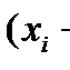Podstawowe funkcje elementarne, ich własności i wykresy. Funkcja potęgowa, jej własności i wykres Przykład wykorzystania funkcji potęgowej

Funkcja potęgowa jest dana wzorem postaci .

Rozważ rodzaje wykresów funkcji potęgowej i właściwości funkcji potęgowej w zależności od wartości wykładnika.

Zacznijmy od funkcji potęgowej z wykładnikiem całkowitym A. W tym przypadku postać wykresów funkcji potęgowych i właściwości funkcji zależą od parzystego lub nieparzystego wykładnika, a także od jego znaku. Dlatego najpierw rozważymy funkcje potęgowe dla nieparzystych dodatnich wartości wykładnika A, następnie - dla parzystego dodatniego, następnie - dla nieparzystych ujemnych wykładników, a na koniec dla parzystego ujemnego A.

Własności funkcji potęgowych o wykładnikach ułamkowych i niewymiernych (oraz rodzaj wykresów takich funkcji potęgowych) zależą od wartości wykładnika A. Rozważymy je, po pierwsze, A od zera do jednego, a po drugie o godz A duże jednostki, po trzecie, z A od minus jeden do zera, po czwarte, kiedy A mniejszy minus jeden.

Na zakończenie tego podrozdziału, dla kompletności, opisujemy funkcję potęgową z zerowym wykładnikiem.

Funkcja potęgowa z nieparzystym dodatnim wykładnikiem.

Rozważmy funkcję potęgową z nieparzystym dodatnim wykładnikiem, to znaczy z a=1,3,5,….

Poniższy rysunek przedstawia wykresy funkcji mocy - linia czarna, - linia niebieska, - linia czerwona, - linia zielona. Na a=1 mamy funkcja liniowa y=x.

Własności funkcji potęgowej o nieparzystym dodatnim wykładniku.

Funkcja potęgowa z parzystym dodatnim wykładnikiem.

Rozważmy funkcję potęgową z parzystym dodatnim wykładnikiem, tj a=2,4,6,….

Jako przykład weźmy wykresy funkcji potęgowych - linia czarna, - linia niebieska, - linia czerwona. Na a=2 mamy funkcję kwadratową, której wykresem jest parabola kwadratowa.

Własności funkcji potęgowej o parzystym dodatnim wykładniku.

Funkcja potęgowa z nieparzystym ujemnym wykładnikiem.

Spójrz na wykresy funkcji potęgi dla nieparzystych ujemnych wartości wykładnika, to znaczy dla a=-1,-3,-5,….

Funkcja zasilania jest funkcją formy y = xp, gdzie p jest daną liczbą rzeczywistą.

Właściwości funkcji potęgowej

1. Jeśli wskaźnik p = 2n- parzysta liczba naturalna:
   • dziedziną definicji są wszystkie liczby rzeczywiste, tj. zbiór R;
   • zbiór wartości - liczby nieujemne, tj. y ≥ 0;
   • funkcja jest parzysta;
   • funkcja jest malejąca na przedziale x ≤ 0 i rosnąca na przedziale x ≥ 0.
   Przykład funkcji z p = 2n: y=x4.


2. Jeśli wskaźnik p = 2n - 1- nieparzysta liczba naturalna:
   • dziedzina definicji - zbiór R;
   • zestaw wartości - zestaw R;
   • funkcja jest nieparzysta;
   • funkcja jest rosnąca na całej osi rzeczywistej.
   Przykład funkcji z p = 2n - 1: y=x5.


3. Jeśli wskaźnik p=-2n, Gdzie N- Liczba naturalna:
   • zestaw wartości - liczby dodatnie y > 0;
   • funkcja jest parzysta;
   • funkcja jest rosnąca w przedziale x 0.
   Przykład funkcji z p = -2n: y = 1/x2.


4. Jeśli wskaźnik p = -(2n - 1), Gdzie N- Liczba naturalna:
   • dziedziną definicji jest zbiór R, z wyjątkiem x = 0;
   • zestaw wartości - zestaw R, z wyjątkiem y = 0;
   • funkcja jest nieparzysta;
   • funkcja jest malejąca w przedziałach x 0.
   Przykład funkcji z p = -(2n - 1): y = 1/x3.


5. Jeśli wskaźnik P jest dodatnią liczbą rzeczywistą niecałkowitą:
   • dziedzina definicji - liczby nieujemne x ≥ 0;
   • zestaw wartości - liczby nieujemne y ≥ 0;
   • funkcja jest rosnąca w przedziale x ≥ 0.
   Przykład funkcji z wykładnikiem p, gdzie p jest dodatnią liczbą rzeczywistą niecałkowitą: y=x4/3.


6. Jeśli wskaźnik P jest ujemną rzeczywistą liczbą niecałkowitą:
   • dziedzina definicji - liczby dodatnie x > 0;
   • zestaw wartości - liczby dodatnie y > 0;
   • funkcja jest malejąca w przedziale x > 0.
   Przykład funkcji z wykładnikiem p, gdzie p jest ujemną rzeczywistą liczbą niecałkowitą: y=x-1/3.

Przypomnij sobie właściwości i wykresy funkcji potęgowych z ujemnym wykładnikiem całkowitym.

Dla parzystego n:

Przykład funkcji:

Wszystkie wykresy takich funkcji przechodzą przez dwa stałe punkty: (1;1), (-1;1). Cechą funkcji tego typu jest ich parzystość, wykresy są symetryczne względem osi op-y.

Ryż. 1. Wykres funkcji

Dla nieparzystego n:

Przykład funkcji:

Wszystkie wykresy takich funkcji przechodzą przez dwa stałe punkty: (1;1), (-1;-1). Cechą funkcji tego typu jest ich dziwność, wykresy są symetryczne względem początku układu.

Ryż. 2. Wykres funkcji

Przypomnijmy główną definicję.

Stopień liczby nieujemnej a z wymiernym dodatnim wykładnikiem nazywamy liczbą.

Stopień liczby dodatniej a z wykładnikiem wymiernym ujemnym nazywamy liczbą.

Dla następujących równości zachodzi:

Na przykład: ; - wyrażenie nie istnieje z definicji stopnia z ujemnym wykładnikiem wymiernym; istnieje, ponieważ wykładnik jest liczbą całkowitą,

Przejdźmy do rozważenia funkcji potęgowych z wykładnikiem wymiernym ujemnym.

Na przykład:

Aby wykreślić tę funkcję, możesz utworzyć tabelę. Zrobimy inaczej: najpierw zbudujemy i przestudiujemy wykres mianownika - znamy go (Rysunek 3).

Ryż. 3. Wykres funkcji

Wykres funkcji mianownika przechodzi przez stały punkt (1;1). Podczas konstruowania wykresu pierwotnej funkcji punkt ten pozostaje, gdy pierwiastek również dąży do zera, funkcja dąży do nieskończoności. I odwrotnie, skoro x dąży do nieskończoności, funkcja dąży do zera (Rysunek 4).

Ryż. 4. Wykres funkcji

Rozważmy jeszcze jedną funkcję z rodziny badanych funkcji.

Ważne, że z definicji

Rozważmy wykres funkcji w mianowniku: , znamy wykres tej funkcji, rośnie w swojej dziedzinie definicji i przechodzi przez punkt (1; 1) (Rysunek 5).

Ryż. 5. Wykres funkcji

Podczas konstruowania wykresu pierwotnej funkcji punkt (1; 1) pozostaje, gdy pierwiastek również dąży do zera, funkcja dąży do nieskończoności. I odwrotnie, skoro x dąży do nieskończoności, funkcja dąży do zera (Rysunek 6).

Ryż. 6. Wykres funkcji

Rozważane przykłady pomagają zrozumieć, jak przebiega wykres i jakie są właściwości badanej funkcji - funkcji z ujemnym wykładnikiem wymiernym.

Wykresy funkcji tej rodziny przechodzą przez punkt (1;1), funkcja maleje w całej dziedzinie definicji.

Zakres funkcji:

Funkcja nie jest ograniczona z góry, ale ograniczona z dołu. Funkcja nie ma wartości maksymalnej ani minimalnej.

Funkcja jest ciągła, przyjmuje wszystkie wartości dodatnie od zera do plus nieskończoności.

Funkcja wypukła w dół (rysunek 15.7)

Na krzywej wzięto punkty A i B, poprowadzono przez nie odcinek, cała krzywa jest pod odcinkiem, warunek ten jest spełniony dla dowolnych dwóch punktów na krzywej, więc funkcja jest wypukła w dół. Ryż. 7.

Ryż. 7. Wypukłość funkcji

Ważne jest, aby zrozumieć, że funkcje tej rodziny są ograniczone od dołu przez zero, ale nie mają najmniejszej wartości.

Przykład 1 - znajdź maksimum i minimum funkcji na przedziale \[(\mathop(lim)_(x\to +\infty ) x^(2n)\ )=+\infty \]

Wykres (ryc. 2).

Rysunek 2. Wykres funkcji $f\left(x\right)=x^(2n)$

Własności funkcji potęgowej z wykładnikiem naturalnym nieparzystym

Dziedziną definicji są wszystkie liczby rzeczywiste.

$f\left(-x\right)=((-x))^(2n-1)=(-x)^(2n)=-f(x)$ jest funkcją nieparzystą.

$f(x)$ jest ciągła w całej dziedzinie definicji.

Zakres to wszystkie liczby rzeczywiste.

$f"\left(x\right)=\left(x^(2n-1)\right)"=(2n-1)\cdot x^(2(n-1))\ge 0$

Funkcja rośnie w całej dziedzinie definicji.

$f\left(x\right)0$, dla $x\in (0,+\infty)$.

$f(""\left(x\right))=(\left(\left(2n-1\right)\cdot x^(2\left(n-1\right))\right))"=2 \left(2n-1\right)(n-1)\cdot x^(2n-3)$

\ \

Funkcja jest wklęsła dla $x\in (-\infty ,0)$ i wypukła dla $x\in (0,+\infty)$.

Wykres (ryc. 3).

Rysunek 3. Wykres funkcji $f\left(x\right)=x^(2n-1)$

Funkcja potęgowa z wykładnikiem całkowitym

Na początek wprowadzimy pojęcie stopnia z wykładnikiem całkowitym.

Definicja 3

Stopień liczby rzeczywistej $a$ z wykładnikiem całkowitym $n$ określa wzór:

Rysunek 4

Rozważmy teraz funkcję potęgową z wykładnikiem całkowitym, jej właściwości i wykres.

Definicja 4

$f\left(x\right)=x^n$ ($n\in Z)$ nazywamy funkcją potęgową z wykładnikiem całkowitym.

Jeśli stopień jest większy od zera, to dochodzimy do przypadku funkcji potęgowej z naturalnym wykładnikiem. Omówiliśmy to już powyżej. Dla $n=0$ otrzymujemy funkcję liniową $y=1$. Rozważanie pozostawiamy czytelnikowi. Pozostaje rozważyć właściwości funkcji potęgowej z ujemnym wykładnikiem całkowitym

Własności funkcji potęgowej z ujemnym wykładnikiem całkowitym

Zakres to $\left(-\infty ,0\right)(0,+\infty)$.

Jeśli wykładnik jest parzysty, to funkcja jest parzysta; jeśli jest nieparzysty, to funkcja jest nieparzysta.

$f(x)$ jest ciągła w całej dziedzinie definicji.

Zakres wartości:

Jeśli wykładnik jest parzysty, to $(0,+\infty)$, jeśli nieparzysty, to $\left(-\infty ,0\right)(0,+\infty)$.

Jeśli wykładnik jest nieparzysty, funkcja maleje jako $x\in \left(-\infty ,0\right)(0,+\infty)$. Dla parzystego wykładnika funkcja maleje jako $x\in (0,+\infty)$. i rośnie jako $x\in \left(-\infty ,0\right)$.

$f(x)\ge 0$ w całej domenie