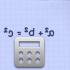Definicja. Twarz boczna- jest to trójkąt, w którym jeden kąt leży na szczycie piramidy, a jego przeciwna strona pokrywa się z bokiem podstawy (wielokąt).

Definicja. Żeberka boczne są wspólne strony ścian bocznych. Piramida ma tyle krawędzi, ile jest rogów wielokąta.

Definicja. wysokość piramidy to prostopadłość opuszczona od góry do podstawy piramidy.

Definicja. Apotema- jest to prostopadła ściana boczna piramidy opuszczona od szczytu piramidy do boku podstawy.

Definicja. Przekrój po przekątnej- jest to odcinek piramidy przez płaszczyznę przechodzącą przez szczyt piramidy i przekątną podstawy.

Definicja. Prawidłowa piramida- Jest to piramida, w której podstawa jest wielokątem foremnym, a wysokość schodzi do środka podstawy.

Objętość i powierzchnia piramidy

Formuła. objętość piramidy przez podstawę i wysokość:

właściwości piramidy

Jeśli wszystkie krawędzie boczne są równe, to wokół podstawy piramidy można zakreślić okrąg, a środek podstawy pokrywa się ze środkiem okręgu. Również prostopadły opuszczony z góry przechodzi przez środek podstawy (koło).

Jeśli wszystkie boczne żebra są równe, to są one nachylone do płaszczyzny podstawy pod tymi samymi kątami.

Żebra boczne są równe, gdy tworzą równe kąty z płaszczyzną podstawy lub jeśli wokół podstawy piramidy można opisać okrąg.

Jeżeli ściany boczne są nachylone do płaszczyzny podstawy pod jednym kątem, wówczas w podstawę piramidy można wpisać okrąg, a wierzchołek piramidy rzutowany jest na jej środek.

Jeżeli ściany boczne są nachylone do płaszczyzny bazowej pod jednym kątem, wówczas apotemy ścian bocznych są równe.

Właściwości regularnej piramidy

1. Wierzchołek piramidy znajduje się w równej odległości od wszystkich rogów podstawy.

2. Wszystkie krawędzie boczne są równe.

3. Wszystkie boczne żebra są nachylone pod tym samym kątem do podstawy.

4. Apothemy wszystkich ścian bocznych są równe.

5. Obszary wszystkich powierzchni bocznych są równe.

6. Wszystkie ściany mają te same dwuścienne (płaskie) kąty.

7. Wokół piramidy można opisać kulę. Środek opisywanej kuli będzie punktem przecięcia pionów przechodzących przez środek krawędzi.

8. Kulę można wpisać w piramidę. Środek wpisanej kuli będzie punktem przecięcia dwusiecznych wychodzących z kąta między krawędzią a podstawą.

9. Jeżeli środek kuli wpisanej pokrywa się ze środkiem kuli opisanej, to suma kątów płaskich na wierzchołku jest równa π lub odwrotnie, jeden kąt jest równy π / n, gdzie n jest liczbą kątów u podstawy piramidy.

Połączenie piramidy z kulą

Kulę można opisać wokół piramidy, gdy u podstawy piramidy leży wielościan, wokół którego można opisać okrąg (warunek konieczny i wystarczający). Środek kuli będzie punktem przecięcia płaszczyzn przechodzących prostopadle przez środki bocznych krawędzi ostrosłupa.

Sferę można zawsze opisać wokół dowolnej trójkątnej lub regularnej piramidy.

Kulę można wpisać w piramidę, jeśli dwusieczne płaszczyzny wewnętrznych kątów dwuściennych piramidy przecinają się w jednym punkcie (warunek konieczny i wystarczający). Ten punkt będzie środkiem kuli.

Połączenie piramidy ze stożkiem

Stożek nazywany jest wpisanym w piramidę, jeśli ich wierzchołki pokrywają się, a podstawa stożka jest wpisana w podstawę piramidy.

Stożek może być wpisany w piramidę, jeśli apotemy piramidy są równe.

Mówi się, że stożek jest opisany wokół piramidy, jeśli ich wierzchołki pokrywają się, a podstawa stożka jest zakreślona wokół podstawy piramidy.

Stożek można opisać wokół piramidy, jeśli wszystkie boczne krawędzie piramidy są sobie równe.

Połączenie piramidy z cylindrem

Mówi się, że piramida jest wpisana w cylinder, jeśli wierzchołek piramidy leży na jednej podstawie cylindra, a podstawa piramidy jest wpisana w inną podstawę cylindra.

Cylinder można zakreślić wokół piramidy, jeśli okrąg można zakreślić wokół podstawy piramidy.

Definicja. Piramida ścięta (pryzmat piramidalny)- Jest to wielościan, który znajduje się między podstawą piramidy a płaszczyzną przekroju równoległą do podstawy. Zatem piramida ma dużą podstawę i mniejszą podstawę, która jest podobna do większej. Boczne powierzchnie są trapezowe.

Definicja. Trójkątna piramida (czworościan)- jest to piramida, w której trzy twarze i podstawa to dowolne trójkąty.

Czworościan ma cztery ściany i cztery wierzchołki i sześć krawędzi, gdzie dowolne dwie krawędzie nie mają wspólnych wierzchołków, ale nie stykają się.

Każdy wierzchołek składa się z trzech ścian i krawędzi, które tworzą kąt trójścienny.

Nazywa się segment łączący wierzchołek czworościanu ze środkiem przeciwległej ściany mediana czworościanu(GM).

Bimedian nazywa się segmentem łączącym punkty środkowe przeciwległych krawędzi, które się nie stykają (KL).

Wszystkie bimediany i mediany czworościanu przecinają się w jednym punkcie (S). W tym przypadku bimediany są podzielone na pół, a mediany w stosunku 3:1 zaczynając od góry.

Definicja. nachylona piramida jest piramidą, w której jedna z krawędzi tworzy z podstawą kąt rozwarty (β).

Definicja. Piramida prostokątna to piramida, w której jedna z bocznych ścian jest prostopadła do podstawy.

Definicja. Ostra piramida kątowa to piramida, w której apotem ma więcej niż połowę długości boku podstawy.

Definicja. rozwarta piramida to piramida, w której apotem jest krótszy niż połowa długości boku podstawy.

Definicja. czworościan foremny Czworościan, którego cztery ściany są trójkątami równobocznymi. Jest to jeden z pięciu regularnych wielokątów. W czworościanie foremnym wszystkie kąty dwuścienne (pomiędzy ścianami) i trójścienne (na wierzchołku) są równe.

Definicja. Czworościan prostokątny nazywa się czworościan, który ma kąt prosty między trzema krawędziami na wierzchołku (krawędzie są prostopadłe). Tworzą się trzy twarze prostokątny trójkątny kąt a twarze są trójkątami prostokątnymi, a podstawą jest dowolny trójkąt. Apotem każdej twarzy jest równy połowie boku podstawy, na który spada apotem.

Definicja. Czworościan izoedryczny Nazywa się czworościan, w którym ściany boczne są sobie równe, a podstawa jest regularnym trójkątem. Twarze takiego czworościanu to trójkąty równoramienne.

Definicja. Czworościan ortocentryczny nazywa się czworościan, w którym wszystkie wysokości (prostopadłe) obniżone od góry do przeciwległej ściany przecinają się w jednym punkcie.

Definicja. gwiezdna piramida Nazywa się wielościan, którego podstawą jest gwiazda.

Definicja. bipiramida- wielościan składający się z dwóch różnych piramid (piramidy można również odciąć), mających wspólną podstawę, a wierzchołki leżą po przeciwnych stronach płaszczyzny podstawy.

Powierzchnia bocznej powierzchni regularnej piramidy jest równa iloczynowi jej apotemu o połowę obwodu podstawy.

Jeśli chodzi o całkowitą powierzchnię, po prostu dodajemy obszar podstawy z boku.

Boczna powierzchnia regularnej piramidy jest równa iloczynowi półobwodu podstawy i apotemu.

Dowód:

Jeżeli bok podstawy to a, liczba boków to n, to boczna powierzchnia piramidy to:

a l n/2 =a n l/2=pl/2

gdzie l jest twierdzeniem, a p jest obwodem podstawy piramidy. Twierdzenie zostało udowodnione.

Ta formuła brzmi tak:

Powierzchnia bocznej powierzchni regularnej piramidy jest równa połowie iloczynu obwodu podstawy i apotemy piramidy.

Całkowitą powierzchnię piramidy oblicza się według wzoru:

S pełny =S bok + S Główny

Jeśli piramida jest nieregularna, jej powierzchnia boczna będzie równa sumie powierzchni jej ścian bocznych.

Objętość piramidy

Tom ostrosłup jest równy jednej trzeciej iloczynu powierzchni podstawy i wysokości.

Dowód. Zaczniemy od trójkątnego pryzmatu. Narysuj płaszczyznę przez wierzchołek A „górnej podstawy pryzmatu i przeciwległą krawędź BC dolnej podstawy. Ta płaszczyzna odetnie trójkątną piramidę A” ABC od pryzmatu. Pozostałą część pryzmatu rozkładamy na rdzeń korpusu, przeciągając płaszczyznę przez przekątne A „C” i „B” C ścian bocznych. Powstałe dwa ciała są również piramidami. Biorąc pod uwagę trójkąt A"B"C" jako podstawę jednego z nich, a C jego wierzchołek, zobaczymy, że jego podstawa i wysokość są takie same jak w pierwszej odciętej piramidzie, a zatem piramidy A"ABC i CA "B"C" są równe. Ponadto obie nowe piramidy CA "B" C "i A" B "BC" są również równe wielkości - stanie się to jasne, jeśli weźmiemy trójkąty BC "i B" CC "dla ich podstawy. Piramidy CA” B „C” i A „B” VS mają wspólny wierzchołek A”, a ich podstawy znajdują się w tej samej płaszczyźnie i są równe, dlatego piramidy są równe wielkości. Tak więc pryzmat jest rozłożone na trzy piramidy o równych rozmiarach, objętość każdej z nich jest równa jednej trzeciej objętości pryzmatu.Ponieważ kształt podstawy jest nieznaczny, to na ogół objętość n-kąta ostrosłup jest równy jednej trzeciej objętości graniastosłupa o tej samej wysokości i tej samej (lub równej) podstawie. Przypominając wzór wyrażający objętość graniastosłupa, V=Sh, otrzymujemy wynik końcowy: V=1/3Sh

Przygotowując się do egzaminu z matematyki, studenci muszą usystematyzować swoją wiedzę z algebry i geometrii. Chciałbym połączyć wszystkie znane informacje, na przykład, jak obliczyć powierzchnię piramidy. Co więcej, począwszy od podstawy i ścian bocznych po całą powierzchnię. Jeśli sytuacja jest jasna z bocznymi ścianami, ponieważ są to trójkąty, podstawa jest zawsze inna.

Co zrobić, gdy znajduje się obszar podstawy piramidy?

Może to być absolutnie dowolna figura: od dowolnego trójkąta do n-kąta. I ta podstawa, oprócz różnicy w liczbie kątów, może być liczbą zwykłą lub nieprawidłową. W zadaniach USE interesujących dzieci w wieku szkolnym u podstawy znajdują się tylko zadania z prawidłowymi liczbami. Dlatego porozmawiamy tylko o nich.

trójkąt prostokątny

To jest równoboczne. Taki, w którym wszystkie boki są równe i oznaczone literą „a”. W takim przypadku obszar podstawy piramidy oblicza się według wzoru:

S = (a 2 * √3) / 4.

Kwadrat

Wzór na obliczenie jego powierzchni jest najprostszy, tutaj „a” to znowu bok:

Arbitralny regularny n-gon

Bok wielokąta ma to samo oznaczenie. Jako liczbę rogów stosuje się łacińską literę n.

S = (n * a 2) / (4 * tg (180º/n)).

Jak postępować przy obliczaniu powierzchni bocznej i całkowitej?

Ponieważ podstawa jest regularną figurą, wszystkie ściany piramidy są równe. Co więcej, każdy z nich jest trójkątem równoramiennym, ponieważ krawędzie boczne są równe. Następnie, aby obliczyć boczną powierzchnię piramidy, potrzebujesz wzoru składającego się z sumy identycznych jednomianów. Liczba terminów zależy od liczby boków podstawy.

Obszar trójkąta równoramiennego oblicza się według wzoru, w którym połowę iloczynu podstawy mnoży się przez wysokość. Ta wysokość w piramidzie nazywa się apotem. Jego oznaczenie to „A”. Ogólny wzór na powierzchnię boczną to:

S \u003d ½ P * A, gdzie P jest obwodem podstawy piramidy.

Zdarzają się sytuacje, w których boki podstawy nie są znane, ale podane są krawędzie boczne (c) i kąt płaski na jej wierzchołku (α). Następnie należy użyć takiego wzoru do obliczenia bocznej powierzchni piramidy:

S = n/2 * w 2 sin α .

Zadanie 1

Stan. Znajdź całkowitą powierzchnię piramidy, jeśli jej podstawa leży o boku 4 cm, a apotem ma wartość √3 cm.

Rozwiązanie. Musisz zacząć od obliczenia obwodu bazy. Ponieważ jest to trójkąt regularny, to P \u003d 3 * 4 \u003d 12 cm Ponieważ znany jest apotem, możesz natychmiast obliczyć pole całej powierzchni bocznej: ½ * 12 * √3 = 6 3 cm 2.

W przypadku trójkąta u podstawy uzyskana zostanie następująca wartość pola: (4 2 * √3) / 4 \u003d 4√3 cm 2.

Aby określić cały obszar, musisz dodać dwie wynikowe wartości: 6√3 + 4√3 = 10√3 cm2.

Odpowiadać. 10√3 cm2.

Zadanie nr 2

Stan. Jest regularna czworokątna piramida. Długość boku podstawy 7 mm, krawędź boczna 16 mm. Musisz znać jego powierzchnię.

Rozwiązanie. Ponieważ wielościan jest czworokątny i regularny, jego podstawa jest kwadratem. Po poznaniu obszarów podstawy i ścian bocznych możliwe będzie obliczenie obszaru piramidy. Wzór na kwadrat podano powyżej. A na bocznych ścianach znane są wszystkie boki trójkąta. Dlatego możesz użyć wzoru Herona do obliczenia ich powierzchni.

Pierwsze obliczenia są proste i prowadzą do tej liczby: 49 mm 2. Dla drugiej wartości musisz obliczyć półobwód: (7 + 16 * 2): 2 = 19,5 mm. Teraz możesz obliczyć powierzchnię trójkąta równoramiennego: √ (19,5 * (19,5-7) * (19,5-16) 2) = √2985,9375 = 54,644 mm 2. Są tylko cztery takie trójkąty, więc obliczając ostateczną liczbę, musisz ją pomnożyć przez 4.

Okazuje się: 49 + 4 * 54,644 \u003d 267,576 mm 2.

Odpowiadać. Pożądana wartość to 267,576 mm 2.

Zadanie nr 3

Stan. W przypadku zwykłej piramidy czworokątnej musisz obliczyć powierzchnię. W nim bok kwadratu ma 6 cm, a wysokość 4 cm.

Rozwiązanie. Najprostszym sposobem jest użycie wzoru z iloczynem obwodu i apotem. Pierwsza wartość jest łatwa do znalezienia. Drugi jest trochę trudniejszy.

Musimy pamiętać twierdzenie Pitagorasa i rozważyć, że jest ono utworzone przez wysokość piramidy i apotem, który jest przeciwprostokątną. Druga noga jest równa połowie boku kwadratu, ponieważ wysokość wielościanu przypada na jego środek.

Pożądany apotem (przeciwprostokątna trójkąta prostokątnego) to √(3 2 + 4 2) = 5 (cm).

Teraz możesz obliczyć żądaną wartość: ½ * (4 * 6) * 5 + 6 2 \u003d 96 (cm 2).

Odpowiadać. 96 cm2.

Zadanie #4

Stan. Prawidłowa strona jej podstawy to 22 mm, boczne żebra to 61 mm. Jaka jest powierzchnia bocznej powierzchni tego wielościanu?

Rozwiązanie. Rozumowanie w nim jest takie samo, jak opisane w zadaniu nr 2. Tylko tam podano piramidę z kwadratem u podstawy, a teraz jest to sześciokąt.

Przede wszystkim powierzchnia podstawy jest obliczana przy użyciu powyższego wzoru: (6 * 22 2) / (4 * tg (180º / 6)) \u003d 726 / (tg30º) \u003d 726√3 cm 2.

Teraz musisz znaleźć półobwód trójkąta równoramiennego, który jest boczną ścianą. (22 + 61 * 2): 2 = 72 cm Pozostaje obliczyć obszar każdego takiego trójkąta za pomocą wzoru Czapla, a następnie pomnożyć go przez sześć i dodać do tego, który okazał się dla baza.

Obliczenia z wykorzystaniem wzoru Czapla: √ (72 * (72-22) * (72-61) 2) \u003d √ 435600 \u003d 660 cm 2. Obliczenia, które dadzą powierzchnię boczną: 660 * 6 \u003d 3960 cm 2. Pozostaje je dodać, aby dowiedzieć się o całej powierzchni: 5217,47≈5217 cm 2.

Odpowiadać. Podstawa - 726√3 cm2, powierzchnia boczna - 3960 cm2, cała powierzchnia - 5217 cm2.

- jest to figura, u podstawy której leży dowolny wielokąt, a ściany boczne są reprezentowane przez trójkąty. Ich wierzchołki leżą w jednym punkcie i odpowiadają wierzchołkowi piramidy.

Piramida może być zróżnicowana - trójkątna, czworokątna, sześciokątna itp. Jego nazwę można określić w zależności od liczby narożników przylegających do podstawy.
Prawidłowa piramida nazywana piramidą, w której boki podstawy, kąty i krawędzie są równe. Również w takiej piramidzie powierzchnia bocznych ścian będzie równa.
Wzór na powierzchnię bocznej powierzchni piramidy jest sumą powierzchni wszystkich jej ścian:
Oznacza to, że aby obliczyć powierzchnię bocznej powierzchni arbitralnej piramidy, konieczne jest znalezienie obszaru każdego pojedynczego trójkąta i dodanie ich do siebie. Jeśli piramida jest ścięta, jej twarze są reprezentowane przez trapezy. Dla prawidłowej piramidy istnieje inna formuła. W nim powierzchnia boczna jest obliczana przez półobwód podstawy i długość apotemu:

Rozważ przykład obliczenia powierzchni bocznej powierzchni piramidy.
Niech zostanie podana regularna piramida czworokątna. Strona podstawowa b= 6 cm i apotem a\u003d 8 cm Znajdź obszar powierzchni bocznej.

U podstawy regularnej czworokątnej piramidy leży kwadrat. Najpierw znajdźmy jego obwód:

Teraz możemy obliczyć powierzchnię bocznej powierzchni naszej piramidy:

Aby znaleźć całkowitą powierzchnię wielościanu, musisz znaleźć obszar jego podstawy. Wzór na powierzchnię podstawy piramidy może się różnić w zależności od tego, który wielokąt leży u podstawy. Aby to zrobić, użyj wzoru na obszar trójkąta, obszar równoległoboku itp.

Rozważ przykład obliczenia powierzchni podstawy piramidy podanej przez nasze warunki. Ponieważ piramida jest regularna, u podstawy ma kwadrat.
kwadratowy obszar obliczona według wzoru: ,
gdzie a jest bokiem kwadratu. Mamy to równe 6 cm, więc powierzchnia podstawy piramidy:

Teraz pozostaje tylko znaleźć całkowitą powierzchnię wielościanu. Wzór na powierzchnię piramidy to suma powierzchni jej podstawy i jej powierzchni bocznej.

Przed przestudiowaniem pytań dotyczących tej figury geometrycznej i jej właściwości konieczne jest zrozumienie niektórych terminów. Kiedy ktoś słyszy o piramidzie, wyobraża sobie ogromne budowle w Egipcie. Tak wyglądają te najprostsze. Ale występują w różnych typach i kształtach, co oznacza, że ​​wzór obliczeniowy dla kształtów geometrycznych będzie inny.

Typy figur

Piramida - figura geometryczna, oznaczający i reprezentujący wiele twarzy. W rzeczywistości jest to ten sam wielościan, u podstawy którego leży wielokąt, a po bokach trójkąty, które łączą się w jednym punkcie - wierzchołku. Liczba składa się z dwóch głównych typów:

• prawidłowy;
• kadłubowy.

W pierwszym przypadku podstawą jest wielokąt foremny. Tutaj wszystkie powierzchnie boczne są równe między sobą a samą figurą ucieszy oko perfekcjonisty.

W drugim przypadku są dwie podstawy - duża na samym dole i mała pomiędzy górą, powtarzająca kształt głównej. Innymi słowy, ścięta piramida to wielościan o przekroju uformowanym równolegle do podstawy.

Terminy i notacja

Podstawowe warunki:

• Regularny (równoboczny) trójkąt Postać o trzech identycznych kątach i równych bokach. W tym przypadku wszystkie kąty wynoszą 60 stopni. Figura jest najprostszą z regularnych wielościanów. Jeśli ta figura leży u podstawy, wówczas taki wielościan będzie nazywany regularnym trójkątnym. Jeśli podstawą jest kwadrat, piramida będzie nazywana regularną piramidą czworokątną.
• Wierzchołek- najwyższy punkt, w którym spotykają się krawędzie. Wysokość wierzchołka tworzy prosta linia biegnąca od szczytu do podstawy piramidy.
• Brzeg jest jedną z płaszczyzn wielokąta. Może mieć kształt trójkąta w przypadku piramidy trójkątnej lub trapezu w przypadku piramidy ściętej.
• Przekrój- płaska figura powstała w wyniku sekcji. Nie mylić z sekcją, ponieważ sekcja pokazuje również, co jest za sekcją.
• Apotema- odcinek narysowany od szczytu piramidy do jej podstawy. Jest to również wysokość twarzy, na której znajduje się drugi punkt wysokości. Ta definicja obowiązuje tylko w odniesieniu do wielościanu foremnego. Na przykład - jeśli nie jest to ścięta piramida, twarz będzie trójkątem. W takim przypadku wysokość tego trójkąta stanie się apotemem.

Formuły powierzchni

Znajdź obszar bocznej powierzchni piramidy każdy rodzaj można zrobić na kilka sposobów. Jeżeli figura nie jest symetryczna i jest wielokątem o różnych bokach, to w takim przypadku łatwiej jest obliczyć całkowitą powierzchnię przez sumę wszystkich powierzchni. Innymi słowy, musisz obliczyć obszar każdej twarzy i dodać je razem.

W zależności od znanych parametrów mogą być wymagane wzory do obliczania kwadratu, trapezu, dowolnego czworoboku itp. Same formuły w różnych przypadkach będzie też inaczej.

W przypadku zwykłej sylwetki odnalezienie obszaru jest znacznie łatwiejsze. Wystarczy znać tylko kilka kluczowych parametrów. W większości przypadków obliczenia są wymagane właśnie dla takich liczb. Dlatego odpowiednie wzory zostaną podane poniżej. W przeciwnym razie musiałbyś namalować wszystko na kilku stronach, co tylko myli i myli.

Podstawowy wzór do obliczeń powierzchnia boczna regularnej piramidy będzie wyglądać tak:

S \u003d ½ Pa (P to obwód podstawy i jest apotemem)

Rozważmy jeden z przykładów. Wielościan ma podstawę z segmentami A1, A2, A3, A4, A5 i wszystkie są równe 10 cm Niech apotem będzie równy 5 cm Najpierw musisz znaleźć obwód. Ponieważ wszystkie pięć ścian podstawy jest takie samo, można je znaleźć w następujący sposób: P \u003d 5 * 10 \u003d 50 cm Następnie stosujemy podstawową formułę: S \u003d ½ * 50 * 5 \u003d 125 cm do kwadratu .

Powierzchnia boczna regularnej trójkątnej piramidy najłatwiejszy do obliczenia. Formuła wygląda tak:

S =½* ab *3, gdzie a jest apotemem, b jest aspektem podstawy. Współczynnik trzy oznacza tutaj liczbę ścian podstawy, a pierwsza część to pole powierzchni bocznej. Rozważ przykład. Biorąc pod uwagę liczbę z apotemem 5 cm i powierzchnią podstawy 8 cm, obliczamy: S = 1/2 * 5 * 8 * 3 = 60 cm do kwadratu.

Boczna powierzchnia piramidy ściętej trochę trudniej to obliczyć. Formuła wygląda tak: S \u003d 1/2 * (p _01 + p _02) * a, gdzie p_01 i p_02 są obwodami podstaw i jest apotemem. Rozważ przykład. Załóżmy, że dla figury czworokątnej wymiary boków podstaw wynoszą 3 i 6 cm, apotem wynosi 4 cm.

Tutaj na początek powinieneś znaleźć obwody podstaw: p_01 \u003d 3 * 4 \u003d 12 cm; p_02=6*4=24 cm Pozostaje podstawić wartości do głównej formuły i uzyskać: S =1/2*(12+24)*4=0,5*36*4=72 cm do kwadratu.

W ten sposób można znaleźć boczną powierzchnię regularnej piramidy o dowolnej złożoności. Uważaj, aby nie pomylić te obliczenia z całkowitą powierzchnią całego wielościanu. A jeśli nadal musisz to zrobić, wystarczy obliczyć powierzchnię największej podstawy wielościanu i dodać ją do powierzchni bocznej powierzchni wielościanu.

Wideo

Aby skonsolidować informacje o tym, jak znaleźć boczną powierzchnię różnych piramid, ten film pomoże ci.