Краткий курс начертательной геометрии

Лекции предназначены для студентов инженерно–технических специальностей

Метод Монжа

Если информацию о расстоянии точки относительно плоскости проекции дать не с помощью числовой отметки, а с помощью второй проекции точки, построенной на второй плоскости проекций, то чертеж называют двухкартинным или комплексным. Основные принципы построения таких чертежей изложены Г. Монжем.
Изложенный Монжем метод - метод ортогонального проецирования, причем берутся две проекции на две взаимно перпендикулярные плоскости проекций, - обеспечивая выразительность, точность и удобоизмеримость изображений предметов на плоскости, был и остается основным методом составления технических чертежей

Рисунок 1.1 Точка в системе трех плоскостей проекций

Модель трех плоскостей проекций показана на рисунке 1.1. Третья плоскость, перпендикулярная и П1, и П2, обозначается буквой П3 и называется профильной. Проекции точек на эту плоскость обозначаются заглавными буквами или цифрами с индексом 3. Плоскости проекций, попарно пересекаясь, определяют три оси 0x, 0y и 0z, которые можно рассматривать как систему декартовых координат в пространстве с началом в точке 0. Три плоскости проекций делят пространство на восемь трехгранных углов - октантов. Как и прежде, будем считать, что зритель, рассматривающий предмет, находится в первом октанте. Для получения эпюра точки в системе трех плоскостей проекций плоскости П1 и П3 вращают до совмещения с плоскостью П2. При обозначении осей на эпюре отрицательные полуоси обычно не указывают. Если существенно только само изображение предмета, а не его положение относительно плоскостей проекций, то оси на эпюре не показывают. Координатами называют числа, которые ставят в соответствие точке для определения ее положения в пространстве или на поверхности. В трехмерном пространстве положение точки устанавливают с помощью прямоугольных декартовых координат x , y и z (абсцисса, ордината и аппликата).

Для определения положения прямой в пространстве существуют следующие методы: 1.Двумя точками (А и В). Рассмотрим две точки в пространстве А и В (рис. 2.1). Через эти точки можно провести прямую линию получим отрезок . Для того чтобы найти проекции этого отрезка на плоскости проекций необходимо найти проекции точек А и В и соединить их прямой. Каждая из проекций отрезка на плоскости проекций меньше самого отрезка: <; <; <.

Рисунок 2.1 Определение положения прямой по двум точкам

2. Двумя плоскостями (a; b). Этот способ задания определяется тем что две непараллельные плоскости пересекаются в пространстве по прямой линии (этот способ подробно рассматривается в курсе элементарной геометрии).

3. Точкой и углами наклона к плоскостям проекций. Зная координаты точки принадлежащей прямой и углы наклона ее к плоскостям проекций можно найти положение прямой в пространстве.

В зависимости от положения прямой по отношению к плоскостям проекций она может занимать как общее, так и частные положения. 1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения (рис.3.1).

2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:

2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями (рис.3.2).

Рисунок 3.2 Горизонтальная прямая

2.2. Прямые параллельные фронтальной плоскости проекций называются фронтальными или фронталями(рис.3.3).

Рисунок 3.3 Фронтальная прямая

2.3. Прямые параллельные профильной плоскости проекций называются профильными (рис. 3.4).

Рисунок 3.4 Профильная прямая

3. Прямые, перпендикулярные плоскостям проекций, называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают:

3.1. Фронтально-проецирующая прямая - АВ (рис. 3.5).

Рисунок 3.5 Фронтально-проецирующая прямая

3.2. Профильно проецирующая прямая - АВ (рис.3.6).

Рисунок 3.6 Профильно-проецирующая прямая

3.3. Горизонтально-проецирующая прямая - АВ (рис.3.7).

Рисунок 3.7 Горизонтально-проецирующая прямая

Плоскость – одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскость обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Некоторые характеристические свойства плоскости: 1. Плоскость есть поверхность, содержащая полностью каждую прямую, соединяющую любые ее точки; 2. Плоскость есть множество точек, равноотстоящих от двух заданных точек.

Способы графического задания плоскостей Положение плоскости в пространстве можно определить:

1. Тремя точками, не лежащими на одной прямой линии (рис.4.1).

Рисунок 4.1 Плоскость заданная тремя точками, не лежащими на одной прямой

2. Прямой линией и точкой, не принадлежащей этой прямой (рис.4.2).

Рисунок 4.2 Плоскость заданная прямой линией и точкой, не принадлежащей этой линии

3. Двумя пересекающимися прямыми (рис.4.3).

Рисунок 4.3 Плоскость заданная двумя пересекающимися прямыми линиями

4. Двумя параллельными прямыми (рис.4.4).

Рисунок 4.4 Плоскость заданная двумя параллельными прямыми линиями

Различное положение плоскости относительно плоскостей проекций

В зависимости от положения плоскости по отношению к плоскостям проекций она может занимать как общее, так и частные положения.

1. Плоскость не перпендикулярная ни одной плоскости проекций называется плоскостью общего положения. Такая плоскость пересекает все плоскости проекций (имеет три следа: - горизонтальный S 1; - фронтальный S 2; - профильный S 3). Следы плоскости общего положения пересекаются попарно на осях в точках ax,ay,az. Эти точки называются точками схода следов, их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций. Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях (рис.5.1).

2. Плоскости перпендикулярные плоскостям проекций – занимают частное положение в пространстве и называются проецирующими. В зависимости от того, какой плоскости проекций перпендикулярна заданная плоскость, различают:

2.1. Плоскость, перпендикулярная горизонтальной плоскости проекций (S ^П1) , называется горизонтально-проецирующей плоскостью. Горизонтальная проекция такой плоскости представляет собой прямую линию, которая одновременно является её горизонтальным следом. Горизонтальные проекции всех точек любых фигур в этой плоскости совпадают с горизонтальным следом (рис.5.2).

Рисунок 5.2 Горизонтально-проецирующая плоскость

2.2. Плоскость, перпендикулярная фронтальной плоскости проекций (S ^П2) - фронтально-проецирующая плоскость. Фронтальной проекцией плоскости S является прямая линия, совпадающая со следом S 2 (рис.5.3).

Рисунок 5.3 Фронтально-проецирующая плоскость

2.3. Плоскость, перпендикулярная профильной плоскости (S ^П3) - профильно-проецирующая плоскость. Частным случаем такой плоскости является биссекторная плоскость (рис.5.4).

Рисунок 5.4 Профильно-проецирующая плоскость

3. Плоскости параллельные плоскостям проекций – занимают частное положение в пространстве и называются плоскостями уровня. В зависимости от того, какой плоскости параллельны исследуемая плоскость, различают:

3.1. Горизонтальная плоскость - плоскость параллельная горизонтальной плоскости проекций (S //П1) - (S ^П2, S ^П3). Любая фигура в этой плоскости проецируется на плоскость П1 без искажения, а на плоскости П2 и П3 в прямые - следы плоскости S 2 и S 3 (рис.5.5).

Рисунок 5.5 Горизонтальная плоскость

3.2. Фронтальная плоскость - плоскость параллельная фронтальной плоскости проекций (S //П2), (S ^П1, S ^П3). Любая фигура в этой плоскости проецируется на плоскость П2 без искажения, а на плоскости П1 и П3 в прямые - следы плоскости S 1 и S 3 (рис.5.6).

Рисунок 5.6 Фронтальная плоскость

3.3. Профильная плоскость - плоскость параллельная профильной плоскости проекций (S //П3), (S ^П1, S ^П2). Любая фигура в этой плоскости проецируется на плоскость П3 без искажения, а на плоскости П1 и П2 в прямые - следы плоскости S 1 и S 2 (рис.5.7).

Рисунок 5.7 Профильная плоскость

Следы плоскости

Следом плоскости называется линия пересечения плоскости с плоскостями проекций. В зависимости от того с какой из плоскостей проекций пересекается данная, различают: горизонтальный, фронтальный и профильный следы плоскости.

Каждый след плоскости является прямой линией, для построения которых необходимо знать две точки, либо одну точку и направление прямой(как для построения любой прямой). На рисунке 5.8 показано нахождение следов плоскости S (АВС). Фронтальный след плоскости S 2, построен, как прямая соединяющая две точки 12 и 22, являющиеся фронтальными следами соответствующих прямых, принадлежащих плоскости S . Горизонтальный следS 1 – прямая, проходящая через горизонтальный след прямой АВ и S x. Профильный следS 3 – прямая соединяющая точки (S y и S z) пересечения горизонтального и фронтального следов с осями.

Рисунок 5.8 Построение следов плоскости

Определение взаимного положения прямой и плоскости - позиционная задача, для решения которой применяется метод вспомогательных секущих плоскостей. Сущность метода заключается в следующем: через прямую проведем вспомогательную секущую плоскость Q и установим относительное положение двух прямых a и b, последняя из которых является линией пересечения вспомогательной секущей плоскости Q и данной плоскости T(рис.6.1).

Рисунок 6.1 Метод вспомогательных секущих плоскостей

Каждому из трех возможных случаев относительного расположения этих прямых соответствует аналогичный случай взаимного расположения прямой и плоскости. Так, если обе прямые совпадают, то прямая а лежит в плоскости T, параллельность прямых укажет на параллельность прямой и плоскости и, наконец, пересечение прямых соответствует случаю когда прямая а пересекает плоскость T. Таким образом возможны три случая относительного расположения прямой и плоскости: Прямая принадлежит плоскости; Прямая параллельна плоскости; Прямая пересекает плоскость, частный случай – прямая перпендикулярна плоскости. Рассмотрим каждый случай.

Прямая линия, принадлежащая плоскости

Аксиома 1. Прямая принадлежит плоскости, если две её точки принадлежат той же плоскости (рис.6.2).

Задача. Дана плоскость (n,k) и одна проекция прямой m2. Требуется найти недостающие проекции прямой m если известно, что она принадлежит плоскости, заданной пересекающимися прямыми n и k. Проекция прямой m2 пересекает прямые n и k в точках В2 и С2, для нахождения недостающих проекций прямой необходимо найти недостающие проекции точек В и С как точек лежащих на прямых соответственно n и k. Таким образом точки В и С принадлежат плоскости заданной пересекающимися прямыми n и k, а прямая m проходит через эти точки, значит согласно аксиоме прямая принадлежит этой плоскости.

Аксиома 2. Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости (рис.6.3).

Задача. Через точку В провести прямую m если известно, что она принадлежит плоскости заданной пересекающимися прямыми n и k. Пусть В принадлежит прямой n лежащей в плоскости заданной пересекающимися прямыми n и k. Через проекцию В2 проведем проекцию прямой m2 параллельно прямой k2, для нахождения недостающих проекций прямой необходимо построить проекцию точки В1, как точки лежащей на проекции прямой n1 и через неё провести проекцию прямой m1 параллельно проекции k1. Таким образом точки В принадлежат плоскости заданной пересекающимися прямыми n и k, а прямая m проходит через эту точку и параллельна прямой k, значит согласно аксиоме прямая принадлежит этой плоскости.

Рисунок 6.3 Прямая имеет с плоскостью одну общую точку и параллельна прямой расположенной в этой плоскости

Главные линии в плоскости

Среди прямых линий, принадлежащих плоскости, особое место занимают прямые, занимающие частное положение в пространстве:

1. Горизонтали h - прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций (h//П1)(рис.6.4).

Рисунок 6.4 Горизонталь

2. Фронтали f - прямые, расположенные в плоскости и параллельные фронтальной плоскости проекций (f//П2)(рис.6.5).

Рисунок 6.5 Фронталь

3. Профильные прямые р - прямые, которые находятся в данной плоскости и параллельны профильной плоскости проекций (р//П3) (рис.6.6). Следует заметить, что следы плоскости можно отнести тоже к главным линиям. Горизонтальный след - это горизонталь плоскости, фронтальный - фронталь и профильный - профильная линия плоскости.

Рисунок 6.6 Профильная прямая

4. Линия наибольшего ската и её горизонтальная проекция образуют линейный угол j , которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций (рис.6.7). Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее.

Рисунок 6.7 Линия наибольшего ската

Взаимное расположение точки и плоскости

Возможны два варианта взаимного расположения точки и плоскости: либо точка принадлежит плоскости, либо нет. Если точка принадлежит плоскости то из трех проекций, определяющих положение точки в пространстве, произвольно задать можно только одну. Рассмотрим пример (рис.6.8): Построение проекции точки А принадлежащей плоскости общего положения заданной двумя параллельными прямыми a(a//b).

Задача. Дано: плоскость T(а,в) и проекция точки А2. Требуется построить проекцию А1 если известно, что точка А лежит в плоскости в,а. Через точку А2 проведем проекцию прямой m2, пересекающую проекции прямых a2 и b2 в точках С2 и В2. Построив проекции точек С1 и В1, определяющие положение m1, находим горизонтальную проекцию точки А.

Рисунок 6.8. Точка, принадлежащая плоскости

Две плоскости в пространстве могут быть либо взаимно параллельны, в частном случае совпадая друг с другом, либо пересекаться. Взаимно перпендикулярные плоскости представляют собой частный случай пересекающихся плоскостей.

1. Параллельные плоскости. Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Это определение хорошо иллюстрируется задачей, через точку В провести плоскость параллельную плоскости, заданной двумя пересекающимися прямыми ab (рис.7.1). Задача. Дано: плоскость общего положения, заданную двумя пересекающимися прямыми ab и точка В. Требуется через точку В провести плоскость, параллельную плоскости ab и задать её двумя пересекающимися прямыми c и d. Согласно определения если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости то эти плоскости параллельны между собой. Для того чтобы провести на эпюре параллельные прямые необходимо воспользоваться свойством параллельного проецирования - проекции параллельных прямых - параллельны между собой d||a, с||b; d1||a1,с1||b1; d2||a2 ,с2||b2; d3||a3,с3||b3.

Рисунок 7.1. Параллельные плоскости

2. Пересекающиеся плоскости, частный случай – взаимно перпендикулярные плоскости. Линия пересечения двух плоскостей является прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям, либо одну точку и направление линии пересечения плоскостей. Рассмотрим построение линии пересечения двух плоскостей, когда одна из них проецирующая (рис.7.2).

Задача. Дано: плоскость общего положения задана треугольником АВС, а вторая плоскость - горизонтально проецирующая T. Требуется построить линию пересечения плоскостей. Решение задачи заключается в нахождении двух точек общих для данных плоскостей, через которые можно провести прямую линию. Плоскость, заданная треугольником АВС можно представить, как прямые линии (АВ), (АС), (ВС). Точка пересечения прямой (АВ) с плоскостью T - точка D, прямой (AС) -F. Отрезок определяет линию пересечения плоскостей. Так как T - горизонтально проецирующая плоскость, то проекция D1F1 совпадает со следом плоскости T1, таким образом остается только построить недостающие проекции на П2 и П3.

Рисунок 7.2. Пересечение плоскости общего положения с горизонтально проецирующей плоскостью

Перейдем к общему случаю. Пусть в пространстве заданы две плоскости общего положения a(m,n) и b (ABC) (рис.7.3).

Рисунок 7.3. Пересечение плоскостей общего положения

Рассмотрим последовательность построения линии пересечения плоскостей a(m//n) и b(АВС). По аналогии с предыдущей задачей для нахождения линии пересечения данных плоскостей проведем вспомогательные секущие плоскости g и d. Найдем линии пересечения этих плоскостей с рассматриваемыми плоскостями. Плоскость g пересекает плоскость a по прямой (12), а плоскость b - по прямой (34). Точка К - точка пересечения этих прямых одновременно принадлежит трем плоскостям a, b и g, являясь таким образом точкой принадлежащей линии пересечения плоскостей a и b. Плоскость d пересекает плоскости a и b по прямым (56) и (7C) соответственно, точка их пересечения М расположена одновременно в трех плоскостях a, b, d и принадлежит прямой линии пересечения плоскостей a и b. Таким образом найдены две точки принадлежащие линии пересечения плоскостей a и b - прямая (КМ).

Некоторого упрощения при построении линии пересечения плоскостей можно достичь, если вспомогательные секущие плоскости проводить через прямые, задающие плоскость.

Взаимно перпендикулярные плоскости. Из стереометрии известно, что две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Через точку А можно провести множество плоскостей перпендикулярных данной плоскости a(f,h). Эти плоскости образуют в пространстве пучок плоскостей, осью которого является перпендикуляр опущенный из точки А на плоскость a . Для того чтобы из точки А провести плоскость перпендикулярную плоскости заданной двумя пересекающимися прямыми hf необходимо из точки А провести прямую n перпендикулярную плоскости hf (горизонтальная проекция n перпендикулярна горизонтальной проекции горизонтали h, фронтальная проекция n перпендикулярна фронтальной проекции фронтали f). Любая плоскость проходящая через прямую n будет перпендикулярна плоскости hf, поэтому для задания плоскости через точки А проводим произвольную прямую m. Плоскость заданная двумя пересекающимися прямыми mn будет перпендикулярна плоскости hf (рис.7.4).

Рисунок 7.4. Взаимно перпендикулярные плоскости

Метод плоскопараллельного перемещения

Изменение взаимного положения проецируемого объекта и плоскостей проекций методом плоскопараллельного перемещения осуществляется путем изменения положения геометрического объекта так, чтобы траектория движения её точек находилась в параллельных плоскостях. Плоскости носители траекторий перемещения точек параллельны какой-либо плоскости проекций (рис. 8.1). Траектория произвольная линия. При параллельном переносе геометрического объекта относительно плоскостей проекций, проекция фигуры хотя и меняет свое положение, но остается конгруэнтной проекции фигуры в ее исходном положении.

Рисунок 8.1 Определение натуральной величины отрезка методом плоскопараллельного перемещения

Свойства плоскопараллельного перемещения:

1. При всяком перемещении точек в плоскости параллельной плоскости П1, её фронтальная проекция перемещается по прямой линии, параллельной оси х.

2. В случае произвольного перемещения точки в плоскости параллельной П2, её горизонтальная проекция перемещается по прямой параллельной оси х.

Метод вращения вокруг оси перпендикулярной плоскости проекций

Плоскости носитель траекторий перемещения точек параллельны плоскости проекций. Траектория - дуга окружности, центр которой находится на оси перпендикулярной плоскости проекций. Для определения натуральной величины отрезка прямой общего положения АВ (рис. 8.2), выберем ось вращения (i) перпендикулярную горизонтальной плоскости проекций и проходящую через В1. Повернем отрезок так, чтобы он стал параллелен фронтальной плоскости проекций (горизонтальная проекция отрезка параллельна оси x). При этом точка А1 переместиться в А"1, а точка В не изменит своего положения. Положение точки А"2 находится на пересечении фронтальной проекции траектории перемещения точки А (прямая линия параллельная оси x) и линии связи проведенной из А"1. Полученная проекция В2 А"2 определяет натуральную величину самого отрезка.

Рисунок 8.2 Определение натуральной величины отрезка методом вращения вокруг оси перпендикулярной горизонтальной плоскости проекций

Метод вращения вокруг оси параллельной плоскости проекций

Рассмотрим этот способ на примере определения угла между пересекающимися прямыми (рис.8.3). Рассмотрим две проекции пересекающихся прямых а и в которые пересекаются в точке К. Для то чтобы определить натуральную величину угла между этими прямыми необходимо произвести преобразование ортогональных проекций так, чтобы прямые стали параллельны плоскости проекций. Воспользуемся способом вращения вокруг линии уровня - горизонтали. Проведем произвольно фронтальную проекцию горизонтали h2 параллельно оси Ох, которая пересекает прямые в точках 12 и 22 . Определив проекции 11 и 11, построим горизонтальную проекцию горизонтали h1 . Траектория движения всех точек при вращении вокруг горизонтали - окружность, которая проецируется на плоскость П1 в виде прямой линии перпендикулярной горизонтальной проекции горизонтали.

Рисунок 8.3 Определение угла между пересекающимися прямыми, вращением вокруг оси параллельной горизонтальной плоскости проекций

Таким образом, траектория движения точки К1 определена прямой К1О1, точка О -центр окружности - траектории движения точки К. Чтобы найти радиус этой окружности найдем методом треугольника натуральную величину отрезка КО.Продолжим прямую К1О1 так чтобы |О1К"1|=|КО| . Точка К"1 соответствует точке К, когда прямые а и в лежат в плоскости параллельной П1 и проведенной через горизонталь - ось вращения. С учетом этого через точку К"1 и точки 11 и 21 проведем прямые, которые лежат теперь в плоскости параллельной П1, а следовательно и угол фи - натуральная величина угла между прямыми а и в.

Метод замены плоскостей проекций

Изменение взаимного положения проецируемой фигуры и плоскостей проекций методом перемены плоскостей проекций, достигается путем замены плоскостей П1 и П2 новыми плоскостями П4 (рис. 8.4). Новые плоскости выбираются перпендикулярно старым. Некоторые преобразования проекций требуют двойной замены плоскостей проекций (рис. 8.5). Последовательный переход от одной системы плоскостей проекций другой необходимо осуществлять, выполняя следующее правило: расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси.

Задача 1: Определить натуральную величину отрезка АВ прямой общего положений (рис. 8.4). Из свойства параллельного проецирования известно, что отрезок проецируется на плоскость в натуральную величину, если он параллелен этой плоскости. Выберем новую плоскость проекций П4, параллельно отрезку АВ и перпендикулярно плоскости П1. Введением новой плоскости, переходим из системы плоскостей П1П2 в систему П1П4 , причем в новой системе плоскостей проекция отрезка А4В4 будет натуральной величиной отрезка АВ.

Рисунок 8.4. Определение натуральной величины отрезка прямой методом замены плоскостей проекций

Задача 2: Определить расстояние от точки C до прямой общего положения, заданной отрезком АВ (рис. 8.5).

Рисунок 8.5. Определение натуральной величины отрезка прямой методом замены плоскостей проекций

Как построить на чертеже прямую линию, лежащую в заданной плоскости? Это построение основано на двух положениях, известных из геометрии.

1. Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие данной плоскости.
2. Прямая принадлежит плоскости, если она проходит через точку, принадлежащую данной плоскости, и параллельна прямой, находящейся в этой плоскости или параллельной ей.

Положим, что пл.α (рис. 106) определена двумя пересекающимися прямыми АВ и СВ, а пл. β - двумя параллельными - DE и FG. Согласно первому положе

нию прямая, пересекающая прямые, определяющие плоскость, находится в данной плоскости.

Отсюда вытекает, что если плоскость задана следами, то прямая принадлежит плоскости, если следы прямой находятся на одноименных с ними следах плоскости (рис. 107).

Положим, что пл. γ (рис. 106) определяется точкой А и прямой ВС. Согласно второму положению прямая, проведенная через точку А параллельно прямой ВС, принадлежит пл. γ. Отсюда прямая принадлежит плоскости, если она параллельна одному из следов этой плоскости и имеет с другим следом общую точку (рис. 108).

Примеры построений на рис. 107 и 108 не должны быть поняты так, что для построения прямой в плоскости надо предварительно строить следы этой плоскости. Это не требуется.

Например, на рис. 109 выполнено построение прямой AM в плоскости, заданной точкой А и прямой, проходящей через точку L. Положим, что прямая AM должна быть параллельна пл. π 1 . Построение начато с проведения проекции А"М" перпендикулярно к линии связи А"А". По точке М" найдена точка М", и затем проведена проекция А"М". Прямая AM отвечает условию: она параллельна пл. π 1 И лежит в данной плоскости, так как проходит через две точки (А и М), заведомо принадлежащие этой плоскости.

Как построить на чертеже точку, лежащую в заданной плоскости? Для того чтобы сделать это, предварительно строят прямую, лежащую в заданной плоскости, и на этой прямой берут точку.

Например, требуется найти фронтальную проекцию точки D, если задана ее горизонтальная проекция D" и известно, что точка D должна лежать в плоскости, определяемой треугольником АВС (рис. 110).

Сначала строят горизонтальную проекцию некоторой прямой так, чтобы точка D могла оказаться на этой прямой, а последняя была бы расположена в данной плоскости. Для этого проводят прямую через точки А" и D" и отмечают точку М", в которой прямая A"D" пересекает отрезок В"С". Построив фронтальную проекцию М" на В"С", получают прямую AM, расположенную в данной плоскости: эта прямая проходит через точки А и М, из которых первая заведомо принадлежит данной плоскости, а вторая в ней построена.

Искомая фронтальная проекция D" точки D должна быть на фронтальной проекции прямой AM.

Другой пример дан на рис. 111. В пл. β, заданной параллельными прямыми АВ и CD, должна находиться точка К, для которой дана лишь горизонтальная проекция - точка К

Через точку К" проведена некоторая прямая, принимаемая в качестве горизонтальной проекции прямой в данной плоскости. По точкам E" и F" строим Е" на А"В" и F" на C"D". Построенная прямая EF принадлежит пл. β, так как проходит через точки Е и F, заведомо принадлежащие плоскости. Если взять точку К" на E"F", го точка К окажется в пл.β

К числу прямых, занимающих особое положение в плоскости, отнесем горизонтали, фронтали 1) и линии наибольшего наклона к плоскостям проекций . Линию наибольшего наклона к пл. π 1 , будем называть линией ската плоскости 2).

Горизонталями плоскости называются прямые, лежащие в пей и параллельные горизонтальной плоскости проекций.

Построим горизонталь плоскости, заданной треугольником АВС. Требуется провести горизонталь через вершину А (рис. 112).

Так как горизонталь плоскости есть прямая, параллельная пл.π 1 , то фронтальную проекцию этой прямой получим, проведя А"К"⊥А"А". Для построения горизонтальной проекции этой горизонтали строим точку К" и проводим прямую через точки А" и К".

Построенная прямая АК действительно является горизонталью данной плоскости: эта прямая лежит в плоскости, так как проходит через две точки, заведомо ей принадлежащие, и параллельна плоскости проекций π 1 .

Теперь рассмотрим построение горизонтали плоскости, заданной следами.

Горизонтальный след плоскости есть одна из ее горизонталей («нулевая» горизонталь). Поэтому построение какой-либо из горизонталей плоскости сводится

к проведению в этой плоскости прямой, параллельной горизонтальному следу плоскости (рис. 108, слева). Горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости; фронтальная проекция горизонтали параллельна оси проекций.

Фронталями плоскости называются прямые, лежащие в ней и параллельные плоскости проекций π 2 .

Пример построения фронтали в плоскости дан на рис. 113. Пост роение выполнено аналогично построению горизонтали (см. рис. 112).

Пусть фронталь проходит через точку А (рис. 113). Начинаем построение с проведения горизонтальной проекции фронтали - прямой А"К", так как направление этой проекции известно: А К"⊥А"А". Затем строим фронтальную проекцию фронтали - прямую А"К".

1)Наряду с горизонталями и фронталями плоскости можно рассматривать также ее профильные прямые - прямые, лежащие в данной плоскости и параллельные пл. π 3 . Для горизонталей, фронталей и профильных прямых встречается общее название - линия уровня. Однако такое название отвечает обычному представлению только о горизонтальности.

2)Для линии ската плоскости распространено название «линия наибольшего ската», но понятие «скат» по отношению к плоскости не требует добавления «наибольший».

Построенная прямая действительно является фронталью данной плоскости: эта прямая лежит в плоскости, так как проходит через две точки, заведомо ей принадлежащие, и параллельна пл, π 2 .

Построим теперь фронталь плоскости, заданной следами. Рассматривая рис, 108, справа, на котором изображена пл. β и прямая МВ, устанавливаем, что эта прямая - фронталь плоскости. Действительно, она параллельна фронтальному следу («нулевой» фронтали) плоскости, Горизонтальная проекция фронтали параллельна оси х, фронтальная проекция фронтали параллельна фронтальному следу плоскости.

Линиями наибольшего наклона плоскости к плоскостям π 1 , π 2 и π 3 называются прямые, лежащие в ней и перпендикулярные или к горизонталям плоскости, или к ее фронталям, или к ее профильным прямым. В первом случае определяется наклон к пл.π 1 , во втором - к пл. π 2 , в третьем - к пл. π 3 . Для проведения линий наибольшего наклона плоскости можно, конечно, соответственно брать ее следы.

Как было сказано выше, линия наибольшего наклона плоскости к пл. к π 1 , называется линией ската плоскости.

Согласно правилам проецирования прямого угла (см, § 15) горизонтальная проекция линии ската плоскости перпендикулярна к горизонтальной проекции горизонтали этой плоскости или к ее горизонтальному следу. Фронтальная проекция линии ската строится после горизонтальной и может занимать различные положения в зависимости от задания плоскости. На рис, 114 изображена линия ската Пл. α: ВК⊥h" 0α . Так как В"К также перпендикулярна к h" 0α , то ∠ВКВ" есть линейный угол

двугранного, образованного плоскостями α и π 1 Следовательно, линия ската плоскости может служить для определения угла наклона этой плоскости к плоскости проекций π 1 .

Аналогично, линия наибольшего наклона плоскости к пл, π 2 служит для определения угла между этой плоскостью и пл, π 2 , а линия наибольшего наклона к пл.π 3 - для определения угла.с пл. π 3 .

На рис, 115 построены линии ската в заданных плоскостях. Угол пл, α с пл.π 1 выражен проекциями - фронтальной в виде угла В"К"В" и горизонтальной в виде отрезка К"В". Определить величину этого угла можно, построив прямоугольный треугольник по катетам, равным К"В" и В"В".

Очевидно, линия наибольшего наклона плоскости определяет положение этой плоскости. Например, если (рис. 115) задана линия ската КВ, то, проведя перпендикулярную к ней горизонтальную прямую AN или задавшись осью проекций х и проведя h" 0α ⊥ К"В", мы вполне определяем плоскость, для которой КВ является линией ската.

Рассмотренные нами прямые особого положения в плоскости, главным образоии горизонтали и фронтали, весьма часто применяются в различных построениях и при решении задач. Это объясняется значительной простотой построения указанных прямых; их поэтому удобно применять в качестве вспомогательных.

На рис. 116 была задана горизонтальная проекция К" точки К. Требовалось найти фронтальную проекцию К", если точка К должна быть в плоскости, заданной двумя параллельными прямыми, проведенными из точек А и В.

Сначала была проведена некоторая прямая линия, проходящая через точку К и лежащая в заданной плоскости. В качестве такой прямой выбрана фронталь МN: ее горизонтальная проекция проведена через данную проекцию К". Затем построены точки М" и N", определяющие фронтальную проекцию фронтали.

Искомая проекция К" должна находиться на прямой M"N".

На рис. 117 слева по данной фронтальной проекции А" точки А, принадлежащей пл.α, найдена ее горизонтальная проекция (А"); построение произведено при помощи горизонтали ЕК. На рис. 117 справа аналогичная задача решена при помощи фронтали MN.

Еще один пример построения недостающей проекции точки, принадлежащей некоторой плоскости, дан на рис. 118. Слева показано задание: линия ската плоскости (АВ) и горизонтальная проекция точки (К"). Справа на рис. 118 показано построение; через точку К" проведена (перпендикулярная к А"В") горизонтальная проекция горизонтали, на которой должна лежать точка К, по точке L" найдена фронтальная проекция этой горизонтали и на ней искомая проекция К".

На рис. 119 дан пример построения второй проекции некоторой плоской кривой, если известна одна проекция (горизонтальная) и пл. α, в которой эта кривая расположена. Взяв на горизонтальной проекции кривой ряд точек, находим при помощи горизонталей точки для построения фронтальной проекции кривой.

Стрелками показан ход построения фронтальной проекции А" по горизонтальной проекции А".

Вопросы к §§ 16-18

1. Как задаетcя плоскость на чертеже?
2. Что такое след плоскости на плоскости проекций?
3. Где располагаются фронтальная проекция горизонтального следа и горизонтальная проекция фронтального следа плоскости?
4. Как определяется на чертеже, принадлежит ли прямая данной плоскости?
5. Как построить на чертеже точку, принадлежащую данной плоскости?
6. Что такое фронталь, горизонталь и линия ската плоскости?
7. Может ли служить линия ската плоскости для определения угла наклона этой плоскости к плоскости проекций π 1 ?
8. Определяет ли прямая линия плоскость, для которой эта прямая является, линией ската?

Точка принадлежит плоскости, если она принадлежит какой-либо прямой этой плоскости.

Прямая принадлежит плоскости, если две ее точки принадлежат плоскости.

Эти два вполне очевидных предложения часто называют условиями принадлежности точки и прямой плоскости.

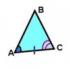
На рис. 3.6 плоскость общего положения задана треугольником АВС. Точки А, В, С принадлежат этой плоскости, так как являются вершинами треугольника из этой плоскости. Прямые (АВ), (ВС), (АС) принадлежат плоскости, так как по две их точки принадлежат плоскости. Точка N принадлежит (AC), D принадлежит (AB), E принадлежит (CD) и, значит, точки N и E принадлежат плоскости (DABC), тогда прямая (NE) принадлежит плоскости (DABC).

Если задана одна проекция точки L, например L 2 , и известно, что точка L принадлежит плоскости (DABC), то для нахождения второй проекции L 1 последовательно находим (A 2 L 2), K 2 , (A 1 K 1), L 1 .

Если условие принадлежности точки плоскости нарушено, то точка не принадлежит плоскости. На рис. 3.6 точка R не принадлежит плоскости (DABC), так как R 2 принадлежит (F 2 K 2), а R 1 не принадлежит (A 1 K 1).

На рис. 3.7 приведен комплексный чертеж горизонтально проецирующей плоскости (DCDE). Точки K и P принадлежат этой плоскости, так как P 1 и K 1 принадлежат прямой (D 1 C 1), являющейся горизонтальной проекцией плоскости (DCDE). Точка N не принадлежит плоскости, так как N 1 не принадлежит (D 1 C 1).

Все точки плоскости (DCDE) проецируются на П 1 в прямую (D 1 C 1). Это следует из того, что плоскость (DCDE) ^ П 1 . В этом же можно убедиться, если проделать для точки P (или любой другой точки) построения, которые были сделаны для точки L (рис. 3.6). Точка P 1 попадет на прямую (D 1 C 1). Таким образом, для того, чтобы определить принадлежность точки горизонтально проецирующей плоскости, фронтальная проекция (DC 2 D 2 E 2) не нужна. Поэтому в дальнейшем проецирующие плоскости будут задаваться только одной проекцией (прямой линией). На рис. 3.7 показана фронтально проецирующая плоскость S, заданная фронтальной проекцией S 2 , а также точки A Î S и B Ï S.

Взаимное положение точки и плоскости сводится к принадлежности или не принадлежности точки плоскости.

При решении многих задач приходится строить линии уровня, принадлежащие плоскостям общего и частного положения. На рис. 3.8 показаны горизонталь h и фронталь f, принадлежащие плоскости общего положения (DABC). Фронтальная проекция h 2 параллельна оси x, поэтому прямая h – горизонталь. Точки 1 и 2 прямой h принадлежат плоскости, поэтому прямая h принадлежит плоскости. Таким образом, прямая h – это горизонталь плоскости (DABC). Обычно порядок построения такой: h 2 ; 1 2 , 2 2 ; 1 1 , 2 1 ; (1 1 2 1) = h 1 . Фронталь f проведена через точку A. Порядок построения: f 1 // x, A 1 Î f 1 ; 3 1 , 3 2 ; (A 2 3 2) = f 2 .

На рис. 3.9 показаны проекции горизонтали и фронтали для фронтально проецирующей плоскости S и горизонтально проецирующей плоскости Г. В плоскости S горизонталь является фронтально проецирующей прямой и проходит через точку A (попытайтесь представить горизонталь как линию пересечения S и плоскости, проходящей через точку A параллельно П 1). Фронталь проходит через точку С. В плоскости Г горизонталь и фронталь проведены через одну точку D. Фронталь является горизонтально проецирующей прямой.

Из рассмотренных выше построений следует, что линию уровня в плоскости можно провести через любую точку этой плоскости.

Совпадение плоскостей можно трактовать как принадлежность одной плоскости другой. Если три точки одной плоскости принадлежат другой плоскости, то эти плоскости совпадают. Упомянутые три точки не должны лежать на одной прямой. На рис. 3.10 плоскость (DDNE) совпадает с плоскостью S(DABC), так как точки D, N, E принадлежат плоскости S(DABC).

Обратим внимание на то, что плоскость S, заданная DABC, теперь может быть задана DDNE. Любая плоскость может быть задана линиями уровня. Для этого необходимо через точку плоскости S(DABC) (например, через точку А) провести в плоскости горизонталь и фронталь, которые и будут задавать плоскость S (на рис. 3.10 построения не показаны). Последовательность построения горизонтали: h 2 // x (A 2 Î h 2); K 2 = h 2 Ç B 2 C 2 ; K 1 Î B 1 C 1 (K 2 K 1 ^ x); A 1 K 1 = h 1 . Последовательность построения фронтали: f 1 // x (A 1 Î f 1); L 1 = f 1 Ç B 1 C 1 ; L 2 Î B 2 C 2 (L 1 L 2 ^ x); A 2 L 2 = f 2 . Можно записать S(DABC) = S(h, f).

ПРЕОБРАЗОВАНИЕ КОМПЛЕКСНОГО ЧЕРТЕЖА

В курсе начертательной геометрии под преобразованием комплексного чертежа фигуры обычно понимается его изменение, вызванное перемещением фигуры в пространстве, или введением новых плоскостей проекций, или использованием других видов проецирования. Применение различных методов (способов) преобразования комплексного чертежа упрощает решение многих задач.

4.1. Метод замены плоскостей проекций

Метод замены плоскостей проекций состоит в том, что вместо одной из плоскостей проекций вводится новая плоскость, перпендикулярная к другой плоскости проекций. На рис. 4.1 показана пространственная схема получения комплексного чертежа точки А в системе (П 1 П 2). Точки А 1 и А 2 – горизонтальная и фронтальная проекции точки А, АА 1 А x А 2 – прямоугольник, плоскость которого перпендикулярна оси x (рис. 2.3).

Новая плоскость П 4 перпендикулярна П 1 . При проецировании точки А на П 4 получим новую проекцию А 4 , фигура АА 1 А 14 А 4 – прямоугольник, плоскость которого перпендикулярна новой оси x 14 = П 4 Ç П 1 . Для получения комплексного чертежа будем рассматривать фигуры, расположенные в плоскостях проекций. Поворотом вокруг оси x 14 совместим П 4 с П 1 , затем поворотом вокруг оси x совместим П 1 (и П 4) с П 2 (на рис. 4.1 направления движения плоскостей П 4 и П 1 показаны штриховыми линиями со стрелками). Полученный чертеж приведен на рис. 4.2. Прямые углы на рис. 4.1, 4.2 помечены дугой с точкой, равные отрезки помечены двумя штрихами (противоположные стороны прямоугольников на рис. 4.1). От комплексного чертежа точки А в системе (П 1 П 2) перешли к комплексному чертежу точки А в системе (П 1 П 4), заменили плоскость П 2 на плоскость П 4 , заменили А 2 на А 4 .

На основе этих построений сформулируем правило замены плоскостей проекций (правило получения новой проекции). Через незаменяемую проекцию проводим новую линию проекционной связи перпендикулярно новой оси, затем от новой оси по линии проекционной связи откладываем отрезок, длина которого равна расстоянию от заменяемой проекции до старой оси, полученная при этом точка и есть новая проекция. Направление новой оси будем брать произвольно. Новое начало координат указывать не будем.

На рис. 4.3 показан переход от комплексного чертежа в системе (П 1 П 2) к комплексному чертежу в системе (П 2 П 4), а затем еще один переход к комплексному чертежу в системе (П 4 П 5). Вместо плоскости П 1 введена плоскость П 4 , перпендикулярная П 2 , затем вместо П 2 введена плоскость П 5 , перпендикулярная П 4 . Используя правило замены плоскостей проекций, можно выполнить любое количество замен плоскостей проекций.

Чтобы прямая лежала в данной плоскости, необходимо, чтобы эта прямая имела с плоскостью две общие точки, которые и определят эту прямую.
Возьмем на данных прямых две произвольно расположенные точки Е и F (Е 1 Е 2 и F 1 F 2 ) и проведем через них прямую k (k 1 и k 2 ). Эта прямая будет расположена в данной плоскости, так как она имеет с ней две общие точки (фиг.232,б).
Изображение на комплексном чертеже прямой, расположенной в плоскости, заданной следами:
а) Возьмем на следах k и L произвольно точки М (М 1 М 2 ) и N (N 1 N 2 ) как следы прямой (фиг.233,а).
б) Проведем через одноименные фронтальные (М 2 и N 2 ) и горизонтальные (М 1 и N 1 ) проекции точек М и N прямые (фиг.233,б).
Прямая MN будет расположена в плоскости а как имеющая с ней две общие точки.
Отсюда следует: для того чтобы прямая принадлежала плоскости, надо, чтобы следы прямой лежали на одноименных следах этой плоскости.

Прямая лежит в плоскости, если имеет с ней одну общую точку и параллельна прямой, лежащей в плоскости. Пусть задана плоскость (фиг.234,а) прямой АВ (А 1 В 1 и A 2 В 2 ) и точкой С (C 1 C 2 ).
Требуется в заданной плоскости провести прямую через заданную точку С .
Проведем через точку С (С 1 С 2 ) прямую параллельно прямой АВ (А 1 В 1 и А 2 В 2 ); эта прямая будет расположена в данной плоскости, так как она имеет с плоскостью общую точку и параллельна прямой, лежащей в данной плоскости (фиг.234,б).
Изображение на комплексном чертеже прямой , расположенной в плоскости и параллельной одному из следов плоскости. Для проведения прямой в заданной следами плоскости а общего положения (прямая должна быть параллельна горизонтальному следу k данной плоскости), возьмем на следе L произвольную точку N (N 1 N 2 ) как точку, лежащую в данной плоскости а (фиг.235,а).
След k принимаем за прямую, лежащую в плоскости П 1 Проведем прямую через точку N 1 параллельно прямой k 1 получим горизонтальную проекцию h 1 прямой h . Фронтальная проекция h 2 прямой h пройдет через точку N 2 и расположится параллельно оси х 12 как прямая, параллельная плоскости П 1 (фиг.235,б).
Прямая h будет принадлежать плоскости а , как имеющая с ней общую точку (след N ) и параллельная прямой (следу к ), лежащей в данной плоскости.
Аналогичное построение будет справедливо и для случая, когда требуется провести прямую в заданной следами плоскости общего положения параллельно фронтальному следу L (фиг.235,в и г).
Прямая h , лежащая в плоскости а , параллельная горизонтальной плоскости проекций П 1 , называется горизонталью данной плоскости (фиг.235,а и б).
Прямая f , лежащая в плоскости а , параллельная фронтальной плоскости проекций П 2 , называется фронталью данной плоскости (фиг.235,в и г).
Отсюда следует, что через всякую точку, лежащую в данной плоскости, можно провести одну горизонталь и одну фронталь. Разобрав различные изображения прямой в плоскости, можно на комплексном чертеже решить обратную задачу, т. е., имея проекции прямой, провести через нее соответствующую плоскость.

Пример 1. Через данный отрезок АВ (А 1 В 1 А 2 В 2 ) провести плоскость общего положения и показать проекции следов этой плоскости (фиг. 236,а).
Зная, что следы прямой должны лежать на одноименных следах плоскости, сначала находим следы прямой, затем выбираем в произвольном месте на оси х 12 точку F 12 схода следов (фиг. 236,б) и, наконец, проводим следы плоскости общего положения (фиг. 236,в).

Пример 2. Через данный отрезок АВ (А 1 В 1 , А 2 В 2 ) провести горизонтально - проектирующую плоскость и показать ее проекцию.
Так как в этом случае горизонтальная проекция прямой должна сливаться с горизонтальной проекцией плоскости, проводим горизонтальную проекцию σ 1 плоскости через горизонтальную проекцию прямой (фиг. 237).
Точка в плоскости. В случае изображения на комплексном чертеже проекций точки, лежащей в данной плоскости, сначала проводят в плоскости вспомогательную прямую, а затем на ней изображают точку.
а) Построить проекции произвольной точки A , принадлежащей плоскости а , заданной следами (фиг.238,а).
Воспользуемся фронталью данной плоскости а как прямой, лежащей в плоскости. Спроектируем одну из фронталей плоскости а , например f (f 1 , f 2 ) (фиг.238,б).
Затем на фронтали проектируем произвольную точку, которую принимаем за заданную точку А (А 1 A 2 ) (фиг.238,в).
Так как обе проекции А 1 и А 2 точки А лежат на проекциях фронтали f плоскости а , то, следовательно, точка А лежит в заданной плоскости а .
Таким же способом можно выполнить построение, воспользовавшись горизонталью h (фиг.238,г)
б) Пусть плоскость задана двумя пересекающимися прямыми АВ (A 1 B 1 , A 2 A 2 ) и ВС (B 1 C 1 , В 2 С 2 ), требуется найти проекции D 1 и D 2 точки D лежащей в заданной плоскости вне этих прямых (фиг.239,а). Зная, что проекции точки должны лежать на проекциях прямой, принадлежащей данной плоскости, проводим вспомогательную прямую EF (E 1 F 1 , E 2 F 2 ) так, чтобы она лежала в данной плоскости (фиг.239,б). Затем на прямой EF (фиг.239,в) проектируем точку D (D 1 D 2 ).

Так как точка D (D 1 D 2 ) лежит на прямой EF (E 1 F 1 , E 2 F 2 ), находящейся в заданной плоскости, следовательно, она принадлежит заданной плоскости.
в) Пусть плоскость σ задана фронтальной проекцией σ 2 . Требуется построить проекции произвольной точки А , принадлежащей данной плоскости.
Так как плоскость σ - фронтально - проектирующая, то по свойству проектирующих плоскостей фронтальная проекция точки, лежащей в этой плоскости, должна сливаться с фронтальной проекцией данной плоскости.
Спроектируем произвольную точку А так, чтобы фронтальная проекция A 2 точки лежала на проекции σ 2 , это и определит, что точка A (A 1 A 2 ) лежит в заданной плоскости (фиг.240).
Такое построение будет справедливо и для остальных проектирующих плоскостей.
Рассмотрим несколько примеров.
Пример I . Дан треугольник AВС (А 1 В 1 С 1 , A 2 B 2 C 2 ) и произвольно расположенная точка D (фиг.241,а); требуется определить, лежит ли точка D (D 1 D 2 ) в плоскости данного треугольника? Порядок проверки указан цифрами на (фиг.241,б).
1 - проводим через точки С 2 и D 2 прямую, получаем точку K 2 ;
2 - проводим вертикальную линию связи, получаем точку К 1 ;
3 - проводим через точки С 1 и К 1 прямую; в данном случае она прошла через точку Ьъ следовательно, точка D (D 1 D 2 ) лежит на прямой СК (С 1 К 1 , С 2 K 2 ), так как ее проекции лежат на проекциях этой прямой и на одной линии связи; прямая СК принадлежит плоскости треугольника ABC (A 1 B 1 C 1 , А 2 В 2 С 2 ), так как имеет с ней две общие точки; следовательно, точка D принадлежит плоскости треугольника.
Пример II . Дан треугольник ABC и расположенная произвольно прямая EF (Е 1 F 1 E 2 F 2 ), требуется определить, лежит ли прямая в плоскости данного треугольника (фиг.242,а)?
Порядок проверки указан цифрами на (фиг.242,б):
1 - продолжаем отрезок E 2 F 2 ; в пересечении с прямыми В 2 А 2 и А 2 С 2 получаем точки Р 2 и Т 2 ;
2 - проводим через точки Р 2 и Т 2 вертикальные линии связи до пересечения с прямыми В 1 А 1 и А 1 С 1 получаем точки Р 1 и Т 1 ;
3 - проведем через точки Р 1 и T 1 прямую; в данном случае прямая сливается с отрезком E 1 F 1 следовательно, прямая РТ принадлежит плоскости треугольника, так как одноименные проекции точек Р и Т лежат на одноименных проекциях прямых ВА и АС , принадлежащих треугольнику, и на одной линии связи; следовательно, прямая EF принадлежит плоскости данного треугольника.

Принадлежность прямой плоскости :

2) прямая принадлежит плоскости, если она проходит через точку, принадлежащую данной плоскости и параллельна какой-нибудь прямой этой плоскости.

Из этих двух признаков принадлежности прямой плоскости можно сделать следующие выводы:

1) если плоскость задана следами, то прямая принадлежит плоскости, если следы прямой лежат на одноименных следах плоскости;

2) прямая принадлежит плоскости, если она с одним следом плоскости имеет общую точку, а другому следу параллельна.

Рассмотрим плоскость Q, общего положения, задана следами (рисунок 17). Прямая NM принадлежит этой плоскости, поскольку ее следы лежат на одноименных следах плоскостей.

На рисунке 18 показана плоскость, заданная пересекающимися прямыми t и n. Чтобы построить прямую, лежащую в этой плоскости, достаточно провести произвольно одну из проекций, например, горизонтальную c1, а затем спроецировать точки пересечения этой прямой с прямыми плоскости на фронтальную плоскость. Фронтальная проекция прямой c2 пройдет через полученные точки.

Рисунок 17 Рисунок 18

Согласно второму положению на рисунке 19 построена прямая h, принадлежащая плоскости Р, - она имеет точку N (N1, N2) общую с плоскостью Р и параллельна прямой, лежащей в плоскости - горизонтальному следу Р1.

Рисунок 19 Рисунок 20

Рассмотрим плоскости частного положения. Если прямая или фигура принадлежит горизонтально-проецирующей плоскости (рисунок 20), то горизонтальные проекции этих геометрических элементов совпадают с горизонтальным следом плоскости.

Если прямая или плоская фигура принадлежит фронтально-проецирующей плоскости, то фронтальные проекции этих геометрических элементов совпадают с фронтальным следом плоскости.

Принадлежность точки плоскости:

Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.

Пример: Дана плоскость Р (a || b). Известна горизонтальная проекция точки В, принадлежащей плоскости Р. Найти фронтальную проекцию точки В (рисунок 21).

На рисунках 22, 23, 24 показано фрагментарно решение этой задачи:

1) проведем через В1 (известную проекцию точки В) любую прямую,

лежащую в плоскости Р, - для этого прямая должна иметь с плоскостью две общие точки. Отметим их на чертеже - М1 и K1;

2) построим фронтальные проекции этих точек по принадлежности точек прямым, т. е. М2 на прямой а, K2 на прямой b. Проведем через фронтальные проекции точек фронтальную проекцию прямой;

Рисунок 21 Рисунок 22