Goniometrické nerovnosti. Goniometrické nerovnice a jejich řešení Jak řešit dvojité goniometrické nerovnice
Ministerstvo školství Běloruské republiky
vzdělávací instituce
„Gomelská státní univerzita
pojmenovaný po Francysk Skaryna"
Matematická fakulta
Katedra algebry a geometrie
Způsobilý k obhajobě
Hlava Oddělení Shemetkov L.A.
Goniometrické rovnice a nerovnice
Práce na kurzu
Vykonavatel:
žákovská skupina M-51
CM. Gorského
Vědecký poradce
Docent
V.G. Safonov
Gomel 2008
ÚVOD
ZÁKLADNÍ METODY ŘEŠENÍ TRIGONOMETRICKÝCH ROVNIC
Faktorizace
Řešení rovnic převodem součinu goniometrických funkcí na součet
Řešení rovnic pomocí trojitých argumentových vzorců
Násobení nějakou goniometrickou funkcí
NESTANDARDNÍ TRIGONOMETRICKÉ ROVNICE
TRIGONOMETRICKÉ NEROVNOSTI
VÝBĚR KOŘENŮ
ÚKOLY PRO SAMOSTATNÉ ŘEŠENÍ
ZÁVĚR
SEZNAM POUŽITÝCH ZDROJŮ
V dávných dobách trigonometrie vznikla v souvislosti s potřebami astronomie, zeměměřictví a stavebnictví, to znamená, že měla čistě geometrický charakter a představovala především<<исчисление хорд>>. Postupem času se do něj začaly prolínat některé analytické body. V první polovině 18. století došlo k prudkému obratu, po kterém trigonometrie nabrala nový směr a posunula se k matematické analýze. Právě v této době se trigonometrické závislosti začaly považovat za funkce.
Goniometrické rovnice jsou jedním z nejobtížnějších témat školního kurzu matematiky. Goniometrické rovnice vznikají při řešení úloh z planimetrie, geometrie těles, astronomie, fyziky a dalších oblastí. Mezi úkoly centralizovaného testování se nacházejí goniometrické rovnice a nerovnice z roku na rok.
Nejdůležitější rozdíl mezi goniometrickými a algebraickými rovnicemi je ten, že algebraické rovnice mají konečný počet kořenů, zatímco goniometrické rovnice mají nekonečný počet, což značně komplikuje výběr kořenů. Dalším specifikem goniometrických rovnic je nejedinečná forma zápisu odpovědi.
Tato práce je věnována metodám řešení goniometrických rovnic a nerovnic.
Diplomová práce se skládá ze 6 částí.
První část obsahuje základní teoretické informace: definice a vlastnosti goniometrických a inverzních goniometrických funkcí; tabulka hodnot goniometrických funkcí pro některé argumenty; vyjádření goniometrických funkcí z hlediska jiných goniometrických funkcí, což je velmi důležité pro převod goniometrických výrazů, zejména těch, které obsahují inverzní goniometrické funkce; kromě základních goniometrických vzorců, dobře známých ze školního kurzu, jsou uvedeny vzorce, které zjednodušují výrazy obsahující inverzní goniometrické funkce.
Druhá část nastiňuje hlavní metody řešení goniometrických rovnic. Uvažuje se řešení elementárních goniometrických rovnic, metoda faktoringu, metody redukce goniometrických rovnic na algebraické. Vzhledem k tomu, že řešení goniometrických rovnic lze zapsat několika způsoby a tvar těchto řešení neumožňuje okamžitě zjistit, zda jsou tato řešení stejná nebo různá, což může<<сбить с толку>> při řešení testů se uvažuje s obecným schématem řešení goniometrických rovnic a podrobně se uvažuje s transformací skupin obecných řešení goniometrických rovnic.
Třetí část se zabývá nestandardními goniometrickými rovnicemi, jejichž řešení jsou založena na funkcionálním přístupu.
Čtvrtá část se zabývá goniometrickými nerovnostmi. Podrobně jsou zvažovány metody řešení elementárních goniometrických nerovnic jak na jednotkové kružnici, tak i grafickou metodou. Je popsán postup řešení neelementárních goniometrických nerovnic pomocí elementárních nerovností a školákům již dobře známá metoda intervalů.
Pátá část představuje nejobtížnější úlohy: kdy je potřeba nejen vyřešit goniometrickou rovnici, ale také z nalezených kořenů vybrat kořeny, které splňují nějakou podmínku. Tato část poskytuje řešení typických úloh pro výběr kořenů. Jsou uvedeny potřebné teoretické informace pro výběr kořenů: rozdělení množiny celých čísel na neprotínající se podmnožiny, řešení rovnic v celých číslech (diofantina).
V šesté části jsou uvedeny úlohy k samostatnému řešení navržené formou testu. 20 testovacích úloh uvádí nejobtížnější úlohy, se kterými se lze v centralizovaném testování setkat.
Elementární goniometrické rovnice
Elementární goniometrické rovnice jsou rovnice tvaru , kde je jedna z goniometrických funkcí: , , , .
Elementární goniometrické rovnice mají nekonečně mnoho kořenů. Například následující hodnoty splňují rovnici: , , atd. Obecný vzorec, podle kterého jsou nalezeny všechny kořeny rovnice, kde , je:
Zde může nabývat libovolných celočíselných hodnot, každá z nich odpovídá určitému kořenu rovnice; v tomto vzorci (stejně jako v jiných vzorcích, kterými se řeší elementární goniometrické rovnice) se nazývá parametr. Obvykle si zapisují, čímž zdůrazňují, že parametr může nabývat libovolných celočíselných hodnot.
Řešení rovnice , kde , se nalézají podle vzorce
Rovnice je vyřešena použitím vzorce
a rovnice --- podle vzorce
Povšimněme si zejména některých speciálních případů elementárních goniometrických rovnic, kdy řešení lze zapsat bez použití obecných vzorců:
Při řešení goniometrických rovnic hraje důležitou roli perioda goniometrických funkcí. Proto uvádíme dvě užitečné věty:
Teorém Pokud --- hlavní perioda funkce, pak číslo je hlavní perioda funkce.
Periody funkcí a se nazývají souměřitelné, pokud existují přirozená čísla a , že .
Teorém Jestliže periodické funkce a , mají úměrné a , pak mají společnou periodu , což je perioda funkcí , , .
Věta říká, jaká je perioda funkce , , , a nemusí to být nutně hlavní perioda. Například hlavní období funkcí a je --- a hlavní období jejich produktu je --- .
Zavedení pomocného argumentu
Standardní způsob převodu výrazů formuláře 
je následující trik: nechť --- úhel daný rovností 
, 
. Neboť existuje jakýkoli a takový úhel. Takto . Pokud , nebo , , , jinak .
Schéma řešení goniometrických rovnic
Hlavní schéma, kterým se budeme řídit při řešení goniometrických rovnic, je následující:
řešení dané rovnice je redukováno na řešení elementárních rovnic. Řešení --- transformace, faktorizace, nahrazení neznámých. Hlavní zásadou je neztratit kořeny. To znamená, že při přechodu na další rovnici (rovnice) se nebojíme výskytu extra (cizí) kořenů, ale záleží nám pouze na tom, aby každá následující rovnice našeho „řetězce“ (nebo soustava rovnic v případě větvení) je důsledkem předchozího. Jednou z možných metod výběru kořenů je kontrola. Hned poznamenáváme, že v případě goniometrických rovnic potíže spojené s výběrem kořenů s ověřováním zpravidla prudce rostou ve srovnání s algebraickými rovnicemi. Koneckonců, musíte zkontrolovat řadu, skládající se z nekonečného počtu členů.
Zvláště je třeba zmínit změnu neznámých při řešení goniometrických rovnic. Ve většině případů se po nezbytné výměně získá algebraická rovnice. Navíc nejsou tak vzácné rovnice, které, i když vypadají trigonometricky, v podstatě nejsou, protože již po prvním kroku --- změny proměnných --- přecházejí v algebraické a k návratu k trigonometrii dochází až na jevišti. řešení elementárních goniometrických rovnic.
Ještě jednou připomeňme: záměnu neznámé je třeba provést co nejdříve, rovnici získanou po záměně je nutné dořešit až do konce včetně fáze výběru kořenů a teprve poté se vrátí k původní neznámý.
Jedním z rysů goniometrických rovnic je, že odpověď v mnoha případech může být zapsána různými způsoby. Dokonce i k vyřešení rovnice 
odpověď lze napsat takto:
1) ve formě dvou sérií: 
, , ;
2) ve standardním tvaru, který je sjednocením výše uvedených řad: , ;
3) od té doby 
, pak lze odpověď napsat jako 
, . (Dále, přítomnost parametru , , nebo v záznamu odpovědi automaticky znamená, že tento parametr nabývá všech možných celočíselných hodnot. Budou stanoveny výjimky.)
Je zřejmé, že uvedené tři případy nevyčerpávají všechny možnosti zápisu odpovědi na uvažovanou rovnici (je jich nekonečně mnoho).
Například pro 
. Proto v prvních dvou případech, pokud , můžeme nahradit za .
Obvykle se odpověď píše na základě odstavce 2. Je užitečné si zapamatovat následující doporučení: pokud práce nekončí řešením rovnice, je třeba ještě provést studii, výběr kořenů, pak nejvhodnější forma záznamu je uvedena v odstavci 1. (Pro rovnici by mělo být uvedeno podobné doporučení.)
Podívejme se na příklad ilustrující to, co bylo řečeno.
Příklad Vyřešte rovnici.
Řešení. Nejviditelnější je následující způsob. Tato rovnice se dělí na dvě: a . Řešením každého z nich a kombinací získaných odpovědí najdeme .
Jiná cesta. Od , tedy nahrazení a pomocí redukčních vzorců. Po drobných transformacích dostaneme , odkud 
.
Na první pohled nemá druhý vzorec oproti prvnímu žádné zvláštní výhody. Vezmeme-li však např. , pak nám vyjde, že , tzn. rovnice má řešení, zatímco první cesta nás vede k odpovědi 
. "Vidět" a dokázat rovnost 
není tak snadné.
Odpovědět. .
Transformace a sjednocení grup obecných řešení goniometrických rovnic
Budeme uvažovat aritmetickou progresi, která se neomezeně rozšiřuje v obou směrech. Termíny této progrese lze rozdělit do dvou skupin termínů umístěných vpravo a vlevo od určitého termínu, nazývaných centrální nebo nulový termín progrese.
Opravíme-li jeden z členů nekonečné progrese nulovým číslem, budeme muset provést dvojité číslování pro všechny zbývající členy: kladné pro členy umístěné vpravo a záporné pro členy umístěné nalevo od nuly.
V obecném případě, pokud je rozdíl progrese nulový člen, vzorec pro jakýkoli (tý) člen nekonečné aritmetické posloupnosti je:
Transformace vzorců pro libovolný člen nekonečné aritmetické posloupnosti
1. Pokud přičteme nebo odečteme rozdíl progrese k nulovému členu, pak se od tohoto progrese nezmění, ale posune se pouze nultý člen, tzn. změní se číslování členů.
2. Pokud je koeficient proměnné vynásoben , pak to povede pouze k permutaci pravé a levé skupiny členů.
3. Jsou-li po sobě jdoucí členy nekonečné progrese
například , , , ..., , aby se centrální členy posloupnosti se stejným rozdílem rovnaly:
pak průběh a řada průběhů vyjadřují stejná čísla.
Příklad Řádek lze nahradit následujícími třemi řádky: , , .
4. Jestliže nekonečné posloupnosti se stejným rozdílem mají čísla jako centrální členy, které tvoří aritmetickou posloupnost s rozdílem , pak tyto řady mohou být nahrazeny jednou posloupností s rozdílem a s centrálním členem rovným kterémukoli z centrálních členů těchto progrese, tzn. -li
pak se tyto průběhy spojí do jednoho:
Příklad
, , , oba se spojují do jedné skupiny, od 
.
Pro transformaci skupin, které mají společná řešení, na skupiny, které nemají společná řešení, se tyto skupiny rozloží na skupiny se společnou tečkou a následně se snažíme výsledné skupiny sloučit, vyjma opakujících se skupin.
Faktorizace
Metoda faktorizace je následující: jestliže
pak libovolné řešení rovnice
je řešení soustavy rovnic
Opačné tvrzení je, obecně řečeno, nepravdivé: ne každé řešení množiny je řešením rovnice. Je to dáno tím, že řešení jednotlivých rovnic nemusí být zahrnuto do oboru definice funkce.
Příklad Vyřešte rovnici.
Řešení. Pomocí základní goniometrické identity znázorníme rovnici ve tvaru
Odpovědět.
; 
.
Převod součtu goniometrických funkcí na součin
Příklad
řešit rovnici 
.
Řešení. Aplikujeme vzorec, získáme ekvivalentní rovnici
Odpovědět. .
Příklad Vyřešte rovnici.
Řešení. V tomto případě byste před použitím vzorců pro součet goniometrických funkcí měli použít redukční vzorec 
. Výsledkem je ekvivalentní rovnice
Odpovědět.
, 
.
Řešení rovnic převodem součinu goniometrických funkcí na součet
Při řešení řady rovnic se používají vzorce.
Příklad řešit rovnici
Řešení.
Odpovědět. , .
Příklad Vyřešte rovnici.
Řešení. Použitím vzorce získáme ekvivalentní rovnici:
Odpovědět. .
Řešení rovnic pomocí redukčních vzorců
Při řešení celé řady goniometrických rovnic hrají klíčovou roli vzorce.
Příklad Vyřešte rovnici.
Řešení. Aplikací vzorce získáme ekvivalentní rovnici.
Odpovědět. ; .
Řešení rovnic pomocí trojitých argumentových vzorců
Příklad Vyřešte rovnici.
Řešení. Aplikujeme vzorec, dostaneme rovnici
Odpovědět. ; .
Příklad
řešit rovnici 
.
Řešení. Použitím vzorců pro snížení stupně získáme: 
. Přihláškou získáme:
Odpovědět. ; .
Rovnost stejnojmenných goniometrických funkcí
Příklad Vyřešte rovnici.
Řešení.
Odpovědět. , .
Příklad
řešit rovnici 
.
Řešení. Pojďme transformovat rovnici.
Odpovědět. .
Příklad Je známo, že a splňují rovnici
Najděte součet.
Řešení. Z rovnice vyplývá, že
Odpovědět. .
Zvažte součty formuláře
Tyto součty lze převést na součin jejich vynásobením a dělením , pak dostaneme
Tato technika může být použita k řešení některých goniometrických rovnic, ale je třeba mít na paměti, že v důsledku toho se mohou objevit cizí kořeny. Zde je zobecnění těchto vzorců:
Příklad Vyřešte rovnici.
Řešení. Je vidět, že množina je řešením původní rovnice. Proto násobení levé a pravé strany rovnice nevede k výskytu dalších kořenů.
My máme 
.
Odpovědět. ; .
Příklad Vyřešte rovnici.
Řešení. Vynásobíme levou a pravou stranu rovnice a použitím vzorců pro převod součinu goniometrických funkcí na součet dostaneme
Tato rovnice je ekvivalentní soustavě dvou rovnic a , odkud a .
Protože kořeny rovnice nejsou kořeny rovnice, měly by být z výsledných množin řešení vyloučeny. Takže v sadě musíte vyloučit .
Odpovědět. a , .
Příklad
řešit rovnici 
.
Řešení. Převedeme výraz:
Rovnice bude zapsána ve tvaru:
Odpovědět. .
Redukce goniometrických rovnic na algebraické
Zmenšení na čtverec
Pokud rovnice vypadá jako
pak to náhrada přivede na čtverec, protože 
() a.
Pokud je místo termínu uvedeno , pak bude požadovaná náhrada .
Rovnice
redukuje na kvadratickou rovnici
prezentace jako 
. Je snadné zkontrolovat, že pro které , nejsou kořeny rovnice, a provedením změny se rovnice zredukuje na kvadratickou.
Příklad Vyřešte rovnici.
Řešení. Přesuňme jej na levou stranu, nahraďme jej a vyjádřeme prostřednictvím a .
Po zjednodušení dostáváme: . Vydělte termín termínem a proveďte substituci:
Když se vrátíme do , najdeme 
.
Rovnice homogenní s ohledem na ,
Uvažujme rovnici tvaru
kde , , , ..., , jsou reálná čísla. V každém členu na levé straně rovnice jsou stupně monočlenů stejné, tj. součet stupňů sinusových a kosinusových je stejný a roven. Taková rovnice se nazývá homogenní vzhledem k a a číslo je voláno indikátor homogenity .
Je jasné, že pokud , pak rovnice bude mít tvar:
jejichž řešením jsou hodnoty, pro které , tedy čísla , . Druhá rovnice, zapsaná v závorkách, je také homogenní, ale stupně jsou o 1 nižší.
Jestliže , pak tato čísla nejsou kořeny rovnice.
Když dostaneme: , a levá strana rovnice (1) nabývá hodnotu .
Takže pro , a , proto lze obě strany rovnice vydělit . V důsledku toho dostaneme rovnici:
který se substitucí snadno redukuje na algebraický:
Homogenní rovnice s indexem homogenity 1. V , máme rovnici .
Jestliže , pak je tato rovnice ekvivalentní rovnici , , odkud , .
Příklad Vyřešte rovnici.
Řešení. Tato rovnice je homogenní prvního stupně. Vydělením obou jeho částí dostaneme: , , , .
Odpovědět. .
Příklad Při , získáme homogenní rovnici tvaru
Řešení.
Jestliže , pak obě strany rovnice vydělíme , dostaneme rovnici 
, který lze snadno zmenšit na čtverec substitucí: 
. Pokud 
, pak má rovnice reálné kořeny , . Původní rovnice bude mít dvě skupiny řešení: , , .
Pokud 
, pak rovnice nemá řešení.
Příklad Vyřešte rovnici.
Řešení. Tato rovnice je homogenní druhého stupně. Vydělte obě strany rovnice , dostaneme: . Nechte tedy , , . , , ; , , .
Odpovědět.
.
Rovnice je redukována na rovnici tvaru
K tomu stačí použít identitu 
Zejména se rovnice redukuje na homogenní, pokud je nahrazena 
, pak dostaneme ekvivalentní rovnici:
Příklad Vyřešte rovnici.
Řešení. Převedeme rovnici na homogenní:
Vydělte obě strany rovnice 
, dostaneme rovnici:
Nechť, pak se dostaneme ke kvadratické rovnici: 
, , 
, 
, .
Odpovědět.
.
Příklad Vyřešte rovnici.
Řešení. Odmocnime obě strany rovnice, protože mají kladné hodnoty: , ,
Nechte, pak dostaneme 
, , .
Odpovědět. .
Rovnice řešené pomocí identit 
Je užitečné znát následující vzorce:
Příklad Vyřešte rovnici.
Řešení. Používáme, dostáváme
Odpovědět.
Nenabízíme samotné vzorce, ale způsob, jak je odvodit:
Tudíž,
Stejně tak .
Příklad
řešit rovnici 
.
Řešení. Převedeme výraz:
Rovnice bude zapsána ve tvaru:
Vezmeme , dostaneme . , . tudíž
Odpovědět. .
Univerzální trigonometrické substituce
Goniometrická rovnice tvaru
kde --- racionální funkci pomocí vzorců -- stejně jako pomocí vzorců -- lze redukovat na racionální rovnici s ohledem na argumenty , , , , načež lze rovnici redukovat na algebraická racionální rovnice s ohledem na použití univerzálních goniometrických substitučních vzorců
Je třeba poznamenat, že použití vzorců může vést ke zúžení ODZ původní rovnice, protože není definována v bodech , takže v takových případech je nutné zkontrolovat, zda jsou úhly kořeny původní rovnice .
Příklad Vyřešte rovnici.
Řešení. Podle zadání. Použitím vzorců a provedením substituce dostaneme
odkud a tedy .
Rovnice formuláře
Rovnice tvaru , kde je polynom, se řeší změnou neznámých
Příklad Vyřešte rovnici.
Řešení. Provedením substituce a zohledněním toho dostaneme
kde,. --- cizí kořen, protože . Kořeny rovnic 
jsou .
Použití omezených funkcí
V praxi centralizovaného testování se nezřídka setkáme s rovnicemi, jejichž řešení je založeno na ohraničenosti funkcí a . Například:
Příklad Vyřešte rovnici.
Řešení. Protože , , pak levá strana nepřesahuje a je rovna , jestliže
Abychom našli hodnoty, které splňují obě rovnice, postupujeme následovně. Vyřešíme jeden z nich, pak mezi nalezenými hodnotami vybereme ty, které vyhovují druhému.
Začněme tím druhým: , . Pak , 
.
Je jasné, že pouze pro sudá čísla bude .
Odpovědět. .
Další nápad je realizován řešením následující rovnice:
Příklad
řešit rovnici 
.
Řešení. Použijme vlastnost exponenciální funkce: , 
.
Přidáním těchto nerovností po členech získáme:
Proto je levá strana této rovnice rovna právě tehdy, když platí obě rovnosti:
tj. může nabývat hodnot , , , nebo může nabývat hodnot , .
Odpovědět. , .
Příklad
řešit rovnici 
.
Řešení., . Tudíž, 
.
Odpovědět. .
Příklad řešit rovnici
Řešení. Označte , pak z definice inverzní goniometrické funkce máme 
a 
.
Jelikož z rovnice plyne nerovnost, tzn. . Od a , potom a . Nicméně, a proto.
Pokud a , tak . Vzhledem k tomu , že bylo dříve stanoveno , pak .
Odpovědět. , .
Příklad řešit rovnici
Řešení. Rozsah platných hodnot rovnice je .
Nejprve si ukažme, že funkce
Pro všechny může nabývat pouze kladných hodnot.
Představme si funkci následovně: .
Od té doby, tj. 
.
Proto, abychom dokázali nerovnost , je nutné to ukázat 
. Za tímto účelem pak obě části této nerovnosti krychlíme
Výsledná číselná nerovnost ukazuje, že . Pokud vezmeme v úvahu i to , pak je levá strana rovnice nezáporná.
Zvažte nyní pravou stranu rovnice.
Protože 
, pak
Je však známo, že 
. Z toho vyplývá, že tj. pravá strana rovnice nepřesahuje . Dříve bylo prokázáno, že levá strana rovnice je nezáporná, takže rovnost v může být pouze v případě, kdy jsou obě její části stejné, a to je možné pouze pro .
Odpovědět. .
Příklad řešit rovnici
Řešení. Označte a 
. Aplikováním Cauchy-Bunyakovského nerovnosti získáme . Z toho tedy vyplývá 
. Na druhou stranu existuje 
. Rovnice tedy nemá kořeny.
Odpovědět. .
Příklad Řešte rovnici:
Řešení. Přepišme rovnici do tvaru:
Odpovědět. .
Funkcionální metody řešení goniometrických a kombinovaných rovnic
Ne každou rovnici lze v důsledku transformací redukovat na rovnici toho či onoho standardního tvaru, pro kterou existuje určitá metoda řešení. V takových případech se ukazuje jako užitečné použít takové vlastnosti funkcí, jako je monotónnost, omezenost, rovnost, periodicita atd. Pokud se tedy jedna z funkcí zmenšuje a druhá na intervalu zvyšuje, pak pokud má rovnice kořen na tomto intervalu, tento kořen je jedinečný, a pak ho lze například najít výběrem. Pokud je funkce omezena shora a , a funkce je omezena zdola a , pak je rovnice ekvivalentní soustavě rovnic
Příklad řešit rovnici
Řešení. Původní rovnici transformujeme do tvaru
a vyřešte jej jako čtverec s ohledem na . Pak dostaneme
Pojďme vyřešit první nastavenou rovnici. Vezmeme-li v úvahu omezenost funkce, dojdeme k závěru, že rovnice může mít kořen pouze na intervalu. V tomto intervalu se funkce zvyšuje a funkce 
klesá. Pokud tedy tato rovnice má kořen, pak je jedinečná. Najdeme výběrem.
Odpovědět. .
Příklad řešit rovnici
Řešení. Nechte, a 
, pak lze původní rovnici zapsat jako funkcionální rovnici . Protože je funkce lichá, pak . V tomto případě dostaneme rovnici
Protože a je monotónní na , rovnice je ekvivalentní rovnici , tzn. 
, který má jeden kořen .
Odpovědět. .
Příklad
řešit rovnici 
.
Řešení. Na základě věty o derivaci komplexní funkce je zřejmé, že funkce 
klesající (funkce klesající, rostoucí, klesající). Z toho je zřejmé, že funkce 
definováno dne , klesající. Tato rovnice má tedy nejvýše jeden kořen. Protože 
, pak
Odpovědět. .
Příklad Vyřešte rovnici.
Řešení. Uvažujme rovnici na třech intervalech.
a) Nechat. Pak na této množině je původní rovnice ekvivalentní rovnici . Která nemá žádná řešení na intervalu, protože 
, , a . Na intervalu původní rovnice také nemá kořeny, protože 
,
b) Nechat. Pak na této množině je původní rovnice ekvivalentní rovnici
jehož kořeny na intervalu jsou čísla , , , .
c) Nechat. Pak na této množině je původní rovnice ekvivalentní rovnici
Která nemá žádná řešení na intervalu, protože , ale . Rovnice také nemá řešení na intervalu, protože , , a .
Odpovědět. , , , .
Metoda symetrie
Metodu symetrie je vhodné použít, když zadání úlohy obsahuje požadavek, aby řešení rovnice, nerovnosti, soustavy atd. bylo jedinečné. nebo přesný údaj o počtu řešení. V tomto případě by měla být detekována jakákoli symetrie daných výrazů.
Je také nutné vzít v úvahu rozmanitost různých možných typů symetrie.
Neméně důležité je důsledné dodržování logických fází uvažování se symetrií.
Obvykle nám symetrie umožňuje stanovit pouze nezbytné podmínky a pak je třeba zkontrolovat jejich dostatečnost.
Příklad Najděte všechny hodnoty parametru, pro které má rovnice jedinečné řešení.
Řešení. Všimněte si, že a jsou sudé funkce, takže levá strana rovnice je sudá funkce.
Pokud tedy existuje řešení rovnice, pak existuje také řešení rovnice. Pokud je jediným řešením rovnice, pak nutné , .
Pojďme vybrat možný hodnoty, vyžadující, aby byl kořenem rovnice.
Okamžitě si všimneme, že jiné hodnoty nemohou splnit podmínku problému.
Zatím ale není známo, zda všichni vybraní skutečně splňují podmínku problému.
Přiměřenost.
1), rovnice bude mít tvar 
.
2), rovnice bude mít tvar:
Pochopitelně pro všechny a 
. Proto je poslední rovnice ekvivalentní systému:
Tak jsme dokázali, že pro , rovnice má jedinečné řešení.
Odpovědět. .
Řešení s průzkumem funkcí
Příklad Dokažte, že všechna řešení rovnice
Celá čísla.
Řešení. Hlavní perioda původní rovnice je . Proto nejprve studujeme tuto rovnici na segmentu .
Převedeme rovnici do tvaru:
Pomocí kalkulačky získáme:
Pokud , pak z předchozích rovností dostaneme:
Řešením výsledné rovnice dostaneme: .
Provedené výpočty poskytují příležitost předpokládat, že kořeny rovnice patřící do intervalu jsou , a .
Přímé ověření tuto hypotézu potvrzuje. Je tedy dokázáno, že kořeny rovnice jsou pouze celá čísla , .
Příklad
Vyřešte rovnici 
.
Řešení. Najděte hlavní periodu rovnice. Hlavním obdobím funkce je . Hlavním obdobím funkce je . Nejmenší společný násobek čísel a je roven . Hlavní perioda rovnice je tedy . Nechte
Je zřejmé, že jde o řešení rovnice. Na intervalu. Funkce je záporná. Další kořeny rovnice by se proto měly hledat pouze na intervalech x a .
Pomocí mikrokalkulačky nejprve najdeme přibližné hodnoty kořenů rovnice. K tomu sestavíme tabulku hodnot funkcí 
na intervalech a ; tj. na intervalech a .
| 0 | 0 | 202,5 | 0,85355342 |
| 3 | -0,00080306 | 207 | 0,6893642 |
| 6 | -0,00119426 | 210 | 0,57635189 |
| 9 | -0,00261932 | 213 | 0,4614465 |
| 12 | -0,00448897 | 216 | 0,34549155 |
| 15 | -0,00667995 | 219 | 0,22934931 |
| 18 | -0,00903692 | 222 | 0,1138931 |
| 21 | -0,01137519 | 225 | 0,00000002 |
| 24 | -0,01312438 | 228 | -0,11145712 |
| 27 | -0,01512438 | 231 | -0,21961736 |
| 30 | -0,01604446 | 234 | -0,32363903 |
| 33 | -0,01597149 | 237 | -0,42270819 |
| 36 | -0,01462203 | 240 | -0,5160445 |
| 39 | -0,01170562 | 243 | -0,60290965 |
| 42 | -0,00692866 | 246 | -0,65261345 |
| 45 | 0,00000002 | 249 | -0,75452006 |
| 48 | 0,00936458 | 252 | -0,81805397 |
| 51 | 0,02143757 | 255 | -0,87270535 |
| 54 | 0,03647455 | 258 | -0,91803444 |
| 57 | 0,0547098 | 261 | -0,95367586 |
| 60 | 0,07635185 | 264 | -0,97934187 |
| 63 | 0,10157893 | 267 | -0,99482505 |
| 66 | 0,1305352 | 270 | -1 |
| 67,5 | 0,14644661 |
Následující hypotézy jsou snadno patrné z tabulky: kořeny rovnice patřící do segmentu jsou čísla: ; ; . Přímé ověření tuto hypotézu potvrzuje.
Odpovědět.
; 
; .
Řešení goniometrických nerovnic pomocí jednotkové kružnice
Při řešení goniometrických nerovnic tvaru , kde je jedna z goniometrických funkcí, je vhodné použít goniometrický kruh, aby bylo řešení nerovnice co nejpřehledněji prezentováno a odpověď zapsána. Hlavní metodou řešení goniometrických nerovností je jejich redukce na nejjednodušší nerovnosti typu . Podívejme se na příklad, jak takové nerovnosti vyřešit.
Příklad Vyřešte nerovnost.
Řešení. Narýsujme si trigonometrickou kružnici a označme na ní body, pro které je pořadnice větší než .
Pro řešení této nerovnosti bude . Je také jasné, že pokud se některé číslo liší od některého čísla z uvedeného intervalu o , pak také nebude menší než . Proto na konce nalezeného segmentu řešení stačí přidat . Nakonec dostaneme, že řešení původní nerovnosti budou všechna 
.
Odpovědět.
.
Pro řešení nerovností s tečnou a kotangens je užitečný koncept přímky tečen a kotangens. Toto jsou čáry a (na obrázku (1) a (2)) dotýkající se trigonometrické kružnice.
Je snadné vidět, že pokud vytvoříte paprsek s počátkem v počátku, který svírá úhel s kladným směrem osy úsečky, pak délka segmentu od bodu k bodu průsečíku tohoto paprsku s přímkou tečny je přesně rovna tečně úhlu, který tento paprsek svírá s osou úsečky. Podobné pozorování platí pro kotangens.
Příklad Vyřešte nerovnost.
Řešení. Označte , pak bude mít nerovnost podobu nejjednoduššího: . Uvažujme interval s délkou rovnou nejmenší kladné periodě (LPP) tečny. Na tomto segmentu pomocí přímky tečen zjistíme, že . Nyní si připomeneme, co je třeba přidat, protože RPE funkce . Tak, 
. Vrátíme-li se k proměnné, dostaneme to.
Odpovědět.
.
Nerovnice s inverzními goniometrickými funkcemi je vhodné řešit pomocí grafů inverzních goniometrických funkcí. Ukažme si, jak se to dělá na příkladu.
Řešení goniometrických nerovnic grafickou metodou
Všimněte si, že pokud --- je periodická funkce, pak k vyřešení nerovnosti je nutné najít její řešení na segmentu, jehož délka je rovna periodě funkce . Všechna řešení původní nerovnosti se budou skládat z nalezených hodnot a také ze všech, které se liší od nalezených libovolným celým počtem period funkce.
Zvažte řešení nerovnice ().
Od té doby nemá nerovnost řešení pro . Jestliže , pak množina řešení nerovnice je množinou všech reálných čísel.
Nechte Funkce sinus má nejmenší kladnou periodu, takže nerovnost lze vyřešit nejprve na segmentu délky , například na segmentu. Vytváříme grafy funkcí a (). jsou dány nerovnostmi tvaru: a odkud,
V tomto příspěvku byly zvažovány metody řešení goniometrických rovnic a nerovnic, a to jak na nejjednodušší, tak na úrovni olympiády. Byly uvažovány hlavní metody řešení goniometrických rovnic a nerovnic, a to jak specifické --- charakteristické pouze pro goniometrické rovnice a nerovnice ---, tak obecné funkční metody pro řešení rovnic a nerovnic, jak jsou aplikovány na goniometrické rovnice.
Práce poskytuje základní teoretické informace: definice a vlastnosti goniometrických a inverzních goniometrických funkcí; vyjádření goniometrických funkcí z hlediska jiných goniometrických funkcí, což je velmi důležité pro převod goniometrických výrazů, zejména těch, které obsahují inverzní goniometrické funkce; kromě základních goniometrických vzorců, dobře známých ze školního kurzu, jsou uvedeny vzorce, které zjednodušují výrazy obsahující inverzní goniometrické funkce. Uvažuje se řešení elementárních goniometrických rovnic, metoda faktoringu, metody redukce goniometrických rovnic na algebraické. Vzhledem k tomu, že řešení goniometrických rovnic lze zapsat několika způsoby a tvar těchto řešení neumožňuje okamžitě určit, zda jsou tato řešení stejná nebo odlišná, uvažuje se o obecném schématu řešení goniometrických rovnic. podrobně je zvažována transformace grup obecných řešení goniometrických rovnic. Podrobně jsou zvažovány metody řešení elementárních goniometrických nerovnic jak na jednotkové kružnici, tak i grafickou metodou. Je popsán postup řešení neelementárních goniometrických nerovnic pomocí elementárních nerovností a školákům již dobře známá metoda intervalů. Jsou uvedena řešení typických úloh pro výběr kořenů. Jsou uvedeny potřebné teoretické informace pro výběr kořenů: rozdělení množiny celých čísel na neprotínající se podmnožiny, řešení rovnic v celých číslech (diofantina).
Výsledky této diplomové práce lze využít jako výukový materiál při přípravě semestrálních prací a diplomových prací, při přípravě volitelných předmětů pro školáky a práci lze využít i při přípravě studentů na přijímací zkoušky a centralizované testování.
Vygodsky Ya.Ya., Příručka elementární matematiky. /Vygodsky Ya.Ya. --- M.: Nauka, 1970.
Igudisman O., Matematika u ústní zkoušky / Igudisman O. --- M .: Iris press, Rolf, 2001.
Azarov A.I., rovnice / Azarov A.I., Gladun O.M., Fedosenko V.S. --- Minsk: Trivium, 1994.
Litviněnko V.N., Workshop o elementární matematice / Litviněnko V.N. --- M .: Vzdělávání, 1991.
Sharygin I.F., Volitelný kurz z matematiky: řešení problémů / Sharygin I.F., Golubev V.I. --- M.: Osvícení, 1991.
Bardushkin V., Goniometrické rovnice. Výběr kořenů / V. Barduškin, A. Prokofjev.// Matematika, č. 12, 2005 s. 23--27.
Vasilevsky A.B., Úkoly pro mimoškolní práci v matematice / Vasilevsky A.B. --- Mn.: Lidová Asveta. 1988. --- 176. léta.
Sapunov P. I., Transformace a sjednocení grup obecných řešení goniometrických rovnic / Sapunov P. I. // Matematická výchova, vydání č. 3, 1935.
Borodin P., Trigonometrie. Materiály k přijímacím zkouškám na Moskevské státní univerzitě [text] / P. Borodin, V. Galkin, V. Panferov, I. Sergejev, V. Tarasov // Matematika č. 1, 2005 str. 36--48.
Samusenko A.V., Matematika: Typické chyby žadatelů: Referenční příručka / Samusenko A.V., Kazachenok V.V. --- Minsk: Higher School, 1991.
Azarov A.I., Funkční a grafické metody pro řešení zkušebních problémů / Azarov A.I., Barvenov S.A., --- Minsk: Aversev, 2004.
Řešení nejjednodušších goniometrických rovnic
Nejprve si připomeňme vzorce pro řešení nejjednodušších goniometrických rovnic.
- $sinx=a$
- $cosx=a$
- $tgx=a$
- $ctgx=a$
Řešení nejjednodušších goniometrických nerovnic.
Abychom vyřešili nejjednodušší goniometrické nerovnice, musíme nejprve vyřešit odpovídající rovnici a poté pomocí goniometrické kružnice najít řešení nerovnice. Uvažujme řešení nejjednodušších goniometrických nerovnic na příkladech.
Příklad 1
$sinx\ge \frac(1)(2)$
Najděte řešení trigonometrické nerovnosti $sinx=\frac(1)(2)$
\ \
Obrázek 1. Řešení nerovnosti $sinx\ge \frac(1)(2)$.
Protože nerovnost má znaménko „větší než nebo rovno“, řešení leží na horním oblouku kružnice (vzhledem k řešení rovnice).
Odpověď: $\left[\frac(\pi )(6)+2\pi n,\frac(5\pi )(6)+2\pi n\right]$.
Příklad 2
Najděte řešení trigonometrické nerovnosti $cosx=\frac(\sqrt(3))(2)$
\ \
Všimněte si řešení na trigonometrické kružnici
Protože nerovnost má znaménko „menší než“, řešení leží na oblouku kružnice umístěné vlevo (vzhledem k řešení rovnice).
Odpověď: $\left(\frac(\pi )(6)+2\pi n,\frac(11\pi )(6)+2\pi n\right)$.
Příklad 3
$tgx\le \frac(\sqrt(3))(3)$
Najděte řešení trigonometrické nerovnosti $tgx=\frac(\sqrt(3))(3)$
\ \
Zde také potřebujeme doménu definice. Jak si pamatujeme, funkce tečny $x\ne \frac(\pi )(2)+\pi n,n\in Z$
Všimněte si řešení na trigonometrické kružnici
Obrázek 3. Řešení nerovnosti $tgx\le \frac(\sqrt(3))(3)$.
Protože nerovnost má znaménko „menší nebo rovno“, řešení leží na obloucích kruhu vyznačených na obrázku 3 modře.
Odpověď: $\ \left(-\frac(\pi )(2)+2\pi n\right.,\left.\frac(\pi )(6)+2\pi n\right]\cup \left (\frac(\pi )(2)+2\pi n,\vpravo.\vlevo.\frac(7\pi )(6)+2\pi n\vpravo]$
Příklad 4
Najděte řešení trigonometrické nerovnosti $ctgx=\sqrt(3)$
\ \
Zde také potřebujeme doménu definice. Jak si pamatujeme, funkce tečny $x\ne \pi n,n\in Z$
Všimněte si řešení na trigonometrické kružnici
Obrázek 4. Řešení nerovnosti $ctgx\le \sqrt(3)$.
Protože nerovnost má znaménko „větší než“, řešení leží na obloucích kruhu vyznačených na obrázku 4 modře.
Odpověď: $\ \left(2\pi n,\frac(\pi )(6)+2\pi n\right)\cup \left(\pi +2\pi n,\frac(7\pi )( 6)+2\pi n\vpravo)$
DEFINICE
Goniometrické nerovnosti jsou nerovnosti, které obsahují proměnnou pod znaménkem goniometrické funkce.
Řešení goniometrických nerovností
Řešení goniometrických nerovností často spočívá v řešení nejjednodušších goniometrických nerovností tvaru: \(\ \sin x a \), \(\ \cos x > a \), \(\ \jméno operátora(tg) x > a \ ), \(\ \ jméno operátora(ctg) x > a \), \(\ \sin x \leq a \), \(\ \cos x \leq a \), \(\ \název_operátora(tg) x \ leq a \), \ (\ \název_operátora(ctg) x \leq a \), \(\ \sin x \geq a \), \(\ \cos \geq a \), \(\ \jméno_operátora(tg ) x \geq a \ ), \(\ \jméno operátora(tg) x \geq a \)
Nejjednodušší goniometrické nerovnice řešíme graficky nebo pomocí jednotkové goniometrické kružnice.
Podle definice je sinus úhlu \(\ \alpha \) pořadnicí bodu \(\ P_(\alpha)(x, y) \) jednotkové kružnice (obr. 1) a kosinus je úsečka tohoto bodu. Této skutečnosti se využívá při řešení nejjednodušších goniometrických nerovnic s kosinusem a sinem pomocí jednotkové kružnice.
Příklady řešení goniometrických nerovnic
Vyřešte nerovnost \(\ \sin x \leq \frac(\sqrt(3))(2) \)
Protože \(\ \left|\frac(\sqrt(3))(2)\right| , má tato nerovnost řešení a lze ji vyřešit dvěma způsoby
První způsob. Vyřešme tuto nerovnost graficky. K tomu sestrojíme ve stejném souřadnicovém systému graf sinus \(\ y=\sin x \) (obr. 2) a přímky \(\ y=\frac(\sqrt(3))( 2) \)
Vyberme intervaly, kde se sinusoida nachází pod grafem přímky \(\ y=\frac(\sqrt(3))(2) \) . Najděte úsečky \(\ x_(1) \) a \(\ x_(2) \) průsečíků těchto grafů: \(\ x_(1)=\pi-\arcsin \frac(\sqrt(3) ))(2)=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_(2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\ frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)
Dostali jsme interval \(\ \left[-\frac(4 \pi)(3) ; \frac(\pi)(3)\right] \), ale protože funkce \(\ y=\sin x \) je periodický a má tečku \(\ 2 \pi \) , pak je odpovědí sjednocení intervalů: \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+ 2 \pi k\vpravo] \), \(\ k \in Z \)
Druhý způsob. Sestrojte jednotkovou kružnici a přímku \(\ y=\frac(\sqrt(3))(2) \) , označte jejich průsečíky \(\ P_(x_(1)) \) a \(\ P_(x_) (2)) \) (obr. 3). Řešením původní nerovnosti bude množina bodů na pořadnici, které jsou menší než \(\ \frac(\sqrt(3))(2) \) . Zjistíme hodnotu \(\ \boldsymbol(I)_(1) \) a \(\ \boldsymbol(I)_(2) \) proti směru hodinových ručiček, \(\ x_(1) Obr.
\(\ x_(1)=\pi-\arcsin \frac(\sqrt(3))(2)=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_ (2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)
Vezmeme-li v úvahu periodicitu funkce sinus, nakonec získáme intervaly \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+2 \ pi\right] \), \(\k\in Z\)
Vyřešte nerovnost \(\ \sin x>2 \)
Sinus je omezená funkce: \(\ |\sin x| \leq 1 \) , a pravá strana této nerovnosti je větší než jedna, takže neexistují žádná řešení.
Vyřešte nerovnost \(\ \cos x>\frac(1)(2) \)
Tuto nerovnost lze řešit dvěma způsoby: graficky a pomocí jednotkové kružnice. Zvažme každou z metod.
První způsob. Znázorněme v jednom souřadnicovém systému funkce, které popisují levou a pravou část nerovnosti, tedy \(\ y=\cos x \) a \(\ y=\frac(1)(2) \) . Vyberme intervaly, kde se graf funkce kosinus \(\ y=\cos x \) nachází nad grafem přímky \(\ y=\frac(1)(2) \) (obr. 4 ).
Najděte úsečky bodů \(\ \boldsymbol(x)_(1) \) a \(\ x_(2) \) - průsečíky grafů funkcí \(\ y=\cos x \ ) a \(\ y=\frac (1)(2) \) , což jsou konce jednoho z intervalů, na kterých platí indikovaná nerovnost. \(\ x_(1)=-\arccos \frac(1)(2)=-\frac(\pi)(3) \); \(\ x_(1)=\arccos \frac(1)(2)=\frac(\pi)(3) \)
Vzhledem k tomu, že kosinus je periodická funkce s periodou \(\ 2 \pi \) , je odpovědí hodnota \(\ x \) z intervalů \(\ \left(-\frac(\pi)(3 )+2 \pi k ; \frac(\pi)(3)+2 \pi k\right) \), \(\ k \in Z \)
Druhý způsob. Sestrojme jednotkovou kružnici a přímku \(\ x=\frac(1)(2) \) (protože osa x odpovídá kosinusům na jednotkové kružnici). Nechť \(\ P_(x_(1)) \) a \(\ P_(x_(2)) \) (obr. 5) jsou průsečíky přímky a jednotkové kružnice. Řešením původní rovnice bude množina úseček, které jsou menší než \(\ \frac(1)(2) \) . Najděte hodnotu \(\ x_(1) \) a \(\ 2 \) , proveďte obchůzku proti směru hodinových ručiček, takže \(\ x_(1) Vezmeme-li v úvahu periodicitu kosinu, nakonec dostaneme intervaly \( \ \left(-\frac (\pi)(3)+2 \pi k ;\frac(\pi)(3)+2 \pi k\vpravo) \),\(\ k \in Z \)
Vyřešte nerovnost \(\ \operatorname(ctg) x \leq-\frac(\sqrt(3))(3) \)
Nakreslete grafy funkcí \(\ y=\jméno operátora(ctg) x \), \(\ y=-\frac(\sqrt(3))(3) \) v jednom souřadnicovém systému
Vyberme intervaly, kde graf funkce \(\ y=\jméno operátora(ctg) x \) není vyšší než graf přímky \(\ y=-\frac(\sqrt(3))(3 ) \) (obr. 6) .
Najděte úsečku bodu \(\ x_(0) \) , což je konec jednoho z intervalů, na kterém je nerovnost \(\ x_(0)=\název operátora(arcctg)\left(-\frac(\ sqrt(3))( 3)\right)=\pi-\jméno operátora (arcctg)\left(\frac(\sqrt(3))(3)\right)=\pi-\frac(\pi)(3 )=\frac(2 \pi)(3) \)
Druhým koncem této mezery je bod \(\ \pi \) a funkce \(\ y=\jméno operátora(ctg) x \) je v tomto bodě nedefinovaná. Jedním z řešení této nerovnosti je tedy interval \(\ \frac(2 \pi)(3) \leq x
Goniometrické nerovnosti se složitým argumentem
Goniometrické nerovnosti se složitým argumentem lze pomocí substituce redukovat na nejjednodušší goniometrické nerovnosti. Po jeho vyřešení se provede obrácená substituce a vyjádří se původní neznámá.
Vyřešte nerovnost \(\ 2 \cos \left(2 x+100^(\circ)\right) \leq-1 \)
Vyjádřete kosinus na pravé straně této nerovnosti: \(\ \cos \left(2 x+100^(\circ)\right) \leq-\frac(1)(2) \)
Provedeme nahrazení \(\ t=2 x+100^(\circ) \) , po kterém se tato nerovnost transformuje na nejjednodušší nerovnost \(\ \cos t \leq-\frac(1)(2) \ )
Vyřešme to pomocí jednotkové kružnice. Sestrojme jednotkovou kružnici a přímku \(\ x=-\frac(1)(2) \) . Jako průsečík přímky a jednotkové kružnice označme \(\ P_(1) \) a \(\ P_(2) \) (obr. 7).
Řešením původní nerovnosti bude množina úseček, které jsou nejvýše \(\ -\frac(1)(2) \). Bod \(\ P_(1) \) odpovídá úhlu \(\ 120^(\circ) \) a bod \(\ P_(2) \) . Při dané kosinové periodě tedy dostaneme \(\ 120^(\circ)+360^(\circ) \cdot n \leq t \leq 240^(\circ)+360^(\circ) \cdot n \ ), \(\ n \in Z \)
Provedeme opačnou substituci \(\ t=2 x+100^(\circ) 120^(\circ)+360^(\circ) \cdot n \leq 2 x+100^(\circ) \leq 240^ (\ circ)+360^(\circ) \cdot n \), \(\ n \in Z \)
Vyjádříme \(\ \mathbf(x) \), k tomu nejprve odečteme \(\ 100^(\circ) 120^(\circ)-100^(\circ)+360^(\circ) \ cdot n \leq 2 x+100^(\circ)-100^(\circ) \leq 240^(\circ)-100^(\circ)+360^(\circ) \cdot n \), \( \ n\v Z\); \(\ 20^(\circ)+360^(\circ) \cdot n \leq 2 x \leq 140^(\circ)+360^(\circ) \cdot n \), \(\ n \in Z\)
a poté vydělte 2 \(\ \frac(20^(\circ)+360^(\circ) \cdot n)(2) \leq \frac(2 x)(2) \leq \frac(140^ (\circ)+360^(\circ) \cdot n)(2) \), \(\ n \in Z \); \(\ 10^(\circ)+180^(\circ) \cdot n \leq x \leq 70^(\circ)+180^(\circ) \cdot n \), \(\ n \in Z \)
Dvojité goniometrické nerovnosti
Vyřešte dvojitou goniometrickou nerovnost \(\ \frac(1)(2)
Zaveďme náhradu \(\ t=\frac(x)(2) \) , pak původní nerovnost bude mít tvar \(\ \frac(1)(2)
Vyřešme to pomocí jednotkové kružnice. Protože ordináta odpovídá sinusu na jednotkové kružnici, vybereme na ní množinu ordinát, která je větší než \(\ x=\frac(1)(2) \) a menší nebo rovna \(\ \frac(\sqrt(2))(2) \) . Na obrázku 8 budou tyto body umístěny na obloucích \(\ P_(t_(1)) \), \(\ P_(t_(2)) \) a \(\ P_(t_(3)) \) , \( \ P_(t_(4)) \) . Nalezneme hodnotu \(\ t_(1) \), \(\ t_(2) \), \(\ t_(3) \), \(\ t_(4) \) , provedeme prohlídku proti směru hodinových ručiček a \ (\ t_(1) \(\ t_(3)=\pi-\arcsin \frac(\sqrt(2))(2)=\pi-\frac(\pi)(4)=\frac(3 \ pi)(4) \); \(\ t_(4)=\pi-\arcsin \frac(1)(2)=\pi-\frac(\pi)(6)=\frac(5 \pi ) (6)\)
Získáme tak dva intervaly, které lze s přihlédnutím k periodicitě funkce sinus zapsat takto \(\ \frac(\pi)(6)+2 \pi k \leq t \frac(\pi) (4)+2 \ pi k \quad \frac(3 \pi)(4)+2 \pi k leq \frac(x)(2) \frac(\pi)(4)+2 \pi k \) , \(\ \frac(3 \pi)(4)+2 \pi k Vyjádřete \(\ \mathbf( x) \), k tomu vynásobíme všechny strany obou nerovností 2, dostaneme \(\ \frac (\pi)(3)+4 \pi k \leq x
METODY ŘEŠENÍ TRIGONOMETRICKÝCH NEROVNOSTÍ
Relevantnost. Historicky měly goniometrické rovnice a nerovnice zvláštní místo ve školních osnovách. Můžeme říci, že trigonometrie je jednou z nejdůležitějších částí školního kurzu a celé matematické vědy obecně.
Goniometrické rovnice a nerovnice zaujímají ve středoškolském matematickém kurzu jedno z ústředních míst, a to jak z hlediska obsahu vzdělávacího materiálu, tak z hlediska metod edukační a poznávací činnosti, které lze a mají být utvářeny během jejich studia a aplikovány při řešení rozsáhlé řada problémů teoretického i aplikovaného charakteru.
Řešení goniometrických rovnic a nerovnic vytváří předpoklady pro systematizaci znalostí studentů souvisejících s veškerým výukovým materiálem z trigonometrie (například vlastnosti goniometrických funkcí, metody transformace goniometrických výrazů apod.) a umožňuje navázat efektivní propojení s probíraná látka v algebře (rovnice, ekvivalence rovnic, nerovnice, shodné transformace algebraických výrazů atd.).
Jinými slovy, úvahy o metodách řešení goniometrických rovnic a nerovnic zahrnují jakýsi přenos těchto dovedností do nového obsahu.
Význam teorie a její četné aplikace jsou důkazem relevance zvoleného tématu. To vám zase umožňuje určit cíle, cíle a předmět výzkumu práce v kurzu.
Účel studia: zobecnit dostupné typy goniometrických nerovnic, základní a speciální metody jejich řešení, vybrat soubor úloh pro řešení goniometrických nerovnic školákem.
Cíle výzkumu:
1. Na základě analýzy dostupné literatury k tématu výzkumu systematizovat materiál.
2. Zadejte soubor úkolů nezbytných k upevnění tématu "Trigometrické nerovnosti."
Předmět studia jsou goniometrické nerovnosti v kurzu školní matematiky.
Předmět studia: typy goniometrických nerovnic a metody jejich řešení.
Teoretický význam je organizovat materiál.
Praktický význam: aplikace teoretických znalostí při řešení problémů; analýza hlavních často používaných metod řešení goniometrických nerovností.
Metody výzkumu : rozbor odborné literatury, syntéza a zobecnění získaných poznatků, rozbor řešení problémů, hledání optimálních metod řešení nerovnic.
§jeden. Typy goniometrických nerovnic a základní metody jejich řešení
1.1. Nejjednodušší goniometrické nerovnosti
Dva goniometrické výrazy spojené znaménkem nebo > se nazývají goniometrické nerovnice.
Vyřešit trigonometrickou nerovnost znamená najít množinu hodnot neznámých zahrnutých v nerovnosti, pod kterými je nerovnost splněna.
Hlavní část goniometrických nerovností se řeší jejich redukcí na řešení nejjednodušších:
Může to být metoda faktorizace, změna proměnné ( 
, 
atd.), kde se nejprve řeší obvyklá nerovnost a poté nerovnice tvaru 
atd., nebo jinými způsoby.
Nejjednodušší nerovnosti se řeší dvěma způsoby: pomocí jednotkové kružnice nebo graficky.
Nechatf(x
je jednou ze základních goniometrických funkcí. K vyřešení nerovnosti 
jeho řešení stačí najít na jednom období, tzn. na libovolném segmentu, jehož délka je rovna periodě funkceF
X
. Pak bude nalezeno řešení původní nerovnostiX
a také ty hodnoty, které se liší od těch nalezených libovolným celým počtem period funkce. V tomto případě je vhodné použít grafickou metodu.
Uveďme příklad algoritmu pro řešení nerovnic 
(
) a 
.
Algoritmus pro řešení nerovnice (
).
1. Formulujte definici sinusu číslaX na jednotkovém kruhu.
3. Na ose y označte bod se souřadnicíA .
4. Tímto bodem nakreslete přímku rovnoběžnou s osou OX a označte její průsečíky s kružnicí.
5. Vyberte oblouk kružnice, jehož všechny body mají pořadnici menší nežA .
6. Určete směr bypassu (proti směru hodinových ručiček) a zapište odpověď přidáním periody funkce na konce intervalu2πn
,
.
Algoritmus pro řešení nerovnice .
1. Formulujte definici tečny číslaX na jednotkovém kruhu.
2. Nakreslete jednotkovou kružnici.
3. Nakreslete čáru tečen a označte na ní bod s pořadnicíA .
4. Připojte tento bod k počátku a označte průsečík výsledného segmentu s jednotkovou kružnicí.
5. Vyberte oblouk kružnice, jehož všechny body mají pořadnici na tečné čáře menší nežA .
6. Uveďte směr procházení a zapište odpověď s přihlédnutím k rozsahu funkce a přidejte tečkupn
,
(číslo na levé straně záznamu je vždy menší než číslo na pravé straně).
Grafický výklad řešení nejjednodušších rovnic a vzorce pro řešení nerovnic v obecném tvaru jsou uvedeny v příloze (Příloha 1 a 2).
Příklad 1
Vyřešte nerovnost 
.
Nakreslete čáru na jednotkovou kružnici 
, která protíná kružnici v bodech A a B.
Všechny hodnotyy
na intervalu NM více
, všechny body oblouku AMB splňují tuto nerovnost. Ve všech úhlech rotace velký 
, ale menší 
,
bude nabývat hodnot větších než
(ale ne více než jeden).
Obr. 1
Řešením nerovnosti tedy budou všechny hodnoty v intervalu 
, tj. 
. Abychom dostali všechna řešení této nerovnice, stačí přidat na konce tohoto intervalu 
, kde 
, tj. 
,
.
Všimněte si, že hodnoty 
a 
jsou kořeny rovnice 
,
těch. 
;
.
Odpovědět: 
, .
1.2. Grafická metoda
V praxi je často užitečná grafická metoda řešení goniometrických nerovnic. Zvažte podstatu metody na příkladu nerovnosti 
:
1. Pokud je argument složitý (odlišný odX ), pak jej nahradímet .
2. Stavíme v jedné souřadnicové rovinětoOy
funkční grafy 
a 
.
3. Najdeme takovédva sousední průsečíky grafů, mezi nimižsinusoidanacházívýše
rovný . Najděte úsečky těchto bodů.
4. Napište dvojitou nerovnost pro argumentt s ohledem na kosinusové období (t bude mezi nalezenými úsečkami).
5. Proveďte zpětnou substituci (vraťte se k původnímu argumentu) a vyjádřete hodnotuX z dvojité nerovnosti zapíšeme odpověď jako číselný interval.
Příklad 2 Vyřešte nerovnici: .
Při řešení nerovnic grafickou metodou je nutné sestavit grafy funkcí co nejpřesněji. Převedeme nerovnost do tvaru:
Sestavme grafy funkcí v jednom souřadnicovém systému 
a 
(obr. 2).
Obr.2
Grafy funkcí se protínají v boděALE
se souřadnicemi 
; 
. Mezi 
body grafu 
pod body grafu 
. A kdy funkční hodnoty jsou stejné. Proto v 
.
Odpovědět: 
.
1.3. Algebraická metoda
Poměrně často lze původní goniometrickou nerovnost dobře zvolenou substitucí redukovat na algebraickou (racionální či iracionální) nerovnost. Tato metoda zahrnuje transformaci nerovnosti, zavedení substituce nebo nahrazení proměnné.
Podívejme se na aplikaci této metody na konkrétních příkladech.
Příklad 3
Redukce na nejjednodušší formu 
.
(obr. 3)
Obr.3
, 
.
Odpovědět: 
,
Příklad 4 Vyřešte nerovnost:
ODZ: 
, 
.
Použití vzorců: 
, 
nerovnost zapíšeme ve tvaru: 
.
Nebo za předpokladu 
po jednoduchých transformacích dostaneme
,
,
.
Řešením poslední nerovnosti intervalovou metodou získáme:
Obr.4
, resp 
. Potom z Obr. 4 následuje 
, kde 
.
Obr.5
Odpovědět: 
, 
.
1.4. Metoda rozmístění
Obecné schéma řešení goniometrických nerovnic intervalovou metodou:
Použití goniometrických vzorců, faktorizace.
Najděte body přerušení a nuly funkce, vložte je na kružnici.
Vezměte si jakýkoli bodNa (ale nenalezen dříve) a zjistěte označení produktu. Pokud je součin kladný, umístěte bod mimo jednotkovou kružnici na paprsek odpovídajícím úhlu. V opačném případě umístěte bod do kruhu.
Pokud se bod vyskytuje sudý početkrát, nazýváme jej bodem sudé násobnosti, pokud je lichý, nazýváme jej bodem liché násobnosti. Nakreslete oblouky následovně: začněte od boduNa , pokud je další bod liché násobnosti, pak oblouk protíná kružnici v tomto bodě, ale pokud je bod sudé násobnosti, pak se neprotíná.
Oblouky za kružnicí jsou kladné mezery; uvnitř kruhu jsou záporné mezery.
Příklad 5 Vyřešte nerovnost
, 
.
Body první série: 
.
Body druhé série: 
.
Každý bod se vyskytuje lichý početkrát, tedy všechny body s lichou násobností.
Znak produktu zjistěte na 
: . Označíme všechny body na jednotkové kružnici (obr. 6):
Rýže. 6
Odpovědět: 
, 
; 
, 
; 
, 
.
Příklad 6 . Vyřešte nerovnost.
Řešení:
Najdeme nuly výrazu .
Dostataem :
,
;
, 
;
, 
;
, 
;
Na jednotkovém kruhu, řady hodnotX
1
znázorněné tečkami 
. SérieX
2
dává body 
. SérieX
3
získáváme dva body 
. Konečně sérieX
4
bude představovat body 
. Všechny tyto body umístíme na jednotkovou kružnici a u každé její násobnosti uvedeme v závorkách.
Nyní nechejte číslo 
budou rovné. Odhad provádíme podle znaménka:
Takže pointaA
by měla být zvolena na nosníku tvořícím úhel 
s paprskemAch,
mimo jednotkový kruh. (Všimněte si, že pomocný paprsekÓ
A
na obrázku to být nemusí. TečkaA
vybráno přibližně.)
Nyní od věciA
ke všem označeným bodům nakreslíme souvislou vlnovku. A v bodech naše čára přechází z jedné oblasti do druhé: pokud byla mimo jednotkový kruh, přechází do něj. Blíží se k bodu 
, úsečka se vrátí do vnitřní oblasti, protože násobnost tohoto bodu je sudá. Podobně v bodě 
(se sudou násobností) čára musí být otočena do vnější oblasti. Nakreslili jsme tedy určitý obrázek znázorněný na obr. 7. Pomáhá zvýraznit požadované oblasti na jednotkovém kruhu. Jsou označeny „+“.
Obr.7
Konečná odpověď:
Poznámka. Pokud vlnovku po projetí všech bodů vyznačených na jednotkové kružnici nelze vrátit do boduA , bez překročení kruhu na „nelegálním“ místě to znamená, že v řešení došlo k chybě, konkrétně byl vynechán lichý počet kořenů.
Odpovědět: .
§2. Soubor úloh pro řešení goniometrických nerovnic
V procesu rozvoje schopnosti školáků řešit trigonometrické nerovnice lze rozlišit i 3 etapy.
1. přípravný,
2. formování dovedností řešit nejjednodušší goniometrické nerovnosti;
3. zavedení goniometrických nerovností jiných typů.
Účelem přípravné fáze je, že je nutné u školáků formovat schopnost používat trigonometrický kruh nebo graf k řešení nerovností, a to:
Schopnost řešit jednoduché nerovnice tvaru ,
, ,
,
využití vlastností funkcí sinus a kosinus;
Schopnost vytvářet dvojité nerovnosti pro oblouky číselné kružnice nebo pro oblouky grafů funkcí;
Schopnost provádět různé transformace goniometrických výrazů.
Tuto etapu se doporučuje implementovat do procesu systematizace znalostí školáků o vlastnostech goniometrických funkcí. Hlavním prostředkem mohou být úkoly nabízené žákům a vykonávané buď pod vedením učitele nebo samostatně, dále dovednosti získané při řešení goniometrických rovnic.
Zde jsou příklady takových úkolů:
1
. Označte bod na jednotkové kružnici 
, pokud
.
2.
V jaké čtvrtině souřadnicové roviny je bod , pokud 
rovná se: 
3.
Označte body na trigonometrickém kruhu , pokud:
4. Přeneste výraz na goniometrické funkcejáčtvrtletí.
A) 
,
b) 
,
v) 
5. Vzhledem k oblouku MR.M - středníjáčtvrtletí,R - středníIIčtvrtletí. Omezte hodnotu proměnnét pro: (složte dvojitou nerovnost) a) oblouk MP; b) RM oblouky.
6. Napište dvojitou nerovnost pro vybrané části grafu:
Rýže. jeden
7.
Řešit nerovnosti 
, 
, 
, 
.
8. Převést výraz .
Na druhém stupni učení se řešit goniometrické nerovnice můžeme nabídnout následující doporučení související s metodikou organizace aktivit žáků. Zároveň je třeba se zaměřit na dovednosti žáků pracovat s goniometrickým kruhem nebo grafem, které vznikají při řešení nejjednodušších goniometrických rovnic.
Za prvé je možné motivovat účelnost získání obecné metody pro řešení nejjednodušších goniometrických nerovností odkazem například na nerovnost tvaru 
.
S využitím znalostí a dovedností získaných v přípravné fázi studenti dostanou navrženou nerovnost do formy 
, ale může být obtížné najít sadu řešení výsledné nerovnosti, protože nelze to řešit pouze pomocí vlastností funkce sinus. Této obtíži se lze vyhnout odkazem na příslušnou ilustraci (řešení rovnice graficky nebo pomocí jednotkového kruhu).
Za druhé by měl učitel žáky upozornit na různé způsoby plnění úkolu, uvést vhodný příklad řešení nerovnice jak graficky, tak pomocí trigonometrické kružnice.
Zvažte takové možnosti řešení nerovnosti .
1. Řešení nerovnice pomocí jednotkové kružnice.
V první lekci o řešení goniometrických nerovnic studentům nabídneme podrobný algoritmus řešení, který v postupné prezentaci odráží všechny základní dovednosti potřebné k řešení nerovnice.
Krok 1.Nakreslete jednotkovou kružnici, označte bod na ose y 
a nakreslete jím přímku rovnoběžnou s osou x. Tato čára bude protínat jednotkovou kružnici ve dvou bodech. Každý z těchto bodů znázorňuje čísla, jejichž sinus je roven .
Krok 2Tato přímka rozdělila kruh na dva oblouky. Vyberme to, na kterém jsou zobrazena čísla, která mají sinus větší než . Tento oblouk je přirozeně umístěn nad nakreslenou přímkou.
Rýže. 2
Krok 3Vyberme si jeden z konců označeného oblouku. Zapišme si jedno z čísel, které tento bod jednotkové kružnice představuje 
.
Krok 4Abychom zvolili číslo odpovídající druhému konci vybraného oblouku, "přejdeme" po tomto oblouku z pojmenovaného konce na druhý. Zároveň si připomínáme, že při pohybu proti směru hodinových ručiček se čísla, která budeme míjet, zvětšují (při opačném směru by se čísla snižovala). Zapišme si číslo, které je znázorněno na jednotkovém kruhu druhým koncem označeného oblouku 
.
Vidíme tedy, že nerovnost splnit čísla, pro která je nerovnost 
. Vyřešili jsme nerovnici pro čísla na stejné periodě funkce sinus. Proto lze všechna řešení nerovnice zapsat jako 
Studenti by měli být požádáni, aby pečlivě zvážili číslo a zjistili, proč všechna řešení nerovnosti lze zapsat ve tvaru 
, 
.
Rýže. 3
Je nutné žáky upozornit, že při řešení nerovnic pro funkci kosinus vedeme přímku rovnoběžnou s osou y.
Grafický způsob řešení nerovnosti.
Stavební grafy 
a 
vzhledem k tomu 
.
Rýže. čtyři
Potom napíšeme rovnici 
a jeho řešení 
, 
, 
, nalezené pomocí vzorců 
, 
, 
.
(Dávánín
hodnoty 0, 1, 2, najdeme tři kořeny složené rovnice). Hodnoty 
jsou tři po sobě jdoucí úsečky průsečíků grafů a . Pochopitelně vždy v intervalu 
nerovnost 
a na intervalu 
- nerovnost 
. Zajímá nás první případ a přičtením na konce tohoto intervalu čísla, které je násobkem periody sinus, získáme řešení nerovnosti tak jako: 
, .
Rýže. 5
Shrnout. K vyřešení nerovnosti , musíte napsat odpovídající rovnici a vyřešit ji. Z výsledného vzorce najděte kořeny 
a 
a zapište odpověď na nerovnici ve tvaru: , .
Za třetí, při grafickém řešení se velmi jasně potvrzuje fakt o množině kořenů příslušné goniometrické nerovnosti.
Rýže. 6
Je třeba studentům ukázat, že cívka, která je řešením nerovnice, se opakuje ve stejném intervalu, který je roven periodě goniometrické funkce. Podobnou ilustraci můžete zvážit také pro graf funkce sinus.
Za čtvrté je vhodné provést práci na aktualizaci studentských metod převodu součtu (rozdílu) goniometrických funkcí na součin, upozornit školáky na roli těchto technik při řešení goniometrických nerovnic.
Taková práce může být organizována samostatným plněním úkolů navržených učitelem ze strany studentů, mezi nimiž vyzdvihujeme následující:
Za páté, studenti musí mít povinnost znázornit řešení každé jednoduché goniometrické nerovnosti pomocí grafu nebo trigonometrické kružnice. Nezapomeňte věnovat pozornost jeho účelnosti, zejména použití kruhu, protože při řešení goniometrických nerovností slouží odpovídající ilustrace jako velmi pohodlný prostředek k upevnění množiny řešení k dané nerovnosti
Seznámení studentů s metodami řešení goniometrických nerovnic, které nejsou nejjednodušší, je vhodné provést podle následujícího schématu: odkazování na konkrétní goniometrickou nerovnici odkazování na odpovídající goniometrickou rovnici společné hledání (učitel - studenti) řešení nezávislé přenesení nalezené techniky na další nerovnosti stejného typu.
Pro systematizaci znalostí studentů z trigonometrie doporučujeme specificky vybírat takové nerovnice, jejichž řešení vyžaduje různé transformace, které lze v procesu řešení realizovat, se zaměřením pozornosti studentů na jejich vlastnosti.
Jako takové produktivní nerovnosti můžeme navrhnout například následující:
Na závěr uvádíme příklad sady úloh pro řešení goniometrických nerovnic.
1. Vyřešte nerovnosti:
2. Vyřešte nerovnosti: 3. Najděte všechna řešení nerovnic: 4. Najděte všechna řešení nerovnic:A) 
, splňující podmínku 
;
b) 
, splňující podmínku 
.
5. Najděte všechna řešení nerovnic:
A) ;
b) ;
v) 
;
G) 
;
E) 
.
6. Vyřešte nerovnice:
A) ;
b) ;
v) ;
G) 
;
e) ;
e) ;
a) 
.
7. Vyřešte nerovnice:
A) 
;
b) ;
v) ;
G).
8. Vyřešte nerovnice:
A) ;
b) ;
v) ;
G) 
;
E) 
;
e) ;
a) 
;
h) .
Úkoly 6 a 7 je vhodné nabídnout žákům studujícím matematiku na pokročilé úrovni, úkol 8 - žákům ve třídách s prohloubeným studiem matematiky.
§3. Speciální metody řešení goniometrických nerovnic
Speciální metody řešení goniometrických rovnic - tedy takové metody, které lze použít pouze k řešení goniometrických rovnic. Tyto metody jsou založeny na využití vlastností goniometrických funkcí a také na využití různých goniometrických vzorců a identit.
3.1. Sektorová metoda
Zvažte sektorovou metodu pro řešení goniometrických nerovností. Řešení nerovnic tvaru 
, kdeP
(
X
)
aQ
(
X
)
- racionální goniometrické funkce (sinus, kosinus, tangens a kotangens do nich vstupují racionálně), podobně jako při řešení racionálních nerovnic. Racionální nerovnice je vhodné řešit metodou intervalů na reálné ose. Její obdobou při řešení racionálních goniometrických nerovnic je metoda výsečí v goniometrickém kruhu, např.sinx
acosx
(
) nebo trigonometrický půlkruh protgx
actgx
(
).
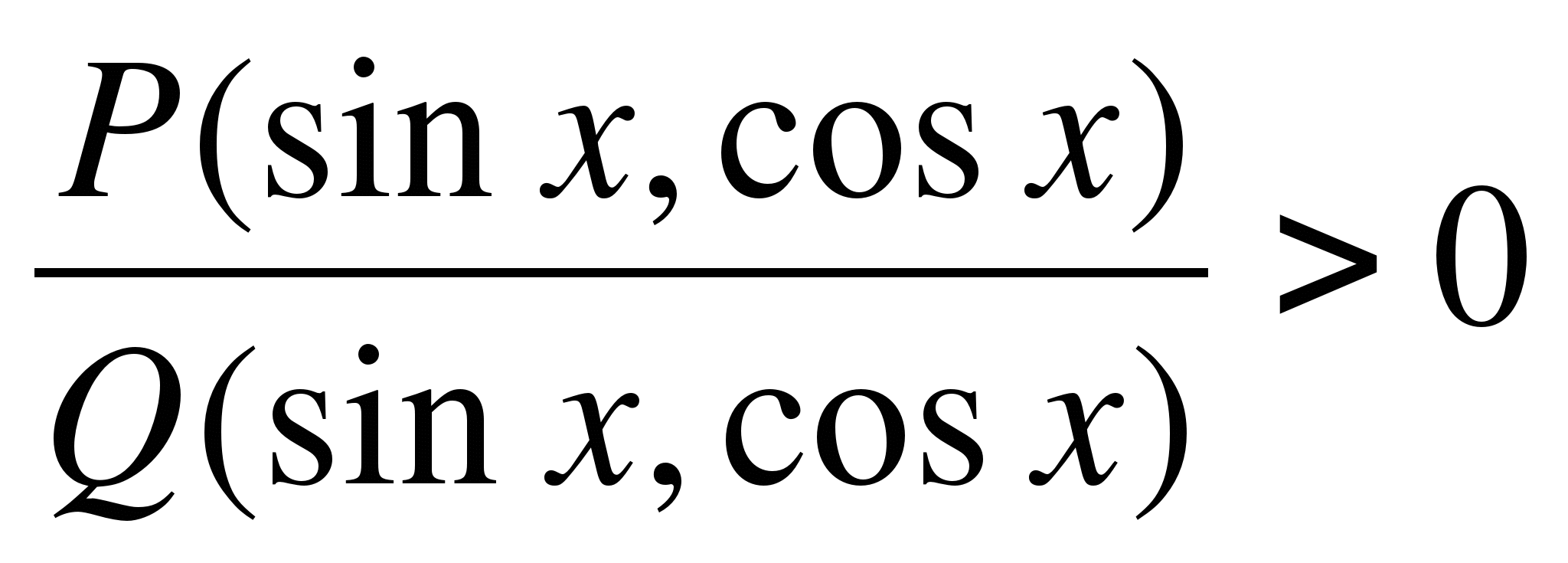
V intervalové metodě každý lineární faktor čitatele a jmenovatele tvaru 
bod na číselné ose 
a při průjezdu tímto bodem změny znamení. V sektorové metodě každý násobitel formuláře 
, kde 
- jedna z funkcísinx
nebocosx
a 
, v trigonometrickém kruhu odpovídají dva úhly 
a 
, které rozdělují kruh na dva sektory. Při průjezdu a funkce změny znamení.
Je třeba mít na paměti následující:
a) Násobitele formuláře 
a 
, kde 
, ponechte znaménko pro všechny hodnoty 
. Takové násobiče čitatele a jmenovatele jsou vyřazeny a mění se (pokud 
) pro každé takové odmítnutí je znaménko nerovnosti obráceno.
b) Násobitele formuláře 
a 
jsou také vyřazeny. Navíc, pokud se jedná o faktory jmenovatele, pak se k ekvivalentnímu systému nerovností přidají nerovnosti tvaru 
a 
. Pokud se jedná o faktory čitatele, pak v ekvivalentním systému omezení odpovídají nerovnostem a v případě přísné počáteční nerovnosti a rovnosti 
a 
v případě nestriktní počáteční nerovnosti. Při shození násobilky 
nebo 
znaménko nerovnosti je obrácené.
Příklad 1
Vyřešte nerovnosti: a) 
, b) 
.
máme funkci, b). Vyřešte nerovnost, kterou máme
3.2. Metoda soustředného kruhu
Tato metoda je obdobou metody paralelních číselných os při řešení soustav racionálních nerovnic.
Zvažte příklad systému nerovností.
Příklad 5
Vyřešte soustavu jednoduchých goniometrických nerovnic 
Nejprve řešíme každou nerovnici zvlášť (obrázek 5). V pravém horním rohu obrázku naznačíme, pro který argument je trigonometrický kruh uvažován.
Obr.5
Dále vytvoříme systém soustředných kruhů pro argumentX . Nakreslíme kružnici a vystínujeme ji podle řešení první nerovnosti, poté nakreslíme kružnici o větším poloměru a vystínujeme ji podle řešení druhé, pak postavíme kružnici pro třetí nerovnost a základní kružnici . Paprsky vedeme ze středu soustavy přes konce oblouků tak, aby protínaly všechny kružnice. Na základní kružnici vytvoříme řešení (obrázek 6).
Obr.6
Odpovědět:
, 
.
Závěr
Všechny cíle kurzu byly splněny. Teoretický materiál je systematizován: jsou uvedeny hlavní typy goniometrických nerovnic a hlavní metody jejich řešení (grafické, algebraické, metoda intervalů, sektorů a metoda soustředných kružnic). U každé metody byl uveden příklad řešení nerovnice. Po teoretické části následovala část praktická. Obsahuje sadu úloh pro řešení goniometrických nerovnic.
Tuto práci mohou studenti využít k samostatné práci. Studenti si mohou ověřit úroveň asimilace tohoto tématu, procvičit si plnění úkolů různé složitosti.
Po prostudování relevantní literatury k této problematice můžeme samozřejmě dojít k závěru, že schopnost a dovednosti řešit goniometrické nerovnice ve školním kurzu algebry a na začátku analýzy jsou velmi důležité, jejichž rozvoj vyžaduje značné úsilí ze strany učitel matematiky.
Proto bude tato práce užitečná pro učitele matematiky, protože umožňuje efektivně organizovat školení studentů na téma "Trigonometrické nerovnosti".
Ve studiu lze pokračovat jeho rozšířením na závěrečnou kvalifikační práci.
Seznam použité literatury
Bogomolov, N.V. Sbírka úloh z matematiky [Text] / N.V. Bogomolov. – M.: Drop, 2009. – 206 s.
Vygodsky, M.Ya. Příručka elementární matematiky [Text] / M.Ya. Vygodsky. – M.: Drop, 2006. – 509 s.
Zhurbenko, L.N. Matematika v příkladech a úlohách [Text] / L.N. Zhurbenko. – M.: Infra-M, 2009. – 373 s.
Ivanov, O.A. Elementární matematika pro školáky, studenty a učitele [Text] / O.A. Ivanov. – M.: MTsNMO, 2009. – 384 s.
Karp, A.P. Úkoly z algebry a začátky rozboru pro organizaci závěrečného opakování a certifikace v 11. ročníku [Text] / A.P. Kapr. – M.: Osvěta, 2005. – 79 s.
Kulanin, E.D. 3000 soutěžních problémů v matematice [Text] / E.D. Kulanin. – M.: Iris-press, 2007. – 624 s.
Leibson, K.L. Sbírka praktických úloh z matematiky [Text] / K.L. Leibson. – M.: Drop, 2010. – 182 s.
Loket, V.V. Problémy s parametry a jejich řešení. Trigonometrie: rovnice, nerovnice, soustavy. Stupeň 10 [Text] / V.V. Loket. – M.: ARKTI, 2008. – 64 s.
Manova, A.N. Matematika. Expresní lektor pro přípravu na zkoušku: účet. příspěvek [Text] / A.N. Manova. - Rostov na Donu: Phoenix, 2012. - 541 s.
Mordkovich, A.G. Algebra a začátek matematické analýzy. 10-11 tříd. Učebnice pro studenty vzdělávacích institucí [Text] / A.G. Mordkovič. – M.: Iris-press, 2009. – 201 s.
Novikov, A.I. Goniometrické funkce, rovnice a nerovnice [Text] / A.I. Novikov. - M.: FIZMATLIT, 2010. - 260 s.
Oganesyan, V.A. Metody výuky matematiky na střední škole: Obecná metodika. Proč. příspěvek pro studenty fyziky. - mat. fak. ped. soudruh. [Text] / V.A. Oganesyan. – M.: Osvěta, 2006. – 368 s.
Olechnik, S.N. Rovnice a nerovnice. Nestandardní metody řešení [Text] / S.N. Olekhnik. - M .: Nakladatelství Factorial, 1997. - 219 s.
Sevrjukov, P.F. Goniometrické, exponenciální a logaritmické rovnice a nerovnice [Text] / P.F. Sevrjukov. – M.: Národní školství, 2008. – 352 s.
Sergejev, I.N. POUŽITÍ: 1000 úloh s odpověďmi a řešeními v matematice. Všechny úkoly skupiny C [Text] / I.N. Sergejev. – M.: Zkouška, 2012. – 301 s.
Sobolev, A.B. Elementární matematika [Text] / A.B. Sobolev. - Jekatěrinburg: GOU VPO USTU-UPI, 2005. - 81 s.
Fenko, L.M. Metoda intervalů při řešení nerovnic a studiu funkcí [Text] / L.M. Fenko. – M.: Drop, 2005. – 124 s.
Friedman, L.M. Teoretické základy metodiky výuky matematiky [Text] / L.M. Friedman. - M .: Knižní dům "LIBROKOM", 2009. - 248 s.
Příloha 1
Grafická interpretace řešení nejjednodušších nerovnic
Rýže. jeden
Rýže. 2
Obr.3
Obr.4
Obr.5
Obr.6
Obr.7
Obr.8
Příloha 2
Řešení nejjednodušších nerovností
