Тригонометрични неравенства. Тригонометрични неравенства и техните решения Как се решават двойни тригонометрични неравенства
Министерство на образованието на Република Беларус
образователна институция
„Гомелски държавен университет
на името на Франциск Скарина"
Факултет по математика
Катедра по алгебра и геометрия
Подходящ за защита
Глава Отдел Шеметков Л.А.
Тригонометрични уравнения и неравенства
Курсова работа
Изпълнител:
студентска група М-51
СМ. Горски
Научен съветник
Старши преподавател
В.Г. Сафонов
Гомел 2008 г
ВЪВЕДЕНИЕ
ОСНОВНИ МЕТОДИ ЗА РЕШАВАНЕ НА ТРИГОНОМЕТРИЧНИ УРАВНЕНИЯ
Факторизация
Решаване на уравнения чрез преобразуване на произведението на тригонометрични функции в сума
Решаване на уравнения с помощта на формули с троен аргумент
Умножение с някаква тригонометрична функция
НЕСТАНДАРТНИ ТРИГОНОМЕТРИЧНИ УРАВНЕНИЯ
ТРИГОНОМЕТРИЧНИ НЕРАВЕНСТВА
ИЗБОР НА КОРЕНИ
ЗАДАЧИ ЗА САМОСТОЯТЕЛНО РЕШАВАНЕ
ЗАКЛЮЧЕНИЕ
СПИСЪК НА ИЗПОЛЗВАНИТЕ ИЗТОЧНИЦИ
В древни времена тригонометрията е възникнала във връзка с нуждите на астрономията, геодезията и строителството, тоест тя е била чисто геометрична по своята същност и е представлявала главно<<исчисление хорд>>. С течение на времето в него започнаха да се вмъкват някои аналитични точки. През първата половина на 18 век настъпва рязък обрат, след който тригонометрията поема в нова посока и се насочва към математическия анализ. По това време тригонометричните зависимости започват да се разглеждат като функции.
Тригонометричните уравнения са една от най-трудните теми в училищния курс по математика. Тригонометричните уравнения възникват при решаването на задачи в планиметрията, геометрията на твърдо тяло, астрономията, физиката и други области. Тригонометрични уравнения и неравенства от година на година се срещат сред задачите на централизираното изпитване.
Най-важната разлика между тригонометричните и алгебричните уравнения е, че алгебричните уравнения имат краен брой корени, докато тригонометричните уравнения имат безкраен брой, което значително усложнява избора на корени. Друга специфика на тригонометричните уравнения е неуникалната форма на записване на отговора.
Дипломната работа е посветена на методите за решаване на тригонометрични уравнения и неравенства.
Дипломната работа се състои от 6 раздела.
Първият раздел съдържа основната теоретична информация: определението и свойствата на тригонометричните и обратните тригонометрични функции; таблица със стойности на тригонометрични функции за някои аргументи; изразяване на тригонометрични функции по отношение на други тригонометрични функции, което е много важно за преобразуване на тригонометрични изрази, особено тези, съдържащи обратни тригонометрични функции; в допълнение към основните тригонометрични формули, добре познати от училищния курс, са дадени формули, които опростяват изрази, съдържащи обратни тригонометрични функции.
Вторият раздел очертава основните методи за решаване на тригонометрични уравнения. Разглеждат се решаването на елементарни тригонометрични уравнения, методът на факторизиране, методите за редуциране на тригонометрични уравнения до алгебрични. С оглед на факта, че решенията на тригонометричните уравнения могат да бъдат записани по няколко начина и формата на тези решения не позволява веднага да се установи дали тези решения са еднакви или различни, което може<<сбить с толку>> при решаване на тестове се разглежда обща схема за решаване на тригонометрични уравнения и се разглежда подробно преобразуването на групи от общи решения на тригонометрични уравнения.
Третият раздел разглежда нестандартни тригонометрични уравнения, чиито решения се основават на функционалния подход.
Четвъртият раздел се занимава с тригонометрични неравенства. Подробно са разгледани методите за решаване на елементарни тригонометрични неравенства, както върху единична окръжност, така и чрез графичен метод. Описан е процесът на решаване на неелементарни тригонометрични неравенства чрез елементарни неравенства и методът на интервалите, вече добре познат на учениците.
Петият раздел представя най-трудните задачи: когато е необходимо не само да се реши тригонометрично уравнение, но и да се изберат корени от намерените корени, които отговарят на дадено условие. Този раздел предоставя решения на типични задачи за избор на корени. Дадена е необходимата теоретична информация за избора на корени: разделяне на множеството от цели числа на непресичащи се подмножества, решение на уравнения в цели числа (диофантово).
В шести раздел са представени задачи за самостоятелно решаване, оформени под формата на тест. В 20-те тестови задачи са изброени най-трудните задачи, които могат да се срещнат при централизирано изпитване.
Елементарни тригонометрични уравнения
Елементарните тригонометрични уравнения са уравнения от вида , където е една от тригонометричните функции: , , , .
Елементарните тригонометрични уравнения имат безкрайно много корени. Например, следните стойности отговарят на уравнението: , , и т.н. Общата формула, по която се намират всички корени на уравнението, където , е:
Тук може да приема всякакви цели числа, като всяка от тях отговаря на определен корен на уравнението; в тази формула (както и в други формули, с които се решават елементарни тригонометрични уравнения) се нарича параметър. Те обикновено записват, като по този начин подчертават, че параметърът може да приема всякакви цели числа.
Решенията на уравнението , където , се намират по формулата
Уравнението се решава чрез прилагане на формулата
и уравнението --- по формулата
Нека специално да отбележим някои специални случаи на елементарни тригонометрични уравнения, когато решението може да бъде написано без използване на общи формули:
При решаването на тригонометрични уравнения периодът на тригонометричните функции играе важна роля. Затова представяме две полезни теореми:
Теорема Ако --- основният период на функцията, тогава числото е основният период на функцията.
Периодите на функциите и се наричат съизмерими, ако има естествени числа и , че .
Теорема Ако периодичните функции и , имат съизмерими и , тогава те имат общ период, който е периодът на функциите , , .
Теоремата казва какъв е периодът на функцията , , , и не е непременно основният период. Например главният период на функциите и е --- , а главният период на техния продукт е --- .
Въвеждане на спомагателен аргумент
Стандартният начин за преобразуване на изрази на формата 
е следният трик: нека --- ъгълът, даден от равенствата 
, 
. За всеки и такъв ъгъл съществува. По този начин . Ако , или , , иначе .
Схема за решаване на тригонометрични уравнения
Основната схема, от която ще се ръководим при решаването на тригонометрични уравнения, е следната:
решението на даденото уравнение се свежда до решаване на елементарни уравнения. Решения --- трансформации, факторизации, заместване на неизвестни. Водещият принцип е да не се губят корените. Това означава, че когато преминаваме към следващото уравнение (уравнения), ние не се страхуваме от появата на допълнителни (странни) корени, а се интересуваме само от това, че всяко следващо уравнение от нашата "верига" (или набор от уравнения в случай на разклоняване) е следствие от предходното. Един възможен метод за избор на корени е проверката. Веднага отбелязваме, че в случай на тригонометрични уравнения трудностите, свързани с избора на корени, с проверката, като правило, рязко се увеличават в сравнение с алгебричните уравнения. В крайна сметка трябва да проверите серията, състояща се от безкраен брой членове.
Специално трябва да се спомене промяната на неизвестните при решаване на тригонометрични уравнения. В повечето случаи след необходимата замяна се получава алгебрично уравнение. Освен това не са толкова редки уравненията, които, въпреки че изглеждат тригонометрични, по същество не са такива, тъй като още след първата стъпка --- промените на променливите --- се превръщат в алгебрични, а връщането към тригонометрията става само на етапа за решаване на елементарни тригонометрични уравнения.
Нека ви напомним още веднъж: замяната на неизвестното трябва да се извърши възможно най-скоро, уравнението, получено след замяната, трябва да бъде решено до края, включително етапа на избор на корените, и едва тогава ще се върне към оригинала неизвестен.
Една от характеристиките на тригонометричните уравнения е, че отговорът в много случаи може да бъде написан по различни начини. Дори за решаване на уравнението 
отговорът може да бъде написан така:
1) под формата на две серии: 
, , ;
2) в стандартна форма, която е обединение на горните серии: , ;
3) защото 
, тогава отговорът може да бъде записан като 
, . (По-нататък наличието на параметъра , , или в записа на отговора автоматично означава, че този параметър приема всички възможни цели числа. Ще бъдат посочени изключения.)
Очевидно трите изброени случая не изчерпват всички възможности за написване на отговора на разглежданото уравнение (те са безкрайно много).
Например за 
. Следователно, в първите два случая, ако , можем да заменим с .
Обикновено отговорът е написан въз основа на параграф 2. Полезно е да запомните следната препоръка: ако работата не завърши с решението на уравнението, все още е необходимо да се проведе изследване, изборът на корени, след това най-удобната форма на запис е посочена в параграф 1. (Трябва да се даде подобна препоръка за уравнението.)
Нека разгледаме пример, илюстриращ казаното.
Пример Решете уравнението.
Решение.Най-очевидният е следният начин. Това уравнение се разделя на две: и . Решавайки всеки от тях и комбинирайки получените отговори, намираме .
Друг начин.Тъй като , тогава, замествайки и от формулите за намаляване. След малки трансформации получаваме , откъде 
.
На пръв поглед втората формула няма особени предимства пред първата. Ако обаче вземем например , тогава се оказва, че , т.е. уравнението има решение, докато първият начин ни води до отговора 
. „Виж“ и докажи равенството 
не е толкова лесно.
Отговор. .
Преобразуване и обединяване на групи от общи решения на тригонометрични уравнения
Ще разгледаме аритметична прогресия, която се простира неограничено в двете посоки. Членовете на тази прогресия могат да бъдат разделени на две групи термини, разположени отдясно и отляво на определен термин, наречен централен или нулев член на прогресията.
Фиксирайки един от членовете на безкрайната прогресия с нулево число, ще трябва да извършим двойно номериране за всички останали членове: положително за членовете, разположени вдясно, и отрицателно за членовете, разположени вляво от нулата.
В общия случай, ако разликата на прогресията е нулев член, формулата за всеки (ти) член на безкрайната аритметична прогресия е:
Трансформации на формула за всеки член на безкрайна аритметична прогресия
1. Ако добавим или извадим разликата на прогресията до нулевия член, тогава прогресията няма да се промени от това, но само нулевият член ще се премести, т.е. номерацията на членовете ще се промени.
2. Ако коефициентът на променлива се умножи по , тогава това ще доведе само до пермутация на дясната и лявата група членове.
3. Ако последователни членове на безкрайна прогресия
например , , , ..., , за да направим централните членове на прогресии със същата разлика равна на:
тогава прогресията и серията от прогресии изразяват едни и същи числа.
Пример Редът може да бъде заменен от следните три реда: , , .
4. Ако безкрайни прогресии с еднаква разлика имат числа като централни членове, които образуват аритметична прогресия с разлика, тогава тези серии могат да бъдат заменени с една прогресия с разлика и с централен член, равен на който и да е от централните членове на тези прогресии, т.е. ако
тогава тези прогресии се комбинират в едно:
Пример
, , , и двете са обединени в една група, тъй като 
.
За да трансформираме групи, които имат общи решения, в групи, които нямат общи решения, тези групи се разлагат на групи с общ период и след това се опитваме да комбинираме получените групи, като изключим повтарящите се.
Факторизация
Методът на факторизиране е следният: ако
тогава всяко решение на уравнението
е решението на набора от уравнения
Обратното твърдение е, най-общо казано, невярно: не всяко решение на множеството е решение на уравнението. Това се дължи на факта, че решенията на отделните уравнения може да не бъдат включени в областта на дефиниране на функцията.
Пример Решете уравнението.
Решение.Използвайки основното тригонометрично тъждество, представяме уравнението във формата
Отговор.
; 
.
Преобразуване на сумата от тригонометрични функции в произведение
Пример
реши уравнението 
.
Решение.Прилагаме формулата, получаваме еквивалентно уравнение
Отговор. .
Пример Решете уравнението.
Решение.В този случай, преди да приложите формулите за сумата на тригонометричните функции, трябва да използвате формулата за редукция 
. В резултат на това получаваме еквивалентно уравнение
Отговор.
, 
.
Решаване на уравнения чрез преобразуване на произведението на тригонометрични функции в сума
При решаването на редица уравнения се използват формули.
Пример реши уравнението
Решение.
Отговор. , .
Пример Решете уравнението.
Решение.Прилагайки формулата, получаваме еквивалентно уравнение:
Отговор. .
Решаване на уравнения с помощта на формули за редукция
При решаването на широк кръг от тригонометрични уравнения формулите играят ключова роля.
Пример Решете уравнението.
Решение.Прилагайки формулата, получаваме еквивалентно уравнение.
Отговор. ; .
Решаване на уравнения с помощта на формули с троен аргумент
Пример Решете уравнението.
Решение.Прилагаме формулата, получаваме уравнението
Отговор. ; .
Пример
реши уравнението 
.
Решение.Прилагайки формулите за понижаване на степента, получаваме: 
. При кандидатстване получаваме:
Отговор. ; .
Равенство на едноименни тригонометрични функции
Пример Решете уравнението.
Решение.
Отговор. , .
Пример
реши уравнението 
.
Решение.Нека трансформираме уравнението.
Отговор. .
Пример Известно е, че и отговарят на уравнението
Намерете сумата.
Решение.От уравнението следва, че
Отговор. .
Помислете за суми на формата
Тези суми могат да бъдат преобразувани в продукт, като се умножат и разделят на , след което получаваме
Тази техника може да се използва за решаване на някои тригонометрични уравнения, но трябва да се има предвид, че в резултат на това могат да се появят външни корени. Ето обобщение на тези формули:
Пример Решете уравнението.
Решение.Вижда се, че наборът е решение на първоначалното уравнение. Следователно умножаването на лявата и дясната страна на уравнението по не води до появата на допълнителни корени.
Ние имаме 
.
Отговор. ; .
Пример Решете уравнението.
Решение.Умножаваме лявата и дясната страна на уравнението по и прилагайки формулите за преобразуване на произведението на тригонометричните функции в сума, получаваме
Това уравнение е еквивалентно на набор от две уравнения и , откъдето и .
Тъй като корените на уравнението не са корените на уравнението, тогава от получените набори от решения трябва да бъдат изключени. Така че в комплекта трябва да изключите .
Отговор.и , .
Пример
реши уравнението 
.
Решение.Нека трансформираме израза:
Уравнението ще бъде написано във формата:
Отговор. .
Свеждане на тригонометрични уравнения до алгебрични
Намаляване до квадрат
Ако уравнението изглежда така
тогава замяната го довежда до квадрат, т.к 
() и.
Ако вместо термина има , тогава необходимата замяна ще бъде .
Уравнението
се свежда до квадратното уравнение
представяне като 
. Лесно е да се провери това, за което , не са корени на уравнението и като се направи промяната, уравнението се свежда до квадратно.
Пример Решете уравнението.
Решение.Нека го преместим в лявата страна, да го заменим с и да изразим чрез и.
След опростяване получаваме: . Разделете термин по термин на , направете замяната:
Връщайки се към , намираме 
.
Уравнения, хомогенни по отношение на ,
Разгледайте уравнение на формата
където , , , ..., , са реални числа. Във всеки член от лявата страна на уравнението степените на мономите са равни, т.е. сумата от степените на синуса и косинуса е еднаква и равна на. Такова уравнение се нарича хомогененспрямо и , и номерът се нарича индикатор за хомогенност .
Ясно е, че ако , тогава уравнението ще приеме формата:
чиито решения са стойностите, за които , т.е. числата , . Второто уравнение, записано в скоби, също е хомогенно, но степените са с 1 по-ниски.
Ако , тогава тези числа не са корените на уравнението.
Когато получим: , и лявата страна на уравнение (1) приема стойността .
И така, за и следователно двете страни на уравнението могат да бъдат разделени на . В резултат на това получаваме уравнението:
което чрез заместване лесно се свежда до алгебричното:
Хомогенни уравнения с индекс на хомогенност 1. При , имаме уравнението .
Ако , то това уравнение е еквивалентно на уравнението , , откъдето , .
Пример Решете уравнението.
Решение.Това уравнение е хомогенно от първа степен. Разделяйки двете му части на получаваме: , , , .
Отговор. .
Пример При , получаваме хомогенно уравнение от формата
Решение.
Ако , тогава разделяме двете страни на уравнението на , получаваме уравнението 
, което може лесно да бъде намалено до квадрат чрез заместване: 
. Ако 
, тогава уравнението има реални корени , . Оригиналното уравнение ще има две групи решения: , , .
Ако 
, тогава уравнението няма решения.
Пример Решете уравнението.
Решение.Това уравнение е хомогенно от втора степен. Разделяме двете страни на уравнението на , получаваме: . Нека тогава , , . , , ; , , .
Отговор.
.
Уравнението се свежда до уравнение от вида
За да направите това, достатъчно е да използвате самоличността 
По-специално, уравнението се свежда до хомогенно, ако се замени с 
, тогава получаваме еквивалентното уравнение:
Пример Решете уравнението.
Решение.Нека преобразуваме уравнението в хомогенно:
Разделете двете страни на уравнението на 
, получаваме уравнението:
Нека , тогава стигаме до квадратното уравнение: 
, , 
, 
, .
Отговор.
.
Пример Решете уравнението.
Решение.Нека повдигнем на квадрат двете страни на уравнението, като се има предвид, че те имат положителни стойности: , ,
Нека, тогава получаваме 
, , .
Отговор. .
Уравнения, решени с помощта на идентичности 
Полезно е да знаете следните формули:
Пример Решете уравнението.
Решение.Използвайки, получаваме
Отговор.
Предлагаме не самите формули, а начина за извеждането им:
Следователно,
По същия начин,.
Пример
реши уравнението 
.
Решение.Нека трансформираме израза:
Уравнението ще бъде написано във формата:
Като вземем, получаваме. , . Следователно
Отговор. .
Универсално тригонометрично заместване
Тригонометрично уравнение на формата
където --- рационална функция с помощта на формули -- , както и с помощта на формули -- може да се сведе до рационално уравнение по отношение на аргументите , , , , след което уравнението може да се сведе до алгебрично рационално уравнение по отношение на използването на универсалните тригонометрични формули за заместване
Трябва да се отбележи, че използването на формули може да доведе до стесняване на ODZ на оригиналното уравнение, тъй като то не е определено в точките, така че в такива случаи е необходимо да се провери дали ъглите са корените на оригиналното уравнение .
Пример Решете уравнението.
Решение.Според задачата. Прилагайки формулите и правейки заместването, получаваме
откъде и следователно, .
Уравнения на формата
Уравнения от вида , където е полином, се решават чрез промяна на неизвестните
Пример Решете уравнението.
Решение.Извършвайки замяната и като вземем предвид това , получаваме
където , . --- външен корен, т.к . Корени на уравнение 
са .
Използване на ограничени функции
В практиката на централизираното тестване не е необичайно да се срещат уравнения, чието решение се основава на ограничеността на функциите и . Например:
Пример Решете уравнението.
Решение.Тъй като , , След това лявата страна не надвишава и е равно на , Ако
За да намерим стойностите, които отговарят на двете уравнения, процедираме по следния начин. Решаваме един от тях, след което сред намерените стойности избираме тези, които удовлетворяват другия.
Да започнем с втория: , . Тогава , 
.
Ясно е, че само за четни числа ще бъде .
Отговор. .
Друга идея се реализира чрез решаване на следното уравнение:
Пример
реши уравнението 
.
Решение.Нека използваме свойството на експоненциалната функция: , 
.
Добавяйки тези неравенства член по член, имаме:
Следователно лявата страна на това уравнение е равна тогава и само ако са валидни двете равенства:
т.е. може да приема стойностите, , или може да приема стойностите, .
Отговор. , .
Пример
реши уравнението 
.
Решение., . Следователно, 
.
Отговор. .
Пример реши уравнението
Решение.Означаваме , тогава от дефиницията на обратната тригонометрична функция имаме 
и 
.
Тъй като , неравенството следва от уравнението, т.е. . Тъй като и , тогава и . Въпреки това и следователно.
Ако и , тогава . Тъй като предварително беше установено, че тогава.
Отговор. , .
Пример реши уравнението
Решение.Обхватът на валидните стойности на уравнението е.
Нека първо покажем, че функцията
За всеки може да приема само положителни стойности.
Нека представим функцията по следния начин: .
Тъй като , тогава , т.е. 
.
Следователно, за да се докаже неравенството, е необходимо да се покаже това 
. За тази цел поставяме на куб и двете части на това неравенство
Полученото числово неравенство показва, че . Ако също вземем предвид, че , тогава лявата страна на уравнението е неотрицателна.
Помислете сега за дясната страна на уравнението.
защото 
, тогава
Известно е обаче, че 
. От тук следва, че , т.е. дясната страна на уравнението не надвишава . По-рано беше доказано, че лявата страна на уравнението е неотрицателна, следователно равенството в може да бъде само в случай, че и двете му части са равни, а това е възможно само за .
Отговор. .
Пример реши уравнението
Решение.Означаваме и 
. Прилагайки неравенството на Коши-Буняковски, получаваме . Оттук следва, че 
. От друга страна, има 
. Следователно уравнението няма корени.
Отговор. .
Пример Решете уравнението:
Решение.Нека пренапишем уравнението във формата:
Отговор. .
Функционални методи за решаване на тригонометрични и комбинирани уравнения
Не всяко уравнение в резултат на трансформации може да бъде сведено до уравнение на една или друга стандартна форма, за която има определен метод за решаване. В такива случаи се оказва полезно да се използват такива свойства на функциите и като монотонност, ограниченост, равномерност, периодичност и т.н. Така че, ако една от функциите намалява, а втората нараства на интервала, тогава ако уравнението има корен на този интервал, този корен е уникален и след това, например, може да бъде намерен чрез селекция. Ако функцията е ограничена отгоре и , а функцията е ограничена отдолу и , тогава уравнението е еквивалентно на системата от уравнения
Пример реши уравнението
Решение.Преобразуваме оригиналното уравнение във формата
и го реши като квадрат по отношение на . Тогава получаваме
Нека да решим първото уравнение. Отчитайки ограничеността на функцията, стигаме до извода, че уравнението може да има корен само на интервала. На този интервал функцията нараства и функцията 
намалява. Следователно, ако това уравнение има корен, то е уникално. Намираме чрез селекция.
Отговор. .
Пример реши уравнението
Решение.Нека , и 
, тогава първоначалното уравнение може да бъде написано като функционално уравнение. Тъй като функцията е странна, тогава . В този случай получаваме уравнението
Тъй като и е монотонно на , уравнението е еквивалентно на уравнението , т.е. 
, който има един корен .
Отговор. .
Пример
реши уравнението 
.
Решение.Въз основа на теоремата за производната на сложна функция е ясно, че функцията 
намаляваща (функция намаляваща, нарастваща, намаляваща). От това става ясно, че функцията 
дефиниран на , намаляващ. Следователно това уравнение има най-много един корен. защото 
, тогава
Отговор. .
Пример Решете уравнението.
Решение.Разгледайте уравнението на три интервала.
а) Нека . Тогава на този набор първоначалното уравнение е еквивалентно на уравнението . Което няма решения на интервала, тъй като 
, , a . На интервала оригиналното уравнение също няма корени, защото 
, a .
б) Нека . Тогава на този набор първоначалното уравнение е еквивалентно на уравнението
чиито корени на интервала са числата , , , .
в) Нека . Тогава на този набор първоначалното уравнение е еквивалентно на уравнението
Което няма решения на интервала, тъй като , но . Уравнението също няма решения на интервала, тъй като , , a .
Отговор. , , , .
Метод на симетрия
Удобно е да се използва методът на симетрия, когато формулировката на задачата съдържа изискването решението на уравнение, неравенство, система и др. да бъде уникално. или точна индикация за броя на разтворите. В този случай трябва да се открие всякаква симетрия на дадените изрази.
Необходимо е също така да се вземе предвид разнообразието от различни възможни видове симетрия.
Също толкова важно е стриктното спазване на логическите етапи в разсъжденията със симетрията.
Обикновено симетрията ни позволява да установим само необходимите условия, след което трябва да проверим тяхната достатъчност.
Пример Намерете всички стойности на параметъра, за които уравнението има уникално решение.
Решение.Обърнете внимание, че и са четни функции, така че лявата страна на уравнението е четна функция.
Така че, ако е решение на уравнение, тогава има и решение на уравнението. Ако е единственото решение на уравнението, тогава необходимо , .
Да изберем възможенстойности, изискващи това да бъде коренът на уравнението.
Веднага отбелязваме, че други стойности не могат да задоволят условието на проблема.
Но все още не е известно дали всички избрани наистина отговарят на условието на проблема.
Адекватност.
1), уравнението ще приеме формата 
.
2), уравнението ще приеме формата:
Очевидно за всички и 
. Следователно последното уравнение е еквивалентно на системата:
Така доказахме, че за , уравнението има единствено решение.
Отговор. .
Решение с изследване на функцията
Пример Докажете, че всички решения на уравнението
Цели числа.
Решение.Основният период на първоначалното уравнение е . Следователно, първо изучаваме това уравнение на сегмента.
Нека преобразуваме уравнението във вида:
С помощта на калкулатор получаваме:
Ако , тогава от предишните равенства получаваме:
Решавайки полученото уравнение, получаваме: .
Извършените изчисления дават възможност да се приеме, че корените на уравнението, принадлежащи на интервала, са , и .
Директната проверка потвърждава тази хипотеза. Така се доказва, че корените на уравнението са само цели числа , .
Пример
Решете уравнението 
.
Решение.Намерете главния период на уравнението. Основният период на функцията е . Основният период на функцията е . Най-малкото общо кратно на числата и е равно на . Следователно главният период на уравнението е . Позволявам .
Очевидно е решение на уравнението. На интервала. Функцията е отрицателна. Следователно други корени на уравнението трябва да се търсят само на интервалите x и .
С помощта на микрокалкулатор първо намираме приблизителните стойности на корените на уравнението. За да направим това, ние съставяме таблица със стойностите на функцията 
на интервали и ; на интервалите и .
| 0 | 0 | 202,5 | 0,85355342 |
| 3 | -0,00080306 | 207 | 0,6893642 |
| 6 | -0,00119426 | 210 | 0,57635189 |
| 9 | -0,00261932 | 213 | 0,4614465 |
| 12 | -0,00448897 | 216 | 0,34549155 |
| 15 | -0,00667995 | 219 | 0,22934931 |
| 18 | -0,00903692 | 222 | 0,1138931 |
| 21 | -0,01137519 | 225 | 0,00000002 |
| 24 | -0,01312438 | 228 | -0,11145712 |
| 27 | -0,01512438 | 231 | -0,21961736 |
| 30 | -0,01604446 | 234 | -0,32363903 |
| 33 | -0,01597149 | 237 | -0,42270819 |
| 36 | -0,01462203 | 240 | -0,5160445 |
| 39 | -0,01170562 | 243 | -0,60290965 |
| 42 | -0,00692866 | 246 | -0,65261345 |
| 45 | 0,00000002 | 249 | -0,75452006 |
| 48 | 0,00936458 | 252 | -0,81805397 |
| 51 | 0,02143757 | 255 | -0,87270535 |
| 54 | 0,03647455 | 258 | -0,91803444 |
| 57 | 0,0547098 | 261 | -0,95367586 |
| 60 | 0,07635185 | 264 | -0,97934187 |
| 63 | 0,10157893 | 267 | -0,99482505 |
| 66 | 0,1305352 | 270 | -1 |
| 67,5 | 0,14644661 |
От таблицата лесно се виждат следните хипотези: корените на уравнението, принадлежащи на отсечката, са числа: ; ; . Директната проверка потвърждава тази хипотеза.
Отговор.
; 
; .
Решаване на тригонометрични неравенства с помощта на единичната окръжност
При решаване на тригонометрични неравенства от вида , където е една от тригонометричните функции, е удобно да се използва тригонометрична окръжност, за да се представи най-ясно решението на неравенството и да се запише отговорът. Основният метод за решаване на тригонометрични неравенства е свеждането им до най-простите неравенства от вида . Нека да разгледаме пример как се решават такива неравенства.
Пример Решете неравенството.
Решение.Нека начертаем тригонометрична окръжност и отбележим върху нея точките, за които ординатата е по-голяма от .
За решението на това неравенство ще бъде . Също така е ясно, че ако някое число се различава от някое число от посочения интервал с , то също няма да бъде по-малко от . Следователно към краищата на намерения сегмент от решението просто трябва да добавите . Накрая получаваме, че решенията на първоначалното неравенство ще бъдат всички 
.
Отговор.
.
За решаване на неравенства с тангенс и котангенс е полезна концепцията за линия от тангенси и котангенси. Това са линиите и съответно (на фигурите (1) и (2)), докосващи тригонометричната окръжност.
Лесно е да се види, че ако изградите лъч с начало в началото, сключвайки ъгъл с положителната посока на абсцисната ос, тогава дължината на сегмента от точката до точката на пресичане на този лъч с линията на допирателната е точно равна на тангенса на ъгъла, който този лъч сключва с абсцисната ос. Подобно наблюдение важи за котангенса.
Пример Решете неравенството.
Решение.Означаваме , тогава неравенството ще приеме формата на най-простото: . Да разгледаме интервал с дължина, равна на най-малкия положителен период (LPP) на тангентата. На този сегмент, използвайки линията на допирателната, установяваме, че . Сега си спомняме какво трябва да се добави, тъй като RPE на функцията. Така, 
. Връщайки се към променливата, получаваме това.
Отговор.
.
Удобно е да се решават неравенства с обратни тригонометрични функции с помощта на графики на обратни тригонометрични функции. Нека покажем как става това с пример.
Решаване на тригонометрични неравенства по графичен метод
Обърнете внимание, че ако --- е периодична функция, тогава за решаване на неравенството е необходимо да се намерят неговите решения на сегмент, чиято дължина е равна на периода на функцията. Всички решения на първоначалното неравенство ще се състоят от намерените стойности, както и всички, които се различават от тези, намерени с всеки цял брой периоди на функцията.
Разгледайте решението на неравенството ().
Тъй като , тогава неравенството няма решения за . Ако , тогава множеството от решения на неравенството е множеството от всички реални числа.
Позволявам . Функцията синус има най-малкия положителен период, така че неравенството може да бъде решено първо върху сегмент с дължина, например върху сегмент. Изграждаме графики на функции и (). са дадени от неравенства от вида: и, откъдето,
В тази статия бяха разгледани методи за решаване на тригонометрични уравнения и неравенства, както най-прости, така и ниво на олимпиада. Разгледани са основните методи за решаване на тригонометрични уравнения и неравенства, както специфични --- характерни само за тригонометрични уравнения и неравенства --- така и общи функционални методи за решаване на уравнения и неравенства, приложени към тригонометричните уравнения.
Дипломната работа предоставя основни теоретични сведения: дефиницията и свойствата на тригонометричните и обратните тригонометрични функции; изразяване на тригонометрични функции по отношение на други тригонометрични функции, което е много важно за преобразуване на тригонометрични изрази, особено тези, съдържащи обратни тригонометрични функции; в допълнение към основните тригонометрични формули, добре познати от училищния курс, са дадени формули, които опростяват изрази, съдържащи обратни тригонометрични функции. Разглеждат се решаването на елементарни тригонометрични уравнения, методът на факторизиране, методите за редуциране на тригонометрични уравнения до алгебрични. С оглед на факта, че решенията на тригонометричните уравнения могат да бъдат записани по няколко начина и формата на тези решения не позволява веднага да се определи дали тези решения са еднакви или различни, се разглежда обща схема за решаване на тригонометрични уравнения и подробно се разглежда преобразуването на групи от общи решения на тригонометрични уравнения. Подробно са разгледани методите за решаване на елементарни тригонометрични неравенства, както върху единична окръжност, така и чрез графичен метод. Описан е процесът на решаване на неелементарни тригонометрични неравенства чрез елементарни неравенства и методът на интервалите, вече добре познат на учениците. Дадени са решенията на типични задачи за избор на корени. Дадена е необходимата теоретична информация за избора на корени: разделяне на множеството от цели числа на непресичащи се подмножества, решение на уравнения в цели числа (диофантово).
Резултатите от тази дипломна работа могат да се използват като образователен материал при подготовката на курсови и дипломни работи, при подготовката на избираеми предмети за ученици, а работата може да се използва и при подготовката на студентите за приемни изпити и централизирано тестване.
Вигодски Я.Я., Наръчник по елементарна математика. /Вигодски Я.Я. --- М.: Наука, 1970.
Игудисман О., Математика на устния изпит / Игудисман О. --- М .: Ирис прес, Ролф, 2001.
Азаров А.И., уравнения / Азаров А.И., Гладун О.М., Федосенко В.С. --- Минск: Тривиум, 1994.
Литвиненко В. Н., Семинар по елементарна математика / Литвиненко В. Н. --- М .: Образование, 1991.
Шаригин И.Ф., Избираем курс по математика: решаване на задачи / Шаригин И.Ф., Голубев В.И. --- М.: Просвещение, 1991.
Бардушкин В., Тригонометрични уравнения. Избор на корени / В. Бардушкин, А. Прокофиев.// Математика, № 12, 2005 с. 23--27.
Василевски A.B., Задачи за извънкласна работа по математика / Vasilevsky A.B. --- Мн.: Народна асвета. 1988. --- 176s.
Сапунов П. И., Преобразуване и обединяване на групи от общи решения на тригонометрични уравнения / Сапунов П. И. // Математическо образование, брой № 3, 1935 г.
Бородин П., Тригонометрия. Материали за приемни изпити в Московския държавен университет [текст] / П. Бородин, В. Галкин, В. Панферов, И. Сергеев, В. Тарасов // Математика № 1, 2005 г. стр. 36--48.
Самусенко А.В., Математика: Типични грешки на кандидатите: Справочник / Самусенко А.В., Казаченок В.В. --- Минск: Висше училище, 1991.
Азаров А.И., Функционални и графични методи за решаване на изпитни задачи / Азаров А.И., Барвенов С.А., --- Минск: Аверсев, 2004.
Решение на най-простите тригонометрични уравнения
Първо, нека си припомним формулите за решаване на най-простите тригонометрични уравнения.
- $sinx=a$
- $cosx=a$
- $tgx=a$
- $ctgx=a$
Решение на най-простите тригонометрични неравенства.
За да решим най-простите тригонометрични неравенства, първо трябва да решим съответното уравнение и след това, използвайки тригонометричната окръжност, да намерим решение на неравенството. Разгледайте решенията на най-простите тригонометрични неравенства чрез примери.
Пример 1
$sinx\ge \frac(1)(2)$
Намерете решение на тригонометричното неравенство $sinx=\frac(1)(2)$
\ \
Фигура 1. Решение на неравенството $sinx\ge \frac(1)(2)$.
Тъй като неравенството има знак „по-голямо или равно“, решението лежи на горната дъга на окръжността (по отношение на решението на уравнението).
Отговор: $\left[\frac(\pi )(6)+2\pi n,\frac(5\pi )(6)+2\pi n\right]$.
Пример 2
Намерете решение на тригонометричното неравенство $cosx=\frac(\sqrt(3))(2)$
\ \
Обърнете внимание на решението на тригонометричната окръжност
Тъй като неравенството има знак „по-малко от“, решението лежи върху дъгата на окръжността, разположена вляво (по отношение на решението на уравнението).
Отговор: $\left(\frac(\pi )(6)+2\pi n,\frac(11\pi )(6)+2\pi n\right)$.
Пример 3
$tgx\le \frac(\sqrt(3))(3)$
Намерете решение на тригонометричното неравенство $tgx=\frac(\sqrt(3))(3)$
\ \
Тук също се нуждаем от домейн на дефиниция. Както си спомняме, допирателната функция $x\ne \frac(\pi )(2)+\pi n,n\in Z$
Обърнете внимание на решението на тригонометричната окръжност
Фигура 3. Решение на неравенството $tgx\le \frac(\sqrt(3))(3)$.
Тъй като неравенството има знак „по-малко или равно на“, решението се намира върху дъгите на кръга, маркиран в синьо на фигура 3.
Отговор: $\ \left(-\frac(\pi )(2)+2\pi n\right.,\left.\frac(\pi )(6)+2\pi n\right]\cup \left (\frac(\pi )(2)+2\pi n,\right.\left.\frac(7\pi )(6)+2\pi n\right]$
Пример 4
Намерете решение на тригонометричното неравенство $ctgx=\sqrt(3)$
\ \
Тук също се нуждаем от домейн на дефиниция. Както си спомняме, допирателната функция $x\ne \pi n,n\in Z$
Обърнете внимание на решението на тригонометричната окръжност
Фигура 4. Решение на неравенството $ctgx\le \sqrt(3)$.
Тъй като неравенството има знак „по-голямо от“, решението се намира върху дъгите на кръга, маркиран в синьо на фигура 4.
Отговор: $\ \left(2\pi n,\frac(\pi )(6)+2\pi n\right)\cup \left(\pi +2\pi n,\frac(7\pi )( 6)+2\pi n\надясно)$
ОПРЕДЕЛЕНИЕ
Тригонометричните неравенства са неравенства, които съдържат променлива под знака на тригонометрична функция.
Решаване на тригонометрични неравенства
Решаването на тригонометрични неравенства често се свежда до решаване на най-простите тригонометрични неравенства от вида: \(\ \sin x a \), \(\ \cos x > a \), \(\ \operatorname(tg) x > a \ ), \(\ \ име на оператор(ctg) x > a \), \(\ \sin x \leq a \), \(\ \cos x \leq a \), \(\ \име на оператор(tg) x \ leq a \), \ (\ \operatorname(ctg) x \leq a \), \(\ \sin x \geq a \), \(\ \cos \geq a \), \(\ \operatorname(tg ) x \geq a \ ), \(\ \operatorname(tg) x \geq a \)
Най-простите тригонометрични неравенства се решават графично или с помощта на единична тригонометрична окръжност.
По дефиниция синусът на ъгъла \(\ \alpha \) е ординатата на точката \(\ P_(\alpha)(x, y) \) от единичната окръжност (фиг. 1), а косинусът е абсцисата на тази точка. Този факт се използва при решаването на най-простите тригонометрични неравенства с косинус и синус с помощта на единичната окръжност.
Примери за решаване на тригонометрични неравенства
Решете неравенството \(\ \sin x \leq \frac(\sqrt(3))(2) \)
Тъй като \(\ \left|\frac(\sqrt(3))(2)\right| , това неравенство има решение и може да бъде решено по два начина
Първи начин. Нека решим това неравенство графично. За да направим това, ние конструираме в същата координатна система графика на синуса \(\ y=\sin x \) (фиг. 2) и правата \(\ y=\frac(\sqrt(3))( 2) \)
Нека изберем интервалите, където синусоидата е разположена под графиката на правата \(\ y=\frac(\sqrt(3))(2) \) . Намерете абсцисите \(\ x_(1) \) и \(\ x_(2) \) на пресечните точки на тези графики: \(\ x_(1)=\pi-\arcsin \frac(\sqrt(3) ))(2 )=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_(2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\ frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)
Получихме интервала \(\ \left[-\frac(4 \pi)(3) ; \frac(\pi)(3)\right] \), но тъй като функцията \(\ y=\sin x \) е периодичен и има период \(\ 2 \pi \) , тогава отговорът е обединението на интервали: \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+ 2 \pi k\right] \), \(\ k \in Z \)
Вторият начин. Постройте единична окръжност и права \(\ y=\frac(\sqrt(3))(2) \) , означете техните пресечни точки \(\ P_(x_(1)) \) и \(\ P_(x_ (2 )) \) (фиг. 3). Решението на първоначалното неравенство ще бъде набор от ординатни точки, които са по-малки от \(\ \frac(\sqrt(3))(2) \) . Нека намерим стойността на \(\ \boldsymbol(I)_(1) \) и \(\ \boldsymbol(I)_(2) \), като се движим обратно на часовниковата стрелка, \(\ x_(1) Фиг. 3
\(\ x_(1)=\pi-\arcsin \frac(\sqrt(3))(2)=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_ (2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)
Като вземем предвид периодичността на функцията синус, накрая получаваме интервалите \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+2 \ pi\right] \), \(\k\in Z\)
Решете неравенството \(\ \sin x>2 \)
Синусът е ограничена функция: \(\ |\sin x| \leq 1 \) и дясната страна на това неравенство е по-голяма от единица, така че няма решения.
Решете неравенството \(\ \cos x>\frac(1)(2) \)
Това неравенство може да се реши по два начина: графично и чрез единична окръжност. Нека разгледаме всеки от методите.
Първи начин. Нека изобразим в една координатна система функциите, които описват лявата и дясната част на неравенството, тоест \(\ y=\cos x \) и \(\ y=\frac(1)(2) \) . Нека изберем интервалите, където графиката на функцията косинус \(\ y=\cos x \) е разположена над графиката на правата \(\ y=\frac(1)(2) \) (фиг. 4 ).
Намерете абсцисите на точките \(\ \boldsymbol(x)_(1) \) и \(\ x_(2) \) - точките на пресичане на графиките на функциите \(\ y=\cos x \ ) и \(\ y=\frac (1)(2) \) , които са краищата на един от интервалите, за които е валидно посоченото неравенство. \(\ x_(1)=-\arccos \frac(1)(2)=-\frac(\pi)(3) \); \(\ x_(1)=\arccos \frac(1)(2)=\frac(\pi)(3) \)
Като се има предвид, че косинусът е периодична функция с период \(\ 2 \pi \) , отговорът е стойността \(\ x \) от интервалите \(\ \left(-\frac(\pi)(3 )+2 \pi k ; \frac(\pi)(3)+2 \pi k\right) \), \(\ k \in Z \)
Вторият начин. Нека построим единична окръжност и права \(\ x=\frac(1)(2) \) (тъй като оста x съответства на косинусите на единичната окръжност). Нека \(\ P_(x_(1)) \) и \(\ P_(x_(2)) \) (фиг. 5) са пресечните точки на правата и единичната окръжност. Решението на първоначалното уравнение ще бъде набор от абсцисни точки, които са по-малки от \(\ \frac(1)(2) \) . Намерете стойността на \(\ x_(1) \) и \(\ 2 \) , като направите обиколка обратно на часовниковата стрелка, така че \(\ x_(1) Като вземем предвид периодичността на косинуса, накрая получаваме интервалите \( \ \left(-\frac (\pi)(3)+2 \pi k ;\frac(\pi)(3)+2 \pi k\десен) \),\(\ k \in Z \)
Решете неравенството \(\ \operatorname(ctg) x \leq-\frac(\sqrt(3))(3) \)
Нека начертаем графики на функции \(\ y=\operatorname(ctg) x \), \(\ y=-\frac(\sqrt(3))(3) \) в една координатна система
Нека изберем интервалите, където графиката на функцията \(\ y=\operatorname(ctg) x \) не е по-висока от графиката на правата \(\ y=-\frac(\sqrt(3))(3 ) \) (фиг. 6) .
Намерете абсцисата на точката \(\ x_(0) \) , която е краят на един от интервалите, на които неравенството \(\ x_(0)=\operatorname(arcctg)\left(-\frac(\ sqrt(3))( 3)\right)=\pi-\име на оператор(arcctg)\left(\frac(\sqrt(3))(3)\right)=\pi-\frac(\pi)(3 )=\frac(2 \pi)(3) \)
Другият край на тази празнина е точката \(\ \pi \) и функцията \(\ y=\operatorname(ctg) x \) е недефинирана в тази точка. Така едно от решенията на това неравенство е интервалът \(\ \frac(2 \pi)(3) \leq x
Тригонометрични неравенства със сложен аргумент
Тригонометричните неравенства със сложен аргумент могат да бъдат сведени до най-простите тригонометрични неравенства с помощта на заместване. След решаването му се извършва обратното заместване и се изразява първоначалното неизвестно.
Решете неравенството \(\ 2 \cos \left(2 x+100^(\circ)\right) \leq-1 \)
Изразете косинуса от дясната страна на това неравенство: \(\ \cos \left(2 x+100^(\circ)\right) \leq-\frac(1)(2) \)
Извършваме замяната \(\ t=2 x+100^(\circ) \) , след което това неравенство се трансформира в най-простото неравенство \(\ \cos t \leq-\frac(1)(2) \ )
Нека го решим с помощта на единичната окръжност. Нека построим единична окръжност и права \(\ x=-\frac(1)(2) \) . Нека означим \(\ P_(1) \) и \(\ P_(2) \) като точки на пресичане на правата и единичната окръжност (фиг. 7).
Решението на първоначалното неравенство ще бъде наборът от абсцисни точки, които са най-много \(\ -\frac(1)(2) \). Точката \(\ P_(1) \) съответства на ъгъла \(\ 120^(\circ) \) , а точката \(\ P_(2) \) . Така, като се има предвид косинус периодът, получаваме \(\ 120^(\circ)+360^(\circ) \cdot n \leq t \leq 240^(\circ)+360^(\circ) \cdot n \ ), \(\ n \in Z \)
Правим обратното заместване \(\ t=2 x+100^(\circ) 120^(\circ)+360^(\circ) \cdot n \leq 2 x+100^(\circ) \leq 240^ (\ circ)+360^(\circ) \cdot n \), \(\ n \in Z \)
Изразяваме \(\ \mathbf(x) \), за да направите това, първо извадете \(\ 100^(\circ) 120^(\circ)-100^(\circ)+360^(\circ) \ cdot n \leq 2 x+100^(\circ)-100^(\circ) \leq 240^(\circ)-100^(\circ)+360^(\circ) \cdot n \), \( \ n\in Z\); \(\ 20^(\circ)+360^(\circ) \cdot n \leq 2 x \leq 140^(\circ)+360^(\circ) \cdot n \), \(\ n \in Z\)
и след това разделете на 2 \(\ \frac(20^(\circ)+360^(\circ) \cdot n)(2) \leq \frac(2 x)(2) \leq \frac(140^ (\circ)+360^(\circ) \cdot n)(2) \), \(\ n \in Z \); \(\ 10^(\circ)+180^(\circ) \cdot n \leq x \leq 70^(\circ)+180^(\circ) \cdot n \), \(\ n \in Z \)
Двойни тригонометрични неравенства
Решете двойното тригонометрично неравенство \(\ \frac(1)(2)
Нека въведем замяната \(\ t=\frac(x)(2) \) , тогава първоначалното неравенство ще приеме формата \(\ \frac(1)(2)
Нека го решим с помощта на единичната окръжност. Тъй като ординатната ос съответства на синуса на единичната окръжност, ние избираме върху нея набора от ординати, който е по-голям от \(\ x=\frac(1)(2) \) и по-малък или равен на \(\ \frac(\sqrt(2))(2 ) \) . На фигура 8 тези точки ще бъдат разположени върху дъгите \(\ P_(t_(1)) \), \(\ P_(t_(2)) \) и \(\ P_(t_(3)) \) , \( \ P_(t_(4)) \) . Нека намерим стойността \(\ t_(1) \), \(\ t_(2) \), \(\ t_(3) \), \(\ t_(4) \) , като направим обиколка обратно на часовниковата стрелка и \ (\ t_(1) \(\ t_(3)=\pi-\arcsin \frac(\sqrt(2))(2)=\pi-\frac(\pi)(4)=\frac(3 \ pi)(4) \); \(\ t_(4)=\pi-\arcsin \frac(1)(2)=\pi-\frac(\pi)(6)=\frac(5 \pi ) (6)\)
По този начин получаваме два интервала, които, като се вземе предвид периодичността на синусовата функция, могат да бъдат записани по следния начин \(\ \frac(\pi)(6)+2 \pi k \leq t \frac(\pi) (4)+2 \ pi k \quad \frac(3 \pi)(4)+2 \pi k leq \frac(x)(2) \frac(\pi)(4)+2 \pi k \) , \(\ \frac(3 \pi)(4)+2 \pi k Express \(\ \mathbf( x) \), за това умножаваме всички страни на двете неравенства по 2, получаваме \(\ \frac (\pi)(3)+4 \pi k \leq x
МЕТОДИ ЗА РЕШАВАНЕ НА ТРИГОНОМЕТРИЧНИ НЕРАВЕНСТВА
Уместност. Исторически на тригонометричните уравнения и неравенства е отделено специално място в училищната програма. Можем да кажем, че тригонометрията е един от най-важните раздели на училищния курс и на цялата математическа наука като цяло.
Тригонометричните уравнения и неравенства заемат едно от централните места в гимназиалния курс по математика, както по отношение на съдържанието на учебния материал, така и на методите на учебно-познавателна дейност, които могат и трябва да се формират по време на изучаването им и да се прилагат за решаване на големи задачи. редица проблеми от теоретичен и приложен характер.
Решаването на тригонометрични уравнения и неравенства създава предпоставки за систематизиране на знанията на учениците, свързани с целия учебен материал по тригонометрия (например свойствата на тригонометричните функции, методи за преобразуване на тригонометрични изрази и др.) и дава възможност за установяване на ефективни връзки с изучавания материал по алгебра (уравнения, еквивалентност на уравнения, неравенства, тъждествени преобразувания на алгебрични изрази и др.).
С други думи, разглеждането на методите за решаване на тригонометрични уравнения и неравенства включва един вид прехвърляне на тези умения към ново съдържание.
Значимостта на теорията и многобройните й приложения са доказателство за актуалността на избраната тема. Това от своя страна ви позволява да определите целите, задачите и предмета на изследване на курсовата работа.
Цел на изследването: обобщете наличните видове тригонометрични неравенства, основни и специални методи за тяхното решаване, изберете набор от задачи за решаване на тригонометрични неравенства от ученици.
Цели на изследването:
1. Въз основа на анализа на наличната литература по темата на изследването систематизирайте материала.
2. Дайте набор от задачи, необходими за консолидиране на темата "Тригонометрични неравенства".
Обект на изследване са тригонометрични неравенства в училищния курс по математика.
Предмет на изследване: видове тригонометрични неравенства и методи за тяхното решаване.
Теоретично значение е да организираме материала.
Практическо значение: прилагане на теоретични знания при решаване на задачи; анализ на основните често срещани методи за решаване на тригонометрични неравенства.
Изследователски методи : анализ на научна литература, синтез и обобщение на придобитите знания, анализ на решаването на проблеми, търсене на оптимални методи за решаване на неравенства.
§едно. Видове тригонометрични неравенства и основни методи за тяхното решаване
1.1. Най-простите тригонометрични неравенства
Два тригонометрични израза, свързани със знак или >, се наричат тригонометрични неравенства.
Решаването на тригонометрично неравенство означава да се намери набор от стойности на неизвестните, включени в неравенството, при които неравенството е изпълнено.
Основната част от тригонометричните неравенства се решават чрез свеждането им до решаването на най-простите:
Това може да е метод на факторизация, промяна на променлива ( 
, 
и т.н.), където първо се решава обичайното неравенство, а след това неравенството на формата 
и т.н. или други начини.
Най-простите неравенства се решават по два начина: с помощта на единичната окръжност или графично.
Позволявамf(x
е една от основните тригонометрични функции. Да се реши неравенството 
достатъчно е да се намери решението му на един период, т.е. на всеки сегмент, чиято дължина е равна на периода на функциятаf
х
. Тогава решението на първоначалното неравенство ще бъде намеренох
, както и тези стойности, които се различават от тези, намерени с произволен брой периоди на функцията. В този случай е удобно да използвате графичния метод.
Нека дадем пример за алгоритъм за решаване на неравенства 
(
) и 
.
Алгоритъм за решаване на неравенството (
).
1. Формулирайте дефиницията на синуса на числох върху единичната окръжност.
3. На оста y маркирайте точка с координатаа .
4. През тази точка начертайте линия, успоредна на оста OX, и маркирайте точките на пресичане на нея с кръга.
5. Изберете дъга от окръжност, всички точки от която имат ордината по-малка ота .
6. Посочете посоката на байпаса (обратно на часовниковата стрелка) и запишете отговора, като добавите периода на функцията към краищата на интервала2πn
,
.
Алгоритъм за решаване на неравенството .
1. Формулирайте определението на тангенса на числох върху единичната окръжност.
2. Начертайте единична окръжност.
3. Начертайте линия от допирателни и маркирайте точка върху нея с ординатаа .
4. Свържете тази точка с началото и маркирайте пресечната точка на получения сегмент с единичната окръжност.
5. Изберете дъга от окръжност, всички точки на която имат ордината на допирателната, по-малка ота .
6. Посочете посоката на обхождане и запишете отговора, като вземете предвид обхвата на функцията, като добавите точкапн
,
(числото от лявата страна на записа винаги е по-малко от числото от дясната страна).
Графична интерпретация на решения на най-простите уравнения и формули за решаване на неравенства в общ вид са дадени в приложението (Приложения 1 и 2).
Пример 1
Решете неравенството 
.
Начертайте линия върху единичната окръжност 
, която пресича окръжността в точки A и B.
Всички ценностиг
на интервала NM повече
, всички точки на дъгата AMB удовлетворяват това неравенство. При всички ъгли на въртене, големи 
, но по-малък 
,
ще приеме стойности по-големи от
(но не повече от един).
Фиг. 1
По този начин решението на неравенството ще бъде всички стойности в интервала 
, т.е. 
. За да получите всички решения на това неравенство, е достатъчно да добавите към краищата на този интервал 
, където 
, т.е. 
,
.
Имайте предвид, че стойностите 
и 
са корените на уравнението 
,
тези. 
;
.
Отговор: 
, .
1.2. Графичен метод
На практика често е полезен графичен метод за решаване на тригонометрични неравенства. Разгледайте същността на метода на примера на неравенството 
:
1. Ако аргументът е сложен (различен отх ), след което го заместваме сT .
2. Изграждаме в една координатна равнинаtoOy
функционални графики 
и 
.
3. Намираме такивадве съседни точки на пресичане на графики, между коитосинусоидаразположенпо-горе
прав . Намерете абсцисите на тези точки.
4. Напишете двойно неравенство за аргументаT , като се има предвид косинус периодът (T ще бъде между намерените абциси).
5. Направете обратно заместване (върнете се към първоначалния аргумент) и изразете стойносттах от двойно неравенство записваме отговора като числов интервал.
Пример 2 Решете неравенството: .
При решаване на неравенства по графичен метод е необходимо да се изградят графики на функции възможно най-точно. Нека трансформираме неравенството във вида:
Нека построим графики на функции в една координатна система 
и 
(фиг. 2).
Фиг.2
Функционалните графики се пресичат в точкаНО
с координати 
; 
. Между 
точки на графиката 
под точките на графиката 
. И когато стойностите на функцията са еднакви. Ето защо при 
.
Отговор: 
.
1.3. Алгебричен метод
Доста често първоначалното тригонометрично неравенство чрез добре подбрана замяна може да бъде сведено до алгебрично (рационално или ирационално) неравенство. Този метод включва трансформиране на неравенството, въвеждане на заместване или заместване на променлива.
Нека разгледаме приложението на този метод на конкретни примери.
Пример 3
Намаляване до най-простата форма 
.
(фиг. 3)
Фиг.3
, 
.
Отговор: 
,
Пример 4 Решете неравенството:
ODZ: 
, 
.
Използване на формули: 
, 
записваме неравенството във вида: 
.
Или, ако приемем 
след прости трансформации получаваме
,
,
.
Решавайки последното неравенство по интервалния метод, получаваме:
Фиг.4
, съответно 
. Тогава от фиг. 4 следва 
, където 
.
Фиг.5
Отговор: 
, 
.
1.4. Метод на разстояние
Общата схема за решаване на тригонометрични неравенства по интервалния метод:
Използвайки тригонометрични формули, разложете на фактори.
Намерете точки на прекъсване и нули на функцията, поставете ги върху кръга.
Вземете всяка точкаДа се (но не е намерен по-рано) и разберете знака на продукта. Ако произведението е положително, тогава поставете точка извън единичната окръжност върху лъча, съответстващ на ъгъла. В противен случай поставете точката вътре в кръга.
Ако една точка се среща четен брой пъти, ние я наричаме точка с четна кратност; ако нечетен брой пъти, ние я наричаме точка с нечетна кратност. Начертайте дъги, както следва: започнете от точкаДа се , ако следващата точка е с нечетна кратност, тогава дъгата пресича окръжността в тази точка, но ако точката е с четна кратност, тогава тя не се пресича.
Дъгите зад кръг са положителни пропуски; вътре в кръга има отрицателни интервали.
Пример 5 Решете неравенството
, 
.
Точки от първата серия: 
.
Точки от втората серия: 
.
Всяка точка се среща нечетен брой пъти, т.е. всички точки са с нечетна множественост.
Разберете знака на продукта на 
: . Маркираме всички точки на единичния кръг (фиг. 6):
Ориз. 6
Отговор: 
, 
; 
, 
; 
, 
.
Пример 6 . Решете неравенството.
Решение:
Нека намерим нулите на израза .
Вземетеаем :
,
;
, 
;
, 
;
, 
;
На единичната окръжност, серийни стойностих
1
представени с точки 
. Сериях
2
дава точки 
. сериях
3
получаваме две точки 
. Най-после сериях
4
ще представляват точки 
. Поставяме всички тези точки върху единичната окръжност, като посочваме в скоби до всяка от нейната множественост.
Сега нека номерът 
ще бъдат равни. Правим оценка по знака:
Така че точкатаА
трябва да се избере върху гредата, образуваща ъгъла 
с лъчо
извън единичната окръжност. (Имайте предвид, че спомагателният лъчО
А
не е задължително да се показва на снимката. ТочкаА
избрано приблизително.)
Сега от точкатаА
изчертаваме вълнообразна непрекъсната линия последователно към всички маркирани точки. И по точките нашата линия преминава от една област в друга: ако е била извън единичния кръг, тогава тя преминава в него. Приближава точката 
, линията се връща във вътрешната област, тъй като кратността на тази точка е четна. По същия начин в точката 
(с равномерна кратност) линията трябва да се завърти към външния регион. И така, начертахме определена картина, изобразена на фиг. 7. Помага да се подчертаят желаните зони върху единичния кръг. Те са отбелязани с "+".
Фиг.7
Окончателен отговор:
Забележка. Ако вълнообразната линия, след преминаване през всички точки, отбелязани на единичната окръжност, не може да се върне в точкатаА , без да пресечете кръга на „незаконно“ място, това означава, че е допусната грешка в решението, а именно, че са пропуснати нечетен брой корени.
Отговор: .
§2. Комплект задачи за решаване на тригонометрични неравенства
В процеса на развитие на способността на учениците да решават тригонометрични неравенства могат да се разграничат и 3 етапа.
1. подготвителен,
2. формиране на умения за решаване на най-прости тригонометрични неравенства;
3. въвеждане на тригонометрични неравенства от други видове.
Целта на подготвителния етап е, че е необходимо да се формира у учениците способността да използват тригонометричен кръг или графика за решаване на неравенства, а именно:
Способност за решаване на прости неравенства от вида ,
, ,
,
използване на свойствата на функциите синус и косинус;
Умение за съставяне на двойни неравенства за дъги от числова окръжност или за дъги от графики на функции;
Възможност за извършване на различни трансформации на тригонометрични изрази.
Препоръчва се този етап да се приложи в процеса на систематизиране на знанията на учениците за свойствата на тригонометричните функции. Основните средства могат да бъдат задачи, предлагани на учениците и изпълнявани под ръководството на учител или самостоятелно, както и придобити умения за решаване на тригонометрични уравнения.
Ето примери за такива задачи:
1
. Маркирайте точка върху единичната окръжност 
, ако
.
2.
В коя четвърт от координатната равнина е точката , ако 
се равнява: 
3.
Маркирайте точки върху тригонометричния кръг , ако:
4. Приведете израза към тригонометрични функцииазчетвъртинки.
а) 
,
б) 
,
в) 
5. Като се има предвид дъгата MR.М - средноазто тримесечие,Р - средноIIто тримесечие. Ограничете стойността на променливаT за: (съставете двойно неравенство) а) дъга MP; б) RM дъги.
6. Напишете двойно неравенство за избраните участъци от графиката:
Ориз. един
7.
Решете неравенства 
, 
, 
, 
.
8. Преобразуване на израз .
На втория етап от обучението за решаване на тригонометрични неравенства можем да предложим следните препоръки, свързани с методиката за организиране на дейността на учениците. В същото време е необходимо да се съсредоточи върху уменията на учениците да работят с тригонометрична окръжност или графика, които се формират по време на решаването на най-простите тригонометрични уравнения.
Първо, възможно е да се мотивира целесъобразността за получаване на общ метод за решаване на най-простите тригонометрични неравенства, като се позовава например на неравенство от формата 
.
Използвайки знанията и уменията, придобити на подготвителния етап, учениците ще приведат предложеното неравенство във формата 
, но може да се окаже трудно да се намери набор от решения на полученото неравенство, тъй като невъзможно е да се реши само с помощта на свойствата на функцията синус. Тази трудност може да бъде избегната, като се обърнете към подходящата илюстрация (решение на уравнението графично или с помощта на единична окръжност).
Второ, учителят трябва да насочи вниманието на учениците към различни начини за изпълнение на задачата, да даде подходящ пример за решаване на неравенството както графично, така и с помощта на тригонометричната окръжност.
Разгледайте такива варианти за решаване на неравенството .
1. Решаване на неравенството чрез единичната окръжност.
В първия урок за решаване на тригонометрични неравенства ще предложим на учениците подробен алгоритъм за решение, който в презентация стъпка по стъпка отразява всички основни умения, необходими за решаване на неравенството.
Етап 1.Начертайте единична окръжност, маркирайте точка на оста y 
и начертайте права линия през него, успоредна на оста x. Тази линия ще пресича единичната окръжност в две точки. Всяка от тези точки изобразява числа, чийто синус е равен на .
Стъпка 2Тази права линия разделя кръга на две дъги. Нека отделим тази, на която се показват числа, които имат синус по-голям от . Естествено, тази дъга се намира над начертаната права линия.
Ориз. 2
Стъпка 3Нека изберем един от краищата на маркираната дъга. Нека запишем едно от числата, които са представени от тази точка от единичната окръжност 
.
Стъпка 4За да изберем число, съответстващо на втория край на избраната дъга, ние "минаваме" по тази дъга от посочения край до другия. В същото време припомняме, че когато се движим обратно на часовниковата стрелка, числата, които ще преминем, се увеличават (при движение в обратна посока числата ще намаляват). Нека запишем числото, което е изобразено на единичната окръжност от втория край на маркираната дъга 
.
Така виждаме, че неравенството отговарят на числата, за които неравенството 
. Решихме неравенството за числа, разположени на един и същ период на функцията синус. Следователно всички решения на неравенството могат да бъдат записани като 
Учениците трябва да бъдат помолени внимателно да разгледат фигурата и да разберат защо са всички решения на неравенството може да се запише във формата 
, 
.
Ориз. 3
Необходимо е да се обърне внимание на учениците върху факта, че при решаване на неравенства за функцията косинус, ние чертаем права линия, успоредна на оста y.
Графичен начин за решаване на неравенството.
Изграждане на диаграми 
и 
, предвид това 
.
Ориз. четири
След това записваме уравнението 
и неговото решение 
, 
, 
, намерени с помощта на формули 
, 
, 
.
(Давамн
стойности 0, 1, 2, намираме три корена на съставеното уравнение). Стойности 
са три последователни абсциси на пресечните точки на графиките и . Очевидно винаги на интервал 
неравенството 
, и на интервала 
- неравенство 
. Интересуваме се от първия случай и след това добавяйки към краищата на този интервал число, което е кратно на периода на синуса, получаваме решение на неравенството като: 
, .
Ориз. 5
Обобщете. Да се реши неравенството , трябва да напишете съответното уравнение и да го решите. От получената формула намерете корените 
и 
, и запишете отговора на неравенството във вида: , .
Трето, фактът за множеството корени на съответното тригонометрично неравенство се потвърждава много ясно при графичното му решаване.
Ориз. 6
Необходимо е да се демонстрира на учениците, че намотката, която е решението на неравенството, се повтаря през същия интервал, равен на периода на тригонометричната функция. Можете също да разгледате подобна илюстрация за графиката на функцията синус.
Четвърто, препоръчително е да се извърши работа по актуализиране на методите на учениците за преобразуване на сумата (разликата) на тригонометричните функции в продукт, за да се привлече вниманието на учениците към ролята на тези техники при решаването на тригонометрични неравенства.
Такава работа може да се организира чрез самостоятелно изпълнение на задачите, предложени от учителя от учениците, сред които изтъкваме следното:
Пето, от учениците трябва да се изисква да илюстрират решението на всяко просто тригонометрично неравенство с помощта на графика или тригонометрична окръжност. Не забравяйте да обърнете внимание на неговата целесъобразност, особено на използването на кръг, тъй като при решаване на тригонометрични неравенства съответната илюстрация служи като много удобно средство за фиксиране на набора от решения на дадено неравенство
Запознаването на учениците с методи за решаване на тригонометрични неравенства, които не са най-простите, е препоръчително да се извършва по следната схема: позоваване на конкретно тригонометрично неравенство позоваване на съответното тригонометрично уравнение съвместно търсене (учител - ученици) на решение независимо прехвърляне на намерената техника към други неравенства от същия тип.
За да систематизираме знанията на учениците по тригонометрия, препоръчваме специално да изберете такива неравенства, чието решение изисква различни трансформации, които могат да бъдат приложени в процеса на решаването му, като фокусирате вниманието на учениците върху техните характеристики.
Като такива продуктивни неравенства можем да предложим например следното:
В заключение даваме пример за набор от задачи за решаване на тригонометрични неравенства.
1. Решете неравенствата:
2. Решете неравенствата: 3. Намерете всички решения на неравенствата: 4. Намерете всички решения на неравенствата:а) 
, отговарящи на условието 
;
б) 
, отговарящи на условието 
.
5. Намерете всички решения на неравенствата:
а) ;
б) ;
в) 
;
G) 
;
д) 
.
6. Решете неравенствата:
а) ;
б) ;
в) ;
G) 
;
д) ;
д) ;
и) 
.
7. Решете неравенствата:
а) 
;
б) ;
в) ;
G) .
8. Решете неравенствата:
а) ;
б) ;
в) ;
G) 
;
д) 
;
д) ;
и) 
;
з) .
Препоръчително е задачите 6 и 7 да се предложат на учениците, изучаващи математика в напреднало ниво, задача 8 - на учениците в паралелки със задълбочено изучаване на математика.
§3. Специални методи за решаване на тригонометрични неравенства
Специални методи за решаване на тригонометрични уравнения - т.е. тези методи, които могат да се използват само за решаване на тригонометрични уравнения. Тези методи се основават на използването на свойствата на тригонометричните функции, както и на използването на различни тригонометрични формули и тъждества.
3.1. Секторен метод
Разгледайте секторния метод за решаване на тригонометрични неравенства. Решение на неравенства от вида 
, къдетоП
(
х
)
иQ
(
х
)
- рационални тригонометрични функции (синуси, косинуси, тангенси и котангенси влизат в тях рационално), подобно на решението на рационални неравенства. Удобно е да се решават рационални неравенства по метода на интервалите върху реалната ос. Негов аналог при решаване на рационални тригонометрични неравенства е методът на секторите в тригонометрична окръжност, заsinx
иcosx
(
) или тригонометричен полукръг заtgx
иctgx
(
).
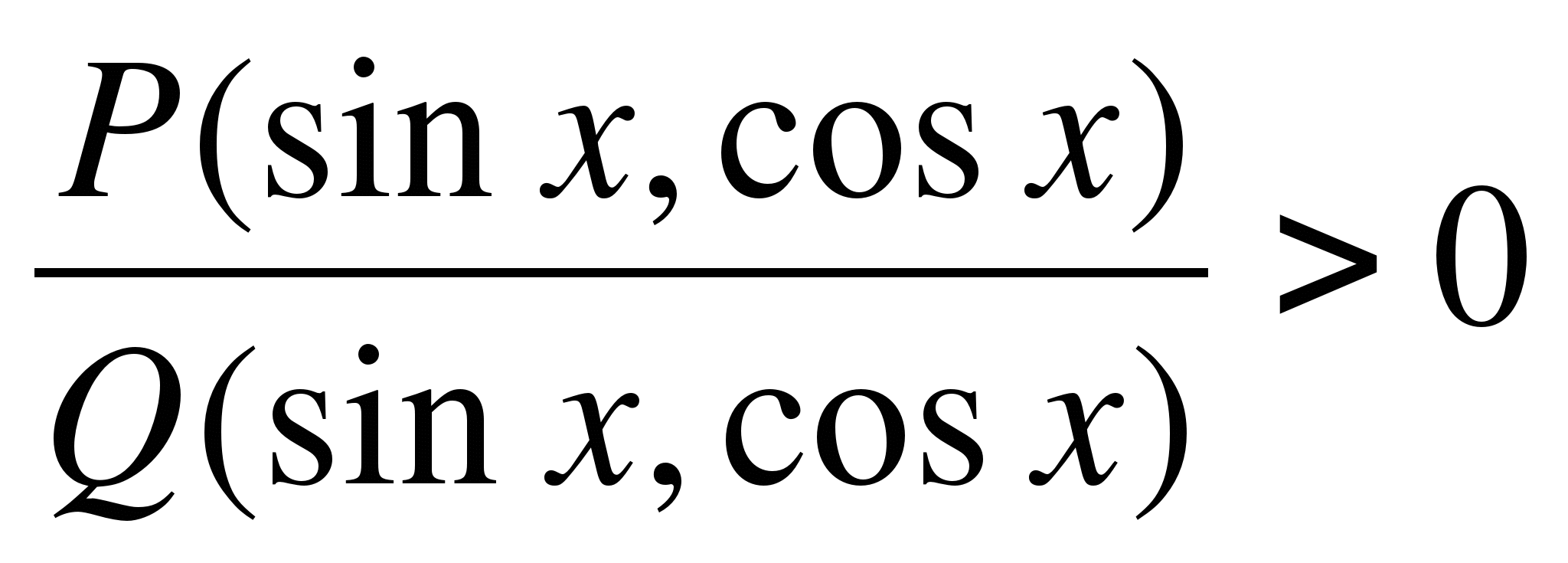
В интервалния метод, всеки линеен фактор на числителя и знаменателя на формата 
точка на числовата ос 
, и при преминаване през тази точка сменя знака. В секторния метод всеки множител на формата 
, където 
- една от функциитеsinx
илиcosx
и 
, в тригонометрична окръжност съответстват два ъгъла 
и 
, които разделят кръга на два сектора. При преминаване през и функция сменя знака.
Трябва да се помни следното:
а) Множители на формата 
и 
, където 
, запазете знака за всички стойности 
. Такива множители на числителя и знаменателя се изхвърлят, променяйки се (ако 
) за всяко такова отхвърляне знакът за неравенство се обръща.
б) Множители на формата 
и 
също се изхвърлят. Освен това, ако това са множители на знаменателя, тогава неравенствата от вида се добавят към еквивалентната система от неравенства 
и 
. Ако това са множители на числителя, то в еквивалентната система от ограничения те съответстват на неравенствата и в случай на строго първоначално неравенство и равенство 
и 
в случай на нестрого начално неравенство. При отпадане на множителя 
или 
знакът за неравенство е обърнат.
Пример 1
Решете неравенства: а) 
, б) 
.
имаме функция, б). Решете неравенството, което имаме
3.2. Метод на концентричния кръг
Този метод е аналогичен на метода на успоредните числени оси при решаване на системи от рационални неравенства.
Помислете за пример за система от неравенства.
Пример 5
Решете система от прости тригонометрични неравенства 
Първо, решаваме всяко неравенство поотделно (Фигура 5). В горния десен ъгъл на фигурата ще посочим за кой аргумент се разглежда тригонометричният кръг.
Фиг.5
След това изграждаме система от концентрични кръгове за аргументах . Чертаем кръг и го защриховаме според решението на първото неравенство, след това рисуваме кръг с по-голям радиус и го защриховаме според решението на второто, след това изграждаме кръг за третото неравенство и основен кръг . Изчертаваме лъчи от центъра на системата през краищата на дъгите, така че да пресичат всички кръгове. Формираме разтвор върху основния кръг (Фигура 6).
Фиг.6
Отговор:
, 
.
Заключение
Всички цели на курсовата работа бяха изпълнени. Теоретичният материал е систематизиран: дадени са основните видове тригонометрични неравенства и основните методи за тяхното решаване (графичен, алгебричен, метод на интервалите, секторите и метод на концентричните окръжности). За всеки метод беше даден пример за решаване на неравенство. Теоретичната част беше последвана от практическата. Съдържа набор от задачи за решаване на тригонометрични неравенства.
Тази курсова работа може да се използва от студентите за самостоятелна работа. Студентите могат да проверят нивото на усвояване на тази тема, да се упражняват при изпълнение на задачи с различна сложност.
След като работихме със съответната литература по този въпрос, очевидно можем да заключим, че способността и уменията за решаване на тригонометрични неравенства в училищния курс по алгебра и началото на анализа са много важни, чието развитие изисква значителни усилия от страна на учителят по математика.
Ето защо тази работа ще бъде полезна за учителите по математика, тъй като дава възможност за ефективно организиране на обучението на учениците по темата "Тригонометрични неравенства".
Проучването може да бъде продължено, като се разшири до крайната квалификационна работа.
Списък на използваната литература
Богомолов, Н.В. Сборник задачи по математика [Текст] / Н.В. Богомолов. – М.: Дропла, 2009. – 206 с.
Вигодски, М.Я. Наръчник по елементарна математика [Текст] / M.Ya. Вигодски. – М.: Дропла, 2006. – 509 с.
Журбенко, Л.Н. Математика в примери и задачи [Текст] / L.N. Журбенко. – М.: Инфра-М, 2009. – 373 с.
Иванов, О.А. Елементарна математика за ученици, студенти и учители [Текст] / O.A. Иванов. – М.: МЦНМО, 2009. – 384 с.
Карп, А.П. Задачи по алгебра и наченки на анализ за организацията на окончателното повторение и удостоверяване в 11. клас [Текст] / A.P. Шаран. – М.: Просвещение, 2005. – 79 с.
Куланин, Е.Д. 3000 състезателни задачи по математика [Текст] / E.D. Куланин. – М.: Ирис-прес, 2007. – 624 с.
Лейбсън, К.Л. Сборник практически задачи по математика [Текст] / К.Л. Лейбсън. – М.: Дропла, 2010. – 182 с.
Лакът, В.В. Задачи с параметри и тяхното решение. Тригонометрия: уравнения, неравенства, системи. 10 клас [Текст] / V.V. Лакът. – М.: АРКТИ, 2008. – 64 с.
Манова, А.Н. Математика. Експресен преподавател за подготовка за изпита: сметка. надбавка [Текст] / A.N. Манова. - Ростов на Дон: Феникс, 2012. - 541 с.
Мордкович, А.Г. Алгебра и началото на математическия анализ. 10-11 клас. Учебник за студенти от образователни институции [Текст] / A.G. Мордкович. – М.: Ирис-прес, 2009. – 201 с.
Новиков, А.И. Тригонометрични функции, уравнения и неравенства [Текст] / A.I. Новиков. - М.: ФИЗМАТЛИТ, 2010. - 260 с.
Оганесян, В.А. Методика на обучението по математика в средното училище: Обща методика. Proc. помощ за студенти по физика. - мат. фак. пед. по-другар. [Текст] / V.A. Оганесян. – М.: Просвещение, 2006. – 368 с.
Олечник, С.Н. Уравнения и неравенства. Нестандартни методи за решаване [Текст] / S.N. Олехник. - М .: Издателство Факториал, 1997. - 219 с.
Севрюков, П.Ф. Тригонометрични, експоненциални и логаритмични уравнения и неравенства [Текст] / P.F. Севрюков. – М.: Народно образование, 2008. – 352 с.
Сергеев, I.N. ИЗПОЛЗВАНЕ: 1000 задачи с отговори и решения по математика. Всички задачи от група C [Текст] / I.N. Сергеев. – М.: Изпит, 2012. – 301 с.
Соболев, А.Б. Елементарна математика [Текст] / A.B. Соболев. - Екатеринбург: GOU VPO USTU-UPI, 2005. - 81 с.
Фенко, Л.М. Методът на интервалите при решаване на неравенства и изучаване на функции [Текст] / L.M. Фенко. – М.: Дропла, 2005. – 124 с.
Фридман, Л.М. Теоретични основи на методиката на обучението по математика [Текст] / L.M. Фридман. - М .: Книжна къща "ЛИБРОКОМ", 2009. - 248 с.
Приложение 1
Графична интерпретация на решения на най-простите неравенства
Ориз. един
Ориз. 2
Фиг.3
Фиг.4
Фиг.5
Фиг.6
Фиг.7
Фиг.8
Приложение 2
Решения на най-простите неравенства
