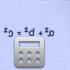Обратното на матрицата е матрица. Намиране на обратната матрица

Матрицата $A^(-1)$ се нарича обратна на квадратната матрица $A$, ако $A^(-1)\cdot A=A\cdot A^(-1)=E$, където $E $ е единичната матрица, чийто ред е равен на реда на матрицата $A$.

Неособена матрица е матрица, чийто детерминант не е равен на нула. Съответно, изродена матрица е тази, чиято детерминанта е равна на нула.

Обратната матрица $A^(-1)$ съществува тогава и само ако матрицата $A$ е неособена. Ако обратната матрица $A^(-1)$ съществува, тогава тя е уникална.

Има няколко начина да намерите обратното на матрица и ще разгледаме два от тях. Тази страница ще обсъди метода на свързаната матрица, който се счита за стандарт в повечето курсове по висша математика. Вторият начин за намиране на обратната матрица (метод на елементарни трансформации), който включва използването на метода на Гаус или метода на Гаус-Джордан, е разгледан във втората част.

Метод на съединена (обединена) матрица

Нека е дадена матрицата $A_(n\times n)$. За да се намери обратната матрица $A^(-1)$, са необходими три стъпки:

Намерете детерминантата на матрицата $A$ и се уверете, че $\Delta A\neq 0$, т.е. че матрицата A е неизродена.
Съставете алгебрични допълнения $A_(ij)$ на всеки елемент от матрицата $A$ и запишете матрицата $A_(n\times n)^(*)=\left(A_(ij) \right)$ от намереното алгебрични допълнения.
Напишете обратната матрица, като вземете предвид формулата $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$.

Матрицата $(A^(*))^T$ често се нарича присъединена (взаимна, съюзна) матрица на $A$.

Ако решението се взема ръчно, тогава първият метод е добър само за матрици с относително малки поръчки: втори (), трети (), четвърти (). За намиране на обратната матрица за матрица от по-висок ред се използват други методи. Например методът на Гаус, който е разгледан във втората част.

Пример #1

Намерете матрица, обратна на матрица $A=\left(\begin(array) (cccc) 5 & -4 &1 & 0 \\ 12 &-11 &4 & 0 \\ -5 & 58 &4 & 0 \\ 3 & - 1 & -9 & 0 \end(array) \right)$.

Тъй като всички елементи от четвъртата колона са равни на нула, тогава $\Delta A=0$ (т.е. матрицата $A$ е изродена). Тъй като $\Delta A=0$, няма матрица, обратна на $A$.

Отговор: матрица $A^(-1)$ не съществува.

Пример #2

Намерете матрицата, обратна на матрицата $A=\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right)$. Пуснете проверка.

Използваме метода на свързаната матрица. Първо, нека намерим детерминантата на дадената матрица $A$:

$$ \Delta A=\left| \begin(array) (cc) -5 & 7\\ 9 & 8 \end(array)\right|=-5\cdot 8-7\cdot 9=-103. $$

Тъй като $\Delta A \neq 0$, тогава обратната матрица съществува, така че ние продължаваме решението. Намиране на алгебрични допълнения

\begin(aligned) & A_(11)=(-1)^2\cdot 8=8; \; A_(12)=(-1)^3\cdot 9=-9;\\ & A_(21)=(-1)^3\cdot 7=-7; \; A_(22)=(-1)^4\cdot (-5)=-5.\\ \end(подравнено)

Съставете матрица от алгебрични допълнения: $A^(*)=\left(\begin(array) (cc) 8 & -9\\ -7 & -5 \end(array)\right)$.

Транспонирайте получената матрица: $(A^(*))^T=\left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right)$ (резултантната матрицата често се нарича присъединена или обединена матрица към матрицата $A$). Използвайки формулата $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, имаме:

$$ A^(-1)=\frac(1)(-103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right) =\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right) $$

Така се намира обратната матрица: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array) \вдясно) $. За да проверите истинността на резултата, е достатъчно да проверите истинността на едно от равенствата: $A^(-1)\cdot A=E$ или $A\cdot A^(-1)=E$. Нека проверим равенството $A^(-1)\cdot A=E$. За да работим по-малко с дроби, ще заместим матрицата $A^(-1)$ не във формата $\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \ end(array)\right)$ но като $-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \ край (масив)\десен)$:

$$ A^(-1)\cdot(A) =-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end( array)\right)\cdot\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right) =-\frac(1)(103)\cdot\left( \begin(array) (cc) -103 & 0 \\ 0 & -103 \end(array)\right) =\left(\begin(array) (cc) 1 & 0 \\ 0 & 1 \end(array) )\вдясно) =E $$

Отговор: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right)$.

Пример #3

Намерете обратната на матрицата $A=\left(\begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right)$. Пуснете проверка.

Нека започнем с изчисляване на детерминантата на матрицата $A$. И така, детерминантата на матрицата $A$ е:

$$ \Delta A=\left| \begin(масив) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(масив) \right| = 18-36+56-12=26. $$

Тъй като $\Delta A\neq 0$, тогава обратната матрица съществува, така че продължаваме решението. Намираме алгебричните допълнения на всеки елемент от дадената матрица:

Съставяме матрица от алгебрични добавки и я транспонираме:

$$ A^*=\left(\begin(array) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37\end(array) \right); \; (A^*)^T=\left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right) . $$

Използвайки формулата $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, получаваме:

$$ A^(-1)=\frac(1)(26)\cdot \left(\begin(масив) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37\end(array) \right)= \left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \end(array) \right) $$

Така че $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 & -3/26 & 37/26 \end(array) \right)$. За да проверите истинността на резултата, е достатъчно да проверите истинността на едно от равенствата: $A^(-1)\cdot A=E$ или $A\cdot A^(-1)=E$. Нека проверим равенството $A\cdot A^(-1)=E$. За да работим по-малко с дроби, ще заместим матрицата $A^(-1)$ не във формата $\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \ \ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end(array) \right)$, но като $\frac(1)(26)\ cdot \left( \begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right)$:

$$ A\cdot(A^(-1)) =\left(\begin(array)(ccc) 1 & 7 & 3 \\ -4 & 9 & 4\\ 0 & 3 & 2\end(array) \right)\cdot \frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\ край (масив) \right) =\frac(1)(26)\cdot\left(\begin(масив) (ccc) 26 & 0 & 0 \\ 0 & 26 & 0 \\ 0 & 0 & 26\end (масив) \right) =\left(\begin(array) (ccc) 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end(array) \right) =E $$

Проверката е преминала успешно, обратната матрица $A^(-1)$ е намерена правилно.

Отговор: $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 /13 & -3/26 & 37/26 \end(array) \right)$.

Пример #4

Намерете матрица, обратна на $A=\left(\begin(array) (cccc) 6 & -5 & 8 & 4\\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7\\ -4 & 8 & -8 & -3 \end(array) \right)$.

За матрица от четвърти ред, намирането на обратната матрица с помощта на алгебрични добавки е малко трудно. Такива примери обаче се срещат в контролните работи.

За да намерите обратната матрица, първо трябва да изчислите детерминантата на матрицата $A$. Най-добрият начин да направите това в тази ситуация е да разширите детерминантата в ред (колона). Избираме всеки ред или колона и намираме алгебричното допълнение на всеки елемент от избрания ред или колона.

Например за първия ред получаваме:

$$ A_(11)=\left|\begin(array)(ccc) 7 & 5 & 2\\ 5 & 3 & 7\\ 8 & -8 & -3 \end(array)\right|=556; \; A_(12)=-\left|\begin(array)(ccc) 9 & 5 & 2\\ 7 & 3 & 7 \\ -4 & -8 & -3 \end(array)\right|=-300 ; $$ $$ A_(13)=\left|\begin(array)(ccc) 9 & 7 & 2\\ 7 & 5 & 7\\ -4 & 8 & -3 \end(array)\right|= -536;\; A_(14)=-\left|\begin(array)(ccc) 9 & 7 & 5\\ 7 & 5 & 3\\ -4 & 8 & -8 \end(array)\right|=-112. $$

Детерминантата на матрицата $A$ се изчислява по следната формула:

$$ \Delta(A)=a_(11)\cdot A_(11)+a_(12)\cdot A_(12)+a_(13)\cdot A_(13)+a_(14)\cdot A_(14) )=6\cdot 556+(-5)\cdot(-300)+8\cdot(-536)+4\cdot(-112)=100. $$

$$ \begin(aligned) & A_(21)=-77;\;A_(22)=50;\;A_(23)=87;\;A_(24)=4;\\ & A_(31) =-93;\;A_(32)=50;\;A_(33)=83;\;A_(34)=36;\\ & A_(41)=473;\;A_(42)=-250 ;\;A_(43)=-463;\;A_(44)=-96. \end(подравнено) $$

Алгебрична допълнителна матрица: $A^*=\left(\begin(array)(cccc) 556 & -300 & -536 & -112\\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36 \\ 473 & -250 & -463 & -96\end(array)\right)$.

Прикачена матрица: $(A^*)^T=\left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96\end(array)\right)$.

Обратна матрица:

$$ A^(-1)=\frac(1)(100)\cdot \left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96 \end(array) \right)= \left(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/ 25 & 1/25 & 9/25 & -24/25 \end(array) \right) $$

Проверката, ако желаете, може да се извърши по същия начин, както в предишните примери.

Отговор: $A^(-1)=\left(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/25 & 9/25 & -24/25 \end(array) \right) $.

Във втората част ще бъде разгледан друг начин за намиране на обратната матрица, който включва използването на трансформации на метода на Гаус или метода на Гаус-Джордан.

Продължаваме да говорим за действия с матрици. А именно, в хода на изучаването на тази лекция ще научите как да намерите обратната матрица. Уча. Дори ако математиката е тясна.

Какво е обратна матрица? Тук можем да направим аналогия с реципрочните числа: разгледайте например оптимистичното число 5 и неговата реципрочна стойност. Произведението на тези числа е равно на едно: . Същото е и с матриците! Произведението на матрица и нейната обратна е - матрица на идентичността, което е матричният аналог на числовата единица. Въпреки това, първо ще решим един важен практически проблем, а именно ще се научим как да намираме тази много обратна матрица.

Какво трябва да знаете и да можете да намерите обратната матрица? Трябва да можеш да решаваш детерминанти. Трябва да разберете какво е матрицаи да можете да извършвате някои действия с тях.

Има два основни метода за намиране на обратната матрица:
като се използва алгебрични добавкии с помощта на елементарни трансформации.

Днес ще изучаваме първия, по-лесен начин.

Да започнем с най-ужасното и неразбираемо. Обмисли квадратматрица . Обратната матрица може да се намери с помощта на следната формула:

Където е детерминантата на матрицата, е транспонираната матрица от алгебрични допълнения на съответните елементи на матрицата.

Концепцията за обратна матрица съществува само за квадратни матрици, матрици "две по две", "три по три" и др.

Нотация: Както вероятно вече сте забелязали, обратната на матрица се обозначава с горен индекс

Да започнем с най-простия случай - матрица две на две. Най-често, разбира се, се изисква "три по три", но въпреки това силно препоръчвам да изучавате по-проста задача, за да научите общия принцип на решението.

Пример:

Намерете обратното на матрица

Ние решаваме. Последователността от действия е удобно разложена на точки.

1) Първо намираме детерминантата на матрицата.

Ако разбирането на това действие не е добро, прочетете материала Как да изчислим детерминантата?

важно!Ако детерминантата на матрицата е НУЛА– обратна матрица НЕ СЪЩЕСТВУВА.

В разглеждания пример, както се оказа, , което означава, че всичко е наред.

2) Намерете матрицата на минорите.

За да разрешим нашия проблем, не е необходимо да знаем какво е непълнолетно лице, но е препоръчително да прочетете статията Как да изчислим детерминантата.

Матрицата на минорите има същите размери като матрицата , т.е. в този случай .
Случаят е малък, остава да намерите четири числа и да ги поставите вместо звездички.

Обратно към нашата матрица
Нека първо разгледаме горния ляв елемент:

Как да го намерите незначителен?
И това се прави по следния начин: УМСТВЕНО зачеркнете реда и колоната, в които се намира този елемент:

Останалият брой е минор на дадения елемент, което записваме в нашата матрица от второстепенни:

Разгледайте следния матричен елемент:

Мислено задраскайте реда и колоната, в които се намира този елемент:

Това, което остава, е минорът на този елемент, който записваме в нашата матрица:

По същия начин разглеждаме елементите на втория ред и намираме техните второстепенни:

Готов.

Просто е. В матрицата на непълнолетните се нуждаете ПРОМЯНА НА ЗНАЦИза две числа:

Точно тези цифри съм оградил!

е матрицата на алгебричните допълнения на съответните елементи на матрицата .

И само нещо…

4) Намерете транспонираната матрица на алгебрични добавки.

е транспонираната матрица от алгебрични добавки на съответните елементи на матрицата.

5) Отговор.

Запомнете нашата формула
Всички намерени!

Така че обратната матрица е:

Най-добре е да оставите отговора такъв, какъвто е. НЯМА НУЖДАразделете всеки елемент от матрицата на 2, като ще се получат дробни числа. Този нюанс е разгледан по-подробно в същата статия. Действия с матрици.

Как да проверите решението?

Трябва да се извърши и матрично умножение

Преглед:

вече споменах матрица на идентичносттае матрица с включени единици главен диагонали нули другаде.

По този начин обратната матрица се намира правилно.

Ако извършите действие, тогава резултатът също ще бъде матрица за идентичност. Това е един от малкото случаи, когато умножението на матрицата е пермутабилно, повече информация можете да намерите в статията Свойства на операциите върху матрици. Матрични изрази. Също така имайте предвид, че по време на проверката константата (дробта) се изнася напред и се обработва в самия край - след умножението на матрицата. Това е стандартен прием.

Нека да преминем към по-често срещан случай в практиката - матрицата три по три:

Пример:

Намерете обратното на матрица

Алгоритъмът е абсолютно същият като в случая две по две.

Намираме обратната матрица по формулата: , където е транспонираната матрица от алгебрични допълнения на съответните елементи на матрицата .

1) Намерете детерминанта на матрицата.

Тук се разкрива детерминантата на първия ред.

Освен това не забравяйте това, което означава, че всичко е наред - съществува обратна матрица.

2) Намерете матрицата на минорите.

Матрицата на минорите има размерността "три по три" и трябва да намерим девет числа.

Ще разгледам подробно няколко непълнолетни:

Разгледайте следния матричен елемент:

УМСТВЕНО задраскайте реда и колоната, в които се намира този елемент:

Останалите четири числа са записани в определителя "две по две"

Тази детерминанта две по две и е минор на дадения елемент. Необходимо е да се изчисли:

Всичко, минорът е намерен, ние го записваме в нашата матрица от минори:

Както може би се досещате, има девет детерминанти две по две за изчисляване. Процесът, разбира се, е досаден, но случаят не е най-трудният, може да бъде и по-лош.

Е, за консолидиране - намиране на друг непълнолетен в снимките:

Опитайте сами да изчислите останалите непълнолетни.

Краен резултат:
е матрицата на минорите на съответните елементи на матрицата .

Това, че всички непълнолетни се оказаха отрицателни, е чиста случайност.

3) Намерете матрицата на алгебричните добавки.

В матрицата на непълнолетните е необходимо ПРОМЯНА НА ЗНАЦИстрого за следните елементи:

В такъв случай:

Намирането на обратната матрица за матрицата „четири по четири“ не се разглежда, тъй като само садистичен учител може да даде такава задача (за ученика да изчисли една детерминанта „четири по четири“ и 16 детерминанти „три по три“) . В моята практика имаше само един такъв случай и клиентът на теста плати за мъките ми доста скъпо =).

В редица учебници, ръководства можете да намерите малко по-различен подход за намиране на обратната матрица, но препоръчвам да използвате горния алгоритъм за решение. Защо? Тъй като вероятността да се объркате в изчисленията и знаците е много по-малка.

Тази тема е една от най-омразните сред студентите. По-лошо, вероятно, само детерминанти.

Номерът е, че самата концепция за обратния елемент (и сега не говоря само за матрици) ни препраща към операцията умножение. Дори в училищната програма умножението се счита за сложна операция, а матричното умножение като цяло е отделна тема, на която имам цял параграф и видео урок, посветен на нея.

Днес няма да навлизаме в детайлите на матричните изчисления. Само запомнете: как се обозначават матриците, как се умножават и какво следва от това.

Преглед: Матрично умножение

Първо, нека се споразумеем за нотацията. Матрица $A$ с размер $\left[ m\times n \right]$ е просто таблица с числа с точно $m$ реда и $n$ колони:

\=\под скоба(\left[ \begin(matrix) ((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) \\ (( a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) \\ ... & ... & ... & ... \\ ((a)_(m1)) & ((a)_(m2)) & ... & ((a)_(mn)) \\\end(matrix) \right])_(n)\]

За да не объркате случайно редове и колони на места (повярвайте ми, на изпита можете да объркате един с двойка - какво да кажем за някои редове там), просто погледнете снимката:

Определяне на индекси за матрични клетки

Какво се случва? Ако поставим стандартната координатна система $OXY$ в горния ляв ъгъл и насочим осите така, че да покриват цялата матрица, тогава всяка клетка от тази матрица може да бъде уникално свързана с координатите $\left(x;y \right) $ - това ще бъде номера на реда и номера на колоната.

Защо координатната система е поставена точно в горния ляв ъгъл? Да, защото именно оттам започваме да четем всякакви текстове. Много лесно се запомня.

Защо оста $x$ сочи надолу, а не надясно? Отново е просто: вземете стандартната координатна система (оста $x$ върви надясно, оста $y$ върви нагоре) и я завъртете така, че да обхваща матрицата. Това е завъртане на 90 градуса по часовниковата стрелка - виждаме резултата от него на снимката.

Като цяло разбрахме как да определим индексите на матричните елементи. Сега нека се заемем с умножението.

Определение. Матриците $A=\left[ m\times n \right]$ и $B=\left[ n\times k \right]$, когато броят на колоните в първата съответства на броя на редовете във втората, са наречена последователна.

В този ред е. Човек може да бъде двусмислен и да каже, че матриците $A$ и $B$ образуват подредена двойка $\left(A;B \right)$: ако те са последователни в този ред, тогава изобщо не е необходимо $B $ и $A$, тези. двойката $\left(B;A \right)$ също е последователна.

Само последователни матрици могат да бъдат умножени.

Определение. Произведението на последователни матрици $A=\left[ m\times n \right]$ и $B=\left[ n\times k \right]$ е новата матрица $C=\left[ m\times k \right ]$ , чиито елементи $((c)_(ij))$ се изчисляват по формулата:

\[((c)_(ij))=\sum\limits_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

С други думи: за да получите елемента $((c)_(ij))$ на матрицата $C=A\cdot B$, трябва да вземете $i$-реда на първата матрица, $j$ -та колона на втората матрица и след това умножете по двойки елементи от този ред и колона. Съберете резултатите.

Да, това е сурово определение. От него веднага следват няколко факта:

Матричното умножение е, най-общо казано, некомутативно: $A\cdot B\ne B\cdot A$;
Умножението обаче е асоциативно: $\left(A\cdot B \right)\cdot C=A\cdot \left(B\cdot C \right)$;
И дори разпределителен: $\left(A+B \right)\cdot C=A\cdot C+B\cdot C$;
И отново дистрибутив: $A\cdot \left(B+C \right)=A\cdot B+A\cdot C$.

Дистрибутивността на умножението трябваше да бъде описана отделно за левия и десния умножител-сума само поради некомутативността на операцията за умножение.

Ако въпреки това се окаже, че $A\cdot B=B\cdot A$, такива матрици се наричат пермутабилни.

Сред всички матрици, които се умножават по нещо там, има специални - тези, които, когато се умножат по произволна матрица $A$, отново дават $A$:

Определение. Матрица $E$ се нарича идентичност, ако $A\cdot E=A$ или $E\cdot A=A$. В случай на квадратна матрица $A$ можем да запишем:

Идентификационната матрица е чест гост при решаването на матрични уравнения. И като цяло, чест гост в света на матриците. :)

И заради това $E$ някой измисли цялата игра, която ще бъде написана по-нататък.

Какво е обратна матрица

Тъй като умножението на матрицата е много отнемаща време операция (трябва да умножите куп редове и колони), концепцията за обратна матрица също не е най-тривиалната. И има нужда от някакво обяснение.

Ключова дефиниция

Е, време е да разберем истината.

Определение. Матрицата $B$ се нарича обратна на матрицата $A$ ако

Обратната матрица се обозначава с $((A)^(-1))$ (да не се бърка със степента!), така че определението може да бъде пренаписано по следния начин:

Изглежда, че всичко е изключително просто и ясно. Но когато се анализира такова определение, веднага възникват няколко въпроса:

Винаги ли съществува обратна матрица? И ако не винаги, тогава как да се определи: кога съществува и кога не?
И кой каза, че такава матрица е точно една? Ами ако за някаква оригинална матрица $A$ има цяла тълпа обратни?
Как изглеждат всички тези "обратни"? И как всъщност ги броите?

Що се отнася до алгоритмите за изчисление - ще говорим за това малко по-късно. Но на останалите въпроси ще отговорим точно сега. Нека ги подредим под формата на отделни твърдения-леми.

Основни свойства

Нека започнем с това как трябва да изглежда матрицата $A$, за да има $((A)^(-1))$. Сега ще се уверим, че и двете от тези матрици трябва да са квадратни и с еднакъв размер: $\left[ n\times n \right]$.

Лема 1. Дадена е матрица $A$ и нейната обратна $((A)^(-1))$. Тогава и двете от тези матрици са квадратни и имат еднакъв ред $n$.

Доказателство. Всичко е просто. Нека матрицата $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ a\times b \right]$. Тъй като продуктът $A\cdot ((A)^(-1))=E$ съществува по дефиниция, матриците $A$ и $((A)^(-1))$ са последователни в този ред:

\[\begin(align) & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end( подравняване)\]

Това е пряко следствие от алгоритъма за умножение на матрици: коефициентите $n$ и $a$ са "транзитни" и трябва да бъдат равни.

В същото време обратното умножение също е дефинирано: $((A)^(-1))\cdot A=E$, така че матриците $((A)^(-1))$ и $A$ са също в съответствие в този ред:

\[\begin(align) & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end( подравняване)\]

Така, без загуба на общост, можем да приемем, че $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ n\times m \right]$. Въпреки това, според дефиницията на $A\cdot ((A)^(-1))=((A)^(-1))\cdot A$, така че размерите на матриците са абсолютно еднакви:

\[\begin(align) & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end(align)\]

Така се оказва, че и трите матрици - $A$, $((A)^(-1))$ и $E$ - са квадратни по размер $\left[ n\times n \right]$. Лемата е доказана.

Е, това вече е добре. Виждаме, че само квадратните матрици са обратими. Сега нека се уверим, че обратната матрица е винаги една и съща.

Лема 2. Дадена е матрица $A$ и нейната обратна $((A)^(-1))$. Тогава тази обратна матрица е уникална.

Доказателство. Да започнем от обратното: нека матрицата $A$ има поне два случая на обратни — $B$ и $C$. Тогава според определението са верни следните равенства:

\[\begin(align) & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \край (подравняване)\]

От лема 1 заключаваме, че и четирите матрици $A$, $B$, $C$ и $E$ са квадратни от един и същи ред: $\left[ n\times n \right]$. Следователно продуктът се определя:

Тъй като матричното умножение е асоциативно (но не комутативно!), можем да напишем:

\[\begin(align) & B\cdot A\cdot C=\left(B\cdot A \right)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \left(A\cdot C \right)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\Стрелка надясно B=C. \\ \край (подравняване)\]

Получихме единствената възможна опция: две копия на обратната матрица са равни. Лемата е доказана.

Горното разсъждение почти дословно повтаря доказателството за уникалността на обратния елемент за всички реални числа $b\ne 0$. Единственото съществено допълнение е вземането под внимание на размерността на матриците.

Все още обаче не знаем нищо за това дали всяка квадратна матрица е обратима. Тук на помощ ни идва детерминантата – това е ключова характеристика за всички квадратни матрици.

Лема 3. Дадена е матрица $A$. Ако матрицата $((A)^(-1))$ съществува, обратна на нея, тогава детерминантата на оригиналната матрица е различна от нула:

\[\ляво| A \right|\ne 0\]

Доказателство. Вече знаем, че $A$ и $((A)^(-1))$ са квадратни матрици с размер $\left[ n\times n \right]$. Следователно за всеки от тях е възможно да се изчисли детерминантата: $\left| A \right|$ и $\left| ((A)^(-1)) \right|$. Детерминантата на продукта обаче е равна на произведението на детерминантите:

\[\ляво| A\cdot B \right|=\left| A \right|\cdot \left| B \right|\Rightarrow \left| A\cdot ((A)^(-1)) \right|=\left| A \right|\cdot \left| ((A)^(-1)) \right|\]

Но според дефиницията на $A\cdot ((A)^(-1))=E$ и детерминантата на $E$ винаги е равна на 1, така че

\[\begin(align) & A\cdot ((A)^(-1))=E; \\ & \left| A\cdot ((A)^(-1)) \right|=\left| E\надясно|; \\ & \left| A \right|\cdot \left| ((A)^(-1)) \right|=1. \\ \край (подравняване)\]

Произведението на две числа е равно на единица само ако всяко от тези числа е различно от нула:

\[\ляво| A \right|\ne 0;\quad \left| ((A)^(-1)) \right|\ne 0.\]

Така се оказва, че $\left| A \right|\ne 0$. Лемата е доказана.

Всъщност това изискване е съвсем логично. Сега ще анализираме алгоритъма за намиране на обратната матрица - и ще стане напълно ясно защо по принцип не може да съществува обратна матрица с нулев детерминант.

Но първо, нека формулираме "спомагателна" дефиниция:

Определение. Изродената матрица е квадратна матрица с размер $\left[ n\times n \right]$, чиято детерминанта е нула.

По този начин можем да твърдим, че всяка обратима матрица е неизродена.

Как да намерим обратната матрица

Сега ще разгледаме универсален алгоритъм за намиране на обратни матрици. Като цяло има два общоприети алгоритъма и днес ще разгледаме втория.

Тази, която ще разгледаме сега, е много ефективна за матрици с размер $\left[ 2\times 2 \right]$ и - отчасти - с размер $\left[ 3\times 3 \right]$. Но като се започне от размера $\left[ 4\times 4 \right]$ е по-добре да не го използвате. Защо - сега ще разберете всичко.

Алгебрични допълнения

Приготви се. Сега ще има болка. Не, не се притеснявайте: красива медицинска сестра в пола, чорапи с дантела не идва при вас и няма да ви постави инжекция в дупето. Всичко е много по-прозаично: алгебричните допълнения и Нейно Величество „Матрицата на съюза“ идват при вас.

Да започнем с основното. Нека има квадратна матрица с размер $A=\left[ n\times n \right]$, чиито елементи се наричат $((a)_(ij))$. Тогава за всеки такъв елемент може да се дефинира алгебрично допълнение:

Определение. Алгебрично допълнение $((A)_(ij))$ към елемента $((a)_(ij))$ в $i$-тия ред и $j$-та колона на матрицата $A=\left [ n \times n \right]$ е конструкция на формата

\[((A)_(ij))=((\left(-1 \right))^(i+j))\cdot M_(ij)^(*)\]

Където $M_(ij)^(*)$ е детерминантата на матрицата, получена от оригиналния $A$ чрез изтриване на същия $i$-ти ред и $j$-та колона.

Отново. Алгебричното допълнение към матричния елемент с координати $\left(i;j \right)$ се означава като $((A)_(ij))$ и се изчислява по схемата:

Първо изтриваме $i$-реда и $j$-тата колона от оригиналната матрица. Получаваме нова квадратна матрица и означаваме нейния детерминант като $M_(ij)^(*)$.
След това умножаваме този детерминант по $((\left(-1 \right))^(i+j))$ - първоначално този израз може да изглежда умопомрачителен, но всъщност просто намираме знака пред $ M_(ij)^(*) $.
Ние броим - получаваме конкретно число. Тези. алгебричното събиране е просто число, а не някаква нова матрица и т.н.

Самата матрица $M_(ij)^(*)$ се нарича допълнителен минор към елемента $((a)_(ij))$. И в този смисъл горната дефиниция на алгебрично допълнение е частен случай на по-сложна дефиниция - тази, която разгледахме в урока за детерминантата.

Важна забележка. Всъщност в математиката за "възрастни" алгебричните добавки се дефинират, както следва:

Вземаме $k$ реда и $k$ колони в квадратна матрица. При тяхното пресичане получаваме матрица с размер $\left[ k\times k \right]$ — нейният детерминант се нарича минор от порядък $k$ и се обозначава с $((M)_(k))$.

След това задраскваме тези "избрани" $k$ реда и $k$ колони. Отново получаваме квадратна матрица - нейният детерминант се нарича допълнителен минор и се означава с $M_(k)^(*)$.

Умножете $M_(k)^(*)$ по $((\left(-1 \right))^(t))$, където $t$ е (внимание!) сумата от числата на всички избрани редове и колони. Това ще бъде алгебричното добавяне.

Обърнете внимание на третата стъпка: всъщност има сума от $2k$ условия! Друго нещо е, че за $k=1$ получаваме само 2 члена - това ще бъдат същите $i+j$ - "координатите" на елемента $((a)_(ij))$, за който сме търси алгебрично допълнение.

Затова днес използваме леко опростена дефиниция. Но както ще видим по-късно, това ще бъде повече от достатъчно. Много по-важно е следното:

Определение. Обединителната матрица $S$ към квадратната матрица $A=\left[ n\times n \right]$ е нова матрица с размер $\left[ n\times n \right]$, която се получава от $A$ чрез заместване на $(( a)_(ij))$ с алгебрични допълнения $((A)_(ij))$:

\\Rightarrow S=\left[ \begin(matrix) ((A)_(11)) & ((A)_(12)) & ... & ((A)_(1n)) \\ (( A)_(21)) & ((A)_(22)) & ... & ((A)_(2n)) \\ ... & ... & ... & ... \\ ((A)_(n1)) & ((A)_(n2)) & ... & ((A)_(nn)) \\\end(matrix) \right]\]

Първата мисъл, която възниква в момента на осъзнаване на това определение е „ето колко трябва да броите общо!“ Спокойно: трябва да броите, но не толкова. :)

Е, всичко това е много хубаво, но защо е необходимо? Но защо.

Основна теорема

Да се върнем малко назад. Спомнете си, лема 3 твърди, че една обратима матрица $A$ винаги е неособена (т.е. нейният детерминант е различен от нула: $\left| A \right|\ne 0$).

Така че обратното също е вярно: ако матрицата $A$ не е изродена, тогава тя винаги е обратима. И дори има схема за търсене $((A)^(-1))$. Виж това:

Теорема за обратната матрица. Нека е дадена квадратна матрица $A=\left[ n\times n \right]$ и нейният детерминант е различен от нула: $\left| A \right|\ne 0$. Тогава обратната матрица $((A)^(-1))$ съществува и се изчислява по формулата:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))\]

И сега – все същото, но с четлив почерк. За да намерите обратната матрица, трябва:

Изчислете детерминантата $\left| A \right|$ и се уверете, че е различно от нула.
Компилирайте обединителната матрица $S$, т.е. пребройте 100500 алгебрични добавки $((A)_(ij))$ и ги поставете на място $((a)_(ij))$.
Транспонирайте тази матрица $S$ и след това я умножете по някакво число $q=(1)/(\left| A \right|)\;$.

И това е! Намерена е обратната матрица $((A)^(-1))$. Нека да разгледаме примери:

\[\left[ \begin(matrix) 3 & 1 \\ 5 & 2 \\\end(matrix) \right]\]

Решение. Да проверим обратимостта. Нека изчислим детерминантата:

\[\ляво| A \дясно|=\ляво| \begin(matrix) 3 & 1 \\ 5 & 2 \\\end(matrix) \right|=3\cdot 2-1\cdot 5=6-5=1\]

Детерминантата е различна от нула. Така че матрицата е обратима. Нека създадем обединителна матрица:

Нека изчислим алгебричните добавки:

\[\begin(align) & ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| 2\вдясно|=2; \\ & ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| 5\вдясно|=-5; \\ & ((A)_(21))=((\left(-1 \right))^(2+1))\cdot \left| 1 \right|=-1; \\ & ((A)_(22))=((\left(-1 \right))^(2+2))\cdot \left| 3\надясно|=3. \\ \край (подравняване)\]

Обърнете внимание: детерминанти |2|, |5|, |1| и |3| са детерминантите на матрици с размер $\left[ 1\times 1 \right]$, а не модули. Тези. ако в детерминантите имаше отрицателни числа, не е необходимо да премахвате "минуса".

Общо нашата матрица на съюза изглежда така:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))=\frac(1)(1)\cdot ( (\left[ \begin(array)(*(35)(r)) 2 & -5 \\ -1 & 3 \\\end(array) \right])^(T))=\left[ \begin (масив)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\край (масив) \right]\]

Добре, всичко свърши. Проблема решен.

Отговор. $\left[ \begin(array)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(array) \right]$

Задача. Намерете обратната матрица:

\[\left[ \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(array) \right] \]

Решение. Отново разглеждаме детерминантата:

\[\begin(align) & \left| \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(array) \right|=\begin(matrix ) \left(1\cdot 2\cdot 1+\left(-1 \right)\cdot \left(-1 \right)\cdot 1+2\cdot 0\cdot 0 \right)- \\ -\left (2\cdot 2\cdot 1+\left(-1 \right)\cdot 0\cdot 1+1\cdot \left(-1 \right)\cdot 0 \right) \\\end(matrix)= \ \ & =\left(2+1+0 \right)-\left(4+0+0 \right)=-1\ne 0. \\ \end(align)\]

Детерминантата е различна от нула - матрицата е обратима. Но сега ще бъде най-тенекиеното: трябва да преброите цели 9 (девет, по дяволите!) Алгебрични добавки. И всеки от тях ще съдържа квалификатора $\left[ 2\times 2 \right]$. Летя:

\[\begin(matrix) ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| \begin(matrix) 2 & -1 \\ 0 & 1 \\\end(matrix) \right|=2; \\ ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| \begin(matrix) 0 & -1 \\ 1 & 1 \\\end(matrix) \right|=-1; \\ ((A)_(13))=((\left(-1 \right))^(1+3))\cdot \left| \begin(matrix) 0 & 2 \\ 1 & 0 \\\end(matrix) \right|=-2; \\ ... \\ ((A)_(33))=((\left(-1 \right))^(3+3))\cdot \left| \begin(matrix) 1 & -1 \\ 0 & 2 \\\end(matrix) \right|=2; \\ \край (матрица)\]

Накратко, матрицата на обединението ще изглежда така:

Следователно обратната матрица ще бъде:

\[((A)^(-1))=\frac(1)(-1)\cdot \left[ \begin(matrix) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end(matrix) \right]=\left[ \begin(array)(*(35)(r))-2 & -1 & 3 \\ 1 & 1 & -1 \ \ 2 & 1 & -2 \\\end(масив) \right]\]

Е, това е всичко. Ето и отговора.

Отговор. $\left[ \begin(array)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end(array) \right ]$

Както можете да видите, в края на всеки пример извършихме проверка. В тази връзка важна забележка:

Не бъдете мързеливи, за да проверите. Умножете оригиналната матрица по намерената обратна - трябва да получите $E$.

Много по-лесно и по-бързо е да извършите тази проверка, отколкото да търсите грешка в следващите изчисления, когато например решавате матрично уравнение.

Алтернативен начин

Както казах, теоремата за обратната матрица работи добре за размерите $\left[ 2\times 2 \right]$ и $\left[ 3\times 3 \right]$ (във последния случай не е толкова "красиво" вече). ”), но за големите матрици започва тъгата.

Но не се притеснявайте: има алтернативен алгоритъм, който може да се използва за спокойно намиране на обратната дори за матрицата $\left[ 10\times 10 \right]$. Но, както често се случва, за да разгледаме този алгоритъм, имаме нужда от малко теоретична подготовка.

Елементарни трансформации

Сред различните трансформации на матрицата има няколко специални - те се наричат елементарни. Има точно три такива трансформации:

Умножение. Можете да вземете $i$-тия ред (колона) и да го умножите по произволно число $k\ne 0$;
Допълнение. Добавете към $i$-тия ред (колона) всеки друг $j$-ти ред (колона), умножен по произволно число $k\ne 0$ (разбира се, $k=0$ също е възможно, но какъв е смисълът от това? ?Нищо няма да се промени обаче).
Пермутация. Вземете $i$-тия и $j$-тия ред (колони) и ги разменете.

Защо тези трансформации се наричат елементарни (за големи матрици те не изглеждат толкова елементарни) и защо има само три от тях - тези въпроси са извън обхвата на днешния урок. Затова няма да навлизаме в подробности.

Друго нещо е важно: ние трябва да извършим всички тези извращения върху свързаната матрица. Да, да, чухте правилно. Сега ще има още едно определение - последното в днешния урок.

Приложена матрица

Със сигурност в училище сте решавали системи от уравнения, използвайки метода на добавяне. Е, ето, извадете друг от един ред, умножете някой ред по число - това е всичко.

И така: сега всичко ще бъде същото, но вече „по възрастен начин“. Готов?

Определение. Нека са дадени матрицата $A=\left[ n\times n \right]$ и матрицата на идентичност $E$ със същия размер $n$. Тогава свързаната матрица $\left[ A\left| E \ дясно. \right]$ е нова $\left[ n\times 2n \right]$ матрица, която изглежда така:

\[\left[ A\left| E \ дясно. \right]=\left[ \begin(array)(rrrr|rrrr)((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) & 1 & 0 & ... & 0 \\((a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... & ... \\((a)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\end(array) \right]\]

Накратко, вземаме матрицата $A$, отдясно й присвояваме матрицата за идентичност $E$ с необходимия размер, разделяме ги с вертикална лента за красота - ето приложената. :)

Каква е уловката? И ето какво:

Теорема. Нека матрицата $A$ е обратима. Разгледайте присъединената матрица $\left[ A\left| E \ дясно. \right]$. Ако използвате елементарни низови трансформациипренесете го във формата $\left[ E\left| Ярък. \right]$, т.е. чрез умножаване, изваждане и пренареждане на редове, за да се получи от $A$ матрицата $E$ отдясно, тогава матрицата $B$, получена отляво, е обратната на $A$:

\[\left[ A\left| E \ дясно. \right]\to \left[ E\left| Ярък. \right]\Rightarrow B=((A)^(-1))\]

Толкова е просто! Накратко, алгоритъмът за намиране на обратната матрица изглежда така:

Напишете свързаната матрица $\left[ A\left| E \ дясно. \right]$;
Извършете елементарни преобразувания на низове, докато вдясно вместо $A$ се появи $E$;
Разбира се, нещо ще се появи и отляво - определена матрица $B$. Това ще бъде обратното;
ПЕЧАЛБИ! :)

Разбира се, много по-лесно е да се каже, отколкото да се направи. Нека да разгледаме няколко примера: за размерите $\left[ 3\times 3 \right]$ и $\left[ 4\times 4 \right]$.

Задача. Намерете обратната матрица:

\[\left[ \begin(array)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end(array) \right]\ ]

Решение. Съставяме приложената матрица:

\[\left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end(масив) \right]\]

Тъй като последната колона на оригиналната матрица е пълна с единици, извадете първия ред от останалите:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\end(масив) \right]\begin(matrix) \downarrow \\ -1 \\ -1 \\\end(matrix)\to \\ & \to \left [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 \\ & 1 \\\end(array) \right] \\ \end(align)\]

Няма повече единици, с изключение на първия ред. Но ние не го докосваме, в противен случай новоотстранените единици ще започнат да се "умножават" в третата колона.

Но можем да извадим втория ред два пъти от последния - получаваме единица в долния ляв ъгъл:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(масив) \right]\begin(matrix) \ \\ \downarrow \\ -2 \\\end(matrix)\to \\ & \left [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right] \\ \end(align)\]

Сега можем да извадим последния ред от първия и два пъти от втория - по този начин ще "нулираме" първата колона:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(масив) \right]\begin(matrix) -1 \\ -2 \\ \стрелка нагоре \\\end(matrix)\to \\ & \ към \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right] \\ \end(align)\]

Умножете втория ред по −1 и след това го извадете 6 пъти от първия и добавете 1 път към последния:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\end(масив) \right]\begin(matrix) \ \\ \left| \cdot \left(-1 \right) \right. \\ \ \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(масив) \right]\begin(matrix) -6 \\ \updownarrow \\ +1 \\\end (матрица)\to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\end(масив) \right] \\ \end(align)\]

Остава само да размените редове 1 и 3:

\[\left[ \begin(array)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 & 32 & -13 \\\end(масив) \right]\]

Готов! Вдясно е необходимата обратна матрица.

Отговор. $\left[ \begin(array)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end(array) \right ]$

Задача. Намерете обратната матрица:

\[\left[ \begin(matrix) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\end(matrix) \right]\]

Решение. Отново съставяме прикачения:

\[\left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right]\]

Нека вземем малко назаем, да се погрижим колко трябва да броим сега ... и да започнем да броим. Като начало ние „нулираме“ първата колона, като извадим ред 1 от редове 2 и 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\край (масив) \right]\begin(matrix) \downarrow \\ -1 \\ -1 \\ \ \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right] \\ \end(align)\]

Наблюдаваме твърде много "минуси" в редове 2-4. Умножете всичките три реда по −1 и след това изгорете третата колона, като извадите ред 3 от останалите:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \end(масив) \right]\begin(matrix) \ \\ \left| \cdot \left(-1 \right) \right. \\ \ляво| \cdot \left(-1 \right) \right. \\ \ляво| \cdot \left(-1 \right) \right. \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & 1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\ \end (масив) \right]\begin(matrix) -2 \\ -1 \\ \updownarrow \\ -2 \\\end(matrix)\to \\ & \to \left[ \begin(array)( rrrr| rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

Сега е време да "изпържим" последната колона от оригиналната матрица: извадете ред 4 от останалите:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(масив ) \right]\begin(matrix) +1 \\ -3 \\ -2 \\ \uparrow \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

Последно хвърляне: "изгорете" втората колона, като извадите ред 2 от ред 1 и 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end( array) \right]\begin(matrix) 6 \\ \updownarrow \\ -5 \\ \ \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

И отново, идентичната матрица отляво, така че обратното отдясно. :)

Отговор. $\left[ \begin(matrix) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\end(matrix) \right]$

Добре, всичко свърши. Направете проверката сами - бракуван съм. :)

Помислете за квадратна матрица. Означаваме с Δ = det A неговия детерминант. Квадрат B е (OM) за квадрат A от същия ред, ако техният продукт A*B = B*A = E, където E е матрицата на идентичност от същия ред като A и B.

Квадрат A се нарича неизроден или неособен, ако неговата детерминанта е различна от нула, и изроден или специален, ако Δ = 0.

Теорема. За да има обратен, е необходимо и достатъчно неговата детерминанта да е различна от нула.

(OM) A, означено с A -1, така че B \u003d A -1 и се изчислява по формулата

, (1)

където А i j - алгебрични добавки на елементи a i j , Δ = detA.

Изчисляването на A -1 по формула (1) за матрици от висок ред е много трудоемко, така че на практика е удобно да се намери A -1 с помощта на метода на елементарните трансформации (EP). Всяко неособено A посредством EP само на колони (или само редове) може да бъде намалено до единица E. Ако EP, изпълнени върху матрицата A, се приложат в същия ред към единица E, тогава резултатът ще бъде A -1 . Удобно е да изпълнявате EP върху A и E едновременно, като напишете и двете една до друга през линията A|E. Ако искате да намерите A -1, трябва да използвате само редове или само колони във вашите реализации.

Намиране на обратната матрица с помощта на алгебрични допълнения

Пример 1. За намерете A -1 .

Решение.Първо намираме детерминантата A
следователно (OM) съществува и можем да го намерим по формулата: , където A i j (i,j=1,2,3) - алгебрични допълнения на елементи a i j от оригинала A.

Алгебричното допълнение на елемента a ij е детерминантата или минорът M ij. Получава се чрез изтриване на колона i и ред j. След това второстепенният се умножава по (-1) i+j , т.е. A ij =(-1) i+j M ij

където .

Намиране на обратната матрица чрез елементарни трансформации

Пример 2. Използвайки метода на елементарните трансформации, намерете A -1 за: A \u003d.

Решение.Приписваме на оригинала A отдясно единица от същия ред: . С помощта на елементарни преобразувания на колони редуцираме лявата „половина“ до единица, като едновременно с това извършваме точно такива преобразувания на дясната „половина“.
За да направите това, разменете първата и втората колона: ~. Добавяме първата към третата колона и първата, умножена по -2, към втората: . От първата колона изваждаме удвоената секунда, а от третата - втората, умножена по 6; . Нека добавим третата колона към първата и втората: . Умножете последната колона по -1: . Квадратната таблица, получена вдясно от вертикалната лента, е обратна на A -1. Така,
.

Обратна матрица за дадена е такава матрица, умножаването на оригиналната, по която дава единична матрица: Задължително и достатъчно условие за наличието на обратна матрица е неравенството на детерминантата на оригиналната (която на свой ред предполага, че матрицата трябва да е квадратна). Ако детерминантата на матрица е равна на нула, тогава тя се нарича изродена и такава матрица няма обратна. Във висшата математика обратните матрици са важни и се използват за решаване на редица проблеми. Например на намиране на обратната матрицаконструиран е матричен метод за решаване на системи от уравнения. Нашият сервизен сайт позволява изчислете обратната матрица онлайндва метода: методът на Гаус-Джордан и използването на матрицата на алгебричните добавки. Първият предполага голям брой елементарни трансформации в рамките на матрицата, вторият - изчисляване на детерминанта и алгебрични добавки към всички елементи. За да изчислите детерминанта на матрица онлайн, можете да използвате другата ни услуга - Изчисляване на детерминанта на матрица онлайн

Намерете обратната матрица на сайта

уебсайтви позволява да намерите обратна матрица онлайнбързо и безплатно. В сайта се правят изчисления от нашия сервиз и се извежда резултат с подробно решение за намиране обратна матрица. Сървърът винаги дава само точния и верен отговор. В задачи по определение обратна матрица онлайн, необходимо е детерминантата матрицибеше различно от нула, иначе уебсайтще отчете невъзможността за намиране на обратната матрица поради факта, че детерминантата на оригиналната матрица е равна на нула. Задача за намиране обратна матрицанамира се в много клонове на математиката, като е една от най-основните концепции на алгебрата и математически инструмент в приложни проблеми. Независим дефиниция на обратна матрицаизисква значителни усилия, много време, изчисления и голямо внимание, за да не се допусне пропуск или малка грешка в изчисленията. Ето защо, нашата услуга намиране на обратната матрица онлайнзначително ще улесни задачата ви и ще се превърне в незаменим инструмент за решаване на математически задачи. Дори ако ти намерете обратна матрицасами, препоръчваме да проверите вашето решение на нашия сървър. Въведете оригиналната си матрица в нашата Изчисли обратна матрица онлайн и проверете отговора си. Нашата система никога не греши и намира обратна матрицададено измерение в режима онлайнмоментално! На сайта уебсайтвписванията на символи са разрешени в елементи матрици, в такъв случай обратна матрица онлайнще бъдат представени в обща символна форма.