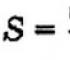Vzorec pro modul přemístění tělesa při rovnoměrně zrychleném pohybu. Rovnice promítání posunutí

Strana 8 z 12

§ 7. Pohyb s rovnoměrně zrychleným
přímočarý pohyb

1. Pomocí grafu závislosti rychlosti na čase můžete získat vzorec pro pohyb tělesa rovnoměrným přímočarým pohybem.

Obrázek 30 ukazuje graf promítání rychlosti rovnoměrného pohybu na ose X od času. Pokud v nějakém bodě nastavíme kolmici k časové ose C, pak dostaneme obdélník OABC. Plocha tohoto obdélníku se rovná součinu stran OA a OC. Ale délka strany OA je rovný v x a délka strany OC - t, tedy S = v x t. Součin průmětu rychlosti na osu X a čas se rovná projekci posunutí, tzn. s x = v x t.

Takto, projekce posunutí pro rovnoměrný přímočarý pohyb se číselně rovná ploše obdélníku ohraničeného souřadnicovými osami, grafem rychlosti a kolmicí zvednutou k časové ose.

2. Obdobným způsobem získáme vzorec pro průmět výchylky při přímočarém rovnoměrně zrychleném pohybu. K tomu nám slouží graf závislosti průmětu rychlosti na ose X od času (obr. 31). Vyberte malou oblast v grafu ab a vypusťte kolmice z bodů A a b na časové ose. Pokud časový interval D t, odpovídající sekci CD na časové ose je malý, pak můžeme předpokládat, že se rychlost během tohoto časového úseku nemění a těleso se pohybuje rovnoměrně. V tomto případě obrázek cabd se od obdélníku liší jen málo a jeho plocha se číselně rovná průmětu pohybu tělesa za čas odpovídající segmentu CD.

Na takové proužky můžete rozbít celou postavu OABC a jeho plocha bude rovna součtu ploch všech proužků. Proto projekce pohybu těla v čase tčíselně se rovná ploše lichoběžníku OABC. Z kurzu geometrie víte, že plocha lichoběžníku se rovná součinu poloviny součtu jeho základen a výšky: S= (OA + před naším letopočtem)OC.

Jak je vidět z obrázku 31, OA = proti 0X , před naším letopočtem = v x, OC = t. Z toho vyplývá, že projekce posunutí je vyjádřena vzorcem: s x= (v x + proti 0X)t.

Při rovnoměrně zrychleném přímočarém pohybu je rychlost tělesa v každém okamžiku rovna v x = proti 0X + a x t, tedy, s x = (2proti 0X + a x t)t.

Odtud:

Abychom získali pohybovou rovnici tělesa, dosadíme do vzorce promítání posunutí její vyjádření rozdílem souřadnic s x = X – X 0 .

Dostaneme: X – X 0 = proti 0X t+ nebo

X = X 0 + proti 0X t + .

Podle pohybové rovnice je možné kdykoli určit souřadnici tělesa, pokud jsou známy počáteční souřadnice, počáteční rychlost a zrychlení tělesa.

3. V praxi se často vyskytují problémy, při kterých je nutné najít posunutí tělesa při rovnoměrně zrychleném přímočarém pohybu, ale čas pohybu není znám. V těchto případech se používá jiný vzorec projekce posunutí. Pojďme na to.

Ze vzorce pro projekci rychlosti rovnoměrně zrychleného přímočarého pohybu v x = proti 0X + a x t vyjádříme čas:

t = .

Dosazením tohoto výrazu do vzorce projekce posunutí dostaneme:

s x = proti 0X + .

Odtud:

s x = , nebo
–= 2a x s x.

Pokud je počáteční rychlost tělesa nulová, pak:

2a x s x.

4. Příklad řešení problému

Lyžař se pohybuje po horském svahu z klidového stavu se zrychlením 0,5 m/s 2 za 20 s a poté se pohybuje po vodorovném úseku po zastavení 40 m. S jakým zrychlením se lyžař pohyboval po vodorovný povrch? Jaká je délka svahu hory?

Dáno:

Řešení

proti 01 = 0

A 1 = 0,5 m/s 2

t 1 = 20 s

s 2 = 40 m

proti 2 = 0

Pohyb lyžaře se skládá ze dvou fází: v první fázi, sestupování ze svahu hory, se lyžař pohybuje s rostoucí rychlostí v absolutní hodnotě; ve druhé fázi, když se pohybuje po vodorovném povrchu, jeho rychlost klesá. Hodnoty související s první fází pohybu budou zapsány s indexem 1 a hodnoty související s druhou fází s indexem 2.

A 2?

s 1?

Propojíme vztažnou soustavu se Zemí, osou X směrujme ve směru rychlosti lyžaře v každé fázi jeho pohybu (obr. 32).

Napišme rovnici pro rychlost lyžaře na konci sjezdu z hory:

proti 1 = proti 01 + A 1 t 1 .

V průmětech na osu X dostaneme: proti 1X = A 1X t. Od průmětů rychlosti a zrychlení na osu X jsou kladné, modul rychlosti lyžaře je: proti 1 = A 1 t 1 .

Napišme rovnici vztahující se k projekcím rychlosti, zrychlení a pohybu lyžaře ve druhé fázi pohybu:

–= 2A 2X s 2X .

Vzhledem k tomu, že počáteční rychlost lyžaře v této fázi pohybu je rovna jeho konečné rychlosti v první fázi

proti 02 = proti 1 , proti 2X= 0 dostaneme

– = –2A 2 s 2 ; (A 1 t 1) 2 = 2A 2 s 2 .

Odtud A 2 = ;

A 2 == 0,125 m/s 2.

Modul pohybu lyžaře v první fázi pohybu se rovná délce sjezdovky. Napišme rovnici pro posun:

s 1X = proti 01X t + .

Proto je délka horského svahu s 1 = ;

s 1 == 100 m.

Odpovědět: A 2 \u003d 0,125 m/s2; s 1 = 100 m.

Otázky k samovyšetření

1. Jako podle grafu průmětu rychlosti rovnoměrného přímočarého pohybu na osu X

2. Jako podle grafu průmětu rychlosti rovnoměrně zrychleného přímočarého pohybu na ose X z času na určení průmětu posunu tělesa?

3. Jaký vzorec se používá k výpočtu průmětu posunutí tělesa při rovnoměrně zrychleném přímočarém pohybu?

4. Jaký vzorec se používá k výpočtu průmětu výchylky tělesa pohybujícího se rovnoměrně zrychleně a přímočarě, pokud je počáteční rychlost tělesa nulová?

Úkol 7

1. Jaký je modul posunutí automobilu za 2 minuty, pokud se během této doby jeho rychlost změnila z 0 na 72 km/h? Jaká je aktuální souřadnice auta t= 2 minuty? Předpokládá se, že počáteční souřadnice je nulová.

2. Vlak se pohybuje počáteční rychlostí 36 km/h a zrychlením 0,5 m/s 2 . Jaký je posun vlaku za 20 s a jeho souřadnice v časovém okamžiku t= 20 s, pokud je počáteční souřadnice vlaku 20 m?

3. Jaký je pohyb cyklisty po dobu 5 s po začátku brzdění, je-li jeho počáteční rychlost při brzdění 10 m/s a zrychlení 1,2 m/s 2? Jaké jsou souřadnice cyklisty v čase t= 5 s, pokud v počátečním okamžiku bylo na počátku?

4. Automobil pohybující se rychlostí 54 km/h se při brzdění na 15 sekund zastaví. Jaký je modul posunutí vozu při brzdění?

5. Dvě auta se pohybují proti sobě ze dvou osad nacházejících se ve vzdálenosti 2 km od sebe. Počáteční rychlost jednoho vozu je 10 m/s a zrychlení je 0,2 m/s 2, počáteční rychlost druhého je 15 m/s a zrychlení je 0,2 m/s 2 . Určete čas a souřadnice místa setkání vozů.

Laboratoř #1

Studium rovnoměrně zrychlené
přímočarý pohyb

Objektivní:

naučit se měřit zrychlení při rovnoměrně zrychleném přímočarém pohybu; experimentálně stanovte poměr drah, které těleso urazí během rovnoměrně zrychleného přímočarého pohybu v po sobě jdoucích stejných časových intervalech.

Zařízení a materiály:

skluz, stativ, kovová koule, stopky, měřicí páska, kovový válec.

Zakázka

1. Jeden konec skluzu upevněte do nohy stativu tak, aby svíral malý úhel s povrchem stolu, na druhý konec skluzu vložte kovový válec.

2. Změřte dráhy, které míček urazí ve 3 po sobě jdoucích časových intervalech rovných 1 s. To lze provést různými způsoby. Na skluz můžete křídou umístit značky, fixovat polohu míče v časových bodech rovných 1 s, 2 s, 3 s a měřit vzdálenosti s_ mezi těmito značkami. Je možné změřit dráhu uvolněním míče pokaždé ze stejné výšky s, prošel kolem něj nejprve za 1 s, pak za 2 s a za 3 s, a pak vypočítej dráhu, kterou urazil míč ve druhé a třetí sekundě. Výsledky měření zaznamenejte do tabulky 1.

3. Najděte poměr dráhy ujeté za druhou sekundu k dráze ujeté za první sekundu a k dráze ujeté za třetí sekundu k dráze ujeté za první sekundu. Udělejte závěr.

4. Změřte dobu, po kterou míč urazil žlab, a vzdálenost, kterou urazil. Vypočítejte jeho zrychlení pomocí vzorce s = .

5. Pomocí experimentálně získané hodnoty zrychlení vypočítejte dráhy, které musí kulička urazit v první, druhé a třetí sekundě svého pohybu. Udělejte závěr.

stůl 1

zkušenostní číslo

Experimentální data

Teoretické výsledky

Čas t , S

Cesta s , cm

Čas t , S

Cesta

s, cm

Zrychlení a, cm/s2

Čast, S

Cesta s , cm

Rychlost (v) je fyzikální veličina, která se číselně rovná dráze (cestám), kterou tělo urazí za jednotku času (t).

Cesta

Dráha (S) - délka trajektorie, po které se těleso pohybovalo, je číselně rovna součinu rychlosti (v) tělesa a času (t) pohybu.

Cestovní čas

Doba pohybu (t) se rovná poměru dráhy (S), kterou urazí těleso, k rychlosti (v) pohybu.

průměrná rychlost

Průměrná rychlost (vav) je rovna poměru součtu úseků dráhy (s 1 s 2, s 3, ...) ujetých tělesem k časovému intervalu (t 1 + t 2 + t 3 + ...), pro které byla tato cesta projeta .

průměrná rychlost je poměr délky dráhy, kterou těleso urazilo, k době, po kterou tuto dráhu urazilo.

průměrná rychlost při nerovnoměrném přímém pohybu: jedná se o poměr celé dráhy k celkovému času.

Dvě po sobě jdoucí fáze s různými rychlostmi: kde

Při řešení problémů - kolik fází pohybu bude mít tolik komponent:

Průměty vektoru posunutí na souřadnicové osy

Projekce vektoru posunutí na osu OX:

Projekce vektoru posunutí na osu OY:

Projekce vektoru na osu je nulová, pokud je vektor kolmý k ose.

Známky průmětů posunutí: průmět je považován za kladný, pokud k pohybu od průmětu začátku vektoru k průmětu konce dochází ve směru osy, a za záporný, je-li proti ose. V tomto příkladu

Pohybový modul je délka vektoru posunutí:

Podle Pythagorovy věty:

Projekce pohybu a úhlu sklonu

V tomto příkladu:

Souřadnicová rovnice (obecně):

Vektor poloměru- vektor, jehož začátek se shoduje s počátkem souřadnic a konec - s polohou těla v daném čase. Průměty vektoru poloměru na souřadnicové osy určují souřadnice tělesa v daném čase.

Vektor poloměru umožňuje nastavit polohu hmotného bodu v daném referenční systém:

Rovnoměrný přímočarý pohyb - definice

Rovnoměrný přímočarý pohyb- pohyb, při kterém se těleso po libovolné stejné časové intervaly posouvá stejně.

Rychlost v rovnoměrném přímočarém pohybu. Rychlost je vektorová fyzikální veličina, která ukazuje, kolik pohybu tělo udělá za jednotku času.

Ve vektorové podobě:

V projekcích na osu OX:

Další jednotky rychlosti:

1 km/h = 1000 m/3600 s,

1 km/s = 1000 m/s,

1 cm/s = 0,01 m/s,

1 m/min = 1 m/60 s.

Měřící zařízení - rychloměr - zobrazuje modul rychlosti.

Znaménko projekce rychlosti závisí na směru vektoru rychlosti a souřadnicové ose:

Graf projekce rychlosti je závislost projekce rychlosti na čase:

Graf rychlosti pro rovnoměrný přímočarý pohyb- přímka rovnoběžná s časovou osou (1, 2, 3).

Pokud graf leží nad časovou osou (.1), pak se těleso pohybuje ve směru osy OX. Pokud je graf umístěn pod časovou osou, pak se těleso pohybuje proti ose OX (2, 3).

Geometrický význam pohybu.

Při rovnoměrném přímočarém pohybu je posunutí určeno vzorcem. Stejný výsledek dostaneme, pokud vypočítáme plochu obrázku pod grafem rychlosti v osách. Abychom určili dráhu a modul posunutí během přímočarého pohybu, je nutné vypočítat plochu obrázku pod grafem rychlosti v osách:

Displacement Projection Plot- závislost průmětu posunutí na čase.

Graf projekce posunutí pro rovnoměrný přímočarý pohyb- přímka vycházející z počátku (1, 2, 3).

Pokud přímka (1) leží nad časovou osou, pak se těleso pohybuje ve směru osy OX a pokud pod osou (2, 3), pak proti ose OX.

Čím větší je tečna sklonu (1) grafu, tím větší je modul rychlosti.

Vykreslete souřadnice- závislost tělesných souřadnic na čase:

Souřadnice grafu pro rovnoměrný přímočarý pohyb - přímky (1, 2, 3).

Pokud se časem souřadnice zvětší (1, 2), pak se těleso pohybuje ve směru osy OX; pokud se souřadnice sníží (3), pak se těleso pohybuje proti směru osy OX.

Čím větší je tečna sklonu (1), tím větší je modul rychlosti.

Pokud se grafy souřadnic dvou těles protínají, pak by se z průsečíku měly snížit kolmice k časové ose a souřadnicové ose.

Relativita mechanického pohybu

Relativitou rozumíme závislost něčeho na volbě vztažné soustavy. Například mír je relativní; relativní pohyb a relativní poloha těla.

Pravidlo sčítání posunů. Vektorový součet posunů

kde je posunutí tělesa vzhledem k pohyblivé vztažné soustavě (RFR); - pohyb PSO vzhledem k pevnému referenčnímu rámci (FRS); - pohyb těla vzhledem k pevné vztažné soustavě (FRS).

Doplnění vektoru:

Sčítání vektorů vedených podél jedné přímky:

Sčítání vektorů na sebe kolmých

Podle Pythagorovy věty

Odvoďme vzorec, který lze použít k výpočtu průmětu vektoru posunutí tělesa pohybujícího se po přímce a rovnoměrně zrychleného po libovolnou dobu. K tomu se podívejme na obrázek 14. Jak na obrázku 14, a, tak na obrázku 14, b, je segment AC grafem průmětu vektoru rychlosti tělesa pohybujícího se konstantním zrychlením a (při počáteční rychlosti v 0).

Rýže. 14. Průmět vektoru posunutí přímočarého a rovnoměrně zrychleného tělesa se číselně rovná ploše S pod grafem.

Připomeňme, že při přímočarém rovnoměrném pohybu tělesa je projekce vektoru posunutí vytvořená tímto tělesem určena stejným vzorcem jako plocha obdélníku uzavřeného pod grafem projekce vektoru rychlosti (viz obr. 6). Proto se projekce vektoru posunutí numericky rovná ploše tohoto obdélníku.

Dokažme, že v případě přímočarého rovnoměrně zrychleného pohybu lze průmět vektoru posunutí sx určit stejným vzorcem jako oblast obrazce uzavřeného mezi grafem AC, osou Ot a segmenty OA a BC, tj. v tomto případě projekce vektoru posunutí číselně rovné ploše obrázku pod grafem rychlosti. K tomu zvolíme na ose Ot (viz obr. 14, a) malý časový interval db. Z bodů dab vedeme kolmice k ose Ot, dokud se neprotnou s grafem promítání vektoru rychlosti v bodech a a c.

Po dobu odpovídající segmentu db se tedy rychlost tělesa změní z v ax na v cx.

Po dostatečně krátkou dobu se projekce vektoru rychlosti velmi mírně změní. Proto se pohyb těla v tomto časovém období jen málo liší od rovnoměrného, tedy od pohybu konstantní rychlostí.

Je možné rozdělit celou plochu postavy OASV, což je lichoběžník, na takové proužky. Proto je projekce vektoru posunutí sx pro časový interval odpovídající segmentu OB číselně rovna ploše S lichoběžníku OASV a je určena stejným vzorcem jako tato oblast.

Podle pravidla uvedeného ve školních kurzech geometrie se plocha lichoběžníku rovná součinu poloviny součtu jeho základen a výšky. Obrázek 14, b ukazuje, že základnami lichoběžníku OASV jsou segmenty OA = v 0x a BC = v x a výška je segment OB = t. Proto,

Protože v x \u003d v 0x + a x t, a S \u003d s x, pak můžeme psát:

Tím jsme získali vzorec pro výpočet průmětu vektoru posunutí při rovnoměrně zrychleném pohybu.

Pomocí stejného vzorce se také vypočítá projekce vektoru posunutí, když se těleso pohybuje s klesajícím modulem rychlosti, pouze v tomto případě budou vektory rychlosti a zrychlení nasměrovány opačnými směry, takže jejich projekce budou mít různá znaménka.

Otázky

Pomocí obrázku 14, a, dokažte, že projekce vektoru posunutí během rovnoměrně zrychleného pohybu se číselně rovná ploše obrázku OASV.
Napište rovnici pro určení průmětu vektoru posunutí tělesa během jeho přímočarého rovnoměrně zrychleného pohybu.

Cvičení 7

Strana 8 z 12

§ 7. Pohyb s rovnoměrně zrychleným
přímočarý pohyb

1. Pomocí grafu závislosti rychlosti na čase můžete získat vzorec pro pohyb tělesa rovnoměrným přímočarým pohybem.

Takto, projekce posunutí pro rovnoměrný přímočarý pohyb se číselně rovná ploše obdélníku ohraničeného souřadnicovými osami, grafem rychlosti a kolmicí zvednutou k časové ose.

Jak je vidět z obrázku 31, OA = proti 0X , před naším letopočtem = v x, OC = t. Z toho vyplývá, že projekce posunutí je vyjádřena vzorcem: s x= (v x + proti 0X)t.

Při rovnoměrně zrychleném přímočarém pohybu je rychlost tělesa v každém okamžiku rovna v x = proti 0X + a x t, tedy, s x = (2proti 0X + a x t)t.

Abychom získali pohybovou rovnici tělesa, dosadíme do vzorce promítání posunutí její vyjádření rozdílem souřadnic s x = X – X 0 .

Dostaneme: X – X 0 = proti 0X t+ nebo

X = X 0 + proti 0X t + .

Podle pohybové rovnice je možné kdykoli určit souřadnici tělesa, pokud jsou známy počáteční souřadnice, počáteční rychlost a zrychlení tělesa.

Ze vzorce pro projekci rychlosti rovnoměrně zrychleného přímočarého pohybu v x = proti 0X + a x t vyjádříme čas:

Dosazením tohoto výrazu do vzorce projekce posunutí dostaneme:

s x = proti 0X + .

s x = , nebo
–= 2a x s x.

Pokud je počáteční rychlost tělesa nulová, pak:

2a x s x.

4. Příklad řešení problému

Dáno:

proti 01 = 0

A 1 = 0,5 m/s 2

t 1 = 20 s

s 2 = 40 m

proti 2 = 0

A 2?

s 1?

Propojíme vztažnou soustavu se Zemí, osou X směrujme ve směru rychlosti lyžaře v každé fázi jeho pohybu (obr. 32).

Napišme rovnici pro rychlost lyžaře na konci sjezdu z hory:

proti 1 = proti 01 + A 1 t 1 .

V průmětech na osu X dostaneme: proti 1X = A 1X t. Od průmětů rychlosti a zrychlení na osu X jsou kladné, modul rychlosti lyžaře je: proti 1 = A 1 t 1 .

Napišme rovnici vztahující se k projekcím rychlosti, zrychlení a pohybu lyžaře ve druhé fázi pohybu:

–= 2A 2X s 2X .

Vzhledem k tomu, že počáteční rychlost lyžaře v této fázi pohybu je rovna jeho konečné rychlosti v první fázi

proti 02 = proti 1 , proti 2X= 0 dostaneme

– = –2A 2 s 2 ; (A 1 t 1) 2 = 2A 2 s 2 .

Odtud A 2 = ;

A 2 == 0,125 m/s 2.

Modul pohybu lyžaře v první fázi pohybu se rovná délce sjezdovky. Napišme rovnici pro posun:

s 1X = proti 01X t + .

Proto je délka horského svahu s 1 = ;

s 1 == 100 m.

Odpovědět: A 2 \u003d 0,125 m/s2; s 1 = 100 m.

Otázky k samovyšetření

1. Jako podle grafu průmětu rychlosti rovnoměrného přímočarého pohybu na osu X

2. Jako podle grafu průmětu rychlosti rovnoměrně zrychleného přímočarého pohybu na ose X z času na určení průmětu posunu tělesa?

3. Jaký vzorec se používá k výpočtu průmětu posunutí tělesa při rovnoměrně zrychleném přímočarém pohybu?

4. Jaký vzorec se používá k výpočtu průmětu výchylky tělesa pohybujícího se rovnoměrně zrychleně a přímočarě, pokud je počáteční rychlost tělesa nulová?

Úkol 7

4. Automobil pohybující se rychlostí 54 km/h se při brzdění na 15 sekund zastaví. Jaký je modul posunutí vozu při brzdění?

Laboratoř #1

Studium rovnoměrně zrychlené
přímočarý pohyb

Objektivní:

Zařízení a materiály:

skluz, stativ, kovová koule, stopky, měřicí páska, kovový válec.

Zakázka

1. Jeden konec skluzu upevněte do nohy stativu tak, aby svíral malý úhel s povrchem stolu, na druhý konec skluzu vložte kovový válec.

3. Najděte poměr dráhy ujeté za druhou sekundu k dráze ujeté za první sekundu a k dráze ujeté za třetí sekundu k dráze ujeté za první sekundu. Udělejte závěr.

4. Změřte dobu, po kterou míč urazil žlab, a vzdálenost, kterou urazil. Vypočítejte jeho zrychlení pomocí vzorce s = .

5. Pomocí experimentálně získané hodnoty zrychlení vypočítejte dráhy, které musí kulička urazit v první, druhé a třetí sekundě svého pohybu. Udělejte závěr.

stůl 1

zkušenostní číslo

Experimentální data

Teoretické výsledky

Čas t , S

Cesta s , cm

Čas t , S

Cesta

s, cm

Zrychlení a, cm/s2

Čast, S

Cesta s , cm

Jak při znalosti brzdné dráhy určit počáteční rychlost vozu a jak se znalostí vlastností pohybu, jako je počáteční rychlost, zrychlení, čas, určit pohyb vozu? Odpovědi dostaneme poté, co se seznámíme s tématem dnešní lekce: "Posun při rovnoměrně zrychleném pohybu, závislost souřadnic na čase při rovnoměrně zrychleném pohybu"

Při rovnoměrně zrychleném pohybu vypadá graf jako přímka stoupající nahoru, protože jeho projekce zrychlení je větší než nula.

Při rovnoměrném přímočarém pohybu bude plocha číselně rovna modulu průmětu přemístění tělesa. Ukazuje se, že tuto skutečnost lze zobecnit nejen pro případ rovnoměrného pohybu, ale i pro jakýkoli pohyb, tedy ukázat, že plocha pod grafem je číselně rovna modulu průmětu posunutí. To se provádí přísně matematicky, ale použijeme grafickou metodu.

Rýže. 2. Graf závislosti rychlosti na čase při rovnoměrně zrychleném pohybu ()

Rozdělme graf průmětu rychlosti od času pro rovnoměrně zrychlený pohyb na malé časové intervaly Δt. Předpokládejme, že jsou tak malé, že se během jejich délky rychlost prakticky neměnila, to znamená, že podmíněně přeměníme graf lineární závislosti na obrázku na žebřík. U každého jeho kroku věříme, že se rychlost příliš nezměnila. Představte si, že časové intervaly Δt jsou nekonečně malé. V matematice se říká: uděláme přechod na limit. V tomto případě se plocha takového žebříku bude neurčitě těsně shodovat s plochou lichoběžníku, která je omezena grafem V x (t). A to znamená, že pro případ rovnoměrně zrychleného pohybu můžeme říci, že modul promítání posunutí je číselně roven ploše ohraničené grafem V x (t): osy úsečky a pořadnice a kolmice snížené k ose úsečky, tedy oblast lichoběžníku OABS, kterou vidíme na obrázku 2.

Problém se změní z fyzického na matematický - nalezení oblasti lichoběžníku. To je standardní situace, kdy si fyzici vymyslí model, který popisuje konkrétní jev, a pak přijde na řadu matematika, která tento model obohatí o rovnice, zákony – to udělá z modelu teorii.

Najdeme oblast lichoběžníku: lichoběžník je obdélníkový, protože úhel mezi osami je 90 0, rozdělíme lichoběžník na dva tvary - obdélník a trojúhelník. Je zřejmé, že celková plocha bude rovna součtu ploch těchto obrázků (obr. 3). Najdeme jejich oblasti: plocha obdélníku se rovná součinu stran, to znamená V 0x t, plocha pravoúhlého trojúhelníku se bude rovnat polovině součinu nohou - 1/2AD BD, dosazením hodnot projekce dostaneme: 1/2t (V x - V 0x), a když si pamatujeme zákon změny rychlosti od času při rovnoměrně zrychleném pohybu: V x (t) = V 0x + axt, je zcela zřejmé, že rozdíl v průmětech rychlostí je roven součinu průmětu zrychlení ax časem t, tedy V x - V 0x = a x t.

Rýže. 3. Určení plochy lichoběžníku ( Zdroj)

Vezmeme-li v úvahu skutečnost, že plocha lichoběžníku je číselně rovna modulu projekce posunutí, dostaneme:

S x (t) \u003d V 0 x t + a x t 2 / 2

Získali jsme zákon závislosti projekce posunu na čase s rovnoměrně zrychleným pohybem ve skalárním tvaru, ve vektorovém tvaru to bude vypadat takto:

(t) = t + t2/2

Odvoďme ještě jeden vzorec pro projekci posunutí, která nebude zahrnovat čas jako proměnnou. Řešíme soustavu rovnic, vyjma času z ní:

S x (t) \u003d V 0 x + a x t 2 / 2

V x (t) \u003d V 0 x + a x t

Představte si, že neznáme čas, pak vyjádříme čas z druhé rovnice:

t \u003d V x - V 0x / a x

Výslednou hodnotu dosaďte do první rovnice:

Dostaneme takový těžkopádný výraz, umocníme ho a dáme podobné:

Získali jsme velmi vhodný výraz promítání posunutí pro případ, kdy neznáme čas pohybu.

Mějme počáteční rychlost vozu, když začalo brzdění, V 0 \u003d 72 km / h, konečná rychlost V \u003d 0, zrychlení a \u003d 4 m / s 2. Zjistěte délku brzdné dráhy. Převedením kilometrů na metry a dosazením hodnot do vzorce dostaneme, že brzdná dráha bude:

S x \u003d 0 - 400 (m/s) 2 / -2 4 m/s 2 \u003d 50 m

Pojďme analyzovat následující vzorec:

S x \u003d (V 0 x + V x) / 2 t

Projekce pohybu je poloviční součet projekcí počáteční a konečné rychlosti, vynásobený dobou pohybu. Připomeňte si vzorec pro průměrnou rychlost

S x \u003d V cf t

V případě rovnoměrně zrychleného pohybu bude průměrná rychlost:

V cf \u003d (V 0 + V k) / 2

Přiblížili jsme se k vyřešení hlavního problému mechaniky rovnoměrně zrychleného pohybu, tedy získání zákona, podle kterého se souřadnice mění s časem:

x(t) \u003d x 0 + V 0 x t + a x t 2 / 2

Abychom se naučili používat tento zákon, rozebereme typický problém.

Auto, pohybující se z klidového stavu, získává zrychlení 2 m / s 2. Najděte vzdálenost ujetou autem za 3 sekundy a za třetí sekundu.

Dáno: V 0 x = 0

Zapišme si zákon, podle kterého se posunutí mění s časem v

rovnoměrně zrychlený pohyb: S x \u003d V 0 x t + a x t 2 /2. 2 c

Na první otázku problému můžeme odpovědět vložením dat:

t 1 \u003d 3 c S 1x \u003d a x t 2 / 2 \u003d 2 3 2 / 2 \u003d 9 (m) - toto je cesta, která šla

c auto za 3 sekundy.

Zjistěte, jak daleko cestoval za 2 sekundy:

S x (2 s) \u003d a x t 2 / 2 \u003d 2 2 2 / 2 \u003d 4 (m)

Takže ty a já víme, že za dvě sekundy auto ujelo 4 metry.

Nyní, když známe tyto dvě vzdálenosti, můžeme najít cestu, kterou cestoval ve třetí sekundě:

S 2x \u003d S 1x + S x (2 s) \u003d 9 - 4 \u003d 5 (m)

Rovnoměrně zrychlený pohyb nazývá se takový pohyb, při kterém vektor zrychlení zůstává nezměněn ve velikosti a směru. Příkladem takového pohybu je pohyb kamene vrženého pod určitým úhlem k horizontu (ignorování odporu vzduchu). V kterémkoli bodě trajektorie se zrychlení kamene rovná zrychlení volného pádu. Studium rovnoměrně zrychleného pohybu je tedy redukováno na studium přímočarého rovnoměrně zrychleného pohybu. V případě přímočarého pohybu jsou vektory rychlosti a zrychlení směrovány podél přímky pohybu. Proto lze rychlost a zrychlení v projekcích na směr pohybu považovat za algebraické veličiny. Při rovnoměrně zrychleném přímočarém pohybu je rychlost tělesa určena vzorcem (1)

V tomto vzorci je rychlost těla při t = 0 (startovací rychlost ), = konst – zrychlení. V průmětu na vybranou osu x bude rovnice (1) zapsána ve tvaru: (2). Na grafu projekce rychlosti υ x ( t), tato závislost má tvar přímky.

Sklon grafu rychlosti lze použít k určení zrychlení A tělo. Odpovídající konstrukce jsou provedeny na Obr. pro graf I Zrychlení se numericky rovná poměru stran trojúhelníku ABC: .

Čím větší je úhel β, který tvoří graf rychlosti s časovou osou, tj. tím větší je sklon grafu ( strmost), tím větší je zrychlení těla.

Pro graf I: υ 0 \u003d -2 m / s, A\u003d 1/2 m/s 2. Pro graf II: υ 0 \u003d 3 m / s, A\u003d -1/3 m/s 2.

Graf rychlosti také umožňuje určit průmět výchylky s tělesa na nějaký čas t. Přidělme na časové ose nějaký malý časový interval Δt. Pokud je toto časové období dostatečně malé, pak je změna rychlosti za toto období malá, to znamená, že pohyb během tohoto časového období lze považovat za rovnoměrný s určitou průměrnou rychlostí, která se rovná okamžité rychlosti υ těleso uprostřed intervalu Δt. Proto bude posunutí Δs během času Δt rovno Δs = υΔt. Toto posunutí se rovná ploše vystínované na obr. pruhy. Rozdělením časového intervalu od 0 do určitého okamžiku t na malé intervaly Δt získáme, že výchylka s za daný čas t při rovnoměrně zrychleném přímočarém pohybu je rovna ploše lichoběžníku ODEF. Odpovídající konstrukce jsou provedeny na Obr. pro rozvrh II. Doba t je rovna 5,5 s.

(3) - výsledný vzorec umožňuje určit posunutí s rovnoměrně zrychleným pohybem, pokud zrychlení není známo.

Dosadíme-li do rovnice (3) výraz pro rychlost (2), dostaneme (4) - tento vzorec slouží k zápisu rovnice pohybu tělesa: (5).

Vyjádříme-li z rovnice (2) čas pohybu (6) a dosadíme do rovnosti (3), pak

Tento vzorec umožňuje určit pohyb v neznámém čase pohybu.

Uvažujme, jak se vypočítá projekce vektoru posunutí tělesa pohybujícího se rovnoměrně zrychleně, je-li jeho počáteční rychlost v 0 rovna nule. V tomto případě rovnice

bude vypadat takto:

Přepišme tuto rovnici tak, že do ní místo průmětů s x a a x dosadíme moduly s a a vektorů

posunutí a zrychlení. Protože v tomto případě vektory sua směřují stejným směrem, mají jejich průměty stejná znaménka. Proto lze rovnici pro moduly vektorů napsat:

Z tohoto vzorce vyplývá, že při přímočarém rovnoměrně zrychleném pohybu bez počáteční rychlosti je modul vektoru posunutí přímo úměrný druhé mocnině časového intervalu, během kterého byl tento pohyb uskutečněn. To znamená, že se zvýšením doby pohybu o nkrát (počítáno od okamžiku zahájení pohybu) se pohyb zvýší n 2krát.

Pokud se například po libovolnou dobu t 1 od začátku pohybu těleso pohnulo

pak se po dobu t 2 \u003d 2t 1 (počítáno od stejného okamžiku jako t 1) bude pohybovat

po dobu t n \u003d nt l - posunutí s n \u003d n 2 s l (kde n je přirozené číslo).

Tato závislost modulu vektoru posuvu na čase při přímočarém rovnoměrně zrychleném pohybu bez počáteční rychlosti je jasně vyjádřena na obrázku 15, kde segmenty OA, OB, OS, OD a OE jsou moduly vektorů posuvu (s 1, s 2, s 3, s 4 a s 5), spáchané tělem, v tomto pořadí, pro časové intervaly t 1 , t 2 = 2t 1 , t 3 = 3t 1 , t 4 = 4t 1 a t 5 = 5t 1 .

Rýže. 15. Vzorce rovnoměrně zrychleného pohybu: OA:OB:OC:OD:0E = 1:4:9:16:25; OA:AB:BC:CD:DE = 1:3:5:7:9

Z tohoto obrázku je zřejmé, že

OA:OB:OS:OD:OE = 1:4:9:16:25, (1)

tj. s nárůstem časových intervalů počítaných od začátku pohybu o celé číslo ve srovnání s ti, moduly odpovídajících vektorů posunutí rostou jako série druhých mocnin po sobě jdoucích přirozených čísel.

Obrázek 15 ukazuje další vzor:

OA:AB:BC:CD:DE = 1:3:5:7:9, (2)

tj. moduly vektorů posunů prováděných tělesem v po sobě jdoucích stejných časových obdobích (z nichž každý je roven ti) jsou propojeny jako řada po sobě jdoucích lichých čísel.

Pravidelnosti (1) a (2) jsou vlastní pouze rovnoměrně zrychlenému pohybu. Lze je tedy použít, je-li třeba určit, zda je pohyb rovnoměrně zrychlený nebo ne.

Určijme například, zda byl pohyb hlemýždě rovnoměrně zrychlený, která se během prvních 20 sekund pohybu posunula o 0,5 cm, ve druhých 20 sekundách o 1,5 cm a ve třetích 20 sekundách o 2,5 cm.

Za tímto účelem zjistíme, kolikrát jsou pohyby provedené ve druhém a třetím časovém intervalu větší než v prvním:

To znamená, že 0,5 cm : 1,5 cm : 2,5 cm = 1 : 3 : 5. Protože tyto poměry jsou řadou po sobě jdoucích lichých čísel, pohyb tělesa se rovnoměrně zrychloval.

V tomto případě byl rovnoměrně zrychlený charakter pohybu odhalen na základě pravidelnosti (2).

Otázky

Jaké vzorce se používají k výpočtu průmětu a modulu vektoru posunutí tělesa při jeho rovnoměrně zrychleném pohybu z klidového stavu?
Kolikrát vzroste modul vektoru posunutí tělesa s prodloužením doby jeho pohybu z klidu nkrát?
Zapište, jak spolu souvisí moduly vektorů posunutí tělesa pohybujícího se rovnoměrně zrychleně z klidového stavu při prodloužení doby jeho pohybu o celé číslo oproti t 1.
Zapište, jak spolu souvisí moduly vektorů posuvů vykonávaných tělesem v po sobě jdoucích stejných časových intervalech, jestliže se toto těleso z klidu pohybuje rovnoměrně zrychleně.
Jaký je účel použití pravidelností (1) a (2)?

Cvičení 8

Vlak odjíždějící ze stanice během prvních 20 s se pohybuje v přímém směru a rovnoměrně zrychluje. Je známo, že ve třetí sekundě od zahájení pohybu vlak ujel 2 m. Určete modul vektoru posunu, který vlak udělal v první sekundě, a modul vektoru zrychlení, se kterým se pohyboval.
Automobil pohybující se rovnoměrně zrychlený z klidu urazí za pátou sekundu zrychlení 6,3 m. Jakou rychlost vyvinulo auto do konce páté sekundy od začátku pohybu?
Některé těleso se během prvních 0,03 s pohybu bez počáteční rychlosti posunulo o 2 mm, během prvních 0,06 s - 8 mm, během prvních 0,09 s - 18 mm. Na základě pravidelnosti (1) dokažte, že během všech 0,09 s se těleso pohybovalo rovnoměrně zrychleně.

Otázky.

1. Podle jakých vzorců se vypočítá průmět a modul vektoru přemístění tělesa při jeho rovnoměrně zrychleném pohybu z klidového stavu?

2. Kolikrát vzroste modul vektoru posunutí tělesa s prodloužením doby jeho pohybu z klidu nkrát?

3. Zapište, jak spolu souvisí moduly vektorů posunutí tělesa pohybujícího se rovnoměrně zrychleně z klidového stavu s prodloužením doby jeho pohybu o celé číslo oproti t 1.

4. Zapište, jak spolu souvisí moduly vektorů posuvů vykonávaných tělesem v po sobě jdoucích stejných časových intervalech, jestliže se toto těleso pohybuje z klidu rovnoměrně zrychleně.

5. K jakému účelu lze použít zákonitosti (3) a (4)?

Pravidelnosti (3) a (4) se používají k určení, zda je pohyb rovnoměrně zrychlený nebo ne (viz str. 33).

Cvičení.

1. Vlak odjíždějící ze stanice během prvních 20 s se pohybuje v přímém směru a rovnoměrně zrychluje. Je známo, že ve třetí sekundě od zahájení pohybu vlak ujel 2 m. Určete modul vektoru posunu, který vlak udělal v první sekundě, a modul vektoru zrychlení, se kterým se pohyboval.