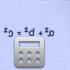The squares indicate their perimeter. How to find the perimeter of a square if its area is known

Many people remember what a square is from a school course. This quadrilateral, which is regular, has absolutely equal angles and sides. Looking around, you can see that we are surrounded by many squares. Every day we encounter them, and sometimes it becomes necessary to find the area and perimeter of this geometric figure. Calculating these values ​​will not be difficult if you take a few minutes to watch this video tutorial explaining the simple rules for making calculations.

Tutorial video “How to find the area and perimeter of a square”

What you need to know about the square?

Before proceeding with the calculations, you need to know some important information about this figure, including:

• all sides of a square are equal;
• all corners of the square are right;
• the area of ​​a square is a way of calculating how much space a figure takes up in two-dimensional space;
• two-dimensional space is a sheet of paper or a computer screen where a square is drawn;
• the perimeter is not an indicator of the fullness of the figure, but allows you to work with its sides;
• perimeter is the sum of all sides of a square;
• when calculating the perimeter, we operate in one-dimensional space, which means fixing the result in meters, not square meters (area).

How to find the area of ​​a square?

The calculation of the area of ​​​​a given figure can be simply and easily explained with an example:

• suppose that the side of the square is 8 meters;
• to calculate the area of ​​any rectangle, you need to multiply the value of one of its sides by the other (8 x 8 \u003d 64);
• since we multiply meters by meters, the result is square meters (m2).

How to find the perimeter of a square?

Knowing that all sides of a given rectangle are equal, you need to do the following manipulations to calculate its perimeter:

• add up all four sides of the square (8 + 8 + 8 + 8 = 32);
• the resulting value will be the perimeter of the square, fixed in meters.

All formulas and calculations given in this article are applicable to any rectangle. It is important to remember that when it comes to other rectangles that are not correct, the value of the sides will be different, for example 4 and 8 meters. This means that in order to find the area of ​​such a rectangle, it will be necessary to multiply the sides of the figure that are different in value, and not the same.

It must also be remembered that the area is measured in square meters, and the perimeter in simple meters. If the perimeter is drawn as one long line, then its value will not change, which indicates that the calculations are carried out in one-dimensional space.

Area is measured in two-dimensional space, as indicated by square meters, which we get by multiplying meters by meters. The area is an indicator of the fullness of a geometric figure, and tells us how much imaginary coverage is needed in order to fill a square or other rectangle.

Simple explanations of the video lesson will allow you to quickly calculate the area and perimeter of not only a square, but also any rectangle. This knowledge of the school course will be useful during the repair of the house or in the garden.

A square is a positive quadrilateral (or rhombus) in which all angles are right and the sides are equal. Like any other regular polygon, square allowed to calculate perimeter and area. If area square already famous, then discover its sides, and after that and perimeter won't be difficult.

Instruction

1. Square square is found by the formula: S = a? This means that in order to calculate the area square, it is necessary to multiply the lengths of its 2 sides by each other. As a result, if you know the area square, then when extracting the root from this value, it is possible to find out the length of the side square.Example: area square 36 cm ?, in order to find out the side of this square, you need to take the square root of the area value. So the side length of a given square 6 cm

2. For finding perimeter a square you need to add the lengths of all its sides. With the help of a formula, this can be expressed as follows: P \u003d a + a + a + a. If we extract the root from the area value square, and after that add the resulting value 4 times, then it is possible to find perimeter square .

3. Example: Given a square with an area of ​​49 cm². It needs to be discovered perimeter.Solution: First you need to take the root of the area square: ?49 = 7 cm Then, by calculating the length of the side square, it is allowed to calculate and perimeter: 7+7+7+7 = 28 cm Answer: perimeter square area 49 cm? is 28 cm

Often, in geometric problems, it is required to find the length of the side of a square, if its other parameters are known - such as area, diagonal or perimeter.

You will need

• Calculator

Instruction

1. If the square area is known, then in order to find the side of the square, you need to extract the square root from the numerical value of the area (because the area of ​​​​the square is equal to the square of its side): a =? S, where a is the length of the side of the square; S is the area of ​​​​the square. Unit the side of a square will be the linear unit of length corresponding to the unit of area. Say, if the area of ​​a square is given in square centimeters, then the length of its side will be obtained primitively in centimeters. Example: The area of ​​​​a square is 9 square meters. Find the length of the side of the square. Solution: a =?

2. In the case when the perimeter of the square is known, to determine the length of the side, it is necessary to divide the numerical value of the perimeter by four (because the square has four sides of identical length): a \u003d P / 4, where: a is the length of the side of the square; P is the perimeter of the square. The unit for the side of the square will be the same linear length unit as the perimeter. Say, if the perimeter of a square is given in centimeters, then the length of its side will also be in centimeters. Example: The perimeter of a square is 20 meters. Find the length of the side of the square. Solution: a=20/4=5 Answer: The length of the side of the square is 5 meters.

3. If the length of the diagonal of the square is known, to the length of its side will be equal to the length of its diagonal divided by the square root of 2 (according to the Pythagorean theorem, because the adjacent sides of the square and the diagonal make up a right-angled isosceles triangle): a \u003d d /? 2 (because .a^2+a^2=d^2), where: a is the length of the side of the square; d is the length of the diagonal of the square. Say, if the diagonal of a square is measured in centimeters, then the length of its side will be in centimeters. Example: The diagonal of a square is 10 meters. Find the length of the side of the square. Solution: a \u003d 10 /? 10/?2, or approximately 1.071 meters.

The square is a beautiful and simple flat geometric figure. It is a rectangle with equal sides. How to discover perimeter square if the length of its side is known?

Instruction

1. Before everyone, it is worth remembering that perimeter is nothing more than the sum of the lengths of the sides of a geometric figure. The square we are considering has four sides. Moreover, by definition square, all these sides are equal to each other. From these premises follows a simple formula for finding perimeter a square – perimeter square equal to the length of the side square multiplied by four: P = 4a, where a is the length of the side square .

Related videos

The perimeter is called the universal length the boundaries of the figure are more often than each on the plane. A square is a positive quadrilateral, either a rhombus, in which all angles are right, or a parallelogram, in which all sides and angles are equal.

You will need

• Geometry knowledge.

Instruction

1. Perimeter square is equal to the sum of the lengths of its sides. Because a square, in its essence, is a quadrilateral, then it has four sides, which means that the perimeter is equal to the sum of the lengths of the four sides, or P = a + b + c + d.

2. A square, as can be seen from the definition, is a true geometric figure, which means that all its sides are equal. So a=b=c=d. Hence P = a+a+a+a or P = 4*a.

3. let side square is 4, that is, a=3. Then the perimeter or length square, according to the obtained formula, will be equal to P = 4*3 or P=12. The number 12 will be the length or, which is the same, the perimeter square .

Related videos

Note!
The perimeter of a square is invariably correct, as is any other length.

Useful advice
Similarly, it is possible to find the perimeter of a rhombus, because the square is a special case of a rhombus with right angles.

The perimeter characterizes the length of a closed silhouette. Like the area, it can be detected by other quantities given in the condition of the problem. Problems on finding the perimeter are extremely common in the school mathematics course.

Instruction

1. Knowing the perimeter and side of the figure, it is possible to find its other side, as well as the area. The perimeter itself, in turn, can be detected by several given sides or by the angle and sides, depending on the conditions of the problem. Also in some cases it is expressed through the area. The perimeter of a rectangle is especially primitive. Draw a rectangle with one side equal to a and a diagonal equal to d. Knowing these two values, use the Pythagorean theorem to find its other side, which is the width of the rectangle. Having found the width of the rectangle, calculate its perimeter in the following way: p=2(a+b). This formula is objective for all rectangles, since each of them has four sides.

2. Pay attention to the fact that the perimeter of a triangle in most problems is found if there is information about one of its corners. However, there are also problems in which all sides of the triangle are known, and then the perimeter can be calculated by simple summation, without the use of trigonometric calculations: p=a+b+c, where a, b and c are the sides. But such problems are rarely found in textbooks, because the method of solving them is clear. More difficult tasks of finding the perimeter of a triangle, solve in stages. Let's say draw an isosceles triangle, in which the base and the angle at it are famous. In order to find its perimeter, first find the sides a and b in the following way: b=c/2cos?. From the fact that a=b (isosceles triangle), make a further summary: a=b=c/2cos?.

3. Calculate the perimeter of a polygon in the same way, adding the lengths of all its sides: p=a+b+c+d+e+f and so on. If the polygon is positive and inscribed in or circumscribed by a circle, calculate the length of one of its sides, and then multiply by their number. Let's say, in order to find the sides of a hexagon inscribed in a circle, proceed as follows: a=R, where a is the side of the hexagon, equal to the radius of the circumscribed circle. Accordingly, if the hexagon is true, then its perimeter is equal to: p=6a=6R. If the circle is inscribed in a hexagon, then the side of the latter is: a=2r?3/3. Accordingly, find the perimeter of such a figure in the following way: p=12r?3/3.

Although the word "perimeter" comes from the Greek designation for a circle, it is customary to call it the total length of the boundaries of any flat geometric figure, including a square. The calculation of this parameter, as usual, is not difficult and can be carried out by several methods, depending on the famous initial data.

Instruction

1. If you know the length of the side of the square (t), then to find its perimeter (p) primitively increase this value four times: p=4*t.

2. If the length of the side is unknown, but the length of the diagonal (c) is given in the conditions of the problem, then this is enough to calculate the length of the sides, and, consequently, the perimeter (p) of the polygon. Use the Pythagorean Theorem, which states that the square of the length of the long side of a right triangle (the hypotenuse) is equal to the sum of the squares of the lengths of the short sides (the legs). In a right triangle made up of 2 adjacent sides of a square and a segment connecting their extreme points, the hypotenuse coincides with the diagonal of the quadrilateral. From this it follows that the length of the side of the square is equal to the ratio of the length of the diagonal to the square root of two. Use this expression in the formula for calculating the perimeter from the previous step: p=4*c/?2.

3. If only the area (S) of a section of the plane bounded by the perimeter of the square is given, then this will be enough to determine the length of one side. Because the area of ​​any rectangle is equal to the product of the lengths of its adjacent sides, then to find the perimeter (p) take the square root of the area, and quadruple the total: p=4*?S.

4. If the radius of the circle described near the square (R) is known, then to find the perimeter of the polygon (p), multiply it by eight and divide the result by the square root of two: p=8*R/?2.

5. If the circle, the radius of which is kept, is inscribed in a square, then calculate its perimeter (p) by simply multiplying the radius (r) by eight: P=8*r.

6. If the square under consideration in the conditions of the problem is described by the coordinates of its vertices, then to calculate the perimeter you will need data on only 2 vertices belonging to one of the sides of the figure. Determine the length of this side, based on the same Pythagorean theorem for a triangle made up of itself and its projections on the coordinate axes, and quadruple the resulting result. Because the lengths of the projections on the coordinate axes are equal to the modulus of the differences between the corresponding coordinates of 2 points (X?; Y? and X?; Y?), then the formula can be written as follows: p=4*? ((X?-X?)? +(Y?-Y?)?).

In the general case, the perimeter is the length of the line that bounds the closed figure. For polygons, the perimeter is the sum of all side lengths. This value can be measured, and for many figures it is easy to calculate if the lengths of the corresponding elements are known.

You will need

• - ruler or tape measure;
• - strong thread;
• - roller rangefinder.

Instruction

1. In order to measure the perimeter of an arbitrary polygon, measure all its sides with a ruler or other measuring device, and then find their sum. Given a quadrilateral with sides of 5, 3, 7 and 4 cm, which are measured with a ruler, find the perimeter by adding them together P = 5 + 3 + 7 + 4 = 19 cm.

2. If the figure is arbitrary and includes not only straight lines, then measure its perimeter with a traditional rope or thread. To do this, position it so that it correctly repeats all the lines that bound the figure, and make a mark on it, if allowed, cut it primitively in order to avoid confusion. After that, using a tape measure or ruler, measure the length of the thread, it will be equal to the perimeter of this figure. Be sure to ensure that the thread repeats the line as accurately as possible for greater accuracy of the result.

3. Measure the perimeter of a difficult geometric figure with a roller rangefinder (curvimeter). To do this, a point is marked on the line, at which the rangefinder roller is installed and rolled along it, until it returns to the starting point. The distance measured by the roller rangefinder will be equal to the perimeter of the figure.

4. Calculate the perimeter of some geometric shapes. Say, in order to find the perimeter of any positive polygon (a convex polygon whose sides are equal), multiply the side length by the number of angles or sides (they are equal). In order to find the perimeter of a true triangle with a side of 4 cm, multiply this number by 3 (P = 4? 3 = 12 cm).

5. To find the perimeter of an arbitrary triangle, add the lengths of all its sides. If all sides are not given, but there are angles between them, find them using the sine or cosine theorem. If two sides of a right triangle are famous, find the third side using the Pythagorean theorem and find their sum. Say, if it is known that the legs of a right triangle are 3 and 4 cm, then the hypotenuse will be equal to? (3? + 4?) = 5 cm. Then the perimeter P = 3 + 4 + 5 = 12 cm.

6. To find the perimeter of a circle, find the circumference of the circle that bounds it. To do this, multiply its radius r by the number??3.14 and the number 2 (P=L=2???r). If the diameter is known, consider that it is equal to two radii.

Perimeter polygon call a closed broken line made up of all its sides. Finding the length of this parameter is reduced to summing the lengths of the sides. If all the segments that form the perimeter of such a two-dimensional geometric figure have identical dimensions, the polygon is called true. In this case, the calculation of the perimeter is much simpler.

Instruction

1. In the simplest case, when we know the length of the side (a) of the correct polygon and the number of vertices (n) in it, to calculate the length of the perimeter (P), simply multiply these two values: P = a * n. Let's say the perimeter length of a true hexagon with a side of 15 cm should be equal to 15 * 6 = 90 cm.

2. Calculate the perimeter of this polygon along the known radius (R) of the circumscribed circle around it is also permissible. To do this, you will first have to express the length of the side using the radius and the number of vertices (n), and then multiply the resulting value by the number of sides. To calculate the length of a side, multiply the radius by the sine of pi divided by the number of vertices, and double the total: R*sin(?/n)*2. If you are more comfortable calculating the trigonometric function in degrees, replace Pi with 180°: R*sin(180°/n)*2. Calculate the perimeter by multiplying the obtained value by the number of vertices: Р = R*sin(?/n)*2*n = R*sin(180°/n)*2*n. Let's say if a hexagon is inscribed in a circle with a radius of 50 cm, its perimeter will have a length of 50*sin(180°/6)*2*6 = 50*0.5*12 = 300 cm.

3. By a similar method, it is possible to calculate the perimeter without knowing the length of the side of the positive polygon, if it is circumscribed about a circle with the famous radius (r). In this case, the formula for calculating the size of the side of the figure will differ from the previous one only by the trigonometric function involved. Replace the sine with the tangent in the formula to get the following expression: r*tg(?/n)*2. Or for calculations in degrees: r*tg(180°/n)*2. To calculate the perimeter, increase the resulting value by a factor equal to the number of vertices polygon: P \u003d r * tg (? / n) * 2 * n \u003d r * tg (180 ° / n) * 2 * n. Let's say the perimeter of an octagon circumscribed near a circle with a radius of 40 cm will be approximately equal to 40*tg(180°/8)*2*8 ? 40 * 0.414 * 16 \u003d 264.96 cm.

A square is a geometric figure consisting of four sides of identical length and four right angles, each of which is equal to 90 °. Determining the area either perimeter a quadrangle, and any one, is required not only when solving problems in geometry, but also in everyday life. This knowledge can become useful, say, during repairs when calculating the required number of materials - floor, wall or ceiling coverings, as well as for laying out lawns and beds, etc.

Instruction

1. To find the area of ​​a square, multiply the length by the width. Because in a square the length and width are identical, then the value of one side is quite square. Thus, the area of ​​a square is equal to the length of its squared side. The area unit can be square millimeters, centimeters, decimeters, meters, kilometers. To determine the area of ​​a square, you can use the formula S = aa, where S is the area of ​​the square, and is the side of the square.

2. Example No. 1. The room has the shape of a square. How much laminate flooring (in sq.m.) will be needed in order to completely cover the floor if the length of one side of the room is 5 meters. Write down the formula: S \u003d aa. Substitute the data specified in the condition into it. Because a \u003d 5 m, therefore, the area will be equal to S (rooms) \u003d 5x5 \u003d 25 sq.m, which means S (laminate) \u003d 25 sq.m.

3. The perimeter is the total length of the figure's border. In a square, the perimeter is the length of all four, and identical, sides. That is, the perimeter of a square is the sum of all its four sides. To calculate the perimeter of a square, it is enough to know the length of one of its sides. The perimeter is measured in millimeters, centimeters, decimeters, meters, kilometers. To determine the perimeter, there is a formula: P \u003d a + a + a + a or P \u003d 4a, where P is the perimeter, and is the length of the side.

4. Example No. 2. For finishing work in a square-shaped room, ceiling plinths are required. Calculate the total length (perimeter) of the skirting boards if one side of the room is 6 meters. Write down the formula P \u003d 4a. Substitute the data indicated in the condition into it: P (rooms) \u003d 4 x 6 \u003d 24 meters. Consequently, the length of the ceiling plinths will also be 24 meters.

Related videos

Note!
The following definitions are objective for a square: A square is a rectangle, one that has sides equal to each other. A square is a special kind of rhombus, in which all of the angles are 90 degrees. Being a positive quadrilateral, it is possible to describe or inscribe a circle around the square. The radius of a circle inscribed in a square can be found by the formula: R = t / 2, where t is the side of the square. If the circle is described around it, then its radius is found as follows: R = (? 2 * t) / 2 Based on these formulas, it is allowed derive new ones to find the perimeter of the square: P = 8*R, where R is the radius of the inscribed circle; P = 4*?2*R, where R is the radius of the circumscribed circle. A square is a unique geometric figure, because it is unconditionally symmetrical, independently on how and where to draw the axis of symmetry.

Square is a geometric figure, which is a quadrilateral with all angles and sides equal. It can also be called rectangle, whose adjacent sides are equal, or rhombus where all angles are equal 90º. Thanks to the absolute symmetry find square or perimeter of the square very easy.

Instruction:

• First, let's define that perimeter called the sum of the lengths of all sides of a flat geometric figure, which is measured by the same quantities as the length. There are two ways to calculate the perimeter of a square.

Through the length of the side and diagonal

• Because the perimeter of the square is determined by the sum of the lengths of all its sides, and the sides of this figure are equal, then you can calculate the value of this value by multiplying the length of one side by the number " 4 ". Accordingly, the formulas will look like this: P = a + a + a + a or P = a * 4 , where R- this is perimeter of the square and a – side length.
• In addition, depending on the condition of the problem, the perimeter of a square can be calculated by multiplying the length of its diagonal by two roots of two: P \u003d 2√2 * d , where R- this is perimeter of the square and d- his diagonal.
• Some tasks require finding perimeter of the square knowing him square . It won't be difficult to do this either. The area of ​​a given figure is equal to the length of its side squared: S = a 2 , where S – square area and a –the length of its side. Or the area is equal to the square value of the length of its diagonal, divided by two: S = d2/2 , where S- still the same square and d – square diagonal.
• Knowing the formulas and the value of the area, it is not difficult to find the length of the side or the length of the diagonal, and then return to the formulas for calculating the perimeter and calculate its value.

Through the radius of the inscribed and circumscribed circle

• Finally, it is important to understand and how to find perimeter of the square if known circle radius described around it (or, on the contrary, inscribed in it). A circle inscribed in a given geometric figure touches the middle of each side, and its radius is equal to half of any side: R in \u003d ½ a , where R in – inscribed circle radius and a – side of a square.
• Circumscribed circle passes through all the vertices of the square and its radius is equal to half the length of the diagonal: R o \u003d ½ d , where R o - this radius of a circle circumscribed about a square and d- his diagonal.
• Therefore, in the first case, the perimeter will be calculated by the formula: R = 8 R in , and in the second: P = 4 x √2 x R o .

Using websites and an online calculator

• If you suddenly for some reason forgot the formulas, then the Internet will help refresh your knowledge. Go to the browser, open the search engine page and type in the appropriate query in the window, for example: " square perimeter formula". The system will give a huge number sites reference character, which will help you in this matter, as well as allow you to cope with solving problems related to other geometric shapes.
• In addition, if you do not want to understand the formulas and calculate the values ​​yourself, then you can use the services online calculators . An example is a website. Chapter " Formulas for the perimeter of geometric shapes» contains theoretical information supported by visual illustrations. If you follow the link " online calculator”, which is located in the window of each figure, then a page for calculations will open in front of you.
• Select in the box below what you are going to calculate based on perimeter of the square(side or diagonal), and then enter the available data. The system will issue result , guided by the established formulas.
• In addition, on the site you will find a lot of other information that can make it easier to work with math problems. If you wish, you can search for more convenient or informative reference sites.
• If you cannot figure out the very course of solving the problem, then here you can ask for help from people who are well versed in the methodology for solving mathematical exercises. They can always be found on the corresponding forums , for example, or.

This material contains geometric figures with measurements. Measurements shown are approximate and may not match actual measurements. Lesson content

The perimeter of a geometric figure

The perimeter of a geometric figure is the sum of all its sides. To calculate the perimeter, you need to measure each side and add the results of the measurements.

Calculate the perimeter of the following figure:

This is a rectangle. We will talk more about this figure later. Now just calculate the perimeter of this rectangle. It is 9 cm long and 4 cm wide.

A rectangle has opposite sides equal. This is visible in the figure. If the length is 9 cm and the width is 4 cm, then the opposite sides will be 9 cm and 4 cm, respectively:

Let's find the perimeter. To do this, add all the sides. You can add them in any order, since the sum does not change from the rearrangement of the places of the terms. The perimeter is often indicated by a capital Latin letter. P(English) perimeters). Then we get:

P= 9 cm + 4 cm + 9 cm + 4 cm = 26 cm.

Since the opposite sides of a rectangle are equal, finding the perimeter is written shorter - add the length and width, and multiply it by 2, which will mean "repeat length and width twice"

P= 2 × (9 + 4) = 18 + 8 = 26 cm.

A square is the same rectangle, but with all sides equal. For example, let's find the perimeter of a square with a side of 5 cm. The phrase "with side 5cm" need to understand how "the length of each side of the square is 5cm"

To calculate the perimeter, add up all the sides:

P= 5 cm + 5 cm + 5 cm + 5 cm = 20 cm

But since all sides are equal, the calculation of the perimeter can be written as a product. The side of the square is 5 cm, and there are 4 such sides. Then this side, equal to 5 cm, must be repeated 4 times

P= 5 cm × 4 = 20 cm

Geometric area

The area of ​​a geometric figure is a number that characterizes the size of this figure.

It should be clarified that in this case we are talking about the area on the plane. In geometry, a plane is any flat surface, for example: a sheet of paper, a plot of land, a table surface.

Area is measured in square units. Square units are squares whose sides are equal to one. For example, 1 square centimeter, 1 square meter or 1 square kilometer.

To measure the area of ​​a figure means to find out how many square units are contained in this figure.

For example, the area of ​​the following rectangle is three square centimeters:

This is because this rectangle contains three squares, each of which has a side equal to one centimeter:

On the right is a square with a side of 1 cm (in this case it is a square unit). If we look at how many times this square enters the rectangle presented on the left, we find that it enters it three times.

The following rectangle has an area of ​​six square centimeters:

This is because this rectangle contains six squares, each of which has a side equal to one centimeter:

Let's say you need to measure the area of ​​the following room:

Let's decide in which squares we will measure the area. In this case, the area is conveniently measured in square meters:

So, our task is to determine how many such squares with a side of 1 m are contained in the original room. Let's fill the whole room with this square:

We see that a square meter is contained in a room 12 times. So the area of ​​the room is 12 square meters.

Rectangle area

In the previous example, we calculated the area of ​​the room by successively checking how many times it contains a square whose side is one meter. The area was 12 square meters.

The room was a rectangle. The area of ​​a rectangle can be calculated by multiplying its length and width.

To calculate the area of ​​a rectangle, you need to multiply its length and width.

Let's go back to the previous example. Let's say we measured the length of the room with a tape measure and it turned out that the length was 4 meters:

Now let's measure the width. Let it be 3 meters:

Multiply the length (4 m) by the width (3 m).

4 x 3 = 12

Like last time, we get twelve square meters. This is explained by the fact that by measuring the length, we thereby find out how many times it is possible to fit a square with a side equal to one meter in this length. We lay four squares in this length:

We then determine how many times this length can be repeated with stacked squares. We find this out by measuring the width of the rectangle:

square area

A square is the same rectangle, but with all sides equal. For example, the following figure shows a square with a side of 3 cm. The phrase "square with side 3cm" means all sides are 3 cm

The area of ​​a square is calculated in the same way as the area of ​​a rectangle - the length is multiplied by the width.

Calculate the area of ​​a square with a side of 3 cm. Multiply the length of 3 cm by the width of 3 cm

In this case, it was required to find out how many squares with a side of 1 cm are contained in the original square. The original square contains nine squares with a side of 1 cm. Indeed, it is so. A square with a side of 1 cm enters the original square nine times:

Multiplying the length by the width, we got the expression 3 × 3, and this is the product of two identical factors, each of which is equal to 3. In other words, the expression 3 × 3 is the second power of the number 3. So the process of calculating the area of ​​​​a square can be written as a power 3 2 .

Therefore, the second power of a number is called the square of a number. When calculating the second power of a number a, a person thereby finds the area of ​​a square with a side a. The operation of raising a number to the second power is called squaring.

Notation

The area is indicated by a capital Latin letter S(English) Square- square). Then the area of ​​a square with a side a cm will be calculated according to the following rule

S = a2

where a is the length of the side of the square. The second degree indicates that two identical factors are multiplied, namely the length and width. It was previously said that all sides of a square are equal, which means that the length and width of the square are equal, expressed through the letter a .

If the task is to determine how many squares with a side of 1 cm are contained in the original square, then cm 2 should be indicated as the area units. This designation replaces the phrase "square centimeter" .

For example, let's calculate the area of ​​a square with a side of 2 cm.

So, a square with a side of 2 cm has an area equal to four square centimeters:

If the task is to determine how many squares with a side of 1 m are contained in the original square, then m 2 should be indicated as units of measurement. This designation replaces the phrase "square meter" .

Calculate the area of ​​a square with a side of 3 meters

So, a square with a side of 3 m has an area equal to nine square meters:

Similar notation is used when calculating the area of ​​a rectangle. But the length and width of the rectangle can be different, so they are denoted by different letters, for example a and b. Then the area of ​​the rectangle, length a and width b calculated according to the following rule:

S = a × b

As in the case of a square, the units for measuring the area of ​​a rectangle can be cm 2, m 2, km 2. These designations replace the phrases "square centimeter", "square meter", "square kilometer" respectively.

For example, let's calculate the area of ​​a rectangle with a length of 6 cm and a width of 3 cm

So, a rectangle 6 cm long and 3 cm wide has an area equal to eighteen square centimeters:

As a unit of measurement, it is allowed to use the phrase "square units" . For example, the entry S = 3 sq. unit means that the area of ​​a square or rectangle is equal to three squares, each of which has a unit side (1 cm, 1 m or 1 km).

Area unit conversion

Area units can be converted from one unit of measure to another. Let's look at a few examples:

Example 1. Express 1 square meter in square centimeters.

1 square meter is a square with a side of 1 m. That is, all four sides have a length equal to one meter.

But 1 m = 100 cm. Then all four sides also have a length equal to 100 cm

Calculate the new area of ​​this square. Multiply the length of 100 cm by the width of 100 cm or square the number 100

S \u003d 100 2 \u003d 10,000 cm 2

It turns out that there are ten thousand square centimeters per square meter.

1 m 2 \u003d 10,000 cm 2

This allows you to multiply any number of square meters by 10,000 in the future and get the area expressed in square centimeters.

To convert square meters to square centimeters, you need to multiply the number of square meters by 10,000.

And to convert square centimeters to square meters, on the contrary, you need to divide the number of square centimeters by 10,000.

For example, let's convert 100,000 cm 2 to square meters. In this case, you can argue like this: if 10,000 cm2 is one square meter, how many times 100,000 cm2 will contain 10 000 cm 2 "

100,000 cm 2: 10,000 cm 2 \u003d 10 m 2

Other units of measurement can be converted in the same way. For example, let's convert 2 km 2 to square meters.

One square kilometer is a square with a side of 1 km. That is, all four sides have a length equal to one kilometer. But 1 km = 1000 m. Hence, all four sides of the square are also equal to 1000 m. Let's find the new area of ​​the square, expressed in square meters. To do this, multiply the length of 1000 m by the width of 1000 m or square the number 1000

S \u003d 1000 2 \u003d 1,000,000 m 2

It turns out that there are one million square meters per square kilometer:

1 km 2 \u003d 1,000,000 m 2

This allows you to multiply any number of square kilometers by 1,000,000 in the future and get the area expressed in square meters.

To convert square kilometers to square meters, you need to multiply the number of square kilometers by 1,000,000.

So, back to our task. It was required to convert 2 km 2 into square meters. Multiply 2 km 2 by 1,000,000

2 km 2 × 1,000,000 \u003d 2,000,000 m 2

And to convert square meters to square kilometers, on the contrary, you need to divide the number of square meters by 1,000,000.

For example, let's convert 3,500,000 m2 to square kilometers. In this case, you can argue like this: if 1,000,000 m2 is one square kilometer, how many times 3,500,000 m2 will contain 1,000,000 m2 "

3,500,000 m 2: 1,000,000 m 2 \u003d 3.5 km 2

Example 2. Express 7 m 2 in square centimeters.

Multiply 7 m 2 by 10,000

7 m 2 \u003d 7 m 2 × 10,000 \u003d 70,000 cm 2

Example 3. Express 5 m 2 13 cm 2 in square centimeters.

5 m 2 13 cm 2 \u003d 5 m 2 × 10,000 + 13 cm 2 \u003d 50,013 cm 2

Example 4. Express 550,000 cm2 in square meters.

Let's find out how many times 550,000 cm 2 contains 10,000 cm 2 each. To do this, we divide 550,000 cm 2 by 10,000 cm 2

550,000 cm 2: 10,000 cm 2 \u003d 55 m 2

Example 5. Express 7 km 2 in square meters.

Multiply 7 km 2 by 1,000,000

7 km 2 × 1,000,000 \u003d 7,000,000 m 2

Example 6. Express 8,500,000 m2 in square kilometers.

Let's find out how many times 8,500,000 m 2 contains 1,000,000 m 2 each. To do this, we divide 8,500,000 m 2 by 1,000,000 m 2

8,500,000 m 2 × 1,000,000 m 2 \u003d 8.5 km 2

Units of land area measurement

It is convenient to measure the areas of small land plots in square meters.

The areas of larger land plots are measured in ares and hectares.

Ar(abbreviated: a) is an area equal to one hundred square meters (100 m 2). In view of the frequent distribution of such an area (100 m 2), it began to be used as a separate unit of measurement.

For example, if it is said that the area of ​​​​a field is 3 a, then you need to understand that these are three squares with an area of ​​\u200b\u200b100 m 2 each, that is:

3 a \u003d 100 m 2 × 3 \u003d 300 m 2

among the people ar often call weaving, since ar is equal to a square, with an area of ​​​​100 m 2. Examples:

1 weave \u003d 100 m 2

2 acres \u003d 200 m 2

10 acres \u003d 1000 m 2

Hectare(abbreviated: ha) is an area equal to 10,000 m 2. For example, if it is said that the area of ​​​​a forest is 20 hectares, then you need to understand that these are twenty squares of 10,000 m 2 each, that is:

20 ha \u003d 10,000 m 2 × 20 \u003d 200,000 m 2

Cuboid and cube

A cuboid is a geometric figure that consists of faces, edges, and vertices. The figure shows a rectangular parallelepiped:

Shown in yellow facets parallelepiped, black ribs, red - peaks.

A rectangular box has a length, width and height. The figure shows where the length, width and height are:

A parallelepiped whose length, width and height are equal is called. The figure shows a cube:

The volume of a geometric figure

The volume of a geometric figure is a number that characterizes the capacity of this figure.

Volume is measured in cubic units. Cubic units mean cubes with a length of 1, a width of 1 and a height of 1. For example, 1 cubic centimeter or 1 cubic meter.

To measure the volume of a figure means to find out how many cubic units fit in this figure.

For example, the volume of the following cuboid is twelve cubic centimeters:

This is because this box contains twelve cubes 1 cm long, 1 cm wide and 1 cm high:

The volume is indicated by a capital Latin letter V. One of the units for measuring volume is the cubic centimeter (cm 3 ). Then the volume V the parallelepiped we have considered is 12 cm 3

V\u003d 12 cm 3

The volume of any parallelepiped is calculated as follows: multiply its length, width and height.

The volume of a cuboid is equal to the product of its length, width and height.

V=abc

where, a- length, b- width, c- height

So, in the previous example, we visually determined that the volume of the parallelepiped is 12 cm 3. But you can measure the length, width and height of a given box and multiply the measurement results. We will get the same result

The volume is calculated in the same way as the volume cuboid- multiply the length, width and height.

For example, let's calculate the volume of a cube whose length is 3 cm. A cube has the same length, width and height. If the length is 3 cm, then the width and height of the cube are equal to the same three centimeters:

We multiply the length, width, height and get a volume equal to twenty-seven cubic centimeters:

V= 3 × 3 × 3 = 27 cm³

Indeed, the original cube contains 27 cubes 1 cm long

When calculating the volume of a given cube, we multiplied the length, width and height. The product is 3 × 3 × 3. This is the product of three factors, each of which is equal to 3. In other words, the product 3 × 3 × 3 is the third power of 3 and can be written as 3 3 .

V\u003d 3 3 \u003d 27 cm 3

Therefore, the third power of a number is called cube number. When calculating the third power of a number a, the person thereby finds the volume of the cube, length a. The operation of raising a number to the third power is also known as cubed.

Thus, the volume of a cube is calculated according to the following rule:

V = a 3

Where a - cube length.

cubic decimeter. Cubic meter

Not all objects of our world are conveniently measured in cubic centimeters. For example, it is more convenient to measure the volume of a room or house in cubic meters (m3). And the volume of a tank, aquarium or refrigerator is more convenient to measure in cubic decimeters (dm 3).

Another name for one cubic decimeter is one liter.

1 dm 3 = 1 liter

Conversion of volume units

Volume units can be converted from one unit of measure to another. Let's look at a few examples:

Example 1. Express 1 cubic meter in cubic centimeters.

One cubic meter is a cube with a side of 1 m. The length, width and height of this cube are equal to one meter.

But 1 m = 100 cm. So the length, width and height are also 100 cm.

Calculate the new volume of the cube, expressed in cubic centimeters. To do this, multiply its length, width and height. Or let's raise the number 100 to the cube:

V \u003d 100 3 \u003d 1,000,000 cm 3

It turns out that one cubic meter accounts for one million cubic centimeters:

1 m 3 \u003d 1,000,000 cm 3

This allows in the future to multiply any number of cubic meters by 1,000,000 and get the volume expressed in cubic centimeters.

To convert cubic meters to cubic centimeters, you need to multiply the number of cubic meters by 1,000,000.

And to convert cubic centimeters to cubic meters, on the contrary, you need to divide the number of cubic centimeters by 1,000,000.

For example, let's convert 300,000,000 cm 3 to cubic meters. In this case, you can argue like this: if 1,000,000 cm3 is one cubic meter, how many times 300,000,000 cm3 will contain 1,000,000 cm 3 "

300,000,000 cm 3: 1,000,000 cm 3 \u003d 300 m 3

Example 2. Express 3 m 3 in cubic centimeters.

Multiply 3 m 3 by 1,000,000

3 m 3 × 1,000,000 \u003d 3,000,000 cm 3

Example 3. Express 60,000,000 cm3 in cubic meters.

Let's find out how many times 60,000,000 cm 3 contains 1,000,000 cm 3 each. To do this, we divide 60,000,000 cm 3 by 1,000,000 cm 3

60,000,000 cm 3: 1,000,000 cm 3 \u003d 60 m 3

The capacity of a tank, can or canister is measured in liters. A liter is also a unit of volume. One liter is equal to one cubic decimeter.

1 liter = 1 dm 3

For example, if the capacity of a jar is 1 liter, this means that the volume of this jar is 1 dm 3 . When solving some problems, it may be useful to be able to convert liters to cubic decimeters and vice versa. Let's look at a few examples.

Example 1. Convert 5 liters to cubic decimetres.

To convert 5 liters to cubic decimeters, just multiply 5 by 1

5 l × 1 \u003d 5 dm 3

Example 2. Convert 6000 liters to cubic meters.

Six thousand liters is six thousand cubic decimeters:

6000 l × 1 = 6000 dm 3

Now let's translate these 6000 dm 3 into cubic meters.

Length, width and height of one cubic meter are equal to 10 dm

If we calculate the volume of this cube in decimeters, we get 1000 dm 3

V\u003d 10 3 \u003d 1000 dm 3

It turns out that one thousand cubic decimeters corresponds to one cubic meter. And to determine how many cubic meters correspond to six thousand cubic decimeters, you need to find out how many times 6,000 dm 3 contains 1,000 dm 3

6,000 dm 3: 1,000 dm 3 \u003d 6 m 3

So, 6000 l \u003d 6 m 3.

Table of squares

In life, you often have to find the areas of various squares. To do this, each time you need to raise the original number to the second power.

The squares of the first 99 natural numbers have already been calculated and entered in a special table called table of squares.

The first row of this table (numbers 0 to 9) is the original number, and the first column (numbers 1 to 9) is the original number.

For example, let's find the square of the number 24 in this table. The number 24 consists of the numbers 2 and 4. More precisely, the number 24 consists of two tens and four ones.

So, select the number 2 in the first column of the table (tens column), and select the number 4 in the first row (line of units). Then, moving to the right of the number 2 and down from the number 4, we find the intersection point. As a result, we will find ourselves in the position where the number 576 is located. So, the square of the number 24 is the number 576

24 2 = 576

Cube table

As in the situation with squares, the cubes of the first 99 natural numbers have already been calculated and entered in a table called cube table.

Calculate the volume of a rectangular parallelepiped, the length of which is 6 cm, the width is 4 cm, the height is 3 cm.

Solution

The number 4 reflects the area sown with wheat. And the number 5 reflects the area sown with flax.
It is said that the areas sown with wheat and flax are proportional to these numbers.

Simply put, how many times the numbers 4 or 5 change, how many times the area sown with wheat or flax will change. 15 hectares were sown with flax. That is, the number 5, which reflects the area sown with flax, has changed 3 times.

Then the number 4, which reflects the area sown with wheat, must be tripled

4 × 3 = 12 ha

Answer: 12 hectares were sown with wheat.

Problem 8. The length of the granary is 42 m, the width is the length, and the height is 0.1 length. Determine how many tons of grain the granary holds if 1 m 3 of it weighs 740 kg.

Solution

Let's determine how many liters per minute are poured through the second pipe:

25 l/min × 0.75 = 18.75 l/min

Let's determine how many liters per minute are poured into the pool through both pipes:

25 l/min + 18.75 l/min = 43.75 l/min

Determine how many liters of water will be poured into the pool in 13 hours 32 minutes

43.75 x 13 h 32 min = 43.75 x 812 min = 35,525 l

1 l \u003d 1 dm 3

35 525 l \u003d 35 525 dm 3

Convert cubic decimeters to cubic meters. This will calculate the volume of the pool:

35 525 dm 3: 1000 dm 3 \u003d 35.525 m 3

Knowing the volume of the pool, you can calculate the height of the pool. Substitute into the literal equation V=abc the values ​​we have. Then we get:

V = 35,525
a = 5.8
b = 3.5
c= x

35.525 = 5.8 x 3.5 x x
35.525 = 20.3× x
x= 1.75 m

c = 1.75

Answer: the height (depth) of the pool is 1.75 m.

Did you like the lesson?
Join our new Vkontakte group and start receiving notifications of new lessons