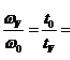Presentation on the topic of volumes of polyhedra. Presentation on the topic "Volume of a polyhedron"
MINISTRY OF EDUCATION AND SCIENCE OF THE RUSSIAN FEDERATION
federal state budget educational institution
higher education
"ULYANOVSK STATE TECHNICAL UNIVERSITY"
Barysh College - branch
Ulyanovsk State technical university
for the implementation of practical work
by discipline
« Mathematics: algebra and the beginnings of analysis, geometry»
for special students 02/09/03 Programming in computer systems, 02/38/01 Economics and accounting (by industry)
2018
Reviewed and approvedcyclic methodological commission
disciplines of the general natural and general professional cycle
Chairman _______ N.A. Zolina
I approve
Deputy director of academic work
I.I. Shmelkova
Lecturer at the Barysh College - a branch of UlSTU D.A. Sovetkin
EXPLANATORY NOTE
The purpose of conducting practical classes is to consolidate and deepen theoretical knowledge in the discipline, as well as the acquisition of practical skills by students.
Before performing each practical lesson, the student is obliged, using the materials of the literature specified in the assignment, to repeat the material covered related to the topic of the practical lesson. Checking the readiness of students is carried out through a survey.
When performing work, students should be given independence, and their creative attitude to work should be encouraged in every possible way.
At the end of the lesson, students draw up a report in which the material on the implementation of the practical lesson should be consecrated in the sequence indicated in the assignment.
After submitting the report, the student receives a credit for the work performed.
Rules for performing practical work:
When performing work, the student must independently study guidelines to carry out specific work; perform the relevant calculations; use reference and technical literature; prepare responses to Control questions. Studying the theoretical justification, the student should keep in mind that the main goal of studying the theory is the ability to apply it in practice to solve practical problems.
After completing the work, the student must submit a report on the work done with the results and conclusions obtained and defend it orally. Reports on practical work are carried out on A4 sheets. The first page is designed according to the rules of design title pages. It is necessary to leave margins 25-30 mm wide for teacher's comments. All schemes and drawings accompanying the implementation of practical work are carried out in pencil in accordance with the requirements of GOST.
Sloppy execution of practical work, non-compliance with accepted rules and poor design of drawings, graphs or diagrams may cause the work to be returned for revision.
The report must contain:
work sequence;
answers to control questions;
conclusion about the work done.
job title;
goal of the work;
PRACTICAL WORK
Topic " Volumes and surface areas of polyhedra and bodies of revolution »
Target: to consolidate the knowledge and skills of finding volumes and surface areas of polyhedra and bodies of revolution.
Time - 2 hours.
Before performing practical work, it is necessary to complete an individual project - to make a polyhedron or a body of revolution on the instructions of the teacher.
List of prisms
1. The figure is a parallelepiped.
Necessary measurements: measure the length, width, height with a ruler.
According to the measurements find:
parallelepiped diagonal
side surface area
total surface area
figure volume.
2. The figure is a right triangular prism ABCA 1 B 1 C 1 .
According to the measurements find:
side surface area
total surface area
figure volume
cross-sectional area through a side ribAA 1 and the middle of the edge of the baseBC
3. Figure - cube ABCDA 1 B 1 C 1 D 1.
Necessary measurements: measure all edges with a ruler.
According to the measurements find:
prism diagonals
side surface area
total surface area
figure volume
Control questions:
Definition of a polyhedron
Definition of a prism
Types of prisms, their definitions
Prism elements
Definition of a parallelepiped, its types and elements
Types of prism sections
Volume of the parallelepiped and prism
List of pyramids
The figure is a tetrahedron.
Necessary measurements: measure all edges with a ruler.
According to the measurements find:
the height of the pyramid
side surface area
total surface area
figure volume
sectional area passing through the lateral edge and apothem of the opposite face
The figure is a quadrangular pyramid.
Necessary measurements: measure all edges with a ruler.
According to the measurements find:
side surface area
total surface area
figure volume
sectional area passing through the diagonal of the base and the side edge
the angle between the side face and the base plane.
The figure is a truncated triangular pyramid.
Necessary measurements: measure all edges with a ruler.
According to the measurements find:
side surface area
total surface area
figure volume
the area of the section passing through the height of the base and the side edge.
The figure is a truncated quadrangular pyramid.
Required measurements: measure with a ruler.
According to the measurements find:
side surface area
total surface area
figure volume
sectional area passing through two opposite side ribs.
Control questions:
Definition of pyramid, truncated pyramid
Types of pyramids, their definitions
pyramid elements
Section types
Pyramid Volume
List of bodies of revolution
1. Cylinder
Necessary measurements: measure the diameter and height of the cylinder with a ruler.
According to the measurements find:
side surface area
total surface area
figure volume
find the area of a section drawn parallel to the axis of the cylinder at a distanceL(to ask each student individually) from her.
Questions:
Cylinder definition
Define right and equilateral cylinder
Cylinder elements
Section types
Cylinder volume
2. Cone
Necessary measurements: measure the generatrix and the diameter of the base with a ruler.
According to the measurements find:
side surface area
total surface area
figure volume
axial area
the angle of inclination of the generatrix to the plane of the base.
Questions:
Definition of cone, truncated cone
Cone elements
Section types
Area and volume of a cone, truncated cone
3. Ball and sphere
Necessary measurements: measure the length of the diametral circle.
According to the measurements find:
shape radius
surface area of a sphere
ball volume
find the cross-sectional area of a sphere or sphere by a plane drawn at a distanceX(set to each student individually) from the center.
Questions:
Definition of a ball, sphere
Types of sections of the ball and sphere
Sphere Equation
Definition of a plane tangent to a ball
Definition of spherical segment, spherical layer and spherical sector
Exercise:
1. Make the necessary measurements according to the figure
2. According to the measurement data, perform the necessary calculations
3. Complete the task in notebooks
4. Answer theoretical questions.
Design requirements: draw a figure, write down the given, write down what needs to be found, the full solution and the answer.
LIST OF SOURCES USED
1. Dadayan A.A. Collection of problems in mathematics: textbook. allowance / A.A. Dadayan. - M.: FORUM: INFRA-M, 2014. - 352 p.
2. Dadayan A.A. Mathematics: textbook. /A.A. Dadayan. - 2nd ed. - M.: FORUM, 2014. -544 p. _
3. Bogomolov N.V. Practical lessons in mathematics, - M .: Nauka, 2011. - 370 p.
4. Algebra and the beginnings of analysis. Mathematics for technical schools at 2 pm Ed. G.N. Yakovlev. – M.: Nauka, 2015. -1002 p.
5. Geometry: Proc. for 10-11 cells. general education institutions / L.S. Atanasyan, V.F. Butuzov, S.B. Kadomtsev and others - 6th ed. - M.: Education, 2013. - 207 p.
6. Alimov Sh. A. et al. Mathematics: algebra and principles of mathematical analysis, geometry. Algebra and the beginning of mathematical analysis (basic and advanced levels). Grades 10-11. - M., 2014.
Class: 11
Goals:
- repeat the types of polyhedra, their elements and volume formulas; show the practical orientation of the topic being studied;
- develop students' practical skills;
- instill interest in the subject.
Equipment:
- a set of all kinds of polyhedra;
- drawings of polygons on the board;
- a poster depicting any modern building;
- projector.
I. Heuristic conversation
(repetition of theoretical material on the topic)
1. Name and write down the formulas for the volumes of a prism, a parallelepiped, a pyramid, a truncated pyramid.
(Vprisms = Sprim. h, Vpara. = abc or Vpara. = Sprim. h, Vpyram. = Sprim. h, V = 
2. What quantities are repeated in all of the above formulas? (Height)
3. Show height on straight and oblique prisms.
4. Can a parallelepiped be called a prism? And the cube? (Yes, these are special cases of a prism)
5. Show the height on a straight and inclined pyramid.
6. What figures can be at the base of a prism and a pyramid? (Triangle, square, rhombus, rectangle, parallelogram, trapezium and other flat figures)
7. Can there be a trapezoid at the base of a parallelepiped? (No, because a parallelepiped is a prism at the base of which is a parallelogram)
8. Consider the polygons on the board. These polygons may lie at the base of the polyhedra we have considered.
On the cards, formulas with calculations of the areas of polygons ( Annex 1
). Correlate these formulas with the figures shown on the board; What is the formula for calculating the area of each of these figures?
9. Which of these formulas is suitable for calculating the floor area of a room? ( a .
b or a 2)
II. Solving problems with practical content
First option:"Service of experts of the sanitary and epidemiological station"
(a “senior expert” is selected who sets out the content of the problem and makes a conclusion based on the results of the solution).
Solution:
V = abc or V = Sbase h
V = 8.5 6 3.6 = 183.6( m 3)
183,6: 30 = 6,12(m 3) air is accounted for by one student.
Expert opinion:
Yes, 30 students can study in the classroom.
Second option:"Meteorological Service"
(a “senior meteorologist” is selected who sets out the content of the task and draws a conclusion based on the results of the solution)
Solution:
The flowerbed is a geometric figure - a straight triangular prism, where h = 20mm, then V = Sprim. h
1) Sosn. =
2) h = 20 mm, 1m = 1000mm, 1mm
= 0,001m, then h = 0.02 m
3) V = 15.3 0.02 = 0.306( m 3) = 306(dm 3)
4) 1dm 3 = 1l(water), then 306 dm 3 = 306 liters of water
The conclusion of the "senior meteorologist":
During the day, 306 liters of precipitation fell on the flower bed.
III. Solving problems for the development of the eye
We often have to ask the question: is it a lot or a little? To learn how to answer such questions, you must constantly develop your eye. Now each of you will have the opportunity to check the quality of your eye.
1) How much do you think cm 3 colognes or lotions are included in this bottle? (The teacher shows the students a bottle in the form of a truncated pyramid or a rectangular parallelepiped).
While the students are giving their guesses, one of them goes to the blackboard, takes the appropriate measurements, and calculates the correct result. Students relate their guesses to this result, thereby testing the quality of their eye.
2) How much m 3 air in our office? (The teacher gives the parameters himself).
IV. "Time out" for the development of spatial imagination
1. A tablet with a drawing of a building is exhibited.
Question: What geometric shapes does this building consist of?
Answer: cuboid, a regular quadrangular pyramid, and so on.
2. What geometric figures meet at your workplace?
V. Laboratory and practical work
Everyone has a model of a polyhedron on the table.
Exercise: Take the necessary measurements, calculate the volume of this figure on a piece of paper.
(Pre-write on the piece of paper the number of the figure and its name).
VI. Crossword puzzle
Students who completed laboratory and practical work earlier than others are invited to solve the crossword puzzle "Polyhedrons".
1. Parallel faces of a prism (base);
2. One of the polyhedra (pyramid);
3. Perpendicular between the bases of the prism (height);
4. A plane intersecting a polyhedron (section);
5. Unit of measurement (meter).
VII. Homework
VIII. Lesson summary
slide 1
slide 2
Polyhedron A polyhedron is a body whose surface consists of finite number flat polygons.
slide 3
A polyhedron is called convex if it lies on one side of any plane containing its face. A polyhedron is called non-convex if there is such a face that the polyhedron is on both sides of the plane containing this face.
slide 4
What is in the everyday sense the volume of a body, in particular a polyhedron? This is how much liquid can be poured inside this polyhedron. Cut off the tops and pour water inside each polyhedron. A convex polyhedron has already been filled, but a non-convex one has not yet. But perhaps the water was poured at different speeds: in order to correctly compare the volumes, we pour the liquid from each polyhedron into identical glasses. The water level in the right glass is higher than in the left one, which means that the volume of a non-convex polyhedron is indeed greater than the volume of a convex one.
slide 5
Many significant achievements of mathematicians Ancient Greece in solving problems of finding cubature (calculating volumes) of bodies are associated with the use of the exhaustion method proposed by Eudoxus of Cnidus (about 408-355 BC). A formula is known that makes it possible to find the volume of a polyhedron if only the lengths of its edges are known. The volume of an arbitrary polyhedron can be calculated by knowing only the lengths of its edges. However, the polyhedron must be of a special form.
slide 6
In the general case, it can be shown that the generalized volumes of polyhedra are the roots of polynomial equations with coefficients that do not depend on the location of the vertices of the polyhedron in space, but are polynomials in the squares of the lengths of its edges. The numerical coefficients of these polynomials are determined by the combinatorial structure of the polyhedron.
Slide 7
The volume of the pyramid Theorem. The volume of a pyramid is equal to one third of the base area multiplied by the height.
Slide 8
