Speed ​​and displacement formulas. Equally accelerated rectilinear motion

Let's try to derive a formula for finding the projection of the displacement vector of a body that moves in a straight line and uniformly accelerated, for any period of time.

To do this, we turn to the graph of the dependence of the projection of the speed of the rectilinear uniformly accelerated motion from time.

The graph of the dependence of the projection of the speed of rectilinear uniformly accelerated motion on time

The figure below shows a graph for the projection of the speed of a body that moves with the initial speed V0 and constant acceleration a.

If we had a uniform rectilinear motion, then to calculate the projection of the displacement vector, it would be necessary to calculate the area of ​​the figure under the graph of the projection of the velocity vector.

Now let us prove that in the case of uniformly accelerated rectilinear motion, the projection of the displacement vector Sx will be determined in the same way. That is, the projection of the displacement vector will be equal to the area of ​​the figure under the graph of the projection of the velocity vector.

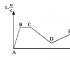
Let us find the area of ​​the figure bounded by the axis оt, by the segments AO and BC, and also by the segment AC.

Let us select a small time interval db on the ot axis. Let us draw perpendiculars to the time axis through these points, until they intersect with the velocity projection graph. Let's mark the points of intersection of a and c. During this period of time, the speed of the body will change from Vax to Vbx.

If we take this interval small enough, then we can assume that the speed remains practically unchanged, and therefore we will deal with uniform rectilinear motion in this interval.

Then we can consider the segment ac as horizontal, and abcd as a rectangle. The area abcd will be numerically equal to the projection of the displacement vector, over a period of time db. We can split the entire area of ​​the OACB figure into such small intervals.

That is, we got that the projection of the displacement vector Sx over the time interval corresponding to the segment OB will be numerically equal to the area S of the trapezoid OACB, and will be determined by the same formula as this area.

Hence,

• S = ((V0x + Vx) / 2) * t.

Since Vx = V0x + ax * t and S = Sx, the resulting formula will take the following form:

• Sx = V0x * t + (ax * t ^ 2) / 2.

We have obtained a formula with which we can calculate the projection of the displacement vector for uniformly accelerated motion.

In the case of uniformly slow motion, the formula will take the following form.

When an accident occurs on the road, experts measure the braking distance. What for? To determine the vehicle speed at the start of braking and the acceleration when braking. All this is necessary to find out the causes of the accident: either the driver exceeded the speed limit, or the brakes were faulty, or everything is in order with the car, and the pedestrian who violated the traffic rules is to blame. How, knowing the braking time and braking distance, to determine the speed and acceleration of body movement?

Find out about geometric sense displacement projections

In the 7th grade, you learned that for any movement, the path is numerically equal to the area of ​​the figure under the graph of the dependence of the modulus of movement speed on the observation time. A similar situation is with the definition of the projection of displacement (Fig. 29.1).

We obtain a formula for calculating the projection of the body's displacement over the time interval from t: = 0 to t 2 = t. Consider uniformly accelerated rectilinear motion, in which the initial velocity and acceleration have the same direction as the OX axis. In this case, the velocity projection graph has the form shown in Fig. 29.2, and the projection of the displacement is numerically equal to the area of ​​the trapezoid OABC:

On the graph, the OA segment corresponds to the projection of the initial velocity v 0 x, the BC segment corresponds to the projection of the final velocity v x, and the OC segment corresponds to the time interval t. Replacing these segments with the appropriate physical quantities and taking into account that s x = S OABC, we obtain the formula for determining the projection of displacement:

Formula (1) is used to describe any uniformly accelerated rectilinear motion.

Determine the movement of the body, the movement graph of which is shown in Fig. 29.1, b, 2 s and 4 s after the start of the timing. Explain the answer.

We write the equation of the projection of displacement

We exclude the variable v x from formula (1). To do this, recall that with uniformly accelerated rectilinear motion v x = v 0 x + a x t. Substituting the expression for v x into formula (1), we get:

Thus, for uniformly accelerated rectilinear motion, the displacement projection equation is obtained:

Rice. 29.3. The graph of the projection of displacement at uniformly accelerated rectilinear motion is a parabola passing through the origin of coordinates: if a x> 0, the branches of the parabola are directed upward (a); if a x<0, ветви параболы направлены вниз (б)

Rice. 29.4. Selection of the coordinate axis in the case of rectilinear motion

So, the graph of the projection of displacement with uniformly accelerated rectilinear movement is a parabola (Fig. 29.3), the top of which corresponds to the turning point:

Since the quantities v 0 x and a x do not depend on the observation time, the dependence s x (ί) is quadratic. For example, if

you can get another formula for calculating the projection of displacement for uniformly accelerated rectilinear motion:

Formula (3) is convenient to use if the problem statement does not deal with the time of motion of the body and does not need to be determined.

Derive formula (3) yourself.

Please note: in each formula (1-3), the projections v x, v 0 x and a x can be either positive or negative, depending on how the vectors v, v 0 and a are directed relative to the OX axis.

Write down the coordinate equation

One of the main tasks of mechanics is to determine the position of the body (body coordinates) at any time. We are considering straight-line motion, so it is sufficient to select one coordinate axis (for example, the OX axis), which is followed by

direct along the movement of the body (fig. 29.4). From this figure we see that regardless of the direction of movement, the x coordinate of the body can be determined by the formula:

Rice. 29.5. With uniformly accelerated rectilinear motion, the plot of the coordinate versus time is a parabola intersecting the x-axis at the point x 0

where x 0 is the initial coordinate (the coordinate of the body at the time of the start of observation); s x - projection of displacement.

therefore, for such a motion, the coordinate equation has the form:

For uniformly accelerated rectilinear motion

After analyzing the last equation, we conclude that the dependence x (ί) is quadratic, therefore the coordinate graph is a parabola (Fig. 29.5).

Learning to solve problems

Let us consider the main stages of solving problems for uniformly accelerated rectilinear motion using examples.

An example of solving the problem

Subsequence

action

1. Carefully read the statement of the problem. Determine which bodies take part in the movement, what is the nature of the movement of the bodies, what parameters of the movement are known.

Problem 1. After the start of braking, the train went to a stop 225 m. What was the speed of the train before braking? Consider that during braking the acceleration of the train is constant and equal to 0.5 m / s 2.

In the explanatory figure, we will direct the OX axis in the direction of the train movement. Since the train decreases its speed, then

2. Write down a brief statement of the problem. If necessary, convert the values ​​of physical quantities into SI units. 2

Problem 2. A pedestrian is walking along a straight section of the road at a constant speed of 2 m / s. A motorcycle catches up with him, which increases its speed, moving with an acceleration of 2 m / s 3. How long will it take for a motorcycle to overtake a pedestrian, if at the time the countdown began, the distance between them was 300 m, and the motorcycle was moving at a speed of 22 m / s? How far will the motorcycle travel in this time?

1. Carefully read the statement of the problem. Find out the nature of the movement of bodies, what parameters of movement are known.

Summing up

For uniformly accelerated rectilinear motion of a body: the projection of displacement is numerically equal to the area of ​​the figure under the projection of the speed of movement - the graph of dependence v x (ί):

3. Make an explanatory drawing, in which show the coordinate axis, positions of bodies, directions of accelerations and velocities.

4. Write down the coordinate equation in general form; using the figure, specify this equation for each body.

5. Considering that at the moment of meeting (overtaking) the coordinates of the bodies are the same, get a quadratic equation.

6. Solve the resulting equation and find the meeting time of the bodies.

7. Calculate the coordinates of the bodies at the time of the meeting.

8. Find the required value and analyze the result.

9. Write down your answer.

this is the geometric meaning of displacement;

the displacement projection equation is:

Control questions

1.What formulas can be used to find the projection of displacement s x for uniformly accelerated rectilinear motion? Print these formulas. 2. Prove that the graph of the body displacement versus observation time is a parabola. How are its branches directed? What moment of movement does the apex of the parabola correspond to? 3. Write down the coordinate equation for uniformly accelerated rectilinear motion. What physical quantities does this equation connect?

Exercise number 29

1. A skier moving at a speed of 1 m / s begins to descend from the mountain. Determine the length of the descent if the skier covered it in 10 seconds. Consider the skier's acceleration to be constant at 0.5 m / s 2.

2. The passenger train changed its speed from 54 km / h to 5 m / s. Determine the distance that the train traveled during braking if the acceleration of the train was constant at 1 m / s 2.

3. The brakes of a passenger car are in good working order if, at a speed of 8 m / s, its braking distance is 7.2 m. Determine the braking time and acceleration of the car.

4. The equations of coordinates of two bodies moving along the OX axis have the form:

1) For each body, determine: a) the nature of the movement; b) the starting coordinate; c) module and direction of initial speed; d) acceleration.

2) Find the time and coordinate of the meeting of the tel.

3) For each body, write down the equations v x (t) and s x (t), build graphs of the projections of speed and displacement.

5. In fig. 1 shows a graph of the projection of the speed of movement for a certain body.

Determine the path and movement of the body 4 s from the start of the countdown. Write down the coordinate equation if at time t = 0 the body was at a point with a coordinate of -20 m.

6. Two cars started moving from one point in one direction, and the second car left 20 seconds later. Both cars are moving uniformly with an acceleration of 0.4 m / s 2. In what time interval after the start of the movement of the first car will the distance between the cars be 240 m?

7. In fig. 2 shows a graph of the dependence of the coordinates of the body on the time of its movement.

Write down the coordinate equation if the acceleration modulus is known to be 1.6 m / s 2.

8. An escalator in the subway rises at a speed of 2.5 m / s. Can a person on an escalator be at rest in a frame of reference related to the Earth? If so, under what conditions? Under these conditions, can the movement of a person be considered a movement by inertia? Justify your answer.

This is tutorial material

In this lesson, we will look at an important characteristic of uneven motion - acceleration. In addition, we will consider uneven motion with constant acceleration. Such a movement is also called uniformly accelerated or equally slowed down. Finally, we will talk about how to graphically depict the dependence of the speed of a body on time for uniformly accelerated motion.

Homework

Having solved the problems for this lesson, you will be able to prepare for questions 1 GIA and questions A1, A2 of the exam.

1. Problems 48, 50, 52, 54 sb. tasks of A.P. Rymkevich, ed. ten.

2. Write down the dependences of the speed on time and draw graphs of the dependence of the body's speed on time for the cases shown in fig. 1, cases b) and d). Mark pivot points on the charts, if any.

3. Consider the following questions and answers:

Question. Is acceleration due to gravity acceleration as defined above?

Answer. Of course it is. Free fall acceleration is the acceleration of a body that falls freely from a certain height (air resistance must be neglected).

Question. What happens if the acceleration of the body is directed perpendicular to the speed of the body?

Answer. The body will move evenly around the circumference.

Question. Can I calculate the tangent of the slope using a protractor and calculator?

Answer. No! Because the acceleration obtained in this way will be dimensionless, and the dimension of the acceleration, as we showed earlier, must have the dimension of m / s 2.

Question. What about movement if the plot of speed versus time is not straight?

Answer. We can say that the acceleration of this body changes with time. Such movement will not be uniformly accelerated.

Page 8 of 12

§ 7. Displacement at uniformly accelerated
straight motion

1. Using the graph of the dependence of speed on time, you can get a formula for the movement of a body with uniform rectilinear motion.

Figure 30 shows a graph of the dependence of the projection of the speed of uniform movement on the axis X from time. If we restore the perpendicular to the time axis at some point C, then we get a rectangle OABC... The area of ​​this rectangle is equal to the product of the sides OA and OC... But the length of the side OA is equal to v x, and the length of the side OC - t, from here S = v x t... Product of the projection of the speed on the axis X and time is equal to the projection of displacement, i.e. s x = v x t.

Thus, the projection of displacement with uniform rectilinear motion is numerically equal to the area of ​​the rectangle bounded by the coordinate axes, the velocity graph and the perpendicular restored to the time axis.

2. We obtain in a similar way the formula for the projection of displacement in rectilinear uniformly accelerated motion. To do this, we will use the graph of the dependence of the projection of the speed on the axis X from time to time (Fig. 31). Select a small area on the graph ab and omit the perpendiculars from points a and b on the time axis. If the time interval D t corresponding to the site cd on the time axis is small, then we can assume that the speed does not change during this time interval and the body moves uniformly. In this case, the figure cabd differs little from a rectangle and its area is numerically equal to the projection of the displacement of the body during the time corresponding to the segment cd.

You can break the whole figure into such strips. OABC, and its area will be equal to the sum of the areas of all stripes. Therefore, the projection of the movement of the body during the time t numerically equal to the area of ​​the trapezoid OABC... From the geometry course, you know that the area of ​​a trapezoid is equal to the product of the half-sum of its bases and the height: S= (OA + BC)OC.

As can be seen from Figure 31, OA = v 0x , BC = v x, OC = t... It follows that the projection of displacement is expressed by the formula: s x= (v x + v 0x)t.

With uniformly accelerated rectilinear motion, the speed of the body at any time is equal to v x = v 0x + a x t, hence, s x = (2v 0x + a x t)t.

Hence:

To obtain the equation of motion of the body, we substitute its expression through the difference of coordinates into the formula for the projection of displacement s x = x – x 0 .

We get: x – x 0 = v 0x t+, or

x = x 0 + v 0x t + .

According to the equation of motion, it is possible to determine the coordinate of the body at any moment of time if the initial coordinate, initial velocity and acceleration of the body are known.

3. In practice, problems are often encountered in which it is necessary to find the displacement of a body with uniformly accelerated rectilinear motion, but the time of motion is unknown. In these cases, a different displacement projection formula is used. Let's get it.

From the formula for the projection of the speed of uniformly accelerated rectilinear motion v x = v 0x + a x t express the time:

t = .

Substituting this expression into the displacement projection formula, we get:

s x = v 0x + .

Hence:

s x = , or
–= 2a x s x.

If the initial velocity of the body is zero, then:

2a x s x.

4. An example of solving the problem

A skier leaves a mountain slope from a state of rest with an acceleration of 0.5 m / s 2 in 20 s and then moves along a horizontal section, having driven 40 m to a stop. With what acceleration did the skier move on a horizontal surface? How long is the slope of the mountain?

Given:	Solution
v 01 = 0 a 1 = 0.5 m / s 2 t 1 = 20 s s 2 = 40 m v 2 = 0	The skier's movement consists of two stages: at the first stage, going down the slope of the mountain, the skier moves with an increasing speed in absolute value; at the second stage, when moving on a horizontal surface, its speed decreases. The values ​​related to the first stage of movement, we write down with the index 1, and for the second stage - with the index 2.
a 2? s 1?

We will connect the frame of reference to the Earth, the axis X direct the skier in the direction of speed at each stage of his movement (Fig. 32).

Let's write the equation for the speed of the skier at the end of the descent from the mountain:

v 1 = v 01 + a 1 t 1 .

In projections on the axis X we get: v 1x = a 1x t... Since the projection of the speed and acceleration on the axis X are positive, the module of the skier's speed is: v 1 = a 1 t 1 .

Let's write down the equation that connects the projections of the speed, acceleration and movement of the skier at the second stage of the movement:

–= 2a 2x s 2x .

Considering that the initial speed of the skier at this stage of movement is equal to his final speed at the first stage

v 02 = v 1 , v 2x= 0 we get

– = –2a 2 s 2 ; (a 1 t 1) 2 = 2a 2 s 2 .

From here a 2 = ;

a 2 == 0.125 m / s 2.

The skier's movement module at the first stage of movement is equal to the length of the mountain slope. Let's write the equation for displacement:

s 1x = v 01x t + .

Hence, the length of the mountain slope is s 1 = ;

s 1 == 100 m.

Answer: a 2 = 0.125 m / s 2; s 1 = 100 m.

Self-test questions

1. As according to the graph of the dependence of the projection of the speed of uniform rectilinear motion on the axis X

2. As according to the graph of the dependence of the projection of the speed of uniformly accelerated rectilinear motion on the axis X from time to time to determine the projection of the movement of the body?

3. What is the formula for calculating the projection of the movement of the body with uniformly accelerated rectilinear motion?

4. What formula is used to calculate the projection of the displacement of a body moving uniformly and rectilinearly if the initial velocity of the body is zero?

Assignment 7

1. What is the modulus of movement of the car in 2 minutes, if during this time its speed has changed from 0 to 72 km / h? What is the coordinate of the car at a time t= 2 minutes? Consider the initial coordinate equal to zero.

2. The train moves with an initial speed of 36 km / h and an acceleration of 0.5 m / s 2. What is the movement of the train in 20 s and its coordinate at the moment of time? t= 20 s, if the initial coordinate of the train is 20 m?

3. What is the movement of a cyclist in 5 seconds after the start of braking, if his initial speed during braking is 10 m / s, and the acceleration is 1.2 m / s 2? What is the coordinate of the cyclist at the moment of time t= 5 s, if at the initial moment of time it was at the origin?

4. A vehicle moving at a speed of 54 km / h stops when braking for 15 seconds. What is the vehicle's modulus of movement during braking?

5. Two cars are moving towards each other from two settlements located at a distance of 2 km from each other. The initial speed of one car is 10 m / s and the acceleration is 0.2 m / s 2, the initial speed of the other is 15 m / s and the acceleration is 0.2 m / s 2. Determine the time and coordinate of the meeting point of the cars.

Laboratory work No. 1

Study of uniformly accelerated
straight motion

Purpose of work:

learn to measure acceleration at uniformly accelerated rectilinear motion; to experimentally establish the ratio of the paths traversed by the body during uniformly accelerated rectilinear motion for successive equal intervals of time.

Devices and materials:

chute, tripod, metal ball, stopwatch, measuring tape, metal cylinder.

Work order

1. Attach one end of the chute to the tripod leg so that it makes a small angle with the table surface. Place a metal cylinder in it at the other end of the chute.

2. Measure the paths traversed by the ball in 3 consecutive intervals of 1 second each. This can be done in different ways. You can put chalk marks on the groove, fixing the position of the ball at times equal to 1 s, 2 s, 3 s, and measure the distances s_ between these labels. You can, each time releasing the ball from the same height, measure the path s, traversed by him first in 1 s, then in 2 s and in 3 s, and then calculate the path traversed by the ball in the second and third seconds. Record the measurement results in Table 1.

3. Find the ratio of the path covered in the second second to the path covered in the first second, and the path covered in the third second to the path covered in the first second. Make a conclusion.

4. Measure the time the ball moved along the chute and the distance traveled. Calculate the acceleration of its movement using the formula s = .

5. Using the experimentally obtained value of acceleration, calculate the paths that the ball must travel in the first, second and third seconds of its movement. Make a conclusion.

Table 1

Experience number	Experimental data					Theoretical results
	Time t , with	Path s , cm	Time t , with	Way s, cm	Acceleration a, cm / s2	Timet, with	Path s , cm
1	1		1

How, knowing the braking distance, to determine the initial speed of the car and how, knowing the characteristics of movement, such as initial speed, acceleration, time, determine the movement of the car? We will receive the answers after we get acquainted with the topic of today's lesson: "Displacement with uniformly accelerated motion, the dependence of the coordinate on time during uniformly accelerated motion"

With uniformly accelerated movement, the graph looks like a straight line going up, since its acceleration projection is greater than zero.

With uniform rectilinear motion, the area will be numerically equal to the modulus of the projection of the displacement of the body. It turns out that this fact can be generalized for the case of not only uniform motion, but also for any motion, that is, it can be shown that the area under the graph is numerically equal to the displacement projection modulus. This is done strictly mathematically, but we will use a graphical method.

Rice. 2. The graph of the dependence of speed on time at uniformly accelerated motion ()

Let's split the graph of the projection of speed versus time for uniformly accelerated motion into small time intervals Δt. Suppose that they are so small that during their length the speed practically did not change, that is, the graph of the linear dependence in the figure, we conditionally turn into a ladder. At every step of it, we believe that the speed has practically not changed. Imagine that we make the time intervals Δt infinitely small. In mathematics, they say: we make the passage to the limit. In this case, the area of ​​such a ladder will be infinitely close to the area of ​​the trapezoid, which is limited by the graph V x (t). And this means that for the case of uniformly accelerated motion, we can say that the displacement projection module is numerically equal to the area bounded by the V x (t) graph: by the abscissa and ordinate axes and the perpendicular dropped on the abscissa axis, that is, the area of ​​the trapezoid OABS, which we see in Figure 2.

The problem turns from a physical into a mathematical problem - finding the area of ​​a trapezoid. This is a standard situation when physicists draw up a model that describes this or that phenomenon, and then mathematics comes into play, which enriches this model with equations, laws - what turns the model into a theory.

We find the area of ​​the trapezoid: the trapezoid is rectangular, since the angle between the axes is 90 0, we divide the trapezoid into two figures - a rectangle and a triangle. Obviously, the total area will be equal to the sum of the areas of these figures (Fig. 3). Let's find their areas: the area of ​​the rectangle is equal to the product of the sides, that is, V 0x t, the area of ​​the right triangle will be equal to half of the product of legs - 1 / 2AD BD, substituting the values ​​of the projections, we get: 1 / 2t (V x - V 0x), a, remembering the law of change in speed from time to uniformly accelerated motion: V x (t) = V 0x + a x t, it is quite obvious that the difference in the projections of the velocities is equal to the product of the projection of the acceleration a x by the time t, that is, V x - V 0x = a x t.

Rice. 3. Determination of the area of ​​the trapezoid ( A source)

Taking into account the fact that the area of ​​the trapezoid is numerically equal to the modulus of the projection of the displacement, we get:

S x (t) = V 0 x t + a x t 2/2

We have obtained the law of the dependence of the projection of displacement on time for uniformly accelerated motion in scalar form, in vector form it will look like this:

(t) = t + t 2/2

Let us derive one more formula for the projection of displacement, which will not include time as a variable. Let's solve the system of equations, excluding time from it:

S x (t) = V 0 x + a x t 2/2

V x (t) = V 0 x + a x t

Imagine that we do not know the time, then we express the time from the second equation:

t = V x - V 0x / a x

Substitute this value into the first equation:

Let's get such a cumbersome expression, square it and give similar ones:

We have obtained a very convenient expression for the projection of displacement for the case when we do not know the time of movement.

Let us assume that the initial speed of the car, when braking began, is V 0 = 72 km / h, the final speed V = 0, and the acceleration a = 4 m / s 2. Find out the length of the braking distance. Converting kilometers to meters and substituting the values ​​into the formula, we get that the braking distance will be:

S x = 0 - 400 (m / s) 2 / -2 · 4 m / s 2 = 50 m

Let's analyze the following formula:

S x = (V 0 x + V x) / 2 t

The projection of displacement is the half-sum of the projections of the initial and final velocities, multiplied by the time of movement. Let's remember the formula for the average speed

S x = V cf t

In the case of uniformly accelerated movement, the average speed will be:

V cf = (V 0 + V k) / 2

We have come close to solving the main problem of the mechanics of uniformly accelerated motion, that is, obtaining a law according to which the coordinate changes with time:

x (t) = x 0 + V 0 x t + a x t 2/2

In order to learn how to use this law, let's analyze a typical problem.

A car, moving from a state of rest, acquires an acceleration of 2 m / s 2. Find the path that the car covered in 3 seconds and in the third second.

Given: V 0 x = 0

Let us write down the law according to which the displacement changes with time at

uniformly accelerated motion: S x = V 0 x t + a x t 2/2. 2 s< Δt 2 < 3.

We can answer the first question of the problem by substituting the data:

t 1 = 3 c S 1х = а х t 2/2 = 2 3 2/2 = 9 (m) - this is the path that has passed

c car in 3 seconds.

Find out how much he drove in 2 seconds:

S x (2 s) = a x t 2/2 = 2 2 2/2 = 4 (m)

So, we know that in two seconds the car drove 4 meters.

Now, knowing these two distances, we can find the path that he traveled in the third second:

S 2x = S 1x + S x (2 s) = 9 - 4 = 5 (m)