Plane normal vector, coordinates of the plane normal vector. The normal vector of the straight line (normal vector) The normal vector of the straight line x 3 has coordinates
When studying the equations of a straight line on a plane and in three-dimensional space, we rely on the algebra of vectors. In this case, the directing vector of the straight line and the normal vector of the straight line are of particular importance. In this article, we will take a closer look at the normal vector of a line. Let's start by defining the normal vector of a straight line, give examples and graphic illustrations. Next, we turn to finding the coordinates of the normal vector of a straight line using the well-known equations of a straight line, while showing detailed solutions to the problems.
Page navigation.
Normal vector of a straight line - definition, examples, illustrations.
To understand the material, you need to have a clear idea of a straight line, a plane, and also know the basic definitions associated with vectors. Therefore, we recommend that you first brush up on the material of the articles, a straight line in a plane, a straight line in space, the idea of a plane, etc.
Let us give the definition of the normal vector of a straight line.
Definition.
Normal vector of a straight line is any nonzero vector lying on any line perpendicular to the given one.
From the definition of the normal vector of a straight line, it is clear that there is an infinite set of normal vectors of a given straight line.
The definition of the normal vector of the straight line and the determination of the direction vector of the straight line allow us to conclude that any normal vector of a given straight line is perpendicular to any direction vector of this straight line.
Let us give an example of a normal vector of a straight line.
Let Oxy be given on the plane. One of the set of normal vectors of the coordinate line Ox is the coordinate vector. Indeed, the vector is nonzero and lies on the coordinate line Oy, which is perpendicular to the Ox axis. The set of all normal vectors of the coordinate line Ox in the rectangular coordinate system Oxy can be specified as 
.
In a rectangular coordinate system Oxyz in three-dimensional space, the normal vector of the straight line Oz is a vector. The coordinate vector is also the normal vector of the straight line Oz. Obviously, any nonzero vector lying in any plane perpendicular to the Oz axis will be the normal vector of the Oz line.
Coordinates of the normal vector of a straight line - finding the coordinates of the normal vector of a straight line using the known equations of this straight line.
If we consider a straight line in a rectangular coordinate system Oxy, then the equation of a straight line on a plane of some kind will correspond to it, and the normal vectors of the straight line will be determined by their coordinates (see the article). This raises the question: "how to find the coordinates of the normal vector of a straight line when we know the equation of this straight line"?
Let us find the answer to the question posed for straight lines given on the plane by equations of various types.
If a straight line on a plane is determined by the general equation of a straight line of the form 
, then the coefficients A and B represent the corresponding coordinates of the normal vector of this straight line.
Example.
Find the coordinates of some normal vector of a straight line 
.
Solution.
Since the straight line is given by the general equation, we can immediately write down the coordinates of its normal vector - they are the corresponding coefficients before the variables x and y. That is, the normal vector of a straight line has coordinates.
Answer:
One of the numbers A or B in the general equation of the line can be zero. This should not confuse you. Let's look at an example.
Example.
Pick any normal line vector.
Solution.
We are given an incomplete general equation of the line. It can be rewritten as 
, from where the coordinates of the normal vector of this straight line are immediately visible:.
Answer:
The equation of a straight line in segments of the form or the equation of a straight line with a slope is easily reduced to the general equation of a straight line, from which the coordinates of the normal vector of this straight line are found.
Example.
Find the coordinates of the normal vector of a straight line.
Solution.
It is very easy to pass from the equation of a straight line in segments to the general equation of a straight line: 
... Therefore, the normal vector of this line has coordinates.
Answer:
If the straight line is defined by the canonical equation of the straight line on the plane of the form or parametric equations of the straight line on the plane of the form 
, then the coordinates of the normal vector are a little more difficult to obtain. From these equations, the coordinates of the directing vector of the straight line are immediately visible -. Find the coordinates of the normal vector of this straight line and allows.
You can also get the coordinates of the normal vector of a straight line, if you bring the canonical equation of a straight line or parametric equations of a straight line to the general equation. For this, the following transformations are performed: 
As a way to prefer - it's up to you.
Let's show solutions of examples.
Example.
Find some normal line vector 
.
Solution.
The direction vector of the straight line is a vector. Normal vector of a straight line is perpendicular to the vector, then it is equal to zero: 
... From this equality, giving n x an arbitrary nonzero real value, we find n y. Let n x = 1, then 
, therefore, the normal vector of the original line has coordinates.
Second solution.
We pass from the canonical equation of the straight line to the general equation:. Now the coordinates of the normal vector of this line are visible.
Answer:
To study the equations of a straight line, you need to have a good understanding of vector algebra. It is important to find the direction vector and the normal vector of the straight line. This article will consider the normal vector of a straight line with examples and figures, finding its coordinates, if the equations of straight lines are known. A detailed solution will be considered.
To make the material easier to assimilate, you need to understand the concepts of line, plane and definitions that are associated with vectors. First, let's get acquainted with the concept of a straight line vector.
Definition 1
The normal vector of the straight line any nonzero vector that lies on any line perpendicular to the given one is called.
It is clear that there is an infinite set of normal vectors located on a given straight line. Consider in the figure below.
We get that the line is perpendicular to one of the two given parallel lines, then its perpendicularity extends to the second parallel line. Hence, we find that the sets of normal vectors of these parallel lines coincide. When the straight lines a and a 1 are parallel, and n → is considered the normal vector of the straight line a, it is also considered the normal vector for the straight line a 1. When the line a has a direct vector, then the vector t · n → is nonzero for any value of the parameter t, and is also normal for the line a.
Using the definition of normal and direction vectors, we can conclude that the normal vector is perpendicular to the direction. Let's look at an example.
If the plane O x y is given, then the set of vectors for O x is the coordinate vector j →. It is considered non-zero and belongs to the coordinate axis O y, perpendicular to O x. The entire set of normal vectors with respect to O x can be written as t j →, t ∈ R, t ≠ 0.
The rectangular system O x y z has a normal vector i → related to the line O z. The vector j → is also considered normal. Hence it is seen that any nonzero vector located in any plane and perpendicular to O z is considered normal for O z.
Coordinates of the normal vector of a straight line - finding the coordinates of the normal vector of a straight line using the known equations of a straight line
When considering a rectangular coordinate system O x y, we find that the equation of a straight line on a plane corresponds to it, and the determination of normal vectors is made by coordinates. If the equation of a straight line is known, but it is necessary to find the coordinates of the normal vector, then it is necessary from the equation A x + B y + C = 0 to identify the coefficients that correspond to the coordinates of the normal vector of the given straight line.
Example 1
A straight line of the form 2 x + 7 y - 4 = 0 _ is given, find the coordinates of the normal vector.
Solution
By condition, we have that the straight line was given by the general equation, which means that it is necessary to write down the coefficients, which are the coordinates of the normal vector. This means that the coordinates of the vector are 2, 7.
Answer: 2 , 7 .
There are times when A or B from the equation equals zero. Let's consider the solution of such a task using an example.
Example 2
Specify the normal vector for the given line y - 3 = 0.
Solution
By hypothesis, we are given the general equation of the straight line, so we write it in this way 0 x + 1 y - 3 = 0. Now we can clearly see the coefficients, which are the coordinates of the normal vector. Hence, we get that the coordinates of the normal vector are 0, 1.
Answer: 0, 1.
If an equation is given in segments of the form x a + y b = 1 or an equation with a slope y = k x + b, then it is necessary to reduce to the general equation of a straight line, where you can find the coordinates of the normal vector of a given straight line.
Example 3
Find the coordinates of the normal vector, given the equation of the straight line x 1 3 - y = 1.
Solution
First, you need to go from the equation in the segments x 1 3 - y = 1 to the general equation. Then we get that x 1 3 - y = 1 ⇔ 3 x - 1 y - 1 = 0.
From this it is seen that the coordinates of the normal vector have a value of 3, - 1.
Answer: 3 , - 1 .
If the line is defined by the canonical equation of the line on the plane x - x 1 a x = y - y 1 a y or by the parametric x = x 1 + a x · λ y = y 1 + a y · λ, then obtaining coordinates becomes more complicated. According to these equations, it can be seen that the coordinates of the direction vector will be a → = (a x, a y). The possibility of finding the coordinates of the normal vector n → is possible due to the condition of perpendicularity of the vectors n → and a →.
It is possible to obtain the coordinates of a normal vector by reducing the canonical or parametric equations of a straight line to the general one. Then we get:
x - x 1 ax = y - y 1 ay ⇔ ay (x - x 1) = ax (y - y 1) ⇔ ay x - ax y + ax y 1 - ay x 1 x = x 1 + ax λ y = y 1 + ay λ ⇔ x - x 1 ax = y - y 1 ay ⇔ ay x - ax y + ax y 1 - ay x 1 = 0
For the solution, you can choose any convenient method.
Example 4
Find the normal vector of a given line x - 2 7 = y + 3 - 2.
Solution
From the straight line x - 2 7 = y + 3 - 2 it is clear that the direction vector will have coordinates a → = (7, - 2). The normal vector n → = (n x, n y) of a given line is perpendicular to a → = (7, - 2).
Let's find out what the dot product is equal to. To find the scalar product of vectors a → = (7, - 2) and n → = (n x, n y), we write a →, n → = 7 n x - 2 n y = 0.
The value of n x is arbitrary, you should find n y. If n x = 1, from this we obtain that 7 1 - 2 n y = 0 ⇔ n y = 7 2.
Hence, the normal vector has coordinates 1, 7 2.
The second way of solving is reduced to the fact that it is necessary to come to the general form of the equation from the canonical one. For this we transform
x - 2 7 = y + 3 - 2 ⇔ 7 (y + 3) = - 2 (x - 2) ⇔ 2 x + 7 y - 4 + 7 3 = 0
The resulting result of the coordinates of the normal vector is 2, 7.
Answer: 2, 7 or 1 , 7 2 .
Example 5
Specify the coordinates of the normal vector of the straight line x = 1 y = 2 - 3 · λ.
Solution
First, you need to perform a transformation to go to the general form of a straight line. Let's execute:
x = 1 y = 2 - 3 λ ⇔ x = 1 + 0 λ y = 2 - 3 λ ⇔ λ = x - 1 0 λ = y - 2 - 3 ⇔ x - 1 0 = y - 2 - 3 ⇔ ⇔ - 3 (x - 1) = 0 (y - 2) ⇔ - 3 x + 0 y + 3 = 0
From here it can be seen that the coordinates of the normal vector are - 3, 0.
Answer: - 3 , 0 .
Let us consider methods for finding the coordinates of a normal vector with the equation of a straight line in space given by a rectangular coordinate system O x y z.
When a line is defined using the equations of intersecting planes A 1 x + B 1 y + C 1 z + D 1 = 0 and A 2 x + B 2 y + C 2 z + D 2 = 0, then the normal vector of the plane refers to A 2 x + B 2 y + C 2 z + D 2 = 0 and A 2 x + B 2 y + C 2 z + D 2 = 0, then we get the vectors in the form n 1 → = (A 1, B 1, C 1) and n 2 → = (A 2, B 2, C 2).
When the line is defined using the canonical equation of the space, which has the form x - x 1 ax = y - y 1 ay = z - z 1 az or parametric, which has the form x = x 1 + ax λ y = y 1 + ay λ z = z 1 + az · λ, hence ax, ay and az are considered the coordinates of the direction vector of the given straight line. Any nonzero vector can be normal for a given straight line, and be perpendicular to the vector a → = (a x, a y, a z). It follows that the coordinates of the normal with parametric and canonical equations are found using the coordinates of a vector that is perpendicular to a given vector a → = (a x, a y, a z).
If you notice an error in the text, please select it and press Ctrl + Enter
Normal vector
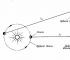
Flat surface with two normals
In differential geometry, normal is a straight line orthogonal (perpendicular) to a tangent line to a certain curve or a tangent plane to a certain surface. Also talk about normal direction.
Normal vector to a surface at a given point is a unit vector applied to a given point and parallel to the normal direction. For each point on a smooth surface, you can specify two normal vectors that differ in direction. If a continuous field of normal vectors can be specified on a surface, then this field is said to define orientation surface (that is, it highlights one of the sides). If this cannot be done, the surface is called unoriented.
Wikimedia Foundation. 2010.
See what "Normal vector" is in other dictionaries:
normal vector- normalės vektorius statusas T sritis fizika atitikmenys: angl. normal vector vok. Normalenvektor, m rus. normal vector, m pranc. vecteur de la normale, m; vecteur normal, m ... Fizikos terminų žodynas
This article or section needs revision. Please improve the article in accordance with the rules for writing articles. Darboux vector is the direction vector of the instantaneous axis of rotation around which the accompanying trihedron of the curve L rotates at ... ... Wikipedia
Electrodynamics of continuous media Electrodynamics of continuous media ... Wikipedia
The Darboux vector is the directing vector of the instantaneous axis of rotation around which the accompanying trihedron of the curve L rotates when the point M moves uniformly along the curve L. The Darboux vector lies in the rectifying plane of the curve L and is expressed through the unit ... ... Wikipedia
Gradient (from lat. Gradiens, genus. Case gradientis walking), a vector showing the direction of the steepest change of a certain value, the value of which changes from one point in space to another (see Fields theory). If the quantity is expressed ... ...
The direction vector d of the instantaneous axis of rotation around the swarm accompanying the trihedron of the curve L rotates with the uniform movement of the point M along the curve L. D. c. lies in the rectifying plane of the curve L and is expressed through the unit vectors of the principal normal ... Encyclopedia of mathematics
This article or section needs revision. Please improve the article in accordance with the rules for writing articles. Hypertop ... Wikipedia
Graphics pipeline is a hardware-software complex for 3D graphics visualization. Contents 1 Elements of a 3D scene 1.1 Hardware 1.2 Programming interfaces ... Wikipedia
A mathematical discipline in which the properties of operations on Vectors of Euclidean space are studied. At the same time, the concept of a vector is a mathematical abstraction of quantities characterized not only by a numerical value, but also ... ... Great Soviet Encyclopedia
This term has other meanings, see Plane. The request "Flatness" is redirected here. A separate article is needed on this topic ... Wikipedia
In order to use the coordinate method, you need to know the formulas well. There are three of them:
At first glance, it looks threatening, but just a little practice and everything will work great.
Task. Find the cosine of the angle between vectors a = (4; 3; 0) and b = (0; 12; 5).
Solution. Since the coordinates of the vectors are given to us, we substitute them into the first formula:
Task. Make an equation for the plane passing through the points M = (2; 0; 1), N = (0; 1; 1) and K = (2; 1; 0), if it is known that it does not pass through the origin.
Solution. The general equation of the plane: Ax + By + Cz + D = 0, but since the desired plane does not pass through the origin of coordinates - the point (0; 0; 0) - then we put D = 1. Since this plane passes through the points M, N and K, then the coordinates of these points should turn the equation into the correct numerical equality.
Substitute instead of x, y and z coordinates of the point M = (2; 0; 1). We have:
A 2 + B 0 + C 1 + 1 = 0 ⇒ 2A + C + 1 = 0;
Similarly, for the points N = (0; 1; 1) and K = (2; 1; 0) we obtain the equations:
A 0 + B 1 + C 1 + 1 = 0 ⇒ B + C + 1 = 0;
A 2 + B 1 + C 0 + 1 = 0 ⇒ 2A + B + 1 = 0;
So, we have three equations and three unknowns. Let's compose and solve the system of equations:
We got that the equation of the plane has the form: - 0.25x - 0.5y - 0.5z + 1 = 0.
Task. The plane is given by the equation 7x - 2y + 4z + 1 = 0. Find the coordinates of the vector perpendicular to the given plane.
Solution. Using the third formula, we get n = (7; - 2; 4) - that's all!
Calculating the coordinates of vectors
But what if there are no vectors in the problem - there are only points lying on straight lines, and you need to calculate the angle between these straight lines? It's simple: knowing the coordinates of the points - the beginning and end of the vector - you can calculate the coordinates of the vector itself.
To find the coordinates of a vector, subtract the coordinates of the beginning from the coordinates of its end.
This theorem works in the same way both on the plane and in space. The expression "subtract coordinates" means that the x coordinate of another point is subtracted from the x coordinate of one point, then the same must be done with the y and z coordinates. Here are some examples:
Task. There are three points in space, given by their coordinates: A = (1; 6; 3), B = (3; - 1; 7) and C = (- 4; 3; - 2). Find the coordinates of vectors AB, AC and BC.
Consider a vector AB: its origin is at point A, and its end is at point B. Therefore, to find its coordinates, it is necessary to subtract the coordinates of point A from the coordinates of point B:
AB = (3 - 1; - 1 - 6; 7 - 3) = (2; - 7; 4).
Similarly, the beginning of the vector AC is still the same point A, but the end is point C. Therefore, we have:
AC = (- 4 - 1; 3 - 6; - 2 - 3) = (- 5; - 3; - 5).
Finally, to find the coordinates of the vector BC, you need to subtract the coordinates of point B from the coordinates of point C:
BC = (- 4 - 3; 3 - (- 1); - 2 - 7) = (- 7; 4; - 9).
Answer: AB = (2; - 7; 4); AC = (- 5; - 3; - 5); BC = (- 7; 4; - 9)
Pay attention to the calculation of the coordinates of the last BC vector: many people make mistakes when working with negative numbers. This concerns the variable y: point B has y = - 1, and point C y = 3. We get exactly 3 - (- 1) = 4, and not 3 - 1, as many believe. Don't make such stupid mistakes!
Calculation of direction vectors for straight lines
If you read Problem C2 carefully, you will be surprised to find that there are no vectors there. There are only straight lines and planes.
Let's start with straight lines. Everything is simple here: on any straight line there are at least two different points and, conversely, any two different points define a single straight line ...
Does anyone understand what is written in the previous paragraph? I didn’t understand it myself, so I’ll explain it easier: in problem C2, straight lines are always given by a pair of points. If we introduce a coordinate system and consider a vector with a beginning and an end at these points, we get the so-called direction vector for a straight line:
Why is this vector needed? The point is that the angle between two straight lines is the angle between their direction vectors. Thus, we pass from incomprehensible straight lines to specific vectors, the coordinates of which are easy to calculate. How easy is it? Take a look at examples:
Task. In the cube ABCDA 1 B 1 C 1 D 1 lines AC and BD 1 are drawn. Find the coordinates of the direction vectors of these lines.
Since the length of the edges of the cube is not specified in the condition, we set AB = 1. We introduce a coordinate system with the origin at point A and axes x, y, z directed along lines AB, AD and AA 1, respectively. The unit segment is equal to AB = 1.
Now let's find the coordinates of the direction vector for the line AC. We need two points: A = (0; 0; 0) and C = (1; 1; 0). From here we get the coordinates of the vector AC = (1 - 0; 1 - 0; 0 - 0) = (1; 1; 0) - this is the direction vector.
Now let's deal with the straight line BD 1. It also has two points: B = (1; 0; 0) and D 1 = (0; 1; 1). We get the direction vector BD 1 = (0 - 1; 1 - 0; 1 - 0) = (- 1; 1; 1).
Answer: AC = (1; 1; 0); BD 1 = (- 1; 1; 1)
Task. In a regular triangular prism ABCA 1 B 1 C 1, all edges of which are equal to 1, lines AB 1 and AC 1 are drawn. Find the coordinates of the direction vectors of these lines.
Let us introduce a coordinate system: the origin is at point A, the x-axis coincides with AB, the z-axis coincides with AA 1, the y-axis forms the OXY plane with the x-axis, which coincides with the ABC plane.
First, let's deal with the straight line AB 1. Everything is simple here: we have points A = (0; 0; 0) and B 1 = (1; 0; 1). We get the direction vector AB 1 = (1 - 0; 0 - 0; 1 - 0) = (1; 0; 1).
Now we will find the direction vector for AC 1. All the same - the only difference is that point C 1 has irrational coordinates. So, A = (0; 0; 0), so we have:
Answer: AB 1 = (1; 0; 1);
A small but very important note about the last example. If the origin of the vector coincides with the origin, the calculations are greatly simplified: the coordinates of the vector are simply equal to the coordinates of the end. Unfortunately, this is only true for vectors. For example, when working with planes, the presence of the origin on them only complicates the calculations.
Calculation of normal vectors for planes
Normal vectors are not vectors that do or do well. By definition, a normal vector (normal) to a plane is a vector perpendicular to that plane.
In other words, a normal is a vector perpendicular to any vector in a given plane. Surely you have met such a definition - however, instead of vectors, we were talking about straight lines. However, just above it was shown that in problem C2 you can operate with any convenient object - even a straight line, even a vector.
Let me remind you once again that any plane is defined in space by the equation Ax + By + Cz + D = 0, where A, B, C and D are some coefficients. Without loss of generality of the solution, we can assume D = 1 if the plane does not pass through the origin, or D = 0 if it does. In any case, the coordinates of the normal vector to this plane are n = (A; B; C).
So, the plane can also be successfully replaced by a vector - the same normal. Any plane is defined in space by three points. How to find the equation of the plane (and hence the normals), we have already discussed at the very beginning of the article. However, this process causes problems for many, so I will give a couple more examples:
Task. Section A 1 BC 1 is drawn in the cube ABCDA 1 B 1 C 1 D 1. Find the normal vector for the plane of this section if the origin is at point A, and the x, y, and z axes coincide with the edges AB, AD and AA 1, respectively.
Since the plane does not go through the origin, its equation looks like this: Ax + By + Cz + 1 = 0, i.e. coefficient D = 1. Since this plane passes through points A 1, B and C 1, the coordinates of these points turn the equation of the plane into the correct numerical equality.
A 0 + B 0 + C 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = - 1;
Similarly, for points B = (1; 0; 0) and C 1 = (1; 1; 1) we obtain the equations:
A 1 + B 0 + C 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = - 1;
A 1 + B 1 + C 1 + 1 = 0 ⇒ A + B + C + 1 = 0;
But we already know the coefficients A = - 1 and C = - 1, so it remains to find the coefficient B:
B = - 1 - A - C = - 1 + 1 + 1 = 1.
We get the equation of the plane: - A + B - C + 1 = 0, Therefore, the coordinates of the normal vector are equal to n = (- 1; 1; - 1).
Task. Section AA 1 C 1 C is drawn in the cube ABCDA 1 B 1 C 1 D 1 C. Find the normal vector for the plane of this section if the origin is at point A and the x, y, and z axes coincide with the edges AB, AD and AA 1 respectively.
In this case, the plane passes through the origin, so the coefficient D = 0, and the plane equation looks like this: Ax + By + Cz = 0. Since the plane passes through the points A1 and C, the coordinates of these points turn the plane equation into the correct numerical equality.
Substitute instead of x, y and z coordinates of the point A 1 = (0; 0; 1). We have:
A 0 + B 0 + C 1 = 0 ⇒ C = 0;
Similarly, for the point C = (1; 1; 0) we get the equation:
A 1 + B 1 + C 0 = 0 ⇒ A + B = 0 ⇒ A = - B;
We put B = 1. Then A = - B = - 1, and the equation of the whole plane has the form: - A + B = 0, Therefore, the coordinates of the normal vector are equal to n = (- 1; 1; 0).
Generally speaking, in the above problems it is necessary to compose a system of equations and solve it. There will be three equations and three variables, but in the second case one of them will be free, i.e. take arbitrary values. That is why we have the right to put B = 1 - without prejudice to the generality of the solution and the correctness of the answer.
Very often in the C2 problem it is required to work with points that divide the segment in half. The coordinates of such points are easily calculated if the coordinates of the ends of the segment are known.
So, let the segment be defined by its ends - points A = (x a; y a; z a) and B = (x b; y b; z b). Then the coordinates of the midpoint of the segment - we denote it by the point H - can be found by the formula:
In other words, the coordinates of the midpoint of a segment are the arithmetic mean of the coordinates of its ends.
Task. The unit cube ABCDA 1 B 1 C 1 D 1 is placed in the coordinate system so that the x, y and z axes are directed along the edges AB, AD and AA 1, respectively, and the origin coincides with point A. Point K is the midpoint of the edge A 1 B 1 . Find the coordinates of this point.
Since point K is the midpoint of the segment A 1 B 1, its coordinates are equal to the arithmetic mean of the coordinates of the ends. Let's write down the coordinates of the ends: A 1 = (0; 0; 1) and B 1 = (1; 0; 1). Now let's find the coordinates of point K:
Task. The unit cube ABCDA 1 B 1 C 1 D 1 is placed in the coordinate system so that the x, y and z axes are directed along the edges AB, AD and AA 1, respectively, and the origin coincides with point A. Find the coordinates of the point L at which they intersect diagonals of the square A 1 B 1 C 1 D 1.
It is known from the planimetry course that the intersection point of the diagonals of a square is equidistant from all its vertices. In particular, A 1 L = C 1 L, i.e. point L is the midpoint of segment A 1 C 1. But A 1 = (0; 0; 1), C 1 = (1; 1; 1), so we have:
Answer: L = (0.5; 0.5; 1)
A plane normal vector is a vector that is perpendicular to a given plane. Obviously, any plane has infinitely many normal vectors. But one will be enough for us to solve problems.
If the plane is given by the general equation , then the vector is the normal vector of the given plane... Just outrageously. All you have to do is "remove" the coefficients from the plane equation.
The promised three screens await, let's go back to Example # 1 and check it out. Let me remind you that there it was required to construct the equation of the plane using a point and two vectors. As a result of the solution, we got the equation. We check:
First, we substitute the coordinates of the point into the resulting equation:
The correct equality is obtained, which means that the point really lies in this plane.
Secondly, we remove the normal vector from the equation of the plane:. Since the vectors are parallel to the plane, and the vector is perpendicular to the plane, the following facts should take place: 
... The perpendicularity of vectors is easy to check with dot product:
Conclusion: the equation of the plane was found correctly.
During my verification, I actually quoted the following theory statement: vector parallel to the plane if and only if 
.
Let's solve an important problem that is relevant to the lesson:
Example 5
Find the unit normal vector of the plane 
.
Solution: A unit vector is a vector whose length is one. Let us denote this vector by. Basically, the landscape looks like this: 
It is quite clear that vectors are collinear.
First, we remove the normal vector from the plane equation:.
How do I find the unit vector? To find the unit vector , necessary every vector coordinate divide by the length of the vector .
Let's rewrite the normal vector in the form and find its length:
According to the above:
Answer: 
Verification: which is what we wanted to verify.
Readers who have carefully studied the last paragraph of the lesson Dot product of vectors probably noticed that unit vector coordinates Are exactly the direction cosines of the vector
:
Let's digress from the analyzed problem: when you are given an arbitrary non-zero vector, and by condition it is required to find its direction cosines (the last tasks of the lesson Dot product of vectors), then you, in fact, find a unit vector collinear to the given one.
In fact, two tasks in one bottle.
The need to find the unit normal vector arises in some problems of mathematical analysis.
We figured out how to fish out the normal vector, now we will answer the opposite question.
