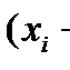बुनियादी प्राथमिक कार्य, उनके गुण और रेखांकन। पावर फ़ंक्शन, इसके गुण और ग्राफ़ पावर फ़ंक्शन का उपयोग करने का एक उदाहरण
पावर फ़ंक्शन फॉर्म के सूत्र द्वारा दिया जाता है।
एक्सपोनेंट के मान के आधार पर पावर फ़ंक्शन के ग्राफ़ के प्रकार और पावर फ़ंक्शन के गुणों पर विचार करें।
आइए पूर्णांक घातांक वाले पावर फ़ंक्शन से प्रारंभ करें ए. इस मामले में, शक्ति कार्यों के रेखांकन का रूप और कार्यों के गुण सम या विषम घातांक पर निर्भर करते हैं, साथ ही इसके संकेत पर भी। इसलिए, हम पहले घातांक के विषम धनात्मक मानों के लिए शक्ति कार्यों पर विचार करते हैं ए, फिर - सकारात्मक के लिए भी, फिर - विषम नकारात्मक घातांक के लिए, और अंत में, नकारात्मक के लिए भी ए.
भिन्नात्मक और अपरिमेय घातांक (साथ ही ऐसे शक्ति कार्यों के रेखांकन के प्रकार) के साथ शक्ति कार्यों के गुण घातांक के मूल्य पर निर्भर करते हैं ए. हम उन पर विचार करेंगे, सबसे पहले, एशून्य से एक तक, और दूसरी बात, पर एबड़ी इकाइयाँ, तीसरी, के साथ एशून्य से एक से शून्य तक, चौथा, जब एछोटा ऋण एक।
इस उपभाग के निष्कर्ष में, पूर्णता के लिए, हम शून्य घातांक वाले एक शक्ति फलन का वर्णन करते हैं।
अजीब सकारात्मक एक्सपोनेंट के साथ पावर फ़ंक्शन।
एक अजीब सकारात्मक एक्सपोनेंट के साथ एक पावर फ़ंक्शन पर विचार करें, यानी एक = 1,3,5,….
नीचे दिया गया चित्र शक्ति कार्यों के ग्राफ दिखाता है - काली रेखा, - नीली रेखा, - लाल रेखा, - हरी रेखा। पर ए = 1अपने पास रैखिक प्रकार्य वाई = एक्स.

विषम धनात्मक घातांक वाले पावर फ़ंक्शन के गुण।
सम धनात्मक प्रतिपादक के साथ शक्ति कार्य।
सम धनात्मक घातांक वाले एक शक्ति फलन पर विचार करें, अर्थात्, के लिए एक = 2,4,6,….
एक उदाहरण के रूप में, आइए पावर फ़ंक्शंस के ग्राफ़ लें - काली रेखा, - नीली रेखा, - लाल रेखा। पर ए = 2हमारे पास एक द्विघात फलन है जिसका ग्राफ है द्विघात परवलय.

सम धनात्मक घातांक वाले शक्ति फलन के गुण।
विषम ऋणात्मक घातांक के साथ शक्ति फलन।
घातांक के विषम ऋणात्मक मानों के लिए, अर्थात्, के लिए शक्ति फलन के आलेखों को देखें एक = -1, -3, -5,….
ऊर्जा समीकरणरूप का कार्य है वाई = एक्सपी, जहाँ p एक दी गई वास्तविक संख्या है।
पावर फ़ंक्शन गुण
- यदि संकेतक पी = 2एन- एक भी प्राकृतिक संख्या:
- परिभाषा का क्षेत्र सभी वास्तविक संख्याएँ हैं, अर्थात् समुच्चय R;
- मानों का समूह - गैर-ऋणात्मक संख्याएँ, अर्थात y ≥ 0;
- कार्य सम है;
- फ़ंक्शन अंतराल x ≤ 0 पर घट रहा है और अंतराल x ≥ 0 पर बढ़ रहा है।
- यदि संकेतक पी = 2एन - 1- विषम प्राकृतिक संख्या:
- परिभाषा का डोमेन - सेट आर;
- मूल्यों का सेट - सेट आर;
- कार्य विषम है;
- फ़ंक्शन पूरे वास्तविक अक्ष पर बढ़ रहा है।
- यदि संकेतक पी=-2एन, कहाँ एन- प्राकृतिक संख्या:
- मूल्यों का सेट - सकारात्मक संख्या y > 0;
- कार्य सम है;
- फ़ंक्शन अंतराल x 0 पर बढ़ रहा है।
- यदि संकेतक पी = - (2एन - 1), कहाँ एन- प्राकृतिक संख्या:
- x = 0 को छोड़कर, परिभाषा का क्षेत्र समुच्चय R है;
- मूल्यों का सेट - सेट आर, y = 0 को छोड़कर;
- कार्य विषम है;
- फ़ंक्शन अंतराल x 0 पर घट रहा है।
- यदि संकेतक पीएक सकारात्मक वास्तविक गैर-पूर्णांक संख्या है:
- परिभाषा का डोमेन - गैर-ऋणात्मक संख्या x ≥ 0;
- मूल्यों का सेट - गैर-ऋणात्मक संख्या y ≥ 0;
- फ़ंक्शन अंतराल x ≥ 0 पर बढ़ रहा है।
- यदि संकेतक पीएक नकारात्मक वास्तविक गैर-पूर्णांक संख्या है:
- परिभाषा का क्षेत्र - धनात्मक संख्या x > 0;
- मूल्यों का सेट - सकारात्मक संख्या y > 0;
- फ़ंक्शन अंतराल x > 0 पर घट रहा है।
नकारात्मक पूर्णांक घातांक वाले पावर फ़ंक्शंस के गुणों और ग्राफ़ को याद करें।
सम n के लिए :
कार्य उदाहरण:
ऐसे कार्यों के सभी ग्राफ दो निश्चित बिंदुओं से होकर गुजरते हैं: (1;1), (-1;1)। इस प्रकार के कार्यों की एक विशेषता उनकी समानता है, रेखांकन ऑप-वाई अक्ष के संबंध में सममित हैं।

चावल। 1. किसी फ़ंक्शन का ग्राफ़
विषम n के लिए, :
कार्य उदाहरण:
ऐसे कार्यों के सभी ग्राफ दो निश्चित बिंदुओं से होकर गुजरते हैं: (1;1), (-1;-1)। इस प्रकार के कार्यों की एक विशेषता उनकी विषमता है, रेखांकन मूल के संबंध में सममित हैं।

चावल। 2. फंक्शन ग्राफ
आइए मुख्य परिभाषा को याद करें।
एक गैर-ऋणात्मक संख्या की डिग्री एक तर्कसंगत सकारात्मक एक्सपोनेंट के साथ एक संख्या कहलाती है।
परिमेय ऋणात्मक घातांक वाली धनात्मक संख्या a की घात संख्या कहलाती है।
निम्नलिखित के लिए समानता रखती है:
![]()
![]()
उदाहरण के लिए: ![]() ; - एक नकारात्मक तर्कसंगत प्रतिपादक के साथ एक डिग्री की परिभाषा से अभिव्यक्ति मौजूद नहीं है; मौजूद है, क्योंकि प्रतिपादक एक पूर्णांक है,
; - एक नकारात्मक तर्कसंगत प्रतिपादक के साथ एक डिग्री की परिभाषा से अभिव्यक्ति मौजूद नहीं है; मौजूद है, क्योंकि प्रतिपादक एक पूर्णांक है, ![]()
आइए हम एक परिमेय ऋणात्मक घातांक वाले शक्ति फलनों पर विचार करें।
![]()
उदाहरण के लिए:
इस फंक्शन को प्लॉट करने के लिए आप एक टेबल बना सकते हैं। हम अन्यथा करेंगे: सबसे पहले, हम भाजक के ग्राफ का निर्माण और अध्ययन करेंगे - हम इसे जानते हैं (चित्र 3)।

चावल। 3. किसी फ़ंक्शन का ग्राफ़
denominator फ़ंक्शन का ग्राफ़ एक निश्चित बिंदु (1;1) से गुजरता है। मूल फ़ंक्शन के ग्राफ़ का निर्माण करते समय, यह बिंदु रहता है, जब जड़ भी शून्य हो जाती है, तो फ़ंक्शन अनंत तक जाता है। और, इसके विपरीत, जैसे x अनंत की ओर प्रवृत्त होता है, फलन शून्य की ओर प्रवृत्त होता है (चित्र 4)।

चावल। 4. फंक्शन ग्राफ
अध्ययन के तहत कार्यों के परिवार से एक और समारोह पर विचार करें।
![]()
यह महत्वपूर्ण है कि परिभाषा के अनुसार
हर में फ़ंक्शन के ग्राफ़ पर विचार करें: , हम इस फ़ंक्शन के ग्राफ़ को जानते हैं, यह परिभाषा के अपने डोमेन में बढ़ता है और बिंदु (1; 1) (चित्र 5) के माध्यम से गुजरता है।

चावल। 5. फंक्शन ग्राफ
मूल फ़ंक्शन के ग्राफ़ का निर्माण करते समय, बिंदु (1; 1) रहता है, जब रूट भी शून्य हो जाता है, तो फ़ंक्शन अनंत तक जाता है। और, इसके विपरीत, जैसे x अनंत की ओर प्रवृत्त होता है, फलन शून्य की ओर प्रवृत्त होता है (चित्र 6)।

चावल। 6. फंक्शन ग्राफ
विचार किए गए उदाहरण यह समझने में मदद करते हैं कि ग्राफ कैसे जाता है और अध्ययन के तहत फ़ंक्शन के गुण क्या हैं - एक नकारात्मक तर्कसंगत प्रतिपादक वाला फ़ंक्शन।
इस परिवार के कार्यों के रेखांकन बिंदु (1; 1) से होकर गुजरते हैं, परिभाषा के पूरे डोमेन में फ़ंक्शन घटता है।
कार्य क्षेत्र: ![]()
समारोह ऊपर से घिरा नहीं है, लेकिन नीचे से घिरा हुआ है। फ़ंक्शन का न तो अधिकतम और न ही न्यूनतम मान है।
कार्य निरंतर है, यह सभी सकारात्मक मूल्यों को शून्य से प्लस अनंत तक ले जाता है।
उत्तल नीचे फलन (चित्र 15.7)
बिंदु A और B को वक्र पर लिया जाता है, उनके माध्यम से एक खंड खींचा जाता है, संपूर्ण वक्र खंड के नीचे होता है, यह स्थिति वक्र पर मनमाना दो बिंदुओं के लिए संतुष्ट होती है, इसलिए कार्य उत्तल नीचे की ओर होता है। चावल। 7.

चावल। 7. एक समारोह की उत्तलता
यह समझना महत्वपूर्ण है कि इस परिवार के कार्य नीचे से शून्य से बंधे हैं, लेकिन उनका सबसे छोटा मूल्य नहीं है।
उदाहरण 1 - अंतराल \[(\mathop(lim)_(x\to +\infty ) x^(2n)\ )=+\infty \] पर अधिकतम और न्यूनतम फ़ंक्शन का पता लगाएं
ग्राफ (चित्र 2)।

चित्रा 2. समारोह का ग्राफ $f\बाएं(x\दाएं)=x^(2n)$
प्राकृतिक विषम घातांक वाले पावर फ़ंक्शन के गुण
परिभाषा का क्षेत्र सभी वास्तविक संख्याएँ हैं।
$f\left(-x\right)=((-x))^(2n-1)=(-x)^(2n)=-f(x)$ एक विषम कार्य है।
$f(x)$ परिभाषा के संपूर्ण डोमेन पर निरंतर है।
परिसर सभी वास्तविक संख्याएँ हैं।
$f"\बाएं(x\दाएं)=\बाएं(x^(2n-1)\दाएं)"=(2n-1)\cdot x^(2(n-1))\ge 0$
परिभाषा के पूरे डोमेन में फ़ंक्शन बढ़ता है।
$f\बाएं(x\दाएं)0$, $x\in (0,+\infty)$ के लिए।
$f(""\बाएं(x\दाएं))=(\बाएं(\बाएं(2n-1\दाएं)\cdot x^(2\बाएं(n-1\दाएं))\दाएं))"=2 \बाएं(2n-1\दाएं)(n-1)\cdot x^(2n-3)$
\ \
फ़ंक्शन $x\in (-\infty ,0)$ के लिए अवतल है और $x\in (0,+\infty)$ के लिए उत्तल है।
ग्राफ (चित्र 3)।

चित्रा 3. समारोह का ग्राफ $f\बाएं(x\दाएं)=x^(2n-1)$
पूर्णांक प्रतिपादक के साथ पावर फ़ंक्शन
आरंभ करने के लिए, हम पूर्णांक घातांक वाली डिग्री की अवधारणा का परिचय देते हैं।
परिभाषा 3
पूर्णांक एक्सपोनेंट $n$ के साथ एक वास्तविक संख्या $a$ की डिग्री सूत्र द्वारा निर्धारित की जाती है:

चित्रा 4
अब एक पूर्णांक एक्सपोनेंट, इसके गुणों और ग्राफ के साथ एक पावर फ़ंक्शन पर विचार करें।
परिभाषा 4
$f\left(x\right)=x^n$ ($n\in Z)$ को पूर्णांक एक्सपोनेंट वाला पावर फ़ंक्शन कहा जाता है।
यदि डिग्री शून्य से अधिक है, तो हम प्राकृतिक एक्सपोनेंट वाले पावर फ़ंक्शन के मामले में आते हैं। ऊपर हम पहले ही विचार कर चुके हैं। $n=0$ के लिए हमें एक रैखिक फलन $y=1$ मिलता है। हम इसका विचार पाठक पर छोड़ते हैं। यह एक नकारात्मक पूर्णांक घातांक वाले पावर फ़ंक्शन के गुणों पर विचार करने के लिए बना हुआ है
ऋणात्मक पूर्णांक घातांक वाले पावर फ़ंक्शन के गुण
गुंजाइश है $\बाएं(-\infty ,0\right)(0,+\infty)$।
यदि घातांक सम है, तो फलन सम है; यदि विषम है, तो फलन विषम है।
$f(x)$ परिभाषा के संपूर्ण डोमेन पर निरंतर है।
मूल्य की सीमा:
यदि घातांक सम है, तो $(0,+\infty)$, यदि विषम है, तो $\बाएं(-\infty ,0\right)(0,+\infty)$।
यदि प्रतिपादक विषम है, तो फ़ंक्शन $x\in \बाएं(-\infty ,0\right)(0,+\infty)$ के रूप में घटता है। सम घातांक के लिए, फ़ंक्शन $x\in (0,+\infty)$ के रूप में घटता है। और $x\in \बाएं(-\infty ,0\right)$ के रूप में बढ़ता है।
$f(x)\ge 0$ पूरे डोमेन पर