Inegalități trigonometrice. Inegalitățile trigonometrice și soluțiile lor Cum se rezolvă inegalitățile trigonometrice duble

Ministerul Educației al Republicii Belarus

instituție educațională

„Universitatea de Stat Gomel

numit după Francysk Skaryna"

Facultatea de Matematică

Departamentul de Algebră și Geometrie

Eligibil pentru apărare

Cap Departamentul Shemetkov L.A.

Ecuații trigonometrice și inegalități

Lucrări de curs

Executor testamentar:

grupa de elevi M-51

CM. Gorsky

Consilier științific

Lector superior

V.G. Safonov

Gomel 2008

INTRODUCERE

METODE DE BAZĂ PENTRU REZOLVAREA ECUATIILOR TRIGONOMETRICE

Factorizarea

Rezolvarea ecuațiilor prin conversia produsului funcțiilor trigonometrice într-o sumă

Rezolvarea ecuațiilor folosind formule cu argument triplu

Înmulțirea cu o funcție trigonometrică

ECUAȚII TRIGONOMETRICE NE-STANDARD

INEGALITATI TRIGONOMETRICE

SELECTAREA RĂDĂCINILOR

SARCINI PENTRU SOLUȚIE INDEPENDENTĂ

CONCLUZIE

LISTA SURSELOR UTILIZATE

În antichitate, trigonometria a apărut în legătură cu nevoile astronomiei, topografiei și construcțiilor, adică era de natură pur geometrică și reprezenta în principal<<исчисление хорд>>. De-a lungul timpului, unele puncte analitice au început să se intersecteze în el. În prima jumătate a secolului al XVIII-lea a avut loc o întorsătură bruscă, după care trigonometria a luat o nouă direcție și a trecut spre analiza matematică. În acest moment, dependențele trigonometrice au început să fie considerate funcții.

Ecuațiile trigonometrice sunt una dintre cele mai dificile subiecte din cursul de matematică din școală. Ecuațiile trigonometrice apar la rezolvarea problemelor din planimetrie, geometrie solidă, astronomie, fizică și alte domenii. Ecuațiile trigonometrice și inegalitățile de la an la an se regăsesc printre sarcinile de testare centralizată.

Cea mai importantă diferență dintre ecuațiile trigonometrice și cele algebrice este că ecuațiile algebrice au un număr finit de rădăcini, în timp ce ecuațiile trigonometrice au un număr infinit, ceea ce complică foarte mult selecția rădăcinilor. O altă specificitate a ecuațiilor trigonometrice este forma non-unica de scriere a răspunsului.

Această teză este dedicată metodelor de rezolvare a ecuațiilor și inegalităților trigonometrice.

Lucrarea de diplomă este formată din 6 secțiuni.

Prima secțiune conține informațiile teoretice de bază: definiția și proprietățile funcțiilor trigonometrice și trigonometrice inverse; tabel de valori ale funcțiilor trigonometrice pentru unele argumente; exprimarea funcțiilor trigonometrice în termenii altor funcții trigonometrice, ceea ce este foarte important pentru conversia expresiilor trigonometrice, în special a celor care conțin funcții trigonometrice inverse; pe lângă formulele trigonometrice de bază, binecunoscute din cursul școlar, se dau formule care simplifică expresiile care conțin funcții trigonometrice inverse.

A doua secțiune prezintă principalele metode de rezolvare a ecuațiilor trigonometrice. Se iau în considerare soluția ecuațiilor trigonometrice elementare, metoda factorizării, metodele de reducere a ecuațiilor trigonometrice la cele algebrice. Având în vedere faptul că soluțiile ecuațiilor trigonometrice pot fi scrise în mai multe moduri, iar forma acestor soluții nu permite să se stabilească imediat dacă aceste soluții sunt identice sau diferite, ceea ce poate<<сбить с толку>> la rezolvarea testelor se are în vedere o schemă generală de rezolvare a ecuațiilor trigonometrice și se consideră în detaliu transformarea grupurilor de soluții generale a ecuațiilor trigonometrice.

A treia secțiune tratează ecuațiile trigonometrice non-standard, ale căror soluții se bazează pe abordarea funcțională.

A patra secțiune tratează inegalitățile trigonometrice. Sunt luate în considerare în detaliu metode de rezolvare a inegalităților trigonometrice elementare, atât pe un cerc unitar, cât și printr-o metodă grafică. Este descris procesul de rezolvare a inegalităților trigonometrice neelementare prin inegalități elementare și metoda intervalelor deja bine cunoscută școlarilor.

Secțiunea a cincea prezintă cele mai dificile sarcini: atunci când este necesar nu numai să se rezolve o ecuație trigonometrică, ci și să se selecteze rădăcini din rădăcinile găsite care îndeplinesc o anumită condiție. Această secțiune oferă soluții pentru sarcinile tipice pentru selectarea rădăcinilor. Informațiile teoretice necesare pentru selecția rădăcinilor sunt date: împărțirea mulțimii de numere întregi în submulțimi care nu se intersectează, soluția ecuațiilor în numere întregi (diofantine).

A șasea secțiune prezintă sarcini pentru soluții independente, concepute sub forma unui test. Cele 20 de sarcini de testare listează cele mai dificile sarcini care pot fi întâlnite în testarea centralizată.

Ecuații trigonometrice elementare

Ecuațiile trigonometrice elementare sunt ecuații de forma , unde este una dintre funcțiile trigonometrice: , , , .

Ecuațiile trigonometrice elementare au infinit de rădăcini. De exemplu, următoarele valori satisfac ecuația: , , , etc. Formula generală prin care se găsesc toate rădăcinile ecuației, unde , este:

Aici poate lua orice valori întregi, fiecare dintre ele corespunde unei anumite rădăcini a ecuației; în această formulă (precum și în alte formule prin care se rezolvă ecuații trigonometrice elementare) se numește parametru. De obicei, ei notează, subliniind astfel că parametrul poate lua orice valoare întreagă.

Soluțiile ecuației , unde , se găsesc prin formula

Ecuația se rezolvă prin aplicarea formulei

iar ecuația --- conform formulei

Să notăm mai ales câteva cazuri speciale de ecuații trigonometrice elementare, când soluția poate fi scrisă fără a folosi formule generale:

La rezolvarea ecuațiilor trigonometrice, perioada funcțiilor trigonometrice joacă un rol important. Prin urmare, prezentăm două teoreme utile:

Teorema Dacă --- perioada principală a funcției, atunci numărul este perioada principală a funcției.

Perioadele funcțiilor și se numesc comensurabile dacă există numere naturale și , că .

Teorema Dacă funcțiile periodice și , au proporționale și , atunci au o perioadă comună , care este perioada funcțiilor , , .

Teorema spune care este perioada funcției , , , și nu este neapărat perioada principală. De exemplu, perioada principală a funcțiilor și este --- , iar perioada principală a produsului lor este --- .

Introducerea unui argument auxiliar

Modul standard de conversie a expresiilor formei este următorul truc: fie --- unghiul dat de egalităţi , . Pentru orice și astfel de unghi există. În acest fel . Dacă , sau , , , altfel .

Schema de rezolvare a ecuatiilor trigonometrice

Schema principală după care ne vom ghida atunci când rezolvăm ecuațiile trigonometrice este următoarea:

soluția ecuației date se reduce la soluția ecuațiilor elementare. Soluții --- transformări, factorizări, înlocuire de necunoscute. Principiul călăuzitor este de a nu pierde rădăcinile. Aceasta înseamnă că atunci când trecem la următoarea ecuație (ecuații), nu ne este frică de apariția unor rădăcini suplimentare (străine), ci ne pasă doar ca fiecare ecuație ulterioară a „lanțului” nostru (sau un set de ecuații în cazul ramificare) este o consecinţă a precedentului. O metodă posibilă pentru selectarea rădăcinilor este verificarea. Observăm imediat că, în cazul ecuațiilor trigonometrice, dificultățile asociate cu selecția rădăcinilor, cu verificare, de regulă, cresc brusc în comparație cu ecuațiile algebrice. La urma urmei, trebuie să verificați seria, formată dintr-un număr infinit de membri.

Mențiune specială trebuie făcută asupra schimbării necunoscutelor în rezolvarea ecuațiilor trigonometrice. În cele mai multe cazuri, după înlocuirea necesară, se obține o ecuație algebrică. Mai mult decât atât, nu sunt atât de rare ecuațiile care, deși sunt trigonometrice în aparență, în esență nu sunt așa, deoarece deja după primul pas --- modificări de variabile --- se transformă în algebrice, iar revenirea la trigonometrie are loc doar pe scenă. de rezolvare a ecuaţiilor trigonometrice elementare.

Să vă reamintim încă o dată: înlocuirea necunoscutului ar trebui să se facă cât mai curând posibil, ecuația obținută după înlocuire trebuie rezolvată până la sfârșit, inclusiv etapa de selectare a rădăcinilor și abia atunci va reveni la original. necunoscut.

Una dintre caracteristicile ecuațiilor trigonometrice este că răspunsul în multe cazuri poate fi scris în diferite moduri. Chiar și pentru a rezolva ecuația raspunsul poate fi scris astfel:

1) sub forma a doua serii: , , ;

2) în formă standard, care este o unire a seriei de mai sus: , ;

3) pentru că , atunci răspunsul poate fi scris ca , . (În continuare, prezența parametrului , , sau în înregistrarea răspunsului înseamnă automat că acest parametru preia toate valorile întregi posibile. Vor fi stipulate excepții.)

Evident, cele trei cazuri enumerate nu epuizează toate posibilitățile de scriere a răspunsului la ecuația luată în considerare (există la infinit de multe).

De exemplu, pentru . Prin urmare, în primele două cazuri, dacă , putem înlocui cu .

De obicei, răspunsul este scris pe baza paragrafului 2. Este util să ne amintim următoarea recomandare: dacă munca nu se termină cu rezolvarea ecuației, este încă necesar să se efectueze un studiu, selectarea rădăcinilor, atunci cea mai convenabilă formă de înregistrare este indicată în paragraful 1. (O recomandare similară ar trebui dată pentru ecuație.)

Să luăm în considerare un exemplu care ilustrează ceea ce s-a spus.

Exemplu Rezolvați ecuația.

Soluţie. Cel mai evident este următorul mod. Această ecuație se împarte în două: și . Rezolvând fiecare dintre ele și combinând răspunsurile obținute, găsim .

Altă cale. Din , atunci, înlocuirea și prin formulele de reducere. După transformări minore, obținem , de unde .

La prima vedere, a doua formulă nu are avantaje deosebite față de prima. Cu toate acestea, dacă luăm, de exemplu, , atunci se dovedește că , i.e. ecuația are o soluție, în timp ce prima cale ne conduce la răspuns . „Vezi” și dovedește egalitatea nu asa de usor.

Răspuns. .

Transformarea și unirea grupurilor de soluții generale ale ecuațiilor trigonometrice

Vom lua în considerare o progresie aritmetică care se extinde la infinit în ambele direcții. Termenii acestei progresii pot fi împărțiți în două grupe de termeni, situați în dreapta și în stânga unui anumit termen, numit termenul central sau zero al progresiei.

Fixând unul dintre termenii progresiei infinite cu un număr zero, va trebui să efectuăm o dublă numerotare pentru toți termenii rămași: pozitiv pentru termenii aflați în dreapta și negativ pentru termenii aflați în stânga zero.

În cazul general, dacă diferența de progresie este termenul zero, formula pentru orice (al-lea) termen al progresiei aritmetice infinite este:

Transformări de formule pentru orice membru al unei progresii aritmetice infinite

1. Dacă adunăm sau scădem diferența de progresie la termenul zero, atunci progresia nu se va schimba de la acesta, ci doar termenul zero se va muta, adică. numerotarea membrilor se va modifica.

2. Dacă coeficientul unei variabile este înmulțit cu , atunci aceasta va avea ca rezultat doar o permutare a grupurilor de termeni din dreapta și din stânga.

3. Dacă membrii succesivi ai unei progresii infinite

de exemplu , , , ..., , pentru a face ca termenii centrali ai progresiilor cu aceeași diferență egali cu:

apoi progresia si seria de progresii exprima aceleasi numere.

Exemplu Rândul poate fi înlocuit cu următoarele trei rânduri: , , .

4. Dacă progresiile infinite cu aceeași diferență au numere ca membri centrali care formează o progresie aritmetică cu o diferență, atunci aceste serii pot fi înlocuite cu o progresie cu o diferență și cu un membru central egal cu oricare dintre membrii centrali ai acestora. progresii, adică dacă

apoi aceste progresii sunt combinate într-una singură:

Exemplu , , , ambele sunt combinate într-un singur grup, deoarece .

Pentru a transforma grupurile care au soluții comune în grupuri care nu au soluții comune, aceste grupuri sunt descompuse în grupuri cu o perioadă comună, iar apoi încercăm să combinăm grupurile rezultate, excluzându-le pe cele repetate.

Factorizarea

Metoda de factorizare este următoarea: dacă

apoi orice soluție a ecuației

este soluția mulțimii de ecuații

Afirmația inversă este, în general, falsă: nu orice soluție a mulțimii este o soluție a ecuației. Acest lucru se datorează faptului că soluțiile ecuațiilor individuale pot să nu fie incluse în domeniul de definire al funcției.

Exemplu Rezolvați ecuația.

Soluţie. Folosind identitatea trigonometrică de bază, reprezentăm ecuația sub formă

Răspuns. ; .

Conversia sumei funcțiilor trigonometrice într-un produs

Exemplu rezolva ecuatia .

Soluţie. Aplicam formula, obtinem o ecuatie echivalenta

Răspuns. .

Exemplu Rezolvați ecuația.

Soluţie.În acest caz, înainte de a aplica formulele pentru suma funcțiilor trigonometrice, ar trebui să utilizați formula de reducere . Ca rezultat, obținem o ecuație echivalentă

Răspuns. , .

Rezolvarea ecuațiilor prin conversia produsului funcțiilor trigonometrice într-o sumă

La rezolvarea unui număr de ecuații se folosesc formule.

Exemplu rezolva ecuatia

Soluţie.

Răspuns. , .

Exemplu Rezolvați ecuația.

Soluţie. Aplicând formula, obținem o ecuație echivalentă:

Răspuns. .

Rezolvarea ecuațiilor folosind formule de reducere

Atunci când se rezolvă o gamă largă de ecuații trigonometrice, formulele joacă un rol cheie.

Exemplu Rezolvați ecuația.

Soluţie. Aplicând formula, obținem o ecuație echivalentă.

Răspuns. ; .

Rezolvarea ecuațiilor folosind formule cu argument triplu

Exemplu Rezolvați ecuația.

Soluţie. Aplicam formula, obtinem ecuatia

Răspuns. ; .

Exemplu rezolva ecuatia .

Soluţie. Aplicând formulele de scădere a gradului, obținem: . Aplicand obtinem:

Răspuns. ; .

Egalitatea funcțiilor trigonometrice cu același nume

Exemplu Rezolvați ecuația.

Soluţie.

Răspuns. , .

Exemplu rezolva ecuatia .

Soluţie. Să transformăm ecuația.

Răspuns. .

Exemplu Se știe că și satisface ecuația

Găsiți suma.

Soluţie. Din ecuație rezultă că

Răspuns. .

Luați în considerare sumele formei

Aceste sume pot fi convertite într-un produs prin înmulțirea și împărțirea lor la , apoi obținem

Această tehnică poate fi folosită pentru a rezolva unele ecuații trigonometrice, dar trebuie avut în vedere că, în consecință, pot apărea rădăcini străine. Iată o generalizare a acestor formule:

Exemplu Rezolvați ecuația.

Soluţie. Se poate observa că mulțimea este o soluție a ecuației inițiale. Prin urmare, înmulțirea părților stânga și dreaptă ale ecuației cu nu duce la apariția unor rădăcini suplimentare.

Avem .

Răspuns. ; .

Exemplu Rezolvați ecuația.

Soluţie.Înmulțim părțile stânga și dreaptă ale ecuației și aplicăm formulele de conversie a produsului funcțiilor trigonometrice într-o sumă, obținem

Această ecuație este echivalentă cu mulțimea a două ecuații și , de unde și .

Deoarece rădăcinile ecuației nu sunt rădăcinile ecuației, atunci din seturile de soluții rezultate ar trebui excluse. Deci, în set, trebuie să excludeți.

Răspuns.și , .

Exemplu rezolva ecuatia .

Soluţie. Să transformăm expresia:

Ecuația se va scrie sub forma:

Răspuns. .

Reducerea ecuațiilor trigonometrice la cele algebrice

Reducerea la pătrat

Dacă ecuația arată ca

apoi înlocuitorul îl aduce la un pătrat, pentru că () și.

Dacă în locul termenului există , atunci înlocuirea necesară va fi .

Ecuația

se reduce la ecuația pătratică

prezentare ca . Este ușor de verificat acela pentru care , nu sunt rădăcini ale ecuației, iar prin efectuarea modificării , ecuația se reduce la una pătratică.

Exemplu Rezolvați ecuația.

Soluţie. Să o mutam în partea stângă, să o înlocuim cu , și să exprimăm prin și .

După simplificări, obținem: . Împărțiți termen cu termen cu , faceți înlocuirea:

Revenind la , găsim .

Ecuații omogene în raport cu ,

Luați în considerare o ecuație de formă

unde , , , ..., , sunt numere reale. În fiecare termen din partea stângă a ecuației, gradele monomiilor sunt egale, adică suma gradelor sinusului și cosinusului este aceeași și egală cu. O astfel de ecuație se numește omogen relativ la și , iar numărul este numit indicator de omogenitate .

Este clar că dacă , atunci ecuația va lua forma:

ale căror soluții sunt valorile pentru care , adică numerele , . A doua ecuație, scrisă între paranteze, este și ea omogenă, dar gradele sunt cu 1 mai mici.

Dacă , atunci aceste numere nu sunt rădăcinile ecuației.

Când obținem: , iar partea stângă a ecuației (1) ia valoarea .

Deci, pentru , și , prin urmare, ambele părți ale ecuației pot fi împărțite la . Ca rezultat, obținem ecuația:

care, prin substituție, se reduce ușor la cea algebrică:

Ecuații omogene cu indice de omogenitate 1. La , avem ecuația .

Dacă , atunci această ecuație este echivalentă cu ecuația , , de unde , .

Exemplu Rezolvați ecuația.

Soluţie. Această ecuație este omogenă de gradul I. Împărțind ambele părți la obținem: , , , .

Răspuns. .

Exemplu La , obținem o ecuație omogenă de formă

Soluţie.

Dacă , atunci împărțim ambele părți ale ecuației la , obținem ecuația , care poate fi ușor redus la un pătrat prin substituție: . În cazul în care un , atunci ecuația are rădăcini reale , . Ecuația inițială va avea două grupe de soluții: , , .

În cazul în care un , atunci ecuația nu are soluții.

Exemplu Rezolvați ecuația.

Soluţie. Această ecuație este omogenă de gradul doi. Împărțim ambele părți ale ecuației la , obținem: . Fie , atunci , , . , , ; , , .

Răspuns. .

Ecuația se reduce la o ecuație de formă

Pentru a face acest lucru, este suficient să folosiți identitatea

În special, ecuația se reduce la una omogenă dacă este înlocuită cu , atunci obținem ecuația echivalentă:

Exemplu Rezolvați ecuația.

Soluţie. Să transformăm ecuația într-una omogenă:

Împărțiți ambele părți ale ecuației la , obținem ecuația:

Fie , atunci ajungem la ecuația pătratică: , , , , .

Răspuns. .

Exemplu Rezolvați ecuația.

Soluţie. Să pătram ambele părți ale ecuației, având în vedere că au valori pozitive: , ,

Lasă, apoi obținem , , .

Răspuns. .

Ecuații rezolvate folosind identități

Este util să cunoașteți următoarele formule:

Exemplu Rezolvați ecuația.

Soluţie. Folosind, primim

Răspuns.

Oferim nu formulele în sine, ci modalitatea de a le deriva:

Prin urmare,

La fel, .

Exemplu rezolva ecuatia .

Soluţie. Să transformăm expresia:

Ecuația se va scrie sub forma:

Luând, primim. , . prin urmare

Răspuns. .

Substituție trigonometrică universală

Ecuația trigonometrică a formei

unde --- o funcție rațională cu ajutorul formulelor -- , precum și cu ajutorul formulelor -- poate fi redusă la o ecuație rațională în raport cu argumentele , , , , după care ecuația poate fi redusă la o ecuația rațională algebrică în ceea ce privește utilizarea formulelor de substituție trigonometrică universală

Trebuie remarcat faptul că utilizarea formulelor poate duce la o îngustare a ODZ a ecuației inițiale, deoarece nu este definită la punctele , așa că în astfel de cazuri este necesar să se verifice dacă unghiurile sunt rădăcinile ecuației originale. .

Exemplu Rezolvați ecuația.

Soluţie. Conform sarcinii. Aplicând formulele și făcând substituția, obținem

de unde și, prin urmare, .

Ecuații de formă

Ecuațiile de forma , unde este un polinom, se rezolvă prin modificarea necunoscutelor

Exemplu Rezolvați ecuația.

Soluţie. Făcând înlocuirea și ținând cont de asta, obținem

Unde , . --- rădăcină străină, deoarece . Rădăcinile ecuației sunteți .

Utilizarea funcțiilor limitate

În practica testării centralizate, nu este neobișnuit să întâlniți ecuații a căror soluție se bazează pe mărginirea funcțiilor și . De exemplu:

Exemplu Rezolvați ecuația.

Soluţie. Deoarece , , atunci partea stângă nu depășește și este egală cu , dacă

Pentru a găsi valorile care satisfac ambele ecuații, procedăm după cum urmează. Rezolvăm una dintre ele, apoi dintre valorile găsite le selectăm pe cele care o satisfac pe cealaltă.

Să începem cu al doilea: , . Apoi , .

Este clar că numai pentru numerele pare va fi .

Răspuns. .

O altă idee se realizează prin rezolvarea următoarei ecuații:

Exemplu rezolva ecuatia .

Soluţie. Să folosim proprietatea funcției exponențiale: , .

Adăugând aceste inegalități termen cu termen, avem:

Prin urmare, partea stângă a acestei ecuații este egală dacă și numai dacă sunt valabile cele două egalități:

adică poate lua valorile, , sau poate lua valorile, .

Răspuns. , .

Exemplu rezolva ecuatia .

Soluţie., . Prin urmare, .

Răspuns. .

Exemplu rezolva ecuatia

Soluţie. Notăm , apoi din definiția funcției trigonometrice inverse pe care o avem și .

Deoarece , inegalitatea rezultă din ecuație, i.e. . De când și , atunci și . Totuși și deci.

Dacă și , atunci . Întrucât s-a stabilit anterior că , atunci .

Răspuns. , .

Exemplu rezolva ecuatia

Soluţie. Intervalul de valori valide ale ecuației este .

Să arătăm mai întâi că funcția

Pentru orice, poate lua doar valori pozitive.

Să reprezentăm funcția astfel: .

Din moment ce, atunci, adică .

Prin urmare, pentru a demonstra inegalitatea, este necesar să se arate că . În acest scop, cubăm ambele părți ale acestei inegalități

Inegalitatea numerică rezultată indică faptul că . Dacă luăm în considerare și faptul că , atunci partea stângă a ecuației este nenegativă.

Luați în considerare acum partea dreaptă a ecuației.

pentru că , apoi

Cu toate acestea, se știe că . De aici rezultă că , i.e. partea dreaptă a ecuaţiei nu depăşeşte . Anterior, s-a dovedit că partea stângă a ecuației este nenegativă, prin urmare, egalitatea în poate fi numai în cazul în care ambele părți sunt egale, iar acest lucru este posibil numai pentru .

Răspuns. .

Exemplu rezolva ecuatia

Soluţie. Notează și . Aplicând inegalitatea Cauci-Bunyakovsky, obținem . De aici rezultă că . Pe de altă parte, există . Prin urmare, ecuația nu are rădăcini.

Răspuns. .

Exemplu Rezolvați ecuația:

Soluţie. Să rescriem ecuația sub forma:

Răspuns. .

Metode funcționale de rezolvare a ecuațiilor trigonometrice și combinate

Nu orice ecuație ca urmare a transformărilor poate fi redusă la o ecuație de una sau alta formă standard, pentru care există o anumită metodă de rezolvare. În astfel de cazuri, se dovedește a fi util să folosiți astfel de proprietăți ale funcțiilor și ca monotonitate, mărginire, uniformitate, periodicitate etc. Deci, dacă una dintre funcții scade, iar a doua crește pe interval, atunci dacă ecuația are o rădăcină pe acest interval, această rădăcină este unică și apoi, de exemplu, poate fi găsită prin selecție. Dacă funcția este mărginită de sus și , iar funcția este mărginită de jos și , atunci ecuația este echivalentă cu sistemul de ecuații

Exemplu rezolva ecuatia

Soluţie. Transformăm ecuația inițială în formă

și rezolvați-l ca un pătrat în raport cu . Apoi primim

Să rezolvăm prima ecuație de mulțime. Ținând cont de mărginirea funcției , ajungem la concluzia că ecuația poate avea rădăcină numai pe interval . În acest interval, funcția crește, iar funcția scade. Prin urmare, dacă această ecuație are o rădăcină, atunci este unică. Găsim prin selecție.

Răspuns. .

Exemplu rezolva ecuatia

Soluţie. Lasă , și , atunci ecuația originală poate fi scrisă ca o ecuație funcțională . Deoarece funcția este impară, atunci . În acest caz, obținem ecuația

Deoarece , și este monotonă pe , ecuația este echivalentă cu ecuația , i.e. , care are o singură rădăcină .

Răspuns. .

Exemplu rezolva ecuatia .

Soluţie. Pe baza teoremei derivatei unei funcții complexe, este clar că funcția descrescătoare (funcție descrescătoare, crescândă, descrescătoare). Din aceasta este clar că funcția definite pe , descrescătoare. Prin urmare, această ecuație are cel mult o rădăcină. pentru că , apoi

Răspuns. .

Exemplu Rezolvați ecuația.

Soluţie. Luați în considerare ecuația pe trei intervale.

a) Fie . Apoi, pe această mulțime, ecuația inițială este echivalentă cu ecuația. Care nu are solutii pe interval, de vreme ce , , A . Pe interval, ecuația originală, de asemenea, nu are rădăcini, deoarece , A .

b) Fie . Apoi, pe această mulțime, ecuația inițială este echivalentă cu ecuația

ale căror rădăcini din interval sunt numerele , , , .

c) Fie . Apoi, pe această mulțime, ecuația inițială este echivalentă cu ecuația

Care nu are soluții asupra intervalului, din moment ce , dar . De asemenea, ecuația nu are soluții pe interval, deoarece , , A .

Răspuns. , , , .

Metoda simetriei

Este convenabil să folosiți metoda simetriei atunci când declarația sarcinii conține cerința ca soluția unei ecuații, inegalități, sistem etc. să fie unică. sau o indicație exactă a numărului de soluții. În acest caz, orice simetrie a expresiilor date ar trebui detectată.

De asemenea, este necesar să se țină cont de varietatea diferitelor tipuri posibile de simetrie.

La fel de importantă este respectarea strictă a etapelor logice în raționamentul cu simetrie.

De obicei, simetria ne permite să stabilim doar condițiile necesare, iar apoi trebuie să verificăm suficiența acestora.

Exemplu Găsiți toate valorile parametrului pentru care ecuația are o soluție unică.

Soluţie. Rețineți că și sunt funcții pare, deci partea stângă a ecuației este o funcție pară.

Deci, dacă este o soluție a unei ecuații, atunci există și o soluție a ecuației. Dacă este singura soluție a ecuației, atunci necesar , .

Să selectăm posibil valori, necesitând ca aceasta să fie rădăcina ecuației.

Observăm imediat că alte valori nu pot satisface condiția problemei.

Dar nu se știe încă dacă toți cei selectați într-adevăr întrunesc condiția problemei.

Adecvarea.

1) , ecuația va lua forma .

2) , ecuația va lua forma:

Evident, pentru toți și . Prin urmare, ultima ecuație este echivalentă cu sistemul:

Astfel, am demonstrat că pentru , ecuația are o soluție unică.

Răspuns. .

Soluție cu explorare a funcției

Exemplu Demonstrați că toate soluțiile ecuației

Numere întregi.

Soluţie. Perioada principală a ecuației originale este . Prin urmare, studiem mai întâi această ecuație pe segmentul .

Să transformăm ecuația în forma:

Cu ajutorul unui calculator obținem:

Dacă , atunci din egalitățile anterioare obținem:

Rezolvând ecuația rezultată, obținem: .

Calculele efectuate oferă o oportunitate de a presupune că rădăcinile ecuației aparținând intervalului sunt , și .

Verificarea directă confirmă această ipoteză. Astfel, se demonstrează că rădăcinile ecuației sunt doar numere întregi , .

Exemplu Rezolvați ecuația .

Soluţie. Aflați perioada principală a ecuației. Perioada principală a funcției este . Perioada principală a funcției este . Cel mai mic multiplu comun al numerelor și este egal cu . Prin urmare, perioada principală a ecuației este . Lăsa .

Evident, este o soluție a ecuației. Pe interval. Funcția este negativă. Prin urmare, alte rădăcini ale ecuației ar trebui căutate numai pe intervalele x și .

Cu ajutorul unui microcalculator, găsim mai întâi valorile aproximative ale rădăcinilor ecuației. Pentru a face acest lucru, alcătuim un tabel cu valorile funcției pe intervale și ; adică pe intervalele și .

0	0	202,5	0,85355342
3	-0,00080306	207	0,6893642
6	-0,00119426	210	0,57635189
9	-0,00261932	213	0,4614465
12	-0,00448897	216	0,34549155
15	-0,00667995	219	0,22934931
18	-0,00903692	222	0,1138931
21	-0,01137519	225	0,00000002
24	-0,01312438	228	-0,11145712
27	-0,01512438	231	-0,21961736
30	-0,01604446	234	-0,32363903
33	-0,01597149	237	-0,42270819
36	-0,01462203	240	-0,5160445
39	-0,01170562	243	-0,60290965
42	-0,00692866	246	-0,65261345
45	0,00000002	249	-0,75452006
48	0,00936458	252	-0,81805397
51	0,02143757	255	-0,87270535
54	0,03647455	258	-0,91803444
57	0,0547098	261	-0,95367586
60	0,07635185	264	-0,97934187
63	0,10157893	267	-0,99482505
66	0,1305352	270	-1
67,5	0,14644661

Din tabel se desprind cu usurinta urmatoarele ipoteze: radacinile ecuatiei apartinand segmentului sunt numere: ; ; . Verificarea directă confirmă această ipoteză.

Răspuns. ; ; .

Rezolvarea inegalităților trigonometrice folosind cercul unitar

La rezolvarea inegalităților trigonometrice de forma , unde este una dintre funcțiile trigonometrice, este convenabil să folosiți un cerc trigonometric pentru a prezenta cât mai clar soluția inegalității și a scrie răspunsul. Principala metodă de rezolvare a inegalităților trigonometrice este reducerea acestora la cele mai simple inegalități de tipul . Să ne uităm la un exemplu despre cum să rezolvăm astfel de inegalități.

Exemplu Rezolvați inegalitatea.

Soluţie. Să desenăm un cerc trigonometric și să marchem pe el punctele pentru care ordonata este mai mare decât .

Căci soluția acestei inegalități va fi . De asemenea, este clar că, dacă un anumit număr diferă de un număr din intervalul indicat prin , atunci va fi, de asemenea, nu mai mic de . Prin urmare, la capetele segmentului găsit al soluției, trebuie doar să adăugați . În cele din urmă, obținem că soluțiile inegalității originale vor fi toate .

Răspuns. .

Pentru a rezolva inegalitățile cu tangentă și cotangentă, este util conceptul unei linii de tangente și cotangente. Acestea sunt liniile și, respectiv (în figura (1) și (2)), care ating cercul trigonometric.

Este ușor de observat că, dacă construiți o rază cu originea la origine, făcând un unghi cu direcția pozitivă a axei absciselor, atunci lungimea segmentului de la punctul până la punctul de intersecție al acestei raze cu linia de tangente este exact egală cu tangentei unghiului pe care această rază îl face cu axa absciselor. O observație similară este valabilă pentru cotangentă.

Exemplu Rezolvați inegalitatea.

Soluţie. Notați , atunci inegalitatea va lua forma celei mai simple: . Se consideră un interval cu o lungime egală cu perioada cea mai puțin pozitivă (LPP) a tangentei. Pe acest segment, folosind dreapta tangentelor, stabilim ca . Acum ne amintim ce trebuie adăugat, deoarece RPE-ul funcției . Asa de, . Revenind la variabilă, obținem asta.

Răspuns. .

Este convenabil să se rezolve inegalitățile cu funcții trigonometrice inverse folosind grafice ale funcțiilor trigonometrice inverse. Să arătăm cum se face acest lucru cu un exemplu.

Rezolvarea inegalităților trigonometrice printr-o metodă grafică

Rețineți că dacă --- este o funcție periodică, atunci pentru a rezolva inegalitatea, este necesar să găsiți soluțiile acesteia pe un segment a cărui lungime este egală cu perioada funcției . Toate soluțiile inegalității inițiale vor consta din valorile găsite, precum și din toate cele care diferă de cele găsite de orice număr întreg de perioade ale funcției.

Luați în considerare soluția inegalității ().

Din moment ce , atunci inegalitatea nu are soluții pentru . Dacă , atunci mulțimea soluțiilor inegalității este mulțimea tuturor numerelor reale.

Lăsa . Funcția sinus are cea mai mică perioadă pozitivă, astfel încât inegalitatea poate fi rezolvată mai întâi pe un segment de lungime , de exemplu, pe un segment. Construim grafice ale funcțiilor și (). sunt date de inegalități de forma: și, de unde,

În această lucrare au fost luate în considerare metode de rezolvare a ecuațiilor și inegalităților trigonometrice, atât cele mai simple, cât și la nivel olimpic. Au fost luate în considerare principalele metode de rezolvare a ecuațiilor și inegalităților trigonometrice, atât specifice --- caracteristice doar pentru ecuațiile și inecuațiile trigonometrice --- cât și metodele funcționale generale de rezolvare a ecuațiilor și inegalităților, aplicate ecuațiilor trigonometrice.

Teza oferă informații teoretice de bază: definiția și proprietățile funcțiilor trigonometrice și trigonometrice inverse; exprimarea funcțiilor trigonometrice în termenii altor funcții trigonometrice, ceea ce este foarte important pentru conversia expresiilor trigonometrice, în special a celor care conțin funcții trigonometrice inverse; pe lângă formulele trigonometrice de bază, binecunoscute din cursul școlar, se dau formule care simplifică expresiile care conțin funcții trigonometrice inverse. Se iau în considerare soluția ecuațiilor trigonometrice elementare, metoda factorizării, metodele de reducere a ecuațiilor trigonometrice la cele algebrice. Având în vedere faptul că soluțiile ecuațiilor trigonometrice pot fi scrise în mai multe moduri, iar forma acestor soluții nu permite să se determine imediat dacă aceste soluții sunt identice sau diferite, se ia în considerare o schemă generală de rezolvare a ecuațiilor trigonometrice și se consideră în detaliu transformarea grupurilor de soluţii generale ale ecuaţiilor trigonometrice. Sunt luate în considerare în detaliu metode de rezolvare a inegalităților trigonometrice elementare, atât pe un cerc unitar, cât și printr-o metodă grafică. Este descris procesul de rezolvare a inegalităților trigonometrice neelementare prin inegalități elementare și metoda intervalelor deja bine cunoscută școlarilor. Sunt oferite soluțiile sarcinilor tipice pentru selectarea rădăcinilor. Informațiile teoretice necesare pentru selecția rădăcinilor sunt date: împărțirea mulțimii de numere întregi în submulțimi care nu se intersectează, soluția ecuațiilor în numere întregi (diofantine).

Rezultatele acestei lucrări de teză pot fi folosite ca material educațional în pregătirea lucrărilor semestriale și a tezelor, în pregătirea opțiunilor pentru școlari, iar lucrarea poate fi folosită și în pregătirea elevilor pentru examenele de admitere și testarea centralizată.

Vygodsky Ya.Ya., Manual de matematică elementară. /Vygodsky Ya.Ya. --- M.: Nauka, 1970.

Igudisman O., Matematica la examenul oral / Igudisman O. --- M .: Iris press, Rolf, 2001.

Azarov A.I., ecuații / Azarov A.I., Gladun O.M., Fedosenko V.S. --- Minsk: Trivium, 1994.

Litvinenko V.N., Atelier de matematică elementară / Litvinenko V.N. --- M .: Educație, 1991.

Sharygin I.F., Curs opțional de matematică: rezolvarea de probleme / Sharygin I.F., Golubev V.I. --- M.: Iluminismul, 1991.

Bardushkin V., Ecuații trigonometrice. Selectarea rădăcinilor / V. Bardushkin, A. Prokofiev.// Matematică, nr. 12, 2005 p. 23--27.

Vasilevsky A.B., Teme de lucru extracurricular la matematică / Vasilevsky A.B. --- Mn.: Asveta Poporului. 1988. --- 176s.

Sapunov P. I., Transformarea și unirea grupelor de soluții generale ale ecuațiilor trigonometrice / Sapunov P. I. // Educația matematică, numărul 3, 1935.

Borodin P., Trigonometrie. Materiale pentru examenele de admitere la Universitatea de Stat din Moscova [text] / P. Borodin, V. Galkin, V. Panferov, I. Sergeev, V. Tarasov // Matematică nr. 1, 2005 p. 36--48.

Samusenko A.V., Matematică: greșeli tipice ale solicitanților: Manual de referință / Samusenko A.V., Kazachenok V.V. --- Minsk: Liceu, 1991.

Azarov A.I., Metode funcționale și grafice pentru rezolvarea problemelor de examinare / Azarov A.I., Barvenov S.A., --- Minsk: Aversev, 2004.

Rezolvarea celor mai simple ecuații trigonometrice

Mai întâi, să ne amintim formulele pentru rezolvarea celor mai simple ecuații trigonometrice.

1. $sinx=a$

1. $cosx=a$

1. $tgx=a$

1. $ctgx=a$

Rezolvarea celor mai simple inegalități trigonometrice.

Pentru a rezolva cele mai simple inegalități trigonometrice, trebuie mai întâi să rezolvăm ecuația corespunzătoare și apoi, folosind cercul trigonometric, să găsim o soluție a inegalității. Luați în considerare soluțiile celor mai simple inegalități trigonometrice prin exemple.

Exemplul 1

$sinx\ge \frac(1)(2)$

Găsiți o soluție la inegalitatea trigonometrică $sinx=\frac(1)(2)$

\ \

Figura 1. Rezolvarea inegalitatii $sinx\ge \frac(1)(2)$.

Deoarece inegalitatea are un semn „mai mare sau egal”, soluția se află pe arcul superior al cercului (în raport cu soluția ecuației).

Răspuns: $\left[\frac(\pi )(6)+2\pi n,\frac(5\pi )(6)+2\pi n\right]$.

Exemplul 2

Găsiți o soluție la inegalitatea trigonometrică $cosx=\frac(\sqrt(3))(2)$

\ \

Notați soluția pe cercul trigonometric

Deoarece inegalitatea are semnul „mai puțin decât”, soluția se află pe arcul de cerc situat la stânga (în raport cu soluția ecuației).

Răspuns: $\left(\frac(\pi )(6)+2\pi n,\frac(11\pi )(6)+2\pi n\right)$.

Exemplul 3

$tgx\le \frac(\sqrt(3))(3)$

Găsiți o soluție la inegalitatea trigonometrică $tgx=\frac(\sqrt(3))(3)$

\ \

Aici avem nevoie și de un domeniu de definiție. După cum ne amintim, funcția tangentă $x\ne \frac(\pi )(2)+\pi n,n\in Z$

Notați soluția pe cercul trigonometric

Figura 3. Rezolvarea inegalității $tgx\le \frac(\sqrt(3))(3)$.

Deoarece inegalitatea are un semn „mai mic sau egal cu”, soluția se află pe arcele de cerc marcate cu albastru în Figura 3.

Răspuns: $\ \left(-\frac(\pi )(2)+2\pi n\right.,\left.\frac(\pi )(6)+2\pi n\right]\cup \left (\frac(\pi )(2)+2\pi n,\dreapta.\left.\frac(7\pi )(6)+2\pi n\right]$

Exemplul 4

Găsiți o soluție la inegalitatea trigonometrică $ctgx=\sqrt(3)$

\ \

Aici avem nevoie și de un domeniu de definiție. După cum ne amintim, funcția tangentă $x\ne \pi n,n\in Z$

Notați soluția pe cercul trigonometric

Figura 4. Rezolvarea inegalității $ctgx\le \sqrt(3)$.

Deoarece inegalitatea are un semn „mai mare decât”, soluția se află pe arcele de cerc marcate cu albastru în Figura 4.

Răspuns: $\ \left(2\pi n,\frac(\pi )(6)+2\pi n\right)\cup \left(\pi +2\pi n,\frac(7\pi )( 6)+2\pi n\dreapta)$

DEFINIȚIE

Inegalitățile trigonometrice sunt inegalități care conțin o variabilă sub semnul unei funcții trigonometrice.

Rezolvarea inegalităților trigonometrice

Soluția inegalităților trigonometrice se rezumă adesea la rezolvarea celor mai simple inegalități trigonometrice de forma: \(\ \sin x a \), \(\ \cos x > a \), \(\ \operatorname(tg) x > a \ ), \(\ \ operatorname(ctg) x > a \), \(\ \sin x \leq a \), \(\ \cos x \leq a \), \(\ \operatorname(tg) x \ leq a \), \ (\ \operatorname(ctg) x \leq a \), \(\ \sin x \geq a \), \(\ \cos \geq a \), \(\ \operatorname(tg ) x \geq a \ ), \(\ \operatorname(tg) x \geq a \)

Cele mai simple inegalități trigonometrice sunt rezolvate grafic sau folosind un cerc trigonometric unitar.

Prin definiție, sinusul unghiului \(\ \alpha \) este ordonata punctului \(\ P_(\alpha)(x, y) \) al cercului unitar (Fig. 1), iar cosinusul este abscisa acestui punct. Acest fapt este folosit în rezolvarea celor mai simple inegalități trigonometrice cu cosinus și sinus folosind cercul unitar.

Exemple de rezolvare a inegalităților trigonometrice

Exercițiu

Rezolvați inegalitatea \(\ \sin x \leq \frac(\sqrt(3))(2) \)

Rezolvat

Deoarece \(\ \left|\frac(\sqrt(3))(2)\right| , această inegalitate are o soluție și poate fi rezolvată în două moduri

Prima cale. Să rezolvăm această inegalitate grafic. Pentru a face acest lucru, construim în același sistem de coordonate un grafic al sinusului \(\ y=\sin x \) (Fig. 2) și al dreptei \(\ y=\frac(\sqrt(3))( 2) \)

Să selectăm intervalele în care se află sinusoida sub graficul dreptei \(\ y=\frac(\sqrt(3))(2) \) . Aflați abscisele \(\ x_(1) \) și \(\ x_(2) \) ale punctelor de intersecție ale acestor grafice: \(\ x_(1)=\pi-\arcsin \frac(\sqrt(3) ))(2 )=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_(2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\ frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)

Am obținut intervalul \(\ \left[-\frac(4 \pi)(3) ; \frac(\pi)(3)\right] \) dar deoarece funcția \(\ y=\sin x \) este periodic și are o perioadă \(\ 2 \pi \), atunci răspunsul este uniunea intervalelor: \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+ 2 \pi k\right] \), \(\ k \in Z \)

A doua cale. Construiți un cerc unitar și o dreaptă \(\ y=\frac(\sqrt(3))(2) \) , notați punctele lor de intersecție \(\ P_(x_(1)) \) și \(\ P_(x_) (2 )) \) (Fig. 3). Soluția inegalității inițiale va fi mulțimea de puncte de ordonate care sunt mai mici decât \(\ \frac(\sqrt(3))(2) \) . Să găsim valoarea \(\ \boldsymbol(I)_(1) \) și \(\ \boldsymbol(I)_(2) \) mergând în sens invers acelor de ceasornic, \(\ x_(1) Fig. 3

\(\ x_(1)=\pi-\arcsin \frac(\sqrt(3))(2)=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_ (2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)

Tinand cont de periodicitatea functiei sinus, obtinem in final intervalele \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+2 \ pi\dreapta] \), \(\k\în Z\)

Răspuns\(\ x \in\left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+2 \pi\right] \), \(\ k \în Z \)

Exercițiu

Rezolvați inegalitatea \(\ \sin x>2 \)

Soluţie

Sinusul este o funcție mărginită: \(\ |\sin x| \leq 1 \) , iar partea dreaptă a acestei inegalități este mai mare decât unu, deci nu există soluții.

Răspuns: Nu există soluții.

Exercițiu

Rezolvați inegalitatea \(\ \cos x>\frac(1)(2) \)

Soluţie

Această inegalitate poate fi rezolvată în două moduri: grafic și folosind un cerc unitar. Să luăm în considerare fiecare dintre metode.

Prima cale. Să descriem într-un sistem de coordonate funcțiile care descriu părțile din stânga și din dreapta ale inegalității, adică \(\ y=\cos x \) și \(\ y=\frac(1)(2) \) . Să selectăm intervalele în care graficul funcției cosinus \(\ y=\cos x \) este situat deasupra graficului dreptei \(\ y=\frac(1)(2) \) (Fig. 4). ).

Aflați abscisele punctelor \(\ \boldsymbol(x)_(1) \) și \(\ x_(2) \) - punctele de intersecție ale graficelor funcțiilor \(\ y=\cos x \ ) și \(\ y=\frac (1)(2) \) , care sunt capetele unuia dintre intervalele pe care se ține inegalitatea indicată. \(\ x_(1)=-\arccos \frac(1)(2)=-\frac(\pi)(3) \); \(\ x_(1)=\arccos \frac(1)(2)=\frac(\pi)(3) \)

Avand in vedere ca cosinusul este o functie periodica, cu perioada \(\ 2 \pi \) , raspunsul este valoarea \(\ x \) din intervalele \(\ \left(-\frac(\pi)(3). )+2 \pi k ; \frac(\pi)(3)+2 \pi k\right) \), \(\ k \in Z \)

A doua cale. Să construim un cerc unitar și o dreaptă \(\ x=\frac(1)(2) \) (deoarece axa x corespunde cosinusului cercului unitar). Fie \(\ P_(x_(1)) \) și \(\ P_(x_(2)) \) (fig. 5) punctele de intersecție ale dreptei și ale cercului unitar. Soluția ecuației inițiale va fi mulțimea punctelor de abscisă care sunt mai mici decât \(\ \frac(1)(2) \) . Aflați valoarea \(\ x_(1) \) și \(\ 2 \) , făcând un tur în sens invers acelor de ceasornic astfel încât \(\ x_(1) Ținând cont de periodicitatea cosinusului, obținem în final intervalele \( \ \left(-\frac (\pi)(3)+2 \pi k ;\frac(\pi)(3)+2 \pi k\right) \),\(\ k \in Z \)

Răspuns: \(\ x \in\left(-\frac(\pi)(3)+2 \pi k ; \frac(\pi)(3)+2 \pi k\right) \), \(\ k \in Z \)

Exercițiu

Rezolvați inegalitatea \(\ \operatorname(ctg) x \leq-\frac(\sqrt(3))(3) \)

Soluţie

Să trasăm grafice ale funcțiilor \(\ y=\operatorname(ctg) x \), \(\ y=-\frac(\sqrt(3))(3) \) într-un singur sistem de coordonate

Să selectăm intervalele în care graficul funcției \(\ y=\operatorname(ctg) x \) nu este mai mare decât graficul dreptei \(\ y=-\frac(\sqrt(3))(3 ) \) (Fig. 6) .

Aflați abscisa punctului \(\ x_(0) \) , care este sfârșitul unuia dintre intervalele pe care inegalitatea \(\ x_(0)=\operatorname(arcctg)\left(-\frac(\) sqrt(3))( 3)\right)=\pi-\operatorname(arcctg)\left(\frac(\sqrt(3))(3)\right)=\pi-\frac(\pi)(3 )=\frac(2 \pi)(3) \)

Celălalt capăt al acestui decalaj este punctul \(\ \pi \) , iar funcția \(\ y=\operatorname(ctg) x \) este nedefinită în acest punct. Astfel, una dintre soluțiile acestei inegalități este intervalul \(\ \frac(2 \pi)(3) \leq x

Răspuns: \(\ x \in\left[\frac(2 \pi)(3)+\pi k ; \pi+\pi k\right) \), \(\ k \in Z \)

Inegalități trigonometrice cu argument complex

Inegalitățile trigonometrice cu un argument complex pot fi reduse la cele mai simple inegalități trigonometrice folosind o substituție. După rezolvare, se face substituția inversă și se exprimă necunoscuta inițială.

Exercițiu

Rezolvați inegalitatea \(\ 2 \cos \left(2 x+100^(\circ)\right) \leq-1 \)

Soluţie

Exprimați cosinusul din partea dreaptă a acestei inegalități: \(\ \cos \left(2 x+100^(\circ)\right) \leq-\frac(1)(2) \)

Efectuăm înlocuirea \(\ t=2 x+100^(\circ) \) , după care această inegalitate se transformă în cea mai simplă inegalitate \(\ \cos t \leq-\frac(1)(2) \ )

Să o rezolvăm folosind cercul unitar. Să construim un cerc unitar și o dreaptă \(\ x=-\frac(1)(2) \) . Să notăm \(\ P_(1) \) și \(\ P_(2) \) ca puncte de intersecție ale dreptei și ale cercului unitar (Fig. 7).

Soluția inegalității inițiale va fi mulțimea punctelor de abscisă, care sunt cel mult \(\ -\frac(1)(2) \). Punctul \(\ P_(1) \) corespunde unghiului \(\ 120^(\circ) \) , iar punctului \(\ P_(2) \) . Astfel, dată fiind perioada cosinus, obținem \(\ 120^(\circ)+360^(\circ) \cdot n \leq t \leq 240^(\circ)+360^(\circ) \cdot n \ ), \(\ n \in Z \)

Facem substituția inversă \(\ t=2 x+100^(\circ) 120^(\circ)+360^(\circ) \cdot n \leq 2 x+100^(\circ) \leq 240^ (\ circ)+360^(\circ) \cdot n \), \(\ n \in Z \)

Exprimăm \(\ \mathbf(x) \), pentru a face acest lucru, mai întâi scădem \(\ 100^(\circ) 120^(\circ)-100^(\circ)+360^(\circ) \ cdot n \leq 2 x+100^(\circ)-100^(\circ) \leq 240^(\circ)-100^(\circ)+360^(\circ) \cdot n \), \( \ n\în Z\); \(\ 20^(\circ)+360^(\circ) \cdot n \leq 2 x \leq 140^(\circ)+360^(\circ) \cdot n \), \(\ n \in Z\)

și apoi, împărțiți la 2 \(\ \frac(20^(\circ)+360^(\circ) \cdot n)(2) \leq \frac(2 x)(2) \leq \frac(140^ (\circ)+360^(\circ) \cdot n)(2) \), \(\ n \in Z \); \(\ 10^(\circ)+180^(\circ) \cdot n \leq x \leq 70^(\circ)+180^(\circ) \cdot n \), \(\ n \in Z \)

Răspuns\(\ x \in\left(10^(\circ)+180^(\circ) \cdot n ; 10^(\circ)+180^(\circ) \cdot n\right) \), \ (\ x \in\left(10^(\circ)+180^(\circ) \cdot n ; 10^(\circ)+180^(\circ) \cdot n\right) \)

Inegalități trigonometrice duble

Exercițiu

Rezolvați inegalitatea trigonometrică dublă \(\ \frac(1)(2)

Soluţie

Să introducem înlocuirea \(\ t=\frac(x)(2) \), atunci inegalitatea inițială va lua forma \(\ \frac(1)(2)

Să o rezolvăm folosind cercul unitar. Deoarece axa ordonatelor corespunde sinusului cercului unitar, selectăm pe ea mulțimea de ordonate a cărora este mai mare decât \(\ x=\frac(1)(2) \) și mai mică sau egală cu \(\ \frac(\sqrt(2))(2 ) \) . În Figura 8, aceste puncte vor fi situate pe arce \(\ P_(t_(1)) \), \(\ P_(t_(2)) \) și \(\ P_(t_(3)) \) , \( \ P_(t_(4)) \) . Să găsim valoarea \(\ t_(1) \), \(\ t_(2) \), \(\ t_(3) \), \(\ t_(4) \) , făcând un tur în sens invers acelor de ceasornic și \ (\ t_(1) \(\ t_(3)=\pi-\arcsin \frac(\sqrt(2))(2)=\pi-\frac(\pi)(4)=\frac(3) \ pi)(4) \); \(\ t_(4)=\pi-\arcsin \frac(1)(2)=\pi-\frac(\pi)(6)=\frac(5 \pi ) (6)\)

Se obține astfel două intervale care, ținând cont de periodicitatea funcției sinus, se pot scrie astfel \(\ \frac(\pi)(6)+2 \pi k \leq t \frac(\pi) (4)+2 \ pi k \quad \frac(3 \pi)(4)+2 \pi k leq \frac(x)(2) \frac(\pi)(4)+2 \pi k \) , \(\ \frac(3 \pi)(4)+2 \pi k Express \(\ \mathbf( x) \), pentru aceasta înmulțim toate laturile ambelor inegalități cu 2, obținem \(\ \frac (\pi)(3)+4 \pi k \leq x

Răspuns\(\ x \in\left(\frac(\pi)(3)+4 \pi k ; \frac(\pi)(2)+4 \pi k\right] \cup\left[\frac( 3 \pi)(2)+4 \pi k ; \frac(5 \pi)(3)+4 \pi k\right) \), \(\ k \in Z \)

METODE DE REZOLVARE A INEGALĂȚILOR TRIGONOMETRICE

Relevanţă. Din punct de vedere istoric, ecuațiilor și inegalităților trigonometrice li s-a acordat un loc special în programa școlară. Putem spune că trigonometria este una dintre cele mai importante secțiuni ale cursului școlar și ale tuturor științelor matematice în general.

Ecuațiile și inegalitățile trigonometrice ocupă unul dintre locurile centrale într-un curs de matematică de liceu, atât în ​​ceea ce privește conținutul materialului educațional, cât și în ceea ce privește metodele de activitate educațională și cognitivă care pot și trebuie formate în timpul studiului lor și aplicate la rezolvarea unei mari probleme. număr de probleme de natură teoretică și aplicativă.

Rezolvarea ecuațiilor și inegalităților trigonometrice creează premisele pentru sistematizarea cunoștințelor elevilor legate de tot materialul educațional din trigonometrie (de exemplu, proprietățile funcțiilor trigonometrice, metode de transformare a expresiilor trigonometrice etc.) și face posibilă stabilirea de conexiuni eficiente cu materialul studiat în algebră (ecuații, echivalență de ecuații, inegalități, transformări identice ale expresiilor algebrice etc.).

Cu alte cuvinte, luarea în considerare a metodelor de rezolvare a ecuațiilor și inegalităților trigonometrice presupune un fel de transfer al acestor abilități la un conținut nou.

Semnificația teoriei și numeroasele ei aplicații sunt o dovadă a relevanței temei alese. Acest lucru, la rândul său, vă permite să determinați scopurile, obiectivele și subiectul cercetării lucrării cursului.

Scopul studiului: generalizează tipurile disponibile de inegalități trigonometrice, metode de bază și speciale pentru rezolvarea acestora, selectează un set de sarcini pentru rezolvarea inegalităților trigonometrice de către școlari.

Obiectivele cercetării:

1. Pe baza analizei literaturii disponibile pe tema de cercetare, sistematizați materialul.

2. Oferă un set de sarcini necesare pentru a consolida tema „Inegalități trigonometrice”.

Obiect de studiu sunt inegalităţi trigonometrice la cursul de matematică şcolară.

Subiect de studiu: tipuri de inegalități trigonometrice și metode de rezolvare a acestora.

Semnificație teoretică este de a organiza materialul.

Semnificație practică: aplicarea cunoștințelor teoretice în rezolvarea problemelor; analiza principalelor metode frecvent întâlnite de rezolvare a inegalităților trigonometrice.

Metode de cercetare : analiza literaturii științifice, sinteza și generalizarea cunoștințelor dobândite, analiza rezolvării problemelor, căutarea metodelor optime de rezolvare a inegalităților.

§unu. Tipuri de inegalități trigonometrice și metode de bază pentru rezolvarea acestora

1.1. Cele mai simple inegalități trigonometrice

Două expresii trigonometrice legate printr-un semn sau > se numesc inegalități trigonometrice.

A rezolva o inegalitate trigonometrică înseamnă a găsi o mulțime de valori ale necunoscutelor incluse în inegalitate, sub care inegalitatea este satisfăcută.

Partea principală a inegalităților trigonometrice este rezolvată prin reducerea lor la rezolvarea celor mai simple:

Aceasta poate fi o metodă de factorizare, schimbare a variabilei (
,
etc.), unde se rezolvă mai întâi inegalitatea obișnuită și apoi inegalitatea formei
etc., sau alte moduri.

Cele mai simple inegalități se rezolvă în două moduri: folosind cercul unitar sau grafic.

Lăsaf(x  este una dintre funcțiile trigonometrice de bază. Pentru a rezolva inegalitatea
este suficient să-și găsești soluția pe o singură perioadă, adică. pe orice segment a cărui lungime este egală cu perioada funcțieif  X  . Apoi se va găsi soluția inegalității originaleX , precum și acele valori care diferă de cele găsite de orice număr întreg de perioade ale funcției. În acest caz, este convenabil să folosiți metoda grafică.

Să dăm un exemplu de algoritm pentru rezolvarea inegalităților
(
) și
.

Algoritm pentru rezolvarea inegalității
(
).

1. Formulați definiția sinusului unui numărX pe cercul unitar.

3. Pe axa y, marcați un punct cu coordonateleA .

4. Prin acest punct, trasați o linie paralelă cu axa OX și marcați punctele de intersecție a acesteia cu cercul.

5. Selectați un arc de cerc, toate punctele căruia au o ordonată mai mică decâtA .

6. Specificați direcția bypass-ului (în sens invers acelor de ceasornic) și notați răspunsul adăugând perioada funcției la capetele intervalului2πn ,
.

Algoritm pentru rezolvarea inegalității
.

1. Formulați definiția tangentei unui numărX pe cercul unitar.

2. Desenați un cerc unitar.

3. Desenați o linie de tangente și marcați un punct pe ea cu o ordonatăA .

4. Conectați acest punct la origine și marcați punctul de intersecție al segmentului rezultat cu cercul unitar.

5. Selectați un arc de cerc, toate punctele căruia au o ordonată pe linia tangentă mai mică decâtA .

6. Indicați direcția de parcurgere și notați răspunsul, ținând cont de sfera funcției, adăugând un punctpn ,
(numărul din partea stângă a înregistrării este întotdeauna mai mic decât numărul din partea dreaptă).

Interpretarea grafică a soluțiilor celor mai simple ecuații și formulele de rezolvare a inegalităților într-o formă generală sunt date în anexă (Anexele 1 și 2).

Exemplul 1 Rezolvați inegalitatea
.

Desenați o linie pe cercul unității
, care intersectează cercul în punctele A și B.

Toate valoriley pe intervalul NM mai mult , toate punctele arcului AMB satisfac această inegalitate. La toate unghiurile de rotație, mare , dar mai mic ,
va lua valori mai mari decât (dar nu mai mult de unul).

Fig.1

Astfel, soluția inegalității va fi toate valorile din interval
, adică
. Pentru a obține toate soluțiile acestei inegalități, este suficient să adăugați la capetele acestui interval
, Unde
, adică
,
. Rețineți că valorile
și
sunt rădăcinile ecuației
,

acestea.
;
.

Răspuns:
,
.

1.2. Metoda grafică

În practică, o metodă grafică pentru rezolvarea inegalităților trigonometrice este adesea utilă. Luați în considerare esența metodei pe exemplul inegalității
:

1. Dacă argumentul este complex (diferit deX ), apoi îl înlocuim cut .

2. Construim într-un singur plan de coordonatetoOy grafice de funcții
și
.

3. Găsim astfeldouă puncte de intersecție adiacente ale graficelor, între caresinusoidsituatde mai sus Drept
. Găsiți abscisele acestor puncte.

4. Scrieți o inegalitate dublă pentru argumentt , având în vedere perioada cosinus (t va fi între abscisele găsite).

5. Faceți o înlocuire inversă (reveniți la argumentul inițial) și exprimați valoareaX dintr-o inegalitate dublă, scriem răspunsul ca un interval numeric.

Exemplul 2 Rezolvați inegalitatea: .

Când rezolvați inegalitățile printr-o metodă grafică, este necesar să construiți grafice ale funcțiilor cât mai precis posibil. Să transformăm inegalitatea în forma:

Să construim grafice ale funcțiilor într-un sistem de coordonate
și
(Fig. 2).

Fig.2

Graficele funcțiilor se intersectează într-un punctDAR cu coordonate
;
. Intre
puncte grafice
sub punctele diagramei
. Și atunci când
valorile funcției sunt aceleași. De aceea
la
.

Răspuns:
.

1.3. Metoda algebrică

Destul de des, inegalitatea trigonometrică inițială, printr-o substituție bine aleasă, poate fi redusă la o inegalitate algebrică (rațională sau irațională). Această metodă implică transformarea inegalității, introducerea unei substituții sau înlocuirea unei variabile.

Să luăm în considerare aplicarea acestei metode pe exemple concrete.

Exemplul 3 Reducere la forma cea mai simplă
.

(Fig. 3)

Fig.3

,
.

Răspuns:
,

Exemplul 4 Rezolvați inegalitatea:

ODZ:
,
.

Folosind formule:
,

scriem inegalitatea sub forma:
.

Sau, presupunând
după simple transformări obținem

,

,

.

Rezolvând ultima inegalitate prin metoda intervalului, obținem:

Fig.4

, respectiv
. Apoi din Fig. 4 urmează
, Unde
.

Fig.5

Răspuns:
,
.

1.4. Metoda de spațiere

Schema generală de rezolvare a inegalităților trigonometrice prin metoda intervalului:

Folosind formule trigonometrice, factorizați.

Găsiți punctele de întrerupere și zerourile funcției, puneți-le pe cerc.

Luați orice punctLa (dar nu a fost găsit mai devreme) și află semnul produsului. Dacă produsul este pozitiv, atunci puneți un punct în afara cercului unitar pe raza corespunzătoare unghiului. În caz contrar, pune punctul în interiorul cercului.

Dacă un punct apare de un număr par, îl numim punct de multiplicitate par; dacă este de un număr impar de ori, îl numim punct de multiplicitate impar. Desenați arce după cum urmează: începeți dintr-un punctLa , dacă următorul punct este de multiplicitate impară, atunci arcul intersectează cercul în acest punct, dar dacă punctul este de multiplicitate pară, atunci nu se intersectează.

Arcurile din spatele unui cerc sunt goluri pozitive; în interiorul cercului sunt goluri negative.

Exemplul 5 Rezolvați inegalitatea

,
.

Puncte din prima serie:
.

Puncte din a doua serie:
.

Fiecare punct apare de un număr impar de ori, adică toate punctele de multiplicitate impară.

Aflați semnul produsului la
: . Marcam toate punctele de pe cercul unitar (Fig. 6):

Orez. 6

Răspuns:
,
;
,
;
,
.

Exemplul 6 . Rezolvați inegalitatea.

Soluţie:

Să găsim zerourile expresiei .

obțineaem :

,
;

,
;

,
;

,
;

Pe cercul unității, valori de serieX 1 reprezentate prin puncte
. SerieX 2 dă puncte
. O serieX 3 obținem două puncte
. În sfârșit, o serieX 4 va reprezenta puncte
. Punem toate aceste puncte pe cercul unitar, indicând în paranteze lângă fiecare multiplicitatea sa.

Acum lăsați numărul va fi egal. Facem o estimare dupa semnul:

Deci ideeaA trebuie ales pe fasciculul care formează unghiul cu grindăOh, în afara cercului unitar. (Rețineți că fasciculul auxiliarO A nu trebuie sa fie aratat in poza. PunctA selectat aproximativ.)

Acum din punct de vedereA trasăm o linie continuă ondulată secvenţial la toate punctele marcate. Și la puncte
linia noastră trece dintr-o regiune în alta: dacă era în afara cercului unitar, atunci trece în el. Apropiindu-se de punct , linia revine în regiunea interioară, deoarece multiplicitatea acestui punct este pară. În mod similar la punct (cu o multiplicitate uniformă) linia trebuie rotită spre regiunea exterioară. Deci, am desenat o anumită imagine descrisă în Fig. 7. Ajută la evidențierea zonelor dorite de pe cercul unității. Sunt marcate cu „+”.

Fig.7

Răspuns final:

Notă. Dacă linia ondulată, după parcurgerea tuturor punctelor marcate pe cercul unitar, nu poate fi returnată la punctA , fără a traversa cercul într-un loc „ilegal”, aceasta înseamnă că a fost făcută o eroare în soluție, și anume, au fost omise un număr impar de rădăcini.

Răspuns: .

§2. Un set de sarcini pentru rezolvarea inegalităților trigonometrice

În procesul de dezvoltare a capacității școlarilor de a rezolva inegalitățile trigonometrice, se pot distinge și 3 etape.

1. pregătitoare,

2. formarea deprinderilor de rezolvare a celor mai simple inegalități trigonometrice;

3. introducerea inegalităţilor trigonometrice de alte tipuri.

Scopul etapei pregătitoare este acela că este necesar să se formeze la școlari capacitatea de a utiliza un cerc sau un grafic trigonometric pentru a rezolva inegalitățile, și anume:

Capacitatea de a rezolva inegalități simple ale formei
,
,
,
, utilizarea proprietăților funcțiilor sinus și cosinus;

Capacitatea de a face inegalități duble pentru arce de cerc numeric sau pentru arce de grafice ale funcțiilor;

Capacitatea de a efectua diverse transformări ale expresiilor trigonometrice.

Se recomandă implementarea acestei etape în procesul de sistematizare a cunoștințelor școlarilor despre proprietățile funcțiilor trigonometrice. Principalele mijloace pot fi sarcinile oferite elevilor și efectuate fie sub îndrumarea unui profesor, fie independent, precum și abilitățile dobândite în rezolvarea ecuațiilor trigonometrice.

Iată exemple de astfel de sarcini:

1 . Marcați un punct pe cercul unității , dacă

.

2. În ce sfert din planul de coordonate se află punctul , dacă este egal cu:

3. Marcați puncte pe cercul trigonometric , dacă:

4. Aduceți expresia la funcțiile trigonometriceeusferturi.

A)
, b)
, în)

5. Având în vedere arcul MR.M - mijloceutrimestrul,R - mijlocIItrimestrul. Restricționați valoarea unei variabilet pentru: (alcătuiți o inegalitate dublă) a) arc MP; b) arcele RM.

6. Scrieți o dublă inegalitate pentru secțiunile selectate ale graficului:

Orez. unu

7. Rezolvați inegalitățile
,
,
,
.

8. Convertiți expresia .

La a doua etapă a învăţării rezolvării inegalităţilor trigonometrice, putem oferi următoarele recomandări legate de metodologia de organizare a activităţilor elevilor. În același timp, este necesar să se concentreze pe abilitățile elevilor de a lucra cu un cerc sau un grafic trigonometric, care se formează în timpul rezolvării celor mai simple ecuații trigonometrice.

În primul rând, este posibil să se motiveze oportunitatea obținerii unei metode generale de rezolvare a celor mai simple inegalități trigonometrice prin referire, de exemplu, la o inegalitate de formă
. Folosind cunoștințele și abilitățile dobândite în etapa pregătitoare, elevii vor aduce în formă inegalitatea propusă
, dar poate fi dificil să găsească un set de soluții la inegalitatea rezultată, deoarece este imposibil de rezolvat numai folosind proprietățile funcției sinus. Această dificultate poate fi evitată prin referire la ilustrația corespunzătoare (rezolvarea grafică a ecuației sau folosind un cerc unitar).

În al doilea rând, profesorul ar trebui să atragă atenția elevilor asupra diferitelor modalități de finalizare a sarcinii, să ofere un exemplu adecvat de rezolvare a inegalității atât grafic, cât și folosind cercul trigonometric.

Luați în considerare astfel de opțiuni pentru rezolvarea inegalității
.

1. Rezolvarea inegalității folosind cercul unitar.

În prima lecție de rezolvare a inegalităților trigonometrice, vom oferi studenților un algoritm de rezolvare detaliat, care într-o prezentare pas cu pas reflectă toate abilitățile de bază necesare rezolvării inegalității.

Pasul 1.Desenați un cerc unitar, marcați un punct pe axa y și trageți o linie dreaptă prin ea paralelă cu axa x. Această linie va intersecta cercul unitar în două puncte. Fiecare dintre aceste puncte descrie numere al căror sinus este egal cu .

Pasul 2Această linie dreaptă a împărțit cercul în două arce. Să-l identificăm pe cel pe care sunt afișate numere care au un sinus mai mare decât . Desigur, acest arc este situat deasupra liniei drepte trasate.

Orez. 2

Pasul 3Să alegem unul dintre capetele arcului marcat. Să notăm unul dintre numerele care este reprezentat de acest punct al cercului unitar .

Pasul 4Pentru a alege un număr corespunzător celui de-al doilea capăt al arcului selectat, „trecem” de-a lungul acestui arc de la capătul numit la celălalt. În același timp, reamintim că la deplasarea în sens invers acelor de ceasornic, numerele pe care le vom trece cresc (când ne deplasăm în sens invers, numerele ar scădea). Să notăm numărul care este reprezentat pe cercul unității de al doilea capăt al arcului marcat .

Astfel, vedem că inegalitatea
satisface numerele pentru care inegalitatea
. Am rezolvat inegalitatea pentru numerele situate pe aceeași perioadă a funcției sinus. Prin urmare, toate soluțiile inegalității pot fi scrise ca

Elevii ar trebui să fie rugați să analizeze cu atenție cifra și să descopere de ce toate soluțiile la inegalitate
poate fi scris sub forma
,
.

Orez. 3

Este necesar să atragem atenția elevilor asupra faptului că atunci când rezolvăm inegalitățile pentru funcția cosinus, trasăm o dreaptă paralelă cu axa y.

Mod grafic de rezolvare a inegalității.

Construirea graficelor
și
, dat fiind
.

Orez. patru

Apoi scriem ecuația
si decizia lui
,
,
, găsit folosind formule
,
,
.

(Dăruindn valorile 0, 1, 2, găsim trei rădăcini ale ecuației compuse). Valori
sunt trei abscise consecutive ale punctelor de intersecție ale graficelor
și
. Evident, mereu la interval
inegalitatea
, iar pe interval
- inegalitatea
. Ne interesează primul caz, iar apoi adăugând la capetele acestui interval un număr care este un multiplu al perioadei sinusurilor, obținem o soluție la inegalitatea
la fel de:
,
.

Orez. 5

Rezuma. Pentru a rezolva inegalitatea
, trebuie să scrieți ecuația corespunzătoare și să o rezolvați. Din formula rezultată găsiți rădăcinile și , și scrieți răspunsul inegalității sub forma: ,
.

În al treilea rând, faptul despre mulțimea de rădăcini a inegalității trigonometrice corespunzătoare este confirmat foarte clar atunci când o rezolvăm grafic.

Orez. 6

Este necesar să le demonstrăm elevilor că bobina, care este soluția inegalității, se repetă în același interval, egal cu perioada funcției trigonometrice. De asemenea, puteți lua în considerare o ilustrație similară pentru graficul funcției sinus.

În al patrulea rând, este recomandabil să se efectueze lucrări de actualizare a metodelor elevilor de conversie a sumei (diferenței) funcțiilor trigonometrice într-un produs, pentru a atrage atenția școlarilor asupra rolului acestor tehnici în rezolvarea inegalităților trigonometrice.

O astfel de muncă poate fi organizată prin îndeplinirea independentă de către elevi a sarcinilor propuse de profesor, dintre care evidențiem următoarele:

În al cincilea rând, elevilor trebuie să li se ceară să ilustreze soluția fiecărei inegalități trigonometrice simple folosind un grafic sau un cerc trigonometric. Asigurați-vă că acordați atenție oportunității sale, în special utilizării unui cerc, deoarece atunci când rezolvați inegalitățile trigonometrice, ilustrația corespunzătoare servește ca un mijloc foarte convenabil de a fixa setul de soluții la o anumită inegalitate.

Cunoașterea elevilor cu metode de rezolvare a inegalităților trigonometrice care nu sunt cele mai simple, este recomandabil să se efectueze după următoarea schemă: referirea la o inegalitate trigonometrică specifică referirea la ecuația trigonometrică corespunzătoare căutarea comună (profesor - elevi) pentru o soluție independentă transferul tehnicii găsite la alte inegalităţi de acelaşi tip.

Pentru a sistematiza cunoștințele de trigonometrie ale elevilor, recomandăm selectarea specifică a unor astfel de inegalități, a căror rezolvare necesită diverse transformări care pot fi implementate în procesul de rezolvare a acesteia, concentrând atenția elevilor asupra trăsăturilor lor.

Ca atare inegalități productive, putem propune, de exemplu, următoarele:

În concluzie, dăm un exemplu de set de probleme pentru rezolvarea inegalităților trigonometrice.

1. Rezolvați inegalitățile:

2. Rezolvați inegalitățile: 3. Găsiți toate soluțiile inegalităților: 4. Găsiți toate soluțiile inegalităților:

A)
, îndeplinind condiția
;

b)
, îndeplinind condiția
.

5. Găsiți toate soluțiile inegalităților:

A) ;

b) ;

în)
;

G)
;

e)
.

6. Rezolvați inegalitățile:

A) ;

b) ;

în);

G)
;

e) ;

e) ;

și)
.

7. Rezolvați inegalitățile:

A)
;

b) ;

în);

G).

8. Rezolvați inegalitățile:

A) ;

b) ;

în);

G)
;

e)
;

e) ;

și)
;

h) .

Este recomandabil să se ofere sarcinile 6 și 7 studenților care studiază matematica la un nivel avansat, sarcina 8 - elevilor din clasele cu studiu aprofundat al matematicii.

§3. Metode speciale de rezolvare a inegalităților trigonometrice

Metode speciale pentru rezolvarea ecuațiilor trigonometrice - adică acele metode care pot fi folosite doar pentru rezolvarea ecuațiilor trigonometrice. Aceste metode se bazează pe utilizarea proprietăților funcțiilor trigonometrice, precum și pe utilizarea diferitelor formule și identități trigonometrice.

3.1. Metoda sectorială

Luați în considerare metoda sectorului pentru rezolvarea inegalităților trigonometrice. Rezolvarea inegalităților de formă

, UndeP ( X ) șiQ ( X ) - funcţiile trigonometrice raţionale (sinusurile, cosinusurile, tangentele şi cotangentele le intră raţional), similar soluţiei inegalităţilor raţionale. Este convenabil să se rezolve inegalitățile raționale prin metoda intervalelor pe axa reală. Analogul său în rezolvarea inegalităților trigonometrice raționale este metoda sectoarelor dintr-un cerc trigonometric, pentrusinx șicosx (
) sau un semicerc trigonometric pentrutgx șictgx (
).

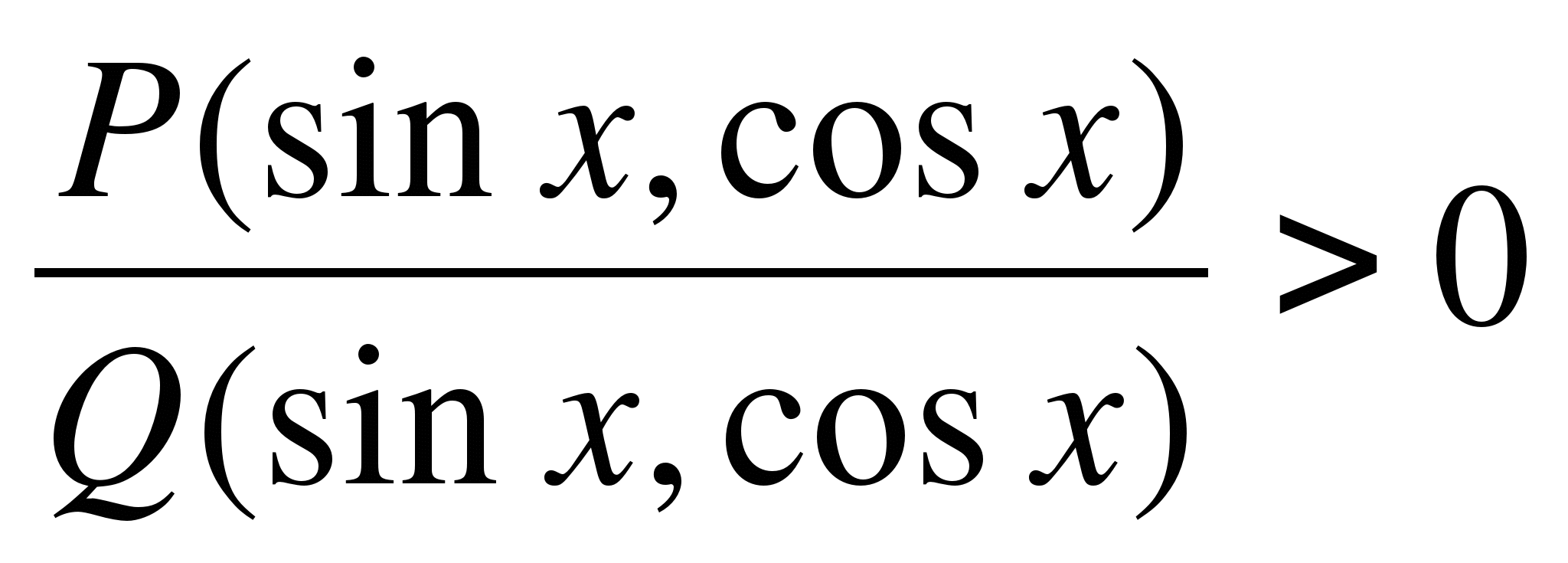
În metoda intervalului, fiecare factor liniar al numărătorului și numitorului formei
punct pe axa numerelor , iar la trecerea prin acest punct
schimba semnul. În metoda sectorului, fiecare multiplicator al formei
, Unde
- una dintre funcțiisinx saucosx și
, într-un cerc trigonometric îi corespund două unghiuri și
, care împart cercul în două sectoare. La trecere prin și funcţie
schimba semnul.

Trebuie reținute următoarele:

a) Multiplicatori ai formei
și
, Unde
, păstrați semnul pentru toate valorile . Astfel de multiplicatori ai numărătorului și numitorului sunt aruncați, schimbându-se (dacă
) pentru fiecare astfel de respingere, semnul de inegalitate este inversat.

b) Multiplicatori ai formei
și
sunt de asemenea aruncate. Mai mult, dacă aceștia sunt factori ai numitorului, atunci inegalitățile de formă sunt adăugate sistemului echivalent de inegalități
și
. Dacă aceștia sunt factori ai numărătorului, atunci în sistemul echivalent de constrângeri ei corespund inegalităților
și
în cazul inegalității inițiale stricte și egalitatea
și
în cazul unei inegalităţi iniţiale nestricte. Când scăpați multiplicatorul
sau
semnul inegalității este inversat.

Exemplul 1 Rezolvați inegalitățile: a)
, b)
. avem o funcție, b). Rezolvați inegalitatea pe care o avem

3.2. Metoda cercului concentric

Această metodă este analogă cu metoda axelor numerice paralele în rezolvarea sistemelor de inegalități raționale.

Luați în considerare un exemplu de sistem de inegalități.

Exemplul 5 Rezolvați un sistem de inegalități trigonometrice simple

În primul rând, rezolvăm fiecare inegalitate separat (Figura 5). În colțul din dreapta sus al figurii, vom indica pentru ce argument este considerat cercul trigonometric.

Fig.5

Apoi, construim un sistem de cercuri concentrice pentru argumentX . Desenăm un cerc și îl umbrim conform soluției primei inegalități, apoi desenăm un cerc de rază mai mare și îl umbrim conform soluției celei de-a doua, apoi construim un cerc pentru a treia inegalitate și un cerc de bază. . Desenăm raze din centrul sistemului prin capetele arcelor, astfel încât acestea să intersecteze toate cercurile. Formăm o soluție pe cercul de bază (Figura 6).

Fig.6

Răspuns:
,
.

Concluzie

Toate obiectivele cursului au fost îndeplinite. Materialul teoretic este sistematizat: sunt date principalele tipuri de inegalități trigonometrice și principalele metode de rezolvare a acestora (grafică, algebrică, metoda intervalelor, sectoarelor și metoda cercurilor concentrice). Pentru fiecare metodă a fost dat un exemplu de rezolvare a unei inegalități. Partea teoretică a fost urmată de partea practică. Conține un set de sarcini pentru rezolvarea inegalităților trigonometrice.

Acest curs poate fi folosit de studenți pentru muncă independentă. Elevii pot verifica nivelul de asimilare a acestei teme, exersează în îndeplinirea sarcinilor de complexitate variată.

După ce am analizat literatura relevantă pe această problemă, putem concluziona, evident, că abilitatea și abilitățile de a rezolva inegalitățile trigonometrice în cursul școlar de algebră și începutul analizei sunt foarte importante, a căror dezvoltare necesită un efort considerabil din partea profesorul de matematică.

Prin urmare, această lucrare va fi utilă profesorilor de matematică, deoarece face posibilă organizarea eficientă a pregătirii elevilor pe tema „Inegalități trigonometrice”.

Studiul poate fi continuat prin extinderea acestuia la lucrarea finală de calificare.

Lista literaturii folosite

Bogomolov, N.V. Culegere de probleme de matematică [Text] / N.V. Bogomolov. – M.: Butarda, 2009. – 206 p.

Vygodsky, M.Ya. Manual de matematică elementară [Text] / M.Ya. Vygodski. – M.: Butarda, 2006. – 509 p.

Zhurbenko, L.N. Matematică în exemple și sarcini [Text] / L.N. Zhurbenko. – M.: Infra-M, 2009. – 373 p.

Ivanov, O.A. Matematică elementară pentru școlari, elevi și profesori [Text] / O.A. Ivanov. – M.: MTsNMO, 2009. – 384 p.

Karp, A.P. Sarcini de algebră și începuturi de analiză pentru organizarea repetiției finale și certificării în clasa a XI-a [Text] / A.P. Crap. – M.: Iluminismul, 2005. – 79 p.

Kulanin, E.D. 3000 de probleme competitive la matematică [Text] / E.D. Kulanin. – M.: Iris-press, 2007. – 624 p.

Leibson, K.L. Culegere de sarcini practice la matematică [Text] / K.L. Leibson. – M.: Butarda, 2010. – 182 p.

Cot, V.V. Probleme cu parametrii și soluția acestora. Trigonometrie: ecuații, inegalități, sisteme. Nota 10 [Text] / V.V. Cot. – M.: ARKTI, 2008. – 64 p.

Manova, A.N. Matematica. Tutor expres pentru pregătirea examenului: cont. indemnizație [Text] / A.N. Manova. - Rostov-pe-Don: Phoenix, 2012. - 541 p.

Mordkovich, A.G. Algebra și începutul analizei matematice. 10-11 clase. Manual pentru studenții instituțiilor de învățământ [Text] / A.G. Mordkovici. – M.: Iris-press, 2009. – 201 p.

Novikov, A.I. Funcții trigonometrice, ecuații și inegalități [Text] / A.I. Novikov. - M.: FIZMATLIT, 2010. - 260 p.

Oganesyan, V.A. Metode de predare a matematicii în liceu: Metodologia generală. Proc. alocație pentru studenții la fizică. - mat. fals. ped. în-tovarăș. [Text] / V.A. Oganesyan. – M.: Iluminismul, 2006. – 368 p.

Olechnik, S.N. Ecuații și inegalități. Metode de rezolvare nestandard [Text] / S.N. Olekhnik. - M .: Editura Factorial, 1997. - 219 p.

Sevriukov, P.F. Ecuații și inecuații trigonometrice, exponențiale și logaritmice [Text] / P.F. Sevriukov. – M.: Educația Națională, 2008. – 352 p.

Sergheev, I.N. UTILIZARE: 1000 de sarcini cu răspunsuri și soluții la matematică. Toate sarcinile grupului C [Text] / I.N. Sergheev. – M.: Examen, 2012. – 301 p.

Sobolev, A.B. Matematică elementară [Text] / A.B. Sobolev. - Ekaterinburg: GOU VPO USTU-UPI, 2005. - 81 p.

Fenko, L.M. Metoda intervalelor în rezolvarea inegalităților și studierea funcțiilor [Text] / L.M. Fenko. – M.: Butarda, 2005. – 124 p.

Friedman, L.M. Fundamentele teoretice ale metodologiei predării matematicii [Text] / L.M. Friedman. - M .: Casa de carte „LIBROKOM”, 2009. - 248 p.

Atasamentul 1

Interpretarea grafică a soluțiilor la cele mai simple inegalități

Orez. unu

Orez. 2

Fig.3

Fig.4

Fig.5

Fig.6

Fig.7

Fig.8

Anexa 2

Soluții la cele mai simple inegalități