Тригонометричні нерівності. Тригонометричні нерівності та їх розв'язання Як вирішувати подвійні тригонометричні нерівності
Міністерство освіти Республіки Білорусь
Заклад освіти
«Гомельський державний університет
імені Франциска Скорини»
Математичний факультет
Кафедра алгебри та геометрії
Допущена до захисту
Зав. кафедрою Шеметков Л.А.
Тригонометричні рівняння та нерівності
Курсова робота
Виконавець:
студент групи М-51
С.М. Горський
Науковий керівник к.ф.- м.н.,
старший викладач
В.Г. Сафонов
Гомель 2008
ВСТУП
ОСНОВНІ МЕТОДИ РІШЕННЯ ТРИГОНОМЕТРИЧНИХ РІВНЯНЬ
Розкладання на множники
Розв'язання рівнянь перетворенням твору тригонометричних функцій на суму
Розв'язання рівнянь із застосуванням формул потрійного аргументу
Примноження на деяку тригонометричну функцію
НЕСТАНДАРТНІ ТРИГОНОМЕТРІЧНІ РІВНЯННЯ
ТРИГОНОМЕТРичні нерівності
ВІДБІР КОРНІВ
ЗАВДАННЯ ДЛЯ САМОСТІЙНОГО РІШЕННЯ
ВИСНОВОК
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
У давнину тригонометрія виникла у зв'язку з потребами астрономії, землемірства та будівельної справи, тобто мала чисто геометричний характер і представляла головним чином<<исчисление хорд>>. Згодом у неї почали вкраплюватись деякі аналітичні моменти. У першій половині 18 століття стався різкий перелом, після чого тригонометрія прийняла новий напрям і змістилася у бік математичного аналізу. Саме в цей час тригонометричні залежності почали розглядати як функції.
Тригонометричні рівняння одна з найскладніших тем у шкільному курсі математики. Тригонометричні рівняння виникають під час вирішення завдань з планіметрії, стереометрії, астрономії, фізики та інших областях. Тригонометричні рівняння та нерівності рік у рік зустрічаються серед завдань централізованого тестування.
Найважливіша відмінність тригонометричних рівнянь від алгебраїчних полягає в тому, що в рівняннях алгебри кінцеве число коренів, а в тригонометричних --- нескінченне, що сильно ускладнює відбір коренів. Ще однією специфікою тригонометричних рівнянь є непомітність форми запису відповіді.
Ця дипломна робота присвячена методам розв'язання тригонометричних рівнянь та нерівностей.
Дипломна робота складається із 6 розділів.
У першому розділі наведено основні теоретичні відомості: визначення та властивості тригонометричних та зворотних тригонометричних функцій; таблиця значень тригонометричних функцій деяких аргументів; вираз тригонометричних функцій через інші тригонометричні функції, що дуже важливо для перетворення тригонометричних виразів, що особливо містять зворотні тригонометричні функції; крім основних тригонометричних формул, добре відомих зі шкільного курсу, наведені формули, що спрощують вирази, що містять зворотні тригонометричні функції.
У другому розділі викладено основні методи розв'язання тригонометричних рівнянь. Розглянуто розв'язок елементарних тригонометричних рівнянь, метод розкладання на множники, методи зведення тригонометричних рівнянь до алгебраїчних. Зважаючи на те, що рішення тригонометричних рівнянь можна записати кількома способами, і вид цих рішень не дозволяє відразу встановити, чи є ці рішення однаковими або різними, що може<<сбить с толку>> при вирішенні тестів, розглянуто загальну схему розв'язання тригонометричних рівнянь і докладно розглянуто перетворення груп загальних рішень тригонометричних рівнянь.
У третьому розділі розглядаються нестандартні тригонометричні рівняння, розв'язання яких ґрунтується на функціональному підході.
У четвертому розділі розглядаються тригонометричні нерівності. Детально розглянуті методи розв'язання елементарних тригонометричних нерівностей, як на одиничному колі, так і графічним методом. Описано процес розв'язання неелементарних тригонометричних нерівностей через елементарні нерівності та вже добре відомий школярам метод інтервалів.
У п'ятому розділі представлені найскладніші завдання: коли необхідно як вирішити тригонометричне рівняння, а й зі знайдених коренів відібрати коріння, задовольняють якомусь умові. У цьому розділі наведено рішення типових завдань на вибір коренів. Наведено необхідні теоретичні відомості для відбору коренів: розбиття безлічі цілих чисел на підмножини, що не перетинаються, розв'язання рівнянь у цілих числах (діафантових).
У шостому розділі подано завдання для самостійного рішення, оформлені у вигляді тесту. У 20 завданнях тесту наведено найскладніші завдання, які можуть зустрітись на централізованому тестуванні.
Елементарні тригонометричні рівняння
Елементарні тригонометричні рівняння -- це рівняння виду , де -- одна з тригонометричних функцій: , , , .
Елементарні тригонометричні рівняння мають безліч коренів. Наприклад, рівняння задовольняють такі значення: , , , і т. д. Загальна формула за якою знаходяться всі корені рівняння , де , така:
Тут може приймати будь-які цілі значення, кожному їх відповідає певний корінь рівняння; у цій формулі (як і в інших формулах, за якими вирішуються елементарні тригонометричні рівняння) називають параметром. Записують зазвичай , підкреслюючи тим самим, що параметр приймати будь-які цілі значення.
Рішення рівняння , де знаходяться за формулою
Рівняння вирішується застосовуючи формулу
а рівняння --- за формулою
Особливо відзначимо деякі окремі випадки елементарних тригонометричних рівнянь, коли рішення може бути записано без застосування загальних формул:
При розв'язанні тригонометричних рівнянь важливу роль відіграє період тригонометричних функцій. Тому наведемо дві корисні теореми:
Теорема Якщо --- основний період функції, то число є основним періодом функції.
Періоди функцій і називаються сумірними, якщо є натуральні числа і , що .
Теорема Якщо періодичні функції і , мають сумірні і , всі вони мають загальний період , що є періодом функцій , , .
У теоремі йдеться про те, що є періодом функції , , , і не обов'язково є основним періодом. Наприклад, основний період функцій і --- , а основний період їхнього твору --- .
Введення допоміжного аргументу
Стандартним шляхом перетворення виразів виду 
є наступний прийом: нехай --- кут, що задається рівностями 
, 
. Для будь-яких і такий кут існує. Таким чином . Якщо, або,,, в інших випадках.
Схема розв'язання тригонометричних рівнянь
Основна схема, якою ми керуватимемося при розв'язанні тригонометричних рівнянь наступна:
Розв'язання заданого рівняння зводиться до розв'язання елементарних рівнянь. Засоби рішення --- перетворення, розкладання на множники, заміна невідомих. Провідний принцип -- не втрачати коріння. Це означає, що при переході до наступного рівняння (рівнянь) ми не побоюємося появи зайвого (стороннього) коріння, а піклуємося лише про те, щоб кожне наступне рівняння нашого "ланцюжка" (або сукупність рівнянь у разі розгалуження) було наслідком попереднього. Одним із можливих методів відбору коренів є перевірка. Відразу зауважимо, що у випадку тригонометричних рівнянь труднощі, пов'язані з відбором коренів, з перевіркою, як правило, різко зростають порівняно з рівняннями алгебри. Адже перевіряти доводиться серії, що складаються з нескінченної кількості членів.
Особливо слід сказати про заміну невідомих під час вирішення тригонометричних рівнянь. Найчастіше після необхідної заміни виходить алгебраїчне рівняння. Більше того, не такі вже й рідкісні рівняння, які, хоч і є тригонометричними на вигляд, по суті такими не є, оскільки вже після першого кроку --- заміни змінних --- перетворюються на алгебраїчні, а повернення до тригонометрії відбувається лише на етапі розв'язання елементарних тригонометричних рівнянь
Ще раз нагадаємо: заміну невідомого слід робити за першої можливості, рівняння, що вийшло після заміни, необхідно вирішити до кінця, включаючи етап відбору коренів, а вже потім повернеться до початкового невідомого.
Одна з особливостей тригонометричних рівнянь полягає в тому, що відповідь у багатьох випадках може бути записана різними способами. Навіть для вирішення рівняння 
відповідь може бути записана так:
1) у вигляді двох серій: 
, , ;
2) у стандартній формі є об'єднання зазначених вище серій: , ;
3) оскільки 
, то відповідь можна записати у вигляді 
, . (Надалі наявність параметра , , або в записі відповіді автоматично означає, що цей параметр набуває всіляких цілісних значень. Винятки будуть обговорюватися.)
Очевидно, що трьома перерахованими випадками не вичерпуються всі можливості для запису відповіді рівняння, що розглядається (їх нескінченно багато).
Наприклад, при справедливій рівності 
. Отже, у двох перших випадках, якщо ми можемо замінити на .
Зазвичай відповідь записується на підставі пункту 2. Корисно запам'ятати таку рекомендацію: якщо на вирішенні рівняння робота не закінчується, необхідно провести дослідження, відбір коренів, то найбільш зручна форма запису, зазначена в пункті 1. (Аналогічну рекомендацію слід дати і для рівняння .)
Розглянемо приклад, що ілюструє сказане.
приклад Вирішити рівняння .
Рішення.Найбільш очевидним є наступний шлях. Це рівняння розпадається на два: і . Вирішуючи кожну з них і поєднуючи отримані відповіді, знайдемо .
Інший шлях.Оскільки , то замінюючи і за формулами зниження ступеня. Після невеликих перетворень отримаємо, звідки 
.
На перший погляд ніяких особливих переваг друга формула в порівнянні з першою не має. Однак, якщо візьмемо, наприклад, то виявиться, що, тобто. рівняння має рішення, тоді як перший спосіб нас призводить до відповіді 
. "Побачити" та довести рівність 
не так просто.
Відповідь. .
Перетворення та об'єднання груп загальних рішень тригонометричних рівнянь
Будемо розглядати арифметичну прогресію, що нескінченно тягнеться в обидві сторони. Члени цієї прогресії можна розбити на дві групи членів, що розташовуються праворуч і ліворуч від деякого члена, що називається центральним або нульовим членом прогресії.
Фіксуючи один із членів нескінченної прогресії нульовим номером, ми повинні будемо вести подвійну нумерацію для всіх членів, що залишилися: позитивну для членів, розташованих праворуч, і негативну для членів, розташованих ліворуч від нульового.
У випадку, якщо різниця прогресії , нульовий член , формула будь-якого (-го) члена нескінченної арифметичної прогресії представляє вид:
Перетворення формули для будь-якого члена нескінченної арифметичної прогресії
1. Якщо до нульового члена додати чи відібрати різницю прогресії , від цього прогресія не зміниться, лише переміститься нульовий член, тобто. зміниться нумерація членів.
2. Якщо коефіцієнт при змінній величині помножити на , то від цього відбудеться лише перестановка правої та лівої груп членів.
3. Якщо послідовні члени нескінченної прогресії
наприклад , , , ..., , зробити центральними членами прогресій з однаковою різницею, що дорівнює :
то прогресія і ряд прогресій висловлюють собою одні й самі числа.
приклад Ряд може бути замінений наступними трьома рядами: , , .
4. Якщо нескінченних прогресій з однаковою різницею мають центральними членами числа, що утворюють арифметичну прогресію з різницею , ці рядів може бути замінені однією прогресією з різницею , і з центральним членом, рівним кожному з центральних членів даних прогресій, тобто. якщо
то ці прогресії об'єднуються в одну:
приклад
, , , обидві об'єднуються в одну групу, оскільки 
.
Для перетворення груп, що мають загальні рішення, в групи, загальних рішень, що не мають дані групи, розкладають на групи із загальним періодом, а потім прагнути об'єднати групи, що виходять, виключивши повторювані.
Розкладання на множники
Метод розкладання на множники полягає в наступному: якщо
то всяке рішення рівняння
є рішення сукупності рівнянь
Зворотне твердження взагалі кажучи невірно: не всяке рішення сукупності є рішенням рівняння. Це пояснюється тим, що розв'язання окремих рівнянь можуть не входити до області визначення функції .
приклад Вирішити рівняння .
Рішення.Використовуючи основне тригонометричне тотожність, рівняння представимо у вигляді
Відповідь.
; 
.
Перетворення суми тригонометричних функцій на твір
приклад
Вирішити рівняння 
.
Рішення.Застосуємо формулу, отримаємо рівносильне рівняння
Відповідь. .
приклад Вирішити рівняння .
Рішення.У цьому випадку, перш ніж застосовувати формули суми тригонометричних функцій, слід використати формулу приведення 
. У результаті отримаємо рівносильне рівняння
Відповідь.
, 
.
Розв'язання рівнянь притвором твору тригонометричних функцій у суму
При розв'язанні низки рівнянь застосовуються формули.
приклад Вирішити рівняння
Рішення.
Відповідь. , .
приклад Вирішити рівняння .
Рішення.Застосувавши формулу, отримаємо рівносильне рівняння:
Відповідь. .
Розв'язання рівнянь із застосуванням формул зниження ступеня
За розв'язання широкого кола тригонометричних рівнянь ключову роль відіграють формули.
приклад Вирішити рівняння .
Рішення.Застосовуючи формулу, отримаємо рівносильне рівняння.
Відповідь. ; .
Розв'язання рівнянь із застосуванням формул потрійного аргументу
приклад Вирішити рівняння .
Рішення.Застосуємо формулу, отримаємо рівняння
Відповідь. ; .
приклад
Вирішити рівняння 
.
Рішення.Застосуємо формули зниження ступеня отримаємо: 
. Застосовуючи отримуємо:
Відповідь. ; .
Рівність однойменних тригонометричних функцій
приклад Вирішити рівняння .
Рішення.
Відповідь. , .
приклад
Вирішити рівняння 
.
Рішення.Перетворимо рівняння.
Відповідь. .
приклад Відомо, що й задовольняють рівняння
Знайти суму.
Рішення.З рівняння випливає, що
Відповідь. .
Розглянемо суми виду
Дані суми можна перетворити на твір, домноживши та розділивши їх на , тоді отримаємо
Зазначений прийом може бути використаний при вирішенні деяких тригонометричних рівнянь, проте слід мати на увазі, що в результаті можлива поява сторонніх коренів. Наведемо узагальнення даних формул:
приклад Вирішити рівняння .
Рішення.Видно, що множина є рішенням вихідного рівняння. Тому множення лівої та правої частини рівняння не призведе до появи зайвого коріння.
Маємо 
.
Відповідь. ; .
приклад Вирішити рівняння .
Рішення.Домножимо ліву та праву частини рівняння на та застосувавши формули перетворення твору тригонометричних функцій у суму, пролучимо
Це рівняння рівносильне сукупності двох рівнянь і , звідки і .
Так як коріння рівняння не є корінням рівняння, то з одержаних множин рішень слід виключити. Значить у багатьох потрібно виключити.
Відповідь.та , .
приклад
Вирішити рівняння 
.
Рішення.Перетворюємо вираз:
Рівняння запишеться у вигляді:
Відповідь. .
Зведення тригонометричних рівнянь до алгебраїчних
Зведені до квадратних
Якщо рівняння має вигляд
то заміна приводить його до квадратного, оскільки 
() в.
Якщо замість доданку буде, то потрібна заміна буде.
Рівняння
зводиться до квадратного рівняння
уявленням як 
. Легко перевірити, що з яких , є корінням рівняння, і, зробивши заміну , рівняння зводиться до квадратного.
приклад Вирішити рівняння .
Рішення.Перенесемо в ліву частину, замінимо її на , і виразимо через і .
Після спрощень отримаємо: . Розділимо почленно на , зробимо заміну:
Повертаючись до , знайдемо 
.
Рівняння, однорідні щодо ,
Розглянемо рівняння виду
де , , , ..., , --- дійсні числа. У кожному доданку лівої частини рівняння ступеня одночленів рівні, т. е. сума ступенів синуса і косинуса та сама і дорівнює. Таке рівняння називається одноріднимщодо і , а число називається показником однорідності .
Ясно, що якщо , то рівняння набуде вигляду:
рішеннями якого є значення , у яких , т. е. числа , . Друге рівняння, записане в дужках, також є однорідним, але ступеня на 1 нижче.
Якщо ж , то ці числа не є корінням рівняння.
При отримаємо: , і ліва частина рівняння (1) набуває значення .
Отже, при , і тому можна розділити обидві частини рівняння на . В результаті отримуємо рівняння:
яке, підстановкою легко зводиться до алгебраїчного:
Однорідні рівняння з показником однорідності 1. При маємо рівняння.
Якщо , це рівняння рівнозначно рівнянню , , звідки , .
приклад Розв'яжіть рівняння.
Рішення.Це рівняння однорідне першого ступеня. Розділимо обидві його частини на отримаємо: , , , .
Відповідь. .
приклад При отримаємо однорідне рівняння виду
Рішення.
Якщо тоді розділимо обидві частини рівняння на , отримаємо рівняння 
, яке підстановкою легко наводиться до квадратного: 
. Якщо 
, то рівняння має дійсне коріння, . Вихідне рівняння матиме дві групи рішень: , , .
Якщо 
, то рівняння немає рішень.
приклад Розв'яжіть рівняння.
Рішення.Це однорідне рівняння другого ступеня. Розділимо обидві честі рівняння на , отримаємо: . Нехай тоді , , . , , ; , , .
Відповідь.
.
До рівняння виду зводиться рівняння
Для цього достатньо скористатися тотожністю 
Зокрема, рівняння зводиться до однорідного, якщо замінити на 
тоді отримаємо рівносильне рівняння:
приклад Розв'яжіть рівняння.
Рішення.Перетворимо рівняння до однорідного:
Розділимо обидві частини рівняння на 
, Отримаємо рівняння:
Нехай тоді приходимо до квадратного рівняння: 
, , 
, 
, .
Відповідь.
.
приклад Розв'яжіть рівняння.
Рішення.Зведемо обидві частини рівняння квадрат, враховуючи, що вони мають позитивні значення: , ,
Нехай тоді отримаємо 
, , .
Відповідь. .
Рівняння, які вирішуються за допомогою тотожностей 
Корисно знати такі формули:
приклад Вирішити рівняння .
Рішення.Використовуючи, отримуємо
Відповідь.
Пропонуємо не самі формули, а спосіб їхнього виведення:
отже,
Аналогічно, .
приклад
Вирішити рівняння 
.
Рішення.Перетворюємо вираз:
Рівняння запишеться у вигляді:
Приймаючи, отримуємо. , . Отже
Відповідь. .
Універсальна тригонометрична підстановка
Тригонометричне рівняння виду
де --- раціональна функція за допомогою фомул -- , а так само за допомогою формул -- можна звести до раціонального рівняння щодо аргументів , , , , після чого рівняння може бути зведене до раціонального алгебраічного рівняння щодо за допомогою формул універсальної тригонометричної підстановки
Слід зазначити, що застосування формул може призводити до звуження ОДЗ вихідного рівняння, оскільки не визначено в точках, тому в таких випадках потрібно перевіряти, чи є кути корінням вихідного рівняння.
приклад Вирішити рівняння .
Рішення.За умовою завдання. Застосувавши формули і зробивши заміну, отримаємо
звідки і, отже, .
Рівняння виду
Рівняння виду , де --- багаточлен, вирішуються за допомогою замін невідомих
приклад Вирішити рівняння .
Рішення.Зробивши заміну та враховуючи, що , отримаємо
звідки , . --- сторонній корінь, т.к. . Корінням рівняння 
є.
Використання обмеженості функцій
У практиці централізованого тестування негаразд рідко зустрічаються рівняння, вирішення яких полягає в обмеженості функцій і . Наприклад:
приклад Вирішити рівняння .
Рішення.Оскільки , , то ліва частина не перевищує і дорівнює, якщо
Для знаходження значень , що задовольняють обох рівнянь, надійде так. Вирішимо одне з них, потім знайдених значень відберемо ті, які задовольняють і іншому.
Почнемо з другого: , . Тоді , 
.
Зрозуміло, що для парних буде .
Відповідь. .
Інша ідея реалізується при вирішенні наступного рівняння:
приклад
Вирішити рівняння 
.
Рішення.Скористаємося властивістю показової функції: , 
.
Склавши почленно ці нерівності матимемо:
Отже, ліва частина даного рівняння дорівнює тоді і тільки тоді, коли виконуються дві рівності:
тобто може набувати значень , , , а може набувати значень , .
Відповідь. , .
приклад
Вирішити рівняння 
.
Рішення., . Отже, 
.
Відповідь. .
приклад Вирішити рівняння
Рішення.Позначимо, тоді з визначення зворотної тригонометричної функції маємо 
і 
.
Оскільки , з рівняння випливає нерівність , тобто . . Оскільки і , і . Однак і тому.
Якщо і , то . Оскільки раніше було встановлено, що , то .
Відповідь. , .
приклад Вирішити рівняння
Рішення.Області допустимих значень рівняння є .
Спочатку покажемо, що функція
За будь-яких може приймати тільки позитивні значення.
Представимо функцію так: .
Оскільки , має місце , тобто . 
.
Отже, для доказу нерівності необхідно показати, що 
. З цією метою зведемо в куб обидві частини цієї нерівності, тоді
Отримана чисельна нерівність свідчить, що . Якщо при цьому ще врахувати, що , то ліва частина рівняння невід'ємна.
Розглянемо тепер праву частину рівняння.
Так як 
, то
Однак відомо, що 
. Звідси випливає, що , тобто. права частина рівняння вбирається у . Раніше було доведено, що ліва частина рівняння невід'ємна, тому рівність може бути тільки в тому випадку, коли обидві його частини рівні , а це можливо лише при .
Відповідь. .
приклад Вирішити рівняння
Рішення.Позначимо і 
. Застосовуючи нерівність Коші-Буняковського, отримуємо . Звідси слідує що 
. З іншого боку має місце 
. Отже, рівняння немає коренів.
Відповідь. .
приклад Вирішити рівняння:
Рішення.Перепишемо рівняння у вигляді:
Відповідь. .
Функціональні методи розв'язання тригонометричних та комбінованих рівнянь
Не всяке рівняння результаті перетворень може бути зведено до рівняння тієї чи іншої стандартного виду, котрій існує певний метод решения. У таких випадках виявляється корисним використовувати такі властивості функцій і , як монотонність, обмеженість, парність, періодичність та ін Так, якщо одна з функцій зменшується, а друга зростає на проміжку , то при наявності у рівняння кореня на цьому проміжку, цей корінь єдиний, і тоді його, наприклад, можна знайти підбором. Якщо ж функція обмежена зверху, причому , а функція обмежена знизу, причому , то рівняння рівносильне системі рівнянь
приклад Вирішити рівняння
Рішення.Перетворимо вихідне рівняння до виду
і вирішимо його як квадратне щодо. Тоді отримаємо,
Вирішимо перше рівняння сукупності. Зваживши на обмеженість функції , приходимо до висновку, що рівняння може мати корінь тільки на відрізку . У цьому проміжку функція зростає, а функція 
зменшується. Отже, якщо це рівняння має корінь, він єдиний. Підбором знаходимо.
Відповідь. .
приклад Вирішити рівняння
Рішення.Нехай і 
тоді вихідне рівняння можна записати у вигляді функціонального рівняння. Оскільки функція непарна, то . У такому разі отримуємо рівняння.
Оскільки , і монотонна на , то рівняння дорівнює рівнянню , тобто. 
, що має єдиний корінь.
Відповідь. .
приклад
Вирішити рівняння 
.
Рішення.На підставі теореми про похідну складну функцію ясно, що функція 
спадна (функція спадна, зростаюча, спадна). Звідси зрозуміло, що функція 
визначена на , спадна. Тому це рівняння має трохи більше одного кореня. Так як 
, то
Відповідь. .
приклад Вирішити рівняння .
Рішення.Розглянемо рівняння на трьох проміжках.
а) Нехай. Тоді на цій множині вихідне рівняння рівносильне рівнянню. Яке на проміжку рішень немає, т. до. 
, , а . На проміжку вихідне рівняння так само немає коренів, т. до. 
, а .
б) Нехай. Тоді на цій множині вихідне рівняння рівносильне рівнянню
корінням якого на проміжку є числа , , , .
в) Нехай. Тоді на цій множині вихідне рівняння рівносильне рівнянню
Яке на проміжку рішень немає, т. до. , а . На проміжку рівняння так само рішень немає, т. до. , , а .
Відповідь. , , , .
Метод симетрії
Метод симетрії зручно застосовувати, як у формулюванні завдання присутня вимога єдиності рішення рівняння, нерівності, системи тощо. або точну вказівку числа рішень. При цьому слід виявити якусь симетрію заданих виразів.
Потрібно також враховувати різноманітність різних можливих видів симетрії.
Не менш важливим є чітке дотримання логічних етапів у міркуваннях із симетрією.
Зазвичай симетрія дозволяє встановити лише необхідні умови, а потім потрібна перевірка їхньої достатності.
приклад Знайти всі значення параметра , у яких рівняння має єдине рішення.
Рішення.Зауважимо, як і --- парні функції, тому ліва частина рівняння є парна функція.
Значить якщо --- рішення рівняння, тобто рішення рівняння. Якщо --- єдине рішення рівняння, то, необхідно , .
Відберемо можливізначення , вимагаючи, щоб було коренем рівняння.
Відразу зазначимо, що інші значення що неспроможні задовольняти умові завдання.
Але поки що не відомо, чи всі відібрані насправді задовольняють умову завдання.
Достатність.
1) , рівняння набуде вигляду 
.
2) , рівняння набуде вигляду:
Очевидно, що для всіх і 
. Отже, останнє рівняння рівносильне системі:
Тим самим ми довели, що при , рівняння має єдине рішення.
Відповідь. .
Рішення з дослідженням функції
приклад Доведіть, що всі рішення рівняння
Цілі числа.
Рішення.Основний період вихідного рівняння дорівнює. Тому спочатку досліджуємо це рівняння на відрізку.
Перетворимо рівняння до виду:
За допомогою мікрокалькулятора отримуємо:
Якщо , то з попередніх рівностей отримуємо:
Розв'язавши отримане рівняння, отримаємо: .
Виконані обчислення дають змогу припустити, що корінням рівняння, що належать відрізку , є , і .
Безпосередня перевірка підтверджує цю гіпотезу. Таким чином, доведено, що корінням рівняння є лише цілі числа .
приклад
Розв'яжіть рівняння 
.
Рішення.Знайдемо основний період рівняння. У функції основний період дорівнює. Основний період функції дорівнює. Найменше загальне кратне чисел і дорівнює. Тому основний період рівняння дорівнює. Нехай.
Вочевидь є рішенням рівняння. На інтервалі. Функція негативна. Тому інше коріння рівняння слід шукати тільки на інтервалах і .
За допомогою мікрокалькулятора спочатку знайдемо наближені значення коренів рівняння. Для цього складаємо таблицю значень функції 
на інтервалах та ; тобто на інтервалах та .
| 0 | 0 | 202,5 | 0,85355342 |
| 3 | -0,00080306 | 207 | 0,6893642 |
| 6 | -0,00119426 | 210 | 0,57635189 |
| 9 | -0,00261932 | 213 | 0,4614465 |
| 12 | -0,00448897 | 216 | 0,34549155 |
| 15 | -0,00667995 | 219 | 0,22934931 |
| 18 | -0,00903692 | 222 | 0,1138931 |
| 21 | -0,01137519 | 225 | 0,00000002 |
| 24 | -0,01312438 | 228 | -0,11145712 |
| 27 | -0,01512438 | 231 | -0,21961736 |
| 30 | -0,01604446 | 234 | -0,32363903 |
| 33 | -0,01597149 | 237 | -0,42270819 |
| 36 | -0,01462203 | 240 | -0,5160445 |
| 39 | -0,01170562 | 243 | -0,60290965 |
| 42 | -0,00692866 | 246 | -0,65261345 |
| 45 | 0,00000002 | 249 | -0,75452006 |
| 48 | 0,00936458 | 252 | -0,81805397 |
| 51 | 0,02143757 | 255 | -0,87270535 |
| 54 | 0,03647455 | 258 | -0,91803444 |
| 57 | 0,0547098 | 261 | -0,95367586 |
| 60 | 0,07635185 | 264 | -0,97934187 |
| 63 | 0,10157893 | 267 | -0,99482505 |
| 66 | 0,1305352 | 270 | -1 |
| 67,5 | 0,14644661 |
З таблиці легко вбачаються такі гіпотези: корінням рівняння, що належать відрізку, є числа: ; ; . Безпосередня перевірка підтверджує цю гіпотезу.
Відповідь.
; 
; .
Розв'язання тригонометричних нерівностей за допомогою одиничного кола
При розв'язанні тригонометричних нерівностей виду , де -- одна з тригонометричних функцій, зручно використовувати тригонометричне коло для того, щоб найбільш наочно уявити рішення нерівності і записати відповідь. Основним методом розв'язання тригонометричних нерівностей є зведення їх до найпростіших нерівностей типу. Розберемо з прикладу, як вирішувати такі нерівності.
приклад Розв'яжіть нерівність.
Рішення.Намалюємо тригонометричне коло і відзначимо у ньому точки, котрим ордината перевершує .
Для вирішення цієї нерівності будуть . Зрозуміло також, якщо деяке число буде відрізнятися від якого-небудь числа із зазначеного інтервалу на , то також буде не менше . Отже, до кінців знайденого відрізка рішення потрібно додати . Остаточно, отримуємо, що рішеннями вихідної нерівності будуть усі 
.
Відповідь.
.
Для вирішення нерівностей з тангенсом та котангенсом корисно поняття про лінію тангенсів та котангенсів. Такими є прямі і відповідно (на малюнку (1) і (2)), що стосуються тригонометричного кола.
Легко помітити, що якщо побудувати промінь з початком на початку координат, що становить кут з позитивним напрямом осі абсцис, то довжина відрізка від точки до точки перетину цього променя з лінією тангенсів точно дорівнює тангенсу кута, який становить цей промінь з віссю абсцис. Аналогічне спостереження має місце й у котангенсу.
приклад Розв'яжіть нерівність.
Рішення.Позначимо , тоді нерівність набуде вигляду найпростішого: . Розглянемо інтервал довжиною, що дорівнює найменшому позитивному періоду (НВП) тангенсу. На цьому відрізку за допомогою лінії тангенсів встановлюємо, що . Згадуємо тепер, що необхідно додати , оскільки функції НПП . Отже, 
. Повертаючись до змінної , отримуємо, що .
Відповідь.
.
Нерівності із зворотними тригонометричними функціями зручно вирішувати з використанням графіків зворотних тригонометричних функцій. Покажемо, як це робиться на прикладі.
Розв'язання тригонометричних нерівностей графічним методом
Зауважимо, що якщо --- періодична функція, то для вирішення нерівності необхідно знайти його рішення на відрізку, довжина якого дорівнює періоду функції . Всі рішення вихідної нерівності будуть складатися зі знайдених значень, а також усіх, що відрізняються від знайдених на будь-яку кількість періодів функції.
Розглянемо розв'язання нерівності ().
Оскільки , то при нерівність рішень немає. Якщо , то безліч розв'язків нерівності --- безліч всіх дійсних чисел.
Нехай. Функція синус має найменший позитивний період, тому нерівність можна вирішити спочатку на відрізку завдовжки, наприклад, на відрізку. Будуємо графіки функцій та (). задаються нерівностями виду: і, звідки,
У роботі були розглянуті методи розв'язання тригонометричних рівнянь і нерівностей, як найпростіших, і олімпіадного рівня. Були розглянуті основні методи розв'язання тригонометричних рівнянь і нерівностей, причому, як специфічні --- характерні тільки для тригонометричних рівнянь і нерівностей,-- так і загальні функціональні методи розв'язання рівнянь і нерівностей, стосовно тригонометричних рівнянь.
У дипломній роботі наведено основні теоретичні відомості: визначення та властивості тригонометричних та зворотних тригонометричних функцій; вираз тригонометричних функцій через інші тригонометричні функції, що дуже важливо для перетворення тригонометричних виразів, що особливо містять зворотні тригонометричні функції; крім основних тригонометричних формул, добре відомих зі шкільного курсу, наведені формули, що спрощують вирази, що містять зворотні тригонометричні функції. Розглянуто розв'язок елементарних тригонометричних рівнянь, метод розкладання на множники, методи зведення тригонометричних рівнянь до алгебраїчних. Зважаючи на те, що рішення тригонометричних рівнянь можна записати декількома способами, і вид цих рішень не дозволяє відразу встановити, чи є ці рішення однаковими або різними, розглянуто загальну схему розв'язання тригонометричних рівнянь і детально розглянуто перетворення груп загальних рішень тригонометричних рівнянь. Детально розглянуті методи розв'язання елементарних тригонометричних нерівностей, як на одиничному колі, так і графічним методом. Описано процес розв'язання неелементарних тригонометричних нерівностей через елементарні нерівності та вже добре відомий школярам метод інтервалів. Наведено рішення типових завдань відбір коренів. Наведено необхідні теоретичні відомості для відбору коренів: розбиття безлічі цілих чисел на підмножини, що не перетинаються, розв'язання рівнянь у цілих числах (діафантових).
Результати даної дипломної роботи можуть бути використані як навчальний матеріал при підготовці курсових та дипломних робіт, при складанні факультативів для школярів, так само робота може застосовуватися при підготовці учнів до вступних іспитів та централізованого тестування.
Вигодський Я.Я., Довідник з елементарної математики. /Вигодський Я.Я. --- М: Наука, 1970.
Ігудісман О., Математика на усному іспиті / Ігудісман О. --- М: Айріс прес, Рольф, 2001.
Азаров А.І., рівняння/Азаров А.І., Гладун О.М., Федосенко В.С. --- Мн.: Трівіум, 1994.
Литвиненко В.М., Практикум з елементарної математики / Литвиненко В.М.--- М.: Просвітництво, 1991.
Шаригін І.Ф., Факультативний курс з математики: вирішення завдань / Шаригін І.Ф., Голубєв В.І. --- М.: Просвітництво, 1991.
Бардушкін Ст, Тригонометричні рівняння. Відбір коренів/В. Бардушкін, А. Прокоф'єв.// Математика, №12, 2005 с. 23-27.
Василевський А.Б., Завдання для позакласної роботи з математики / Васильєв А.Б. --- Мн.: Народна освіта. 1988. --- 176с.
Сапунов П. І., Перетворення та об'єднання груп загальних рішень тригонометричних рівнянь / Сапунов П. І. // Математичне просвітництво, випуск №3, 1935.
Бородін П., Тригонометрія. Матеріали вступних іспитів у МГУ [текст] / П.Бородін, В.Галкін, В.Панферов, І.Сергєєв, В.Тарасов // Математика №1, 2005 с. 36-48.
Самусенко А.В., Математика: Типові помилки абітурієнтів: Довідковий посібник / Самусенко А.В., Козаченок В.В.--- Мн.: Вища школа, 1991.
Азаров А.І., Функціональний та графічний методи вирішення екзаменаційних завдань/Азаров А.І., Барвенов С.А.,--- Мн.: Аверсев, 2004.
Вирішення найпростіших тригонометричних рівнянь
Для початку згадаємо формули для вирішення найпростіших тригонометричних рівнянь.
- $sinx=a$
- $cosx=a$
- $tgx=a$
- $ctgx=a$
Вирішення найпростіших тригонометричних нерівностей.
Для вирішення найпростіших тригонометричних нерівностей нам спочатку необхідно вирішити відповідне рівняння, а потім, використовуючи тригонометричне коло, знайти розв'язання нерівності. Розглянемо розв'язання найпростіших тригонометричних нерівностей на прикладах.
Приклад 1
$sinx\ge \frac(1)(2)$
Знайдемо розв'язання тригонометричної нерівності $sinx=\frac(1)(2)$
\ \
Малюнок 1. Розв'язання нерівності $ sinx \ ge \ frac (1) (2) $.
Оскільки нерівність має знак «більше чи одно», то рішення лежить на верхній дузі кола (щодо розв'язання рівняння).
Відповідь: $\left[\frac(\pi )(6)+2\pi n,\frac(5\pi )(6)+2\pi n\right]$.
Приклад 2
Знайдемо розв'язання тригонометричної нерівності $cosx=\frac(\sqrt(3))(2)$
\ \
Зазначимо рішення на тригонометричному колі
Оскільки нерівність має знак «менше», то рішення лежить на дузі кола, розташованого ліворуч (щодо розв'язання рівняння).
Відповідь: $\left(\frac(\pi )(6)+2\pi n,\frac(11\pi )(6)+2\pi n\right)$.
Приклад 3
$tgx\le \frac(\sqrt(3))(3)$
Знайдемо розв'язання тригонометричної нерівності $tgx=\frac(\sqrt(3))(3)$
\ \
Тут також нам знадобиться область визначення. Як ми пам'ятаємо у функції тангенсу $x\ne \frac(\pi )(2)+\pi n,n\in Z$
Зазначимо рішення на тригонометричному колі
Малюнок 3. Розв'язання нерівності $tgx\le \frac(\sqrt(3))(3)$.
Оскільки нерівність має знак «менше чи одно», то рішення лежить на дугах кола, позначених синім малюнку 3.
Відповідь: $ \ \ left (-\ frac (\ pi ) (2) + 2 \ pi n \ right., \ left. \ frac (\ pi ) (6) + 2 \ pi n \ right] \ cup \ left (\frac(\pi )(2)+2\pi n,\right.\left.\frac(7\pi )(6)+2\pi n\right]$
Приклад 4
Знайдемо розв'язання тригонометричної нерівності $ctgx=\sqrt(3)$
\ \
Тут також нам знадобиться область визначення. Як ми пам'ятаємо у функції тангенсу $ x \ ne \ pi n, n \ in Z $
Зазначимо рішення на тригонометричному колі
Рисунок 4. Вирішення нерівності $ctgx\le \sqrt(3)$.
Оскільки нерівність має знак «більше», то рішення лежить на дугах кола, позначених синім малюнку 4.
Відповідь: $ \ \ left (2 \ pi n, \ frac (\ pi ) (6) + 2 \ pi n \ right) \ cup \ left (\ pi +2 \ pi n, \ frac (7 \ pi ) ( 6) +2 \ pi n \ right) $
ВИЗНАЧЕННЯ
Тригонометричними нерівностями називаються нерівності, які містять змінну під знаком тригонометричної функції.
Розв'язання тригонометричних нерівностей
Розв'язання тригонометричних нерівностей найчастіше зводиться до вирішення найпростіших тригонометричних нерівностей виду: \(\ sin x a \), \(\ cos x > a \), \(\ operatorname(tg) x > a \), \(\ \ operatorname(ctg) x > a \), \(\ \sin x \leq a \), \(\ \cos x \leq a \), \(\ operatorname(tg) x \leq a \), \ (\operatorname(ctg) x \leq a \), \(\ sin x \geq a \), \(\ cos \geq a \), \(\ operatorname(tg) x \geq a \) ), \(\ \operatorname(tg) x \geq a \)
Вирішуються найпростіші тригонометричні нерівності графічно або за допомогою одиничного тригонометричного кола.
За визначенням, синусом кута \(\\alpha\) є ординатою точки \(\P_(\alpha)(x, y)\) одиничного кола (рис. 1), а косинусом - абсцис цієї точки. Цей факт використовується при вирішенні найпростіших тригонометричних нерівностей з косинус і синус за допомогою одиничного кола.
Приклади розв'язання тригонометричних нерівностей
Вирішити нерівність \(\ \sin x \leq \frac(\sqrt(3))(2) \)
Оскільки \(\ \left|\frac(\sqrt(3))(2)\right| , то ця нерівність має розв'язання і її можна вирішити двома способами
Перший метод. Вирішимо цю нерівність графічно. Для цього побудуємо в одній системі координат графік синуса \(\ y=\sin x \) (рис. 2) і прямий \(\ y=\frac(\sqrt(3))(2) \)
Виділимо проміжки, на яких синусоїда розташована нижче графіка прямої \(\ y = \ frac (\ sqrt (3)) (2) \) . Знайдемо абсциси \(\ x_(1) \) і \(\ x_(2) \) точок перетину цих графіків: \(\ x_(1)=\pi-\arcsin \frac(\sqrt(3))(2 )=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_(2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\ frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)
Отримали інтервал \(\ \left[-\frac(4 \pi)(3) ; \frac(\pi)(3)\right] \) але так як функцію \(\ y=\sin x \) періодична і має період \(\ 2 \pi \) , то відповіддю буде об'єднання інтервалів: \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+ 2 \pi k\right] \), \(\ k \in Z \)
Другий спосіб. Побудуємо одиничне коло і пряму \(\ y=\frac(\sqrt(3))(2) \) , точки їх перетину позначимо \(\ P_(x_(1)) \) і \(\ P_(x_(2) )) \) (рис. 3). Вирішенням вихідної нерівності буде безліч точок ординати, яких менше \(\\frac(\sqrt(3))(2)\). Знайдемо значення \(\ \boldsymbol(I)_(1) \) і \(\ \boldsymbol(I)_(2) \) , здійснюючи обхід проти годинникової стрілки, \(\ x_(1)).
\(\ x_(1)=\pi-\arcsin \frac(\sqrt(3))(2)=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_ (2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)
Враховуючи періодичність функції синус, остаточно отримаємо інтервали \(\ left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+2 \pi\right] \), \(\k \in Z\)
Розв'язати нерівність \(\ \sin x>2 \)
Синус – функція обмежена: \(\ |\sin x| \leq 1 \) , а права частина даної нерівності більше одиниці, тому рішень немає.
Розв'язати нерівність \(\ \cos x>\frac(1)(2) \)
Цю нерівність можна вирішити двома способами: графічно та за допомогою одиничного кола. Розглянемо кожен із способів.
Перший метод. Зобразимо в одній системі координат функції, що описують ліву і праву частини нерівності, тобто \(\ y = \ cos x \) і \ (\ y = \ frac (1) (2) \). Виділимо проміжки, на яких графік функції косинус \(\ y=\ cos x \) розташований вище графіка прямої \(\ y=\frac(1)(2) \) (рис. 4).
Знайдемо абсциси точок \(\ \boldsymbol(x)_(1) \) і \(\ x_(2) \) – точок перетину графіків функцій \(\ y=\cos x \) і \(\ y=\frac (1)(2) \) , які є кінцями одного із проміжків, на якому виконується зазначена нерівність. \(\ x_(1)=-\arccos \frac(1)(2)=-\frac(\pi)(3) \); \(\ x_(1)=\arccos \frac(1)(2)=\frac(\pi)(3) \)
Враховуючи, що косинус – функція періодична, з періодом \(\ 2 \pi \) , відповіддю буде значення \(\ x \) з проміжків \(\ \left(-\frac(\pi)(3)+2 \pi k ; \frac(\pi)(3)+2 \pi k\right) \), \(\ k \in Z \)
Другий спосіб. Побудуємо одиничну окружність і пряму \(\ x = \ frac (1) (2) \) (бо на одиничному колі косинус відповідає вісь абсцис). Позначимо \(\ P_(x_(1)) \) і \(\ P_(x_(2)) \) (рис. 5) - точки перетину прямого та одиничного кола. Розв'язанням вихідного рівняння буде безліч точок абсциси, яких менше \(\\frac(1)(2)\). Знайдемо значення \(\ x_(1) \) і \(\ 2 \) , здійснюючи обхід проти годинникової стрілки так, щоб \(\ x_(1) Враховуючи періодичність косинуса, остаточно отримаємо інтервали \(\ \left(-\frac) (\pi)(3)+2 \pi k ; \frac(\pi)(3)+2 \pi k\right) \),\(\ k \in Z \)
Розв'язати нерівність \(\ \operatorname(ctg) x \leq-\frac(\sqrt(3))(3) \)
Побудуємо в одній системі координат графіки функцій \(\ y=\operatorname(ctg) x \), \(\ y=-\frac(\sqrt(3))(3) \)
Виділимо проміжки, на яких графік функції \(\ y=\operatorname(ctg) x \) розташований не вище графіка прямої \(\ y=-\frac(\sqrt(3))(3) \) (рис. 6) .
Знайдемо абсцис точки \(\ x_(0) \) , яка є кінцем одного з проміжків, на якому нерівність \(\ x_(0)=\operatorname(arcctg)\left(-\frac(\sqrt(3)))( 3)\right)=\pi-\operatorname(arcctg)\left(\frac(\sqrt(3))(3)\right)=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) \)
Іншим кінцем цього проміжку є точка \(\pi\) , а функція \(\y=\operatorname(ctg) x \) у цій точці невизначена. Таким чином, одним з розв'язанням даної нерівності є проміжок \(\ \frac(2 \pi)(3) \leq x
Тригонометричні нерівності зі складним аргументом
Тригонометричні нерівності зі складним аргументом можна звести до найпростіших тригонометричних нерівностей за допомогою заміни. Після його рішення робиться зворотна заміна та виражається вихідна невідома.
Розв'язати нерівність \(\ 2 \cos \left(2 x+100^(\circ)\right) \leq-1 \)
Виразимо у правій частині даної нерівності косинус: \(\ \cos \left(2 x+100^(\circ)\right) \leq-\frac(1)(2) \)
Ведемо заміну \(\ t=2 x+100^(\circ) \) , після чого ця нерівність перетворюється до найпростішої нерівності \(\ \cos t \leq-\frac(1)(2) \)
Вирішимо його, використовуючи одиничне коло. Побудуємо одиничне коло і пряму \(\x=-\frac(1)(2)\). Позначимо \(\ P_(1) \) та \(\ P_(2) \) – точки перетину прямого та одиничного кола (рис. 7).
Вирішенням вихідної нерівності буде безліч точок абсциси, яких не більше \(\ -\frac(1)(2) \). Точці \(\P_(1)\) відповідає кут \(\120^(\circ)\), а точці \(\P_(2)\). Таким чином, враховуючи період косинуса, отримаємо \(\ 120^(\circ)+360^(\circ) \cdot n \leq t \leq 240^(\circ)+360^(\circ) \cdot n \) , \(\ n \in Z \)
Зробимо зворотну заміну \(\ t=2 x+100^(\circ) 120^(\circ)+360^(\circ) \cdot n \leq 2 x+100^(\circ) \leq 240^(\ circ)+360^(\circ) \cdot n \), \(\ n \in Z \)
Виразимо \(\ \mathbf(x) \), для початку цього з кожної частини нерівності віднімемо \(\ 100^(\circ) 120^(\circ)-100^(\circ)+360^(\circ) \ cdot n \leq 2 x+100^(\circ)-100^(\circ) \leq 240^(\circ)-100^(\circ)+360^(\circ) \cdot n \), \( \n\in Z\); \(\ 20^(\circ)+360^(\circ) \cdot n \leq 2 x \leq 140^(\circ)+360^(\circ) \cdot n \), \(\ n \in Z \)
а потім розділимо на 2 \(\ \frac(20^(\circ)+360^(\circ) \cdot n)(2) \leq \frac(2 x)(2) \leq \frac(140^ (\circ)+360^(\circ) \cdot n)(2) \), \(\ n \in Z \); \(\ 10^(\circ)+180^(\circ) \cdot n \leq x \leq 70^(\circ)+180^(\circ) \cdot n \), \(\ n \in Z \)
Подвійні тригонометричні нерівності
Розв'язати подвійну тригонометричну нерівність \(\ \frac(1)(2)
Введемо заміну \(\ t=\frac(x)(2) \), тоді вихідна нерівність набуде вигляду \(\ \frac(1)(2)
Вирішимо його, використовуючи одиничне коло. Так як на одиничному колі синусу відповідає вісь ординат, виділимо на ній безліч ординати яких більше \(\ x=\frac(1)(2) \) і менше або одно \(\ \ frac(\sqrt(2))(2 ) \) . На малюнку 8 ці точки будуть розташовані на дугах \(\ P_(t_(1)) \), \(\ P_(t_(2)) \) та \(\ P_(t_(3)) \), \( \P_(t_(4))\). Знайдемо значення \(\ t_(1) \), \(\ t_(2) \), \(\ t_(3) \), \(\ t_(4) \) , здійснюючи обхід проти годинникової стрілки, причому \ (\ t_(1) \(\ t_(3)=\pi-\arcsin \frac(\sqrt(2))(2)=\pi-\frac(\pi)(4)=\frac(3 \) pi) (4) \); (6) \)
Таким чином, отримуємо два інтервали, які, враховуючи періодичність функції синус, можна записати наступним чином \(\ frac(\pi)(6)+2 \pi k \leq t \frac(\pi)(4)+2 \ pi k \quad \frac(3 \pi)(4)+2 \pi k Зробимо зворотну заміну \(\ t=\frac(x)(2) \frac(\pi)(6)+2 \pi k \ leq \frac(x)(2) \frac(\pi)(4)+2 \pi k \), \(\ \frac(3 \pi)(4)+2 \pi kВиразимо \(\ \mathbf( x) \), для цього помножимо всі сторони шпалери нерівностей на 2, отримаємо \(\ \frac(\pi)(3)+4 \pi k \leq x
МЕТОДИ РІШЕННЯ ТРИГОНОМЕТРИЧНИХ НЕРАВЕНСТВ
Актуальність. Історично склалося, що тригонометричним рівнянням та нерівностям приділялося особливе місце у шкільному курсі. Можна сміливо сказати, що тригонометрія одна із найважливіших розділів шкільного курсу і всієї математичної науки загалом.
Тригонометричні рівняння та нерівності займають одне з центральних місць у курсі математики середньої школи, як за змістом навчального матеріалу, так і за способами навчально-пізнавальної діяльності, які можуть і повинні бути сформовані при їх вивченні та застосовані до вирішення великої кількості завдань теоретичного та прикладного характеру .
Розв'язання тригонометричних рівнянь і нерівностей створює передумови для систематизації знань учнів, пов'язаних з усім навчальним матеріалом по тригонометрії (наприклад, властивості тригонометричних функцій, прийоми перетворення тригонометричних виразів і т.д.) і дає можливість встановити дієві зв'язки з вивченим матеріалом з алгебри рівносильність рівнянь, нерівності, тотожні перетворення алгебраїчних виразів тощо).
Інакше висловлюючись, розгляд прийомів розв'язання тригонометричних рівнянь і нерівностей передбачає свого роду перенесення цих умінь нового зміст.
Значимість теорії та її численні застосування є підтвердженням актуальності обраної теми. Це у свою чергу дозволяє визначити цілі, завдання та предмет дослідження курсової роботи.
Мета дослідження: узагальнити наявні типи тригонометричних нерівностей, основні та спеціальні методи їх вирішення, підібрати комплекс завдань для вирішення тригонометричних нерівностей школярами.
Завдання дослідження:
1. На основі аналізу наявної літератури на тему дослідження систематизувати матеріал.
2. Навести комплекс завдань, необхідний закріплення теми «Тригонометричні нерівності».
Об'єктом дослідження є тригонометричні нерівності у шкільному курсі математики.
Предмет дослідження: типи тригонометричних нерівностей та методи їх вирішення.
Теоретична значимість полягає у систематизації матеріалу.
Практична значимість: застосування теоретичних знань у вирішенні завдань; аналіз основних часто зустрічаються способів розв'язання тригонометричних нерівностей.
Методи дослідження : аналіз наукової літератури, синтез та узагальнення отриманих знань, аналіз вирішення завдань, пошук оптимального методу розв'язання нерівностей.
§1. Типи тригонометричних нерівностей та основні методи їх вирішення
1.1. Найпростіші тригонометричні нерівності
Два тригонометричні вирази, з'єднані між собою знаком або >, називаються тригонометричними нерівностями.
Вирішити тригонометричну нерівність – це означає, знайти безліч значень невідомих, які входять у нерівність, у яких нерівність виконується.
Основна частина тригонометричних нерівностей вирішується зведенням їх до вирішення найпростіших:
Це може бути метод розкладання на множники, заміни змінного ( 
, 
і т.д.), де спочатку вирішується звичайна нерівність, а потім нерівність виду 
і т.д., чи інші способи.
Найпростіші нерівності вирішуються двома способами: за допомогою одиничного кола або графічно.
Нехайf(х
- Одна з основних тригонометричних функцій. Для вирішення нерівності 
досить визначити його рішення одному періоді, тобто. на будь-якому відрізку, довжина якого дорівнює періоду функціїf
x
. Тоді рішенням вихідної нерівності будуть усі знайденіx
, і навіть ті значення, які від знайдених будь-яку цілу кількість періодів функції. У цьому зручно використовувати графічний метод.
Наведемо приклад алгоритму розв'язання нерівностей 
(
) та 
.
Алгоритм розв'язання нерівності (
).
1. Сформулюйте визначення синуса числаx на одиничному колі.
3. На осі ординат позначте крапку з координатоюa .
4. Через цю точку проведіть пряму, паралельну до осі OX, і позначте точки перетину її з колом.
5. Виділіть дугу кола, всі точки якого мають ординату, меншуa .
6. Вкажіть напрямок обходу (проти годинникової стрілки) та запишіть відповідь, додавши до кінців проміжку період функції2πn
,
.
Алгоритм розв'язання нерівності .
1. Сформулюйте визначення тангенсу числаx на одиничному колі.
2. Намалюйте одиничне коло.
3. Проведіть лінію тангенсів і позначте крапку з ординатоюa .
4. З'єднайте цю точку з початком координат і позначте точку перетину отриманого відрізка з одиничним колом.
5. Виділіть дугу кола, всі точки якого мають на лінії тангенсів ординату, меншуa .
6. Вкажіть напрямок обходу та запишіть відповідь з урахуванням області визначення функції, додавши періодπn
,
(число, що стоїть у записі зліва, завжди менше числа, що стоїть праворуч).
Графічна інтерпретація рішень найпростіших рівнянь та формули розв'язання нерівностей у загальному вигляді зазначені у додатку (Додатки 1 та 2).
приклад 1.
Розв'яжіть нерівність 
.
На одиничному колі проводимо пряму 
, яка перетинає коло в точках A та B.
Усі значенняy
на проміжку NM більше
, всі точки дуги AMB задовольняють цю нерівність. При всіх кутах повороту, великих 
, але менших 
,
прийматиме значення більше
(Але не більше одиниці).
Рис.1
Таким чином, розв'язанням нерівності будуть усі значення на інтервалі 
, тобто. 
. Для того, щоб отримати всі рішення цієї нерівності, достатньо до кінця цього проміжку додати 
, де 
, тобто. 
,
.
Зауважимо, що значення 
і 
є корінням рівняння 
,
тобто. 
;
.
Відповідь: 
, .
1.2. Графічний метод
Насправді досить часто виявляється корисним графічний спосіб розв'язання тригонометричних нерівностей. Розглянемо сутність методу з прикладу нерівності 
:
1. Якщо аргумент – складний (відмінний відх ), то замінюємо його наt .
2. Будуємо в одній координатній площиніtOy
графіки функцій 
і 
.
3. Знаходимо такідві сусідні точки перетину графіків, між якимисинусоїдарозташовуєтьсявище
прямий . Знаходимо абсциси цих точок.
4. Записуємо подвійну нерівність для аргументуt , враховуючи період косинуса (t буде між знайденими абсцисами).
5. Робимо зворотну заміну (повертаємося до початкового аргументу) та виражаємо значеннях з подвійної нерівності, записуємо відповідь у вигляді числового проміжку.
приклад 2. Вирішити нерівність: .
При розв'язанні нерівностей графічним методом необхідно якнайточніше побудувати графіки функцій. Перетворимо нерівність до виду:
Побудуємо в одній системі координат графіки функцій 
і 
(Рис. 2).
Рис.2
Графіки функцій перетинаються у точціА
з координатами 
; 
. На проміжку 
точки графіка 
нижче точок графіка 
. А при Значення функції збігаються. Тому при 
.
Відповідь: 
.
1.3. Алгебраїчний метод
Досить часто вихідна тригонометрична нерівність шляхом вдало обраної підстановки вдається звести до алгебраїчної (раціональної або ірраціональної) нерівності. Цей метод передбачає перетворення нерівності, введення підстановки чи заміну змінної.
Розглянемо на прикладах застосування цього методу.
приклад 3.
Приведення до найпростішого вигляду 
.
(Рис. 3)
Рис.3
, 
.
Відповідь: 
,
приклад 4. Вирішити нерівність:
ОДЗ: 
, 
.
Використовуючи формули: 
, 
запишемо нерівність у вигляді: 
.
Або, вважаючи 
після нескладних перетворень отримаємо
,
,
.
Вирішуючи останню нерівність методом інтервалів, отримуємо:
Рис.4
відповідно 
. Тоді із рис. 4 слід 
, де 
.
Рис.5
Відповідь: 
, 
.
1.4. Метод інтервалів
Загальна схема розв'язання тригонометричних нерівностей методом інтервалів:
За допомогою тригонометричних формул розкласти на множники.
Знайти точки розриву та нулі функції, поставити їх на коло.
Взяти будь-яку точкуДо (але не знайдену раніше) та з'ясувати знак твору. Якщо твір позитивно, то поставити крапку за одиничним колом на промені, що відповідає куту. Інакше точку поставити всередині кола.
Якщо точка зустрічається парне число разів, назвемо її точкою парної кратності, якщо непарне число разів – точкою непарної кратності. Провести дуги наступним чином: почати з точкиДо Якщо наступна точка непарної кратності, то дуга перетинає коло в цій точці, якщо ж точка парної кратності, то не перетинає.
Дуги за колом – позитивні проміжки; всередині кола - негативні проміжки.
Приклад 5. Розв'язати нерівність
, 
.
Крапки першої серії: 
.
Точки другої серії: 
.
Кожна точка зустрічається непарне число разів, тобто всі точки непарної кратності.
З'ясуємо знак твору при 
: . Зазначимо всі крапки на одиничному колі (рис.6):
Рис. 6
Відповідь: 
, 
; 
, 
; 
, 
.
Приклад 6 . Розв'яжіть нерівність.
Рішення:
Знайдемо нулі вирази .
Отримайaeм :
,
;
, 
;
, 
;
, 
;
На одиничному колі значення серіїх
1
представлені точками 
. Серіях
2
дає крапки 
. Із серіїх
3
отримуємо дві точки 
. Зрештою, серіюх
4
будуть представляти точки 
. Нанесемо всі ці крапки на одиничне коло, вказавши в дужках поруч із кожною їх кратність.
Нехай тепер число 
буде рівним. Робимо прикидку за знаком:
Значить, точкуA
слід вибрати на промені, що утворює кут 
з променемОх,
поза одиничного кола. (Зауважимо, що допоміжний проміньПро
A
зовсім не обов'язково зображати малюнку. КрапкаA
вибирається приблизно.)
Тепер від точкиA
ведемо хвилеподібну безперервну лінію послідовно до всіх зазначених точок. Причому в точках наша лінія переходить з однієї області в іншу: якщо вона знаходилася поза одиничним колом, то переходить усередину неї. Підійшовши до точки 
, Лінія повертається у внутрішню область, так як кратність цієї точки парна. Аналогічно у точці 
(з парною кратністю) лінію доводиться повернути до зовнішньої області. Отже, накреслили якусь картинку, зображену на рис. 7. Вона допомагає виділити на одиничному колі шукані області. Вони позначені знаком «+».
Рис.7
Остаточна відповідь:
Примітка. Якщо хвилеподібну лінію після обходу нею всіх зазначених на одиничному колі точок не вдається повернути до точкиA , не перетинаючи коло в «незаконному» місці, то це означає, що у рішенні допущено помилку, а саме пропущено непарну кількість коренів.
Відповідь: .
§2. Комплекс завдань щодо розв'язання тригонометричних нерівностей
У процесі формування у школярів умінь вирішувати тригонометричні нерівності, також можна виділити 3 етапи.
1. підготовчий,
2. формування умінь вирішувати найпростіші тригонометричні нерівності;
3. запровадження тригонометричних нерівностей інших видів.
Мета підготовчого етапу полягає в тому, що необхідно сформувати у школярів вміння використовувати тригонометричне коло або графік для вирішення нерівностей, а саме:
Вміння вирішувати найпростіші нерівності виду ,
, ,
,
за допомогою властивостей функцій синус та косинус;
Вміння складати подвійні нерівності для дуг числового кола або для дуг графіків функцій;
Вміння виконувати різні перетворення тригонометричних виразів.
Реалізувати цей етап рекомендується у процесі систематизації знань школярів про властивості тригонометричних функцій. Основним засобом можуть бути завдання, пропоновані учням і виконувані або під керівництвом вчителя, або самостійно, а як і навички напрацьовані під час вирішення тригонометричних рівнянь.
Наведемо приклади таких завдань:
1
. Позначте на одиничному колі крапку 
, якщо
.
2.
У якій чверті координатної площини розташована точка , якщо 
одно: 
3.
Позначте на тригонометричному колі точки , якщо:
4. Наведіть вираз до тригонометричних функційIчверті.
а) 
,
б) 
,
в) 
5. Дано дугу МР.М – серединаI-ї чверті,Р – серединаII-ї чверті. Обмежити значення змінноїt для: (скласти подвійну нерівність) а) дуги МР; б) дуги РМ.
6. Записати подвійну нерівність для виділених ділянок графіка:
Рис. 1
7.
Розв'яжіть нерівності 
, 
, 
, 
.
8. Перетворити вираз .
З другого краю етапі навчання розв'язання тригонометричних нерівностей можна запропонувати такі рекомендації, пов'язані з методикою організації діяльності учнів. При цьому потрібно орієнтуватися на вміння, що вже є у учнів, працювати з тригонометричним колом або графіком, сформовані під час вирішення найпростіших тригонометричних рівнянь.
По-перше, мотивувати доцільність отримання загального прийому вирішення найпростіших тригонометричних нерівностей можна, звернувшись, наприклад, до нерівності виду 
.
Використовуючи знання та вміння, набуті на підготовчому етапі, учні приведуть запропоновану нерівність до виду 
, але може бути важко знайти множини рішень отриманого нерівності, т.к. Тільки використовуючи властивості функції синус вирішити його неможливо. Ці труднощі можна уникнути, якщо звернутися до відповідної ілюстрації (рішення рівняння графічно або за допомогою одиничного кола).
По-друге, вчитель повинен звернути увагу учнів на різні способи виконання завдання, дати відповідний зразок вирішення нерівності та графічним способом та за допомогою тригонометричного кола.
Розглянемо такі варіанти розв'язання нерівності .
1. Вирішення нерівності за допомогою одиничного кола.
На першому занятті за розв'язанням тригонометричних нерівностей запропонуємо учням докладний алгоритм розв'язання, який у покроковому поданні відбиває всі основні вміння, необхідні вирішення нерівності.
Крок 1.Накреслимо одиничне коло, відзначимо на осі ординат крапку 
і проведемо через неї пряму, паралельну осі абсцис. Ця пряма перетне одиничне коло у двох точках. Кожна з цих точок зображує числа, синус яких дорівнює .
Крок 2Ця пряма розділила коло на дві дуги. Виділимо ту їх, де зображуються числа, мають синус більший, ніж . Звичайно, ця дуга розташована вище проведеної прямої.
Рис. 2
Крок 3Виберемо один із кінців зазначеної дуги. Запишемо одне з чисел, яке зображується цією точкою одиничного кола 
.
Крок 4.Для того щоб вибрати число, що відповідає другому кінцю виділеної дуги, "пройдемо" цією дугою з названого кінця до іншого. При цьому нагадаємо, що при русі проти годинникової стрілки числа, які ми проходитимемо, збільшуються (при русі в протилежному напрямку числа б зменшувалися). Запишемо число, яке зображується на одиничному колі другим кінцем зазначеної дуги 
.
Таким чином, ми бачимо, що нерівність задовольняють числа, котрим справедлива нерівність 
. Ми вирішили нерівність для чисел, що розташовані на одному періоді функції синус. Тому всі рішення нерівності можуть бути записані у вигляді 
Учням потрібно запропонувати уважно розглянути малюнок та розібратися, чому всі рішення нерівності можуть бути записані у вигляді 
, 
.
Рис. 3
Необхідно звернути увагу учнів те що, що за розв'язання нерівностей для функції косинус, пряму проводимо паралельно осі ординат.
Графічний спосіб розв'язання нерівності.
Будуємо графіки 
і 
, враховуючи що 
.
Рис. 4
Потім записуємо рівняння 
та його рішення 
, 
, 
, знайдене за допомогою формул 
, 
, 
.
(Надаючиn
значення 0, 1, 2, знаходимо три корені складеного рівняння). Значення 
є трьома послідовними абсцисами точок перетину графіків і . Очевидно, що завжди на інтервалі 
виконується нерівність 
, а на інтервалі 
– нерівність 
. Нас цікавить перший випадок, і тоді додавши до кінців цього проміжку число, кратне періоду синуса, отримаємо розв'язання нерівності у вигляді: 
, .
Рис. 5
Підведемо підсумок. Щоб вирішити нерівність , Треба скласти відповідне рівняння та вирішити його. З отриманої формули знайти коріння 
і 
, і записати відповідь нерівності у вигляді: , .
По-третє, факт безлічі коренів відповідного тригонометричного нерівності дуже наочно підтверджується під час вирішення його графічним способом.
Рис. 6
Необхідно продемонструвати учням, що виток, який є розв'язком нерівності, повторюється через один і той же проміжок, що дорівнює періоду тригонометричної функції. Також можна розглянути аналогічну ілюстрацію для графіка функції синус.
По-четверте, доцільно провести роботу з актуалізації в учнів прийомів перетворення суми (різниці) тригонометричних функцій на твір, звернути увагу школярів на роль цих прийомів під час вирішення тригонометричних нерівностей.
Організувати таку роботу можна через самостійне виконання учнями запропонованих вчителем завдань, серед яких виділимо такі:
По-п'яте, від учнів необхідно вимагати обов'язкової ілюстрації розв'язання кожної найпростішої тригонометричної нерівності за допомогою графіка або тригонометричного кола. Обов'язково слід звернути увагу на її доцільність, особливо на застосування кола, тому що при розв'язанні тригонометричних нерівностей відповідна ілюстрація є дуже зручним засобом фіксації множини рішень даної нерівності.
Знайомство учнів із прийомами розв'язання тригонометричних нерівностей, які є найпростішими, доцільно здійснювати за такою схемою: звернення до конкретному тригонометричному нерівності звернення до відповідного тригонометричного рівняння спільний пошук (вчитель – учні) прийому рішення самостійне перенесення знайденого прийому.
Щоб систематизувати знання учнів про тригонометрію, рекомендуємо спеціально підібрати такі нерівності, розв'язання яких потребує різних перетворень, які можуть бути реалізовані в процесі його вирішення, акцентувати учнів на їх особливостях.
Як такі продуктивні нерівності можна запропонувати, наприклад, такі:
На закінчення наведемо приклад комплексу завдань щодо розв'язання тригонометричних нерівностей.
1. Розв'яжіть нерівності:
2. Розв'яжіть нерівності: 3. Знайдіть усі розв'язки нерівностей: 4. Знайдіть усі розв'язки нерівностей:а) 
, які задовольняють умові 
;
б) 
, які задовольняють умові 
.
5. Знайдіть усі розв'язки нерівностей:
а) ;
б) ;
в) 
;
г) 
;
д) 
.
6. Розв'яжіть нерівності:
а) ;
б) ;
в);
г) 
;
д);
е);
ж) 
.
7. Розв'яжіть нерівності:
а) 
;
б) ;
в);
г).
8. Розв'яжіть нерівності:
а) ;
б) ;
в);
г) 
;
д) 
;
е);
ж) 
;
з).
Завдання 6 та 7 доцільно запропонувати учням, які вивчають математику на підвищеному рівні, завдання 8 – учням класів із поглибленим вивченням математики.
§3. Спеціальні методи розв'язання тригонометричних нерівностей
Спеціальні методи розв'язання тригонометричних рівнянь - тобто ті методи, які можна використовувати тільки для розв'язання тригонометричних рівнянь. Ці методи ґрунтуються на використанні властивостей тригонометричних функцій, а також на використанні різних тригонометричних формул та тотожностей.
3.1. Метод секторів
Розглянемо метод секторів на вирішення тригонометричних нерівностей. Вирішення нерівностей виду 
, деP
(
x
)
іQ
(
x
)
– раціональні тригонометричні функції (синуси, косинуси, тангенси та котангенси входять до них раціонально), аналогічно рішенню раціональних нерівностей. Раціональні нерівності зручно вирішувати методом інтервалів на числовій осі. Його аналогом при вирішенні раціональних тригонометричних нерівностей є метод секторів у тригонометричному колі,sinx
іcosx
(
) або тригонометричному півкрузі дляtgx
іctgx
(
).
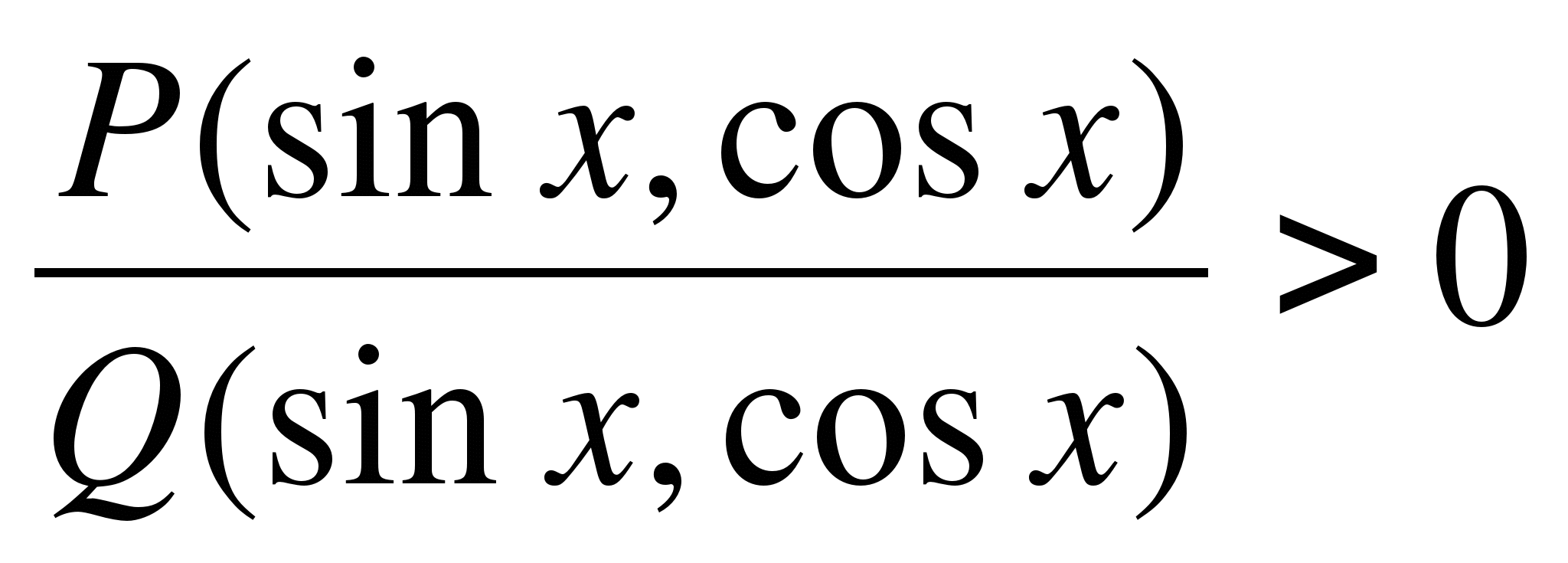
У методі інтервалів кожному лінійному множнику чисельника та знаменника виду 
на числовій осі відповідає точка 
, і при переході через цю точку змінює знак. У методі секторів кожному множнику виду 
, де 
- одна з функційsinx
абоcosx
і 
, у тригонометричному колі відповідають два кути. 
і 
які ділять коло на два сектори. При переході через і функція змінює знак.
Необхідно пам'ятати таке:
а) Множники виду 
і 
, де 
, зберігають знак для всіх значень 
. Такі множники чисельника та знаменника відкидають, змінюючи (якщо 
) при кожному такому відкиданні знак нерівності на протилежний.
б) Множники виду 
і 
також відкидаються. При цьому, якщо це множники знаменника, то до еквівалентної системи нерівностей додаються нерівності виду 
і 
. Якщо це множники чисельника, то в еквівалентній системі обмежень їм відповідають нерівності і у разі суворої вихідної нерівності та рівності 
і 
у разі не суворої вихідної нерівності. При відкиданні множника 
або 
знак нерівності змінюється протилежний.
приклад 1.
Вирішити нерівності: а) 
, б) 
.
маємо функція; б) . Розв'язати нерівність Маємо,
3.2. Метод концентричних кіл
Цей метод є аналогом методу паралельних числових осей під час вирішення систем раціональних нерівностей.
Розглянемо приклад системи нерівностей.
Приклад 5.
Вирішити систему найпростіших тригонометричних нерівностей 
Спочатку вирішимо кожну нерівність окремо (рисунок 5). У правому верхньому кутку малюнка будемо вказувати для якого аргументу розглядається тригонометричне коло.
Рис.5
Далі будуємо систему концентричних кіл для аргументух . Малюємо коло і заштриховуємо його згідно з рішенням першої нерівності, потім малюємо коло більшого радіусу і заштриховуємо його згідно з рішенням другого, далі будуємо коло для третьої нерівності та базове коло. З центру системи через кінці дуг проводимо промені так, щоб вони перетинали всі кола. На базовому колі формуємо рішення (рисунок 6).
Рис.6
Відповідь:
, 
.
Висновок
Усі завдання курсового дослідження було виконано. Систематизовано теоретичний матеріал: наведено основні типи тригонометричних нерівностей та основні методи їх вирішення (графічний, алгебраїчний, метод інтервалів, секторів та метод концентричних кіл). До кожного методу було наведено приклад розв'язання нерівності. За теоретичною частиною слідувала практична. У ній складено комплекс завдань у вирішенні тригонометричних нерівностей.
Ця курсова може бути використана учнями для самостійної роботи. Школярі можуть проконтролювати рівень засвоєння цієї теми, потренуватися у виконанні завдань різної складності.
Пропрацювавши відповідну літературу з цього питання, очевидно, можна дійти невтішного висновку у тому, що вміння і навички вирішувати тригонометричні нерівності у шкільному курсі алгебри і почав аналізу є дуже важливими, розвиток яких потребує значних зусиль з боку вчителя математики.
Тому дана робота буде корисна вчителям математики, оскільки дає можливість ефективно організувати підготовку учнів на тему «Тригонометричні нерівності».
Дослідження можна продовжити, розширивши його до випускної кваліфікаційної роботи.
Список використаної літератури
Богомолов, Н.В. Збірник завдань з математики [Текст]/Н.В. Богомолов. - М.: Дрофа, 2009. - 206 с.
Вигодський, М.Я. Довідник з елементарної математики [Текст]/М.Я. Вигодський. - М.: Дрофа, 2006. - 509 с.
Журбенка, Л.М. Математика в прикладах та завданнях [Текст] / Л.М. Журбенка. - М.: Інфра-М, 2009. - 373 с.
Іванов, О.А. Елементарна математика для школярів, студентів та викладачів [Текст]/О.А. Іванов. - М.: МЦНМО, 2009. - 384 с.
Карп, А.П. Завдання з алгебри та початків аналізу для організації підсумкового повторення та проведення атестації в 11 класі [Текст]/А.П. Короп. - М.: Просвітництво, 2005. - 79 с.
Куланін, О.Д. 3000 конкурсних завдань з математики [Текст]/Є.Д. Куланін. - М.: Айріс-прес, 2007. - 624 с.
Лейбсон, К.Л. Збірник практичних завдань з математики [Текст]/К.Л. Лейбсон. - М.: Дрофа, 2010. - 182 с.
Лікоть, В.В. Завдання з параметрами та їх вирішення. Тригонометрія: рівняння, нерівності, системи. 10 клас [Текст]/В.В. Лікоть. - М.: АРКТІ, 2008. - 64 с.
Манова, О.М. Математика. Експрес-репетитор для підготовки до ЄДІ: навч. посібник [Текст]/О.М. Манова. - Ростов-на-Дону: Фенікс, 2012. - 541 с.
Мордковіч, А.Г. Алгебра та початку математичного аналізу. 10-11 класи. Підручник для учнів загальноосвітніх установ [Текст]/А.Г. Мордкович. - М.: Айріс-прес, 2009. - 201 с.
Новіков, А.І. Тригонометричні функції, рівняння та нерівності [Текст]/А.І. Новіков. - М.: ФІЗМАТЛІТ, 2010. - 260 с.
Оганесян, В.А. Методика викладання математики у неповній середній школі: Загальна методика. Навч. посібник для студентів фіз. - мат. фак. пед. ін-тов. [Текст]/В.А. Оганесян. - М.: Просвітництво, 2006. - 368 с.
Олехнік, С.М. Рівняння та нерівності. Нестандартні методи вирішення [Текст]/С.М. Олехник. - М.: Вид-во Факторіал, 1997. - 219 с.
Севрюков, П.Ф. Тригонометричні, показові та логарифмічні рівняння та нерівності [Текст] / П.Ф. Севрюків. - М.: Народна освіта, 2008. - 352 с.
Сергєєв, І.М. ЄДІ: 1000 завдань з відповідями та рішеннями з математики. Усі завдання групи С [Текст]/І.М. Сергєєв. - М.: Іспит, 2012. - 301 с.
Соболєв, А.Б. Елементарна математика [Текст]/А.Б. Соболєв. - Єкатеринбург: ГОУ ВПО УГТУ-УПІ, 2005. - 81 с.
Фенько, Л.М. Метод інтервалів у вирішенні нерівностей та дослідженні функцій [Текст]/Л.М. Фенько. - М.: Дрофа, 2005. - 124 с.
Фрідман, Л.М. Теоретичні засади методики навчання математики [Текст]/Л.М. Фрідман. - М.: Книжковий дім «ЛІБРОКОМ», 2009. - 248 с.
Додаток 1
Графічна інтерпретація рішень найпростіших нерівностей
Рис. 1
Рис. 2
Рис.3
Рис.4
Рис.5
Рис.6
Рис.7
Рис.8
Додаток 2
Вирішення найпростіших нерівностей
