Trigonometrik tengsizliklar. Trigonometrik tengsizliklar va ularning yechimlari Ikki tomonlama trigonometrik tengsizliklarni yechish usullari
Belarus Respublikasi Ta'lim vazirligi
ta'lim muassasasi
"Gomel davlat universiteti
Fransisk Skarina nomi bilan atalgan.
Matematika fakulteti
Algebra va geometriya kafedrasi
Himoya qilish huquqiga ega
Bosh Kafedra Shemetkov L.A.
Trigonometrik tenglamalar va tengsizliklar
Kurs ishi
Ijrochi:
talabalar guruhi M-51
SM. Gorskiy
Ilmiy maslahatchi
Katta o‘qituvchi
V.G. Safonov
Gomel 2008 yil
KIRISH
TRIGONOMETRIK TENGLAMALARNI YECHISHNING ASOSIY USULLARI
Faktorizatsiya
Trigonometrik funksiyalarning ko`paytmasini yig`indiga aylantirish orqali tenglamalarni yechish
Uch argumentli formulalar yordamida tenglamalarni yechish
Ayrim trigonometrik funktsiyaga ko'paytirish
NOSTANDART TRIGONOMETRİK TENGLAMALAR
TRIGONOMETRIK TENGSIZLIKLAR
ILDIZLARNI TANLASH
MUSTAQIL YECHI UCHUN VAZIFALAR
XULOSA
FOYDALANILGAN MANBALAR RO'YXATI
Qadim zamonlarda trigonometriya astronomiya, geodeziya va qurilish ehtiyojlari bilan bog'liq holda paydo bo'lgan, ya'ni u sof geometrik xususiyatga ega bo'lgan va asosan ifodalangan.<<исчисление хорд>>. Vaqt o'tishi bilan ba'zi tahliliy fikrlar unga aralasha boshladi. 18-asrning birinchi yarmida keskin burilish yuz berdi, shundan soʻng trigonometriya yangi yoʻnalish oldi va matematik analizga oʻtdi. Aynan shu davrda trigonometrik bog'liqliklar funksiyalar sifatida ko'rib chiqila boshlandi.
Trigonometrik tenglamalar maktab matematika kursining eng qiyin mavzularidan biridir. Trigonometrik tenglamalar planimetriya, qattiq geometriya, astronomiya, fizika va boshqa sohalarga oid masalalarni yechishda yuzaga keladi. Trigonometrik tenglamalar va tengsizliklar yildan-yilga markazlashgan test vazifalari orasida topiladi.
Trigonometrik va algebraik tenglamalarning eng muhim farqi shundaki, algebraik tenglamalar chekli sonli ildizlarga ega, trigonometrik tenglamalar esa cheksiz songa ega, bu esa ildizlarni tanlashni ancha murakkablashtiradi. Trigonometrik tenglamalarning yana bir o'ziga xos xususiyati javob yozishning o'ziga xos bo'lmagan shaklidir.
Ushbu tezis trigonometrik tenglamalar va tengsizliklarni yechish usullariga bag'ishlangan.
Diplom ishi 6 bo'limdan iborat.
Birinchi bo'limda asosiy nazariy ma'lumotlar mavjud: trigonometrik va teskari trigonometrik funktsiyalarning ta'rifi va xossalari; ba'zi argumentlar uchun trigonometrik funktsiyalar qiymatlari jadvali; trigonometrik funktsiyalarni boshqa trigonometrik funktsiyalar bilan ifodalash, bu trigonometrik ifodalarni, ayniqsa teskari trigonometrik funktsiyalarni o'z ichiga olganlarni aylantirish uchun juda muhimdir; maktab kursidan yaxshi ma'lum bo'lgan asosiy trigonometrik formulalarga qo'shimcha ravishda, teskari trigonometrik funktsiyalarni o'z ichiga olgan ifodalarni soddalashtiradigan formulalar berilgan.
Ikkinchi bo'limda trigonometrik tenglamalarni yechishning asosiy usullari ko'rsatilgan. Elementar trigonometrik tenglamalarni yechish, faktoring usuli, trigonometrik tenglamalarni algebraik tenglamalarga keltirish usullari ko'rib chiqiladi. Trigonometrik tenglamalar yechimlari bir necha usulda yozilishi mumkinligini va bu yechimlarning shakli bu yechimlarning bir xil yoki boshqacha ekanligini darhol aniqlashga imkon bermaydi.<<сбить с толку>> testlarni yechishda trigonometrik tenglamalarni yechishning umumiy sxemasi ko'rib chiqiladi va trigonometrik tenglamalarning umumiy yechimlari guruhlarini o'zgartirish batafsil ko'rib chiqiladi.
Uchinchi bo'limda nostandart trigonometrik tenglamalar ko'rib chiqiladi, ularning echimlari funktsional yondashuvga asoslangan.
To'rtinchi bo'lim trigonometrik tengsizliklar bilan bog'liq. Elementar trigonometrik tengsizliklarni birlik aylanada ham, grafik usulda ham yechish usullari batafsil ko‘rib chiqiladi. Elementar bo'lmagan trigonometrik tengsizliklarni elementar tengsizliklar orqali yechish jarayoni va maktab o'quvchilariga allaqachon yaxshi ma'lum bo'lgan intervallar usuli tasvirlangan.
Beshinchi bo'lim eng qiyin vazifalarni taqdim etadi: faqat trigonometrik tenglamani yechish kerak bo'lganda, balki topilgan ildizlardan biron bir shartni qondiradigan ildizlarni tanlash kerak bo'lganda. Ushbu bo'lim ildizlarni tanlash uchun odatiy vazifalarni hal qiladi. Ildizlarni tanlash uchun zaruriy nazariy ma'lumotlar berilgan: butun sonlar to'plamini kesishmaydigan kichik to'plamlarga bo'lish, butun sonlarda tenglamalarni yechish (diofantin).
Oltinchi bo'limda test shaklida ishlab chiqilgan mustaqil hal qilish uchun topshiriqlar keltirilgan. 20 ta test topshiriqlarida markazlashtirilgan test sinovlarida duch keladigan eng qiyin vazifalar sanab o‘tilgan.
Elementar trigonometrik tenglamalar
Elementar trigonometrik tenglamalar ko'rinishdagi tenglamalar bo'lib, bu erda trigonometrik funksiyalardan biri: , , , .
Elementar trigonometrik tenglamalar cheksiz ko'p ildizlarga ega. Masalan, quyidagi qiymatlar tenglamani qanoatlantiradi: , , , va hokazo. Tenglamaning barcha ildizlari topiladigan umumiy formula, bu erda ,:
Bu erda u har qanday butun qiymatlarni qabul qilishi mumkin, ularning har biri tenglamaning ma'lum bir ildiziga mos keladi; bu formulada (shuningdek, elementar trigonometrik tenglamalar yechiladigan boshqa formulalarda) deyiladi. parametr. Ular odatda yozib oladilar va shu bilan parametr har qanday butun qiymatlarni qabul qilishi mumkinligini ta'kidlaydilar.
Tenglamaning yechimlari , bu erda , formula bo'yicha topiladi
Tenglama formulani qo'llash orqali echiladi
va tenglama --- formula bo'yicha
Elementar trigonometrik tenglamalarning ba'zi maxsus holatlariga alohida e'tibor qaratamiz, bunda yechim umumiy formulalarsiz yozilishi mumkin:
Trigonometrik tenglamalarni yechishda trigonometrik funksiyalar davri muhim rol o'ynaydi. Shuning uchun biz ikkita foydali teoremani keltiramiz:
Teorema Agar --- funktsiyaning bosh davri bo'lsa, u holda son funktsiyaning bosh davri hisoblanadi.
Funksiyalarning davrlari va agar natural sonlar mavjud bo'lsa, mutanosib deb ataladi va , bu .
Teorema Agar davriy funksiyalar va , mutanosib va ga ega bo lsa, u holda ular umumiy davrga ega bo lib, bu funksiyalarning davri , , .
Teorema , , , funksiyaning davri nima ekanligini aytadi va asosiy davr bo'lishi shart emas. Masalan, va funksiyalarining bosh davri --- , ularning hosilasining bosh davri esa --- dir.
Yordamchi dalil bilan tanishtirish
Shakl ifodalarini konvertatsiya qilishning standart usuli 
quyidagi nayrangdir: --- tenglik bilan berilgan burchak bo'lsin 
, 
. Har qanday va bunday burchak uchun mavjud. Shunday qilib . Agar , yoki , , , aks holda.
Trigonometrik tenglamalarni yechish sxemasi
Trigonometrik tenglamalarni echishda biz rahbarlik qiladigan asosiy sxema quyidagicha:
berilgan tenglamaning yechimi elementar tenglamalar yechimiga keltiriladi. Yechimlar --- o'zgartirishlar, faktorlarga ajratish, noma'lumlarni almashtirish. Asosiy tamoyil - ildizlarni yo'qotmaslik. Bu shuni anglatadiki, keyingi tenglamaga (tenglamalarga) o'tishda biz qo'shimcha (tashqi) ildizlarning paydo bo'lishidan qo'rqmaymiz, lekin biz faqat "zanjir" ning har bir keyingi tenglamasi (yoki tenglamalar to'plami) haqida qayg'uramiz. shoxlanish) oldingisining natijasidir. Ildizlarni tanlashning mumkin bo'lgan usullaridan biri tekshirishdir. Darhol shuni ta'kidlaymizki, trigonometrik tenglamalarda ildizlarni tanlash, tekshirish bilan bog'liq qiyinchiliklar, qoida tariqasida, algebraik tenglamalarga nisbatan keskin ortadi. Axir siz cheksiz ko'p a'zolardan iborat seriyani tekshirishingiz kerak.
Trigonometrik tenglamalarni yechishda noma'lumlarning o'zgarishini alohida ta'kidlab o'tish kerak. Ko'pgina hollarda, kerakli almashtirishdan so'ng, algebraik tenglama olinadi. Bundan tashqari, tenglamalar juda kam uchraydi, ular trigonometrik ko'rinishga ega bo'lsa-da, aslida bunday emas, chunki birinchi bosqichdan keyin --- o'zgaruvchilarning o'zgarishi ---- algebraiklarga aylanadi va trigonometriyaga qaytish faqat sahnada sodir bo'ladi. elementar trigonometrik tenglamalarni yechish.
Yana bir bor eslatib o'tamiz: noma'lumni almashtirish imkon qadar tezroq amalga oshirilishi kerak, almashtirishdan keyin olingan tenglama oxirigacha, shu jumladan ildizlarni tanlash bosqichida hal qilinishi kerak va shundan keyingina u asl holatiga qaytadi. noma'lum.
Trigonometrik tenglamalarning xususiyatlaridan biri shundaki, ko'p hollarda javob turli yo'llar bilan yozilishi mumkin. Hatto tenglamani yechish uchun ham 
javob quyidagicha yozilishi mumkin:
1) ikki qator shaklida: 
, , ;
2) yuqoridagi qatorlar birlashmasi bo'lgan standart shaklda: , ;
3) beri 
, keyin javob quyidagicha yozilishi mumkin 
, . (Keyinchalik, javob yozuvida , yoki parametrining mavjudligi avtomatik ravishda bu parametr barcha mumkin bo'lgan butun qiymatlarni qabul qilishini bildiradi. Istisnolar ko'zda tutiladi.)
Shubhasiz, sanab o'tilgan uchta holat ko'rib chiqilayotgan tenglamaga javob yozish uchun barcha imkoniyatlarni tugatmaydi (ularning cheksiz ko'pi bor).
Masalan, uchun 
. Shuning uchun, birinchi ikki holatda, agar , bilan almashtira olamiz .
Odatda, javob 2-band asosida yoziladi. Quyidagi tavsiyani eslash foydali bo'ladi: agar ish tenglamaning echimi bilan tugamasa, hali ham tadqiqot o'tkazish, ildizlarni tanlash kerak, keyin ro'yxatga olishning eng qulay shakli 1-bandda ko'rsatilgan. (Tenglama uchun shunga o'xshash tavsiyalar berilishi kerak).
Keling, aytilganlarni ko'rsatadigan misolni ko'rib chiqaylik.
Misol Tenglamani yeching.
Yechim. Eng aniq - quyidagi yo'l. Bu tenglama ikkiga bo'linadi: va . Ularning har birini yechish va olingan javoblarni birlashtirib, biz topamiz.
Boshqa yo'l. dan beri, keyin, almashtirish va kamaytirish formulalari bilan. Kichkina o'zgarishlardan so'ng, biz qaerdan olamiz 
.
Bir qarashda, ikkinchi formula birinchisiga nisbatan alohida afzalliklarga ega emas. Biroq, masalan, ni oladigan bo'lsak, ma'lum bo'ladiki, , ya'ni. tenglamaning yechimi bor, birinchi yo'l esa bizni javobga olib boradi 
. "Ko'ring" va tenglikni isbotlang 
unchalik oson emas.
Javob. .
Trigonometrik tenglamalarning umumiy yechimlari guruhlarini o'zgartirish va birlashtirish
Ikkala yo'nalishda ham cheksiz cho'ziladigan arifmetik progressiyani ko'rib chiqamiz. Ushbu progressiyaning shartlarini progressiyaning markaziy yoki nol hadi deb ataladigan ma'lum bir haddan o'ng va chap tomonda joylashgan ikkita atama guruhiga bo'lish mumkin.
Cheksiz progressiyaning shartlaridan birini nol raqam bilan belgilab, qolgan barcha a'zolar uchun ikkita raqamlashni amalga oshirishimiz kerak bo'ladi: o'ngda joylashgan atamalar uchun ijobiy va nolning chap tomonida joylashgan hadlar uchun salbiy.
Umumiy holatda, progressiyaning ayirmasi nol had bo'lsa, cheksiz arifmetik progressiyaning istalgan (inchi) hadi uchun formula:
Cheksiz arifmetik progressiyaning istalgan a'zosi uchun formulalarni o'zgartirish
1. Agar progressiyaning ayirmasini nol hadga qo’shsak yoki ayirasak, bundan progressiya o’zgarmaydi, faqat nol had harakat qiladi, ya’ni. a'zolarning raqamlanishi o'zgaradi.
2. Agar o'zgaruvchining koeffitsienti ga ko'paytirilsa, bu faqat a'zolarning o'ng va chap guruhlarini almashtirishga olib keladi.
3. Cheksiz progressiyaning ketma-ket a'zolari bo'lsa
masalan , , , ..., , bir xil farqli progressiyalarning markaziy hadlarini quyidagiga teng qilish uchun:
keyin progressiya va progressiyalar qatori bir xil sonlarni ifodalaydi.
Misol Qator quyidagi uchta qator bilan almashtirilishi mumkin: , , .
4. Agar ayirmasi bir xil boʻlgan cheksiz progressiyalar ayirmali arifmetik progressiyani tashkil etuvchi markaziy aʼzolar kabi raqamlarga ega boʻlsa, bu qatorlar ayirmali bitta progressiyaga va shularning markaziy aʼzolaridan biriga teng boʻlgan markaziy aʼzo bilan almashtirilishi mumkin. progressiyalar, ya'ni. agar
keyin bu progressiyalar bittaga birlashtiriladi:
Misol
, , , ikkalasi bir guruhga birlashtiriladi, chunki 
.
Umumiy yechimga ega bo'lgan guruhlarni umumiy yechimga ega bo'lmagan guruhlarga aylantirish uchun bu guruhlar umumiy davrga ega bo'lgan guruhlarga bo'linadi, so'ngra takrorlanuvchilarni hisobga olmaganda, hosil bo'lgan guruhlarni birlashtirishga harakat qilamiz.
Faktorizatsiya
Faktorizatsiya usuli quyidagicha: agar
keyin tenglamaning istalgan yechimi
tenglamalar to‘plamining yechimidir
Qarama-qarshi bayonot, umuman olganda, noto'g'ri: to'plamning har bir yechimi tenglamaning yechimi emas. Buning sababi, individual tenglamalar yechimlari funksiyani aniqlash sohasiga kiritilmasligi mumkin.
Misol Tenglamani yeching.
Yechim. Asosiy trigonometrik identifikatsiyadan foydalanib, biz tenglamani shaklda ifodalaymiz
Javob.
; 
.
Trigonometrik funktsiyalar yig'indisini mahsulotga aylantirish
Misol
tenglamani yeching 
.
Yechim. Biz formulani qo'llaymiz, ekvivalent tenglamani olamiz
Javob. .
Misol Tenglamani yeching.
Yechim. Bunday holda, trigonometrik funktsiyalar yig'indisi uchun formulalarni qo'llashdan oldin siz qisqartirish formulasidan foydalanishingiz kerak. 
. Natijada ekvivalent tenglamani olamiz
Javob.
, 
.
Trigonometrik funksiyalarning ko`paytmasini yig`indiga aylantirish orqali tenglamalarni yechish
Bir qator tenglamalarni yechishda formulalardan foydalaniladi.
Misol tenglamani yeching
Yechim.
Javob. , .
Misol Tenglamani yeching.
Yechim. Formuladan foydalanib, biz ekvivalent tenglamani olamiz:
Javob. .
Tenglamalarni kamaytirish formulalari yordamida yechish
Keng doiradagi trigonometrik tenglamalarni yechishda formulalar asosiy rol o‘ynaydi.
Misol Tenglamani yeching.
Yechim. Formulani qo'llash orqali biz ekvivalent tenglamani olamiz.
Javob. ; .
Uch argumentli formulalar yordamida tenglamalarni yechish
Misol Tenglamani yeching.
Yechim. Biz formulani qo'llaymiz, biz tenglamani olamiz
Javob. ; .
Misol
tenglamani yeching 
.
Yechim. Darajani pasaytirish uchun formulalarni qo'llash orqali biz quyidagilarni olamiz: 
. Qo'llash orqali biz quyidagilarni olamiz:
Javob. ; .
Xuddi shu nomdagi trigonometrik funksiyalarning tengligi
Misol Tenglamani yeching.
Yechim.
Javob. , .
Misol
tenglamani yeching 
.
Yechim. Keling, tenglamani aylantiramiz.
Javob. .
Misol Ma'lumki va tenglamani qanoatlantiring
Yig'indini toping.
Yechim. Bu tenglamadan kelib chiqadi
Javob. .
Shakl summalarini ko'rib chiqing
Ushbu summalarni ko'paytirish va bo'lish orqali mahsulotga aylantirish mumkin, keyin biz olamiz
Ushbu texnikadan ba'zi trigonometrik tenglamalarni echishda foydalanish mumkin, ammo buning natijasida begona ildizlar paydo bo'lishi mumkinligini yodda tutish kerak. Mana bu formulalarning umumlashtirilishi:
Misol Tenglamani yeching.
Yechim. Ko'rinib turibdiki, to'plam dastlabki tenglamaning yechimi hisoblanadi. Shuning uchun tenglamaning chap va o'ng tomonlarini ko'paytirish ortiqcha ildizlarning paydo bo'lishiga olib kelmaydi.
Bizda ... bor 
.
Javob. ; .
Misol Tenglamani yeching.
Yechim. Biz tenglamaning chap va o'ng tomonlarini ko'paytiramiz va trigonometrik funktsiyalar mahsulotini yig'indiga aylantirish uchun formulalarni qo'llaymiz, biz olamiz
Bu tenglama ikkita tenglamalar to'plamiga ekvivalent va , buning uchun va.
Tenglamaning ildizlari tenglamaning ildizlari bo'lmaganligi sababli, natijada olingan echimlar to'plamidan chiqarib tashlash kerak. Shunday qilib, to'plamda siz istisno qilishingiz kerak.
Javob. va , .
Misol
tenglamani yeching 
.
Yechim. Keling, ifodani o'zgartiramiz:
Tenglama quyidagi shaklda yoziladi:
Javob. .
Trigonometrik tenglamalarni algebraik tenglamalarga keltirish
Kvadratga qisqartirish
Agar tenglama o'xshash bo'lsa
keyin almashtirish kvadratga olib keladi, chunki 
() va.
Agar muddat o'rniga mavjud bo'lsa, unda kerakli almashtirish bo'ladi.
Tenglama
kvadrat tenglamaga qisqartiradi
sifatida taqdimot 
. Qaysi biri tenglamaning ildizi emasligini tekshirish oson va o'zgartirishni amalga oshirib, tenglama kvadratik tenglamaga keltiriladi.
Misol Tenglamani yeching.
Yechim. Keling, uni chap tomonga o'tkazamiz, uni bilan almashtiramiz va va orqali ifodalaymiz.
Soddalashtirilgandan so'ng biz quyidagilarni olamiz: . Atamani atama ga ajrating, almashtirishni bajaring:
ga qaytsak, topamiz 
.
ga nisbatan bir jinsli tenglamalar,
Shaklning tenglamasini ko'rib chiqing
bu yerda , , , ..., , haqiqiy sonlar. Tenglamaning chap tomonidagi har bir hadda monomiallarning darajalari teng, ya'ni sinus va kosinus darajalarining yig'indisi bir xil va tengdir. Bunday tenglama deyiladi bir hil va ga nisbatan va raqam chaqiriladi bir xillik ko'rsatkichi .
Ma'lumki, agar bo'lsa, tenglama quyidagi shaklni oladi:
ularning yechimlari qiymatlari bo'lgan qiymatlar, ya'ni raqamlar. Qavs ichida yozilgan ikkinchi tenglama ham bir hil, ammo darajalar 1 ga pastroq.
Agar bo'lsa, bu raqamlar tenglamaning ildizi emas.
Qachonki: , va tenglamaning chap tomoni (1) qiymatini oladi.
Demak, uchun, va, demak, tenglamaning ikkala tomonini ga bo’lish mumkin. Natijada biz tenglamani olamiz:
Bu almashtirish orqali algebraikga osonlikcha tushiriladi:
Bir jinslilik indeksli bir jinsli tenglamalar 1. At , bizda tenglama mavjud.
Agar , u holda bu tenglama , , qaerdan , tenglamasiga ekvivalentdir.
Misol Tenglamani yeching.
Yechim. Bu tenglama birinchi darajali bir hildir. Uning ikkala qismini ga ajratsak: , , , .
Javob. .
Misol da, shaklning bir jinsli tenglamasini olamiz
Yechim.
Agar bo'lsa, tenglamaning ikkala tomonini ga bo'lsak, tenglamani olamiz 
, uni almashtirish orqali osongina kvadratga qisqartirish mumkin: 
. Agar a 
, u holda tenglama haqiqiy ildizlarga ega bo'ladi, . Dastlabki tenglama ikkita yechim guruhiga ega bo'ladi: , , .
Agar a 
, u holda tenglamaning yechimlari yo'q.
Misol Tenglamani yeching.
Yechim. Bu tenglama ikkinchi darajali bir hildir. Tenglamaning ikkala tomonini ga ajratsak, quyidagilarga erishamiz: . Keling, keyin, , . , , ; , , .
Javob.
.
Tenglama shakldagi tenglamaga keltiriladi
Buning uchun identifikatsiyadan foydalanish kifoya 
Xususan, tenglama bilan almashtirilsa, bir hil tenglamaga kamayadi 
, keyin biz ekvivalent tenglamani olamiz:
Misol Tenglamani yeching.
Yechim. Keling, tenglamani bir hil tenglamaga aylantiramiz:
Tenglamaning ikkala tomonini ga bo'ling 
, biz tenglamani olamiz:
, keyin kvadrat tenglamaga kelamiz: 
, , 
, 
, .
Javob.
.
Misol Tenglamani yeching.
Yechim. Tenglamaning ikkala tomonini kvadratga aylantiramiz, ularning ijobiy qiymatlari bor: , ,
Mayli, keyin olamiz 
, , .
Javob. .
Identifikatsiyalar yordamida yechilgan tenglamalar 
Quyidagi formulalarni bilish foydalidir:
Misol Tenglamani yeching.
Yechim. Foydalanish, biz olamiz
Javob.
Biz formulalarning o'zini emas, balki ularni olish yo'lini taklif qilamiz:
Binobarin,
Xuddi shunday, .
Misol
tenglamani yeching 
.
Yechim. Keling, ifodani o'zgartiramiz:
Tenglama quyidagi shaklda yoziladi:
Olib, olamiz. , . Natijada
Javob. .
Universal trigonometrik almashtirish
Shaklning trigonometrik tenglamasi
Bu erda --- formulalar yordamida ratsional funktsiya --, shuningdek formulalar yordamida -- , , , argumentlariga nisbatan ratsional tenglamaga keltirilishi mumkin, shundan so'ng tenglamani qisqartirish mumkin. universal trigonometrik almashtirish formulalaridan foydalanishga nisbatan algebraik ratsional tenglama
Shuni ta'kidlash kerakki, formulalardan foydalanish dastlabki tenglamaning ODZ ning torayishiga olib kelishi mumkin, chunki u nuqtalarda aniqlanmagan, shuning uchun bunday hollarda burchaklar asl tenglamaning ildizlari ekanligini tekshirish kerak. .
Misol Tenglamani yeching.
Yechim. Vazifaga ko'ra. Formulalarni qo'llash va almashtirishni amalga oshirib, biz olamiz
qayerdan va shuning uchun, .
Shakl tenglamalari
Ko'phad bo'lgan shakldagi tenglamalar noma'lumlarni o'zgartirish orqali yechiladi
Misol Tenglamani yeching.
Yechim. O'zgartirishni amalga oshirib, buni hisobga olsak, biz olamiz
qayerda,. --- begona ildiz, chunki . Tenglama ildizlari 
bor.
Cheklangan funksiyalardan foydalanish
Markazlashtirilgan test amaliyotida yechimi va funksiyalarining chegaralanganligiga asoslangan tenglamalarni uchratish kam uchraydi. Masalan:
Misol Tenglamani yeching.
Yechim. Chunki , , keyin chap tomoni oshmaydi va ga teng, agar
Ikkala tenglamani qanoatlantiradigan qiymatlarni topish uchun biz quyidagicha harakat qilamiz. Biz ulardan birini hal qilamiz, keyin topilgan qiymatlar orasidan ikkinchisini qanoatlantiradiganlarini tanlaymiz.
Ikkinchisidan boshlaylik: , . Keyin, 
.
Faqat juft sonlar uchun bo'lishi aniq.
Javob. .
Boshqa bir fikr quyidagi tenglamani yechish orqali amalga oshiriladi:
Misol
tenglamani yeching 
.
Yechim. Eksponensial funksiya xossasidan foydalanamiz: , 
.
Ushbu tengsizliklarni atama bo'yicha qo'shsak, bizda:
Shuning uchun, bu tenglamaning chap tomoni teng bo'ladi, agar va faqat ikkita tenglik bajarilsa:
ya'ni , , qiymatlarini olishi mumkin yoki qiymatlarni olishi mumkin, .
Javob. , .
Misol
tenglamani yeching 
.
Yechim., . Binobarin, 
.
Javob. .
Misol tenglamani yeching
Yechim. ni belgilang, keyin bizda mavjud bo'lgan teskari trigonometrik funktsiyaning ta'rifidan 
va 
.
Chunki, tengsizlik tenglamadan kelib chiqadi, ya'ni. . beri va , keyin va . Biroq, va shuning uchun.
Agar va bo'lsa, u holda. Ilgari aniqlangani uchun, keyin.
Javob. , .
Misol tenglamani yeching
Yechim. Tenglamaning haqiqiy qiymatlari diapazoni .
Avval funksiya ekanligini ko'rsatamiz
Har qanday kishi uchun u faqat ijobiy qiymatlarni qabul qilishi mumkin.
Funksiyani quyidagicha ifodalaymiz: .
O'shandan beri, ya'ni, 
.
Shuning uchun tengsizlikni isbotlash uchun buni ko'rsatish kerak 
. Shu maqsadda biz bu tengsizlikning ikkala qismini kub qilamiz
Olingan son tengsizlik shuni ko'rsatadi. ni ham hisobga olsak, tenglamaning chap tomoni manfiy emas.
Endi tenglamaning o'ng tomonini ko'rib chiqing.
Chunki 
, keyin
Biroq, bu ma'lum 
. Bu erdan kelib chiqadiki, ya'ni. tenglamaning o'ng tomoni dan oshmaydi. Ilgari tenglamaning chap tomoni manfiy emasligi isbotlangan edi, shuning uchun undagi tenglik faqat uning ikkala qismi teng bo'lganda bo'lishi mumkin va bu faqat uchun mumkin.
Javob. .
Misol tenglamani yeching
Yechim. Belgilang va 
. Koshi-Bunyakovskiy tengsizligini qo'llagan holda, biz . Demak, bundan kelib chiqadi 
. Boshqa tomondan, bor 
. Shuning uchun tenglamaning ildizlari yo'q.
Javob. .
Misol Tenglamani yeching:
Yechim. Tenglamani quyidagi shaklda qayta yozamiz:
Javob. .
Trigonometrik va kombinatsiyalangan tenglamalarni yechishning funksional usullari
O'zgartirishlar natijasida har bir tenglamani ma'lum bir hal qilish usuli mavjud bo'lgan u yoki bu standart shakldagi tenglamaga keltirish mumkin emas. Bunday hollarda funksiyalarning monotonlik, chegaralanganlik, tekislik, davriylik kabi xossalarini qo‘llash foydali bo‘lib chiqadi. Demak, funksiyalardan biri kamaysa, ikkinchisi intervalda ortib ketsa, tenglama bu oraliqdagi ildiz, bu ildiz noyobdir va keyin, masalan, uni tanlash orqali topish mumkin. Agar funktsiya yuqoridan va , va funksiya pastdan chegaralangan bo'lsa, va, u holda tenglama tenglamalar tizimiga ekvivalent bo'ladi.
Misol tenglamani yeching
Yechim. Dastlabki tenglamani shaklga o'tkazamiz
ga nisbatan kvadrat shaklida yeching. Keyin olamiz
Birinchi to‘plam tenglamasini yechamiz. Funksiyaning chegaralanganligini hisobga olib, tenglama faqat intervalda ildizga ega bo'lishi mumkin degan xulosaga kelamiz. Bu oraliqda funktsiya ortadi va funktsiya 
kamayadi. Shuning uchun, agar bu tenglamaning ildizi bo'lsa, u yagonadir. Tanlov orqali topamiz.
Javob. .
Misol tenglamani yeching
Yechim. Keling, va 
, keyin asl tenglamani funktsional tenglama sifatida yozish mumkin. Funktsiya g'alati bo'lgani uchun . Bunday holda, biz tenglamani olamiz
, va monotonik bo'lgani uchun, tenglama tenglamaga ekvivalent, ya'ni. 
, bu bitta ildizga ega.
Javob. .
Misol
tenglamani yeching 
.
Yechim. Murakkab funktsiyaning hosilasi haqidagi teoremaga asoslanib, funktsiya 
kamayuvchi (funksiyaning kamayishi, ortishi, kamayishi). Bundan ma'lum bo'ladiki, funktsiya 
da aniqlangan, kamaygan. Shuning uchun bu tenglama ko'pi bilan bitta ildizga ega. Chunki 
, keyin
Javob. .
Misol Tenglamani yeching.
Yechim. Tenglamani uchta oraliqda ko'rib chiqing.
a) ruxsat bering. U holda bu to'plamda asl tenglama tenglamaga ekvivalent bo'ladi. Qaysi intervalda hech qanday yechimlari bor, beri 
, , a. Intervalda asl tenglamaning ham ildizlari yo'q, chunki 
, a.
b) ruxsat bering. Keyin ushbu to'plamda asl tenglama tenglamaga ekvivalent bo'ladi
oraliqdagi ildizlari , , , raqamlari.
c) ruxsat bering. Keyin ushbu to'plamda asl tenglama tenglamaga ekvivalent bo'ladi
Qaysi oraliqda yechimlari yo'q, chunki , lekin . Tenglamaning oraliq bo'yicha yechimlari ham yo'q, chunki , , a.
Javob. , , , .
Simmetriya usuli
Simmetriya usulini topshiriq bayonida tenglama, tengsizlik, sistema va h.k.larning yechimi yagona bo‘lishi talabi mavjud bo‘lsa, qo‘llash qulay. yoki yechimlar sonining aniq ko'rsatkichi. Bunday holda, berilgan ifodalarning har qanday simmetriyasini aniqlash kerak.
Bundan tashqari, simmetriyaning mumkin bo'lgan turlarining xilma-xilligini hisobga olish kerak.
Simmetriya bilan fikr yuritishda mantiqiy bosqichlarga qat'iy rioya qilish ham bir xil darajada muhimdir.
Odatda, simmetriya bizga faqat kerakli shartlarni o'rnatishga imkon beradi, keyin esa ularning etarliligini tekshirishimiz kerak.
Misol Tenglama yagona yechimga ega bo'lgan parametrning barcha qiymatlarini toping.
Yechim. E'tibor bering va ular juft funktsiyalardir, shuning uchun tenglamaning chap tomoni juft funktsiyadir.
Shunday qilib, agar tenglamaning yechimi bo'lsa, unda tenglamaning yechimi ham mavjud. Agar tenglamaning yagona yechimi bo'lsa, u holda zarur , .
Keling, tanlaymiz mumkin qiymatlar, bu tenglamaning ildizi bo'lishini talab qiladi.
Biz darhol ta'kidlaymizki, boshqa qiymatlar muammoning holatini qondira olmaydi.
Ammo tanlanganlarning barchasi muammoning shartini qondiradimi yoki yo'qmi hali noma'lum.
Adekvatlik.
1) , tenglama shaklni oladi 
.
2) , tenglama quyidagi ko'rinishga ega bo'ladi:
Shubhasiz, hamma uchun va 
. Shunday qilib, oxirgi tenglama tizimga ekvivalentdir:
Shunday qilib, , uchun tenglama yagona yechimga ega ekanligini isbotladik.
Javob. .
Funktsiyalarni o'rganish bilan yechim
Misol Tenglamaning barcha yechimlari ekanligini isbotlang
Butun sonlar.
Yechim. Dastlabki tenglamaning asosiy davri . Shuning uchun biz birinchi navbatda ushbu tenglamani segmentda o'rganamiz.
Tenglamani quyidagi shaklga aylantiramiz:
Kalkulyator yordamida biz quyidagilarni olamiz:
Agar bo'lsa, oldingi tengliklardan biz quyidagilarni olamiz:
Hosil bo'lgan tenglamani yechish orqali quyidagilarga erishamiz: .
Amalga oshirilgan hisob-kitoblar oraliqga tegishli tenglamaning ildizlarini , va deb hisoblash imkoniyatini beradi.
To'g'ridan-to'g'ri tekshirish bu farazni tasdiqlaydi. Shunday qilib, tenglamaning ildizlari faqat butun sonlar ekanligi isbotlangan.
Misol
Tenglamani yeching 
.
Yechim. Tenglamaning asosiy davrini toping. Funktsiyaning asosiy davri . Funktsiyaning asosiy davri . Sonlarning eng kichik umumiy karrali va ga teng. Demak, tenglamaning asosiy davri . Mayli.
Shubhasiz, bu tenglamaning yechimi. Intervalda. Funktsiya salbiy. Shuning uchun tenglamaning boshqa ildizlarini faqat x va oraliqlardan izlash kerak.
Mikrokalkulyator yordamida biz birinchi navbatda tenglama ildizlarining taxminiy qiymatlarini topamiz. Buning uchun funksiya qiymatlari jadvalini tuzamiz 
intervallar bo'yicha va ; ya'ni intervallarda va .
| 0 | 0 | 202,5 | 0,85355342 |
| 3 | -0,00080306 | 207 | 0,6893642 |
| 6 | -0,00119426 | 210 | 0,57635189 |
| 9 | -0,00261932 | 213 | 0,4614465 |
| 12 | -0,00448897 | 216 | 0,34549155 |
| 15 | -0,00667995 | 219 | 0,22934931 |
| 18 | -0,00903692 | 222 | 0,1138931 |
| 21 | -0,01137519 | 225 | 0,00000002 |
| 24 | -0,01312438 | 228 | -0,11145712 |
| 27 | -0,01512438 | 231 | -0,21961736 |
| 30 | -0,01604446 | 234 | -0,32363903 |
| 33 | -0,01597149 | 237 | -0,42270819 |
| 36 | -0,01462203 | 240 | -0,5160445 |
| 39 | -0,01170562 | 243 | -0,60290965 |
| 42 | -0,00692866 | 246 | -0,65261345 |
| 45 | 0,00000002 | 249 | -0,75452006 |
| 48 | 0,00936458 | 252 | -0,81805397 |
| 51 | 0,02143757 | 255 | -0,87270535 |
| 54 | 0,03647455 | 258 | -0,91803444 |
| 57 | 0,0547098 | 261 | -0,95367586 |
| 60 | 0,07635185 | 264 | -0,97934187 |
| 63 | 0,10157893 | 267 | -0,99482505 |
| 66 | 0,1305352 | 270 | -1 |
| 67,5 | 0,14644661 |
Jadvaldan quyidagi farazlarni osongina ko'rish mumkin: segmentga tegishli tenglamaning ildizlari sonlar: ; ; . To'g'ridan-to'g'ri tekshirish bu farazni tasdiqlaydi.
Javob.
; 
; .
Birlik aylana yordamida trigonometrik tengsizliklarni yechish
Trigonometrik funksiyalardan biri bo'lgan shakldagi trigonometrik tengsizliklarni yechishda tengsizlikning yechimini eng aniq ko'rsatish va javobni yozish uchun trigonometrik doiradan foydalanish qulay. Trigonometrik tengsizliklarni yechishning asosiy usuli ularni eng oddiy turdagi tengsizliklarga kamaytirishdir. Keling, bunday tengsizliklarni qanday yechish misolini ko'rib chiqaylik.
Misol Tengsizlikni yeching.
Yechim. Trigonometrik doira chizamiz va uning ustida ordinatasi dan katta bo'lgan nuqtalarni belgilaymiz.
Bu tengsizlikning yechimi uchun bo'ladi. Bundan tashqari, agar biron bir raqam ko'rsatilgan oraliqdan qaysidir raqamdan farq qilsa, u ham dan kam bo'lmasligi aniq. Shuning uchun, yechimning topilgan segmentining oxiriga faqat qo'shishingiz kerak . Nihoyat, biz asl tengsizlikning yechimlari hammasi bo'lishini tushunamiz 
.
Javob.
.
Tangens va kotangens bilan tengsizliklarni yechish uchun teglar va kotangenslar chizig'i tushunchasi foydalidir. Bular trigonometrik doiraga tegib, navbati bilan (1 va (2)-rasmda) chiziqlar.
Ko'rinib turibdiki, agar siz kelib chiqishi bo'lgan nurni abscissa o'qining musbat yo'nalishi bilan burchak hosil qilgan holda qursangiz, u holda segmentning uzunligi ushbu nurning kesishgan nuqtasidan chiziq chizig'i bilan kesishadi. tangenslar bu nurning abscissa o'qi bilan yasagan burchak tangensiga to'liq teng. Xuddi shunday kuzatuv kotangent uchun ham amal qiladi.
Misol Tengsizlikni yeching.
Yechim. ni belgilang, u holda tengsizlik eng sodda shaklni oladi: . Tangensning eng kichik ijobiy davriga (LPP) teng uzunlikdagi intervalni ko'rib chiqing. Ushbu segmentda tangentlar chizig'idan foydalanib, biz buni aniqlaymiz. Endi biz nima qo'shish kerakligini eslaymiz, chunki funktsiyaning RPE . Shunday qilib, 
. O'zgaruvchiga qaytsak, biz buni olamiz.
Javob.
.
Teskari trigonometrik funksiyalar bilan tengsizliklarni teskari trigonometrik funksiyalarning grafiklaridan foydalanib yechish qulay. Keling, bu qanday amalga oshirilishini misol bilan ko'rsatamiz.
Trigonometrik tengsizliklarni grafik usulda yechish
E'tibor bering, agar --- davriy funktsiya bo'lsa, unda tengsizlikni echish uchun uzunligi funktsiya davriga teng bo'lgan segmentda uning echimlarini topish kerak. Asl tengsizlikning barcha yechimlari topilgan qiymatlardan, shuningdek, funktsiya davrlarining har qanday butun soni bilan topilganlardan farq qiladigan barcha qiymatlardan iborat bo'ladi.
() tengsizlikning yechimini ko'rib chiqing.
Chunki tengsizlikning yechimlari yo'q. Agar bo'lsa, u holda tengsizlikning yechimlari to'plami barcha haqiqiy sonlar to'plamidir.
Mayli. Sinus funktsiyasi eng kichik musbat davrga ega, shuning uchun tengsizlik birinchi navbatda uzunlik segmentida, masalan, segmentda echilishi mumkin. Biz va () funktsiyalarning grafiklarini quramiz. shakldagi tengsizliklar bilan beriladi: va, buning uchun,
Ushbu maqolada eng oddiy va olimpiada darajasidagi trigonometrik tenglamalar va tengsizliklarni yechish usullari ko'rib chiqildi. Trigonometrik tenglamalar va tengsizliklarni yechishning asosiy usullari, ham o'ziga xos --- faqat trigonometrik tenglamalar va tengsizliklar uchun xarakterli ---- va trigonometrik tenglamalarga nisbatan qo'llaniladigan tenglamalar va tengsizliklarni echishning umumiy funktsional usullari ko'rib chiqildi.
Tezisda asosiy nazariy ma’lumotlar berilgan: trigonometrik va teskari trigonometrik funksiyalarning ta’rifi va xossalari; trigonometrik funktsiyalarni boshqa trigonometrik funktsiyalar bilan ifodalash, bu trigonometrik ifodalarni, ayniqsa teskari trigonometrik funktsiyalarni o'z ichiga olganlarni aylantirish uchun juda muhimdir; maktab kursidan yaxshi ma'lum bo'lgan asosiy trigonometrik formulalarga qo'shimcha ravishda, teskari trigonometrik funktsiyalarni o'z ichiga olgan ifodalarni soddalashtiradigan formulalar berilgan. Elementar trigonometrik tenglamalarni yechish, faktoring usuli, trigonometrik tenglamalarni algebraik tenglamalarga keltirish usullari ko'rib chiqiladi. Trigonometrik tenglamalar yechimlari bir necha usulda yozilishi mumkinligini va bu yechimlarning shakli bu yechimlarning bir xil yoki boshqacha ekanligini darhol aniqlashga imkon bermasligini hisobga olib, trigonometrik tenglamalarni yechishning umumiy sxemasi ko‘rib chiqiladi va trigonometrik tenglamalarning umumiy yechimlari guruhlarini o'zgartirish batafsil ko'rib chiqiladi. Elementar trigonometrik tengsizliklarni birlik aylanada ham, grafik usulda ham yechish usullari batafsil ko‘rib chiqiladi. Elementar bo'lmagan trigonometrik tengsizliklarni elementar tengsizliklar orqali yechish jarayoni va maktab o'quvchilariga allaqachon yaxshi ma'lum bo'lgan intervallar usuli tasvirlangan. Ildizlarni tanlash bo'yicha tipik vazifalarning echimlari berilgan. Ildizlarni tanlash uchun zaruriy nazariy ma'lumotlar berilgan: butun sonlar to'plamini kesishmaydigan kichik to'plamlarga bo'lish, butun sonlarda tenglamalarni yechish (diofantin).
Ushbu bitiruv malakaviy ishining natijalari kurs va dissertatsiyalar tayyorlashda, maktab o‘quvchilari uchun fakultativ fanlarni tayyorlashda o‘quv materiali sifatida, ish esa talabalarni kirish imtihonlari va markazlashtirilgan test sinovlariga tayyorlashda ham qo‘llanilishi mumkin.
Vygodskiy Ya.Ya., Boshlang'ich matematika bo'yicha qo'llanma. /Vigodskiy Ya.Ya. --- M.: Nauka, 1970 yil.
Igudisman O., og'zaki imtihonda matematika / Igudisman O. --- M .: Iris press, Rolf, 2001.
Azarov A.I., tenglamalar / Azarov A.I., Gladun O.M., Fedosenko V.S. --- Minsk: Trivium, 1994 yil.
Litvinenko V.N., Boshlang'ich matematika bo'yicha seminar / Litvinenko V.N. --- M .: Ta'lim, 1991 yil.
Sharygin I.F., Matematikaning ixtiyoriy kursi: muammolarni hal qilish / Sharygin I.F., Golubev V.I. --- M.: Ma'rifat, 1991 yil.
Bardushkin V., Trigonometrik tenglamalar. Ildizlarni tanlash / V. Bardushkin, A. Prokofyev.// Matematika, No 12, 2005 bet. 23--27.
Vasilevskiy A.B., Matematikadan sinfdan tashqari ishlar uchun topshiriqlar / Vasilevskiy A.B. --- Mn.: Xalq Asvetasi. 1988. --- 176-yillar.
Sapunov P. I., Trigonometrik tenglamalarning umumiy yechimlari guruhlarini o'zgartirish va birlashtirish / Sapunov P. I. // Matematik ta'lim, 1935 yil 3-son.
Borodin P., Trigonometriya. Moskva davlat universitetiga kirish imtihonlari materiallari [matn] / P. Borodin, V. Galkin, V. Panferov, I. Sergeev, V. Tarasov // Matematika No 1, 2005 y. 36--48.
Samusenko A.V., Matematika: Abituriyentlarning odatiy xatolari: Ma'lumotnoma / Samusenko A.V., Kazachenok V.V. --- Minsk: Oliy maktab, 1991 yil.
Azarov A.I., Imtihon muammolarini hal qilishning funktsional va grafik usullari / Azarov A.I., Barvenov S.A., --- Minsk: Aversev, 2004.
Eng oddiy trigonometrik tenglamalarni yechish
Birinchidan, eng oddiy trigonometrik tenglamalarni yechish formulalarini eslaylik.
- $sinx=a$
- $cosx=a$
- $tgx=a$
- $ctgx=a$
Eng oddiy trigonometrik tengsizliklarni yechish.
Eng oddiy trigonometrik tengsizliklarni yechish uchun avvalo tegishli tenglamani yechishimiz kerak, keyin esa trigonometrik aylana yordamida tengsizlikning yechimini topishimiz kerak. Eng oddiy trigonometrik tengsizliklarning yechimlarini misollar orqali ko'rib chiqing.
1-misol
$sinx\ge \frac(1)(2)$
$sinx=\frac(1)(2)$ trigonometrik tengsizlikning yechimini toping
\ \
1-rasm. $sinx\ge \frac(1)(2)$ tengsizlikni yechish.
Tengsizlik "katta yoki teng" belgisiga ega bo'lganligi sababli, yechim aylananing yuqori yoyida yotadi (tenglamaning yechimiga nisbatan).
Javob: $\left[\frac(\pi )(6)+2\pi n,\frac(5\pi )(6)+2\pi n\right]$.
2-misol
$cosx=\frac(\sqrt(3))(2)$ trigonometrik tengsizlikning yechimini toping.
\ \
Trigonometrik doiradagi yechimga e'tibor bering
Tengsizlik “kichik” belgisiga ega bo'lganligi sababli, yechim chap tomonda joylashgan aylananing yoyida yotadi (tenglamaning yechimiga nisbatan).
Javob: $\left(\frac(\pi )(6)+2\pi n,\frac(11\pi )(6)+2\pi n\right)$.
3-misol
$tgx\le \frac(\sqrt(3))(3)$
$tgx=\frac(\sqrt(3))(3)$ trigonometrik tengsizlikning yechimini toping.
\ \
Bu erda bizga ta'rif sohasi ham kerak. Esda tutganimizdek, Z$ da tangens funksiyasi $x\ne \frac(\pi )(2)+\pi n,n\
Trigonometrik doiradagi yechimga e'tibor bering
3-rasm. $tgx\le \frac(\sqrt(3))(3)$ tengsizlikni yechish.
Tengsizlik “kichik yoki teng” belgisiga ega bo'lganligi sababli, yechim 3-rasmda ko'k rang bilan belgilangan doira yoylarida yotadi.
Javob: $\ \left(-\frac(\pi )(2)+2\pi n\right.,\left.\frac(\pi )(6)+2\pi n\right]\chashka \chap (\frac(\pi )(2)+2\pi n,\o‘ng.\chap.\frac(7\pi )(6)+2\pi n\o‘ng]$
4-misol
$ctgx=\sqrt(3)$ trigonometrik tengsizlikning yechimini toping
\ \
Bu erda bizga ta'rif sohasi ham kerak. Esda tutganimizdek, Z$ da tangens funksiyasi $x\ne \pi n,n\
Trigonometrik doiradagi yechimga e'tibor bering
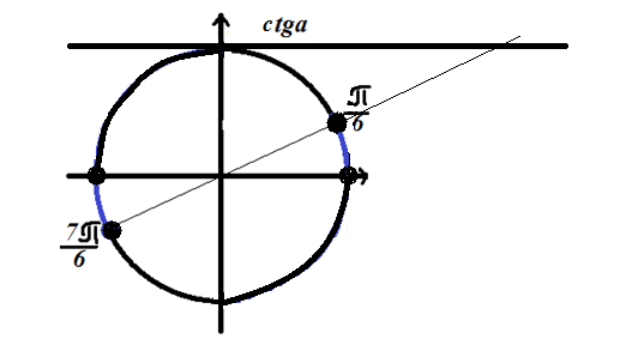
4-rasm. $ctgx\le \sqrt(3)$ tengsizligi yechimi.
Tengsizlik “kattaroq” belgisiga ega bo‘lgani uchun yechim 4-rasmda ko‘k rang bilan belgilangan aylana yoylarida yotadi.
Javob: $\ \left(2\pi n,\frac(\pi )(6)+2\pi n\right)\chashka \left(\pi +2\pi n,\frac(7\pi )( 6)+2\pi n\o‘ng)$
TA'RIF
Trigonometrik tengsizliklar - trigonometrik funktsiya belgisi ostida o'zgaruvchini o'z ichiga olgan tengsizliklar.
Trigonometrik tengsizliklarni yechish
Trigonometrik tengsizliklarni yechish ko'pincha quyidagi ko'rinishdagi eng oddiy trigonometrik tengsizliklarni echishga to'g'ri keladi: \(\ \sin x a \), \(\ \cos x > a \), \(\ \operatorname(tg) x > a \ ), \(\ \ operator nomi(ctg) x > a \), \(\ \sin x \leq a \), \(\ \cos x \leq a \), \(\ \operator nomi(tg) x \ leq a \), \ (\ \operatorname(ctg) x \leq a \), \(\ \sin x \geq a \), \(\ \cos \geq a \), \(\ \operatorname(tg) ) x \geq a \ ), \(\ \operator nomi(tg) x \geq a \)
Eng oddiy trigonometrik tengsizliklar grafik yoki birlik trigonometrik aylana yordamida yechiladi.
Ta'rifga ko'ra, burchakning sinusi \(\ \alpha \) birlik doirasining \(\ P_(\alpha)(x, y) \) nuqtasining ordinatasi (1-rasm), kosinus esa bu nuqtaning abscissasi. Bu fakt kosinus va sinus bilan eng oddiy trigonometrik tengsizliklarni birlik doirasi yordamida yechishda ishlatiladi.
Trigonometrik tengsizliklarni yechishga misollar
Tengsizlikni yeching \(\ \sin x \leq \frac(\sqrt(3))(2) \)
\(\ \left|\frac(\sqrt(3))(2)\right| boʻlgani uchun bu tengsizlik yechimga ega va uni ikki yoʻl bilan yechish mumkin.
Birinchi yo'l. Keling, bu tengsizlikni grafik tarzda yechaylik. Buning uchun bir xil koordinatalar sistemasida sinus \(\ y=\sin x \) (2-rasm) va \(\ y=\frac(\sqrt(3))( to'g'ri chiziq) grafigini tuzamiz. 2) \)
Sinusoid to'g'ri chiziq grafigidan pastda joylashgan intervallarni tanlaymiz \(\ y=\frac(\sqrt(3))(2) \) . Ushbu grafiklarning kesishish nuqtalarining \(\ x_(1) \) va \(\ x_(2) \) abscissalarini toping: \(\ x_(1)=\pi-\arcsin \frac(\sqrt(3) ))(2 )=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_(2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\ frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)
Biz \(\ \left[-\frac(4 \pi)(3) ; \frac(\pi)(3)\right] \) oralig'ini oldik, lekin \(\ y=\sin x \) funktsiyasidan beri davriy bo'lib, \(\ 2 \pi \) davriga ega bo'lsa, javob oraliqlar birligi bo'ladi: \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7) \pi)(3)+ 2 \pi k\o'ng] \), \(\ k \in Z \)
Ikkinchi yo'l. Birlik aylana va chiziqni quring \(\ y=\frac(\sqrt(3))(2) \) , ularning kesishish nuqtalarini \(\ P_(x_(1)) \) va \(\ P_(x_) belgilang. (2 )) \) (3-rasm). Asl tengsizlikning yechimi \(\ \frac(\sqrt(3))(2) \) dan kichik bo'lgan ordinata nuqtalari to'plami bo'ladi. \(\ \boldsymbol(I)_(1) \) va \(\ \boldsymbol(I)_(2) \) qiymatini soat miliga teskari yo'nalishda harakat qilib topamiz, \(\ x_(1) 3-rasm.
\(\ x_(1)=\pi-\arcsin \frac(\sqrt(3))(2)=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_ (2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)
Sinus funksiyasining davriyligini hisobga olib, biz nihoyat \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+2 \ intervallarni olamiz. pi\o'ng] \), \(\k\in Z\)
Tengsizlikni yeching \(\ \sin x>2 \)
Sinus chegaralangan funksiya: \(\ |\sin x| \leq 1 \) , va bu tengsizlikning o'ng tomoni birdan katta, shuning uchun yechimlar yo'q.
Tengsizlikni yeching \(\ \cos x>\frac(1)(2) \)
Bu tengsizlikni ikki usulda yechish mumkin: grafik va birlik doirasi yordamida. Keling, usullarning har birini ko'rib chiqaylik.
Birinchi yo'l. Bir koordinatalar sistemasida tengsizlikning chap va o'ng qismlarini tavsiflovchi funksiyalarni tasvirlaymiz, ya'ni \(\ y=\cos x \) va \(\ y=\frac(1)(2) \) . \(\ y=\cos x \) kosinus funksiya grafigi \(\ y=\frac(1)(2) \) toʻgʻri chiziq grafigi ustida joylashgan oraliqlarni tanlaymiz (4-rasm). ).
\(\ \boldsymbol(x)_(1) \) va \(\ x_(2) \) nuqtalarining abtsissalarini toping - \(\ y=\cos x \ funksiyalar grafiklarining kesishish nuqtalari. ) va \(\ y=\frac (1)(2) \) , ular ko'rsatilgan tengsizlik o'rinli bo'lgan intervallardan birining uchlaridir. \(\ x_(1)=-\arccos \frac(1)(2)=-\frac(\pi)(3) \); \(\ x_(1)=\arccos \frac(1)(2)=\frac(\pi)(3) \)
Kosinus davriy funktsiya ekanligini hisobga olsak, \(\ 2 \pi \) nuqtaga ega, javob \(\ \left(-\frac(\pi)(3) oraliqlaridan \(\ x \) qiymati hisoblanadi. )+2 \pi k; \frac(\pi)(3)+2 \pi k\o'ng) \), \(\ k \in Z \)
Ikkinchi yo'l. Birlik aylana va to'g'ri chiziq quramiz \(\ x=\frac(1)(2) \) (chunki x o'qi birlik doiradagi kosinuslarga mos keladi). \(\ P_(x_(1)) \) va \(\ P_(x_(2)) \) (5-rasm) chiziq va birlik doiraning kesishish nuqtalari bo'lsin. Asl tenglamaning yechimi \(\ \frac(1)(2) \) dan kichik bo'lgan abscissa nuqtalari to'plami bo'ladi. \(\ x_(1) \) va \(\ 2 \) qiymatini toping, soat miliga teskari yo'nalishda aylanamiz, shunda \(\ x_(1) Kosinusning davriyligini hisobga olib, biz nihoyat intervallarni olamiz \( \ \left(-\frac (\pi)(3)+2 \pi k;\frac(\pi)(3)+2 \pi k\right) \),\(\ k \in Z \)
Tengsizlikni yeching \(\ \operatorname(ctg) x \leq-\frac(\sqrt(3))(3) \)
\(\ y=\operatorname(ctg) x \), \(\ y=-\frac(\sqrt(3))(3) \) funksiyalarning grafiklarini bitta koordinata tizimida tuzamiz.
\(\ y=\operatorname(ctg) x \) funksiya grafigi \(\ y=-\frac(\sqrt(3))(3) to‘g‘ri chiziq grafigidan yuqori bo‘lmagan intervallarni tanlaymiz. ) \) (6-rasm) .
\(\ x_(0) \) nuqtaning abssissasini toping, bu tengsizlik \(\ x_(0)=\operatorname(arcctg)\left(-\frac(\) sodir bo'ladigan oraliqlardan birining oxiri hisoblanadi. sqrt(3))( 3)\o'ng)=\pi-\operator nomi(arcctg)\left(\frac(\sqrt(3))(3)\o'ng)=\pi-\frac(\pi)(3) )=\frac(2 \pi)(3) \)
Bu bo'shliqning boshqa uchi \(\ \pi \) nuqtasi bo'lib, \(\ y=\operatorname(ctg) x \) funksiyasi bu nuqtada aniqlanmagan. Shunday qilib, bu tengsizlikning yechimlaridan biri \(\ \frac(2 \pi)(3) \leq x intervalidir.
Murakkab argumentli trigonometrik tengsizliklar
Murakkab argumentli trigonometrik tengsizliklarni almashtirish yordamida eng oddiy trigonometrik tengsizliklarga keltirish mumkin. Uni yechigach, teskari almashtirish amalga oshiriladi va asl noma'lum ifodalanadi.
Tengsizlikni yeching \(\ 2 \cos \left(2 x+100^(\circ)\right) \leq-1 \)
Ushbu tengsizlikning o'ng tomonidagi kosinusni ifodalang: \(\ \cos \left(2 x+100^(\circ)\right) \leq-\frac(1)(2) \)
Biz almashtirishni amalga oshiramiz \(\ t=2 x+100^(\circ) \) , shundan so'ng bu tengsizlik eng oddiy tengsizlikka aylantiriladi \(\ \cos t \leq-\frac(1)(2) \ )
Keling, uni birlik doirasi yordamida hal qilaylik. Birlik aylana va chiziq quramiz \(\ x=-\frac(1)(2) \) . Chiziq va birlik doiraning kesishish nuqtalari sifatida \(\ P_(1) \) va \(\ P_(2) \) ni belgilaymiz (7-rasm).
Asl tengsizlikning yechimi eng ko'p \(\ -\frac(1)(2) \) bo'lgan abscissa nuqtalari to'plami bo'ladi. \(\ P_(1) \) nuqtasi burchakka mos keladi \(\ 120^(\circ) \) , va nuqta \(\ P_(2) \) . Shunday qilib, kosinus davrini hisobga olsak, biz \(\ 120^(\circ)+360^(\circ) \cdot n \leq t \leq 240^(\circ)+360^(\circ) \cdot n \ ni olamiz. ), \(\ n \in Z \)
Biz teskari almashtirishni amalga oshiramiz \(\ t=2 x+100^(\circ) 120^(\circ)+360^(\circ) \cdot n \leq 2 x+100^(\circ) \leq 240^ (\ circ)+360^(\circ) \cdot n \), \(\ n \in Z \)
Biz \(\ \mathbf(x) \) ifodalaymiz, buning uchun avval \(\ 100^(\circ) 120^(\circ)-100^(\circ)+360^(\circ) \ cdot ayirishimiz kerak. n \leq 2 x+100^(\circ)-100^(\circ) \leq 240^(\circ)-100^(\circ)+360^(\circ) \cdot n \), \( \ n\in Z\); \(\ 20^(\circ)+360^(\circ) \cdot n \leq 2 x \leq 140^(\circ)+360^(\circ) \cdot n \), \(\ n \in Z\)
va keyin 2 ga bo'ling \(\ \frac(20^(\circ)+360^(\circ) \cdot n)(2) \leq \frac(2 x)(2) \leq \frac(140^ (\circ)+360^(\circ) \cdot n)(2) \), \(\ n \in Z \); \(\ 10^(\circ)+180^(\circ) \cdot n \leq x \leq 70^(\circ)+180^(\circ) \cdot n \), \(\ n \in Z \)
Ikki tomonlama trigonometrik tengsizliklar
Ikki trigonometrik tengsizlikni yeching \(\ \frac(1)(2)
\(\ t=\frac(x)(2) \) almashtirishni kiritamiz, keyin asl tengsizlik \(\ \frac(1)(2) ko'rinishini oladi.
Keling, uni birlik doirasi yordamida hal qilaylik. Ordinata o'qi birlik aylanasidagi sinusga to'g'ri kelganligi sababli, biz uning ustida \(\ x=\frac(1)(2) \) dan katta va \(\ dan kichik yoki teng bo'lgan ordinatalar to'plamini tanlaymiz. \ frac (\ sqrt (2)) (2 ) \) . 8-rasmda bu nuqtalar \(\ P_(t_(1)) \), \(\ P_(t_(2)) \) va \(\ P_(t_(3)) \) yoylarida joylashgan bo'ladi. , \( \ P_(t_(4)) \) . Qiymatni topamiz \(\ t_(1) \), \(\ t_(2) \), \(\ t_(3) \), \(\ t_(4) \) , soat miliga teskari yoʻnalishda aylanib, va \ (\ t_(1) \(\ t_(3)=\pi-\arcsin \frac(\sqrt(2))(2)=\pi-\frac(\pi)(4)=\frac(3) \ pi)(4) \); \(\ t_(4)=\pi-\arcsin \frac(1)(2)=\pi-\frac(\pi)(6)=\frac(5 \pi) ) (6)\)
Shunday qilib, biz ikkita intervalni olamiz, ular sinus funksiyasining davriyligini hisobga olgan holda, quyidagi tarzda yozilishi mumkin \(\ \frac(\pi)(6)+2 \pi k \leq t \frac(\pi) (4)+2 \ pi k \quad \frac(3 \pi)(4)+2 \pi k leq \frac(x)(2) \frac(\pi)(4)+2 \pi k \) , \(\ \frac(3 \pi)(4)+2 \pi k Express \(\ \mathbf( x) \), buning uchun ikkala tengsizlikning barcha tomonlarini 2 ga ko'paytiramiz, \(\ \frac ni olamiz. (\pi)(3)+4 \pi k \leq x
TRIGONOMETRIK TENGSIZLIKLARNI YECHISH USULLARI
Muvofiqlik. Tarixan trigonometrik tenglamalar va tengsizliklar maktab o‘quv dasturida alohida o‘rin tutgan. Aytishimiz mumkinki, trigonometriya maktab kursining va umuman butun matematika fanining eng muhim bo'limlaridan biridir.
Trigonometrik tenglamalar va tengsizliklar o'rta maktab matematika kursida o'quv materialining mazmuni bo'yicha ham, ularni o'rganish jarayonida shakllantirilishi mumkin bo'lgan va yaratilishi kerak bo'lgan o'quv va kognitiv faoliyat usullari bo'yicha ham markaziy o'rinlardan birini egallaydi va katta muammolarni hal qilishda qo'llaniladi. nazariy va amaliy xarakterdagi muammolar soni.
Trigonometrik tenglamalar va tengsizliklarni yechish o‘quvchilarning trigonometriya bo‘yicha barcha o‘quv materialiga (masalan, trigonometrik funksiyalarning xossalari, trigonometrik ifodalarni o‘zgartirish usullari va boshqalar) oid bilimlarini tizimlashtirish uchun zarur shart-sharoitlarni yaratadi va ular bilan samarali aloqalarni o‘rnatish imkonini beradi. algebra fanidan o‘rganilayotgan material (tenglamalar, tenglamalar ekvivalentligi, tengsizliklar, algebraik ifodalarni bir xil o‘zgartirishlar va boshqalar).
Boshqacha qilib aytganda, trigonometrik tenglamalar va tengsizliklarni yechish usullarini ko'rib chiqish ushbu ko'nikmalarni yangi mazmunga o'tkazishni o'z ichiga oladi.
Nazariyaning ahamiyati va uning ko'plab qo'llanilishi tanlangan mavzuning dolzarbligidan dalolat beradi. Bu, o'z navbatida, kurs ishining maqsadi, vazifalari va tadqiqot mavzusini aniqlash imkonini beradi.
Tadqiqot maqsadi: trigonometrik tengsizliklarning mavjud turlarini, ularni yechishning asosiy va maxsus usullarini umumlashtirish, maktab o‘quvchilari tomonidan trigonometrik tengsizliklarni yechish uchun topshiriqlar to‘plamini tanlash.
Tadqiqot maqsadlari:
1. Tadqiqot mavzusi bo'yicha mavjud adabiyotlarni tahlil qilish asosida materialni tizimlashtirish.
2. “Trigonometrik tengsizliklar” mavzusini mustahkamlash uchun zarur bo’lgan topshiriqlar to’plamini bering.
O'rganish ob'ekti maktab matematika kursidagi trigonometrik tengsizliklardir.
O'rganish mavzusi: trigonometrik tengsizliklar turlari va ularni yechish usullari.
Nazariy ahamiyati materialni tartibga solishdan iborat.
Amaliy ahamiyati: nazariy bilimlarni masalalar yechishda qo‘llash; trigonometrik tengsizliklarni yechishning asosiy tez-tez uchraydigan usullarini tahlil qilish.
Tadqiqot usullari : ilmiy adabiyotlarni tahlil qilish, olingan bilimlarni sintez va umumlashtirish, masalalarni yechish tahlili, tengsizliklarni yechishning optimal usullarini izlash.
§bir. Trigonometrik tengsizliklar turlari va ularni yechishning asosiy usullari
1.1. Eng oddiy trigonometrik tengsizliklar
yoki > belgisi bilan bogʻlangan ikkita trigonometrik ifoda trigonometrik tengsizliklar deyiladi.
Trigonometrik tengsizlikni yechish deganda tengsizlikka kiritilgan noma'lumlar qiymatlari to'plamini topish tushuniladi, bunda tengsizlik qondiriladi.
Trigonometrik tengsizliklarning asosiy qismi ularni eng oddiylarini yechishgacha kamaytirish orqali yechiladi:
Bu faktorizatsiya, o'zgaruvchini o'zgartirish usuli bo'lishi mumkin ( 
, 
va hokazo), bu erda birinchi navbatda odatiy tengsizlik, keyin esa shaklning tengsizligi hal qilinadi 
va boshqalar yoki boshqa usullar.
Eng oddiy tengsizliklar ikki usulda yechiladi: birlik doirasi yordamida yoki grafik.
Maylif(x
asosiy trigonometrik funksiyalardan biridir. Tengsizlikni yechish uchun 
uning yechimini bir davrda topish kifoya, ya'ni. uzunligi funksiya davriga teng bo'lgan har qanday segmentdaf
x
. Shunda asl tengsizlikning yechimi topiladix
, shuningdek, funktsiya davrlarining har qanday butun soni bilan topilgan qiymatlardan farq qiladigan qiymatlar. Bunday holda, grafik usuldan foydalanish qulay.
Tengsizliklarni yechish algoritmiga misol keltiramiz 
(
) va 
.
Tengsizlikni yechish algoritmi (
).
1. Sonning sinus ta’rifini tuzingx birlik aylanasida.
3. Y o'qida koordinatali nuqtani belgilanga .
4. Shu nuqta orqali OX o'qiga parallel chiziq o'tkazing va uning aylana bilan kesishgan nuqtalarini belgilang.
5. Barcha nuqtalari ordinatasidan kichik bo'lgan aylana yoyini tanlanga .
6. Aylanib o‘tish yo‘nalishini belgilang (soat miliga teskari) va oraliq uchlariga funksiya davrini qo‘shib javobni yozing.2p
,
.
Tengsizlikni yechish algoritmi .
1. Son tangensining ta’rifini tuzingx birlik aylanasida.
2. Birlik doirasini chizing.
3. Tangenslar chizig‘ini chizing va undagi nuqtani ordinata bilan belgilanga .
4. Bu nuqtani koordinata boshiga ulang va hosil bo'lgan segmentning birlik doirasi bilan kesishgan nuqtasini belgilang.
5. Doira yoyini tanlang, uning barcha nuqtalari tangens chiziqda ordinatasidan kichik bo'ladi.a .
6. O'tish yo'nalishini ko'rsating va javobni funktsiya doirasini hisobga olgan holda, nuqta qo'shib yozing.pn
,
(yozuvning chap tomonidagi raqam har doim o'ng tarafdagi raqamdan kamroq).
Eng oddiy tenglamalar yechimlarining grafik talqini va tengsizliklarni umumiy shaklda yechish formulalari ilovada keltirilgan (1 va 2-ilovalar).
1-misol
Tengsizlikni yeching 
.
Birlik doirasiga chiziq chizing 
, u aylanani A va B nuqtalarda kesib o'tadi.
Barcha qadriyatlary
NM oralig'ida ko'proq
, AMB yoyining barcha nuqtalari bu tengsizlikni qanoatlantiradi. Barcha aylanish burchaklarida, katta 
, lekin kichikroq 
,
dan kattaroq qiymatlarni qabul qiladi
(lekin bittadan ko'p emas).
1-rasm
Shunday qilib, tengsizlikning yechimi intervaldagi barcha qiymatlar bo'ladi 
, ya'ni. 
. Ushbu tengsizlikning barcha yechimlarini olish uchun ushbu intervalning uchlarini qo'shish kifoya 
, qayerda 
, ya'ni. 
,
.
E'tibor bering, qiymatlar 
va 
tenglamaning ildizlaridir 
,
bular. 
;
.
Javob: 
, .
1.2. Grafik usul
Amalda trigonometrik tengsizliklarni echishning grafik usuli ko'pincha foydalidir. Tengsizlik misolida usulning mohiyatini ko'rib chiqing 
:
1. Agar argument murakkab bo'lsa (farqliX ), keyin uni bilan almashtiramizt .
2. Biz bitta koordinatali tekislikda quramiztoOy
funksiya grafiklari 
va 
.
3. Biz shunday topamizgrafiklarning kesishishning ikkita qo'shni nuqtasi, ular orasidasinusoidjoylashganyuqorida
To'g'riga . Ushbu nuqtalarning abstsissalarini toping.
4. Argument uchun qo‘sh tengsizlikni yozingt , kosinus davrini hisobga olgan holda (t topilgan abscissalar orasida bo'ladi).
5. Teskari almashtirishni bajaring (asl argumentga qayting) va qiymatni ifodalangX qo'sh tengsizlikdan javobni son oralig'i sifatida yozamiz.
2-misol Tengsizlikni yeching: .
Tengsizliklarni grafik usulda yechishda funksiyalar grafiklarini iloji boricha aniq qurish kerak. Tengsizlikni quyidagi shaklga aylantiramiz:
Bitta koordinata tizimidagi funksiyalar grafiklarini tuzamiz 
va 
(2-rasm).
2-rasm
Funktsiya grafiklari bir nuqtada kesishadiLEKIN
koordinatalari bilan 
; 
. Orasida 
grafik nuqtalari 
diagramma nuqtalari ostida 
. Va qachon funktsiya qiymatlari bir xil. Shunung uchun da 
.
Javob: 
.
1.3. Algebraik usul
Ko'pincha, dastlabki trigonometrik tengsizlik, to'g'ri tanlangan almashtirish orqali algebraik (ratsional yoki irratsional) tengsizlikka tushirilishi mumkin. Bu usul tengsizlikni o'zgartirish, almashtirishni kiritish yoki o'zgaruvchini almashtirishni o'z ichiga oladi.
Keling, ushbu usulning qo'llanilishini aniq misollarda ko'rib chiqaylik.
3-misol
Eng oddiy shaklga qisqartirish 
.
(3-rasm)
3-rasm
, 
.
Javob: 
,
4-misol Tengsizlikni yeching:
ODZ: 
, 
.
Formulalardan foydalanish: 
, 
tengsizlikni quyidagi shaklda yozamiz: 
.
Yoki, faraz qilsak 
oddiy o'zgarishlardan keyin biz olamiz
,
,
.
Oxirgi tengsizlikni oraliq usuli bilan yechib, biz quyidagilarga erishamiz:
4-rasm
, mos ravishda 
. Keyin rasmdan. 4 tasi 
, qayerda 
.
5-rasm
Javob: 
, 
.
1.4. Bo'shliq usuli
Trigonometrik tengsizliklarni intervalli usulda yechishning umumiy sxemasi:
Trigonometrik formulalardan foydalanib, faktorlarga ajrating.
Funktsiyaning uzilish nuqtalari va nollarini toping, ularni aylanaga qo'ying.
Har qanday nuqtani olingKimga (lekin ilgari topilmagan) va mahsulotning belgisini bilib oling. Agar mahsulot ijobiy bo'lsa, u holda burchakka mos keladigan nurga birlik doirasi tashqarisida nuqta qo'ying. Aks holda, nuqtani doira ichiga qo'ying.
Agar nuqta juft marta sodir bo'lsa, biz uni juft ko'plik nuqtasi deb ataymiz; agar toq bo'lsa, uni toq ko'plik nuqtasi deb ataymiz. Yoylarni quyidagicha chizing: nuqtadan boshlangKimga , agar keyingi nuqta toq ko'plik bo'lsa, u holda bu nuqtada yoy aylana bilan kesishadi, lekin agar nuqta juft ko'plik bo'lsa, u holda kesishmaydi.
Doira orqasidagi yoylar ijobiy bo'shliqlardir; aylana ichida manfiy intervallar mavjud.
5-misol Tengsizlikni yeching
, 
.
Birinchi seriyaning nuqtalari: 
.
Ikkinchi seriyaning nuqtalari: 
.
Har bir nuqta toq marta, ya'ni toq ko'plikdagi barcha nuqtalar sodir bo'ladi.
Mahsulot belgisini quyidagi manzilda bilib oling 
: . Birlik doirasidagi barcha nuqtalarni belgilaymiz (6-rasm):
Guruch. 6
Javob: 
, 
; 
, 
; 
, 
.
6-misol . Tengsizlikni yeching.
Yechim:
Keling, ifodaning nollarini topamiz .
Olingaem :
,
;
, 
;
, 
;
, 
;
Birlik doirasida, ketma-ket qiymatlarX
1
nuqtalar bilan ifodalanadi 
. SeriyaX
2
ball beradi 
. Bir qatorX
3
ikkita ochko olamiz 
. Nihoyat, seriyaX
4
nuqtalarni ifodalaydi 
. Biz bu nuqtalarning barchasini birlik doirasiga qo'yamiz, uning har bir ko'pligi yonidagi qavslar ichida ko'rsatamiz.
Endi raqamga ruxsat bering 
teng bo'ladi. Biz belgi bo'yicha taxmin qilamiz:
Demak, nuqtaA
burchakni tashkil etuvchi nurda tanlanishi kerak 
nur bilanOh,
birlik doirasidan tashqarida. (Yordamchi nurga e'tibor beringO
A
u rasmda ko'rsatilishi shart emas. NuqtaA
taxminan tanlangan.)
Endi nuqtadanA
barcha belgilangan nuqtalarga ketma-ket to'lqinli uzluksiz chiziq chizamiz. Va nuqtalarda bizning chiziq bir mintaqadan ikkinchisiga o'tadi: agar u birlik doirasidan tashqarida bo'lsa, u holda unga o'tadi. Nuqtaga yaqinlashish 
, chiziq ichki mintaqaga qaytadi, chunki bu nuqtaning ko'pligi juft. Xuddi shu nuqtada 
(tekis ko'plik bilan) chiziqni tashqi hududga aylantirish kerak. Shunday qilib, biz rasmda tasvirlangan ma'lum bir rasmni chizdik. 7. Birlik doirasidagi kerakli joylarni ajratib ko'rsatishga yordam beradi. Ular "+" belgisi bilan belgilanadi.
7-rasm
Yakuniy javob:
Eslatma. Agar to'lqinli chiziq, birlik doirasida belgilangan barcha nuqtalarni kesib o'tgandan so'ng, nuqtaga qaytarilmasaA , aylanani "noqonuniy" joyda kesib o'tmasdan, bu yechimda xatolikka yo'l qo'yilganligini anglatadi, ya'ni toq sonli ildizlar o'tkazib yuborilgan.
Javob: .
§2. Trigonometrik tengsizliklarni yechish uchun topshiriqlar to'plami
Maktab o'quvchilarining trigonometrik tengsizliklarni yechish qobiliyatini rivojlantirish jarayonida 3 bosqichni ham ajratib ko'rsatish mumkin.
1. tayyorgarlik,
2. eng oddiy trigonometrik tengsizliklarni yechish malakalarini shakllantirish;
3. boshqa turdagi trigonometrik tengsizliklarni kiritish.
Tayyorgarlik bosqichining maqsadi shundan iboratki, maktab o'quvchilarida tengsizliklarni echish uchun trigonometrik doira yoki grafikdan foydalanish qobiliyatini shakllantirish kerak, xususan:
Shaklning oddiy tengsizliklarini yechish qobiliyati ,
, ,
,
sinus va kosinus funksiyalarining xossalaridan foydalanish;
Sonli aylana yoylari yoki funksiyalar grafiklari yoylari uchun qo‘sh tengsizliklar yasay olish;
Trigonometrik ifodalarni turli xil o'zgartirishlarni amalga oshirish qobiliyati.
Ushbu bosqichni maktab o'quvchilarining trigonometrik funktsiyalarning xususiyatlari haqidagi bilimlarini tizimlashtirish jarayonida amalga oshirish tavsiya etiladi. Asosiy vositalar talabalarga taklif qilinadigan va o'qituvchi rahbarligida yoki mustaqil ravishda bajariladigan vazifalar, shuningdek, trigonometrik tenglamalarni yechishda olingan ko'nikmalar bo'lishi mumkin.
Mana shunday vazifalarga misollar:
1
. Birlik doirasiga nuqta belgilang 
, agar
.
2.
Nuqta koordinata tekisligining qaysi choragida joylashgan , agar 
teng: 
3.
Trigonometrik doiradagi nuqtalarni belgilang , agar:
4. Ifodani trigonometrik funksiyalarga keltiringIchorak.
a) 
,
b) 
,
ichida) 
5. MR yoyi berilgan.M - o'rtadaIchorak,R - o'rtadaIIth chorak. O'zgaruvchining qiymatini cheklasht uchun: (qo'sh tengsizlik tuzing) a) yoy MP; b) RM yoylari.
6. Grafikning tanlangan bo'limlari uchun ikkita tengsizlikni yozing:
Guruch. bitta
7.
Tengsizliklarni yechish 
, 
, 
, 
.
8. Ifodani aylantirish .
Trigonometrik tengsizliklarni yechishni o'rganishning ikkinchi bosqichida o'quvchilar faoliyatini tashkil etish metodikasi bilan bog'liq quyidagi tavsiyalarni berishimiz mumkin. Bunda o’quvchilarning eng oddiy trigonometrik tenglamalarni yechish jarayonida hosil bo’ladigan trigonometrik doira yoki grafik bilan ishlash malakalariga e’tibor qaratish lozim.
Birinchidan, eng oddiy trigonometrik tengsizliklarni echishning umumiy usulini olishning maqsadga muvofiqligini, masalan, shaklning tengsizligiga murojaat qilish orqali rag'batlantirish mumkin. 
.
Tayyorgarlik bosqichida olingan bilim va ko'nikmalardan foydalanib, talabalar taklif qilingan tengsizlikni shaklga keltiradilar 
, lekin natijada paydo bo'lgan tengsizlikka yechimlar to'plamini topish qiyin bo'lishi mumkin, chunki uni faqat sinus funksiya xossalari yordamida yechish mumkin emas. Tegishli rasmga murojaat qilish (tenglamani grafik yoki birlik doirasi yordamida hal qilish) orqali bu qiyinchilikning oldini olish mumkin.
Ikkinchidan, o'qituvchi o'quvchilar e'tiborini topshiriqni bajarishning turli usullariga qaratishi, tengsizlikni grafik va trigonometrik doiradan foydalangan holda yechishning tegishli misolini keltirishi kerak.
Tengsizlikni yechishning bunday variantlarini ko'rib chiqing .
1. Birlik doirasi yordamida tengsizlikni yechish.
Trigonometrik tengsizliklarni yechish bo‘yicha birinchi darsda biz o‘quvchilarga bosqichma-bosqich taqdimotda tengsizlikni yechish uchun zarur bo‘lgan barcha asosiy ko‘nikmalarni aks ettiruvchi batafsil yechim algoritmini taklif qilamiz.
1-qadam.Birlik doirasini chizing, y o'qida nuqtani belgilang 
va u orqali x o'qiga parallel to'g'ri chiziq o'tkazing. Bu chiziq birlik doirasini ikki nuqtada kesib o'tadi. Ushbu nuqtalarning har biri sinusi teng bo'lgan raqamlarni tasvirlaydi .
2-qadamBu to'g'ri chiziq doirani ikki yoyga bo'ldi. Sinusi kattaroq raqamlar ko'rsatilganini ajratib ko'rsatamiz . Tabiiyki, bu yoy chizilgan to'g'ri chiziq ustida joylashgan.
Guruch. 2
3-qadamBelgilangan yoyning uchlaridan birini tanlaymiz. Keling, birlik doirasining bu nuqtasi bilan ifodalangan raqamlardan birini yozamiz 
.
4-qadamTanlangan yoyning ikkinchi uchiga mos keladigan raqamni tanlash uchun biz ushbu yoy bo'ylab nomlangan uchidan ikkinchisiga "o'tamiz". Shu bilan birga, biz eslaymizki, soat sohasi farqli o'laroq, biz o'tadigan raqamlar ko'payadi (qarama-qarshi yo'nalishda harakatlanayotganda raqamlar kamayadi). Belgilangan yoyning ikkinchi uchiga birlik aylanasida tasvirlangan raqamni yozamiz 
.
Shunday qilib, biz tengsizlikni ko'ramiz tengsizlik yuzaga keladigan raqamlarni qanoatlantiring 
. Sinus funksiyasining bir davrida joylashgan sonlar uchun tengsizlikni yechdik. Shuning uchun tengsizlikning barcha yechimlarini quyidagicha yozish mumkin 
Talabalardan rasmni diqqat bilan ko'rib chiqish va tengsizlikning barcha echimlari nima uchun ekanligini aniqlashni so'rash kerak shaklida yozilishi mumkin 
, 
.
Guruch. 3
Kosinus funksiyasi uchun tengsizliklarni yechishda y o'qiga parallel to'g'ri chiziq o'tkazamiz, deb o'quvchilar e'tiborini qaratish lozim.
Tengsizlikni grafik yechish usuli.
Qurilish sxemalari 
va 
, sharti bilan; inobatga olgan holda 
.
Guruch. to'rtta
Keyin tenglamani yozamiz 
va uning qarori 
, 
, 
, formulalar yordamida topilgan 
, 
, 
.
(Beribn
qiymatlari 0, 1, 2, biz tuzilgan tenglamaning uchta ildizini topamiz). Qiymatlar 
grafiklarning kesishish nuqtalarining ketma-ket uchta abtsissasi va . Shubhasiz, har doim intervalda 
tengsizlik 
, va intervalda 
- tengsizlik 
. Bizni birinchi holat qiziqtiradi va keyin bu oraliqning uchlariga sinus davrining karrali sonini qo'shsak, biz tengsizlikning yechimini olamiz. sifatida: 
, .
Guruch. 5
Xulosa qiling. Tengsizlikni yechish uchun , mos keladigan tenglamani yozib, uni yechish kerak. Olingan formuladan ildizlarni toping 
va 
, va tengsizlikning javobini quyidagi shaklda yozing: , .
Uchinchidan, tegishli trigonometrik tengsizlikning ildizlar to'plami haqidagi fakt uni grafik tarzda yechishda juda aniq tasdiqlanadi.
Guruch. 6
Tengsizlikning yechimi bo'lgan g'altakning trigonometrik funktsiya davriga teng bo'lgan bir xil intervalda takrorlanishini talabalarga ko'rsatish kerak. Sinus funksiyasining grafigi uchun shunga o'xshash rasmni ham ko'rib chiqishingiz mumkin.
To`rtinchidan, o`quvchilarning trigonometrik funksiyalar yig`indisini (ayrimini) ko`paytmaga aylantirish usullarini yangilash bo`yicha ishlarni olib borish, maktab o`quvchilarining e`tiborini trigonometrik tengsizliklarni yechishda bu usullarning roliga qaratish maqsadga muvofiqdir.
Bunday ishlarni talabalar tomonidan o'qituvchi tomonidan taklif qilingan vazifalarni mustaqil ravishda bajarish orqali tashkil etilishi mumkin, ular orasida biz quyidagilarni ajratib ko'rsatamiz:
Beshinchidan, o‘quvchilardan har bir oddiy trigonometrik tengsizlikning yechimini grafik yoki trigonometrik aylana yordamida tasvirlab berish talab qilinishi kerak. Uning maqsadga muvofiqligiga, ayniqsa aylanadan foydalanishga e'tibor bering, chunki trigonometrik tengsizliklarni echishda tegishli rasm berilgan tengsizlikka yechimlar to'plamini o'rnatish uchun juda qulay vosita bo'lib xizmat qiladi.
Talabalarni eng oddiy bo'lmagan trigonometrik tengsizliklarni yechish usullari bilan tanishtirish, uni quyidagi sxema bo'yicha bajarish tavsiya etiladi: ma'lum bir trigonometrik tengsizlikka murojaat qilib, tegishli trigonometrik tenglamani birgalikda qidirish (o'qituvchi - talabalar) mustaqil yechim uchun. topilgan texnikani bir xil turdagi boshqa tengsizliklarga o'tkazish.
Talabalarning trigonometriya bo'yicha bilimlarini tizimlashtirish uchun biz o'quvchilar e'tiborini ularning xususiyatlariga qaratib, uni hal qilish jarayonida amalga oshirilishi mumkin bo'lgan turli xil o'zgarishlarni talab qiladigan bunday tengsizliklarni alohida tanlashni tavsiya qilamiz.
Bunday samarali tengsizliklar sifatida, masalan, quyidagilarni taklif qilishimiz mumkin:
Xulosa qilib, biz trigonometrik tengsizliklarni yechish uchun masalalar to'plamiga misol keltiramiz.
1. Tengsizliklarni yeching:
2. Tengsizliklarni yeching: 3. Tengsizliklarning barcha yechimlarini toping: 4. Tengsizliklarning barcha yechimlarini toping:a) 
, shartni qondirish 
;
b) 
, shartni qondirish 
.
5. Tengsizliklarning barcha yechimlarini toping:
a) ;
b) ;
ichida) 
;
G) 
;
e) 
.
6. Tengsizliklarni yeching:
a) ;
b) ;
ichida);
G) 
;
e) ;
e) ;
va) 
.
7. Tengsizliklarni yeching:
a) 
;
b) ;
ichida);
G) .
8. Tengsizliklarni yeching:
a) ;
b) ;
ichida);
G) 
;
e) 
;
e) ;
va) 
;
h) .
6 va 7-topshiriqlarni matematikani yuqori bosqichda o'rganayotgan talabalarga, 8-topshiriqni matematikani chuqur o'rganadigan sinf o'quvchilariga taklif qilish maqsadga muvofiqdir.
§3. Trigonometrik tengsizliklarni yechishning maxsus usullari
Trigonometrik tenglamalarni echishning maxsus usullari - ya'ni faqat trigonometrik tenglamalarni echish uchun ishlatilishi mumkin bo'lgan usullar. Bu usullar trigonometrik funksiyalarning xossalaridan foydalanishga, shuningdek, turli trigonometrik formulalar va identifikatsiyalardan foydalanishga asoslangan.
3.1. Sektor usuli
Trigonometrik tengsizliklarni echishning sektor usulini ko'rib chiqing. Shaklning tengsizliklarini yechish 
, qayerdaP
(
x
)
vaQ
(
x
)
- ratsional trigonometrik funksiyalar (sinuslar, kosinuslar, tangenslar va kotangentlar ularga ratsional ravishda kiradi), xuddi ratsional tengsizliklarni yechish kabi. Ratsional tengsizliklarni haqiqiy o'qdagi intervallar usuli bilan yechish qulay. Ratsional trigonometrik tengsizliklarni echishda uning analogi trigonometrik doiradagi sektorlar usulidir.sinx
vacosx
(
) yoki trigonometrik yarim doira uchuntgx
vactgx
(
).
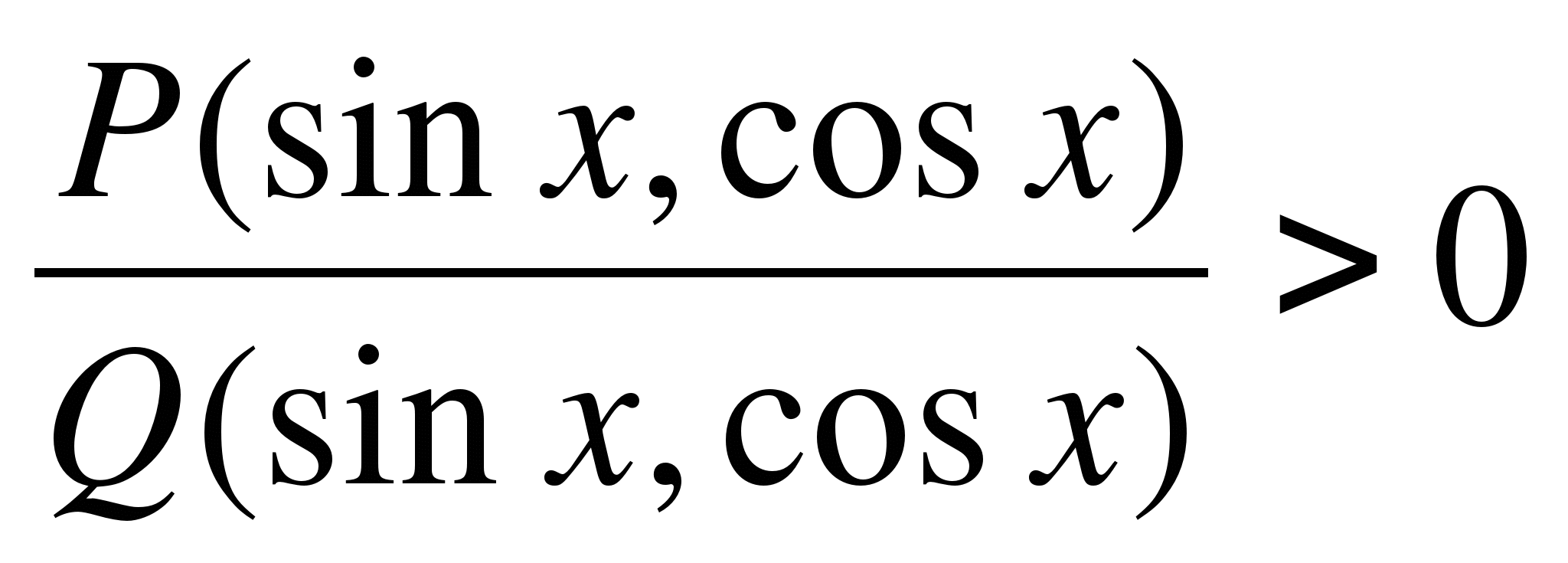
Intervalli usulda shaklning pay va maxrajining har bir chiziqli omili 
raqam o'qi ustidagi nuqta 
, va bu nuqtadan o'tayotganda belgisini o'zgartiradi. Sektor usulida shaklning har bir ko'paytmasi 
, qayerda 
- funksiyalaridan birisinx
yokicosx
va 
, trigonometrik doirada ikkita burchak mos keladi 
va 
, ular doirani ikki sektorga ajratadi. O'tayotganda va funktsiyasi belgisini o'zgartiradi.
Quyidagilarni yodda tutish kerak:
a) shaklning ko‘paytmalari 
va 
, qayerda 
, barcha qiymatlar uchun belgini saqlang 
. Numerator va maxrajning bunday ko'paytmalari o'chiriladi, o'zgaradi (agar 
) har bir bunday rad etish uchun tengsizlik belgisi teskari bo'ladi.
b) shaklning ko‘paytmalari 
va 
ham tashlanadi. Bundan tashqari, agar bu maxraj omillari bo'lsa, unda shakldagi tengsizliklar tengsizliklarning ekvivalent tizimiga qo'shiladi. 
va 
. Agar bular hisoblagichning omillari bo'lsa, u holda ekvivalent cheklovlar tizimida ular tengsizliklarga mos keladi. va qat'iy boshlang'ich tengsizlik, va tenglik taqdirda 
va 
qat'iy bo'lmagan boshlang'ich tengsizlik holatida. Ko'paytirgichni tushirganda 
yoki 
tengsizlik belgisi teskari.
1-misol
Tengsizliklarni yeching: a) 
, b) 
.
funksiyamiz bor, b). Bizdagi tengsizlikni yeching
3.2. Konsentrik doira usuli
Bu usul ratsional tengsizliklar sistemalarini yechishda parallel sonli o`qlar usuliga o`xshaydi.
Tengsizliklar tizimining misolini ko'rib chiqing.
5-misol
Oddiy trigonometrik tengsizliklar sistemasini yeching 
Birinchidan, har bir tengsizlikni alohida yechamiz (5-rasm). Rasmning yuqori o'ng burchagida trigonometrik doira qaysi argument uchun ko'rib chiqilishini ko'rsatamiz.
5-rasm
Keyinchalik, argument uchun konsentrik doiralar tizimini quramizX . Biz aylana chizamiz va uni birinchi tengsizlikning yechimiga qarab soya qilamiz, keyin kattaroq radiusli doira chizamiz va ikkinchisining yechimiga ko'ra uni soya qilamiz, keyin uchinchi tengsizlik uchun doira va asos aylanasini quramiz. . Biz nurlarni tizimning markazidan yoylarning uchlari orqali o'tkazamiz, shunda ular barcha doiralarni kesib o'tadi. Asosiy doirada eritma hosil qilamiz (6-rasm).
6-rasm
Javob:
, 
.
Xulosa
Kurs ishining barcha maqsadlari bajarildi. Nazariy material tizimlashtirilgan: trigonometrik tengsizliklarning asosiy turlari va ularni yechishning asosiy usullari (grafik, algebraik, intervallar usuli, sektorlar va konsentrik doiralar usuli) berilgan. Har bir usul uchun tengsizlikni yechish misoli keltirildi. Nazariy qismdan so‘ng amaliy qism o‘tkazildi. Unda trigonometrik tengsizliklarni yechish uchun vazifalar to‘plami mavjud.
Ushbu kurs ishi talabalar tomonidan mustaqil ish uchun foydalanishi mumkin. Talabalar ushbu mavzuni o'zlashtirish darajasini tekshirishlari, turli xil murakkablikdagi vazifalarni bajarishda mashq qilishlari mumkin.
Ushbu masala bo'yicha tegishli adabiyotlarni o'rganib chiqib, aniq xulosaga kelishimiz mumkinki, algebra fani maktab kursida trigonometrik tengsizliklarni yechish qobiliyati va ko'nikmalari va tahlilning boshlanishi juda muhim bo'lib, ularni rivojlantirish katta kuch talab qiladi. matematika o'qituvchisi.
Shuning uchun bu ish matematika o’qituvchilari uchun foydali bo’ladi, chunki bu o’quvchilarni “Trigonometrik tengsizliklar” mavzusi bo’yicha o’qitishni samarali tashkil etish imkonini beradi.
O'qishni yakuniy malakaviy ishgacha kengaytirish orqali davom ettirish mumkin.
Foydalanilgan adabiyotlar ro'yxati
Bogomolov, N.V. Matematikadan muammolar to'plami [Matn] / N.V. Bogomolov. – M.: Bustard, 2009. – 206 b.
Vygodskiy, M.Ya. Boshlang'ich matematika bo'yicha qo'llanma [Matn] / M.Ya. Vygodskiy. – M.: Bustard, 2006. – 509 b.
Zhurbenko, L.N. Misollar va topshiriqlarda matematika [Matn] / L.N. Jurbenko. – M.: Infra-M, 2009. – 373 b.
Ivanov, O.A. Maktab o'quvchilari, talabalar va o'qituvchilar uchun boshlang'ich matematika [Matn] / O.A. Ivanov. – M.: MTsNMO, 2009. – 384 b.
Karp, A.P. 11-sinfda yakuniy takrorlash va attestatsiyani tashkil etish uchun algebra bo'yicha vazifalar va tahlilning boshlanishi [Matn] / A.P. Karp. – M.: Ma’rifat, 2005. – 79 b.
Kulanin, E.D. Matematikadan 3000 ta raqobatdosh masala [Matn] / E.D. Kulanin. – M.: Iris-press, 2007. – 624 b.
Leibson, K.L. Matematikadan amaliy topshiriqlar to'plami [Matn] / K.L. Leybson. – M.: Bustard, 2010. – 182 b.
Tirsak, V.V. Parametrlar bilan bog'liq muammolar va ularni hal qilish. Trigonometriya: tenglamalar, tengsizliklar, sistemalar. 10-sinf [Matn] / V.V. Tirsak. – M.: ARKTI, 2008. – 64 b.
Manova, A.N. Matematika. Imtihonga tayyorgarlik ko'rish uchun ekspress repetitor: hisob. nafaqa [Matn] / A.N. Manova. - Rostov-na-Donu: Feniks, 2012. - 541 p.
Mordkovich, A.G. Algebra va matematik analizning boshlanishi. 10-11 sinflar. Ta'lim muassasalari talabalari uchun darslik [Matn] / A.G. Mordkovich. – M.: Iris-press, 2009. – 201 b.
Novikov, A.I. Trigonometrik funksiyalar, tenglamalar va tengsizliklar [Matn] / A.I. Novikov. - M.: FIZMATLIT, 2010. - 260 b.
Oganesyan, V.A. O`rta maktabda matematika o`qitish metodikasi: Umumiy metodika. Proc. fizika talabalari uchun nafaqa. - mat. fak. ped. o'rtoq. [Matn] / V.A. Oganesyan. – M.: Ma’rifat, 2006. – 368 b.
Olechnik, S.N. Tenglamalar va tengsizliklar. Nostandart yechim usullari [Matn] / S.N. Olekhnik. - M .: Faktorial nashriyoti, 1997. - 219 b.
Sevryukov, P.F. Trigonometrik, ko'rsatkichli va logarifmik tenglamalar va tengsizliklar [Matn] / P.F. Sevryukov. – M.: Xalq ta’limi, 2008. – 352 b.
Sergeev, I.N. FOYDALANISH: matematikadan javoblar va yechimlar bilan 1000 ta vazifa. C guruhining barcha vazifalari [Matn] / I.N. Sergeev. – M.: Imtihon, 2012. – 301 b.
Sobolev, A.B. Boshlang'ich matematika [Matn] / A.B. Sobolev. - Yekaterinburg: GOU VPO USTU-UPI, 2005. - 81 p.
Fenko, L.M. Tengsizliklarni yechish va funktsiyalarni o'rganishda intervallar usuli [Matn] / L.M. Fenko. – M.: Bustard, 2005. – 124 b.
Fridman, L.M. Matematika o'qitish metodikasining nazariy asoslari [Matn] / L.M. Fridman. - M .: "LIBROKOM" kitob uyi, 2009. - 248 b.
1-ilova
Eng oddiy tengsizliklar yechimlarining grafik talqini
Guruch. bitta
Guruch. 2
3-rasm
4-rasm
5-rasm
6-rasm
7-rasm
8-rasm
2-ilova
Eng oddiy tengsizliklar yechimlari
