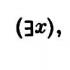Kvantifikátory obecnosti a existence. Kvantifikátory Význam formule predikátové logiky
1. Kvantifikátory.
2. Univerzální kvantifikátor.
3. Kvantifikátor existence.
4. Pojem formule predikátové logiky. Význam vzorce
predikátová logika.
5. Ekvivalentní formule predikátové logiky.
Koncept kvantifikátoru
Kvantifikátor - (z latinského quantum - kolik), logickýkvantitativní operace
oblast objektů, na které se výraz vztahuje,
získaný v důsledku jeho použití.
V běžném jazyce nositelé takových vlastností
slova jako "všechny", "každý", "některé",
"existuje",
"dostupný",
"žádný",
"žádný",
"jeden", "několik", "nekonečně mnoho",
"konečné číslo", stejně jako všechny kvantitativní
číslice.
Operace pro predikát
Pro predikáty jsou zavedeny dva novéve srovnání s výrokovými logickými operacemi:
obecný kvantifikátor
kvantifikátor existence
Obecný kvantifikátor
Nechť P(x) je unární predikát definovaný napředmětová sada M.
Univerzální tvrzení odpovídající
predikátu P(x) se nazývá následující příkaz:
„každý prvek množiny M vyhovuje
predikát P(x)"
nebo
"pro každé x je predikát splněn"
Tento příkaz je označen - (x)P(x)
Výrok (x)P(x) se považuje za pravdivý, jestliže
predikát P(x) je shodně pravdivý i nepravdivý
v opačném případě.
Obecný kvantifikátor
Symbol x se nazývá kvantifikátorproměnná x se čte takto:
"za všechny x"
"za každé x"
"pro libovolné x"
shodnost v
Výraz (x)P(x) zní: „pro všechna x, P(x)“, nebo
"pro každé x, P(x)."
Například x(x=x) je skutečný univerzální
a x(x>2) je falešný univerzální
prohlášení.
konečná množina (a1,a2,…am), pak:
P(x) P(a1) P(a2) ... P(am)
Obecný kvantifikátor
Tedy obecný kvantifikátorlze chápat jako operátor
konjunkce podle kvantifikovatelných
variabilní.
Kvantifikátor existence
Existenciálníprohlášení,
relevantní
predikát
P(x),
volal
výrok „existuje prvek množiny M,
uspokojující
predikát
P(x)",
který
se značí x P(x) a považuje se za pravdivé, jestliže
predikát P(x) je splnitelný, ale jinak je nepravdivý
pouzdro.
Symbol x se nazývá existenciální kvantifikátor a
výraz x, ve kterém je tento kvantifikátor předřazen
proměnná x se čte takto:
„Existuje x takových, že...“
"pro nějaké x,..."
Kvantifikátor existence
NAPŘÍKLADx(x>2) – pravdivé existenciální tvrzení
x(x=x+1) je nepravdivé existenciální tvrzení.
Jestliže P(x) je unární predikát definovaný na
konečná množina (a1,a2,…am), pak
P(x) P(a1) P(a2) ... P(am)
Kvantifikátor existence
Takže kvantifikátorexistenci lze chápat jako
operátor disjunkce by
kvantifikovaná proměnná.
10. Příklady
Příklady záznamů vzorců a jejich slovních vyjádření:x(x 2 1 (x 1)(x 1)) Pro všechna x je predikát splněn...
x(x0)
nerovnost...
x(x0)
Za všechny x, spravedlivé....
y (5 y 5)
Existuje y takové, že 5+y=5
y(y 2 y 1 0)
Pro všechna y je predikát splněn
y(y 2 y 1 0)
Existuje y, že….
x(x x)
Pro některé x pravda
3
2
11. Vzorce predikátové logiky
Predikátová logika má následující symboliku:Symboly p, q, r, ... jsou výrokové proměnné, které berou
dvě hodnoty: 1 - pravda, 0 - nepravda.
Předmětové proměnné – x, y, z, …, které běží
hodnoty z nějaké množiny M;
x0, y0, z0 – předmětové konstanty, tedy hodnoty předmětu
proměnné.
P(·), Q(·), F(·), … - jednomístné predikátové proměnné;
Q(·,·,…,·), R(·,·, …,·) je n-místných predikátových proměnných.
P0(·), Q0(·,·, …,·) jsou symboly konstantních predikátů.
Symboly logických operací: , .
Symboly kvantifikátorových operací: x, x.
Pomocné znaky: závorky, čárky.
12. Vzorce predikátové logiky
Předmětová proměnná se nazývá volná, pokud jenenásleduje bezprostředně za kvantifikátorem a není součástí
rozsah kvantifikátoru na této proměnné, všechny ostatní
proměnné,
doručená pošta
PROTI
vzorec
jsou nazývány
připojeno.
y z (P(x,y) P(y,z))
Vzorce predikátové logiky jsou:
Každé predikátové písmeno a predikátové písmeno s
následované předmětovými proměnnými v závorkách.
Výrazy ve tvaru F G, F G, G, F G, F G, (y)F,
(y)G, kde F a G jsou predikátové logické formule, proměnná
mysl.
13. Vzorce predikátové logiky
Každý výrok je zároveň variabilní akonstanta, je formule (elementární).
A
Jestliže F(·,·, …,·) je n-ární predikátová proměnná
nebo konstantní predikát a x1, x2,…, xn jsou objektivní
proměnné nebo předmětové konstanty (ne
jsou nutně všechny odlišné), pak F(x1, x2,…, xn) je
vzorec. Tento vzorec se nazývá elementární, in
jeho předmětové proměnné jsou volné, nikoli
přidružené kvantifikátory.
14. Vzorce predikátové logiky
Jestliže A a B jsou vzorce a takové, že jsou stejnépředmětná proměnná není v jednom z nich
vázaný a volný v druhém, pak slova A B,
A B, A B jsou vzorce. V těchto vzorcích ty
proměnné, které byly v původních vzorcích
svobodní jsou svobodní a ti, kteří byli
připojeny, jsou připojeny.
Je-li A vzorec, pak A je vzorec a znak
předmětové proměnné při přechodu ze vzorce A na
vzorec A se nemění.
15. Vzorce predikátové logiky
Jestliže A(x) je vzorec, ve kterém je podmětvolně vstupuje proměnná x, pak slova xA(x) a
xA(x) jsou formule, navíc předmět
proměnná je v nich zahrnuta připojena.
Každé slovo kromě těch jmenovaných
vzorce v předchozích odstavcích není
vzorec.
16. Vzorce predikátové logiky
Například pokud P(x) a Q(x,y) jsou jednoduché advojité predikáty a q, r jsou proměnné
příkazy, pak vzorce budou výrazy:
q, P(x), P(x) Q(x, y), xP(x) xQ(x, y), (Q(x, y) q) r
0
Například slovo není vzorec: xQ(x, y) P(x)
Zde je porušena podmínka klauzule 3, protože vzorec
xQ(x,y) se proměnná x jeví jako vázaná a ve vzorci
P(x) proměnná x vstupuje volně.
Z definice formule predikátové logiky je zřejmé, že
každá formule výrokové algebry je
formule predikátové logiky.
17. Výklad predikátové formule
Výklad vzorce predikátového počtuse nazývá konkretizace množin, ze kterých
předmětové proměnné nabývají hodnot a
Specifikace
vztahy
A
relevantní
sady pravdy pro každé písmeno predikátu.
18. Vzorce predikátového počtu
identickýpravda v
žádný
výklady,
těch.
univerzálně platné
identický
Nepravdivé
na
žádný
výklady,
těch.
kontroverzní
proveditelný
(vzorce,
pravda
což závisí
z
výklady)
19. Význam formule predikátové logiky
Jako příklad zvažte vzorecy z (P(x, y) P(y, z))
Ve vzorci je definován dvoumístný predikát P(x, y).
množina MхM, kde M=(0,1,2,…,n,…), tzn. MxM=NxN.
Vzorec obsahuje predikát proměnné P(x,y), předmět
proměnné x,y,z, z nichž dvě y a z jsou spojeny kvantifikátory,
a x je zdarma.
Pojďme vzít
za
charakteristický
význam
predikát
P(x,y)
pevný predikát P0(x,y): „x
Pak pro hodnoty y menší než x0=5 je predikát P0(x0,y)
má hodnotu „nepravda“ a implikaci P(x,y) P(y,z), když
všechny z M mají hodnotu „true“, tzn. prohlášení
má význam „pravda“.
20. Ekvivalentní formule predikátové logiky
Definice 1.ekvivalent na doméně M, pokud vezmou
stejné logické hodnoty pro všechny zahrnuté hodnoty
z proměnných přiřazených k oblasti M.
Definice 2.
Jsou volány dvě predikátové logické formule A a B
ekvivalentní, pokud jsou rovnocenné v jakékoli oblasti.
21. Ekvivalentní formule predikátové logiky
Nechť A(x) a B(x) jsou proměnné predikáty a C je proměnnápříkaz (nebo vzorec neobsahující x). Pak mají
umístit následující ekvivalence:
22. Ekvivalentní formule predikátové logiky
PříkladPredikát Matka(x,y) znamená, že x je matkou y.
Pak y xMatka(x,y) znamená, že každý člověk má
matka, je pravdivé tvrzení.
x yMatka(x,y) znamená, že existuje matka všech lidí, což
je další tvrzení, na kterém závisí pravdivost
množiny hodnot, které y může nabývat: pokud ano
mnoho bratří a sester, pak je to pravda, jinak
případě je to nepravdivé.
Tedy přeskupení univerzálních kvantifikátorů a
existence může změnit význam a význam výrazu.
23. Zákony logických operací (obecně platné formule predikátové logiky)
24. Cvičení
Najděte negaci následujících vzorců25. Cvičení
ACvičení
Dokažte rovnocennost
x(A(x) B(x)) xA(x) xB(x)
Nechť predikáty A(x) a B(x) jsou shodně nepravdivé. Pak to bude
nepravda a predikát A(x) B(x)
x(A(x) B(x))
V tomto případě budou prohlášení nepravdivá
xA(x) xB(x)
Nechť alespoň jeden z predikátů (například A(x)) ne
stejně falešné. Pak to nebude identicky nepravdivé a
predikát A(x) B(x)
V tomto případě budou tvrzení xA(x) x(A(x) B(x)) pravdivá
To znamená, že původní vzorce budou také pravdivé
Proto: x(A(x) B(x)) xA(x) xB(x)
26.
Na vlastní pěstPro podrobnější studium materiálu
čteme sami:
UČEBNICE: „Matematická logika a teorie
algoritmy",
autor Igoshin V.I.
Strany 157-164
Strany 165-178
Strany 178-183
27.
Domácí práceDokažte rovnocennost
C xA(x) x(C A(x))
Dokažte, že vzorec je obecně platný
A V (P(x) Q(x)) xP(x) xQ(x)
Dokažte, že vzorec je nekonzistentní
A x((F (x) F (x)) (F (x) F (x)))
Funkční povaha predikátu znamená zavedení dalšího pojmu - kvantifikátor. (kvantové – z latiny „kolik“) Kvantifikátorové operace lze považovat za zobecnění operací konjunkce a disjunkce v případě konečných a nekonečných oblastí.
Obecný kvantifikátor (všichni, všichni, všichni, jakýkoli (všichni – „všichni“)). Odpovídající slovní výraz zní takto:
"Pro každé x platí P(x)." Výskyt proměnné ve vzorci může být vázán, pokud se proměnná nachází buď bezprostředně za znaménkem kvantifikátoru, nebo v rozsahu kvantifikátoru, za kterým se proměnná objevuje. Všechny ostatní výskyty jsou volné, přechod z P(x) na x(Px) nebo (Px) se nazývá vazba proměnné x nebo připojení kvantifikátoru k proměnné x (nebo k predikátu P) nebo kvantifikace proměnné x. Zavolá se proměnná, ke které je připojen kvantifikátor příbuzný, je volána nesouvisející kvantizační proměnná volný, uvolnit.
Například proměnná x v predikátu P(x) se nazývá volná (x je libovolné z M), ve výroku P(x) se proměnná x nazývá vázaná proměnná.
Ekvivalence je pravdivá: P(x 1)P(x 2)…P(x n),
P(x) – predikát definovaný na množině M=(x 1,x 2 ...x 4)
Kvantifikátor existence(existovat – „existovat“). Odpovídající slovní výraz je: "Existuje x takové, že P(x) je pravdivé." Výrok xP(x) již nezávisí na x, proměnná x je spojena kvantifikátorem.
Ekvivalence je spravedlivá:
xP(x) = P(x 1)P(x 2)…P(x n), kde
P(x) je predikát definovaný na množině M=(x 1 ,x 2 …x n ).
Obecný kvantifikátor a existenční kvantifikátor se nazývají duální, někdy se používá zápis kvantifikátoru! - "existuje, a navíc jen jeden."
Je zřejmé, že výrok xP(x) je pravdivý pouze v jedinečném případě, kdy P(x) je shodně pravdivý predikát, a výrok je nepravdivý pouze tehdy, je-li P(x) shodně nepravdivý predikát.
Operace s kvantifikátorem platí také pro predikáty s více místy. Aplikace kvantifikátorové operace na predikát P(x,y) vzhledem k proměnné x dává do souladu s dvoumístným predikátem P(x,y) jednomístný predikát xP(x,y) nebo xP( x,y), v závislosti na y a nezávisle na x.
Na dvoumístný predikát můžete použít operace kvantifikátoru na obě proměnné. Pak dostaneme osm výroků:
1. P(x,y); 2. P(x,y);
3. P(x,y); 4. P(x,y);
5. P(x,y); 6. P(x,y);
7. P(x,y); 8. P(x,y)
Příklad 3 Zvažte možné možnosti připojení kvantifikátorů k predikátu P(x,y) – “X děleno y“, definované na množině přirozených čísel (bez nuly) N. Uveďte slovní formulace přijatých výroků a určete jejich pravdivost.
Operace připojení kvantifikátorů vede k následujícím vzorcům:
Tvrzení „pro libovolná dvě přirozená čísla je jedno dělitelné druhým“ (nebo 1) všechna přirozená čísla jsou dělitelná libovolným přirozeným číslem; 2) libovolné přirozené číslo je dělitelem libovolného přirozeného čísla) nepravda;
Tvrzení „existují dvě přirozená čísla, z nichž první je dělitelné druhým“ (1. „existuje přirozené číslo x, které je dělitelné nějakým číslem y“; 2. „existuje přirozené číslo y, které je dělitelem některá čísla přirozených čísel x") jsou pravdivá;
Tvrzení „existuje přirozené číslo, které je dělitelné libovolným přirozeným číslem“ je nepravdivé;
Tvrzení „pro každé přirozené číslo existuje přirozené číslo, které je dělitelné prvním“ (nebo pro každé přirozené číslo existuje dělenec) je pravdivé;
Tvrzení „pro každé přirozené číslo x existuje přirozené číslo y, kterým je dělitelné“ (nebo „pro každé přirozené číslo existuje dělitel“) je pravdivé;
Tvrzení „existuje přirozené číslo, které je dělitelem každého přirozeného čísla“ je pravdivé (takový dělitel je jedna).
V obecném případě se změnou pořadí kvantifikátorů mění význam výroku a jeho logický význam, tzn. například výroky P(x,y) a P(x,y) jsou různé.
Nechť predikát P(x,y) znamená, že x je matkou y, pak P(x,y) znamená, že každý člověk má matku – pravdivé tvrzení. P(x,y) znamená, že existuje matka všech lidí. Pravdivost tohoto tvrzení závisí na množině hodnot, které y může nabývat: pokud je to množina sourozenců, pak je pravdivá, jinak je nepravdivá. Přeskupení kvantifikátorů univerzálnosti a existence tedy může změnit samotný význam a význam výrazu.
a) nahraďte počáteční znaménko (nebo) opačným
b) před zbytek predikátu dejte znaménko
Operátor s jehož pomocí asi k.-l. samostatný objekt se přemění na prohlášení o kolekci (množině) takových objektů.
V logice se používají dva základní kódy: kód obecnosti „V“ a kód existence „E“. V přirozeném jazyce jsou vzdálenými sémantickými analogy konceptu komunity slova „všichni“, „jakýkoli“, „všichni“; sémantickými analogy K. existence jsou slova „nějaký“, „existuje“. Pomocí K dat lze jakýkoli atributivní výrok typu P(x), že objekt x je inherentní v P, transformovat na odpovídající kvantifikátorový výrok typu VxP(x) a typu ZxP(x). V obsahu samotný kvantifikátorový vzorec „VxP(x)“ zní jako „pro všechna x existuje P(x)“ a vzorec „ExP(x)“ - jako „pro některé x existuje P(x)“. Příkaz ve tvaru VxP(x) je pravdivý, pokud má libovolné x vlastnost P; a je nepravdivé, pokud alespoň jedno x nemá vlastnost P. Podobně výrok ve tvaru ZxP(x) je pravdivý, pokud alespoň jedno x má vlastnost P; a nepravda, pokud žádné x nemá vlastnost P.
Na základě základních kvantifikátorových vzorců „VxP(x)“, „ExP(x)“ lze konstruovat další, složitější kvantifikátorové vzorce. Logické vztahy mezi takovými formulemi jsou studovány v predikátové logice. Zejména vzorec „ZxP(x)“ je logicky ekvivalentní vzorci „“) VxKVANTITOR| P(x)“ a vzorec „VxP(x)“ je ekvivalentní vzorci „“) Eх) P(x)“, kde „“)“ jsou negace.
V implicitní podobě byly logiky používány již Aristotelem, ale v přísném věcném a formálním smyslu byly poprvé zavedeny do logiky G. Frege.
Filosofie: Encyklopedický slovník. - M.: Gardariki. Editoval A.A. Ivina. 2004 .
(z lat. kvantum - kolik), predikátový logický operátor, aplikovaný na vzorce obsahující pouze jednu volnou proměnnou (prohlášení). Existují K. komunity, označené symbolem (z Angličtina vše - všechno), a K. existence (od existovat - existovat): xP(x) je interpretováno (cm. Výklad) jako „pro všechna x platí vlastnost P“ a xP(x) – jako „existuje x tak, že vlastnost?(x)“ platí. Li (vesmír) je konečný, pak xP(x) je ekvivalentní konjunkci všech formulí P (A), kde a je prvek předmětové oblasti. Podobně je xP(x) ekvivalentní disjunkci všech formulí ve tvaru? (A). Pokud je předmětná oblast nekonečná, pak xP (X) a xP(x) lze interpretovat jako nekonečno, respektive disjunkci. Úvod do K. v logice vícemístných predikátů (tj. nezadaný) způsobuje nerozhodnutelnost predikátového počtu. Různé vztahy mezi principy obecnosti a existence a logickými konektivy výrokové logiky jsou formalizovány v predikátovém počtu.
Filosofický encyklopedický slovník. - M.: Sovětská encyklopedie. Ch. střih: L. F. Iljičev, P. N. Fedosejev, S. M. Kovalev, V. G. Panov. 1983 .
(z lat. kvantové - jak moc) - logické. operátor aplikovaný na log. výrazy a udávání veličin. charakteristika domény objektů (a někdy domény predikátů), která zahrnuje to, co je získáno jako výsledek aplikace K. Jak logické Prostředky výrokové logiky k vyjádření forem obecných, partikulárních a individuálních soudů nestačí, v predikátové logice, získané rozšířením výrokové logiky zavedením principů, jsou takové soudy vyjádřitelné. Tedy například čtyři základní. formy soudů tradic. logiky „Všechna A jsou B“, „Ne A je B“, „Některá A jsou B“ a „Některá A nejsou B“ lze zapsat (pokud pomineme předpokládaný požadavek aristotelské logiky na neprázdnost A). v obecných soudech) pomocí symboliky vysvětlené níže takto: ∀(x) (A (x) ⊃ B (x)), ∀(x) (A (x) ⊃ B(x)), ∃(x) (A (x) & B (x)) a ∃ (x) (A (x) & B (x)). Úvod K. umožňuje zapsat jej formalizovaným logickým způsobem. jazyk vyjadřování přírody. jazyky obsahující množství. charakteristika k.-l. předmětové nebo predikátové oblasti. Přirozeně V jazycích jsou nositeli takových vlastností tzv. kvantifikační slova, mezi které patří zejména veličiny. číslovky, zájmena „všechny“, „každý“, „některé“, sloveso „existuje“, přídavná jména „jakýkoli“, „každý“, „jeden“, příslovce „nekonečně mnoho“ atd. Ukazuje se, že všechna uvedená kvantifikační slova vyjádřit formalismem. jazyky a logika V kalkulu stačí dva nejpoužívanější. K.: K. obecnost (nebo obecnost), obvykle označovaná symbolem ∀ (obrácené písmeno A - počáteční písmeno anglického slova „all“, německého „alle“ atd.), a K. existence, obvykle označovaná symbolem ∃ (obrácené písmeno E je počáteční písmeno anglického slova „exist“, německého „existieren“ atd.); za znaménky ∀ a ∃ v zápisu kvantorické proměnné následuje písmeno určité abecedy, nazývané kvantifikátorová proměnná, která se obvykle považuje za součást zápisu kvantorické proměnné: ∀x, ∀y, ∀F, ∃x, ∃α atd. Pro K. obecnosti se také používají následující zápisy:
pro existenci K.:

Znak K. se umístí před výraz, na který se K. vztahuje (operace aplikace K. se často nazývá kvantifikace); tento výraz je uzavřen v závorkách (které se často vynechávají, pokud to nevede k nejednoznačnosti). Výraz ∀x (A (x)) obsahující obecný princip zní jako „Pro všechna x platí, že A (x)“, nebo „Pro každé x platí, že A (x)“; Výraz ∃x (A(x)) obsahující K. existence se čte jako „Existuje x takové, že A (x)“ nebo „Pro některé x platí A(x)“. V obou těchto případech se obecně nepředpokládá, že výraz A(x) skutečně závisí na proměnné x (nemusí obsahovat vůbec žádné proměnné, tj. může označovat určitý výrok, v tomto případě nikoli změnit význam tohoto prohlášení). Nicméně hlavní účelem K. jsou výroky z výrazu, který závisí na proměnné kvantifikátoru, nebo alespoň snížení počtu proměnných, na kterých tento výraz, jakožto otevřený (otevřený) vzorec (viz uzavřený vzorec), závisí. Například výraz (y>0&z>0&x=y-z) obsahuje tři proměnné (x, y a z) a stává se výrokem (pravda nebo nepravda), když k.-l. def. nahrazení těchto proměnných jmény určitých objektů z rozsahu jejich hodnot. Výraz ∃ z(y>0&z>0&x = y-z) závisí pouze na dvou proměnných (x a y) a ∃y∃z (y>0&z>0& &x = y –z) - na jednom x. Poslední formule tedy vyjadřuje určitou vlastnost (jednomístnou). Nakonec vzorec ∃х∃у∃z (y>0&z>0&x=y–z) vyjadřuje zcela definovaný prohlášení.
Dr. příklady vzorců obsahujících K.: 1) ∀x(x>0); 2) ∃x(x>0); 3) ∀х (2+2=5); 4) ∃x (2+2=4); 5) ∀x (x = x)& (x+2=y); 6) x ∃y jsou části vzorce napravo od nich a definiční obor vzorce (x = z⊃x ≠ 0).Výskyt určité proměnné ve znaménku vzorce nebo v akční doména vzorce obsahujícího tuto proměnnou , se nazývá vázaný výskyt proměnné ve vzorci. V ostatních případech se výskyt proměnné nazývá volný. Stejná se může objevit v určitém vzorci na jednom místě v vázaný tvar, a na jiném.místě - na volném místě.To je např. vzorec 5: první tři (počítáno zleva) výskyty proměnné x v něm jsou spojené, poslední je volný. Někdy říkají, že proměnná je v daném vzorci spojena, pokud jsou všechny její výskyty v tomto vzorci spojeny. V matematice a logice lze jakýkoli výraz obsahující volnou proměnnou považovat (v neformálním přístupu) za to, že v obvyklém smyslu slova závisí na různých hodnotách této proměnné; tím, že této proměnné dáme různé významy (tj. nahradíme všechny její volné výskyty jménem určitého objektu patřícího do rozsahu hodnot této proměnné), získáme různé (obecně řečeno) významy tohoto výrazu v závislosti na hodnotě. proměnné, tj. z konstanty nahrazené místo toho. Pokud jde o vázané proměnné, výrazy, které je uzavírají, na nich ve skutečnosti nezávisí. Například výraz ∃x(x = 2y) v závislosti na y (které je v něm volně obsaženo) je ekvivalentní výrazům ∃z(z = 2y), ∃u(u = 2y) atd. Toto je logické výrazy z přidružených proměnných v nich obsažených se nacházejí v tzv. pravidlo pro přejmenování souvisejících proměnných, postulované nebo odvozené v dep. logický počet (viz Proměnná, Predikátový počet).
Výše uvedený výklad významu K. souvisel s obsahem log. teorie. Pokud jde o správné výpočty. smyslu (tzv. formální systémy), pak v nich nemá vůbec smysl hovořit o „smyslu“ toho či onoho kalkulu, který je zde prostě určitým symbolem kalkulu. Otázka smyslu (významu) kalkulu se zcela vztahuje k oblasti interpretace kalkulu. Při aplikaci na K. můžeme hovořit minimálně o třech výkladech: klasickém, intuicionistickém a konstruktivním, odpovídajícím různým pojetím existence a univerzality v logice a matematice (viz Intuicionismus, Konstruktivní logika). V klasickém i intuicionistickém (konstruktivním) predikátovém kalkulu jsou metody inference v případech, kdy originál nebo dokazované formule obsahují formuli, popsány stejným tzv. predikátovým kalkulem. kvantifikační postuláty, např. Bernaysovy postuláty.
Principy obecnosti a existence nevyčerpávají druhy principů používané v logice Rozsáhlé principy jsou t. zv. omezené kvantové rovnice tvaru ∀xP(x)A(x) nebo ∃xQ(x)A(x), ve kterých je rozsah změny kvantifikátorové proměnné x „omezován“ nějakým speciálním predikát P(x) (nebo Q(x)). Omezené K. se pomocí stop redukují na K. obecnosti a existence. ekvivalence: ∀xP(x)A(x) KVANTITOR ∀x(P(x) ⊃A(x)) a ∃xQ(x)A(x) KVANTITOR ∃x(Q(x)&A(x)). Často používané K. jednoznačnosti ∃!xA(x) („existuje jedinečné x takové, že A(x)“) je vyjádřeno například také K. obecnosti a existence. tedy: xA(x) KVANTITOR ∃xA(x)& ∀y∀z(A(y)&A(z)⊃y=z).
Používají se i další typy výpočtů, na které se pojem omezený výpočet nevztahuje, jedná se o „numerické“ výpočty ve tvaru ∃xnA(x) („existuje právě n různých x takových, že A(x)“), používá se v intuicionistické logice výpočtu „kvazi-existence“ ∃ xA(x), nebo („není pravda, že neexistuje x takové, že A(x)“); s t.zr. klasický v logice Q. „kvazi-existence“ se neliší od Q. existence, v intuicionistické logice věta ∃xA(x), která neříká nic o existenci algoritmu pro nalezení takového x, že A( x), ve skutečnosti tvrdí pouze „kvazi“ takových x a K. nekonečno ∃x∞A(x) („existuje nekonečně mnoho x takových, že A(x)“). Výrazy obsahující principy nekonečna a číselné členy lze také zapsat pomocí termínů obecnosti a existence. V rozšířeném predikátovém počtu se koeficienty berou nejen u předmětových proměnných, ale i u predikátových proměnných, tzn. jsou uvažovány vzorce ve tvaru ∃F∀xF(x), ∀Ф∃у(Ф(y)) atd.
lit.: Gilbert D. a Ackerman V., Základy teoretické logiky, přel. z angličtiny, M., 1947, str. 81-108; Tarski A., Úvod do logiky a metodologie deduktivních věd, přel. z angličtiny, M., 1948, asi. 36-42, 100-102, 120-23; Kleene S.K., Úvod do metamatematiky, přel. z angličtiny, M., 1957, str. 72-80, 130-38; Church A., Úvod do matematické logiky, přel. z angličtiny, díl 1, str. 42–48; Kuzněcov A.V., Logické kontury algoritmu, překlad ze standardizovaného ruského jazyka do informačně logického jazyka, in: Abstrakty zpráv z konference o zpracování informací, strojovém překladu a automatickém čtení textu, M., 1961; Mostowski A., O zobecnění kvantifikátorů, "Fundam. math.", 1957, t. j. 44, č. 1, s. 12–36; Hailperin T., Teorie omezené kvantifikace, I–II, "J. Symb. Logic", 1957, v. 22, č. 1, str. 19–35, č. 2, s. 113–29.
Yu, Gastev. Moskva.
Filosofická encyklopedie. V 5 svazcích - M.: Sovětská encyklopedie. Redakce F. V. Konstantinova. 1960-1970 .
Synonyma:
Podívejte se, co je „QUANTITOR“ v jiných slovnících:
Podstatné jméno, počet synonym: 1 operátor (24) Slovník synonym ASIS. V.N. Trishin. 2013… Slovník synonym
kvantifikátor- - Tematika telekomunikací, základní pojmy EN kvantifikátor... Technická příručka překladatele
Kvantifikátor je obecný název pro logické operace, které omezují doménu pravdivosti predikátu a vytvářejí výrok. Nejčastěji zmiňovaný: Kvantifikátor univerzálnosti (označení: , zní: „pro všechny...“, „pro každého...“ nebo „každý...“ ... Wikipedie
Obecný název pro logické operace, které používají predikát P(x) ke konstrukci výroku, který charakterizuje doménu pravdivosti predikátu P(x). V matematice V logice se nejčastěji používá kvantifikátor univerzálnosti a kvantifikátor existence Výrok znamená... ... Matematická encyklopedie
Kvantifikátor- (z latinského quantum kolik) symbol používaný k označení určitých operací matematické logiky, zároveň logická operace, která udává kvantitativní charakteristiku pole objektů, ke kterým se výraz dostal v ... ... Počátky moderní přírodní vědy
Kromě nám známých logických operací pro predikáty jsou zavedeny dvě nové: operace připojování kvantifikátorů existence a obecnosti.
"pro všechny X" (pro každého X, pro každého X) je nazýván obecný kvantifikátor a je určeno X.
Výrok „existuje X" (pro některé X, alespoň pro jednoho X, existuje něco takového X) je nazýván kvantifikátor existence a je určeno X.
Tvrzení „je jen jeden“ X“ (pro jeden význam X) je nazýván kvantifikátor jedinečnosti : ! X.
Například: "Všechny keře jsou rostliny." Tento příkaz obsahuje obecný kvantifikátor („vše“). Výrok „existují čísla, která jsou násobky 5 "obsahuje existenciální kvantifikátor ("existovat").
Abychom získali výrok z vícemístného predikátu, je nutné propojit každou proměnnou s kvantifikátory. Například, Li P(x;y) je tedy dvoumístný predikát (xX) (yY) P(x; y)- prohlášení.
Pokud není každá proměnná spojena kvantifikátorem, pak to, co se získá, není výrok, ale predikát v závislosti na proměnné, která není spojena kvantifikátorem. Tedy pokud před predikátem P(x;y) vložte kvantifikátor y, pak dostaneme predikát (yY) P(x; y), v závislosti na proměnné X.
Pojďme zjistit, které z následujících vět jsou výroky a které predikáty: a) existuje takový X, Co x+y = 2;
b) pro jakékoli X A na existuje rovnost x + y = y + x.
Řešení: Pojďme identifikovat logickou strukturu těchto vět.
a) Věta „Existuje taková věc“ X, Co x + y = 2“ lze zapsat ve tvaru (xR) x + y = 2. Protože pouze proměnná x je spojena s kvantifikátorem, je daná věta se dvěma proměnnými predikátem.
b) Nabídka „pro jakékoli X A na dochází x + y = y + x“ lze zapsat ve tvaru : (xR) (yR) x + y = y + x, Kde obě proměnné spolu souvisí. Proto je tato věta konstatováním.
Pokud žádná objektivní proměnná ve vzorci není spojena s kvantifikátorem, pak je volána volné proměnné.
Například: (x) xy=uh. Tady je proměnná na není vázán žádným kvantifikátorem, je tedy volný. Pravdivost daného tvrzení na něm nezávisí.
Kvantifikátory (x) (x) jsou nazývány dvojí navzájem.
Stejnojmenné kvantifikátory lze zaměnit, což nemá vliv na pravdivost tvrzení.
Například: (y) (x) x + y = 5. Tento prohlášení má to samé význam, co a (x) (y) x + y = 5.
U odlišných kvantifikátorů může změna pořadí vést ke změně pravdivosti tvrzení.
Například: (x) (y) x<у , tj. pro libovolné číslo X je jich víc na- pravdivé tvrzení.
Pojďme si vyměnit kvantifikátory: (x) (y) x
V souvislosti se zavedením kvantifikátorů je třeba vzít v úvahu následující:
1. Formule predikátové logiky nemůže obsahovat stejnou účelovou proměnnou, která by byla v jedné části formule vázána a v jiné volná.
2. Stejná proměnná nemůže být v oblasti kvantifikátorů, které jsou navzájem duální.
Porušení těchto podmínek se nazývá proměnná kolize.
Jak se stanoví pravdivostní hodnota výroku s kvantifikátorem?
Dokázat tvrzení obecným kvantifikátorem musíte se ujistit, že při dosazování každé z hodnot X do predikátu P(x) to druhé se promění ve pravdivé tvrzení. Jestliže množina X je konečná, pak toto může být děláno výčtem všech případů; je-li množina X nekonečná, pak je nutné provést uvažování v obecné formě.
Prohlášení (x) P(x) false, pokud lze takovou hodnotu zadat AX, při kterém P(x) se změní v nepravdivé tvrzení R(a). Proto, vyvrátit tvrzení obecným kvantifikátorem Stačí uvést příklad.
Prohlášení (x) P(x) true, pokud lze takovou hodnotu zadat AX, při kterém P(x) promění v pravdivé tvrzení R(a). Proto v pořádku ověřit pravdivost tvrzení pomocí kvantifikátoru existence , stačí uvést příklad a tím to dokázat.
V následujících situacích ověřit nepravdivost tvrzení s kvantifikátorem existence (x) P(x), je nutné ověřit nepravdivost každého P(x), P(x), …, P(x). Pokud je sada X To lze samozřejmě provést i hrubou silou. Pokud je jich mnoho X nekonečně, pak je nutné usuzovat v obecné formě.
Příklady.
1. Najděte pravdivostní hodnotu „mezi čísly“ 1, 2, 3, 4 existuje prvočíslo."
Řešení: Výrok obsahuje existenciální kvantifikátor a lze jej tedy reprezentovat jako disjunkci výroků: „ 1 - prvočíslo" nebo " 2 - prvočíslo" nebo " 3 - prvočíslo" nebo " 4 - Prvočíslo". K prokázání pravdivosti disjunkce stačí pravdivost alespoň jednoho tvrzení, například „ 3 je prvočíslo, které je pravdivé. Proto je původní tvrzení také pravdivé.
2. Dokažme, že každý čtverec je obdélník.
Řešení: Příkaz obsahuje obecný kvantifikátor. Proto může být prezentován jako spojení: „čtverec - obdélník“ a „čtverec - obdélník“ a „čtverec - obdélník“ atd. Protože všechny tyto výroky jsou pravdivé, pak spojení těchto výroků je pravdivé, proto je pravdivá původní věta.
3. "Každý trojúhelník je rovnoramenný." Toto je nepravdivé tvrzení. K ověření stačí nakreslit trojúhelník, který není rovnoramenný.a
Sestavit negaci výroku s kvantifikátory nutné:
1) nahradit kvantifikátor obecnosti kvantifikátorem existence a kvantifikátor existence kvantifikátorem obecnosti;
2) nahraďte predikát jeho negací.
Příklad. Formulujme negaci pro následující tvrzení:
a) všechny prvky sady Z dokonce; b) některá slovesa odpovídají na otázku „co dělat?“.
Řešení: a) Nahraďme kvantifikátor obecnosti kvantifikátorem existence a jeho tvrzení jeho negací: některé prvky množiny Z zvláštní.
b) Nahraďme kvantifikátor existence kvantifikátorem obecnosti a jeho vyjádření negací: všechna slovesa neodpovídají na otázku „co dělat?“
Predikát (lat. praedicatum- uvedl, zmínil, řekl) - jakýkoli matematický výrok, ve kterém je alespoň jedna proměnná. Predikát je hlavním předmětem studia v logice prvního řádu.
Predikát je výraz s logickými proměnnými, které mají smysl pro jakékoli platné hodnoty těchto proměnných.
Výrazy: x > 5, x > y – predikáty.
Predikát ( n-místní, popř n-ary) je funkce se sadou hodnot (0,1) (nebo „false“ a „true“), které jsou definovány na množině. Tedy každá množina prvků množiny M charakterizováno buď jako „pravda“ nebo „nepravda“.
Predikát může být spojen s matematickým vztahem: jestliže n-ka patří do relace, pak na ní predikát vrátí 1. Zejména unární predikát definuje vztah příslušnosti k určité množině.
Predikát je jedním z prvků logiky prvního a vyšších řádů. Počínaje logikou druhého řádu lze kvantifikátory umístit na predikáty ve vzorcích.
Predikát se nazývá stejně pravdivé a piš:
pokud na libovolné sadě argumentů nabývá hodnotu 1.
Predikát se nazývá stejně nepravdivé a piš:
pokud na libovolné sadě argumentů nabývá hodnoty 0.
Predikát se nazývá proveditelný, pokud má hodnotu 1 alespoň na jedné sadě argumentů.
Protože predikáty mají pouze dva významy, jsou na ně použitelné všechny operace Booleovy algebry, například: negace, implikace, konjunkce, disjunkce atd.
Kvantifikátor je obecný název pro logické operace, které omezují doménu pravdivosti predikátu. Nejčastěji zmiňované:
Univerzální kvantifikátor(označení: zní: „pro všechny...“, „pro všechny...“ nebo „každý...“, „jakýkoli...“, „pro všechny...“).
Kvantifikátor existence(označení: , zní: „existuje...“ nebo „bude nalezen...“).
Příklady
Označme P(X) predikát" X dělitelné 5." Pomocí obecného kvantifikátoru můžeme formálně napsat následující tvrzení (samozřejmě nepravdivá):
jakékoli přirozené číslo je dělitelné 5;
každé přirozené číslo je násobkem 5;
všechna přirozená čísla jsou násobky 5;
následujícím způsobem:
![]() .
.
Následující (již pravdivá) tvrzení používají existenciální kvantifikátor:
existují přirozená čísla, která jsou násobky 5;
existuje přirozené číslo, které je násobkem 5;
alespoň jedno přirozené číslo je dělitelné 5.
Jejich formální zápis:
![]() .Úvod do konceptu
.Úvod do konceptu
Nechť je na množině X prvočísel dán predikát P(x): "Prvočíslo x je liché." Před tento predikát dosadíme slovo „jakýkoli“. Dostaneme nepravdivé tvrzení „jakékoli prvočíslo x je liché“ (tento výrok je nepravdivý, protože 2 je prvočíslo sudé).
Dosazením slova „existuje“ před daný predikát P(x) získáme pravdivé tvrzení „Existuje prvočíslo x, které je liché“ (např. x = 3).
Z predikátu tedy můžete udělat výrok tak, že před predikát umístíte slova „vše“, „existuje“ atd., v logice nazývaná kvantifikátory.
Kvantifikátory v matematické logice
Příkaz znamená, že rozsah proměnné X zahrnuto do domény pravdivosti predikátu P(X).
(„Pro všechny hodnoty (x) platí tvrzení.)
Výrok znamená, že doména pravdivosti predikátu P(X) je neprázdný.
(„Existuje (x), pro které je tvrzení pravdivé“).
Otázka 31 Graf a jeho prvky. Základní pojmy. Incidence, multiplicita, smyčka, spojitost. Typy grafů. Trasa v grafu a její délka. Klasifikace cest. Matice sousedství orientovaných a neorientovaných grafů.
V matematické teorii grafů a informatice je graf souborem neprázdné množiny vrcholů a množiny dvojic vrcholů.
Objekty jsou reprezentovány jako vrcholy nebo uzly grafu a spojení jsou reprezentována jako oblouky nebo hrany. Pro různé oblasti použití se typy grafů mohou lišit směrovostí, omezením počtu spojení a dalšími údaji o vrcholech nebo hranách.
Cesta (nebo řetězec) v grafu je konečná posloupnost vrcholů, ve které je každý vrchol (kromě posledního) připojen k dalšímu v posloupnosti vrcholů hranou.
Orientovaná cesta v digrafu je konečná posloupnost vrcholů v i, pro které všechny páry ( v i,v i+ 1) jsou (orientované) hrany.
Cyklus je cesta, na které se první a poslední vrchol shodují. V tomto případě je délka cesty (nebo cyklu) počtem jejích součástí žebra. Všimněte si, že pokud vrcholy u A proti jsou konce nějaké hrany, pak podle této definice posloupnost ( u,proti,u) je cyklus. Aby se předešlo takovým „degenerovaným“ případům, jsou zavedeny následující pojmy.
Cesta (nebo cyklus) se nazývá jednoduchá, pokud se její okraje neopakují; elementární, pokud je jednoduchý a jeho vrcholy se neopakují. Je snadné vidět, že:
Každá cesta spojující dva vrcholy obsahuje elementární cestu spojující stejné dva vrcholy.
Jakékoliv jednoduché neelementární cesta obsahuje elementární cyklus.
Žádný jednoduchý cyklus procházející nějakým vrcholem (nebo hranou) obsahuje základní(pod)cyklus procházející stejným vrcholem (nebo hranou).
Smyčka je elementární cyklus.
Graf nebo neorientovaný graf G je objednaný pár G: = (PROTI,E
PROTI
E jedná se o množinu dvojic (v případě neorientovaného grafu neuspořádaných) vrcholů, zvaných hrany.
PROTI(a proto E, jinak by šlo o multimnožinu) jsou obvykle považovány za konečné množiny. Mnoho dobrých výsledků získaných pro konečné grafy není pravdivých (nebo se nějakým způsobem liší). nekonečné grafy. Řada úvah se totiž v případě nekonečných množin stává nepravdivými.
Vrcholy a hrany grafu se také nazývají prvky grafu, počet vrcholů v grafu | PROTI| - pořadí, počet hran | E| - velikost grafu.
Vrcholy u A proti se nazývají koncové vrcholy (nebo jednoduše konce) hrany E = {u,proti). Tyto vrcholy zase spojuje hrana. Dva koncové vrcholy stejné hrany se nazývají sousední.
Říká se, že dvě hrany sousedí, pokud mají společný koncový vrchol.
Dvě hrany se nazývají násobky, pokud se množiny jejich koncových vrcholů shodují.
Hrana se nazývá smyčka, pokud se její konce shodují, tzn E = {proti,proti}.
stupeň deg PROTI vrcholy PROTI zavolejte počet hran, které k němu patří (v tomto případě se smyčky počítají dvakrát).
O vrcholu se říká, že je izolovaný, pokud není koncem žádné hrany; visící (nebo list), pokud se jedná o konec právě jedné hrany.
Orientovaný graf (zkrácený digraph) G je objednaný pár G: = (PROTI,A), pro které jsou splněny tyto podmínky:
PROTI je neprázdná množina vrcholů nebo uzlů,
A je to soubor (uspořádaných) párů odlišných vrcholů, nazývaných oblouky nebo směrované hrany.
Oblouk je uspořádaná dvojice vrcholů (v, w), kde je vrchol proti nazvaný začátek a w- konec oblouku. Dá se říci, že oblouk vede shora proti na vrchol w.
Smíšený graf
Smíšený graf G je graf, ve kterém některé hrany mohou být směrovány a některé mohou být neorientované. Psáno jako uspořádaná trojka G: = (PROTI,E,A), kde PROTI, E A A definovány stejně jako výše.
Orientované a neorientované grafy jsou speciální případy smíšených grafů.
Izomorfní grafy (?)
Graf G se nazývá izomorfní vůči grafu H, pokud existuje bijekce F z množiny vrcholů grafu G do množiny vrcholů grafu H, který má následující vlastnost: if v grafu G z vrcholu je hrana A na vrchol B, pak v grafu H F(A) na vrchol F(B) a naopak - pokud je v grafu H z vrcholu je hrana A na vrchol B, pak v grafu G z vrcholu musí být hrana F − 1 (A) na vrchol F − 1 (B). V případě orientovaného grafu musí tato bijekce zachovat i orientaci hrany. V případě váženého grafu musí bijekce zachovat i váhu hrany.
Matice sousedství grafu G s konečným počtem vrcholů n(číslované od 1 do n) je čtvercová matice A velikost n, ve kterém je hodnota prvku a ij rovný počtu hran od i vrchol grafu v j-tý vrchol.
Někdy, zejména v případě neorientovaného grafu, může smyčka (hrana z i vrchol do sebe) se počítá jako dvě hrany, tedy hodnota diagonálního prvku a ii v tomto případě se rovná dvojnásobku počtu smyček kolem i vrchol.
Matice sousedství jednoduchého grafu (neobsahujícího žádné smyčky nebo více hran) je binární matice a obsahuje nuly na hlavní diagonále.
Otázka 32 Funkce. Způsoby zadání. Klasifikace funkcí. Základní elementární funkce a jejich grafy. Složení funkcí. Elementární funkce.
Funkce je matematický pojem, který odráží vztah mezi prvky množin. Můžeme říci, že funkce je „zákon“, podle kterého každý prvek jedné množiny (tzv doména definice ) je uveden do korespondence s některým prvkem jiné množiny (tzv rozsah hodnot ).
Matematický koncept funkce vyjadřuje intuitivní představu o tom, jak jedna veličina zcela určuje hodnotu jiné veličiny. Tedy hodnotu proměnné X jednoznačně definuje význam výrazu X 2, a hodnota měsíce jednoznačně určuje hodnotu měsíce následujícího, také jakákoliv osoba může být srovnávána s jinou osobou - svým otcem. Podobně některé předem vytvořené algoritmy vytvářejí určitá výstupní data na základě měnících se vstupních dat.
Metody pro specifikaci funkce
Analytická metoda
Funkce je matematický objekt, který je binární relací, která splňuje určité podmínky. Funkci lze zadat přímo jako množinu uspořádaných dvojic, například: existuje funkce . Tato metoda je však zcela nevhodná pro funkce na nekonečných množinách (což jsou obvyklé reálné funkce: mocninná, lineární, exponenciální, logaritmická atd.).
Chcete-li zadat funkci, použijte výraz: . přičemž X je proměnná, která prochází doménou definice funkce a y- rozsah hodnot. Tento záznam označuje přítomnost funkčního vztahu mezi prvky množin. X A y může procházet libovolnými soubory objektů jakékoli povahy. Mohou to být čísla, vektory, matice, jablka, barvy duhy. Vysvětlíme na příkladu:
Nechť je soubor jablko, letadlo, hruška, židle a mnoho muž, lokomotiva, náměstí. Definujme funkci f takto: (jablko, osoba), (letadlo, lokomotiva), (hruška, čtverec), (židle, osoba). Zavedeme-li proměnnou x procházející množinou a proměnnou y procházející množinou, lze zadanou funkci analyticky specifikovat jako: .
Číselné funkce lze zadat podobně. Například: kde x prochází množinou reálných čísel a definuje nějakou funkci f. Je důležité pochopit, že výraz sám o sobě není funkcí. Funkce jako objekt je množina (uspořádaných dvojic). A tento výraz jako objekt je rovností dvou proměnných. Definuje funkci, ale není jednou.
V mnoha odvětvích matematiky je však možné pomocí f(x) označit jak funkci samotnou, tak i analytický výraz, který ji definuje. Tato syntaktická konvence je mimořádně pohodlná a oprávněná.
Grafická metoda
Numerické funkce lze také zadat pomocí grafu. Nechť je reálná funkce n proměnných.
Uvažujme nějaký (n+1)-rozměrný lineární prostor nad polem reálných čísel (protože funkce je reálná). Zvolme v tomto prostoru libovolný základ (). Každý bod funkce je spojen s vektorem: . Budeme mít tedy množinu lineárních prostorových vektorů odpovídajících bodům dané funkce podle zadaného pravidla. Body odpovídajícího afinního prostoru budou tvořit určitou plochu.
Vezmeme-li euklidovský prostor volných geometrických vektorů (směrovaných segmentů) jako lineární prostor a počet argumentů funkce f nepřesáhne 2, lze zadanou množinu bodů vizuálně znázornit ve formě kresby (grafu ). Pokud se navíc původní báze považuje za ortonormální, získáme „školní“ definici grafu funkce.
Pro funkce 3 a více argumentů není tato reprezentace použitelná kvůli nedostatku geometrické intuice vícerozměrných prostorů.
Pro takové funkce však lze přijít s vizuální semi-geometrickou reprezentací (například každá hodnota čtvrté souřadnice bodu může být spojena s určitou barvou v grafu)
Proporcionální veličiny. Pokud proměnné y A x jsou přímo úměrné
y = k x,

Kde k- konstantní hodnota ( faktor proporcionality).
Plán přímá úměrnost– přímka procházející počátkem souřadnic a tvořící přímku s osou Xúhel, jehož tečna je rovna k: opálení = k(obr. 8). Proto se také nazývá koeficient proporcionality sklon. Obrázek 8 ukazuje tři grafy pro k = 1/3, k= 1 a k = 3 .
Lineární funkce. Pokud proměnné y A X souvisí rovnicí 1. stupně:
A x + B y = C ,
kde je alespoň jedno z čísel A nebo B není roven nule, pak graf této funkční závislosti je přímka. Li C= 0, pak projde počátkem, jinak ne. Grafy lineárních funkcí pro různé kombinace A,B,C jsou znázorněny na obr.9.

Inverzní úměrnost. Pokud proměnné y A x jsou nepřímo úměrné, pak je funkční vztah mezi nimi vyjádřen rovnicí:
y = k / X,
Kde k- konstantní hodnota.
 Inverzně proporcionální graf – hyperbola(obr. 10). Tato křivka má dvě větve. Hyperboly jsou získány, když se kruhový kužel protíná s rovinou (pro kuželosečky viz část „Kužel“ v kapitole „Stereometrie“). Jak je znázorněno na obr. 10, součin souřadnic bodů hyperboly je konstantní hodnota, v našem příkladu rovna 1. V obecném případě je tato hodnota rovna k, což vyplývá z rovnice hyperboly: xy = k.
Inverzně proporcionální graf – hyperbola(obr. 10). Tato křivka má dvě větve. Hyperboly jsou získány, když se kruhový kužel protíná s rovinou (pro kuželosečky viz část „Kužel“ v kapitole „Stereometrie“). Jak je znázorněno na obr. 10, součin souřadnic bodů hyperboly je konstantní hodnota, v našem příkladu rovna 1. V obecném případě je tato hodnota rovna k, což vyplývá z rovnice hyperboly: xy = k.
Hlavní vlastnosti a vlastnosti hyperboly:
X 0, rozsah: y 0 ;
Funkce je monotónní (klesající) při X< 0a v x> 0, ale ne
celkově monotónní díky bodu zlomu X = 0);
Neohraničená funkce, nespojitá v bodě X= 0, liché, neperiodické;
- Funkce nemá žádné nuly.
Kvadratická funkce. Toto je funkce: y = sekera 2 + bx + C, Kde a, b, c- trvalé, A b=C= 0 a y = sekera 2. Graf této funkce čtvercová parabola - OY, který se nazývá osa paraboly.Tečka Ó vrchol paraboly.

Kvadratická funkce. Toto je funkce: y = sekera 2 + bx + C, Kde a, b, c- trvalé, A 0. V nejjednodušším případě máme: b=C= 0 a y = sekera 2. Graf této funkce čtvercová parabola - křivka procházející počátkem souřadnic (obr. 11). Každá parabola má osu symetrie OY, který se nazývá osa paraboly.Tečka Ó nazýváme průsečík paraboly s její osou vrchol paraboly.
Graf funkce y = sekera 2 + bx + C- také čtvercová parabola stejného typu jako y = sekera 2, ale jeho vrchol neleží v počátku, ale v bodě se souřadnicemi:

Tvar a umístění čtvercové paraboly v souřadnicovém systému zcela závisí na dvou parametrech: koeficientu A na X 2 a diskriminační D:D=b 2 – 4ac. Tyto vlastnosti vyplývají z analýzy kořenů kvadratické rovnice (viz odpovídající část v kapitole „Algebra“). Všechny možné různé případy pro čtvercovou parabolu jsou na obr. 12.
 Hlavní charakteristiky a vlastnosti čtvercové paraboly:
Hlavní charakteristiky a vlastnosti čtvercové paraboly:
Rozsah definice funkce: < X+ (tj. X R), a oblast
hodnoty: … (Odpovězte si na tuto otázku sami!);
Funkce jako celek není monotónní, ale vpravo nebo vlevo od vrcholu
chová se jako monotónní;
Funkce je neomezená, spojitá všude, i když b = C = 0,
a neperiodické;
- na D< 0 не имеет нулей.
 Exponenciální funkce. Funkce y = a x, Kde A- volá se kladné konstantní číslo exponenciální funkce.Argument X přijímá jakékoli platné hodnoty; funkce jsou považovány za hodnoty pouze kladná čísla, protože jinak máme vícehodnotovou funkci. Ano, funkce y = 81X má v X= 1/4 čtyř různých hodnot: y = 3, y = 3, y = 3 i A y = 3 i(Zkontrolujte prosím!). Ale považujeme to pouze za hodnotu funkce y= 3. Grafy exponenciální funkce pro A= 2 a A= 1/2 jsou uvedeny na obr. 17. Procházejí bodem (0, 1). Na A= 1 máme graf přímky rovnoběžné s osou X, tj. funkce se změní na konstantní hodnotu rovnou 1. Když A> 1 exponenciální funkce roste a při 0< A < 1 – убывает. Основные характеристики и свойства показательной функции:
Exponenciální funkce. Funkce y = a x, Kde A- volá se kladné konstantní číslo exponenciální funkce.Argument X přijímá jakékoli platné hodnoty; funkce jsou považovány za hodnoty pouze kladná čísla, protože jinak máme vícehodnotovou funkci. Ano, funkce y = 81X má v X= 1/4 čtyř různých hodnot: y = 3, y = 3, y = 3 i A y = 3 i(Zkontrolujte prosím!). Ale považujeme to pouze za hodnotu funkce y= 3. Grafy exponenciální funkce pro A= 2 a A= 1/2 jsou uvedeny na obr. 17. Procházejí bodem (0, 1). Na A= 1 máme graf přímky rovnoběžné s osou X, tj. funkce se změní na konstantní hodnotu rovnou 1. Když A> 1 exponenciální funkce roste a při 0< A < 1 – убывает. Основные характеристики и свойства показательной функции:
Rozsah definice funkce: < X+ (tj. X R);
rozsah: y> 0 ;
Funkce je monotónní: zvyšuje se s A> 1 a klesá na 0< A < 1;
- Funkce nemá žádné nuly.
 Logaritmická funkce. Funkce y=log a x, Kde A– volá se konstantní kladné číslo, které se nerovná 1 logaritmický. Tato funkce je inverzní k exponenciální funkci; její graf (obr. 18) získáme otočením grafu exponenciální funkce kolem sečny 1. souřadnicového úhlu.
Logaritmická funkce. Funkce y=log a x, Kde A– volá se konstantní kladné číslo, které se nerovná 1 logaritmický. Tato funkce je inverzní k exponenciální funkci; její graf (obr. 18) získáme otočením grafu exponenciální funkce kolem sečny 1. souřadnicového úhlu.
Hlavní charakteristiky a vlastnosti logaritmické funkce:
Rozsah definice funkce: X> 0 a rozsah hodnot: < y+
(tj. y R);
Toto je monotónní funkce: zvyšuje se jako A> 1 a klesá na 0< A < 1;
Funkce je neomezená, všude spojitá, neperiodická;
Funkce má jednu nulu: X = 1.
Goniometrické funkce. Při konstrukci goniometrických funkcí používáme radián míra úhlů.Poté funkce y= hřích X je znázorněno grafem (obr. 19). Tato křivka se nazývá sinusoida.

Graf funkce y= cos X znázorněné na obr. 20; to je také sinusovka vyplývající z pohybu grafu y= hřích X podél osy X doleva o 2

Z těchto grafů jsou zřejmé charakteristiky a vlastnosti těchto funkcí:
Doména: < X+ rozsah hodnot: 1 y +1;
Tyto funkce jsou periodické: jejich perioda je 2;
Omezené funkce (| y| , všude kontinuální, ne monotónní, ale
mající tzv intervaly monotónnosti, uvnitř kterého jsou
chovat se jako monotónní funkce (viz grafy na obr. 19 a obr. 20);
Funkce mají nekonečný počet nul (další podrobnosti viz sekce
"trigonometrické rovnice").
Funkční grafy y= opálení X A y=dětská postýlka X jsou znázorněny na obr. 21 a obr. 22, v tomto pořadí.

Z grafů je zřejmé, že tyto funkce jsou: periodické (jejich perioda ,
neomezené, obecně ne monotónní, ale mají intervaly monotónnosti
(které?), nespojité (jaké body nespojitosti tyto funkce mají?). Kraj
definice a rozsah hodnot těchto funkcí:
Funkce y= Arcin X(obr.23) a y= Arccos X(obr. 24) vícehodnotový, neomezený; jejich definiční obor, respektive rozsah hodnot: 1 X+1 a < y+ . Protože tyto funkce jsou vícehodnotové, nedělejte to
uvažovány v elementární matematice, jejich hlavní hodnoty jsou považovány za inverzní goniometrické funkce: y= arcsin X A y= arccos X; jejich grafy jsou na obr. 23 a obr. 24 zvýrazněny tlustými čarami.
Funkce y= arcsin X A y= arccos X mají následující vlastnosti a vlastnosti:
Obě funkce mají stejný definiční obor: 1 X +1 ;
jejich rozsah hodnot: /2 y/2 pro y= arcsin X a 0 y Pro y= arccos X;
(y= arcsin X– zvýšení funkce; y= arccos X - klesající);
Každá funkce má jednu nulu ( X= 0 pro funkci y= arcsin X A
X= 1 pro funkci y= arccos X).

Funkce y= Arktan X(obr.25) a y= Arccot X(obr. 26) - vícehodnotové, neomezené funkce; jejich doména definice: X+ . Jejich hlavní významy y= arktan X A y= arccot X jsou považovány za inverzní goniometrické funkce; jejich grafy jsou na obr. 25 a obr. 26 zvýrazněny tučnými větvemi.
Funkce y= arktan X A y= arccot X mají následující vlastnosti a vlastnosti:
Obě funkce mají stejnou definiční doménu: X + ;
jejich rozsah hodnot: /2<y < /2 для y= arktan X a 0< y < для y= arccos X;
Funkce jsou omezené, neperiodické, spojité a monotónní
(y= arktan X– zvýšení funkce; y= arccot X - klesající);
Pouze funkce y= arktan X má jedinou nulu ( X= 0);
funkce y= arccot X nemá nuly.
Složení funkcí
Jsou-li zadány dvě mapy a , kde , pak má smysl „mapa mezi koncovými body“ od do , daná vzorcem , která se nazývá složení funkcí a a je označena .

obr. 1.30 Zobrazení od konce do