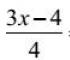Tasks for the application of the Pythagorean theorem. Start in Science Doc in Pythagorean Theorems

Make sure the triangle you are given is a right triangle, as the Pythagorean theorem only applies to right triangles. In right triangles, one of the three angles is always 90 degrees.

• A right angle in a right triangle is indicated by a square instead of a curve, which represents non-right angles.

Label the sides of the triangle. Designate the legs as "a" and "b" (the legs are sides intersecting at right angles), and the hypotenuse as "c" (the hypotenuse is the largest side of a right triangle that lies opposite the right angle).

Determine which side of the triangle you want to find. The Pythagorean theorem allows you to find any side of a right triangle (if the other two sides are known). Determine which side (a, b, c) needs to be found.

• For example, given a hypotenuse equal to 5, and given a leg equal to 3. In this case, you need to find the second leg. We will return to this example later.
• If the other two sides are unknown, it is necessary to find the length of one of the unknown sides in order to be able to apply the Pythagorean theorem. To do this, use the basic trigonometric functions (if you are given the value of one of the non-right angles).

Substitute in the formula a 2 + b 2 \u003d c 2 the values ​​\u200b\u200bgiven to you (or the values ​​\u200b\u200bfound by you). Remember that a and b are legs and c is the hypotenuse.

• In our example, write: 3² + b² = 5².

Square each known side. Or leave the exponents - you can square the numbers later.

• In our example, write: 9 + b² = 25.

Isolate the unknown side on one side of the equation. To do this, transfer the known values ​​to the other side of the equation. If you find the hypotenuse, then in the Pythagorean theorem it is already isolated on one side of the equation (so nothing needs to be done).

• In our example, move 9 to the right side of the equation to isolate the unknown b². You will get b² = 16.

Take the square root of both sides of the equation. At this stage, there is an unknown (squared) on one side of the equation, and an intercept (number) on the other side.

• In our example, b² = 16. Take the square root of both sides of the equation and get b = 4. So the second leg is 4 .

Use the Pythagorean theorem in everyday life, as it can be applied in a large number of practical situations. To do this, learn to recognize right triangles in everyday life - in any situation in which two objects (or lines) intersect at right angles, and a third object (or line) connects (diagonally) the tops of the first two objects (or lines), you can use the Pythagorean theorem to find the unknown side (if the other two sides are known).

• Example: Given a ladder leaning against a building. The bottom of the stairs is 5 meters from the base of the wall. The top of the stairs is 20 meters from the ground (up the wall). What is the length of the ladder?
  • "5 meters from the base of the wall" means that a = 5; "is 20 meters from the ground" means that b = 20 (that is, you are given two legs of a right triangle, since the wall of the building and the surface of the Earth intersect at right angles). The length of the ladder is the length of the hypotenuse, which is unknown.
    • a² + b² = c²
    • (5)² + (20)² = c²
    • 25 + 400 = c²
    • 425 = c²
    • c = √425
    • c = 20.6. Thus, the approximate length of the stairs is 20.6 meters.

Those who are interested in the history of the Pythagorean theorem, which is studied in the school curriculum, will also be curious about such a fact as the publication in 1940 of a book with three hundred and seventy proofs of this seemingly simple theorem. But it intrigued the minds of many mathematicians and philosophers of different eras. In the Guinness Book of Records, it is recorded as a theorem with the maximum number of proofs.

History of the Pythagorean theorem

Associated with the name of Pythagoras, the theorem was known long before the birth of the great philosopher. So, in Egypt, during the construction of structures, the ratio of the sides of a right-angled triangle was taken into account five thousand years ago. The Babylonian texts mention the same ratio of the sides of a right triangle 1200 years before the birth of Pythagoras.

The question arises why then the story says - the emergence of the Pythagorean theorem belongs to him? There can be only one answer - he proved the ratio of the sides in the triangle. He did what those who simply used the aspect ratio and the hypotenuse, established by experience, did not do centuries ago.

From the life of Pythagoras

The future great scientist, mathematician, philosopher was born on the island of Samos in 570 BC. Historical documents preserved information about the father of Pythagoras, who was a gem carver, but there is no information about his mother. They said about the born boy that he was an outstanding child who showed a passion for music and poetry from childhood. Historians attribute Hermodamant and Pherekides of Syros to the teachers of young Pythagoras. The first introduced the boy into the world of the Muses, and the second, being a philosopher and founder of the Italian school of philosophy, directed the young man's gaze to the logos.

At the age of 22 (548 BC), Pythagoras went to Naucratis to study the language and religion of the Egyptians. Further, his path lay in Memphis, where, thanks to the priests, having passed through their ingenious tests, he comprehended Egyptian geometry, which, perhaps, prompted the inquisitive young man to prove the Pythagorean theorem. History will later ascribe this name to the theorem.

Captured by the king of Babylon

On his way home to Hellas, Pythagoras is captured by the king of Babylon. But being in captivity benefited the inquisitive mind of the novice mathematician, he had a lot to learn. Indeed, in those years, mathematics in Babylon was more developed than in Egypt. He spent twelve years studying mathematics, geometry and magic. And, perhaps, it was the Babylonian geometry that was involved in the proof of the ratio of the sides of the triangle and the history of the discovery of the theorem. Pythagoras had enough knowledge and time for this. But that this happened in Babylon, there is no documentary confirmation or refutation of this.

In 530 BC Pythagoras flees from captivity to his homeland, where he lives at the court of the tyrant Polycrates in the status of a semi-slave. Such a life does not suit Pythagoras, and he retires to the caves of Samos, and then goes to the south of Italy, where the Greek colony of Croton was located at that time.

Secret monastic order

On the basis of this colony, Pythagoras organized a secret monastic order, which was a religious union and a scientific society at the same time. This society had its charter, which spoke about the observance of a special way of life.

Pythagoras argued that in order to understand God, a person must know such sciences as algebra and geometry, know astronomy and understand music. Research work was reduced to the knowledge of the mystical side of numbers and philosophy. It should be noted that the principles preached at that time by Pythagoras make sense in imitation at the present time.

Many of the discoveries made by the disciples of Pythagoras were attributed to him. Nevertheless, in short, the history of the creation of the Pythagorean theorem by ancient historians and biographers of that time is directly associated with the name of this philosopher, thinker and mathematician.

The teachings of Pythagoras

Perhaps the historians were inspired by the statement of the great Greek that the proverbial triangle with its legs and hypotenuse encoded all the phenomena of our life. And this triangle is the "key" to solving all the problems that arise. The great philosopher said that one should see a triangle, then we can assume that the problem is two-thirds solved.

Pythagoras told about his teaching only to his students orally, without making any notes, keeping it secret. Unfortunately, the teachings of the greatest philosopher have not survived to this day. Some of it has leaked out, but it is impossible to say how much is true and how much is false in what has become known. Even with the history of the Pythagorean theorem, not everything is certain. Historians of mathematics doubt the authorship of Pythagoras, in their opinion, the theorem was used many centuries before his birth.

Pythagorean theorem

It may seem strange, but there are no historical facts of the proof of the theorem by Pythagoras himself - neither in the archives, nor in any other sources. In the modern version, it is believed that it belongs to none other than Euclid himself.

There is evidence of one of the greatest historians of mathematics, Moritz Kantor, who discovered on a papyrus stored in the Berlin Museum, written by the Egyptians around 2300 BC. e. equality, which read: 3² + 4² = 5².

Briefly from the history of the Pythagorean theorem

The formulation of the theorem from the Euclidean "Beginnings" in translation sounds the same as in the modern interpretation. There is nothing new in its reading: the square of the side opposite the right angle is equal to the sum of the squares of the sides adjacent to the right angle. The fact that the ancient civilizations of India and China used the theorem is confirmed by the treatise Zhou Bi Suan Jin. It contains information about the Egyptian triangle, which describes the aspect ratio as 3:4:5.

No less interesting is another Chinese mathematical book "Chu-pei", which also mentions the Pythagorean triangle with an explanation and drawings that coincide with the drawings of the Hindu geometry of Baskhara. About the triangle itself, the book says that if a right angle can be decomposed into its component parts, then the line that connects the ends of the sides will be equal to five, if the base is three, and the height is four.

The Indian treatise "Sulva Sutra", dating back to about the 7th-5th centuries BC. e., tells about the construction of a right angle using the Egyptian triangle.

Proof of the theorem

In the Middle Ages, students considered proving a theorem too difficult. Weak students learned theorems by heart, without understanding the meaning of the proof. In this regard, they received the nickname "donkeys", because the Pythagorean theorem was an insurmountable obstacle for them, like a bridge for a donkey. In the Middle Ages, students came up with a playful verse on the subject of this theorem.

To prove the Pythagorean theorem in the easiest way, you should simply measure its sides, without using the concept of areas in the proof. The length of the side opposite the right angle is c, and the a and b adjacent to it, as a result we get the equation: a 2 + b 2 \u003d c 2. This statement, as mentioned above, is verified by measuring the lengths of the sides of a right triangle.

If we start the proof of the theorem by considering the area of ​​the rectangles built on the sides of the triangle, we can determine the area of ​​the entire figure. It will be equal to the area of ​​a square with a side (a + b), and on the other hand, the sum of the areas of four triangles and the inner square.

(a + b) 2 = 4 x ab/2 + c 2 ;

a 2 + 2ab + b 2 ;

c 2 = a 2 + b 2 , which was to be proved.

The practical significance of the Pythagorean theorem is that it can be used to find the lengths of segments without measuring them. During the construction of structures, distances, placement of supports and beams are calculated, centers of gravity are determined. The Pythagorean theorem is also applied in all modern technologies. They did not forget about the theorem when creating movies in 3D-6D dimensions, where, in addition to the usual 3 values: height, length, width, time, smell and taste are taken into account. How are tastes and smells related to the theorem, you ask? Everything is very simple - when showing a film, you need to calculate where and what smells and tastes to direct in the auditorium.

It's only the beginning. Boundless scope for discovering and creating new technologies awaits inquisitive minds.

Pythagoras is a Greek scientist who lived about 2500 years ago (564-473 BC).

Let a right triangle be given whose sides a, b and with(Fig. 267).

Let's build squares on its sides. The areas of these squares are respectively a 2 , b 2 and with 2. Let's prove that with 2 = a 2 +b 2 .

Let us construct two squares MKOR and M'K'O'R' (Fig. 268, 269), taking for the side of each of them a segment equal to the sum of the legs of the right triangle ABC.

Having completed the constructions shown in Figures 268 and 269 in these squares, we will see that the MKOR square is divided into two squares with areas a 2 and b 2 and four equal right triangles, each of which is equal to right triangle ABC. The square M'K'O'R' is divided into a quadrilateral (it is shaded in Figure 269) and four right-angled triangles, each of which is also equal to the triangle ABC. The shaded quadrilateral is a square, since its sides are equal (each is equal to the hypotenuse of the triangle ABC, i.e. with), and the angles are straight lines ∠1 + ∠2 = 90°, whence ∠3 = 90°).

Thus, the sum of the areas of the squares built on the legs (in Figure 268 these squares are shaded) is equal to the area of ​​the MKOR square without the sum of the areas of four equal triangles, and the area of ​​the square built on the hypotenuse (in Figure 269 this square is also shaded) is equal to the area of ​​the square M'K'O'R', equal to the square of MKOR, without the sum of the areas of four similar triangles. Therefore, the area of ​​the square built on the hypotenuse of a right triangle is equal to the sum of the areas of the squares built on the legs.

We get the formula with 2 = a 2 +b 2 , where with- hypotenuse, a and b- legs of a right triangle.

The Pythagorean theorem can be summarized as follows:

The square of the hypotenuse of a right triangle is equal to the sum of the squares of the legs.

From the formula with 2 = a 2 +b 2 you can get the following formulas:

a 2 = with 2 - b 2 ;

b 2 = with 2 - a 2 .

These formulas can be used to find the unknown side of a right triangle given two of its sides.

For example:

a) if legs are given a= 4 cm, b\u003d 3 cm, then you can find the hypotenuse ( with):

with 2 = a 2 +b 2 , i.e. with 2 = 4 2 + 3 2 ; with 2 = 25, whence with= √25 = 5(cm);

b) if the hypotenuse is given with= 17 cm and leg a= 8 cm, then you can find another leg ( b):

b 2 = with 2 - a 2 , i.e. b 2 = 17 2 - 8 2 ; b 2 = 225, whence b= √225 = 15 (cm).

Corollary: If in two right triangles ABC and A 1 B 1 C 1 hypotenuse with and with 1 are equal, and the leg b triangle ABC is greater than the leg b 1 triangle A 1 B 1 C 1,

then the leg a triangle ABC is less than the leg a 1 triangle A 1 B 1 C 1 .

Indeed, based on the Pythagorean theorem, we get:

a 2 = with 2 - b 2 ,

a 1 2 = with 1 2 - b 1 2

In the written formulas, the minuends are equal, and the subtrahend in the first formula is greater than the subtrahend in the second formula, therefore, the first difference is less than the second,

i.e. a 2 a 1 2 . Where a a 1 .

1

Shapovalova L.A. (station Egorlykskaya, MBOU ESOSH No. 11)

1. Glazer G.I. History of mathematics at school VII - VIII grades, a guide for teachers, - M: Education, 1982.

2. Dempan I.Ya., Vilenkin N.Ya. "Behind the pages of a mathematics textbook" Handbook for students in grades 5-6. – M.: Enlightenment, 1989.

3. Zenkevich I.G. "Aesthetics of the Mathematics Lesson". – M.: Enlightenment, 1981.

4. Litzman V. The Pythagorean theorem. - M., 1960.

5. Voloshinov A.V. "Pythagoras". - M., 1993.

6. Pichurin L.F. "Beyond the Pages of an Algebra Textbook". - M., 1990.

7. Zemlyakov A.N. "Geometry in the 10th grade." - M., 1986.

8. Newspaper "Mathematics" 17/1996.

9. Newspaper "Mathematics" 3/1997.

10. Antonov N.P., Vygodskii M.Ya., Nikitin V.V., Sankin A.I. "Collection of Problems in Elementary Mathematics". - M., 1963.

11. Dorofeev G.V., Potapov M.K., Rozov N.Kh. "Mathematics Handbook". - M., 1973.

12. Shchetnikov A.I. "The Pythagorean doctrine of number and magnitude". - Novosibirsk, 1997.

13. “Real numbers. Irrational expressions» Grade 8. Tomsk University Press. – Tomsk, 1997.

14. Atanasyan M.S. "Geometry" grade 7-9. – M.: Enlightenment, 1991.

15. URL: www.moypifagor.narod.ru/

16. URL: http://www.zaitseva-irina.ru/html/f1103454849.html.

This academic year, I got acquainted with an interesting theorem, known, as it turned out, from ancient times:

"The square built on the hypotenuse of a right triangle is equal to the sum of the squares built on the legs."

Usually the discovery of this statement is attributed to the ancient Greek philosopher and mathematician Pythagoras (VI century BC). But the study of ancient manuscripts showed that this statement was known long before the birth of Pythagoras.

I wondered why, in this case, it is associated with the name of Pythagoras.

Relevance of the topic: The Pythagorean theorem is of great importance: it is used in geometry literally at every step. I believe that the works of Pythagoras are still relevant, because wherever we look, everywhere we can see the fruits of his great ideas, embodied in various branches of modern life.

The purpose of my research was: to find out who Pythagoras was, and what relation he has to this theorem.

Studying the history of the theorem, I decided to find out:

Are there other proofs of this theorem?

What is the significance of this theorem in people's lives?

What role did Pythagoras play in the development of mathematics?

From the biography of Pythagoras

Pythagoras of Samos is a great Greek scientist. Its fame is associated with the name of the Pythagorean theorem. Although now we already know that this theorem was known in ancient Babylon 1200 years before Pythagoras, and in Egypt 2000 years before him a right-angled triangle with sides 3, 4, 5 was known, we still call it by the name of this ancient scientist.

Almost nothing is known for certain about the life of Pythagoras, but a large number of legends are associated with his name.

Pythagoras was born in 570 BC on the island of Samos.

Pythagoras had a handsome appearance, wore a long beard, and a golden diadem on his head. Pythagoras is not a name, but a nickname that the philosopher received for always speaking correctly and convincingly, like a Greek oracle. (Pythagoras - "persuasive speech").

In 550 BC, Pythagoras makes a decision and goes to Egypt. So, an unknown country and an unknown culture opens up before Pythagoras. Much amazed and surprised Pythagoras in this country, and after some observations of the life of the Egyptians, Pythagoras realized that the path to knowledge, protected by the caste of priests, lies through religion.

After eleven years of study in Egypt, Pythagoras goes to his homeland, where along the way he falls into Babylonian captivity. There he gets acquainted with the Babylonian science, which was more developed than the Egyptian. The Babylonians knew how to solve linear, quadratic and some types of cubic equations. Having escaped from captivity, he could not stay long in his homeland because of the atmosphere of violence and tyranny that reigned there. He decided to move to Croton (a Greek colony in northern Italy).

It is in Croton that the most glorious period in the life of Pythagoras begins. There he established something like a religious-ethical brotherhood or a secret monastic order, whose members were obliged to lead the so-called Pythagorean way of life.

Pythagoras and the Pythagoreans

Pythagoras organized in a Greek colony in the south of the Apennine Peninsula a religious and ethical brotherhood, such as a monastic order, which would later be called the Pythagorean Union. The members of the union had to adhere to certain principles: firstly, to strive for the beautiful and glorious, secondly, to be useful, and thirdly, to strive for high pleasure.

The system of moral and ethical rules, bequeathed by Pythagoras to his students, was compiled into a kind of moral code of the Pythagoreans "Golden Verses", which were very popular in the era of Antiquity, the Middle Ages and the Renaissance.

The Pythagorean system of studies consisted of three sections:

Teachings about numbers - arithmetic,

Teachings about figures - geometry,

Teachings about the structure of the universe - astronomy.

The education system laid down by Pythagoras lasted for many centuries.

The school of Pythagoras did much to give geometry the character of a science. The main feature of the Pythagorean method was the combination of geometry with arithmetic.

Pythagoras dealt a lot with proportions and progressions and, probably, with the similarity of figures, since he is credited with solving the problem: “Construct a third one, equal in size to one of the data and similar to the second, based on the given two figures.”

Pythagoras and his students introduced the concept of polygonal, friendly, perfect numbers and studied their properties. Arithmetic, as a practice of calculation, did not interest Pythagoras, and he proudly declared that he "put arithmetic above the interests of the merchant."

Members of the Pythagorean Union were residents of many cities in Greece.

The Pythagoreans also accepted women into their society. The Union flourished for more than twenty years, and then the persecution of its members began, many of the students were killed.

There were many different legends about the death of Pythagoras himself. But the teachings of Pythagoras and his disciples continued to live.

From the history of the creation of the Pythagorean theorem

It is currently known that this theorem was not discovered by Pythagoras. However, some believe that it was Pythagoras who first gave its full proof, while others deny him this merit. Some attribute to Pythagoras the proof which Euclid gives in the first book of his Elements. On the other hand, Proclus claims that the proof in the Elements is due to Euclid himself. As we can see, the history of mathematics has almost no reliable concrete data on the life of Pythagoras and his mathematical activity.

Let's start our historical review of the Pythagorean theorem with ancient China. Here the mathematical book of Chu-pei attracts special attention. This essay says this about the Pythagorean triangle with sides 3, 4 and 5:

"If a right angle is decomposed into its component parts, then the line connecting the ends of its sides will be 5 when the base is 3 and the height is 4."

It is very easy to reproduce their method of construction. Take a rope 12 m long and tie it to it along a colored strip at a distance of 3 m. from one end and 4 meters from the other. A right angle will be enclosed between sides 3 and 4 meters long.

Geometry among the Hindus was closely connected with the cult. It is highly probable that the hypotenuse squared theorem was already known in India around the 8th century BC. Along with purely ritual prescriptions, there are works of a geometrically theological nature. In these writings, dating back to the 4th or 5th century BC, we meet with the construction of a right angle using a triangle with sides 15, 36, 39.

In the Middle Ages, the Pythagorean theorem defined the limit, if not of the greatest possible, then at least of good mathematical knowledge. The characteristic drawing of the Pythagorean theorem, which is now sometimes turned by schoolchildren, for example, into a top hat dressed in a robe of a professor or a man, was often used in those days as a symbol of mathematics.

In conclusion, we present various formulations of the Pythagorean theorem translated from Greek, Latin and German.

Euclid's theorem reads (literal translation):

"In a right triangle, the square of the side spanning the right angle is equal to the squares on the sides that enclose the right angle."

As you can see, in different countries and different languages ​​there are different versions of the formulation of the familiar theorem. Created at different times and in different languages, they reflect the essence of one mathematical pattern, the proof of which also has several options.

Five Ways to Prove the Pythagorean Theorem

ancient chinese evidence

In an ancient Chinese drawing, four equal right-angled triangles with legs a, b and hypotenuse c are stacked so that their outer contour forms a square with side a + b, and the inner one forms a square with side c, built on the hypotenuse

a2 + 2ab + b2 = c2 + 2ab

Proof by J. Gardfield (1882)

Let us arrange two equal right-angled triangles so that the leg of one of them is a continuation of the other.

The area of ​​the trapezoid under consideration is found as the product of half the sum of the bases and the height

On the other hand, the area of ​​the trapezoid is equal to the sum of the areas of the resulting triangles:

Equating these expressions, we get:

The proof is simple

This proof is obtained in the simplest case of an isosceles right triangle.

Probably, the theorem began with him.

Indeed, it is enough just to look at the tiling of isosceles right triangles to see that the theorem is true.

For example, for the triangle ABC: the square built on the hypotenuse AC contains 4 initial triangles, and the squares built on the legs contain two. The theorem has been proven.

Proof of the ancient Hindus

A square with a side (a + b), can be divided into parts either as in fig. 12. a, or as in fig. 12b. It is clear that parts 1, 2, 3, 4 are the same in both figures. And if equals are subtracted from equals (areas), then equals will remain, i.e. c2 = a2 + b2.

Euclid's proof

For two millennia, the most common was the proof of the Pythagorean theorem, invented by Euclid. It is placed in his famous book "Beginnings".

Euclid lowered the height BH from the vertex of the right angle to the hypotenuse and proved that its extension divides the square completed on the hypotenuse into two rectangles, the areas of which are equal to the areas of the corresponding squares built on the legs.

The drawing used in the proof of this theorem is jokingly called "Pythagorean pants". For a long time he was considered one of the symbols of mathematical science.

Application of the Pythagorean Theorem

The significance of the Pythagorean theorem lies in the fact that most of the theorems of geometry can be derived from it or with its help and many problems can be solved. In addition, the practical significance of the Pythagorean theorem and its inverse theorem is that they can be used to find the lengths of segments without measuring the segments themselves. This, as it were, opens the way from a straight line to a plane, from a plane to volumetric space and beyond. It is for this reason that the Pythagorean theorem is so important for humanity, which seeks to discover more dimensions and create technologies in these dimensions.

Conclusion

The Pythagorean theorem is so famous that it is difficult to imagine a person who has not heard about it. I learned that there are several ways to prove the Pythagorean theorem. I studied a number of historical and mathematical sources, including information on the Internet, and realized that the Pythagorean theorem is interesting not only for its history, but also because it occupies an important place in life and science. This is evidenced by the various interpretations of the text of this theorem given by me in this paper and the ways of its proofs.

So, the Pythagorean theorem is one of the main and, one might say, the most important theorem of geometry. Its significance lies in the fact that most of the theorems of geometry can be deduced from it or with its help. The Pythagorean theorem is also remarkable in that in itself it is not at all obvious. For example, the properties of an isosceles triangle can be seen directly on the drawing. But no matter how much you look at a right triangle, you will never see that there is a simple relation between its sides: c2 = a2 + b2. Therefore, visualization is often used to prove it. The merit of Pythagoras was that he gave a full scientific proof of this theorem. The personality of the scientist himself, whose memory is not accidentally preserved by this theorem, is interesting. Pythagoras is a wonderful speaker, teacher and educator, the organizer of his school, focused on the harmony of music and numbers, goodness and justice, knowledge and a healthy lifestyle. He may well serve as an example for us, distant descendants.

Bibliographic link

Tumanova S.V. SEVERAL WAYS TO PROVE THE PYTHAGOREAN THEOREM // Start in science. - 2016. - No. 2. - P. 91-95;
URL: http://science-start.ru/ru/article/view?id=44 (date of access: 02/28/2020).

According to van der Waerden, it is very likely that the ratio in general form was already known in Babylon around the 18th century BC. e.

Approximately 400 BC. e., according to Proclus, Plato gave a method for finding Pythagorean triples, combining algebra and geometry. Around 300 B.C. e. in the "Elements" of Euclid appeared the oldest axiomatic proof of the Pythagorean theorem.

Wording

The main formulation contains algebraic operations - in a right triangle, the lengths of the legs of which are equal a (\displaystyle a) and b (\displaystyle b), and the length of the hypotenuse is c (\displaystyle c), the relation is fulfilled:

.

An equivalent geometric formulation is also possible, resorting to the concept of area figure: in a right triangle, the area of ​​the square built on the hypotenuse is equal to the sum of the areas of the squares built on the legs. In this form, the theorem is formulated in Euclid's Principia.

Inverse Pythagorean Theorem- the statement about the rectangularity of any triangle, the lengths of the sides of which are related by the relation a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)). As a consequence, for any triple of positive numbers a (\displaystyle a), b (\displaystyle b) and c (\displaystyle c), such that a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)), there is a right triangle with legs a (\displaystyle a) and b (\displaystyle b) and hypotenuse c (\displaystyle c).

Proof of

At least 400 proofs of the Pythagorean theorem have been recorded in the scientific literature, which is explained both by the fundamental value for geometry and by the elementarity of the result. The main directions of proofs are: algebraic use of the ratios of elements triangle (such, for example, is the popular similarity method), area method, there are also various exotic proofs (for example, using differential equations).

Through similar triangles

Euclid's classical proof aims to establish the equality of the areas between the rectangles formed by dissecting the square above the hypotenuse with the height from the right angle with the squares above the legs.

The construction used for the proof is as follows: for a right triangle with a right angle C (\displaystyle C), squares over the legs and and squares over the hypotenuse A B I K (\displaystyle ABIK) height is being built C H (\displaystyle CH) and the beam that continues it s (\displaystyle s), dividing the square above the hypotenuse into two rectangles and . The proof is aimed at establishing the equality of the areas of the rectangle A H J K (\displaystyle AHJK) with a square over the leg A C (\displaystyle AC); the equality of the areas of the second rectangle, which is a square above the hypotenuse, and the rectangle above the other leg is established in a similar way.

Equality of the areas of a rectangle A H J K (\displaystyle AHJK) and A C E D (\displaystyle ACED) established through the congruence of triangles △ A C K ​​(\displaystyle \triangle ACK) and △ A B D (\displaystyle \triangle ABD), the area of ​​each of which is equal to half the area of ​​squares A H J K (\displaystyle AHJK) and A C E D (\displaystyle ACED) respectively, in connection with the following property: the area of ​​a triangle is equal to half the area of ​​a rectangle if the figures have a common side, and the height of the triangle to the common side is the other side of the rectangle. The congruence of triangles follows from the equality of two sides (sides of squares) and the angle between them (composed of a right angle and an angle at A (\displaystyle A).

Thus, the proof establishes that the area of ​​the square above the hypotenuse, composed of rectangles A H J K (\displaystyle AHJK) and B H J I (\displaystyle BHJI), is equal to the sum of the areas of the squares above the legs.

Proof of Leonardo da Vinci

The area method also includes the proof found by Leonardo da Vinci. Let there be a right triangle △ A B C (\displaystyle \triangle ABC) right angle C (\displaystyle C) and squares A C E D (\displaystyle ACED), B C F G (\displaystyle BCFG) and A B H J (\displaystyle ABHJ)(see picture). In this proof on the side H J (\displaystyle HJ) the latter, a triangle is constructed to the outside, congruent △ A B C (\displaystyle \triangle ABC), moreover, reflected both relative to the hypotenuse and relative to the height to it (that is, J I = B C (\displaystyle JI=BC) and H I = A C (\displaystyle HI=AC)). Straight C I (\displaystyle CI) splits the square built on the hypotenuse into two equal parts, since triangles △ A B C (\displaystyle \triangle ABC) and △ J H I (\displaystyle \triangle JHI) are equal in construction. The proof establishes the congruence of quadrilaterals C A J I (\displaystyle CAJI) and D A B G (\displaystyle DABG), the area of ​​each of which, on the one hand, is equal to the sum of half the areas of the squares on the legs and the area of ​​the original triangle, on the other hand, to half the area of ​​the square on the hypotenuse plus the area of ​​the original triangle. In total, half the sum of the areas of the squares over the legs is equal to half the area of ​​the square over the hypotenuse, which is equivalent to the geometric formulation of the Pythagorean theorem.

Proof by the infinitesimal method

There are several proofs using the technique of differential equations. In particular, Hardy is credited with a proof using infinitesimal leg increments a (\displaystyle a) and b (\displaystyle b) and hypotenuse c (\displaystyle c), and preserving the similarity with the original rectangle, that is, ensuring the fulfillment of the following differential relations:

d a d c = c a (\displaystyle (\frac (da)(dc))=(\frac (c)(a))), d b d c = c b (\displaystyle (\frac (db)(dc))=(\frac (c)(b))).

By the method of separation of variables, a differential equation is derived from them c d c = a d a + b d b (\displaystyle c\ dc=a\,da+b\,db), whose integration gives the relation c 2 = a 2 + b 2 + C o n s t (\displaystyle c^(2)=a^(2)+b^(2)+\mathrm (Const) ). Application of initial conditions a = b = c = 0 (\displaystyle a=b=c=0) defines a constant as 0, which results in the assertion of the theorem.

The quadratic dependence in the final formula appears due to the linear proportionality between the sides of the triangle and the increments, while the sum is due to the independent contributions from the increment of different legs.

Variations and Generalizations

Similar geometric shapes on three sides

An important geometric generalization of the Pythagorean theorem was given by Euclid in the "Beginnings", moving from the areas of squares on the sides to the areas of arbitrary similar geometric figures: the sum of the areas of such figures built on the legs will be equal to the area of ​​a figure similar to them, built on the hypotenuse.

The main idea of ​​this generalization is that the area of ​​such a geometric figure is proportional to the square of any of its linear dimensions and, in particular, to the square of the length of any side. Therefore, for similar figures with areas A (\displaystyle A), B (\displaystyle B) and C (\displaystyle C) built on legs with lengths a (\displaystyle a) and b (\displaystyle b) and hypotenuse c (\displaystyle c) accordingly, there is a relation:

A a 2 = B b 2 = C c 2 ⇒ A + B = a 2 c 2 C + b 2 c 2 C (\displaystyle (\frac (A)(a^(2)))=(\frac (B )(b^(2)))=(\frac (C)(c^(2)))\,\Rightarrow \,A+B=(\frac (a^(2))(c^(2) ))C+(\frac (b^(2))(c^(2)))C).

Since according to the Pythagorean theorem a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)), then it is done.

In addition, if it is possible to prove without resorting to the Pythagorean theorem that for the areas of three similar geometric figures on the sides of a right triangle, the relation A + B = C (\displaystyle A+B=C), then using the reverse of the proof of Euclid's generalization, we can derive the proof of the Pythagorean theorem. For example, if on the hypotenuse we construct a right triangle congruent to the initial one with area C (\displaystyle C), and on the legs - two similar right-angled triangles with areas A (\displaystyle A) and B (\displaystyle B), then it turns out that the triangles on the legs are formed as a result of dividing the initial triangle by its height, that is, the sum of two smaller areas of the triangles is equal to the area of ​​the third, thus A + B = C (\displaystyle A+B=C) and, applying the relation for similar figures, the Pythagorean theorem is derived.

Cosine theorem

The Pythagorean theorem is a special case of the more general cosine theorem which relates the lengths of the sides in an arbitrary triangle:

a 2 + b 2 − 2 a b cos ⁡ θ = c 2 (\displaystyle a^(2)+b^(2)-2ab\cos (\theta )=c^(2)),

where is the angle between the sides a (\displaystyle a) and b (\displaystyle b). If the angle is 90°, then cos ⁡ θ = 0 (\displaystyle \cos \theta =0), and the formula simplifies to the usual Pythagorean theorem.

Arbitrary triangle

There is a generalization of the Pythagorean theorem to an arbitrary triangle, operating solely on the ratio of the lengths of the sides, it is believed that it was first established by the Sabian astronomer Sabit ibn Kurra. In it, for an arbitrary triangle with sides, an isosceles triangle with a base on the side c (\displaystyle c), the vertex coinciding with the vertex of the original triangle, opposite the side c (\displaystyle c) and angles at the base equal to the angle θ (\displaystyle \theta ) opposite side c (\displaystyle c). As a result, two triangles are formed, similar to the original one: the first one with sides a (\displaystyle a), the lateral side of the inscribed isosceles triangle far from it, and r (\displaystyle r)- side parts c (\displaystyle c); the second is symmetrical to it from the side b (\displaystyle b) with a party s (\displaystyle s)- the relevant part of the side c (\displaystyle c). As a result, the relation is fulfilled:

a 2 + b 2 = c (r + s) (\displaystyle a^(2)+b^(2)=c(r+s)),

which degenerates into the Pythagorean theorem at θ = π / 2 (\displaystyle \theta =\pi /2). The ratio is a consequence of the similarity of the formed triangles:

c a = a r , c b = b s ⇒ c r + c s = a 2 + b 2 (\displaystyle (\frac (c)(a))=(\frac (a)(r)),\,(\frac (c) (b))=(\frac (b)(s))\,\Rightarrow \,cr+cs=a^(2)+b^(2)).

Pappus area theorem

Non-Euclidean geometry

The Pythagorean theorem is derived from the axioms of Euclidean geometry and is invalid for non-Euclidean geometry - the fulfillment of the Pythagorean theorem is tantamount to the postulate of Euclidean parallelism.

In non-Euclidean geometry, the relationship between the sides of a right triangle will necessarily be in a form different from the Pythagorean theorem. For example, in spherical geometry, all three sides of a right triangle, which bound the octant of the unit sphere, have length π / 2 (\displaystyle \pi /2), which contradicts the Pythagorean theorem.

Moreover, the Pythagorean theorem is valid in hyperbolic and elliptic geometry, if the requirement that the triangle is rectangular is replaced by the condition that the sum of the two angles of the triangle must be equal to the third.

spherical geometry

For any right triangle on a sphere with radius R (\displaystyle R)(for example, if the angle in the triangle is right) with sides a , b , c (\displaystyle a,b,c) the relationship between the sides is:

cos ⁡ (c R) = cos ⁡ (a R) ⋅ cos ⁡ (b R) (\displaystyle \cos \left((\frac (c)(R))\right)=\cos \left((\frac (a)(R))\right)\cdot \cos \left((\frac (b)(R))\right)).

This equality can be derived as a special case of the spherical cosine theorem, which is valid for all spherical triangles:

cos ⁡ (c R) = cos ⁡ (a R) ⋅ cos ⁡ (b R) + sin ⁡ (a R) ⋅ sin ⁡ (b R) ⋅ cos ⁡ γ (\displaystyle \cos \left((\frac ( c)(R))\right)=\cos \left((\frac (a)(R))\right)\cdot \cos \left((\frac (b)(R))\right)+\ sin \left((\frac (a)(R))\right)\cdot \sin \left((\frac (b)(R))\right)\cdot \cos \gamma ). ch ⁡ c = ch ⁡ a ⋅ ch ⁡ b (\displaystyle \operatorname (ch) c=\operatorname (ch) a\cdot \operatorname (ch) b),

where ch (\displaystyle \operatorname (ch) )- hyperbolic cosine. This formula is a special case of the hyperbolic cosine theorem, which is valid for all triangles:

ch ⁡ c = ch ⁡ a ⋅ ch ⁡ b − sh ⁡ a ⋅ sh ⁡ b ⋅ cos ⁡ γ (\displaystyle \operatorname (ch) c=\operatorname (ch) a\cdot \operatorname (ch) b-\operatorname (sh) a\cdot \operatorname (sh) b\cdot \cos \gamma ),

where γ (\displaystyle \gamma )- an angle whose vertex is opposite to a side c (\displaystyle c).

Using the Taylor series for the hyperbolic cosine ( ch ⁡ x ≈ 1 + x 2 / 2 (\displaystyle \operatorname (ch) x\approx 1+x^(2)/2)) it can be shown that if the hyperbolic triangle decreases (that is, when a (\displaystyle a), b (\displaystyle b) and c (\displaystyle c) tend to zero), then the hyperbolic relations in a right triangle approach the relation of the classical Pythagorean theorem.

Application

Distance in two-dimensional rectangular systems

The most important application of the Pythagorean theorem is to determine the distance between two points in a rectangular system coordinates: distance s (\displaystyle s) between points with coordinates (a , b) (\displaystyle (a,b)) and (c , d) (\displaystyle (c,d)) equals:

s = (a − c) 2 + (b − d) 2 (\displaystyle s=(\sqrt ((a-c)^(2)+(b-d)^(2)))).

For complex numbers, the Pythagorean theorem gives a natural formula for finding the modulus complex number - for z = x + y i (\displaystyle z=x+yi) it is equal to the length