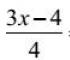Solving equations with brackets. Solving simple linear equations

An equation with one unknown, which, after opening the brackets and reducing like terms, takes the form

ax + b = 0, where a and b are arbitrary numbers, is called linear equation with one unknown. Today we will figure out how to solve these linear equations.

For example, all equations:

2x + 3 \u003d 7 - 0.5x; 0.3x = 0; x / 2 + 3 \u003d 1/2 (x - 2) - linear.

The value of the unknown that turns the equation into a true equality is called decision or the root of the equation .

For example, if in the equation 3x + 7 \u003d 13 we substitute the number 2 instead of the unknown x, then we get the correct equality 3 2 + 7 \u003d 13. This means that the value x \u003d 2 is the solution or the root of the equation.

And the value x \u003d 3 does not turn the equation 3x + 7 \u003d 13 into a true equality, since 3 2 + 7 ≠ 13. Therefore, the value x \u003d 3 is not a solution or a root of the equation.

The solution of any linear equations is reduced to the solution of equations of the form

ax + b = 0.

We transfer the free term from the left side of the equation to the right side, while changing the sign in front of b to the opposite, we get

If a ≠ 0, then x = – b/a .

Example 1 Solve the equation 3x + 2 =11.

We transfer 2 from the left side of the equation to the right, while changing the sign in front of 2 to the opposite, we get
3x \u003d 11 - 2.

Let's do the subtraction, then
3x = 9.

To find x, you need to divide the product by a known factor, that is,
x = 9:3.

So the value x = 3 is the solution or the root of the equation.

Answer: x = 3.

If a = 0 and b = 0, then we get the equation 0x \u003d 0. This equation has infinitely many solutions, since when multiplying any number by 0, we get 0, but b is also 0. The solution to this equation is any number.

Example 2 Solve the equation 5(x - 3) + 2 = 3 (x - 4) + 2x - 1.

Let's expand the brackets:
5x - 15 + 2 \u003d 3x - 12 + 2x - 1.

5x - 3x - 2x \u003d - 12 - 1 + 15 - 2.

Here are similar members:
0x = 0.

Answer: x is any number.

If a = 0 and b ≠ 0, then we get the equation 0x = - b. This equation has no solutions, since when multiplying any number by 0, we get 0, but b ≠ 0.

Example 3 Solve the equation x + 8 = x + 5.

Let us group the terms containing unknowns on the left side, and the free terms on the right side:
x - x \u003d 5 - 8.

Here are similar members:
0x = - 3.

Answer: no solutions.

On the figure 1 the scheme for solving the linear equation is shown

Let us compose a general scheme for solving equations with one variable. Consider the solution of example 4.

Example 4 Let's solve the equation

1) Multiply all terms of the equation by the least common multiple of the denominators, equal to 12.

2) After reduction we get
4 (x - 4) + 3 2 (x + 1) - 12 = 6 5 (x - 3) + 24x - 2 (11x + 43)

3) To separate members containing unknown and free members, open the brackets:
4x - 16 + 6x + 6 - 12 \u003d 30x - 90 + 24x - 22x - 86.

4) We group in one part the terms containing unknowns, and in the other - free terms:
4x + 6x - 30x - 24x + 22x \u003d - 90 - 86 + 16 - 6 + 12.

5) Here are similar members:
- 22x = - 154.

6) Divide by - 22 , We get
x = 7.

As you can see, the root of the equation is seven.

In general, such equations can be solved as follows:

a) bring the equation to an integer form;

b) open brackets;

c) group the terms containing the unknown in one part of the equation, and the free terms in the other;

d) bring similar members;

e) solve an equation of the form aх = b, which was obtained after bringing like terms.

However, this scheme is not required for every equation. When solving many simpler equations, one has to start not from the first, but from the second ( Example. 2), third ( Example. thirteen) and even from the fifth stage, as in example 5.

Example 5 Solve the equation 2x = 1/4.

We find the unknown x \u003d 1/4: 2,
x = 1/8 .

Consider the solution of some linear equations encountered in the main state exam.

Example 6 Solve equation 2 (x + 3) = 5 - 6x.

2x + 6 = 5 - 6x

2x + 6x = 5 - 6

Answer: - 0.125

Example 7 Solve the equation - 6 (5 - 3x) \u003d 8x - 7.

– 30 + 18x = 8x – 7

18x - 8x = - 7 +30

Answer: 2.3

Example 8 Solve the Equation

3(3x - 4) = 4 7x + 24

9x - 12 = 28x + 24

9x - 28x = 24 + 12

Example 9 Find f(6) if f (x + 2) = 3 7's

Decision

Since we need to find f(6), and we know f (x + 2),
then x + 2 = 6.

We solve the linear equation x + 2 = 6,
we get x \u003d 6 - 2, x \u003d 4.

If x = 4 then
f(6) = 3 7-4 = 3 3 = 27

Answer: 27.

If you still have questions, there is a desire to understand the solution of equations more thoroughly, sign up for my lessons in the SCHEDULE. I will be glad to help you!

TutorOnline also recommends watching a new video tutorial from our tutor Olga Alexandrovna, which will help you understand both linear equations and others.

site, with full or partial copying of the material, a link to the source is required.

An equation with one unknown, which, after opening the brackets and reducing like terms, takes the form

ax + b = 0, where a and b are arbitrary numbers, is called linear equation with one unknown. Today we will figure out how to solve these linear equations.

For example, all equations:

2x + 3 \u003d 7 - 0.5x; 0.3x = 0; x / 2 + 3 \u003d 1/2 (x - 2) - linear.

The value of the unknown that turns the equation into a true equality is called decision or the root of the equation .

And the value x \u003d 3 does not turn the equation 3x + 7 \u003d 13 into a true equality, since 3 2 + 7 ≠ 13. Therefore, the value x \u003d 3 is not a solution or a root of the equation.

The solution of any linear equations is reduced to the solution of equations of the form

ax + b = 0.

We transfer the free term from the left side of the equation to the right side, while changing the sign in front of b to the opposite, we get

If a ≠ 0, then x = – b/a .

Example 1 Solve the equation 3x + 2 =11.

We transfer 2 from the left side of the equation to the right, while changing the sign in front of 2 to the opposite, we get
3x \u003d 11 - 2.

Let's do the subtraction, then
3x = 9.

To find x, you need to divide the product by a known factor, that is,
x = 9:3.

So the value x = 3 is the solution or the root of the equation.

Answer: x = 3.

Example 2 Solve the equation 5(x - 3) + 2 = 3 (x - 4) + 2x - 1.

Let's expand the brackets:
5x - 15 + 2 \u003d 3x - 12 + 2x - 1.

5x - 3x - 2x \u003d - 12 - 1 + 15 - 2.

Here are similar members:
0x = 0.

Answer: x is any number.

If a = 0 and b ≠ 0, then we get the equation 0x = - b. This equation has no solutions, since when multiplying any number by 0, we get 0, but b ≠ 0.

Example 3 Solve the equation x + 8 = x + 5.

Let us group the terms containing unknowns on the left side, and the free terms on the right side:
x - x \u003d 5 - 8.

Here are similar members:
0x = - 3.

Answer: no solutions.

On the figure 1 the scheme for solving the linear equation is shown

Let us compose a general scheme for solving equations with one variable. Consider the solution of example 4.

Example 4 Let's solve the equation

1) Multiply all terms of the equation by the least common multiple of the denominators, equal to 12.

2) After reduction we get
4 (x - 4) + 3 2 (x + 1) - 12 = 6 5 (x - 3) + 24x - 2 (11x + 43)

3) To separate members containing unknown and free members, open the brackets:
4x - 16 + 6x + 6 - 12 \u003d 30x - 90 + 24x - 22x - 86.

4) We group in one part the terms containing unknowns, and in the other - free terms:
4x + 6x - 30x - 24x + 22x \u003d - 90 - 86 + 16 - 6 + 12.

5) Here are similar members:
- 22x = - 154.

6) Divide by - 22 , We get
x = 7.

As you can see, the root of the equation is seven.

In general, such equations can be solved as follows:

a) bring the equation to an integer form;

b) open brackets;

c) group the terms containing the unknown in one part of the equation, and the free terms in the other;

d) bring similar members;

e) solve an equation of the form aх = b, which was obtained after bringing like terms.

Example 5 Solve the equation 2x = 1/4.

We find the unknown x \u003d 1/4: 2,
x = 1/8 .

Consider the solution of some linear equations encountered in the main state exam.

Example 6 Solve equation 2 (x + 3) = 5 - 6x.

2x + 6 = 5 - 6x

2x + 6x = 5 - 6

Answer: - 0.125

Example 7 Solve the equation - 6 (5 - 3x) \u003d 8x - 7.

– 30 + 18x = 8x – 7

18x - 8x = - 7 +30

Answer: 2.3

Example 8 Solve the Equation

3(3x - 4) = 4 7x + 24

9x - 12 = 28x + 24

9x - 28x = 24 + 12

Example 9 Find f(6) if f (x + 2) = 3 7's

Decision

Since we need to find f(6), and we know f (x + 2),
then x + 2 = 6.

We solve the linear equation x + 2 = 6,
we get x \u003d 6 - 2, x \u003d 4.

If x = 4 then
f(6) = 3 7-4 = 3 3 = 27

Answer: 27.

If you still have questions, there is a desire to deal with the solution of equations more thoroughly,. I will be glad to help you!

TutorOnline also recommends watching a new video tutorial from our tutor Olga Alexandrovna, which will help you understand both linear equations and others.

blog.site, with full or partial copying of the material, a link to the source is required.

Parentheses are used to indicate the order in which actions are performed in numeric and alphabetic expressions, as well as in expressions with variables. It is convenient to pass from an expression with brackets to an identically equal expression without brackets. This technique is called parenthesis opening.

To expand brackets means to rid the expression of these brackets.

Another point deserves special attention, which concerns the peculiarities of writing solutions when opening brackets. We can write the initial expression with brackets and the result obtained after opening the brackets as equality. For example, after opening the parentheses, instead of the expression
3−(5−7) we get the expression 3−5+7. We can write both of these expressions as the equality 3−(5−7)=3−5+7.

And one more important point. In mathematics, to reduce entries, it is customary not to write a plus sign if it is the first in an expression or in brackets. For example, if we add two positive numbers, for example, seven and three, then we write not +7 + 3, but simply 7 + 3, despite the fact that seven is also a positive number. Similarly, if you see, for example, the expression (5 + x) - know that there is a plus in front of the bracket, which is not written, and there is a plus + (+5 + x) in front of the five.

Bracket expansion rule for addition

When opening brackets, if there is a plus before the brackets, then this plus is omitted along with the brackets.

Example. Open the brackets in the expression 2 + (7 + 3) Before the brackets plus, then the characters in front of the numbers in the brackets do not change.

2 + (7 + 3) = 2 + 7 + 3

The rule for expanding brackets when subtracting

If there is a minus before the brackets, then this minus is omitted along with the brackets, but the terms that were in the brackets change their sign to the opposite. The absence of a sign before the first term in parentheses implies a + sign.

Example. Open brackets in expression 2 − (7 + 3)

There is a minus before the brackets, so you need to change the signs before the numbers from the brackets. There is no sign in brackets before the number 7, which means that the seven is positive, it is considered that the + sign is in front of it.

2 − (7 + 3) = 2 − (+ 7 + 3)

When opening the brackets, we remove the minus from the example, which was before the brackets, and the brackets themselves 2 − (+ 7 + 3), and change the signs that were in the brackets to the opposite ones.

2 − (+ 7 + 3) = 2 − 7 − 3

Expanding parentheses when multiplying

If there is a multiplication sign in front of the brackets, then each number inside the brackets is multiplied by the factor in front of the brackets. At the same time, multiplying a minus by a minus gives a plus, and multiplying a minus by a plus, like multiplying a plus by a minus, gives a minus.

Thus, parentheses in products are expanded in accordance with the distributive property of multiplication.

Example. 2 (9 - 7) = 2 9 - 2 7

When multiplying parenthesis by parenthesis, each term of the first parenthesis is multiplied with every term of the second parenthesis.

(2 + 3) (4 + 5) = 2 4 + 2 5 + 3 4 + 3 5

In fact, there is no need to remember all the rules, it is enough to remember only one, this one: c(a−b)=ca−cb. Why? Because if we substitute one instead of c, we get the rule (a−b)=a−b. And if we substitute minus one, we get the rule −(a−b)=−a+b. Well, if you substitute another bracket instead of c, you can get the last rule.

Expand parentheses when dividing

If there is a division sign after the brackets, then each number inside the brackets is divisible by the divisor after the brackets, and vice versa.

Example. (9 + 6) : 3=9: 3 + 6: 3

How to expand nested parentheses

If the expression contains nested brackets, then they are expanded in order, starting with external or internal.

At the same time, when opening one of the brackets, it is important not to touch the other brackets, just rewriting them as they are.

Example. 12 - (a + (6 - b) - 3) = 12 - a - (6 - b) + 3 = 12 - a - 6 + b + 3 = 9 - a + b

Have you been looking for how to solve an equation with brackets? . A detailed solution with a description and explanations will help you deal with even the most difficult task and how to solve equations in brackets is no exception. We will help you prepare for homework, tests, olympiads, as well as for admission to a university. And no matter what example, no matter what math query you enter, we already have a solution. For example, "how to solve an equation with brackets."

The use of various mathematical problems, calculators, equations and functions is widespread in our lives. They are used in many calculations, construction of structures and even sports. Mathematics has been used by man since ancient times, and since then their use has only increased. However, now science does not stand still and we can enjoy the fruits of its activities, such as, for example, an online calculator that can solve problems such as how to solve an equation with brackets, how to solve equations in brackets, how to solve an equation with brackets, How to solve an equation with brackets How to solve an equation with brackets On this page you will find a calculator that will help you solve any question, including how to solve an equation with brackets. (for example, how to solve an equation with brackets).

Where can I solve any problem in mathematics, as well as how to solve an equation with brackets Online?

You can solve the problem of how to solve an equation with brackets on our website. A free online solver will allow you to solve an online problem of any complexity in a matter of seconds. All you have to do is just enter your data into the solver. You can also watch the video instruction and learn how to correctly enter your task on our website. And if you have any questions, you can ask them in the chat at the bottom left of the calculator page.

Linear equations. Solution, examples.

Attention!
There are additional
material in Special Section 555.
For those who strongly "not very..."
And for those who "very much...")

Linear equations.

Linear equations are not the most difficult topic in school mathematics. But there are some tricks there that can puzzle even a trained student. Shall we figure it out?)

A linear equation is usually defined as an equation of the form:

ax + b = 0 where a and b- any numbers.

2x + 7 = 0. Here a=2, b=7

0.1x - 2.3 = 0 Here a=0.1, b=-2.3

12x + 1/2 = 0 Here a=12, b=1/2

Nothing complicated, right? Especially if you do not notice the words: "where a and b are any numbers"... And if you notice, but carelessly think about it?) After all, if a=0, b=0(any numbers are possible?), then we get a funny expression:

But that's not all! If, say, a=0, a b=5, it turns out something quite absurd:

What strains and undermines confidence in mathematics, yes ...) Especially in exams. But of these strange expressions, you also need to find X! Which doesn't exist at all. And, surprisingly, this X is very easy to find. We will learn how to do it. In this lesson.

How to recognize a linear equation in appearance? It depends on what appearance.) The trick is that linear equations are called not only equations of the form ax + b = 0 , but also any equations that are reduced to this form by transformations and simplifications. And who knows if it is reduced or not?)

A linear equation can be clearly recognized in some cases. Say, if we have an equation in which there are only unknowns in the first degree, yes numbers. And the equation doesn't fractions divided by unknown , it is important! And division by number, or a numeric fraction - that's it! For example:

This is a linear equation. There are fractions here, but there are no x's in the square, in the cube, etc., and there are no x's in the denominators, i.e. No division by x. And here is the equation

cannot be called linear. Here x's are all in the first degree, but there is division by expression with x. After simplifications and transformations, you can get a linear equation, and a quadratic one, and anything you like.

It turns out that it is impossible to find out a linear equation in some intricate example until you almost solve it. It's upsetting. But in assignments, as a rule, they don’t ask about the form of the equation, right? In tasks, equations are ordered decide. This makes me happy.)

Solution of linear equations. Examples.

The entire solution of linear equations consists of identical transformations of equations. By the way, these transformations (as many as two!) underlie the solutions all equations of mathematics. In other words, the decision any The equation begins with these same transformations. In the case of linear equations, it (the solution) on these transformations ends with a full-fledged answer. It makes sense to follow the link, right?) Moreover, there are also examples of solving linear equations.

Let's start with the simplest example. Without any pitfalls. Let's say we need to solve the following equation.

x - 3 = 2 - 4x

This is a linear equation. Xs are all to the first power, there is no division by X. But, actually, we don't care what the equation is. We need to solve it. The scheme here is simple. Collect everything with x's on the left side of the equation, everything without x's (numbers) on the right.

To do this, you need to transfer - 4x to the left side, with a change of sign, of course, but - 3 - to the right. By the way, this is first identical transformation of equations. Surprised? So, they didn’t follow the link, but in vain ...) We get:

x + 4x = 2 + 3

We give similar, we consider:

What do we need to be completely happy? Yes, so that there is a clean X on the left! Five gets in the way. Get rid of the five with second identical transformation of equations. Namely, we divide both parts of the equation by 5. We get a ready-made answer:

An elementary example, of course. This is for a warm-up.) It is not very clear why I recalled identical transformations here? OK. We take the bull by the horns.) Let's decide something more impressive.

For example, here is this equation:

Where do we start? With X - to the left, without X - to the right? Could be so. Little steps along the long road. And you can immediately, in a universal and powerful way. Unless, of course, in your arsenal there are identical transformations of equations.

I ask you a key question: What do you dislike the most about this equation?

95 people out of 100 will answer: fractions ! The answer is correct. So let's get rid of them. So we start right away with second identical transformation. What do you need to multiply the fraction on the left by so that the denominator is completely reduced? That's right, 3. And on the right? By 4. But math allows us to multiply both sides by the same number. How do we get out? Let's multiply both sides by 12! Those. to a common denominator. Then the three will be reduced, and the four. Do not forget that you need to multiply each part entirely. Here's what the first step looks like:

Expanding the brackets:

Note! Numerator (x+2) I took in brackets! This is because when multiplying fractions, the numerator is multiplied by the whole, entirely! And now you can reduce fractions and reduce:

Opening the remaining parentheses:

Not an example, but pure pleasure!) Now we recall the spell from the lower grades: with x - to the left, without x - to the right! And apply this transformation:

Here are some like:

And we divide both parts by 25, i.e. apply the second transformation again:

That's all. Answer: X=0,16

Take note: to bring the original confusing equation to a pleasant form, we used two (only two!) identical transformations- translation left-right with a change of sign and multiplication-division of the equation by the same number. This is the universal way! We will work in this way any equations! Absolutely any. That is why I keep repeating these identical transformations all the time.)

As you can see, the principle of solving linear equations is simple. We take the equation and simplify it with the help of identical transformations until we get the answer. The main problems here are in the calculations, and not in the principle of the solution.

But ... There are such surprises in the process of solving the most elementary linear equations that they can drive into a strong stupor ...) Fortunately, there can be only two such surprises. Let's call them special cases.

Special cases in solving linear equations.

Surprise first.

Suppose you come across an elementary equation, something like:

2x+3=5x+5 - 3x - 2

Slightly bored, we transfer with X to the left, without X - to the right ... With a change of sign, everything is chin-chinar ... We get:

2x-5x+3x=5-2-3

We believe, and ... oh my! We get:

In itself, this equality is not objectionable. Zero is really zero. But X is gone! And we must write in the answer, what x is equal to. Otherwise, the solution doesn't count, yes...) A dead end?

Calm! In such doubtful cases, the most general rules save. How to solve equations? What does it mean to solve an equation? It means, find all values of x that, when substituted into the original equation, will give us the correct equality.

But we have the correct equality already happened! 0=0, where really?! It remains to figure out at what x's this is obtained. What values of x can be substituted into original equation if these x's still shrink to zero? Come on?)

Yes!!! Xs can be substituted any! What do you want. At least 5, at least 0.05, at least -220. They will still shrink. If you don't believe me, you can check it.) Substitute any x values in original equation and calculate. All the time the pure truth will be obtained: 0=0, 2=2, -7.1=-7.1 and so on.

Here is your answer: x is any number.

The answer can be written in different mathematical symbols, the essence does not change. This is a completely correct and complete answer.

Surprise second.

Let's take the same elementary linear equation and change only one number in it. This is what we will decide:

2x+1=5x+5 - 3x - 2

After the same identical transformations, we get something intriguing:

Like this. Solved a linear equation, got a strange equality. Mathematically speaking, we have wrong equality. And in simple terms, this is not true. Rave. But nevertheless, this nonsense is quite a good reason for the correct solution of the equation.)

Again, we think on the basis of general rules. What x, when substituted into the original equation, will give us correct equality? Yes, none! There are no such xes. Whatever you substitute, everything will be reduced, nonsense will remain.)

Here is your answer: there are no solutions.

This is also a perfectly valid answer. In mathematics, such answers often occur.

Like this. Now, I hope, the loss of x's in the process of solving any (not just linear) equation will not bother you at all. The matter is familiar.)

Now that we have dealt with all the pitfalls in linear equations, it makes sense to solve them.

If you like this site...

By the way, I have a couple more interesting sites for you.)

You can practice solving examples and find out your level. Testing with instant verification. Learning - with interest!)

you can get acquainted with functions and derivatives.