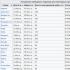
The random variable is given by the following row of the distribution. Distribution law of a discrete random variable

LAW OF DISTRIBUTION AND CHARACTERISTICS

RANDOM VARIABLES

Random variables, their classification and methods of description.

A random quantity is a quantity that, as a result of experiment, can take on one or another value, but which one is not known in advance. For a random variable, therefore, you can only specify values, one of which it will definitely take as a result of experiment. In what follows we will call these values ​​possible values ​​of the random variable. Since a random variable quantitatively characterizes the random result of an experiment, it can be considered as a quantitative characteristic of a random event.

Random variables are usually denoted by capital letters of the Latin alphabet, for example, X..Y..Z, and their possible values ​​by corresponding small letters.

There are three types of random variables:

Discrete; Continuous; Mixed.

Discrete is a random variable whose number of possible values ​​forms a countable set. In turn, a set whose elements can be numbered is called countable. The word "discrete" comes from the Latin discretus, meaning "discontinuous, consisting of separate parts".

Example 1. A discrete random variable is the number of defective parts X in a batch of nproducts. Indeed, the possible values ​​of this random variable are a series of integers from 0 to n.

Example 2. A discrete random variable is the number of shots before the first hit on the target. Here, as in Example 1, the possible values ​​can be numbered, although in the limiting case the possible value is an infinitely large number.

Continuous is a random variable whose possible values ​​continuously fill a certain interval of the numerical axis, sometimes called the interval of existence of this random variable. Thus, on any finite interval of existence, the number of possible values ​​of a continuous random variable is infinitely large.

Example 3. A continuous random variable is the monthly electricity consumption of an enterprise.

Example 4. A continuous random variable is the error in measuring height using an altimeter. Let it be known from the operating principle of the altimeter that the error lies in the range from 0 to 2 m. Therefore, the interval of existence of this random variable is the interval from 0 to 2 m.

Law of distribution of random variables.

A random variable is considered fully specified if its possible values ​​are indicated on the numerical axis and the distribution law is established.

Law of distribution of a random variable is a relation that establishes a connection between the possible values ​​of a random variable and the corresponding probabilities.

A random variable is said to be distributed according to a given law, or subject to a given distribution law. A number of probabilities, distribution function, probability density, and characteristic function are used as distribution laws.

The distribution law gives a complete probable description of a random variable. According to the distribution law, one can judge before experiment which possible values ​​of a random variable will appear more often and which less often.

For a discrete random variable, the distribution law can be specified in the form of a table, analytically (in the form of a formula) and graphically.

The simplest form of specifying the distribution law of a discrete random variable is a table (matrix), which lists in ascending order all possible values ​​of the random variable and their corresponding probabilities, i.e.

Such a table is called a distribution series of a discrete random variable. 1

Events X 1, X 2,..., X n, consisting in the fact that as a result of the test, the random variable X will take the values ​​x 1, x 2,... x n, respectively, are inconsistent and the only possible ones (since the table lists all possible values ​​of a random variable), i.e. form a complete group. Therefore, the sum of their probabilities is equal to 1. Thus, for any discrete random variable

(This unit is somehow distributed among the values ​​of the random variable, hence the term "distribution").

The distribution series can be depicted graphically if the values ​​of the random variable are plotted along the abscissa axis, and their corresponding probabilities are plotted along the ordinate axis. The connection of the obtained points forms a broken line called a polygon or polygon of the probability distribution (Fig. 1).

Example The lottery includes: a car worth 5,000 den. units, 4 TVs costing 250 den. units, 5 video recorders worth 200 den. units A total of 1000 tickets are sold for 7 days. units Draw up a distribution law for the net winnings received by a lottery participant who bought one ticket.

Solution. Possible values ​​of the random variable X - the net winnings per ticket - are equal to 0-7 = -7 money. units (if the ticket did not win), 200-7 = 193, 250-7 = 243, 5000-7 = 4993 den. units (if the ticket has the winnings of a VCR, TV or car, respectively). Considering that out of 1000 tickets the number of non-winners is 990, and the indicated winnings are 5, 4 and 1, respectively, and using the classical definition of probability, we obtain.

Discrete random Variables are random variables that take only values ​​that are distant from each other and that can be listed in advance.
Law of distribution
The distribution law of a random variable is a relationship that establishes a connection between the possible values ​​of a random variable and their corresponding probabilities.
The distribution series of a discrete random variable is the list of its possible values ​​and the corresponding probabilities.
The distribution function of a discrete random variable is the function:
,
determining for each value of the argument x the probability that the random variable X will take a value less than this x.

Expectation of a discrete random variable
,
where is the value of a discrete random variable; - the probability of a random variable accepting X values.
If a random variable takes a countable set of possible values, then:
.
Mathematical expectation of the number of occurrences of an event in n independent trials:
,

Dispersion and standard deviation of a discrete random variable
Dispersion of a discrete random variable:
or .
Variance of the number of occurrences of an event in n independent trials
,
where p is the probability of the event occurring.
Standard deviation of a discrete random variable:
.

Example 1
Draw up a law of probability distribution for a discrete random variable (DRV) X – the number of k occurrences of at least one “six” in n = 8 throws of a pair of dice. Construct a distribution polygon. Find the numerical characteristics of the distribution (distribution mode, mathematical expectation M(X), dispersion D(X), standard deviation s(X)). Solution: Let us introduce the notation: event A – “when throwing a pair of dice, a six appears at least once.” To find the probability P(A) = p of event A, it is more convenient to first find the probability P(Ā) = q of the opposite event Ā - “when throwing a pair of dice, a six never appeared.”
Since the probability of a “six” not appearing when throwing one die is 5/6, then according to the probability multiplication theorem
P(Ā) = q = = .
Respectively,
P(A) = p = 1 – P(Ā) = .
The tests in the problem follow the Bernoulli scheme, so d.s.v. magnitude X- number k the occurrence of at least one six when throwing two dice obeys the binomial law of probability distribution:

where = is the number of combinations of n By k.

The calculations carried out for this problem can be conveniently presented in the form of a table:
Probability distribution d.s.v. X º k (n = 8; p = ; q = )

k
Pn(k)

Polygon (polygon) of probability distribution of a discrete random variable X shown in the figure:

Rice. Probability distribution polygon d.s.v. X=k.
The vertical line shows the mathematical expectation of the distribution M(X).

Let us find the numerical characteristics of the probability distribution of d.s.v. X. The distribution mode is 2 (here P 8(2) = 0.2932 maximum). The mathematical expectation by definition is equal to:
M(X) = = 2,4444,
Where xk = k– value taken by d.s.v. X. Variance D(X) we find the distribution using the formula:
D(X) = = 4,8097.
Standard deviation (RMS):
s( X) = = 2,1931.

Example2
Discrete random variable X given by the distribution law

Find the distribution function F(x) and plot it.

Solution. If , then (third property).
If, then. Really, X can take the value 1 with probability 0.3.
If, then. Indeed, if it satisfies the inequality
, then equals the probability of an event that can occur when X will take the value 1 (the probability of this event is 0.3) or the value 4 (the probability of this event is 0.1). Since these two events are incompatible, then according to the addition theorem, the probability of an event is equal to the sum of the probabilities 0.3 + 0.1 = 0.4. If, then. Indeed, the event is certain, therefore its probability is equal to one. So, the distribution function can be written analytically as follows:

Graph of this function:
Let us find the probabilities corresponding to these values. By condition, the probabilities of failure of the devices are equal: then the probabilities that the devices will work during the warranty period are equal:




The distribution law has the form:

In applications of probability theory, the quantitative characteristics of the experiment are of primary importance. A quantity that can be quantitatively determined and which, as a result of an experiment, can take on different values ​​depending on the case is called random variable.

Examples of random variables:

1. The number of times an even number of points appears in ten throws of a die.

2. The number of hits on the target by a shooter who fires a series of shots.

3. The number of fragments of an exploding shell.

In each of the examples given, the random variable can only take on isolated values, that is, values ​​that can be numbered using a natural series of numbers.

Such a random variable, the possible values ​​of which are individual isolated numbers, which this variable takes with certain probabilities, is called discrete.

The number of possible values ​​of a discrete random variable can be finite or infinite (countable).

Law of distribution A discrete random variable is a list of its possible values ​​and their corresponding probabilities. The distribution law of a discrete random variable can be specified in the form of a table (probability distribution series), analytically and graphically (probability distribution polygon).

When carrying out an experiment, it becomes necessary to evaluate the value being studied “on average.” The role of the average value of a random variable is played by a numerical characteristic called mathematical expectation, which is determined by the formula

Where x 1 , x 2 ,.. , x n– random variable values X, A p 1 ,p 2 , ... , p n– the probabilities of these values ​​(note that p 1 + p 2 +…+ p n = 1).

Example. Shooting is carried out at the target (Fig. 11).

A hit in I gives three points, in II – two points, in III – one point. The number of points scored in one shot by one shooter has a distribution law of the form

To compare the skill of shooters, it is enough to compare the average values ​​of the points scored, i.e. mathematical expectations M(X) And M(Y):

M(X) = 1 0,4 + 2  0,2 + 3  0,4 = 2,0,

M(Y) = 1 0,2 + 2  0,5 + 3  0,3 = 2,1.

The second shooter gives on average a slightly higher number of points, i.e. it will give better results when fired repeatedly.

Let us note the properties of the mathematical expectation:

1. The mathematical expectation of a constant value is equal to the constant itself:

M(C) = C.

2. The mathematical expectation of the sum of random variables is equal to the sum of the mathematical expectations of the terms:

M =(X 1 + X 2 +…+ X n)= M(X 1)+ M(X 2)+…+ M(X n).

3. The mathematical expectation of the product of mutually independent random variables is equal to the product of the mathematical expectations of the factors

M(X 1 X 2 … X n) = M(X 1)M(X 2)… M(X n).

4. The mathematical negation of the binomial distribution is equal to the product of the number of trials and the probability of an event occurring in one trial (task 4.6).

M(X) = pr.

To assess how a random variable “on average” deviates from its mathematical expectation, i.e. In order to characterize the spread of values ​​of a random variable in probability theory, the concept of dispersion is used.

Variance random variable X is called the mathematical expectation of the squared deviation:

D(X) = M[(X - M(X)) 2 ].

Dispersion is a numerical characteristic of the dispersion of a random variable. From the definition it is clear that the smaller the dispersion of a random variable, the more closely its possible values ​​are located around the mathematical expectation, that is, the better the values ​​of the random variable are characterized by its mathematical expectation.

From the definition it follows that the variance can be calculated using the formula

.

It is convenient to calculate the variance using another formula:

D(X) = M(X 2) - (M(X)) 2 .

The dispersion has the following properties:

1. The variance of the constant is zero:

D(C) = 0.

2. The constant factor can be taken out of the dispersion sign by squaring it:

D(CX) = C 2 D(X).

3. The variance of the sum of independent random variables is equal to the sum of the variance of the terms:

D(X 1 + X 2 + X 3 +…+ X n)= D(X 1)+ D(X 2)+…+ D(X n)

4. The variance of the binomial distribution is equal to the product of the number of trials and the probability of the occurrence and non-occurrence of an event in one trial:

D(X) = npq.

In probability theory, a numerical characteristic equal to the square root of the variance of a random variable is often used. This numerical characteristic is called the mean square deviation and is denoted by the symbol

.

It characterizes the approximate size of the deviation of a random variable from its average value and has the same dimension as the random variable.

4.1. The shooter fires three shots at the target. The probability of hitting the target with each shot is 0.3.

Construct a distribution series for the number of hits.

Solution. The number of hits is a discrete random variable X. Each value x n random variable X corresponds to a certain probability P n .

The distribution law of a discrete random variable in this case can be specified near distribution.

In this problem X takes values ​​0, 1, 2, 3. According to Bernoulli's formula

,

Let's find the probabilities of possible values ​​of the random variable:

R 3 (0) = (0,7) 3 = 0,343,

R 3 (1) =0,3(0,7) 2 = 0,441,

R 3 (2) =(0,3) 2 0,7 = 0,189,

R 3 (3) = (0,3) 3 = 0,027.

By arranging the values ​​of the random variable X in increasing order, we obtain the distribution series:

X n

Note that the amount

means the probability that the random variable X will take at least one value from among the possible ones, and this event is reliable, therefore

.

4.2 .There are four balls in the urn with numbers from 1 to 4. Two balls are taken out. Random value X– the sum of the ball numbers. Construct a distribution series of a random variable X.

Solution. Random variable values X are 3, 4, 5, 6, 7. Let's find the corresponding probabilities. Random variable value 3 X can be accepted in the only case when one of the selected balls has the number 1, and the other 2. The number of possible test outcomes is equal to the number of combinations of four (the number of possible pairs of balls) of two.

Using the classical probability formula we get

Likewise,

R(X= 4) =R(X= 6) =R(X= 7) = 1/6.

The sum 5 can appear in two cases: 1 + 4 and 2 + 3, so

.

X has the form:

Find the distribution function F(x) random variable X and plot it. Calculate for X its mathematical expectation and variance.

Solution. The distribution law of a random variable can be specified by the distribution function

F(x) = P(X x).

Distribution function F(x) is a non-decreasing, left-continuous function defined on the entire number line, while

F (- )= 0,F (+ )= 1.

For a discrete random variable, this function is expressed by the formula

.

Therefore in this case

Distribution function graph F(x) is a stepped line (Fig. 12)

	F(x)

Expected valueM(X) is the weighted arithmetic average of the values X 1 , X 2 ,……X n random variable X with scales ρ 1, ρ 2, …… , ρ n and is called the mean value of the random variable X. According to the formula

M(X)= x 1 ρ 1 + x 2 ρ 2 +……+ x n ρ n

M(X) = 3·0.14+5·0.2+7·0.49+11·0.17 = 6.72.

Dispersion characterizes the degree of dispersion of the values ​​of a random variable from its average value and is denoted D(X):

D(X)=M[(HM(X)) 2 ]= M(X 2) –[M(X)] 2 .

For a discrete random variable, the variance has the form

or it can be calculated using the formula

Substituting the numerical data of the problem into the formula, we get:

M(X 2) = 3 2 ∙ 0,14+5 2 ∙ 0,2+7 2 ∙ 0,49+11 2 ∙ 0,17 = 50,84

D(X) = 50,84-6,72 2 = 5,6816.

4.4. Two dice are rolled twice at the same time. Write the binomial law of distribution of a discrete random variable X- the number of occurrences of an even total number of points on two dice.

Solution. Let us introduce a random event

A= (two dice with one throw resulted in a total of even number of points).

Using the classical definition of probability we find

R(A)= ,

Where n - the number of possible test outcomes is found according to the rule

multiplication:

n = 6∙6 =36,

m - number of people favoring the event A outcomes - equal

m= 3∙6=18.

Thus, the probability of success in one trial is

ρ = P(A)= 1/2.

The problem is solved using a Bernoulli test scheme. One challenge here will be rolling two dice once. Number of such tests n = 2. Random variable X takes values ​​0, 1, 2 with probabilities

R 2 (0) =,R 2 (1) =∙,R 2 (2) =

The required binomial distribution of a random variable X can be represented as a distribution series:

X n
ρ n

4.5 . In a batch of six parts there are four standard parts. Three parts were selected at random. Construct a probability distribution of a discrete random variable X– the number of standard parts among those selected and find its mathematical expectation.

Solution. Random variable values X are the numbers 0,1,2,3. It's clear that R(X=0)=0, since there are only two non-standard parts.

R(X=1) =
=1/5,

R(X= 2) =
= 3/5,

R(X=3) =
= 1/5.

Distribution law of a random variable X Let's present it in the form of a distribution series:

X n
ρ n

Expected value

M(X)=1 ∙ 1/5+2 ∙ 3/5+3 ∙ 1/5=2.

4.6 . Prove that the mathematical expectation of a discrete random variable X- number of occurrences of the event A V n independent trials, in each of which the probability of an event occurring is equal to ρ – equal to the product of the number of trials by the probability of the occurrence of an event in one trial, that is, to prove that the mathematical expectation of the binomial distribution

M(X) =n . ρ ,

and dispersion

D(X) =n.p. .

Solution. Random value X can take values ​​0, 1, 2..., n. Probability R(X= k) is found using Bernoulli’s formula:

R(X=k)= R n(k)= ρ To (1-ρ ) n- To

Distribution series of a random variable X has the form:

X n
ρ n	q n	ρq n- 1	ρq n- 2		ρ n

Where q= 1- ρ .

For the mathematical expectation we have the expression:

M(X)=ρq n - 1 +2 ρ 2 q n - 2 +…+.n ρ n

In the case of one test, that is, with n= 1 for random variable X 1 – number of occurrences of the event A- the distribution series has the form:

X n
ρ n

M(X 1)= 0∙q + 1 ∙ p = p

D(X 1) = p – p 2 = p(1- p) = pq.

If X k – number of occurrences of the event A in which test, then R(X To)= ρ And

X=X 1 +X 2 +….+X n .

From here we get

M(X)=M(X 1 )+M(X 2)+ … +M(X n)= nρ,

D(X)=D(X 1)+D(X 2)+ ... +D(X n)=npq.

4.7. The quality control department checks products for standardness. The probability that the product is standard is 0.9. Each batch contains 5 products. Find the mathematical expectation of a discrete random variable X- the number of batches, each of which will contain 4 standard products - if 50 batches are subject to inspection.

Solution. The probability that there will be 4 standard products in each randomly selected batch is constant; let's denote it by ρ .Then the mathematical expectation of the random variable X equals M(X)= 50∙ρ.

Let's find the probability ρ according to Bernoulli's formula:

ρ=P 5 (4)== 0,94∙0,1=0,32.

M(X)= 50∙0,32=16.

4.8 . Three dice are thrown. Find the mathematical expectation of the sum of the dropped points.

Solution. You can find the distribution of a random variable X- the sum of the dropped points and then its mathematical expectation. However, this path is too cumbersome. It is easier to use another technique, representing a random variable X, the mathematical expectation of which needs to be calculated, in the form of a sum of several simpler random variables, the mathematical expectation of which is easier to calculate. If the random variable X i is the number of points rolled on i– th bones ( i= 1, 2, 3), then the sum of points X will be expressed in the form

X = X 1 + X 2 + X 3 .

To calculate the mathematical expectation of the original random variable, all that remains is to use the property of mathematical expectation

M(X 1 + X 2 + X 3 )= M(X 1 )+ M(X 2)+ M(X 3 ).

It's obvious that

R(X i = K)= 1/6, TO= 1, 2, 3, 4, 5, 6, i= 1, 2, 3.

Therefore, the mathematical expectation of the random variable X i looks like

M(X i) = 1/6∙1 + 1/6∙2 +1/6∙3 + 1/6∙4 + 1/6∙5 + 1/6∙6 = 7/2,

M(X) = 3∙7/2 = 10,5.

4.9. Determine the mathematical expectation of the number of devices that failed during testing if:

a) the probability of failure for all devices is the same R, and the number of devices under test is equal to n;

b) probability of failure for i – of the device is equal to p i , i= 1, 2, … , n.

Solution. Let the random variable X is the number of failed devices, then

X = X 1 + X 2 + … + X n ,

X i =

It's clear that

R(X i = 1)= R i , R(X i = 0)= 1– R i ,i= 1, 2, … ,n.

M(X i)= 1∙R i + 0∙(1-R i)=P i ,

M(X)=M(X 1)+M(X 2)+ … +M(X n)=P 1 +P 2 + … + P n .

In case “a” the probability of device failure is the same, that is

R i =p,i= 1, 2, … ,n.

M(X)= n.p..

This answer could be obtained immediately if we notice that the random variable X has a binomial distribution with parameters ( n, p).

4.10. Two dice are thrown simultaneously twice. Write the binomial law of distribution of a discrete random variable X - the number of rolls of an even number of points on two dice.

Solution. Let

A=(rolling an even number on the first die),

B =(rolling an even number on the second dice).

Getting an even number on both dice in one throw is expressed by the product AB. Then

R (AB) = R(A)∙R(IN) =
.

The result of the second throw of two dice does not depend on the first, so Bernoulli's formula applies when

n = 2,p = 1/4, q = 1– p = 3/4.

Random value X can take values ​​0, 1, 2 , the probability of which can be found using Bernoulli’s formula:

R(X= 0)= P 2 (0) = q 2 = 9/16,

R(X= 1)= P 2 (1)= C ,R∙q = 6/16,

R(X= 2)= P 2 (2)= C , R 2 = 1/16.

Distribution series of a random variable X:

4.11. The device consists of a large number of independently operating elements with the same very small probability of failure of each element over time t. Find the average number of refusals over time t elements, if the probability that at least one element will fail during this time is 0.98.

Solution. Number of people who refused over time t elements – random variable X, which is distributed according to Poisson's law, since the number of elements is large, the elements work independently and the probability of failure of each element is small. Average number of occurrences of an event in n tests equals

M(X) = n.p..

Since the probability of failure TO elements from n expressed by the formula

R n (TO)
,

where  = n.p., then the probability that not a single element will fail during the time t we get at K = 0:

R n (0)= e -  .

Therefore, the probability of the opposite event is in time t at least one element fails – equal to 1 - e -  . According to the conditions of the problem, this probability is 0.98. From Eq.

1 - e -  = 0,98,

e -  = 1 – 0,98 = 0,02,

from here  = -ln 0,02  4.

So, in time t operation of the device, on average 4 elements will fail.

4.12 . The dice are rolled until a “two” comes up. Find the average number of throws.

Solution. Let's introduce a random variable X– the number of tests that must be performed until the event of interest to us occurs. The probability that X= 1 is equal to the probability that during one throw of the dice a “two” will appear, i.e.

R(X= 1) = 1/6.

Event X= 2 means that on the first test the “two” did not come up, but on the second it did. Probability of event X= 2 is found by the rule of multiplying the probabilities of independent events:

R(X= 2) = (5/6)∙(1/6)

Likewise,

R(X= 3) = (5/6) 2 ∙1/6, R(X= 4) = (5/6) 2 ∙1/6

etc. We obtain a series of probability distributions:

					(5/6) To ∙1/6

The average number of throws (trials) is the mathematical expectation

M(X) = 1∙1/6 + 2∙5/6∙1/6 + 3∙(5/6) 2 ∙1/6 + … + TO (5/6) TO -1 ∙1/6 + … =

1/6∙(1+2∙5/6 +3∙(5/6) 2 + … + TO (5/6) TO -1 + …)

Let's find the sum of the series:

TOg TO -1 = (g TO) g 
.

Hence,

M(X) = (1/6) (1/ (1 – 5/6) 2 = 6.

Thus, you need to make an average of 6 throws of the dice until a “two” comes up.

4.13. Independent tests are carried out with the same probability of occurrence of the event A in every test. Find the probability of an event occurring A, if the variance of the number of occurrences of an event in three independent trials is 0.63 .

Solution. The number of occurrences of an event in three trials is a random variable X, distributed according to the binomial law. The variance of the number of occurrences of an event in independent trials (with the same probability of occurrence of the event in each trial) is equal to the product of the number of trials by the probabilities of the occurrence and non-occurrence of the event (problem 4.6)

D(X) = npq.

By condition n = 3, D(X) = 0.63, so you can R find from equation

0,63 = 3∙R(1-R),

which has two solutions R 1 = 0.7 and R 2 = 0,3.

A distribution series of a discrete random variable is given. Find the missing probability and plot the distribution function. Calculate the mathematical expectation and variance of this quantity.

The random variable X takes only four values: -4, -3, 1 and 2. It takes each of these values ​​with a certain probability. Since the sum of all probabilities must be equal to 1, the missing probability is equal to:

0,3 + ? + 0,1 + 0,4 = 1,

Let's compose the distribution function of the random variable X. It is known that the distribution function , then:

Hence,

Let's plot the function F(x) .

The mathematical expectation of a discrete random variable is equal to the sum of the products of the value of the random variable and the corresponding probability, i.e.

We find the variance of a discrete random variable using the formula:

APPLICATION

Elements of combinatorics Here: - factorial of a number

Actions on events An event is any fact that may or may not happen as a result of an experience. Merging Events A And IN- this event WITH which consists of an appearance or event A, or events IN, or both events simultaneously. Designation: ; Crossing Events A And IN- this event WITH, which consists of the simultaneous occurrence of both events. Designation: ;

Classic definition of probability Probability of event A is the ratio of the number of experiments , favorable for the occurrence of an event A, to the total number of experiments :

Probability multiplication formula Probability of event can be found using the formula: - probability of event A, - probability of event IN, - probability of event IN provided that the event A has already happened. If events A and B are independent (the occurrence of one does not affect the occurrence of the other), then the probability of the event is equal to:

Formula for adding probabilities The probability of an event can be found using the formula: Probability of event A, Probability of event IN, - probability of co-occurrence of events A And IN. If events A and B are incompatible (cannot occur simultaneously), then the probability of the event is equal to:

Total Probability Formula Let the event A can happen simultaneously with one of the events , , …, - let's call them hypotheses. Also known - probability of execution i-th hypothesis and - probability of occurrence of event A when executing i-th hypothesis. Then the probability of the event A can be found by the formula:

Bernoulli scheme Let there be n independent tests. Probability of occurrence (success) of an event A in each of them is constant and equal p, the probability of failure (i.e. the event not occurring A) q = 1 - p. Then the probability of occurrence k success in n tests can be found using Bernoulli's formula: Most likely number of successes in the Bernoulli scheme, this is the number of occurrences of a certain event that has the highest probability. Can be found using the formula:

Random variables discrete continuous (for example, the number of girls in a family with 5 children) (for example, the time the kettle works properly) Numerical characteristics of discrete random variables Let a discrete quantity be given by a distribution series: X R , , …, - values ​​of a random variable X; , , …, are the corresponding probability values. Distribution function Distribution function of a random variable X is a function defined on the entire number line and equal to the probability that X there will be less X:

Questions for the exam

Event. Operations on random events.

The concept of probability of an event.

Rules for adding and multiplying probabilities. Conditional probabilities.

Total probability formula. Bayes' formula.

Bernoulli scheme.

Random variable, its distribution function and distribution series.

Basic properties of the distribution function.

Expected value. Properties of mathematical expectation.

Dispersion. Properties of dispersion.

Probability distribution density of a one-dimensional random variable.

Types of distributions: uniform, exponential, normal, binomial and Poisson distribution.

Local and integral theorems of Moivre-Laplace.

Law and distribution function of a system of two random variables.

Distribution density of a system of two random variables.

Conditional laws of distribution, conditional mathematical expectation.

Dependent and independent random variables. Correlation coefficient.

Sample. Sample processing. Polygon and frequency histogram. Empirical distribution function.

The concept of estimating distribution parameters. Requirements for assessment. Confidence interval. Construction of intervals for estimating mathematical expectation and standard deviation.

Statistical hypotheses. Consent criteria.