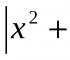Care este greutatea unei poziții în sistemul numeric. Ce este un sistem numeric? Ce sisteme numerice sunt utilizate de experți pentru a comunica cu un computer

Cunoașterea cu Leaf

Inventatorul Listik a venit cu un dispozitiv pentru transmiterea numerelor. Dispozitivul său a transmis mesaje sub forma unui lanț de semnale scurte și lungi. În notele sale, Listik a notat un semnal scurt cu numărul „0”, iar unul lung cu numărul „1”. La transmiterea numerelor, el a folosit următorul cod pentru fiecare cifră:

Numărul 12, format din numerele 1 și 2, Broșură a notat pentru transmisie după cum urmează:

Dispozitivul a transmis acest mesaj într-un lanț de astfel de semnale: trei scurte, una lungă, două scurte, una lungă și una scurtă.

Numărul 77 conform sistemului Listik a fost codificat după cum urmează:

Codificarea informațiilor

Codificarea este traducerea informațiilor într-un formular convenabil pentru transmisie sau stocare.

De exemplu, textele sunt codificate folosind litere și semne de punctuație. Mai mult, una și aceeași înregistrare poate fi codificată în moduri diferite: în rusă, în engleză, în chineză ...

Numerele sunt codificate folosind numere. Numerele cu care suntem obișnuiți se numesc numere arabe. Cifrele romane sunt uneori folosite. În acest caz, metoda de codificare a informațiilor se schimbă. De exemplu, 12 și XII sunt modalități diferite de a scrie același număr.

Muzica poate fi codificată folosind caractere speciale - note. Indicatoarele rutiere sunt mesaje codificate către șoferi și pietoni folosind pictograme.

Mărfurile din magazin sunt marcate cu un cod de bare, care conține informații despre produs și producătorul acestuia.

Un cod de bare este o secvență de dungi alb-negru care codifică informații într-o formă ușor de citit de dispozitivele tehnice. În plus, o serie de numere pot fi plasate sub codul de bare.

Informațiile sunt întotdeauna stocate și transmise sub formă de coduri. Nu puteți stoca doar informații, fără un operator de transport. În același mod, este imposibil să stocați și să transmiteți doar informații: are întotdeauna o formă, adică este codificată.

Codificare binară

Codarea binară este codificarea informațiilor folosind zerouri și unele. Pentru tehnologiile informatice, această metodă de prezentare a informațiilor s-a dovedit a fi foarte convenabilă.

Ideea este că computerele sunt construite pe elemente care pot fi în două stări posibile. Un astfel de stat este desemnat prin numărul 0, celălalt prin numărul 1.

Un exemplu de dispozitiv binar este un bec obișnuit. Poate fi în una din cele două stări: pornit (starea 1) sau oprit (starea 0).

Puteți construi memorie electrică pe becuri și puteți stoca în ea, de exemplu, numere folosind codul binar al Leaf.

Sunt necesare patru becuri pentru a stoca fiecare cifră zecimală. Acesta este modul în care vă puteți aminti numărul 6:

Puneți întrerupătoarele în poziția dorită - și să mergem să bem ceai! Dacă electricitatea nu este oprită, informațiile vor fi salvate.

Becurile, desigur, nu sunt potrivite pentru producția de computere: sunt mari, se ard rapid, sunt scumpe (la urma urmei sunt milioane) și încălzesc mult mediul.

În computerele moderne, un dispozitiv electronic, un tranzistor, este folosit ca element de memorie.

Tranzistorul poate trece curent prin el însuși (starea 1) sau nu (starea 0).

A existat o perioadă în care fiecare tranzistor a fost fabricat separat și a avut dimensiuni semnificative.

Acum, tranzistoarele, ca și alte elemente electronice, sunt realizate într-un mod similar cu imprimarea fotografiilor. unu microcircuit de mărimea unei unghii, câteva milioane de tranzistoare pot fi „imprimate”.

Codul pe care Listik l-a folosit pentru a codifica mesajele este de fapt folosit pentru a lucra cu numerele dintr-un computer.

Cu codarea binară, nu trebuie să te uiți deloc la acest tabel, dar amintește-ți regula simplă pentru traducerea unui cod binar într-o cifră zecimală.

Cel din cod din primul loc din dreapta dă numărul
lo 1, pe al doilea - 2, pe al treilea - 4, pe al patrulea - 8. Pentru a obține cifra zecimală, se adaugă numerele. De exemplu, codul „0101” este tradus în cifra 5 (suma numerelor 4 și 1).

Aceeași regulă poate fi utilizată și pentru decodare. De exemplu, cifra 6 este scrisă ca suma numerelor 4 și 2, ceea ce înseamnă că codul său va fi „0110”.

O tabletă cu numere scrise în sistemul numeric care a fost folosit în Babilonul antic. În jurul anului 1700 î.Hr. Descifrat în 1945.

Sisteme numerice

Codul frunzei și codarea numerelor

Lecția anterioară v-a arătat cum să scrieți numere folosind zerouri și unele. Broșură codifică fiecare cifră numărul patru binar semne.

Deci, numărul 102 din codul Leaf este scris folosind 12 caractere binare:

Broșură codifică separat fiecare din 10 cifre și folosește 4 cifre binare pentru aceasta. Dar patru caractere binare pot codifica nu 10, ci 16 valori:

Se pare că 6 coduri Leaf (care este mai mult de jumătate din 10) sunt irosite!

Este posibil să codificați mai economic?

Puteți, dacă codificați nu numere(din care se colectează numărul) și imediat numerele! Deci, numărul 102, cu această metodă de codare, poate fi scris nu în douăsprezece, ci doar în șapte cifre binare (salvăm 5 cifre):

Această codificare va fi acoperită în acest tutorial. Dar să începem în ordine.

Sistem de numere zecimale

După cum știți, numerele sunt construite din numere și există doar zece numere, iată-le:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Cum se pot scrie numere mari cu doar zece cifre? Vom vedea acest lucru acum, dar mai întâi, să ne amintim definiția:

Se numește modul de scriere a numerelor sistemul numeric.

Cuvant erudit socoteală, consonant cu cuvântul „calcul” înseamnă deja „mod de scriere a numerelor”. Dar matematicienilor li s-a părut că fraza notaţie suna mai bine. Nu contează, vom stăpâni acest termen cu două cuvinte! Acum să ne ocupăm de asta sistemul numeric, cu care sunt obișnuiți.

Uită-te la numărul 253. În această intrare, prima cifră din dreapta (se numește cifră cel mai puțin semnificativă) înseamnă „trei unii”, cinci înseamnă „cinci zeci” și doi ( cea mai mare cifră) - "doua sute".

Se pare: 253 = 2 · 100 + 5 · 10 + 3 · 1.

Vorbim: "Două sute cincizeci și trei"... Aceasta înseamnă numărul care se obține prin adăugarea:

două sute (2 100 = doua sute),

cinci zeci (5 10 = cincizeci) și

trei unități (3 1 = Trei).

Vedem că valoarea cifrei din înregistrarea numerelor depinde de pozițiiîn care se află cifra. Pozițiile cifrei sunt numite diferit descărcări numere.

Cifra cea mai puțin semnificativă înseamnă unități:

A doua cifră din dreapta înseamnă zeci:

A treia cifră din dreapta înseamnă sute:

Vedem că contribuția cifrei la număr crește de la dreapta la stânga.

Sisteme numerice în care depinde contribuția unei cifre la un număr poziții numerele din intrare sunt numite sisteme de numere poziționale.

Sistemul numeric care ne este familiar este pozițional, așa cum am văzut. Rețineți că în bază se presupune că este numărul 10 - numărul de cifre utilizate.

Cea mai mică cifră arată numărul de unități din număr, a doua din dreapta - numărul de zeci (1 · 10). Al treilea arată sute (10 10), al patrulea arată mii (10 100) și așa mai departe.

Numărăm ca unități, unitățile se adună la zeci (zece unități sunt înlocuite cu unul zece), zeci - în sute (zece zeci sunt înlocuite cu o sută) și așa mai departe.

Numărul 10 este baza sistemului numeric obișnuit, de aceea este numit sistem zecimal, sau de sistemul numeric bază 10.

Uită-te din nou la modul în care 2789 se traduce într-un număr.

Numărul se obține prin adăugare depozite numere incluse în acesta:

Contribuția fiecărei cifre este obținută prin înmulțirea acelei cifre cu un multiplicator dependent de poziție asociat cu raza sistemului.

Multiplicatorii de poziție sunt calculați conform următoarei reguli:

1. Multiplicatorul primei poziții (dreapta) este 1 .

2. Înmulțitorul fiecărei poziții următoare se obține prin înmulțirea bazei sistemului (numărul 10 ) printr-un factor al poziției anterioare.

Se vor apela multiplicatorii de poziție greutățile pozițiilor, sau greutăți poziționale.

Numărul este egal cu suma depozitelor. Contribuția este egală cu produsul figurii și greutatea pozițională. Greutatea primei poziții este 1, a doua este 10, a treia este 100 și așa mai departe. Adică, greutatea fiecărei poziții (cu excepția primei) se obține din greutatea celei anterioare prin înmulțirea cu baza sistemului. Greutatea primei poziții este egală cu una.

Iată cum: s-au înmulțit, au adăugat și nu au suspectat! Se pare că scriem numere în notația pozițională bazată pe zece! De ce baza sistemului nostru este egală cu 10? Ei bine, acest lucru este de înțeles: la urma urmei, avem 10 degete, este convenabil să numărăm îndoindu-le în ordine.

Dar pentru un computer, așa cum știți deja, sistemul binar este mai familiar, adică baza pozițională doi.

Sistem de numere binare

Există doar două cifre în sistemul binar:

Dacă în sistemul zecimal greutățile poziției se obțin înmulțind cu zece, atunci în sistemul binar - înmulțind cu două:

Se pare: 1011 2 = 1 2 · 4 + 0· 2 · 2 + 1 2 · 1 + 1 1 .

În sistemul binar, acestea sunt considerate a fi unele, cele se adaugă la două (două sunt înlocuite cu unul două), două - în patru (două două sunt înlocuite cu unul patru) și așa mai departe.

Când este necesar să se clarifice în ce sistem este scris un număr, baza sistemului i se atribuie de jos:

1011 2 - numărul este scris în sistemul binar.

Nu este dificil să-l convertiți în sistemul zecimal, trebuie doar să efectuați operațiile de multiplicare și adunare:

1011 2 = 1 2 · 4 + 0· 2 · 2 + 1 2 · 1 + 1 1 =

1 8 + 0 4 + 1 2 + 1 1 = 11 10.

Conversie binară în zecimală

În sistemul binar, contribuția unuia pe primul loc din dreapta este numărul 1, în al doilea - 2, în al treilea - 4, în al patrulea - 8 și așa mai departe. Contribuțiile de zerouri, desigur, sunt egale cu zero, indiferent de pozițiile lor.

Primim următoarea regulă:

Pentru a converti de la binar la zecimal, trebuie să scrieți greutatea poziției sale deasupra fiecărei cifre binare și să adăugați numerele scrise deasupra celor.

10111 2 = 16 + 4 + 2 + 1 = 23 10 .

Un alt exemplu, numărul 100110:

100110 2 = 32 + 4 + 2 = 38 10 .

Conversie de la zecimal la binar

Pentru a converti de la zecimal la binar, vom folosi schema anterioară cu greutăți de poziție:

Să se convertească numărul 26 în sistemul binar. Selectăm începutul numărului binar (cea mai semnificativă cifră) conform schemei. 32 este mult, așa că începem cu 16:

O parte din numărul original, și anume 16, este codificată, rămâne să codeze 26 - 16 = 10. Luați 8 (cea mai mare greutate pozițională posibilă):

Rămâne să codificăm 10 - 8 = 2. Patru sunt multe. Scriem în poziția 0 și luăm 2:

Am codificat întregul număr, ceea ce înseamnă că ultima cifră ar trebui să fie zero:

Se pare: 26 10 = 11010 2.

Regula pentru conversia de la zecimal la binar poate fi formulată după cum urmează.

Pentru a înțelege mai bine acest algoritm, lucrați pe banca testerului. Faceți clic pe buton Resetați, formeaza un numar. Apoi apăsați butonul start: veți vedea cum efectuează Tester algoritmul de conversie binară pas cu pas.

Vă rugăm să rețineți: în înregistrarea algoritmului, elementul care va fi executat este evidențiat. după apăsând butonul start... De exemplu, dacă elementul este evidențiat „Repetați până când numărul devine zero”, apoi după ce faceți clic pe start Testerul va verifica numărul curent pentru egalitate la zero și va decide dacă se repetă în continuare.

(Efectuați lucrări cu Testerul pe pagina aplicației electronice.)

Sisteme poziționale cu alte baze

Vasya iubește sistemul zecimal, computerul său iubește binarul, iar matematicienii curioși adoră diferite sisteme de numere poziționale, deoarece puteți lua orice număr ca bază, nu doar 2 sau 10.

Să luăm ca exemplu un sistem numeric ternar.

Sistem de numere ternare

Sistemul numeric ternar folosește, după cum ați putea ghici, trei numere:

În sistemul ternar, acestea sunt considerate a fi unități, unele sunt adăugate la trei (trei sunt înlocuite cu un triplu), trei - la nouă (trei trei sunt înlocuite cu un nouă) și așa mai departe.

Interesant este că în 1958, sub conducerea N.P. Brusentsov, computerul Setun a fost creat la Universitatea de Stat din Moscova și funcționa cu numere nu în sistem binar, ci în sistem ternar! Primul prototip „Setun” este prezentat în fotografie:

Conversia de la ternar la zecimal

Să denotăm în diagramă contribuțiile poziționale ale cifrelor din sistemul numeric ternar:

Pentru a converti la sistemul zecimal, adăugați cifrele înmulțite cu greutățile lor poziționale (pozițiile cu zero cifre, desigur, pot fi omise):

10212 3 = 1 81 + 2 9 + 1 3 + 2 1 = 104 10 .

În sistemul binar, am renunțat la multiplicare (nu are rost să înmulțim cu 1). Există un număr 2 în sistemul ternar, deci trebuie să dublați greutățile poziționale corespunzătoare.

Conversie de la zecimal la ternar

Să fie tradus numărul 196 în sistemul ternar. Selectăm începutul numărului ternar în conformitate cu schema. 243 este mult, așa că începem cu 81 și numărul 2 (2 81< 196):

O parte din numărul original, și anume 162 = 2 · 81, este codificată, rămâne să codeze 196 - 162 = 34. Luați 27 și numărul 1 (numărul 2 dă 54, care este prea mult):

Rămâne să codificați 34 - 1 · 27 = 7. Poziția cu greutatea 9 dă prea mult, scrieți 0 în ea și luați poziția cu greutatea 3 și numărul 2:

Rămâne să codificați 7 - 2 · 3 = 1. Aceasta este exact valoarea cifrei rămase cel mai puțin semnificative:

Se pare: 196 10 = 21021 3.

Sisteme poziționale: reguli de bază

Să formulăm regulile generale pentru construirea numerelor în sistemele numerice poziționale.

Numărul este scris în cifre, de exemplu:

Pentru a determina valoarea unui număr, trebuie să multiplicați numerele cu greutățile pozițiilor lor și să adăugați rezultatele.

Pozițiile sunt numerotate de la dreapta la stânga. Greutatea primei poziții este 1.

Greutatea fiecărei poziții următoare se obține din greutatea celei anterioare prin înmulțirea cu baza sistemului.

Se pare că greutatea celei de-a doua poziții este întotdeauna egală cu baza sistemului.

Baza sistemului arată numărul de cifre care sunt utilizate în acest sistem. Deci, într-un sistem de bază 10, există zece cifre, într-un sistem de bază 5, cinci cifre.

Să vedem un exemplu. Dacă intrarea

înseamnă un număr în sistemul de bază 5, atunci este egal cu

3242 5 = 3 125 + 2 25 + 4 5 + 2 1 = 447 10 .

Aceeași intrare în sistemul de bază 6 înseamnă numărul

3242 6 = 3 216 + 2 36 + 4 6 + 2 1 = 746 10 .

Sisteme numerice nepoziționale

Sistemele numerice poziționale nu au apărut imediat, oamenii primitivi au desemnat numărul unor obiecte ca fiind egal cu numărul altora (erau considerați pietricele, bețe, oase).

Au fost folosite și metode mai convenabile de numărare: crestături pe un băț, liniuțe pe o piatră, noduri pe o frânghie.

Uneori, oamenii moderni folosesc și un astfel de sistem numeric, observând, de exemplu, numărul de zile care au trecut de crestături.

Acesta este un exemplu sistem de număr de unități nepozițional: folosit pentru numărare singur număr (piatră, baston, os, liniuță, nod ...), iar contribuția acestei figuri nu depinde de locul (poziția) ei, este întotdeauna egală cu o unitate.

Este clar că este mult mai convenabil să folosiți sisteme de numere poziționale.

Acțiuni asupra numerelor

Acțiunile asupra numerelor din sistemul pozițional cu orice bază sunt efectuate în același mod ca și în sistemul zecimal: se bazează pe tabelele de adunare și multiplicare a cifrelor sistemelor numerice corespunzătoare.

Ar fi ciudat dacă în diferite sisteme ar trebui să adăugați, să scădeți, să înmulțiți și să împărțiți în diferite moduri! Într-adevăr, în toate sistemele numerice, numerele sunt construite în același mod, ceea ce înseamnă că acțiunile asupra lor trebuie efectuate în același mod.

Să ne uităm la câteva exemple.

Plus

5 + 7 = 12. În bitul cel mai puțin semnificativ scriem 2 și adăugăm unul la bitul următor.

Să construim un tabel de adăugare octal:

Conform tabelului de adunare 5 + 7 = 14 8. Scriem 4 în cifra cea mai puțin semnificativă și adăugăm una la cifra următoare.

Scădere

Ocupăm 1 în a doua cifră și scădem 7 din numărul 15. În mod similar în sistemul octal:

Ocupăm 1 în a doua cifră și scădem 7 din numărul 15 8. Conform tabelului de adunare din linia 7, găsim numărul 15. Numărul coloanei corespunzătoare dă rezultatul diferenței - numărul 6.

Acest lucru este probabil convenabil pentru păianjeni
sistem de numere octale!

Multiplicare

2 7 = 14. Scriem 4, iar 1 merge la „minte” (adăugați la categoria următoare). 4 · 7 = 28. Scriem 9 (8 plus 1 din „minte”) și 2 trecem la următoarea categorie.

Să construim un tabel de multiplicare octal:

2 7 = 16 8. Scriem 6, iar 1 merge la „minte” (adăugați la categoria următoare). 4 7 = 34 8. Scriem 5 (4 plus 1 din „minte”) și 3 trecem la cifra următoare.

Divizia

3 5< 17 < 4·5, поэтому первая цифра результата - 3. Из 17 вычитаем 5·3 = 15. К разности 2 приписываем цифру 5, получается 25. 25 = 5 ·5. Из 25 вычитаем 25=5·5, получается 0 - деление закончено.

În tabelul de înmulțire din linia 5 găsim numărul corespunzător 17 8 = 5 3:

Aceasta înseamnă că prima cifră a rezultatului este 3. Din 17 8 scădem 17 8 = 5 · 3. Diferenței 0 îi atribuim ultima cifră 5. 5 = 5 · 1. Se scade 5 din 5, rezultă 0 - împărțirea s-a terminat.

Intrebari si raspunsuri

1. Dați o definiție termenului „sistem numeric”.

2. Dați o definiție termenului „sistem de număr pozițional”.

3. Explicați principiile construirii numerelor în notație zecimală folosind exemplul numărului 548.

4. Ce se numește greutatea unei poziții? Spuneți-ne algoritmul pentru găsirea greutății unei poziții. Care este greutatea celei de-a treia poziții din dreapta în notația zecimală a numărului? Și în binar? Și în ternar?

5. Ce se înțelege prin externare? Ce loc este numărul 5 din numărul zecimal 1532?

6. Ce se numește contribuția numerelor? Care este contribuția numărului 7 la 1745 10? Și contribuția numărului 4 la numărul 1432 5?

7. Dați o definiție termenului „baza sistemului de numere poziționale”. Cum este legată baza unui sistem de numărul de cifre din acest sistem? Câte cifre există în sistemul numeric cu 5 arii? Și în hexazecimal? Dar un sistem de bază 25?

8. Unde este cea mai puțin semnificativă cifră din înregistrarea numerelor? Și cel mai mare?

9. Spuneți algoritmului pentru conversia unui număr binar în sistemul numeric zecimal și efectuați acest algoritm pentru numărul 101101 2.

10. Spuneți algoritmului pentru conversia unui număr zecimal într-un sistem de numere binare și efectuați acest algoritm pentru numărul 50 10.

11. Cum se convertește un număr din orice sistem de numere poziționale în sistemul zecimal? Explicația se bazează pe exemplul unui sistem cu o bază 4.

Hometasks

Opțiunea 1. Efectuată fără computer, „pe hârtie”

1. Citiți strunguri de limbă, înlocuind numerele binare cu zecimale:

A mancat bine
100001 2 plăcinte cu plăcintă,
Da, toate cu brânză de vaci.

Au fost 101000 2 șoareci,
Adus 101000 2 grosz,
Un 10 2 șoareci sunt mai mici
Au purtat câte 10 2 gros.

2. Rezolvați puzzle-urile cu litere binare:

3. Efectuați calculele și notați răspunsul în notație zecimală:

1) 100 2 5 8 =

2) 100 3 + 100 5 =

3) 10 9 10 100 - 10 900 =

4) 33 4 + 44 5 =

5) 15 6 + 51 8 =

4. Traduceți numerele date în sistemele numerice indicate:

Opțiunea 2. Efectuată pe computer

1. Scrieți expresia aritmetică pentru rezolvarea următoarei probleme și calculați răspunsul:

Inteligența noastră Malvina
Se ocupă de Pinocchio
Și l-am cumpărat pentru el
De ce are nevoie cel mai mult:
10 2 coperte, 11 2 rigle
Și pentru 111 autocolante de 2 ruble.
Pe coperte - Barmaley,
Prețul fiecăruia este de 101 2 ruble.
Pe conducătorii pe care i-am cumpărat
101010 2 ruble au fost suficiente.
Cât au costat achizițiile?
La reflecție - o jumătate de minut.

2. Încercați să utilizați programul standard Calculator pentru a converti numerele dintr-o poezie în notația zecimală obișnuită ( Vedere- Inginerie, Cos- reprezentarea binară a unui număr, Dec- reprezentarea zecimală a numărului). Utilizați Calculatorul pentru a nota algoritmi pentru conversia numerelor de la binar la zecimal și invers, de la zecimal la binar.

Opțiunea 3. Pentru curioși

1. Dovediți că scrierea 10 în orice sistem numeric pozițional înseamnă un număr egal cu baza acestui sistem.

2. Determinați baza sistemului de numere poziționale b pentru fiecare egalitate:

1) 10 b = 50 10 ;

2) 11 b = 6 10 ;

3) 100 b = 64 10 ;

4) 101 b = 26 10 ;

5) 50 b = 30 10 ;

6) 99 b = 909 10 ;

7) 21 b = 15 6 ;

8) 10 2 b = 100 b ;

9) 12 2 b = 22 b ;

10) 14 b· b = 104 b .

p ALIGN = "JUSTIFY"> 3. Sistemul numeric hexazecimal utilizează 16 cifre. Primele zece cifre coincid cu cifrele sistemului zecimal, iar ultimele sunt notate cu litere din alfabetul latin:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

	Valoare

Să traducem, de exemplu, numărul A8 16 în sistemul zecimal:

A8 16 = 10 16 + 8 1 = 168 10 .

Găsiți semnificația numărului în fiecare sarcină X:

1) 25 16 = X 10 ; 4) 170 10 = X 16 ;

2) AB 16 = X 10 ; 5) 2569 10 = X 16 ;

3) FD 16 = X 10 ; 6) 80 32 = X 16 .

4. Finalizați următoarele sarcini.

1) Găsiți greutatea celei de-a treia poziții în înregistrarea numerică dacă știți că greutatea celei de-a doua poziții este 7. Numerotarea pozițiilor de la dreapta la stânga.

2) Sistemul numeric folosește 5 cifre. Găsiți greutatea celei de-a patra poziții din dreapta în notația numerică.

3) Numărul se scrie sub forma a două unități: 11. În ce sistem numeric se scrie dacă în zecimal este egal cu 21?

4) Într-un anumit sistem numeric, numărul arată ca 100. Câte cifre folosește acest sistem numeric dacă în sistemul zecimal numărul este 2500?

5) Două numere sunt scrise ca 100, dar în sisteme cu rază diferită. Se știe că baza primului sistem este de două ori cea a celui de-al doilea. Ce număr este mai mare și de câte ori?

6) Găsiți baza sistemului, dacă se știe că numărul 101 scris în acest sistem înseamnă numărul zecimal 37.

7) În ce sistem numeric, pentru a dubla un număr, trebuie să adăugați zero la dreapta intrării sale?

8) Înmulțirea cu 10 în sistemul zecimal înseamnă adăugarea zero la dreapta la număr. Formulați regula înmulțirii cu 10 bîntr-un sistem cu bază b.

5. Formulează un algoritm pentru conversia unui număr din sistemul numeric zecimal în sistem ternar.

6. Construiți tabele de adunare și înmulțire pentru sistemul de patru ori. Folosind aceste tabele, efectuați următoarele acțiuni asupra numerelor dintr-o coloană (rămânând în sistemul numeric cuaternar):

1.a) 1021 4 + 333 4;

b) 3333 4 + 3210 4;

2. a) 321 4 - 123 4;

b) 1000 4 - 323 4;

3. a) 13 4 · 12 4;

b) 302 4 23 4;

4.a) 1123 4:13 4;

b) 112003 4: 101 4.

7. Construiți tabele de adunare și multiplicare pentru sistemul de numere binare. Folosind aceste tabele, efectuați următoarele acțiuni asupra numerelor dintr-o coloană (rămase în sistemul de numere binare):

1.a) 1001 2 + 1010 2;

b) 10111 2 + 1110 2;

2. a) 1110 2 - 101 2;

b) 10000 2 - 111 2;

3. a) 101 2 · 11 2;

b) 1110 2 · 101 2;

4.a) 1000 110 2: 101 2;

b) 100000100 2: 1101 2.

Atelier

Pe paginile aplicației electronice, lucrați cu codificatorul performer.

Exercițiile conțin următoarele grupuri de sarcini:

Zecimal

1. De la binar la zecimal

2. De la ternar la zecimal

3. De la cinci la zecimale

4. De la hexazecimal la zecimal

Din zecimal

1. Zecimal la Binar

2. De la zecimal la ternar

3. De la zecimal la cinci

4. De la zecimal la hexazecimal

Clasa 1 de creditare

2. 1101 2 = ? 10

3. 11101 2 = ? 10

Clasa 2 de creditare

10. 1001 2 = ? 16

Material didactic

Sisteme de numere poziționale

În sistemul numeric pozițional, un număr este scris ca un lanț de caractere speciale:

a n a n - 1 ... A 2 A 1 (1)

Simboluri a i sunt numite cifre... Ele indică cantități ordinale numărabile, începând de la zero și până la valoarea cu un număr mai puțin. q numit bază sistemul numeric. Adică dacă q- bază, apoi valorile cifrelor se află în interval (inclusiv limite).

Poziția cifrei în înregistrarea numărului (1) se numește poziţie, sau descărcare.

Notă 1. În aceste pagini, termenul „poziție” este preferat. În primul rând, cuvântul „poziție” este în acord cu conceptul „sistem de numere poziționale”, iar în al doilea rând, termenul „greutate pozițională” sau „greutate de poziție” sună mai bine, mai clar și mai simplu decât „greutate pe biți” sau „greutate pe biți” . Cu toate acestea, profesorul poate și trebuie să le reamintească elevilor din când în când că „poziția” și „rangul” sunt termeni echivalenți.

Observație 2. Definiția sistemului numeric pozițional dat în textele pentru elev nu este complet corectă. Dependența contribuției figurii doar de poziție nu este suficientă. De exemplu, în sistemul numerelor romane, contribuția cifrei depinde și de poziție (numerele IV și VI sunt diferite), dar acest sistem nu este pozițional. O definiție exactă poate fi considerată întregul set de reguli pentru construirea unui număr, dat în acest context pentru un profesor (adică, împreună cu faptul dependenței poziționale, definiția include: finitudinea setului de cifre și regula pentru găsirea unui număr prin înregistrarea acestuia).

Pozițiile sunt numerotate de la dreapta la stânga. Se numește numărul din prima poziție tanarul cifra unui număr, în ultimul - senior.

Fiecare poziție este asociată cu un număr, pe care îl vom numi greutatea sa ( poziția de ponderare).

Ponderile poziției sunt determinate în conformitate cu următoarea regulă recursivă:

1. Greutatea celei mai mici poziții este 1.

2. Greutatea fiecărei poziții următoare se obține din greutatea celei anterioare prin înmulțirea cu baza sistemului.

Lasa q- baza sistemului numeric. Apoi regula pentru calcularea greutăților poziționale w i poate fi scris mai concis ca o formulă recurentă:

1. w 1 = 1.

2. w i = w i-unu · q(pentru toți eu > 1).

În sistemul numeric pozițional, înregistrarea

a n a n - 1 ... A 2 A 1 (1)

înseamnă număr N, egală cu suma produselor de cifre după greutățile lor de poziție:

N = a n· w n + a n-unu · w n–1 + ... + A 2 w 2 + A unu · w 1 . (2)

Produsul unei cifre după greutatea sa pozițională (adică a i· w i) va fi chemat contribuția pozițională a numerelor.

Formula (2) stă la baza regulilor de traducere a numerelor dintr-un sistem în altul, propuse în textele pentru elev.

În sistemul zecimal, numerele sunt scrise folosind zece caractere arabe: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Greutățile poziționale ale acestui sistem sunt: ..., 1000, 100, 10, 1.

4627 10 = 4 1000 + 6 100 + 2 10 + 7 1.

În sistemul binar, numerele sunt scrise folosind două caractere arabe: 0 și 1. Greutăți poziționale ale acestui sistem: ..., 256, 128, 64, 32, 16, 8, 4, 2, 1.

De exemplu, intrarea 10101 este „decriptată” astfel:

10101 2 = 1 16 + 0 8 + 1 4 + 0 2 + 1 1.

Rețineți că regula recursivă pentru calcularea ponderilor implică acest lucru w i = q i–1 și, prin urmare, notația (2) este echivalentă cu notația tradițională sub forma unui polinom de putere:

N = a n· q n–1 + a n-unu · q n–2 + ... + A 2 q + A 1 . (3)

Dovedim acest lucru prin inducție. Baza de inducție la eu= 1 este bifat direct: w 1 = q 0 = 1.

Ipoteza inducției: afirmația să fie adevărată pentru unii n:

w n = q n–1 .

Să dovedim că va fi valabil și pentru n + 1.
Adică vom dovedi validitatea egalității:

w n + 1 = q n.

Într-adevăr, w n+1 = w n· q(conform definiției recursive a greutății poziției) și w n = q n–1 prin ipoteză de inducție. Se pare:

w n + 1 = w n· q = q n-unu · q = q n.

Să dovedim că orice număr este reprezentabil în forma (1) (Teorema 1) într-un mod unic (Teorema 2).

Teorema 1 (existență). Orice număr m poate fi reprezentat sub forma (1) pentru oricare q > 1.

Dovezi. Să o dovedim prin inducție. Pentru m = 0
și m= 1 este ușor să construiți reprezentarea necesară - acestea sunt 0 și respectiv 1 (pentru oricare q> 1). Să presupunem că am reușit să reprezentăm numărul m sub forma (1). Să găsim apoi o reprezentare pentru m+ 1. Pentru a face acest lucru, este suficient să convertiți suma

a n q n–1 + a n-unu · q n–2 + ... + A 2 q + A 1 + 1 pentru a forma (1).

În cazul în care un A 1 < (q-1), atunci reprezentarea dorită se obține prin înlocuirea cifrei A 1 pe A " 1 = A 1 + 1.

În cazul în care un A 1 = (q–1), obținem transferul unității în următoarea poziție:

a n q n F - 1 + a n-unu · q n–2 + ... + (A 2 + 1) q + 0.

Apoi, rezonăm într-un mod similar. În cazul în care un A 2 < (q-1), atunci reprezentarea dorită se obține prin înlocuirea cifrei A 2 pe A " 2 = A 2 + 1. Dacă A 2 = (q–1), atunci A 2 este înlocuit cu zero și unul este transferat în poziția următoare.

Sau pe unele eu < n vom termina construcția sau vom obține un record de 1000 ... 0 - unul și n zerouri la dreapta. Dovada este completă.

Înainte de teorema 2, demonstrăm lema.

Lemă. Contribuția fiecărei cifre diferite de zero din înregistrarea (1) depășește suma contribuțiilor cifrelor situate în dreapta acesteia.

a n a n - 1 ... A 2 A 1 . (1)

Dovezi. Să dovedim asta pentru orice n > 1:

a n q n–1 > a n-unu · q n–2 + ... + A 2 q+ A 1 .

Numere a i se află în interval, ceea ce înseamnă că este suficient să demonstrați inegalitatea pentru cea mai mică cifră diferită de zero din stânga și cifrele maxime din dreapta:

q n - 1> ( q-unu)· q n–2 + ... + (q-unu)· q + (q–1).

În partea dreaptă, eliminăm factorul ( q–1) în afara parantezei:

(q-unu)· q n–2 + ... + (q-unu)· q + (q–1) =

= (q-unu)·( q n–2 + ... + q + 1).

Calculăm suma progresiei geometrice din ultima paranteză folosind formula bine-cunoscută:

(q-unu)·( q n–2 + ... + q + 1) =

= (q-unu)·( q n–1 –1)/(q–1) = q n–1 – 1.

Obținem o inegalitate evidentă care dovedește lema:

q n - 1> q n–1 – 1.

Teorema 2 (unicitate). Numărul în forma (1) este reprezentat în singurul mod.

Dovezi. Din lema rezultă că numerele care au un număr diferit de cifre în notație (zerourile nesemnificative din stânga nu sunt numărate) nu pot fi egale: un număr cu un număr mare de cifre este întotdeauna mai mare. Prin urmare, este necesar doar să demonstreze că dacă a i nu este egal b i pentru toți eu de la 1 la n apoi înregistrează

a n a n - 1 ... A 2 A 1 (4)

b n b n - 1 ... b 2 b 1 (5)

nu poate însemna același număr.

Să analizăm înregistrările (4) și (5) de la stânga la dreapta în căutarea cifrelor nepotrivite. Lăsați-l să fie a kși b k lăsați-l să plece a k – b k = d.

Pe k- locul al doilea, a fost o diferență în d· q k-unu . Această diferență ar trebui compensată prin contribuțiile pozițiilor situate în dreapta. Dar acest lucru este imposibil, întrucât, conform lemei, suma contribuțiilor pozițiilor situate la dreapta este întotdeauna mai mică decât contribuția poziției actuale. Teorema este dovedită.

Conversia în zecimal

Pentru a traduce numerele dintr-un sistem radix qîn sistemul zecimal, puteți utiliza formula (2), efectuând multiplicare și adunare în ea.

N = a n· w n + a n-unu · w n–1 + ... + A 2 w 2 + A unu · w 1 (2)

La traducerea dintr-un sistem binar, este implicată doar adăugarea (deoarece nu puteți înmulți cu 1). Astfel, obținem regula de traducere formulată în sala de lectură:

Pentru a converti de la binar la zecimal, trebuie să scrieți greutatea poziției sale deasupra fiecărei cifre binare și să adăugați numerele scrise deasupra unităților.

Deci, de exemplu, pentru numărul 10111 obținem:

10111 2 = 16 + 4 + 2 + 1 = 23 10

Regula generală a transferului din q-ar sistem la zecimale sună astfel:

Pentru a transfera de la q-ar sistem în zecimal, trebuie să notați greutatea poziției sale deasupra fiecărei cifre și să găsiți suma produselor cifrelor după greutățile lor de poziție (adică să găsiți suma contribuțiilor poziționale).

Deci, de exemplu, pentru numărul 10212 3 obținem:

Adăugăm numerele înmulțite cu greutățile lor poziționale (pozițiile cu zero cifre, desigur, pot fi omise):

10212 3 = 1 81 + 2 9 + 1 3 + 2 1 = 104 10 .

Traducere în q- personal

Pentru a converti numerele de la zecimal la radix q vom continua să ne bazăm pe formula (2):

N = a n· w n + a n-unu · w n–1 + ... + A 2 w 2 + A unu · w 1 . (2)

Algoritmul traducerii.

I. Repetați până când numărul devine zero:

1. Găsiți prima poziție din stânga, a cărei greutate nu depășește numărul curent. Scrieți în poziție cifra maximă posibilă, astfel încât contribuția sa pozițională (produsul cifrei în funcție de greutate) să nu depășească numărul curent.

2. Reduceți numărul curent cu contribuția poziției construite.

II. Scrieți zerouri în pozițiile neocupate de cifrele construite.

În fiecare poziție, se ia cifra maximă posibilă, deoarece, conform lemei, contribuția acestei cifre nu poate fi compensată de cifrele situate în dreapta. Algoritmul va funcționa datorită existenței dovedite (teorema 1) și unicității (teorema 2) a reprezentării unui număr în forma (1).

Pentru un sistem binar, obținem o variantă a algoritmului dat în material pentru elev.

Pentru a converti în binar, trebuie să creați un șablon cu greutăți de cifre binare:

Numărul este tradus conform următorului algoritm:

I. Repetați până când numărul devine zero:

1. Scrieți 1 în prima poziție din stânga, a cărui greutate nu depășește numărul curent.

2. Reduceți numărul curent cu greutatea unității construite.

II. Scrieți zerouri în pozițiile neocupate de unele.

În practică, această metodă de traducere se dovedește a fi mult mai ușoară și mai rapidă decât algoritmul tradițional cu găsirea reziduurilor.

La conversia de la un sistem zecimal la un sistem ternar, trebuie să se ia în considerare atât greutățile poziționale în sine, cât și dublarea lor. Pentru o traducere rapidă, puteți construi un tabel, ale cărui linii corespund pozițiilor numerelor, coloanelor - numerelor și celulelor - contribuțiilor numărului la număr, în funcție de poziția sa în înregistrare număr:


poziția 729
poziția 243
poziția 81
poziția 27
poziția 9
poziția 3
poziția 1

Să presupunem că contribuția numărului 2 în poziția 243 este numărul 486, iar în poziția 9 este numărul 18.

Pentru a traduce într-un sistem ternar, trebuie să scanați tabelul linie cu linie în căutarea celui mai mare număr care nu depășește valoarea curentă.

De exemplu, să convertim numărul 183 în sistem ternar. O valoare adecvată este situată în al treilea rând și prima coloană:


poziția 729
poziția 243
poziția 81
poziția 27
poziția 9
poziția 3
poziția 1

Prin urmare, numărul ternar începe cu cifra 2:

183 10 = 202?? 3

Pentru numărul 21-18 = 3 există o semnificație exactă în tabel, traducerea este terminată:

183 10 = 20210 3 .

Pentru sistemele cu o bază mare, tabelele corespunzătoare vor fi, desigur, mai voluminoase. Ca un ultim exemplu, să construim un tabel pentru conversia într-un sistem numeric hexazecimal:

Lăsați numărul 4255 să fie convertit în sistemul hexazecimal. Căutăm primul număr din tabel (de la stânga la dreapta, rând cu rând, începând de sus), care se dovedește a fi cel mult numărul original 4255:

Primim prima cifră 1 în poziția 4096:

Rămâne să codificați 4255 - 4096 = 159.

Saltem rândul 256 (cifra corespunzătoare va fi 0), iar în linia 16 găsim valoarea adecvată 144:

Obținem numerele în pozițiile 256 și 16:

Rămâne să codificăm 159 - 144 = 15. Este clar că aceasta este valoarea cifrei mai puțin semnificative:

Se pare: 4255 10 = 109F 16.

Acțiuni asupra numerelor

Această secțiune este prezentată în material pentru elev în mod schematic, în scop informativ.

O lecție separată, mare și destul de interesantă poate fi dedicată subiectului, dar există deja o mulțime de materiale - este dificil să înțelegi imensitatea!

Într-o versiune simplă, introductivă, se arată că acțiunile asupra numerelor din orice sistem numeric sunt efectuate în același mod ca și în sistemul zecimal. Este ciudat dacă ar fi altfel, deoarece numerele din toate sistemele de poziție sunt construite în conformitate cu aceleași reguli, ceea ce înseamnă că acțiunile asupra lor trebuie efectuate în același mod.

Secțiunea este susținută de teme pentru opțiunea 3. Aceste exerciții pot fi recomandate elevilor curioși ca sarcini individuale.

Capitolul 4. Bazele aritmetice ale computerelor

4.1. Ce este un sistem numeric?

Există sisteme numerice poziționale și nepoziționale.

În sistemele numerice nepoziționale greutatea unei cifre (adică contribuția pe care o aduce la valoarea numărului) nu depinde de poziția eiîn notația numărului. Deci, în sistemul numeric roman din numărul XXXII (treizeci și doi), greutatea figurii X în orice poziție este doar zece.

În sistemele numerice poziționale greutatea fiecărei cifre se modifică în funcție de poziția (poziția) acesteia în secvența de cifre care reprezintă numărul. De exemplu, în numărul 757,7, primele șapte înseamnă 7 sute, al doilea - 7 unități, iar al treilea - 7 zecimi din unul.

Aceeași notație a numărului 757.7 înseamnă o expresie stenogramă

700 + 50 + 7 + 0,7 = 7 . 10 2 + 5 . 10 1 + 7 . 10 0 + 7 . 10 -1 = 757,7.

Orice sistem numeric pozițional se caracterizează prin bază.

Orice număr natural poate fi luat ca bază a sistemului - doi, trei, patru etc. Prin urmare, nenumărate sisteme de poziționare posibile: binar, ternar, cuaternar etc. Scrierea numerelor în fiecare dintre sistemele radix qînseamnă expresie stenogramă

A n-1 q n-1 + a n-2 q n-2 + ... + a 1 q 1 + a 0 q 0 + a -1 q -1 + ... + a -m q -m ,

Unde A eu - numere numerice; n și m - numărul cifrelor întregi și, respectiv, fracționare.
De exemplu:

4.2. Cum sunt generate numerele întregi în sistemele numerice poziționale?

În fiecare sistem numeric, numerele sunt ordonate în funcție de semnificațiile lor: 1 este mai mare decât 0, 2 este mai mare decât 1 etc.

A avansa numărul 1 înseamnă a-l înlocui cu 2, a avansa numărul 2 înseamnă a-l înlocui cu 3 etc. Promovare cu cifre mari(de exemplu, cifrele 9 în zecimal) înseamnă înlocuirea acestuia cu 0... Într-un sistem binar care folosește doar două cifre, 0 și 1, avansarea 0 înseamnă înlocuirea acestuia cu 1, iar avansarea 1 înseamnă înlocuirea acestuia cu 0.

Numerele întregi din orice sistem numeric sunt generate folosind Regulile contului [44 ]:

Aplicând această regulă, să scriem primele zece numere întregi

în binar: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;

în sistemul ternar: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;

în sistemul de cinci ori: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;

în octal: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.

4.3. Ce sisteme numerice utilizează specialiștii pentru a comunica cu un computer?

În plus față de zecimal, sunt utilizate pe scară largă sistemele cu o bază care este o putere întreagă de 2, și anume:

binar(se folosesc numerele 0, 1);

octal(se folosesc numerele 0, 1, ..., 7);

hexazecimal(pentru primii întregi de la zero la nouă, cifrele 0, 1, ..., 9 sunt folosite, iar pentru următorii numere întregi de la zece la cincisprezece, caracterele A, B, C, D, E, F sunt utilizate ca cifre).

Este util să ne amintim intrarea în aceste sisteme numerice pentru primele două zeci de numere întregi:

Dintre toate sistemele numerice mai ales simplu prin urmare interesant pentru implementarea tehnică în sisteme de număr binar de calculatoare.

4.4. De ce oamenii folosesc zecimale și computerele folosesc binare?

Oamenii preferă sistemul zecimal, probabil pentru că din cele mai vechi timpuri au numărat cu degetele, iar oamenii au zece degete pe mâini și picioare. Nu întotdeauna și nu pretutindeni oamenii folosesc sistemul numeric zecimal. În China, de exemplu, sistemul numeric de cinci ori a fost folosit mult timp.

Și computerele folosesc un sistem binar, deoarece are o serie de avantaje față de alte sisteme:

pentru a-l implementa, aveți nevoie dispozitive tehnice cu două stări stabile(există curent - nu există curent, magnetizat - nu magnetizat etc.) și nu, de exemplu, cu zece, ca în zecimal;

prezentarea informațiilor prin intermediul a doar două state în mod fiabilși anti-blocare;

eventual Aplicație pentru aparatul de algebră booleană să efectueze transformări logice ale informației;

aritmetica binară este mult mai simplă decât zecimalul.

Dezavantajul sistemului binar este creșterea rapidă a numărului de cifre necesare pentru a scrie numere.

4.5. De ce computerele folosesc și sisteme de număr octal și hexazecimal?

Un sistem binar, convenabil pentru computere, este incomod pentru oameni din cauza greutății sale și a înregistrării neobișnuite.

Conversia numerelor din zecimal în binar și invers se face de către mașină. Cu toate acestea, pentru a utiliza un computer profesional, trebuie să învățați să înțelegeți mașina de cuvinte. Pentru aceasta, au fost dezvoltate sistemele octal și hexadecimal.

Numerele din aceste sisteme sunt citite aproape la fel de ușor ca cele zecimale, necesită, respectiv, de trei (octale) și de patru (hexazecimale) ori mai puține cifre decât în sistemul binar (la urma urmei, numerele 8 și 16 sunt, respectiv, al treilea și a patra puteri ale numărului 2) ...

De exemplu:

De exemplu,

4.6. Cum se convertește un număr întreg din sistem zecimal în orice alt sistem numeric pozițional?

Exemplu: Să convertim numărul 75 din sistemul zecimal în binar, octal și hexazecimal:

Răspuns: 75 10 = 1 001 011 2 = 113 8 = 4B 16.

4.7. Cum se traduce numărul zecimal corect în orice alt sistem numeric pozițional?

Pentru a traduce numărul zecimal corectF a radixq necesarF înmulțit cuq , scris în același sistem zecimal, apoi înmulțiți partea fracțională a produsului rezultat cuq, și așa mai departe, până când partea fracționată a următorului produs devine egală cu zero sau se atinge acuratețea necesară a numărului F înq -sistem asociat. Reprezentarea părții fracționate a unui numărF în noul sistem numeric, va exista o succesiune de părți întregi ale lucrărilor obținute, scrise în ordinea primirii lor și descrise de una q -un număr. Dacă precizia necesară a conversiei numericeF estek zecimale, atunci eroarea absolută maximă este egală cuq - (k + 1) / 2.

Exemplu. Să convertim numărul 0,36 din sistemul zecimal în binar, octal și hexazecimal:

4.8. Cum se convertește un număr din binar (octal, hexazecimal) în zecimal?

Conversia unui număr în sistemul zecimalX înregistrat înq -numeral sistem (q = 2, 8 sau 16) în formăX q = (a n A n-1 ... A 0 , A -1 A -2 ... A -m ) q se reduce la calcularea valorii polinomului

X 10 = a n q n + a n-1 q n-1 + ... + a 0 q 0 + a -1 q -1 + a -2 q -2 + ... + a -m q -m

prin intermediul aritmeticii zecimale.

Exemple:

4.9. Tabel rezumativ al traducerilor de numere întregi de la un sistem numeric la altul

Luați în considerare numai acele sisteme numerice care sunt utilizate în computere - zecimal, binar, octal și hexadecimal. Pentru claritate, luăm un număr zecimal arbitrar, de exemplu 46, și pentru acesta efectuăm toate traducerile consecutive posibile de la un sistem numeric la altul. Ordinea traducerilor este determinată în conformitate cu figura:

Această figură folosește următoarele convenții:

bazele sistemelor numerice sunt scrise în cercuri;

săgețile indică direcția traducerii;

numărul de lângă săgeată înseamnă numărul de serie al exemplului corespunzător din tabelul rezumat 4.1.

De exemplu: înseamnă o traducere de la binar la hexazecimal, care are un număr de secvență 6 în tabel.

Tabel pivot al traducerilor întregiDouăsecțiuni- teoria statisticii ... statistici, informatică ca discipline ... KR (electronic versiune ediții). „.... Statistici microeconomice EP: Manual. alocație... - M.: Delo, 2000. ... revista. internetul- Site-uri web Rosstat ...

& formarea bazelor de date deschise cu resurse informaționale &

Raport

Ediții de referință. Bibliografic beneficii. Secțiune 1. Publicații de referință ... ale procedurilor de conciliere. internetul-versiune jurnalul oferă acces ... URSS / internetul-Scor constădeDouă departamente: ... specialiști ai Biroului informaticăși telecomunicații ...

Notaţie este o metodă de scriere a unui număr folosind un set specificat de caractere speciale (numere).

Notaţie:

oferă o reprezentare a unui set de numere (întregi și / sau reale);

dă fiecărui număr o reprezentare unică (sau cel puțin o reprezentare standard);

afișează structura algebrică și aritmetică a unui număr.

Scrierea unui număr într-un anumit sistem numeric se numește codul numeric.

Se afișează o poziție separată în afișarea unui număr descărcare, ceea ce înseamnă că numărul poziției este numărul de rang.

Numărul de biți dintr-un număr este numit amărăciuneși se potrivește cu lungimea acestuia.

Sistemele numerice sunt împărțite în poziționalși non-pozițional. Sistemele de numere poziționale sunt împărțite

pe omogenși amestecat.

sistem de numere octale, sistem de numere hexazecimale și alte sisteme de numere.

Traducerea sistemelor numerice. Numerele pot fi traduse de la un sistem numeric la altul.

Tabel de corespondență a numerelor din diferite sisteme numerice.