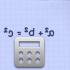Matritsaning teskarisi matritsadir. Teskari matritsani topish

Agar $A^(-1)\cdot A=A\cdot A^(-1)=E$ boʻlsa, $A^(-1)$ matritsasi $A$ kvadrat matritsasiga teskari deyiladi, bunda $E $ identifikatsiya matritsasi bo'lib, uning tartibi $A$ matritsasining tartibiga teng.

Yagona bo'lmagan matritsa - bu determinanti nolga teng bo'lmagan matritsa. Shunga ko'ra, degenerativ matritsa determinanti nolga teng bo'lgan matritsadir.

Teskari $A^(-1)$ matritsasi $A$ matritsasi birlik boʻlmagan taqdirdagina mavjud boʻladi. Agar $A^(-1)$ teskari matritsasi mavjud boʻlsa, u yagona hisoblanadi.

Matritsaning teskarisini topishning bir qancha usullari mavjud va biz ulardan ikkitasini ko‘rib chiqamiz. Ushbu sahifada ko'pgina oliy matematika kurslarida standart hisoblangan qo'shma matritsa usuli muhokama qilinadi. Gauss usuli yoki Gauss-Jordan usulidan foydalanishni o'z ichiga olgan teskari matritsani topishning ikkinchi usuli (elementar o'zgartirishlar usuli) ikkinchi qismda ko'rib chiqiladi.

Qo'shma (birlashma) matritsa usuli

$A_(n\times n)$ matritsasi berilsin. $A^(-1)$ teskari matritsasini topish uchun uchta qadam kerak:

1. $A$ matritsasining determinantini toping va $\Delta A\neq 0$, ya'ni. A matritsasi degenerativ emas.
2. $A$ matritsasining har bir elementining $A_(ij)$ algebraik toʻldiruvchilarini tuzing va topilganlardan $A_(n\times n)^(*)=\left(A_(ij) \right)$ matritsasini yozing. algebraik to‘ldiruvchilar.
3. $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$ formulasini hisobga olgan holda teskari matritsani yozing.

$(A^(*))^T$ matritsasi koʻpincha $A$ ning qoʻshma (oʻzaro, ittifoqdosh) matritsasi deb ataladi.

Agar qaror qo'lda qabul qilingan bo'lsa, unda birinchi usul faqat nisbatan kichik tartibli matritsalar uchun yaxshi bo'ladi: ikkinchi (), uchinchi (), to'rtinchi (). Yuqori tartibli matritsa uchun teskari matritsani topish uchun boshqa usullardan foydalaniladi. Masalan, ikkinchi qismda muhokama qilinadigan Gauss usuli.

№1 misol

$A=\left(\begin(massiv) (cccc) 5 & -4 &1 & 0 \\ 12 &-11 &4 & 0 \\ -5 & 58 &4 & 0 \\ 3 & - 1 matritsasiga teskari matritsani toping. & -9 & 0 \end(massiv) \o'ng)$.

To'rtinchi ustunning barcha elementlari nolga teng bo'lganligi sababli, $\Delta A=0$ (ya'ni, $A$ matritsasi degeneratsiyalangan). $\Delta A=0$ ekan, $A$ ga teskari matritsa yo'q.

Javob: $A^(-1)$ matritsasi mavjud emas.

№2 misol

$A=\left(\begin(massiv) (cc) -5 & 7 \\ 9 & 8 \end(massiv)\right)$ matritsasiga teskari matritsani toping. Tekshirishni o'tkazing.

Biz qo'shma matritsa usulidan foydalanamiz. Avval berilgan $A$ matritsasining determinantini topamiz:

$$ \Delta A=\chap| \begin(massiv) (cc) -5 & 7\\ 9 & 8 \end(massiv)\right|=-5\cdot 8-7\cdot 9=-103. $$

$\Delta A \neq 0$ bo'lgani uchun teskari matritsa mavjud, shuning uchun biz yechimni davom ettiramiz. Algebraik to‘ldiruvchilarni topish

\begin(hizalangan) & A_(11)=(-1)^2\cdot 8=8; \; A_(12)=(-1)^3\cdot 9=-9;\\ & A_(21)=(-1)^3\cdot 7=-7; \; A_(22)=(-1)^4\cdot (-5)=-5.\\ \end(hizalangan)

Algebraik to‘ldiruvchilar matritsasini tuzing: $A^(*)=\left(\begin(massiv) (cc) 8 & -9\\ -7 & -5 \end(massiv)\right)$.

Olingan matritsani ko'chiring: $(A^(*))^T=\left(\begin(massiv) (cc) 8 & -7\\ -9 & -5 \end(massiv)\right)$ (natijadagi matritsa ko'pincha $A$ matritsasiga qo'shma yoki birlashma matritsa deb ataladi). $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$ formulasidan foydalanib, bizda:

$$ A^(-1)=\frac(1)(-103)\cdot \left(\begin(massiv) (cc) 8 & -7\\ -9 & -5 \end(massiv)\o'ng) =\left(\begin(massiv) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(massiv)\o'ng) $$

Shunday qilib, teskari matritsa topiladi: $A^(-1)=\left(\begin(massiv) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(massiv) \o'ng) $. Natijaning haqiqatini tekshirish uchun tengliklardan birining haqiqatini tekshirish kifoya: $A^(-1)\cdot A=E$ yoki $A\cdot A^(-1)=E$. $A^(-1)\cdot A=E$ tengligini tekshiramiz. Kasrlar bilan kamroq ishlash uchun biz $A^(-1)$ matritsasini $\left(\begin(massiv) (cc) -8/103 & 7/103\\ 9/103 shaklida emas, balki almashtiramiz. & 5/103 \ end(massiv)\right)$ lekin $-\frac(1)(103)\cdot \left(\begin(massiv) (cc) 8 & -7\\ -9 & -5 \ end(massiv)\o'ng)$:

$$ A^(-1)\cdot(A) =-\frac(1)(103)\cdot \left(\begin(massiv) (cc) 8 & -7\\ -9 & -5 \end( massiv)\o'ng)\cdot\left(\begin(massiv) (cc) -5 & 7 \\ 9 & 8 \end(massiv)\o'ng) =-\frac(1)(103)\cdot\left( \begin(massiv) (cc) -103 & 0 \\ 0 & -103 \end(massiv)\o'ng) =\left(\begin(massiv) (cc) 1 & 0 \\ 0 & 1 \end(massiv) )\o‘ng) =E $$

Javob: $A^(-1)=\left(\begin(massiv) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(massiv)\oʻng)$.

№3 misol

$A=\left(\begin(massiv) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(massiv) \right)$ matritsasining teskarisini toping. Tekshirishni o'tkazing.

Keling, $A$ matritsasining determinantini hisoblashdan boshlaylik. Demak, $A$ matritsasining determinanti:

$$ \Delta A=\chap| \begin(massiv) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(massiv) \o'ng| = 18-36+56-12=26. $$

$\Delta A\neq 0$ bo'lgani uchun teskari matritsa mavjud, shuning uchun biz yechimni davom ettiramiz. Berilgan matritsaning har bir elementining algebraik to‘ldiruvchilarini topamiz:

$$ \begin(aligned) & A_(11)=(-1)^(2)\cdot\left|\begin(massiv)(cc) 9 & 4\\ 3 & 2\end(massiv)\o'ng| =6;\; A_(12)=(-1)^(3)\cdot\left|\begin(massiv)(cc) -4 &4 \\ 0 & 2\end(massiv)\right|=8;\; A_(13)=(-1)^(4)\cdot\left|\begin(massiv)(cc) -4 & 9\\ 0 & 3\end(massiv)\right|=-12;\\ & A_(21)=(-1)^(3)\cdot\left|\begin(massiv)(cc) 7 & 3\\ 3 & 2\end(massiv)\right|=-5;\; A_(22)=(-1)^(4)\cdot\left|\begin(massiv)(cc) 1 & 3\\ 0 & 2\end(massiv)\right|=2;\; A_(23)=(-1)^(5)\cdot\left|\begin(massiv)(cc) 1 & 7\\ 0 & 3\end(massiv)\right|=-3;\\ & A_ (31)=(-1)^(4)\cdot\left|\begin(massiv)(cc) 7 & 3\\ 9 & 4\end(massiv)\right|=1;\; A_(32)=(-1)^(5)\cdot\left|\begin(massiv)(cc) 1 & 3\\ -4 & 4\end(massiv)\right|=-16;\; A_(33)=(-1)^(6)\cdot\left|\begin(massiv)(cc) 1 & 7\\ -4 & 9\end(massiv)\right|=37. \end(hizalangan) $$

Biz algebraik qo'shimchalar matritsasini tuzamiz va uni almashtiramiz:

$$ A^*=\left(\begin(massiv) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37\end(massiv) \o'ng); \; (A^*)^T=\left(\begin(massiv) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(massiv) \oʻng) . $$

$A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$ formulasidan foydalanib, biz quyidagilarni olamiz:

$$ A^(-1)=\frac(1)(26)\cdot \left(\begin(massiv) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 va 37\end(massiv) \o'ng)= \left(\begin(massiv) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \end(massiv) \o'ng) $$

Shunday qilib, $A^(-1)=\left(\begin(massiv) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 & -3/26 & 37/26 \end(massiv) \o'ng)$. Natijaning haqiqatini tekshirish uchun tengliklardan birining haqiqatini tekshirish kifoya: $A^(-1)\cdot A=E$ yoki $A\cdot A^(-1)=E$. $A\cdot A^(-1)=E$ tengligini tekshiramiz. Kasrlar bilan kamroq ishlash uchun $A^(-1)$ matritsasini $\left(\begin(massiv) (ccc) 3/13 & -5/26 & 1/26 \ shaklida emas, balki almashtiramiz. \ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end(massiv) \o'ng)$, lekin $\frac(1)(26)\ cdot \left( \begin(massiv) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(massiv) \o'ng)$:

$$ A\cdot(A^(-1)) =\left(\begin(massiv)(ccc) 1 & 7 & 3 \\ -4 & 9 & 4\\ 0 & 3 & 2\end(massiv) \right)\cdot \frac(1)(26)\cdot \left(\begin(massiv) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\ end(massiv) \o'ng) =\frac(1)(26)\cdot\left(\begin(massiv) (ccc) 26 & 0 & 0 \\ 0 & 26 & 0 \\ 0 & 0 & 26\end (massiv) \o'ng) =\left(\begin(massiv) (ccc) 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end(massiv) \o'ng) =E $$

Tekshiruv muvaffaqiyatli o'tdi, $A^(-1)$ teskari matritsasi to'g'ri topildi.

Javob: $A^(-1)=\left(\begin(massiv) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 /13 & -3/26 & 37/26 \end(massiv) \o'ng)$.

4-misol

$A=\left(\begin(massiv) (cccc) 6 & -5 & 8 & 4\\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7\\ -4 & 8 ning teskari matritsasini toping. & -8 & -3 \end(massiv) \o'ng)$.

To'rtinchi tartibli matritsa uchun algebraik qo'shimchalar yordamida teskari matritsani topish biroz qiyin. Biroq bunday misollar nazorat ishlarida uchraydi.

Teskari matritsani topish uchun avval $A$ matritsasining determinantini hisoblash kerak. Bunday vaziyatda buni amalga oshirishning eng yaxshi yo'li determinantni ketma-ket (ustun) kengaytirishdir. Biz har qanday satr yoki ustunni tanlaymiz va tanlangan satr yoki ustunning har bir elementining algebraik to'ldiruvchisini topamiz.

Masalan, birinchi qator uchun biz quyidagilarni olamiz:

$$ A_(11)=\left|\begin(massiv)(ccc) 7 & 5 & 2\\ 5 & 3 & 7\\ 8 & -8 & -3 \end(massiv)\right|=556; \; A_(12)=-\left|\begin(massiv)(ccc) 9 & 5 & 2\\ 7 & 3 & 7 \\ -4 & -8 & -3 \end(massiv)\o'ng|=-300 ; $$ $$ A_(13)=\left|\begin(massiv)(ccc) 9 & 7 & 2\\ 7 & 5 & 7\\ -4 & 8 & -3 \end(massiv)\o'ng|= -536;\; A_(14)=-\left|\begin(massiv)(ccc) 9 & 7 & 5\\ 7 & 5 & 3\\ -4 & 8 & -8 \end(massiv)\right|=-112. $$

$A$ matritsasining determinanti quyidagi formula bilan hisoblanadi:

$$ \Delta(A)=a_(11)\cdot A_(11)+a_(12)\cdot A_(12)+a_(13)\cdot A_(13)+a_(14)\cdot A_(14) )=6\cdot 556+(-5)\cdot(-300)+8\cdot(-536)+4\cdot(-112)=100. $$

$$ \begin(hizalangan) & A_(21)=-77;\;A_(22)=50;\;A_(23)=87;\;A_(24)=4;\\ & A_(31) =-93;\;A_(32)=50;\;A_(33)=83;\;A_(34)=36;\\ & A_(41)=473;\;A_(42)=-250 ;\;A_(43)=-463;\;A_(44)=-96. \end(hizalangan) $$

Algebraik to‘ldiruvchi matritsasi: $A^*=\left(\begin(massiv)(cccc) 556 & -300 & -536 & -112\\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36 \\ 473 & -250 & -463 & -96\end(massiv)\o'ng)$.

Biriktirilgan matritsa: $(A^*)^T=\left(\begin(massiv) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96\end(massiv)\o'ng)$.

Teskari matritsa:

$$ A^(-1)=\frac(1)(100)\cdot \left(\begin(massiv) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96 \end(massiv) \oʻng)= \left(\begin(massiv) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/ 25 & 1/25 & 9/25 & -24/25 \end(massiv) \o'ng) $$

Agar so'ralsa, tekshirish avvalgi misollardagi kabi amalga oshirilishi mumkin.

Javob: $A^(-1)=\left(\begin(massiv) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/25 & 9/25 & -24/25 \end(massiv) \o'ng) $.

Ikkinchi bo'limda teskari matritsani topishning boshqa usuli ko'rib chiqiladi, bu Gauss usuli yoki Gauss-Jordan usulini o'zgartirishdan foydalanishni o'z ichiga oladi.

Biz matritsalar bilan harakatlar haqida gapirishni davom ettiramiz. Ya'ni, ushbu ma'ruzani o'rganish jarayonida siz teskari matritsani qanday topishni o'rganasiz. O'rganing. Matematika qiyin bo'lsa ham.

Teskari matritsa nima? Bu erda biz o'zaro o'xshashliklar bilan taqqoslashimiz mumkin: masalan, optimistik raqam 5 va uning o'zaroligini ko'rib chiqing. Bu sonlarning ko'paytmasi bittaga teng: . Matritsalar bilan ham xuddi shunday! Matritsa va uning teskari ko'paytmasi - identifikatsiya matritsasi, bu raqamli birlikning matritsa analogidir. Biroq, birinchi navbatda, biz muhim amaliy masalani hal qilamiz, ya'ni biz bu juda teskari matritsani qanday topishni o'rganamiz.

Teskari matritsani bilish va topa olish uchun nimani bilishingiz kerak? Siz qaror qabul qilishingiz kerak determinantlar. Siz nima ekanligini tushunishingiz kerak matritsa va ular bilan ba'zi harakatlarni bajara olish.

Teskari matritsani topishning ikkita asosiy usuli mavjud:
yordamida algebraik qo'shimchalar va elementar transformatsiyalardan foydalanish.

Bugun biz birinchi, osonroq yo'lni o'rganamiz.

Keling, eng dahshatli va tushunarsizidan boshlaylik. O'ylab ko'ring kvadrat matritsa. Teskari matritsani quyidagi formula yordamida topish mumkin:

Matritsaning determinanti qayerda, matritsaning tegishli elementlarining algebraik to'ldiruvchilarining ko'chirilgan matritsasi.

Teskari matritsa tushunchasi faqat kvadrat matritsalar uchun mavjud, matritsalar "ikkidan ikki", "uchdan uch" va hokazo.

Belgilash: Siz allaqachon payqaganingizdek, matritsaning teskarisi ustun belgisi bilan belgilanadi

Keling, eng oddiy holatdan boshlaylik - ikki-ikki matritsa. Ko'pincha, albatta, "uchdan uch" talab qilinadi, ammo shunga qaramay, men yechimning umumiy tamoyilini o'rganish uchun oddiyroq vazifani o'rganishni qat'iy tavsiya qilaman.

Misol:

Matritsaning teskarisini toping

Biz qaror qilamiz. Harakatlar ketma-ketligi qulay tarzda nuqtalarga bo'linadi.

1) Avval matritsaning determinantini topamiz.

Agar ushbu harakatni tushunish yaxshi bo'lmasa, materialni o'qing Determinantni qanday hisoblash mumkin?

Muhim! Agar matritsaning determinanti bo'lsa NO- teskari matritsa MAVJUD EMAS.

Ko'rib chiqilayotgan misolda, ma'lum bo'lishicha, , bu hamma narsa tartibda ekanligini anglatadi.

2) Voyaga etmaganlar matritsasini toping.

Muammoni hal qilish uchun voyaga etmagan bola nima ekanligini bilish shart emas, ammo maqolani o'qish tavsiya etiladi. Determinantni qanday hisoblash mumkin.

Voyaga etmaganlar matritsasi matritsa bilan bir xil o'lchamlarga ega, ya'ni bu holda .
Ish kichik, to'rtta raqamni topib, ularni yulduzcha o'rniga qo'yish kerak.

Bizning matritsamizga qaytish
Keling, avval yuqori chap elementni ko'rib chiqaylik:

Uni qanday topish mumkin kichik?
Va bu shunday amalga oshiriladi: ushbu element joylashgan qator va ustunni aqliy ravishda kesib tashlang:

Qolgan raqam berilgan elementning kichik qismi, biz voyaga etmaganlar matritsasida yozamiz:

Quyidagi matritsa elementini ko'rib chiqing:

Ushbu element joylashgan qator va ustunni aqliy ravishda kesib tashlang:

Qolgan narsa bu elementning kichik qismi bo'lib, biz uni matritsamizga yozamiz:

Xuddi shunday, biz ikkinchi qatorning elementlarini ko'rib chiqamiz va ularning kichiklarini topamiz:


Tayyor.

Bu oddiy. Voyaga etmaganlar matritsasida sizga kerak BELGILARI O'ZGARTIRISh ikki raqam uchun:

Men bu raqamlarni aylana oldim!

- matritsaning mos keladigan elementlarining algebraik to'ldiruvchilari matritsasi.

Va shunchaki bir narsa ...

4) Algebraik qo‘shimchalarning ko‘chirilgan matritsasini toping.

- matritsaning tegishli elementlarining algebraik to'ldiruvchilarining ko'chirilgan matritsasi.

5) Javob.

Bizning formulamizni eslang
Hammasi topildi!

Shunday qilib, teskari matritsa:

Javobni avvalgidek qoldirgan ma'qul. KERAKMAS matritsaning har bir elementini 2 ga bo'ling, chunki kasr sonlar olinadi. Ushbu nuance xuddi shu maqolada batafsilroq muhokama qilinadi. Matritsalar bilan amallar.

Yechimni qanday tekshirish mumkin?

Matritsalarni ko'paytirish ham bajarilishi kerak

Imtihon:

allaqachon aytib o'tilgan identifikatsiya matritsasi birliklar yoqilgan matritsadir asosiy diagonali va boshqa joylarda nollar.

Shunday qilib, teskari matritsa to'g'ri topildi.

Agar siz biror amalni bajarsangiz, natijada identifikatsiya matritsasi ham bo'ladi. Bu matritsalarni ko'paytirish o'zgaruvchan bo'lgan bir nechta holatlardan biridir, qo'shimcha ma'lumotni maqolada topishingiz mumkin. Matritsalar ustida amallarning xossalari. Matritsali ifodalar. Shuni ham yodda tutingki, tekshirish paytida doimiy (kasr) oldinga keltiriladi va eng oxirida - matritsani ko'paytirishdan keyin qayta ishlanadi. Bu standart qabul qilish.

Keling, amaliyotda keng tarqalgan holatga o'tamiz - uch-uch matritsa:

Misol:

Matritsaning teskarisini toping

Algoritm ikki-ikki holat bilan bir xil.

Teskari matritsani quyidagi formula bo'yicha topamiz: , bu erda matritsaning mos elementlarining algebraik to'ldiruvchilarining ko'chirilgan matritsasi .

1) Matritsa determinantini toping.

Bu erda determinant ochiladi birinchi qatorda.

Bundan tashqari, buni unutmang, bu hamma narsa yaxshi ekanligini anglatadi - teskari matritsa mavjud.

2) Voyaga etmaganlar matritsasini toping.

Voyaga etmaganlar matritsasi "uchdan uch" o'lchamiga ega , va biz to'qqizta raqamni topishimiz kerak.

Men bir nechta voyaga etmaganlarni batafsil ko'rib chiqaman:

Quyidagi matritsa elementini ko'rib chiqing:

Ushbu element joylashgan qator va ustunni aqliy ravishda kesib tashlang:

Qolgan to'rtta raqam "ikkidan ikkiga" determinantida yoziladi.

Bu ikki-ikki determinant va berilgan elementning kichik qismidir. Buni hisoblash kerak:


Hamma narsa, kichik topiladi, biz uni voyaga etmaganlar matritsasiga yozamiz:

Siz taxmin qilganingizdek, hisoblash uchun to'qqizta ikkitadan ikkiga determinant mavjud. Jarayon, albatta, qayg'uli, lekin ish eng qiyin emas, bundan ham battar bo'lishi mumkin.

Xo'sh, birlashtirish uchun - rasmlarda boshqa kichikni toping:

Voyaga etmaganlarning qolgan qismini o'zingiz hisoblashga harakat qiling.

Yakuniy natija:
- matritsaning mos keladigan elementlarining kichiklari matritsasi.

Voyaga etmaganlarning hammasi salbiy bo'lib chiqqani aniq tasodifdir.

3) Algebraik qo‘shimchalar matritsasini toping.

Voyaga etmaganlar matritsasida bu zarur BELGILARI O'ZGARTIRISh qat'iy quyidagi elementlar uchun:

Ushbu holatda:

"To'rtdan to'rtga" matritsa uchun teskari matritsani topish e'tiborga olinmaydi, chunki bunday vazifani faqat sadist o'qituvchi berishi mumkin (talaba uchun bitta "to'rtdan to'rt" determinantni va 16 ta "uchdan uch" determinantni hisoblash) . Mening amaliyotimda faqat bitta holat bo'lgan va sinov mijozi mening azoblarim uchun juda qimmatga tushdi =).

Bir qator darsliklarda, qo'llanmalarda siz teskari matritsani topishda biroz boshqacha yondashuvni topishingiz mumkin, ammo men yuqoridagi yechim algoritmidan foydalanishni tavsiya qilaman. Nega? Chunki hisob-kitoblar va belgilarda chalkashib ketish ehtimoli ancha past.

Bu mavzu talabalar orasida eng nafratlangan mavzulardan biridir. Bundan ham yomoni, ehtimol, faqat determinantlar.

Ayyorlik shundaki, teskari element tushunchasining o'zi (va men hozir faqat matritsalar haqida gapirmayapman) bizni ko'paytirish operatsiyasiga ishora qiladi. Hatto maktab o'quv dasturida ham ko'paytirish murakkab operatsiya hisoblanadi va matritsalarni ko'paytirish umuman alohida mavzu bo'lib, menda butun paragraf va unga bag'ishlangan video dars bor.

Bugun biz matritsali hisob-kitoblarning tafsilotlariga kirmaymiz. Esda tuting: matritsalar qanday belgilanadi, ular qanday ko'paytiriladi va bundan nima kelib chiqadi.

Ko‘rib chiqish: Matritsalarni ko‘paytirish

Avvalo, notatsiya haqida kelishib olaylik. $A$ oʻlchamli $\left[ m\times n \right]$ matritsasi shunchaki $m$ satrlari va $n$ ustunlari boʻlgan raqamlar jadvalidir:

\=\ underbrace(\left[ \begin(matritsa) ((a)_(11)) & ((a)_(12)) & ... & (a)_(1n)) \\ (( a)_(21)) & (a)_(22)) & ... & (a)_(2n)) \\ ... & ... & ... & ... \\ ((a)_(m1)) & (a)_(m2)) & ... & ((a)_(mn)) \\\end(matritsa) \o'ng])_(n)\]

Joylardagi satrlar va ustunlarni tasodifan chalkashtirib yubormaslik uchun (ishonasizmi, imtihonda siz birini ikkilik bilan aralashtirib yuborishingiz mumkin - u erdagi qatorlar haqida nima deyishimiz mumkin), shunchaki rasmga qarang:

Matritsa hujayralari uchun indekslarni aniqlash

Nima bo'lyapti? Agar biz $OXY$ standart koordinata tizimini yuqori chap burchakka joylashtirsak va o‘qlarni butun matritsani qamrab oladigan tarzda yo‘naltirsak, u holda bu matritsaning har bir katakchasi $\left(x;y \right) koordinatalari bilan yagona bog‘lanishi mumkin. $ - bu qator va ustun raqami bo'ladi.

Nima uchun koordinatalar tizimi aynan yuqori chap burchakda joylashgan? Ha, chunki u erdan biz har qanday matnni o'qishni boshlaymiz. Buni eslab qolish juda oson.

Nima uchun $x$ o'qi o'ngga emas, pastga qaratilgan? Shunga qaramay, hamma narsa oddiy: standart koordinata tizimini oling ($x$ o'qi o'ngga, $y$ o'qi yuqoriga ko'tariladi) va uni matritsani o'rab oladigan tarzda aylantiring. Bu soat yo'nalishi bo'yicha 90 daraja aylanish - biz uning natijasini rasmda ko'ramiz.

Umuman olganda, biz matritsa elementlarining indekslarini qanday aniqlashni aniqladik. Endi ko'paytirish bilan shug'ullanamiz.

Ta'rif. $A=\left[ m\times n \right]$ va $B=\left[ n\times k \right]$ matritsalari, birinchisidagi ustunlar soni ikkinchisidagi qatorlar soniga toʻgʻri kelganda, shunday boʻladi. izchil deb ataladi.

Bu tartibda. $A$ va $B$ matritsalari $\left(A;B \right)$ tartiblangan juftlikni tashkil qiladi, deyish mumkin: agar ular shu tartibda izchil boʻlsa, $B boʻlishi shart emas. $ va $A$, bular. $\left(B;A \right)$ juftligi ham mos keladi.

Faqat izchil matritsalarni ko'paytirish mumkin.

Ta'rif. $A=\left[ m\times n \right]$ va $B=\left[ n\times k \right]$ matritsalarining koʻpaytmasi yangi $C=\left[ m\times k \right] matritsasidir. ]$ , uning elementlari $((c)_(ij))$ formula bilan hisoblanadi:

\[((c)_(ij))=\sum\limits_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

Boshqacha qilib aytganda: $C=A\cdot B$ matritsasining $((c)_(ij))$ elementini olish uchun birinchi matritsaning $i$-qatorini, $j$ ni olish kerak. -ikkinchi matritsaning ustuni, so'ngra ushbu qator va ustundan elementlarni juft qilib ko'paytiring. Natijalarni qo'shing.

Ha, bu qattiq ta'rif. Undan darhol bir nechta faktlar kelib chiqadi:

1. Matritsalarni ko'paytirish, umuman olganda, kommutativ emas: $A\cdot B\ne B\cdot A$;
2. Biroq, ko'paytirish assotsiativdir: $\left(A\cdot B \right)\cdot C=A\cdot \left(B\cdot C \right)$;
3. Va hatto distributiv: $\left(A+B \right)\cdot C=A\cdot C+B\cdot C$;
4. Va yana tarqatuvchi: $A\cdot \left(B+C \o'ng)=A\cdot B+A\cdot C$.

Ko'paytirishning distributivligini faqat ko'paytirish amalining o'zgarmasligi sababli chap va o'ng ko'paytma yig'indisi uchun alohida tavsiflash kerak edi.

Agar shunga qaramay $A\cdot B=B\cdot A$ ekanligi aniqlansa, bunday matritsalar almashtiriladigan deyiladi.

U erda biror narsaga ko'paytiriladigan barcha matritsalar orasida o'ziga xoslari bor - ular har qanday $A$ matritsasiga ko'paytirilganda yana $A$ ni beradi:

Ta'rif. Agar $A\cdot E=A$ yoki $E\cdot A=A$ boʻlsa, $E$ matritsasi identifikatsiya deb ataladi. $A$ kvadrat matritsasi bo'lsa, biz quyidagilarni yozishimiz mumkin:

Identifikatsiya matritsasi matritsa tenglamalarini echishda tez-tez mehmon hisoblanadi. Va umuman, matritsalar dunyosida tez-tez mehmon. :)

Va bu $E$ tufayli, kimdir keyingi yoziladigan barcha o'yinlarni o'ylab topdi.

Teskari matritsa nima

Matritsani ko'paytirish juda ko'p vaqt talab qiladigan operatsiya bo'lganligi sababli (siz qatorlar va ustunlarni ko'paytirishingiz kerak), teskari matritsa tushunchasi ham eng ahamiyatsiz narsa emas. Va bu qandaydir tushuntirishga muhtoj.

Kalit ta'rifi

Xo'sh, haqiqatni bilish vaqti keldi.

Ta'rif. $B$ matritsasi agar $A$ matritsasiga teskari deyiladi

Teskari matritsa $((A)^(-1))$ bilan belgilanadi (daraja bilan adashtirmaslik kerak!), shuning uchun ta'rifni quyidagicha qayta yozish mumkin:

Hamma narsa juda oddiy va tushunarli bo'lib tuyuladi. Ammo bunday ta'rifni tahlil qilganda darhol bir nechta savollar tug'iladi:

1. Teskari matritsa har doim mavjudmi? Va agar har doim bo'lmasa, unda qanday aniqlash mumkin: qachon mavjud va qachon yo'q?
2. Va bunday matritsa aynan bitta deb kim aytdi? Agar biron bir original $A$ matritsasi uchun teskari ma'lumotlar to'plami bo'lsa-chi?
3. Bu barcha "teskarilar" nimaga o'xshaydi? Va aslida ularni qanday hisoblaysiz?

Hisoblash algoritmlariga kelsak - bu haqda biroz keyinroq gaplashamiz. Ammo qolgan savollarga hozir javob beramiz. Keling, ularni alohida tasdiqlar-lemmalar shaklida tuzamiz.

Asosiy xususiyatlar

Keling, $A$ matritsasi $((A)^(-1))$ boʻlishi uchun qanday koʻrinishidan boshlaylik. Endi biz ushbu matritsalarning ikkalasi ham kvadrat va bir xil o'lchamda bo'lishi kerakligiga ishonch hosil qilamiz: $\left[ n\times n \right]$.

Lemma 1. $A$ matritsasi va uning teskarisi $((A)^(-1))$ berilgan. U holda bu matritsalarning ikkalasi ham kvadrat va bir xil tartib $n$.

Isbot. Hammasi oddiy. $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ a\times b \right]$ matritsasi boʻlsin. $A\cdot ((A)^(-1))=E$ mahsuloti taʼrifi boʻyicha mavjud boʻlgani uchun $A$ va $((A)^(-1))$ matritsalari shu tartibda mos keladi:

\[\begin(align) & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end( tekislash)\]

Bu matritsani ko'paytirish algoritmining bevosita natijasidir: $n$ va $a$ koeffitsientlari "tranzit" bo'lib, ular teng bo'lishi kerak.

Shu bilan birga, teskari ko'paytirish ham aniqlanadi: $((A)^(-1))\cdot A=E$, shuning uchun $((A)^(-1))$ va $A$ matritsalari ushbu tartibda ham mos keladi:

\[\begin(align) & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end( tekislash)\]

Shunday qilib, umumiylikni yo'qotmasdan, $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ n\times m \right]$ deb taxmin qilishimiz mumkin. Biroq, $A\cdot ((A)^(-1))=((A)^(-1))\cdot A$ taʼrifiga koʻra, matritsalarning oʻlchamlari aynan bir xil:

\[\begin(align) & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end(align)\]

Shunday qilib, har uchala matritsa - $A$, $((A)^(-1))$ va $E$ $\left[ n\times n \right]$ oʻlchamida kvadrat ekanligi maʼlum boʻldi. Lemma isbotlangan.

Xo'sh, bu allaqachon yaxshi. Biz faqat kvadrat matritsalar teskari bo'lishini ko'ramiz. Endi teskari matritsa har doim bir xil ekanligiga ishonch hosil qilaylik.

Lemma 2. $A$ matritsasi va uning teskarisi $((A)^(-1))$ berilgan. Keyin bu teskari matritsa noyobdir.

Isbot. Qarama-qarshi tomondan boshlaylik: $A$ matritsasida kamida ikkita teskari holatlar bo'lsin — $B$ va $C$. Keyin, ta'rifga ko'ra, quyidagi tengliklar to'g'ri bo'ladi:

\[\begin(align) & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \end (tekislash)\]

Lemma 1dan shunday xulosaga keldikki, barcha to'rtta $A$, $B$, $C$ va $E$ matritsalari bir xil tartibdagi kvadratdir: $\left[ n\times n \right]$. Shunday qilib, mahsulot tasniflanadi:

Matritsalarni ko'paytirish assotsiativ bo'lgani uchun (lekin kommutativ emas!), Biz yozishimiz mumkin:

\[\begin(align) & B\cdot A\cdot C=\left(B\cdot A \right)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \left(A\cdot C \right)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\O'ng strelka B=C. \\ \end (tekislash)\]

Biz yagona mumkin bo'lgan variantni oldik: teskari matritsaning ikkita nusxasi teng. Lemma isbotlangan.

Yuqoridagi mulohaza barcha $b\ne 0$ haqiqiy sonlar uchun teskari elementning yagonaligini isbotini deyarli so'zma-so'z takrorlaydi. Faqatgina muhim qo'shimcha matritsalarning o'lchamini hisobga olishdir.

Biroq, har qanday kvadrat matritsa teskari emasligi haqida hali hech narsa bilmaymiz. Bu erda determinant bizning yordamimizga keladi - bu barcha kvadrat matritsalar uchun asosiy xususiyatdir.

Lemma 3. $A$ matritsasi berilgan. Agar unga teskari $((A)^(-1))$ matritsasi mavjud boʻlsa, asl matritsaning determinanti nolga teng emas:

\[\chap| A \o'ng|\ne 0\]

Isbot. Biz allaqachon bilamizki, $A$ va $((A)^(-1))$ $\left[ n\times n \right]$ oʻlchamdagi kvadrat matritsalardir. Shuning uchun ularning har biri uchun determinantni hisoblash mumkin: $\left| A \right|$ va $\left| ((A)^(-1)) \o'ng|$. Biroq, mahsulotning aniqlovchisi aniqlovchilarning mahsulotiga teng:

\[\chap| A\cdot B \o'ng|=\chap| A \right|\cdot \left| B \o'ng|\O'ngga \chap| A\cdot ((A)^(-1)) \right|=\left| A \right|\cdot \left| ((A)^(-1)) \o'ng|\]

Lekin $A\cdot ((A)^(-1))=E$ taʼrifiga koʻra va $E$ ning determinanti har doim 1 ga teng, shuning uchun

\[\begin(align) & A\cdot ((A)^(-1))=E; \\ & \chap| A\cdot ((A)^(-1)) \right|=\left| E\o'ng|; \\ & \chap| A \right|\cdot \left| ((A)^(-1)) \o'ng|=1. \\ \end (tekislash)\]

Ikki raqamning mahsuloti bittaga teng bo'ladi, agar bu raqamlarning har biri noldan farq qilsa:

\[\chap| A \right|\ne 0;\quad \left| ((A)^(-1)) \o'ng|\ne 0.\]

Shunday qilib, $\left| A \o'ng|\ne 0$. Lemma isbotlangan.

Aslida, bu talab juda mantiqiy. Endi biz teskari matritsani topish algoritmini tahlil qilamiz - va nima uchun printsipial jihatdan nol determinant bilan teskari matritsa mavjud bo'lmasligi aniq bo'ladi.

Ammo birinchi navbatda "yordamchi" ta'rifni tuzamiz:

Ta'rif. Degenerativ matritsa $\left[ n\times n \right]$ oʻlchamdagi kvadrat matritsa boʻlib, determinanti nolga teng.

Shunday qilib, biz har qanday teskari matritsa buzilmagan deb aytishimiz mumkin.

Teskari matritsani qanday topish mumkin

Endi biz teskari matritsalarni topishning universal algoritmini ko'rib chiqamiz. Umuman olganda, ikkita umumiy qabul qilingan algoritm mavjud va biz bugun ikkinchisini ham ko'rib chiqamiz.

Endi ko'rib chiqiladigan $\left[ 2\times 2 \right]$ va qisman - $\left[ 3\times 3 \right]$ o'lchamli matritsalar uchun juda samarali. Lekin $\left[ 4\times 4 \right]$ oʻlchamidan boshlab, undan foydalanmaslik yaxshiroqdir. Nima uchun - endi siz hamma narsani tushunasiz.

Algebraik qo'shimchalar

Tayyor bo'l. Endi og'riq bo'ladi. Yo'q, xavotir olmang: yubka kiygan chiroyli hamshira, dantelli paypoq sizga kelmaydi va dumbangizga ukol ham qilmaydi. Hammasi ko'proq prozaik: algebraik qo'shimchalar va Janobi Oliylari "Union matritsasi" sizga keladi.

Asosiysidan boshlaylik. Elementlari $((a)_(ij))$ deb nomlangan $A=\left[ n\times n \right]$ oʻlchamli kvadrat matrisa boʻlsin. Keyin, har bir bunday element uchun algebraik to'ldiruvchini aniqlash mumkin:

Ta'rif. $((A)_(ij))$ algebraik toʻldiruvchi $((a)_(ij))$ elementiga $i$-chi qator va $A=\chap matritsaning $j$-chi ustuni. [ n \times n \right]$ - shaklning qurilishi

\[((A)_(ij))=((\left(-1 \o'ng))^(i+j))\cdot M_(ij)^(*)\]

Bu yerda $M_(ij)^(*)$ bir xil $i$-chi qator va $j$-chi ustunni oʻchirish yoʻli bilan asl $A$ dan olingan matritsaning determinantidir.

Yana bir marta. Koordinatalari $\left(i;j \right)$ boʻlgan matritsa elementining algebraik toʻldiruvchisi $((A)_(ij))$ sifatida belgilanadi va quyidagi sxema boʻyicha hisoblanadi:

1. Birinchidan, biz $i$-qatorni va $j$-th ustunini asl matritsadan oʻchirib tashlaymiz. Biz yangi kvadrat matritsani olamiz va uning determinantini $M_(ij)^(*)$ deb belgilaymiz.
2. Keyin bu determinantni $((\left(-1 \right))^(i+j))$ ga ko'paytiramiz - dastlab bu ibora hayratlanarlidek tuyulishi mumkin, lekin aslida biz $ ning oldidagi belgini topamiz. M_(ij)^(*) $.
3. Biz hisoblaymiz - biz aniq raqamni olamiz. Bular. algebraik qo'shilish faqat son, qandaydir yangi matritsa emas va hokazo.

$M_(ij)^(*)$ matritsasining oʻzi $((a)_(ij))$ elementining toʻldiruvchi minori deyiladi. Va shu ma'noda, algebraik to'ldiruvchining yuqoridagi ta'rifi yanada murakkab ta'rifning alohida holatidir - biz determinant haqidagi darsda ko'rib chiqdik.

Muhim eslatma. Aslida, "kattalar" matematikasida algebraik qo'shimchalar quyidagicha aniqlanadi:

1. Biz kvadrat matritsada $k$ satr va $k$ ustunlarini olamiz. Ularning kesishgan joyida $\left[ k\times k \right]$ o‘lchamdagi matritsani olamiz — uning determinanti $k$ tartibli minor deyiladi va $((M)_(k))$ bilan belgilanadi.
2. Keyin biz ushbu "tanlangan" $k$ qatorlari va $k$ ustunlarini kesib tashlaymiz. Yana kvadrat matritsani olamiz - uning determinanti komplementar minor deb ataladi va $M_(k)^(*)$ bilan belgilanadi.
3. $M_(k)^(*)$ ni $((\left(-1 \o'ng))^(t))$ ga ko'paytiring, bu erda $t$ (hozir e'tibor bering!) tanlangan barcha qatorlar raqamlari yig'indisi. va ustunlar. Bu algebraik qo'shimcha bo'ladi.

Uchinchi qadamni ko'rib chiqing: aslida 2 ming dollarlik shartlar mavjud! Yana bir narsa shundaki, $k=1$ uchun biz atigi 2 ta atama olamiz - bular bir xil $i+j$ bo'ladi - $((a)_(ij))$ elementining "koordinatalari", biz ular uchun algebraik to‘ldiruvchini qidiradi.

Shunday qilib, bugungi kunda biz biroz soddalashtirilgan ta'rifdan foydalanamiz. Ammo keyinroq ko'rib turganimizdek, bu etarli bo'ladi. Eng muhimi quyidagilar:

Ta'rif. $S$ kvadrat matritsaga $A=\left[ n\times n \right]$ birlashma matritsasi $A$ dan olingan $\left[ n\times n \right]$ oʻlchamdagi yangi matritsadir. $(( a)_(ij))$ algebraik toʻldiruvchilar bilan $((A)_(ij))$ oʻrniga:

\\O'ng strelka S=\chap[ \begin(matritsa) ((A)_(11)) & ((A)_(12)) & ... & (A)_(1n)) \\ (( A)_(21)) & ((A)_(22)) & ... & ((A)_(2n)) \\ ... & ... & ... & ... \\ ((A)_(n1)) & ((A)_(n2)) & ... & ((A)_(nn)) \\\end(matritsa) \o'ng]\]

Ushbu ta'rifni amalga oshirish paytida paydo bo'ladigan birinchi fikr - bu "jami siz qancha hisoblashingiz kerak!" Dam oling: hisoblashingiz kerak, lekin unchalik emas. :)

Xo'sh, bularning barchasi juda yoqimli, lekin nima uchun bu kerak? Lekin nega.

Asosiy teorema

Bir oz orqaga qaytaylik. Esingizda bo'lsin, 3-Lemma $A$ inversiyali matritsa har doim birlik emas (ya'ni uning determinanti nolga teng emas: $\left| A \right|\ne 0$) ekanligini ta'kidlagan.

Demak, buning aksi ham to'g'ri: agar $A$ matritsasi degenerativ bo'lmasa, u har doim teskari bo'ladi. Va hatto $((A)^(-1))$ qidiruv sxemasi ham mavjud. Tekshirib ko'r:

Teskari matritsa teoremasi. $A=\left[ n\times n \right]$ kvadrat matritsasi berilsin va uning determinanti nolga teng: $\left| A \o'ng|\ne 0$. Keyin $((A)^(-1))$ teskari matritsasi mavjud va quyidagi formula bilan hisoblanadi:

\[((A)^(-1))=\frac(1)(\chap| A \o'ng|)\cdot ((S)^(T))\]

Va endi - hammasi bir xil, lekin o'qiladigan qo'l yozuvida. Teskari matritsani topish uchun sizga kerak bo'ladi:

1. $\left| determinantini hisoblang \right|$ va uning nolga teng emasligiga ishonch hosil qiling.
2. Birlashma matritsasini $S$ kompilyatsiya qilish, ya'ni. $((A)_(ij))$ 100500 algebraik qo'shimchalarni hisoblang va ularni $((a)_(ij))$ o'rniga qo'ying.
3. Ushbu $S$ matritsasini joyiga qo'ying va keyin uni qandaydir songa ko'paytiring $q=(1)/(\left| A \right|)\;$.

Va tamom! $((A)^(-1))$ teskari matritsasi topildi. Keling, misollarni ko'rib chiqaylik:

\[\left[ \begin(matritsa) 3 & 1 \\ 5 & 2 \\\end(matritsa) \o'ng]\]

Yechim. Keling, teskarilikni tekshiramiz. Determinantni hisoblaymiz:

\[\chap| A \o'ng|=\chap| \begin(matritsa) 3 & 1 \\ 5 & 2 \\\end(matritsa) \o'ng|=3\cdot 2-1\cdot 5=6-5=1\]

Aniqlovchi noldan farq qiladi. Shunday qilib, matritsa teskari bo'ladi. Keling, birlashma matritsasini yaratamiz:

Keling, algebraik qo'shimchalarni hisoblaymiz:

\[\begin(align) & ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| 2\right|=2; \\ & ((A)_(12))=((\left(-1 \o'ng))^(1+2))\cdot \left| 5\o'ng|=-5; \\ & ((A)_(21))=((\left(-1 \o'ng))^(2+1))\cdot \left| 1 \right|=-1; \\ & ((A)_(22))=((\left(-1 \o'ng))^(2+2))\cdot \left| 3\o'ng|=3. \\ \end (tekislash)\]

E'tibor bering: determinantlar |2|, |5|, |1| va |3| $\left[ 1\times 1 \right]$ oʻlchamdagi matritsalarning determinantlari boʻlib, modullar emas. Bular. agar determinantlarda salbiy sonlar bo'lsa, "minus" ni olib tashlash kerak emas.

Umuman olganda, bizning ittifoq matritsasi quyidagicha ko'rinadi:

\[((A)^(-1))=\frac(1)(\chap| A \o'ng|)\cdot ((S)^(T))=\frac(1)(1)\cdot ( (\left[ \begin(massiv)(*(35)(r)) 2 & -5 \\ -1 & 3 \\\end(massiv) \o'ng])^(T))=\left[ \begin (massiv)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(massiv) \o'ng]\]

OK, endi hammasi tugadi. Muammo hal qilindi.

Javob. $\left[ \begin(massiv)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(massiv) \right]$

Vazifa. Teskari matritsani toping:

\[\left[ \begin(massiv)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(massiv) \o'ng] \]

Yechim. Yana determinantni ko'rib chiqamiz:

\[\begin(align) & \left| \begin(massiv)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(massiv) \right|=\begin(matritsa) ) \left(1\cdot 2\cdot 1+\left(-1 \o'ng)\cdot \left(-1 \o'ng)\cdot 1+2\cdot 0\cdot 0 \o'ng)- \\ -\chap (2\cdot 2\cdot 1+\left(-1 \o'ng)\cdot 0\cdot 1+1\cdot \left(-1 \o'ng)\cdot 0 \o'ng) \\\end(matritsa)= \ \ & =\left(2+1+0 \o'ng)-\left(4+0+0 \o'ng)=-1\ne 0. \\ \end(tuzalash)\]

Determinant noldan farq qiladi - matritsa teskari. Ammo endi bu eng tiniq bo'ladi: siz 9 (to'qqiz, la'nat!) algebraik qo'shimchalarni hisoblashingiz kerak. Va ularning har biri $\left[ 2\times 2 \right]$ kvalifikatsiyasini o'z ichiga oladi. Uchib ketdi:

\[\begin(matritsa) ((A)_(11))=((\left(-1 \o'ng))^(1+1))\cdot \left| \begin(matritsa) 2 & -1 \\ 0 & 1 \\\end(matritsa) \o'ng|=2; \\ ((A)_(12))=((\left(-1 \o'ng))^(1+2))\cdot \left| \begin(matritsa) 0 & -1 \\ 1 & 1 \\\end(matritsa) \o'ng|=-1; \\ ((A)_(13))=((\left(-1 \o'ng))^(1+3))\cdot \left| \begin(matritsa) 0 & 2 \\ 1 & 0 \\\end(matritsa) \right|=-2; \\ ... \\ ((A)_(33))=((\left(-1 \o'ng))^(3+3))\cdot \left| \begin(matritsa) 1 & -1 \\ 0 & 2 \\\end(matritsa) \o'ng|=2; \\ \end (matritsa)\]

Qisqasi, birlashma matritsasi quyidagicha ko'rinadi:

Shunday qilib, teskari matritsa quyidagicha bo'ladi:

\[((A)^(-1))=\frac(1)(-1)\cdot \left[ \begin(matritsa) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end(matritsa) \o'ng]=\left[ \begin(massiv)(*(35)(r))-2 & -1 & 3 \\ 1 & 1 & -1 \ \ 2 & 1 & -2 \\\end(massiv) \o'ng]\]

Xo'sh, hammasi shu. Mana javob.

Javob. $\left[ \begin(massiv)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end(massiv) \o'ng ]$

Ko'rib turganingizdek, har bir misol oxirida biz tekshirishni amalga oshirdik. Shu munosabat bilan muhim eslatma:

Tekshirish uchun dangasa bo'lmang. Asl matritsani topilgan teskarisiga ko'paytiring - siz $E$ olishingiz kerak.

Masalan, siz matritsali tenglamani yechsangiz, keyingi hisob-kitoblarda xato izlashdan ko'ra, ushbu tekshiruvni bajarish ancha oson va tezroq.

Alternativ usul

Aytganimdek, teskari matritsa teoremasi $\left[ 2\times 2 \right]$ va $\left[ 3\times 3 \right]$ oʻlchamlari uchun yaxshi ishlaydi (oxirgi holatda u unchalik “chiroyli” emas. endi). ”), lekin katta matritsalar uchun qayg'u boshlanadi.

Lekin tashvishlanmang: $\left[ 10\times 10 \right]$ matritsasi uchun ham teskarisini tinchgina topish uchun ishlatilishi mumkin bo'lgan muqobil algoritm mavjud. Ammo, tez-tez bo'lgani kabi, ushbu algoritmni ko'rib chiqish uchun bizga biroz nazariy ma'lumot kerak.

Elementar transformatsiyalar

Matritsaning turli xil o'zgarishlari orasida bir nechta maxsuslari mavjud - ular elementar deb ataladi. Aynan uchta o'zgarishlar mavjud:

1. Ko'paytirish. Siz $i$-chi qatorni (ustun) olib, uni istalgan $k\ne 0$ songa ko'paytirishingiz mumkin;
2. Qo'shish. $i$-chi qatorga (ustun) har qanday boshqa $j$-chi qatorni (ustunni) istalgan raqamga ko'paytiring $k\ne 0$ (albatta, $k=0$ ham bo'lishi mumkin, ammo buning nima keragi bor? bundan? ?Hech narsa o'zgarmaydi).
3. Permutatsiya. $i$-th va $j$-th qatorlarni (ustunlarni) oling va ularni almashtiring.

Nima uchun bu o'zgarishlar elementar deb ataladi (katta matritsalar uchun ular unchalik elementar ko'rinmaydi) va nima uchun ulardan faqat uchtasi bor - bu savollar bugungi dars doirasidan tashqarida. Shuning uchun biz tafsilotlarga kirmaymiz.

Yana bir narsa muhim: biz barcha bu buzilishlarni tegishli matritsada bajarishimiz kerak. Ha, ha, siz to'g'ri eshitdingiz. Endi yana bitta ta'rif bo'ladi - bugungi darsda oxirgi.

Biriktirilgan matritsa

Shubhasiz, maktabda siz qo'shish usuli yordamida tenglamalar tizimini yechgansiz. Xo'sh, mana, bitta satrdan boshqasini olib tashlang, bir qatorni raqamga ko'paytiring - barchasi shu.

Shunday qilib: endi hamma narsa bir xil bo'ladi, lekin allaqachon "kattalarcha". Tayyormisiz?

Ta'rif. $A=\left[ n\times n \right]$ matritsasi va bir xil kattalikdagi $E$ identifikatsiya matritsasi $n$ berilsin. Keyin bog'langan matritsa $\left[ A\left| E\to'g'ri. \right]$ yangi $\left[ n\times 2n \right]$ matritsasi boʻlib, u quyidagicha koʻrinadi:

\[\left[ A\left| E\to'g'ri. \right]=\left[ \begin(massiv)(rrrr|rrrr)((a)_(11)) & (a)_(12)) & ... & (a)_(1n)) & 1 & 0 & ... & 0 \\((a)_(21)) & ((a)_(22)) & ... & (a)_(2n)) & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... & ... \\((a)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\end(massiv) \o'ng]\]

Xulosa qilib aytganda, biz $A$ matritsasini olamiz, oʻng tomonda unga kerakli oʻlchamdagi $E$ identifikatsiya matritsasi tayinlaymiz, ularni goʻzallik uchun vertikal chiziq bilan ajratamiz – mana biriktirilgan. :)

Tushunish nima? Va mana nima:

Teorema. $A$ matritsasi teskari boʻlsin. $\left[ A\left| qo'shma matritsasini ko'rib chiqing E\to'g'ri. \right]$. Agar foydalansangiz elementar qator transformatsiyalari uni $\left[ E\left| shakliga keltiring B\o'ng. \right]$, ya'ni. $A$ dan oʻngdagi $E$ matritsasini olish uchun qatorlarni koʻpaytirish, ayirish va qayta tartiblash orqali, chap tomonda olingan $B$ matritsasi $A$ ga teskari hisoblanadi:

\[\left[ A\left| E\to'g'ri. \right]\to \chap[ E\left| B\o'ng. \o'ng]\O'ng strelka B=((A)^(-1))\]

Bu juda oddiy! Qisqacha aytganda, teskari matritsani topish algoritmi quyidagicha ko'rinadi:

1. Bog'langan $\left[ A\left| matritsasini yozing E\to'g'ri. \right]$;
2. $A$ oʻrniga oʻng tomon $E$ paydo boʻlguncha elementar satr konvertatsiyasini bajaring;
3. Albatta, chap tomonda ham biror narsa paydo bo'ladi - ma'lum bir matritsa $B$. Bu teskari bo'ladi;
4. FOYDA! :)

Albatta, qilishdan ko'ra aytish osonroq. Keling, bir nechta misollarni ko'rib chiqaylik: $\left[ 3\times 3 \right]$ va $\left[ 4\times 4 \right]$ o'lchamlari uchun.

Vazifa. Teskari matritsani toping:

\[\left[ \begin(massiv)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end(massiv) \o'ng]\ ]

Yechim. Biz biriktirilgan matritsani tuzamiz:

\[\left[ \begin(massiv)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 va 1 \\\end(massiv) \o'ng]\]

Asl matritsaning oxirgi ustuni birlar bilan to'ldirilganligi sababli, qolganlardan birinchi qatorni olib tashlang:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\end(massiv) \o'ng]\boshlash(matritsa) \pastga strelka \\ -1 \\ -1 \\\end(matritsa)\to \\ & \chapga [ \begin(massiv)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(massiv) \o'ng] \\ \end(hizala)\]

Birinchi qatordan tashqari boshqa birliklar yo'q. Lekin biz unga tegmaymiz, aks holda yangi olib tashlangan birliklar uchinchi ustunda "ko'payishni" boshlaydi.

Ammo biz ikkinchi qatorni oxirgisidan ikki marta ayirishimiz mumkin - biz pastki chap burchakda birlik olamiz:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(massiv) \o'ng]\begin(matritsa) \\\ \pastga strelka \\ -2 \\\end(matritsa)\to \\ & \chap [ \begin(massiv)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(massiv) \o'ng] \\ \end(hizala)\]

Endi biz birinchi qatordan oxirgi qatorni, ikkinchisidan esa ikki marta ayirishimiz mumkin - shu tarzda biz birinchi ustunni "noldan chiqaramiz":

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(massiv) \o'ng]\begin(matritsa) -1 \\ -2 \\ \uparrow \\\end(matritsa)\to \\ & \ to \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(massiv) \o'ng] \\ \end(hizala)\]

Ikkinchi qatorni -1 ga ko'paytiring, so'ngra uni birinchisidan 6 marta ayirib, oxirgisiga 1 marta qo'shing:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\end(massiv) \o'ng]\begin(matritsa) \ \\ \chap| \cdot \left(-1 \o'ng) \o'ng. \\ \ \\\end(matritsa)\to \\ & \to \chap[ \begin(massiv)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(massiv) \o'ng]\boshlash(matritsa) -6 \\ \yuqoriga -pastga \\ +1 \\\end (matritsa)\to \\ & \to \chap[ \begin(massiv)(rrr|rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\end(massiv) \o'ng] \\ \end(tizalash)\]

Faqat 1 va 3 qatorlarni almashtirish uchun qoladi:

\[\left[ \begin(massiv)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 & 32 & -13 \\\end(massiv) \o'ng]\]

Tayyor! O'ng tomonda kerakli teskari matritsa mavjud.

Javob. $\left[ \begin(massiv)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end(massiv) \o'ng ]$

Vazifa. Teskari matritsani toping:

\[\left[ \begin(matritsa) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\end (matritsa) \o'ng]\]

Yechim. Biz yana biriktirilganni tuzamiz:

\[\left[ \begin(massiv)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(massiv) \oʻng]\]

Keling, bir oz qarz olaylik, hozir qancha hisoblashimiz kerakligi haqida tashvishlanamiz ... va hisoblashni boshlaymiz. Boshlash uchun 2 va 3-qatorlardan 1-qatorni ayirib, birinchi ustunni “nolga chiqaramiz”:

\[\begin(align) & \left[ \begin(massiv)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(massiv) \o'ng]\begin(matritsa) \pastga strelka \\ -1 \\ -1 \\ \ \\\end(matritsa)\to \\ & \to \chap[ \begin(massiv)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(massiv) \o'ng] \\ \end(hizalang)\]

Biz 2-4 qatorlarda juda ko'p "minuslar" ni kuzatamiz. Barcha uchta qatorni -1 ga ko'paytiring va qolganlardan 3-qatorni ayirib, uchinchi ustunni yoqib yuboring:

\[\begin(align) & \left[ \begin(massiv)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \end(massiv) \o'ng]\begin(matritsa) \ \\ \chap| \cdot \left(-1 \o'ng) \o'ng. \\ \chap| \cdot \left(-1 \o'ng) \o'ng. \\ \chap| \cdot \left(-1 \o'ng) \o'ng. \\\end(matritsa)\to \\ & \to \chap[ \begin(massiv)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & ​​1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\ \end (massiv) \o'ng]\begin(matritsa) -2 \\ -1 \\ \yuqoriga qarab \\ -2 \\\end(matritsa)\to \\ & \chapga[ \begin(massiv)( rrrr| rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(massiv) \o'ng] \\ \end(hizalang)\]

Endi asl matritsaning oxirgi ustunini "qovurish" vaqti keldi: qolganidan 4-qatorni ayirib tashlang:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(massiv ) \right]\begin(matritsa) +1 \\ -3 \\ -2 \\ \uparrow \\\end(matritsa)\to \\ & \chapga[ \begin(massiv)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(massiv) \o'ng] \\ \end(tuzalash)\]

Yakuniy rulon: 1 va 3-qatordan 2-qatorni ayirish orqali ikkinchi ustunni "yoqib yuboring":

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end( massiv) \o'ng]\begin(matritsa) 6 \\ \updownarrow \\ -5 \\ \ \\\end(matritsa)\to \\ & \chapga[ \begin(massiv)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(massiv) \o'ng] \\ \end(hizalang)\]

Va yana, chapdagi identifikatsiya matritsasi, shuning uchun o'ngdagi teskari. :)

Javob. $\left[ \begin(matritsa) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\end(matritsa) \o'ng]$

OK, endi hammasi tugadi. Tekshirishni o'zingiz bajaring - men o'chirildim. :)

Kvadrat matritsani ko'rib chiqing. Uning determinantini D = det A bilan belgilang. Agar ularning mahsuloti A * B = B * A = E bo'lsa, bir xil tartibli A kvadrat uchun B kvadrati (OM) dir, bu erda E - A va B bilan bir xil tartibdagi o'ziga xoslik matritsasi.

A kvadrati, agar uning determinanti nolga teng bo'lsa, degenerativ bo'lmagan yoki yagona bo'lmagan, D = 0 bo'lsa, degenerativ yoki maxsus deyiladi.

Teorema. A ning teskari bo‘lishi uchun uning determinanti noldan farq qilishi zarur va yetarli.

(OM) A, A -1 bilan belgilanadi, shuning uchun B \u003d A -1 va formula bilan hisoblanadi

, (1)

bu yerda A i j - a i j elementlarining algebraik to'ldiruvchisi, D = detA.

Yuqori tartibli matritsalar uchun (1) formula bo'yicha A -1 ni hisoblash juda mashaqqatli, shuning uchun amalda elementar o'zgartirishlar (EP) usuli yordamida A -1 ni topish qulay. Faqat ustunlardan (yoki faqat satrlardan) iborat EP yordamida har qanday yagona bo'lmagan A ni E birligiga qisqartirish mumkin. Agar A matritsasi bo'yicha bajarilgan RaIlar E birligiga bir xil tartibda qo'llanilsa, natija A -1 bo'ladi. A|E chizig'i orqali ikkalasini yonma-yon yozib, bir vaqtning o'zida A va E da RaI bajarish qulay. Agar siz A -1 ni topmoqchi bo'lsangiz, konvertatsiya qilishda faqat satrlardan yoki faqat ustunlardan foydalaning.

Teskari matritsani algebraik to‘ldiruvchilar yordamida topish

1-misol. Uchun A -1 ni toping.

Yechim. Avval determinant A ni topamiz
demak, (OM) mavjud va uni quyidagi formula bilan topishimiz mumkin: , bu yerda A i j (i,j=1,2,3) - asl A ning a i j elementlarining algebraik toʻldiruvchilari.

a ij elementning algebraik to'ldiruvchisi aniqlovchi yoki minor M ij bo'ladi. U ustun i va j qatorni o'chirish orqali olinadi. Keyin minor (-1) i+j ga ko'paytiriladi, ya'ni. A ij =(-1) i+j M ij

qayerda .

Elementar transformatsiyalar yordamida teskari matritsani topish

2-misol. Elementar transformatsiyalar usulidan foydalanib, A -1 ni toping: A \u003d.

Yechim. Biz o'ngdagi asl A ga bir xil tartibdagi birlikni kiritamiz: . Elementar ustun o'zgarishlari yordamida biz chap "yarim" ni bitta birlikka qisqartiramiz va bir vaqtning o'zida o'ng "yarim" da aynan shunday o'zgarishlarni amalga oshiramiz.
Buning uchun birinchi va ikkinchi ustunlarni almashtiring: ~. Birinchi ustunni uchinchi ustunga, ikkinchisini esa -2 ga ko'paytiramiz: . Birinchi ustundan biz ikki barobar ko'p soniyani olib tashlaymiz, uchinchidan esa - ikkinchisi 6 ga ko'paytiriladi; . Birinchi va ikkinchi ustunga uchinchi ustunni qo'shamiz: . Oxirgi ustunni -1 ga ko'paytiring: . Vertikal chiziqning o'ng tomonida olingan kvadrat jadval A -1 ning teskarisidir. Shunday qilib,
.

Berilgan matritsa uchun teskari matritsa shunday matritsa bo'lib, asl matritsani ko'paytirish orqali o'ziga xos matritsani beradi: Teskari matritsa mavjudligi uchun majburiy va etarli shart - bu asl determinantning tengsizligi (qaysi o'z navbatida matritsa kvadrat bo'lishi kerakligini anglatadi). Agar matritsaning determinanti nolga teng bo'lsa, u degenerativ deb ataladi va bunday matritsaning teskarisi yo'q. Oliy matematikada teskari matritsalar muhim ahamiyatga ega bo‘lib, ular qator masalalarni yechishda qo‘llaniladi. Masalan, on teskari matritsani topish tenglamalar sistemasini yechishning matritsa usuli qurilgan. Bizning xizmat saytimiz ruxsat beradi teskari matritsani onlayn hisoblang ikkita usul: Gauss-Jordan usuli va algebraik qo'shimchalar matritsasidan foydalanish. Birinchisi, matritsa ichidagi ko'p sonli elementar o'zgarishlarni nazarda tutadi, ikkinchisi - barcha elementlarga determinant va algebraik qo'shimchalarni hisoblash. Matritsa determinantini onlayn hisoblash uchun siz bizning boshqa xizmatimizdan foydalanishingiz mumkin - Matritsa determinantini onlayn hisoblash

.

Saytdagi teskari matritsani toping

veb-sayt topishga imkon beradi teskari matritsa onlayn tez va bepul. Saytda hisob-kitoblar bizning xizmatimiz tomonidan amalga oshiriladi va natija topish uchun batafsil echim bilan ko'rsatiladi. teskari matritsa. Server har doim faqat aniq va to'g'ri javob beradi. Ta'rifi bo'yicha vazifalarda teskari matritsa onlayn, aniqlovchi bo'lishi kerak matritsalar noldan farqli edi, aks holda veb-sayt asl matritsaning determinanti nolga teng bo'lganligi sababli teskari matritsani topishning iloji yo'qligi haqida xabar beradi. Vazifani topish teskari matritsa matematikaning ko'plab sohalarida mavjud bo'lib, algebraning eng asosiy tushunchalaridan biri va amaliy masalalarda matematik vositadir. Mustaqil teskari matritsa ta'rifi hisob-kitoblarda sirpanish yoki kichik xatolikka yo'l qo'ymaslik uchun katta kuch, ko'p vaqt, hisob-kitoblar va katta ehtiyotkorlik talab etiladi. Shuning uchun bizning xizmatimiz teskari matritsani onlayn topish vazifangizni sezilarli darajada osonlashtiradi va matematik muammolarni hal qilishda ajralmas vositaga aylanadi. Agar siz teskari matritsani toping o'zingiz uchun yechimingizni serverimizda tekshirishni tavsiya qilamiz. Asl matritsangizni bizning Inverse Matrix Onlayn hisob-kitobimizga kiriting va javobingizni tekshiring. Bizning tizimimiz hech qachon xato qilmaydi va topadi teskari matritsa rejimida berilgan o'lcham onlayn darhol! Saytda veb-sayt elementlarda belgilar kiritishga ruxsat beriladi matritsalar, Ushbu holatda teskari matritsa onlayn umumiy ramziy shaklda taqdim etiladi.