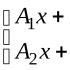Обобщение и основни формули.

Задача No1

Логиката е проста: ще правим както преди, независимо че сега тригонометричните функции имат по-сложен аргумент!

Ако решим уравнение от вида:

Тогава ще запишем следния отговор:

Или (тъй като)

Но сега нашата роля се играе от този израз:

Тогава можем да напишем:

Нашата цел с вас е да се уверим, че лявата страна стои просто, без никакви „примеси“!

Нека постепенно се отървем от тях!

Първо, нека премахнем знаменателя при: за да направите това, умножете нашето равенство по:

Сега нека се отървем от него, като разделим двете части:

Сега нека се отървем от осемте:

Полученият израз може да бъде записан като 2 серии от решения (по аналогия с квадратно уравнение, където добавяме или изваждаме дискриминанта)

Трябва да намерим най-големия отрицателен корен! Ясно е, че трябва да подредим.

Нека първо да разгледаме първия епизод:

Ясно е, че ако вземем, тогава в резултат ще получим положителни числа, но те не ни интересуват.

Така че трябва да го приемете отрицателно. Нека бъде.

Когато коренът ще бъде по-тесен:

И трябва да намерим най-големия негатив!! Това означава, че вървенето в негативна посока тук вече няма смисъл. И най-големият отрицателен корен за тази редица ще бъде равен на.

Сега нека да разгледаме втората серия:

И отново заместваме: , след това:

Не се интересувам!

Тогава няма смисъл да увеличавате повече! Да го намалим! Нека тогава:

пасва!

Нека бъде. Тогава

След това - най-големият отрицателен корен!

Отговор:

Задача No2

Решаваме отново, независимо от комплексния косинус аргумент:

Сега изразяваме отново отляво:

Умножете двете страни по

Разделете двете страни на

Остава само да го преместите надясно, като промените знака му от минус на плюс.

Отново получаваме 2 серии от корени, едната с и другата с.

Трябва да намерим най-големия отрицателен корен. Да видим първия епизод:

Ясно е, че ще получим първия отрицателен корен при, той ще бъде равен на и ще бъде най-големият отрицателен корен в 1 серия.

За втората серия

Първият отрицателен корен също ще бъде получен при и ще бъде равен на. Тъй като, тогава е най-големият отрицателен корен на уравнението.

Отговор: .

Задача No3

Ние решаваме, независимо от сложния допирателен аргумент.

Сега не изглежда сложно, нали?

Както преди, изразяваме от лявата страна:

Е, това е страхотно, тук има само една серия корени! Нека отново намерим най-големия минус.

Ясно е, че се оказва, ако го оставите. И този корен е равен.

Отговор:

Сега се опитайте сами да разрешите следните задачи.

Домашна работа или 3 задачи за самостоятелно решаване.

Решете уравнението.
Решете уравнението.
В отговора на pi-shi-th-най-малкия-възможен корен.
Решете уравнението.
В отговора на pi-shi-th-най-малкия-възможен корен.

Готов? Да проверим. Няма да описвам подробно целия алгоритъм на решението, струва ми се, че вече му беше обърнато достатъчно внимание по-горе.

Е, всичко наред ли е? О, тези гадни синуси, винаги има някакъв проблем с тях!

Е, сега можете да решавате прости тригонометрични уравнения!

Вижте решенията и отговорите:

Задача No1

Да изразим

Най-малкият положителен корен се получава, ако поставим, тъй като, тогава

Отговор:

Задача No2

Най-малкият положителен корен се получава при.

Ще бъде равно.

Отговор: .

Задача No3

Когато получим, когато имаме.

Отговор: .

Това знание ще ви помогне да решите много проблеми, които ще срещнете на изпита.

Ако кандидатствате за оценка „5“, тогава просто трябва да продължите към четене на статията за средно нивокойто ще бъде посветен на решаването на по-сложни тригонометрични уравнения (задача C1).

СРЕДНО НИВО

В тази статия ще опиша решаване на по-сложни тригонометрични уравненияи как да изберете техните корени. Тук ще черпя по следните теми:

Тригонометрични уравнения за ниво начинаещи (виж по-горе).

По-сложните тригонометрични уравнения са основата за напреднали проблеми. Те изискват както решаване на самото уравнение в общ вид, така и намиране на корените на това уравнение, принадлежащи към определен интервал.

Решаването на тригонометрични уравнения се свежда до две подзадачи:

Решаване на уравнението
Избор на корен

Трябва да се отбележи, че второто не винаги е необходимо, но в повечето примери изборът все още е необходим. Но ако не е задължително, тогава можем да ви съчувстваме - това означава, че уравнението е доста сложно само по себе си.

Моят опит в анализирането на проблеми с C1 показва, че те обикновено се разделят на следните категории.

Четири категории задачи с повишена сложност (бивш C1)

Уравнения, които се свеждат до факторизация.
Уравнения, приведени до форма.
Уравнения, решени чрез промяна на променлива.
Уравнения, които изискват допълнителен избор на корени поради ирационалност или знаменател.

Казано по-просто: ако те хванат едно от уравненията на първите три вида, тогава се считайте за късметлия. За тях, като правило, допълнително трябва да изберете корени, принадлежащи към определен интервал.

Ако срещнете уравнение от тип 4, тогава имате по-малко късмет: трябва да се занимавате с него по-дълго и по-внимателно, но доста често не изисква допълнителен избор на корени. Въпреки това ще анализирам този тип уравнения в следващата статия, а тази ще посветя на решаването на уравнения от първите три вида.

Уравнения, които се свеждат до факторизация

Най-важното нещо, което трябва да запомните, за да решите този тип уравнение, е

Както показва практиката, като правило това знание е достатъчно. Нека да разгледаме някои примери:

Пример 1. Уравнение, намалено до разлагане на множители с помощта на формулите за редукция и синус на двоен ъгъл

Решете уравнението
Намерете всички корени на това уравнение, които лежат над разреза

Тук, както обещах, формулите за намаляване работят:

Тогава моето уравнение ще изглежда така:

Тогава моето уравнение ще приеме следната форма:

Един късоглед студент може да каже: сега ще намаля двете страни, ще получа най-простото уравнение и ще се радвам на живота! И горчиво ще сгреши!

ЗАПОМНЕТЕ: НИКОГА НЕ МОЖЕТЕ ДА НАМАЛИТЕ ДВЕТЕ СТРАНИ НА ТРИГОНОМЕТРИЧНО УРАВНЕНИЕ С ФУНКЦИЯ, СЪДЪРЖАЩА НЕИЗВЕСТНО! ТАКА ЗАГУБВАШ КОРЕНИТЕ СИ!

И така, какво да правя? Да, просто е, преместете всичко на една страна и извадете общия множител:

Е, разложихме го на фактори, ура! Сега да решим:

Първото уравнение има корени:

И второто:

Това завършва първата част от проблема. Сега трябва да изберете корените:

Разликата е следната:

Или може да се напише и така:

Е, нека вземем корените:

Първо, нека поработим с първия епизод (и най-малкото е по-прост!)

Тъй като нашият интервал е изцяло отрицателен, няма нужда да вземаме неотрицателни, те пак ще дадат неотрицателни корени.

Да вземем, значи - много е, не улучва.

Нека бъде тогава - не го ударих отново.

Още един опит - тогава - да, разбрах! Първият корен е открит!

Стрелям отново: след това удрям отново!

Ами още веднъж : : - това вече е полет.

Така че от първата серия има 2 корена, принадлежащи на интервала: .

Работим с втората серия (изграждаме на степен според правилото):

Подстрелване!

Отново липсва!

Схванах го!

Полет!

Така моят интервал има следните корени:

Това е алгоритъмът, който ще използваме за решаване на всички други примери. Нека се упражним заедно с още един пример.

Пример 2. Уравнение, намалено до разлагане на множители с помощта на редукционни формули

Решете уравнението

Решение:

Отново прословутите формули за намаляване:

Не се опитвайте да намалите отново!

Първото уравнение има корени:

И второто:

Сега отново търсенето на корени.

Ще започна с втория епизод, вече знам всичко за него от предишния пример! Погледнете и се уверете, че корените, принадлежащи на интервала, са както следва:

Сега първият епизод и е по-прост:

Ако - подходящо

Ако и това е добре

Ако вече е полет.

Тогава корените ще бъдат както следва:

Самостоятелна работа. 3 уравнения.

Е, ясна ли ви е техниката? Решаването на тригонометрични уравнения вече не изглежда толкова трудно? След това бързо решете следните задачи сами и след това ще решим други примери:

Решете уравнението
Намерете всички корени на това уравнение, които лежат над интервала.
Решете уравнението
Посочете корените на уравнението, които лежат над разреза
Решете уравнението
Намерете всички корени на това уравнение, които лежат между тях.

Уравнение 1.

И отново формулата за намаляване:

Първа серия от корени:

Втора серия от корени:

Започваме селекцията за празнината

Отговор: , .

Уравнение 2. Проверка на самостоятелна работа.

Доста сложно групиране в фактори (ще използвам формулата за синус на двоен ъгъл):

тогава или

Това е общо решение. Сега трябва да изберем корените. Проблемът е, че не можем да кажем точната стойност на ъгъл, чийто косинус е равен на една четвърт. Следователно не мога просто да се отърва от аркосинуса - такъв срам!

Това, което мога да направя, е да разбера, че така, така, тогава.

Нека създадем таблица: interval:

Е, чрез болезнени търсения стигнахме до разочароващото заключение, че нашето уравнение има един корен на посочения интервал: \displaystyle arccos\frac(1)(4)-5\pi

Уравнение 3: Тест за самостоятелна работа.

Страшно изглеждащо уравнение. Въпреки това, той може да бъде решен съвсем просто чрез прилагане на формулата за синус на двоен ъгъл:

Нека го намалим с 2:

Нека групираме първия член с втория и третия с четвъртия и извадим общите множители:

Ясно е, че първото уравнение няма корени, а сега нека разгледаме второто:

Като цяло щях да се спра малко по-късно върху решаването на такива уравнения, но тъй като се оказа, няма какво да правя, трябва да го реша ...

Уравнения от вида:

Това уравнение се решава чрез разделяне на двете страни на:

Така нашето уравнение има една поредица от корени:

Трябва да намерим тези, които принадлежат на интервала: .

Нека изградим таблица отново, както направих по-рано:

Отговор: .

Уравнения, приведени до вида:

Е, сега е време да преминем към втората част от уравненията, особено след като вече разказах какво представлява решението на тригонометричните уравнения от нов тип. Но си струва да повторим, че уравнението е от вида

Решено чрез разделяне на двете страни на косинус:

Решете уравнението
Посочете корените на уравнението, които лежат над разреза.
Решете уравнението
Посочете корените на уравнението, които лежат между тях.

Пример 1.

Първият е доста прост. Преместете се надясно и приложете формулата за двоен ъглов косинус:

да! Уравнение от вида: . Разделям двете части на

Извършваме корен скрининг:

празнина:

Отговор:

Пример 2.

Всичко също е доста тривиално: нека отворим скобите вдясно:

Основна тригонометрична идентичност:

Синус на двоен ъгъл:

Накрая получаваме:

Скрининг на корените: интервал.

Отговор: .

Е, как ви харесва техниката, не е ли много сложна? Надявам се не. Веднага можем да направим резервация: в чистата си форма уравненията, които веднага се свеждат до уравнение за допирателната, са доста редки. Обикновено този преход (деление по косинус) е само част от по-сложен проблем. Ето един пример за упражнение:

Решете уравнението
Намерете всички корени на това уравнение, които лежат над разреза.

Да проверим:

Уравнението може да бъде решено веднага; достатъчно е да разделите двете страни на:

Скрининг на корена:

Отговор: .

По един или друг начин все още не сме срещали уравнения от вида, който току-що разгледахме. Въпреки това е твърде рано да го наричаме ден: все още има още един „слой“ от уравнения, които не сме анализирали. Така:

Решаване на тригонометрични уравнения чрез промяна на променливи

Тук всичко е прозрачно: разглеждаме внимателно уравнението, опростяваме го възможно най-много, правим заместване, решаваме го, правим обратно заместване! На думи всичко е много лесно. Да видим в действие:

Пример.

Решете уравнението: .
Намерете всички корени на това уравнение, които лежат над разреза.

Е, тук самата подмяна ни се подсказва!

Тогава нашето уравнение ще се превърне в това:

Първото уравнение има корени:

А второто е така:

Сега нека намерим корените, принадлежащи на интервала

Отговор: .

Нека да разгледаме един малко по-сложен пример заедно:

Решете уравнението
Посочете корените на даденото уравнение, лежащи над-лежащи между тях.

Тук замяната не се вижда веднага, освен това не е много очевидна. Нека първо да помислим: какво можем да направим?

Можем например да си представим

И в същото време

Тогава моето уравнение ще приеме формата:

А сега внимание, фокус:

Нека разделим двете страни на уравнението на:

Изведнъж вие и аз имаме относително квадратно уравнение! Нека направим замяна, тогава получаваме:

Уравнението има следните корени:

Неприятна втора серия от корени, но нищо не може да се направи! Избираме корени в интервала.

Ние също трябва да вземем предвид това

От и тогава

Отговор:

За да затвърдите това, преди да разрешите проблемите сами, ето още едно упражнение за вас:

Решете уравнението
Намерете всички корени на това уравнение, които лежат между тях.

Тук трябва да си държите очите отворени: сега имаме знаменатели, които могат да бъдат нула! Затова трябва да сте особено внимателни към корените!

Първо, трябва да пренаредя уравнението, така че да мога да направя подходящо заместване. Сега не мога да измисля нищо по-добро от това да пренапиша тангенса по отношение на синус и косинус:

Сега ще премина от косинус към синус, използвайки основната тригонометрична идентичност:

И накрая, ще доведа всичко до общ знаменател:

Сега мога да премина към уравнението:

Но при (тоест при).

Сега всичко е готово за подмяна:

Тогава или

Имайте предвид обаче, че ако, тогава в същото време!

Кой страда от това? Проблемът с тангенса е, че той не е дефиниран, когато косинусът е равен на нула (възниква деление на нула).

Така корените на уравнението са:

Сега отсяваме корените в интервала:


	- пасва
	- прекаляване

Така нашето уравнение има един корен в интервала и той е равен.

Виждате: появата на знаменател (също като допирателната, води до определени трудности с корените! Тук трябва да сте по-внимателни!).

Е, вие и аз почти приключихме с анализа на тригонометричните уравнения, остава много малко - да решите две задачи сами. Ето ги и тях.

Решете уравнението
Намерете всички корени на това уравнение, които лежат над разреза.
Решете уравнението
Посочете корените на това уравнение, разположени над разреза.

Решихте ли? Не е ли много трудно? Да проверим:

Ние работим по формулите за намаление:
Заместете в уравнението:
Нека пренапишем всичко чрез косинуси, за да направим по-лесно замяната:
Сега е лесно да направите замяна:
Ясно е, че това е външен корен, тъй като уравнението няма решения. Тогава:
Търсим корените, от които се нуждаем в интервала
Отговор: .
Тук веднага се вижда замяната:
Тогава или

- пасва! - пасва!
- пасва! - пасва!
- много! - също много!
Отговор:

Е, това е вече! Но решаването на тригонометрични уравнения не свършва дотук; изоставаме в най-трудните случаи: когато уравненията съдържат ирационалност или различни видове „комплексни знаменатели“. Ще разгледаме как се решават такива задачи в статия за напреднало ниво.

НАПРЕДНАЛО НИВО

В допълнение към тригонометричните уравнения, обсъдени в предишните две статии, ще разгледаме друг клас уравнения, които изискват още по-внимателен анализ. Тези тригонометрични примери съдържат или ирационалност, или знаменател, което прави анализа им по-труден. Възможно е обаче да срещнете тези уравнения в част C на изпитната работа. Въпреки това, всеки облак има сребърна подплата: за такива уравнения, като правило, вече не се повдига въпросът кой от неговите корени принадлежи към даден интервал. Нека не се заобикаляме, а да преминем направо към тригонометричните примери.

Пример 1.

Решете уравнението и намерете корените, които принадлежат на отсечката.

Решение:

Имаме знаменател, който не трябва да е равен на нула! Тогава решаването на това уравнение е същото като решаването на системата

Нека решим всяко от уравненията:

А сега второто:

Сега нека да разгледаме серията:

Ясно е, че тази опция не ни подхожда, тъй като в този случай нашият знаменател се нулира (вижте формулата за корените на второто уравнение)

Ако, тогава всичко е наред и знаменателят не е нула! Тогава корените на уравнението са както следва: , .

Сега избираме корените, принадлежащи на интервала.


	- неподходящ	- пасва
	- пасва	- пасва
	свръхубийство	свръхубийство

Тогава корените са както следва:

Виждате ли, дори появата на малко смущение във формата на знаменателя значително повлия на решението на уравнението: изхвърлихме поредица от корени, които анулираха знаменателя. Нещата могат да станат още по-сложни, ако попаднете на тригонометрични примери, които са ирационални.

Пример 2.

Решете уравнението:

Решение:

Е, поне не е нужно да отнемате корените и това е добре! Нека първо решим уравнението, независимо от ирационалността:

И така, това ли е всичко? Не, уви, би било твърде лесно! Трябва да помним, че под корена могат да се появят само неотрицателни числа. Тогава:

Решението на това неравенство е:

Сега остава да разберем дали част от корените на първото уравнение неволно са се озовали там, където неравенството не важи.

За да направите това, можете отново да използвате таблицата:


	: , Но	Не!
		да
		да

Така един от корените ми „изпадна“! Оказва се, ако го оставите. Тогава отговорът може да бъде написан по следния начин:

Отговор:

Виждате ли, коренът изисква още повече внимание! Нека го направим по-сложно: нека сега имам тригонометрична функция под моя корен.

Пример 3.

Както досега: първо ще решаваме всеки поотделно, а след това ще мислим какво сме направили.

Сега второто уравнение:

Сега най-трудното нещо е да разберем дали под аритметичния корен се получават отрицателни стойности, ако заместим корените от първото уравнение там:

Числото трябва да се разбира като радиани. Тъй като радианът е приблизително градуси, тогава радианите са от порядъка на градуси. Това е ъгълът на втората четвърт. Какъв е знакът на косинуса на втората четвърт? Минус. Какво ще кажете за синуса? плюс. И така, какво можем да кажем за израза:

По-малко от нула е!

Това означава, че не е коренът на уравнението.

Сега е времето.

Нека сравним това число с нула.

Котангенсът е функция, намаляваща на 1 четвърт (колкото по-малък е аргументът, толкова по-голям е котангенсът). радианите са приблизително градуси. В същото време

тъй като, тогава и следователно
,

Отговор: .

Може ли да стане по-сложно? Моля те! Ще бъде по-трудно, ако коренът все още е тригонометрична функция, а втората част на уравнението отново е тригонометрична функция.

Колкото повече тригонометрични примери, толкова по-добре, вижте по-долу:

Пример 4.

Коренът не е подходящ поради ограничения косинус

Сега второто:

В същото време, по дефиниция на корен:

Трябва да запомним единичната окръжност: а именно тези четвъртини, където синусът е по-малък от нула. Какви са тези квартали? Трети и четвърти. Тогава ще се интересуваме от онези решения на първото уравнение, които се намират в третата или четвъртата четвърт.

Първата серия дава корени, разположени на пресечната точка на третата и четвъртата четвърт. Втората серия - диаметрално противоположна на нея - поражда корени, лежащи на границата на първата и втората четвърт. Следователно този сериал не е подходящ за нас.

Отговор: ,

И отново тригонометрични примери с "трудна ирационалност". Не само, че отново имаме тригонометричната функция под корена, но сега тя е и в знаменателя!

Пример 5.

Е, нищо не може да се направи - правим както досега.

Сега работим със знаменателя:

Не искам да решавам тригонометричното неравенство, така че ще направя нещо хитро: ще взема и ще заменя моята поредица от корени в неравенството:

Ако - е четно, тогава имаме:

тъй като всички ъгли на изгледа лежат в четвъртата четвърт. И отново свещеният въпрос: какъв е знакът на синуса в четвъртата четвърт? Отрицателна. След това неравенството

Ако -нечетно, тогава:

В коя четвърт се намира ъгълът? Това е ъгълът на втората четвърт. Тогава всички ъгли отново са ъглите на втората четвърт. Синусът там е положителен. Точно това, от което се нуждаете! И така, серията:

пасва!

Справяме се с втората серия от корени по същия начин:

Заменяме в нашето неравенство:

Ако - дори, тогава

Първа четвърт ъгли. Синусът там е положителен, което означава, че серията е подходяща. Сега, ако - странно, тогава:

пасва също!

Е, сега записваме отговора!

Отговор:

Е, това беше може би най-трудоемкият случай. Сега ви предлагам задачи, които да решите сами.

обучение

Решете и намерете всички корени на уравнението, които принадлежат на отсечката.

Решения:

Първо уравнение:
или
ODZ на корен:
Второ уравнение:
Избор на корени, които принадлежат на интервала
Отговор:

Или
или
Но

Нека разгледаме:. Ако - дори, тогава
- не става!
Ако - странно, : - подходящо!
Това означава, че нашето уравнение има следната поредица от корени:
или
Избор на корени в интервала:


	- неподходящ	- пасва
	- пасва	- много
	- пасва	много

Отговор: , .

Или
Тъй като, тогава допирателната не е дефинирана. Веднага изхвърляме тази серия от корени!

Втора част:

В същото време според ДЗ се изисква т.к

Проверяваме корените, намерени в първото уравнение:

Ако знакът:

Първа четвърт ъгли, където тангентата е положителна. Не става!
Ако знакът:

Четвърта четвърт ъгъл. Там тангенсът е отрицателен. Пасва. Записваме отговора:

Отговор: , .

Разгледахме заедно сложни тригонометрични примери в тази статия, но вие трябва да решите уравненията сами.

ОБОБЩЕНИЕ И ОСНОВНИ ФОРМУЛИ

Тригонометрично уравнение е уравнение, в което неизвестното е строго под знака на тригонометричната функция.

Има два начина за решаване на тригонометрични уравнения:

Първият начин е използването на формули.

Вторият начин е чрез тригонометричния кръг.

Позволява ви да измервате ъгли, да намирате техните синуси, косинуси и др.

Доста често срещаме проблеми с повишена сложност тригонометрични уравнения, съдържащи модул. Повечето от тях изискват евристичен подход за решаване, който е напълно непознат за повечето ученици.

Предложените по-долу задачи имат за цел да ви запознаят с най-типичните техники за решаване на тригонометрични уравнения, съдържащи модул.

Задача 1. Намерете разликата (в градуси) на най-малкия положителен и най-големия отрицателен корен на уравнението 1 + 2sin x |cos x| = 0.

Решение.

Нека разширим модула:

1) Ако cos x ≥ 0, тогава оригиналното уравнение ще приеме формата 1 + 2sin x · cos x = 0.

Използвайки формулата за синус на двоен ъгъл, получаваме:

1 + sin 2x = 0; sin 2x = -1;

2x = -π/2 + 2πn, n € Z;

x = -π/4 + πn, n € Z. Тъй като cos x ≥ 0, тогава x = -π/4 + 2πk, k € Z.

2) Ако cos x< 0, то заданное уравнение имеет вид 1 – 2sin x · cos x = 0. По формуле синуса двойного угла, имеем:

1 – sin 2x = 0; грях 2x = 1;

2x = π/2 + 2πn, n € Z;

x = π/4 + πn, n € Z. Тъй като cos x< 0, то x = 5π/4 + 2πk, k € Z.

3) Най-големият отрицателен корен на уравнението: -π/4; най-малкият положителен корен на уравнението: 5π/4.

Необходимата разлика: 5π/4 – (-π/4) = 6π/4 = 3π/2 = 3 180°/2 = 270°.

Отговор: 270°.

Задача 2. Намерете (в градуси) най-малкия положителен корен на уравнението |tg x| + 1/cos x = tan x.

Решение.

Нека разширим модула:

1) Ако tan x ≥ 0, тогава

tan x + 1/cos x = tan x;

Полученото уравнение няма корени.

2) Ако tg x< 0, тогда

Tg x + 1/cos x = tg x;

1/cos x – 2tg x = 0;

1/cos x – 2sin x / cos x = 0;

(1 – 2sin x) / cos x = 0;

1 – 2sin x = 0 и cos x ≠ 0.

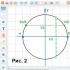
Използвайки фигура 1 и условието tg x< 0 находим, что x = 5π/6 + 2πn, где n € Z.

3) Най-малкият положителен корен на уравнението е 5π/6. Нека преобразуваме тази стойност в градуси:

5π/6 = 5 180°/6 = 5 30° = 150°.

Отговор: 150°.

Задача 3. Намерете броя на различните корени на уравнението sin |2x| = cos 2x на интервала [-π/2; π/2].

Решение.

Нека напишем уравнението във формата sin|2x| – cos 2x = 0 и разгледаме функцията y = sin |2x| – cos 2x. Тъй като функцията е четна, ще намерим нейните нули за x ≥ 0.

sin 2x – cos 2x = 0; Нека разделим двете страни на уравнението на cos 2x ≠ 0, получаваме:

tg 2x – 1 = 0;

2x = π/4 + πn, n € Z;

x = π/8 + πn/2, n € Z.

Използвайки паритета на функцията, намираме, че корените на оригиналното уравнение са числа от формата

± (π/8 + πn/2), където n € Z.

Интервал [-π/2; π/2] принадлежат на числата: -π/8; π/8.

И така, два корена на уравнението принадлежат на дадения интервал.

Отговор: 2.

Това уравнение може да се реши и чрез отваряне на модула.

Задача 4. Намерете броя на корените на уравнението sin x – (|2cos x – 1|)/(2cos x – 1) · sin 2 x = sin 2 x на интервала [-π; 2π].

Решение.

1) Разгледайте случая, когато 2cos x – 1 > 0, т.е. cos x > 1/2, тогава уравнението приема формата:

sin x – sin 2 x = sin 2 x;

sin x – 2sin 2 x = 0;

sin x(1 – 2sin x) = 0;

sin x = 0 или 1 – 2sin x = 0;

sin x = 0 или sin x = 1/2.

Използвайки фигура 2 и условието cos x > 1/2, намираме корените на уравнението:

x = π/6 + 2πn или x = 2πn, n € Z.

2) Разгледайте случая, когато 2cos x – 1< 0, т.е. cos x < 1/2, тогда исходное уравнение принимает вид:

sin x + sin 2 x = sin 2 x;

x = 2πn, n € Z.

Използвайки фигура 2 и условието cos x< 1/2, находим, что x = π + 2πn, где n € Z.

Комбинирайки двата случая, получаваме:

x = π/6 + 2πn или x = πn.

3) Интервал [-π; 2π] принадлежат на корените: π/6; -π; 0; π; 2π.

Така даденият интервал съдържа пет корена на уравнението.

Отговор: 5.

Задача 5. Намерете броя на корените на уравнението (x – 0,7) 2 |sin x| + sin x = 0 на интервала [-π; 2π].

Решение.

1) Ако sin x ≥ 0, тогава първоначалното уравнение приема формата (x – 0,7) 2 sin x + sin x = 0. След като извадим общия множител sin x извън скоби, получаваме:

sin x((x – 0,7) 2 + 1) = 0; тъй като (x – 0,7) 2 + 1 > 0 за всички реални x, тогава sinx = 0, т.е. x = πn, n € Z.

2) Ако sin x< 0, то -(x – 0,7) 2 sin x + sin x = 0;

sin x((x – 0,7) 2 – 1) = 0;

sinx = 0 или (x – 0,7) 2 + 1 = 0. Тъй като sin x< 0, то (x – 0,7) 2 = 1. Извлекаем квадратный корень из левой и правой частей последнего уравнения, получим:

x – 0,7 = 1 или x – 0,7 = -1, което означава x = 1,7 или x = -0,3.

Като се има предвид условието sinx< 0 получим, что sin (-0,3) ≈ sin (-17,1°) < 0 и sin (1,7) ≈ sin (96,9°) >0, което означава, че само числото -0,3 е коренът на оригиналното уравнение.

3) Интервал [-π; 2π] принадлежат на числата: -π; 0; π; 2π; -0,3.

Така уравнението има пет корена на даден интервал.

Отговор: 5.

Можете да се подготвите за уроци или изпити, като използвате различни образователни ресурси, които са достъпни в Интернет. В момента всеки човек просто трябва да използва нови информационни технологии, тъй като тяхното правилно и най-важното целесъобразно използване ще спомогне за повишаване на мотивацията при изучаването на предмета, ще повиши интереса и ще помогне за по-доброто усвояване на необходимия материал. Но не забравяйте, че компютърът не ви учи да мислите, получената информация трябва да бъде обработена, разбрана и запомнена. Затова можете да се обърнете за помощ към нашите онлайн преподаватели, които ще ви помогнат да разберете как да решите проблемите, които ви интересуват.

Все още имате въпроси? Не знаете как да решавате тригонометрични уравнения?
За да получите помощ от преподавател, регистрирайте се.
Първият урок е безплатен!

уебсайт, при пълно или частично копиране на материал се изисква връзка към източника.


	- пасва!	- пасва!
	- пасва!	- пасва!
	- много!	- също много!