Was sind die Zeichen dafür, dass Dreiecke gleich sind? Das erste Zeichen der Gleichheit der Dreiecke

Eine geometrische Figur, die aus drei Segmenten besteht, die drei Punkte verbinden, die nicht zur gleichen Geraden gehören.

Die Seiten des Dreiecks bilden an den Eckpunkten des Dreiecks drei Winkel. Umschreiben, Dreieck ist ein Polygon mit drei Winkeln .

Praktische Bedeutung Zeichen der Gleichheit von Dreiecken läuft auf Folgendes hinaus: dem Wortlaut entsprechend Dreiecke sind gleich, wenn es möglich ist, sie so zu überlagern, dass sie zusammenfallen; Die Implementierung einer Dreiecksüberlappung kann jedoch manchmal schwierig und manchmal unmöglich sein.

Tests auf Gleichheit von Dreiecken ermöglichen es, die Überlappung von Dreiecken durch das Finden und Vergleichen einzelner Grundkomponenten (Seiten und Winkel) zu ersetzen und so die Gleichheit von Dreiecken zu begründen.

3. Alle drei Seiten:

Sie heben auch hervor viertes Zeichen, der im Schulmathematikkurs nicht so umfassend behandelt wird wie die drei vorherigen. Es ist wie folgt formuliert:

Wenn zwei Seiten des ersten Dreiecks jeweils gleich zwei Seiten des zweiten Dreiecks sind und der Winkel gegenüber der größeren dieser Seiten im ersten Dreieck gleich dem Winkel gegenüber der entsprechenden Seite im zweiten Dreieck ist, dann sind diese Dreiecke sind gleich.

Zeichen der Gleichheit von Dreiecken

Dreiecke, deren entsprechende Seiten gleich sind, nennt man kongruent.

Satz (das erste Zeichen der Gleichheit von Dreiecken).
Wenn zwei Seiten und der Winkel zwischen ihnen eines Dreiecks jeweils gleich zwei Seiten und der Winkel zwischen ihnen eines anderen Dreiecks sind, dann sind solche Dreiecke kongruent.

Satz (zweites Kriterium für die Gleichheit von Dreiecken).
Wenn eine Seite und zwei benachbarte Winkel eines Dreiecks jeweils gleich einer Seite und zwei benachbarten Winkeln eines anderen Dreiecks sind, dann sind solche Dreiecke kongruent.

Satz (Drittes Kriterium für die Gleichheit von Dreiecken).
Wenn drei Seiten eines Dreiecks jeweils gleich drei Seiten eines anderen Dreiecks sind, dann sind solche Dreiecke kongruent.

Ähnlichkeitszeichen von Dreiecken

Dreiecke, deren Winkel gleich und deren ähnliche Seiten proportional sind, heißen ähnlich: , wobei der Ähnlichkeitskoeffizient ist.

Ich unterschreibe die Ähnlichkeit von Dreiecken. Wenn zwei Winkel eines Dreiecks jeweils gleich zwei Winkeln eines anderen sind, dann sind diese Dreiecke ähnlich.

II Zeichen der Ähnlichkeit von Dreiecken. Wenn drei Seiten eines Dreiecks proportional zu drei Seiten eines anderen Dreiecks sind, dann sind die Dreiecke ähnlich.

III Zeichen der Ähnlichkeit von Dreiecken. Wenn zwei Seiten eines Dreiecks proportional zu zwei Seiten eines anderen Dreiecks sind und die Winkel zwischen diesen Seiten gleich sind, dann sind die Dreiecke ähnlich.

1) auf zwei Seiten und der Winkel zwischen ihnen

Nachweisen:

Die Dreiecke ABC und A 1 B 1 C 1 haben einen Winkel A gleich A 1, AB gleich A 1 B 1 und AC gleich A 1 C 1. Beweisen wir, dass die Dreiecke kongruent sind.

Lassen Sie uns das Dreieck ABC auferlegen (oder symmetrisch dazu) auf das Dreieck A 1 B 1 C 1, so dass Winkel A mit Winkel A 1 ausgerichtet ist. Da AB=A 1 B 1 und AC=A 1 C 1, dann fällt B mit B 1 und C mit C 1 zusammen. Das bedeutet, dass das Dreieck A 1 B 1 C 1 mit dem Dreieck ABC zusammenfällt und es daher auch ist gleich dem Dreieck ABC.

Der Satz ist bewiesen.

2) entlang der Seite und angrenzender Ecken

Nachweisen:

Es seien ABC und A 1 B 1 C 1 zwei Dreiecke, in denen AB gleich A 1 B 1, Winkel A gleich Winkel A 1 und Winkel B gleich Winkel B 1 ist. Beweisen wir, dass sie gleich sind.

Lassen Sie uns das Dreieck ABC auferlegen (oder symmetrisch dazu) auf das Dreieck A 1 B 1 C 1, so dass AB mit A 1 B 1 zusammenfällt. Da ∠BAC =∠B 1 A 1 C 1 und ∠ABC=∠A 1 B 1 C 1, dann fällt Strahl AC mit A 1 C zusammen 1, und BC wird mit B 1 C 1 zusammenfallen. Daraus folgt, dass der Scheitelpunkt C mit C 1 zusammenfällt. Dies bedeutet, dass das Dreieck A 1 B 1 C 1 mit dem Dreieck ABC zusammenfällt und daher gleich dem Dreieck ABC ist.

Der Satz ist bewiesen.

3) auf drei Seiten

Nachweisen :

Betrachten Sie die Dreiecke ABC und A l B l C 1, in denen AB = A 1 B 1, BC = B l C 1 CA = C 1 A 1. Lassen Sie uns beweisen, dass ΔАВС =ΔA 1 B 1 C 1.

Wenden wir das Dreieck ABC an (oder symmetrisch dazu) zum Dreieck A 1 B 1 C 1, sodass Scheitelpunkt A mit Scheitelpunkt A 1 ausgerichtet ist, Scheitelpunkt B mit Scheitelpunkt B 1 ausgerichtet ist und die Scheitelpunkte C und C 1 auf gegenüberliegenden Seiten der Geraden A 1 B 1 liegen. Betrachten wir drei Fälle:

1) Strahl C 1 C verläuft innerhalb des Winkels A 1 C 1 B 1. Da nach den Bedingungen des Satzes die Seiten AC und A 1 C 1, BC und B 1 C 1 gleich sind, sind die Dreiecke A 1 C 1 C und B 1 C 1 C gleichschenklig. Nach dem Satz über die Eigenschaft der Winkel eines gleichschenkligen Dreiecks ist ∠1 = ∠2, ∠3 = ∠4, also ∠ACB=∠A 1 C 1 B 1 .

2) Strahl C 1 C fällt mit einer der Seiten dieses Winkels zusammen. A liegt auf CC 1. AC=A 1 C 1, BC=B 1 C 1, C 1 BC - gleichschenklig, ∠ACB=∠A 1 C 1 B 1.

3) Strahl C 1 C verläuft außerhalb des Winkels A 1 C 1 B 1. AC=A 1 C 1, BC=B 1 C 1, was bedeutet ∠1 = ∠2, ∠1+∠3 = ∠2+∠4, ∠ACB=∠A 1 C 1 B 1.

Also, AC=A 1 C 1, BC=B 1 C 1, ∠C=∠C 1. Daher sind die Dreiecke ABC und A 1 B 1 C 1 gleich
das erste Kriterium für die Gleichheit von Dreiecken.

Der Satz ist bewiesen.

2. Teilen eines Segments in n gleiche Teile.

Zeichnen Sie einen Strahl durch A und legen Sie n gleiche Segmente darauf an. Zeichnen Sie eine Gerade durch B und A n und parallele Linien dazu durch die Punkte A 1 - A n -1. Markieren wir ihre Schnittpunkte mit AB. Wir erhalten n Segmente, die nach dem Satz von Thales gleich sind.

Satz von Thales. Legt man auf einer von zwei Geraden nacheinander mehrere gleiche Segmente an und zieht durch deren Enden parallele Linien, die die zweite Gerade schneiden, so schneidet man auf der zweiten Geraden gleiche Segmente ab.

Nachweisen. AB=CD

1. Zeichnen Sie gerade Linien durch die Punkte A und C parallel zur anderen Seite des Winkels. Wir erhalten zwei Parallelogramme AB 2 B 1 A 1 und CD 2 D 1 C 1. Nach der Eigenschaft eines Parallelogramms: AB 2 = A 1 B 1 und CD 2 = C 1 D 1.

2. ΔABB 2 =ΔCDD 2 ABB 2 CDD 2 BAB 2 DCD 2 und sind gleich, basierend auf dem zweiten Kriterium für die Gleichheit von Dreiecken:
AB = CD nach dem Satz,
als entsprechende, am Schnittpunkt der Parallelen BB 1 und DD 1 gerade Linie BD gebildete.

3. Ebenso stellt sich heraus, dass jeder der Winkel gleich dem Winkel mit dem Scheitelpunkt am Schnittpunkt der Sekanten ist. AB 2 = CD 2 als entsprechende Elemente in kongruenten Dreiecken.

4. A 1 B 1 = AB 2 = CD 2 = C 1 D 1

Podgorny Maxim

Forschungspapiermaterial kann für Geometrieclubs in der 7. Klasse verwendet werden

Herunterladen:

Vorschau:

MBU DO der Stadt Rostow am Don „Palast der Kreativität von Kindern und Jugendlichen“

Don-Akademie der Wissenschaften für junge Forscher, benannt nach. Yu. A. Zhdanova

Mathematik

Thema: „Nichtstandardisierte Sätze zur Gleichheit von Dreiecken“

Podgorny Maxim, 7. Klasse,

MBOU-Sekundarschule Nr. 3,

Aufsicht:

Oleynikova Ljudmila Alexandrowna,

Mathematiklehrer,

MBOU-Sekundarschule Nr. 3,

Salsk, Region Rostow

Rostow am Don

2017

Einleitung……………………………………………………….………………3

Hauptteil

Zeichen der Gleichheit von Dreiecken…………………………………………… 4

Nicht standardmäßige Gleichheitszeichen von Dreiecken………………………….7

Fazit…………………………………………………………………………… 10

Referenzen…………………………………………………………… 11

Anwendung

Einführung.

Relevanz:

Das Dreieck ist eine der Hauptfiguren der Planimetrie. Ich habe oft von Gymnasiasten gehört, dass sie bei der Vorbereitung auf das Einheitliche Staatsexamen oft die Gleichheit von Dreiecken nachweisen müssen. Und die Kenntnis der Grundzeichen erweist sich als unzureichend. Ich wollte wissen, ob es möglich ist, die Gleichheit von Dreiecken mit anderen Parametern zu beweisen. Im Geometrielehrbuch, aus dem die Schüler unserer Schule lernen (Autoren L.S. Atanasyan, V.F. Butuzov usw. Geometrie 7-9), werden nur 3 Gleichheitszeichen von Dreiecken berücksichtigt. Ich habe mir die Lehrmaterialien anderer Autoren angesehen. Aber selbst in ihnen werden nur drei bekannte Theoreme zum Studium vorgeschlagen.

Hypothese:

Lassen sich neben den drei bekannten noch weitere Kriterien für die Gleichheit von Dreiecken formulieren?

Um sicherzustellen, dass die Antwort auf diese Frage nicht nur mich betrifft, habe ich eine soziologische Umfrage unter Schülern der Klassen 7-11 durchgeführt (siehe Anhang 1).

Meine Annahmen wurden bestätigt. Die meisten Schüler kennen nur drei Zeichen dafür, dass Dreiecke gleich sind.

Ziel meiner Forschung war es daher, neue Anzeichen für die Gleichheit von Dreiecken zu finden.

Aufgaben:

ΘStudieren Sie die Literatur zum untersuchten Thema.

ΘGeben Sie die Anzahl der Zeichen an, die dafür sorgen, dass Dreiecke gleich sind.

ΘDemonstrieren Sie Ihren Klassenkameraden und Schülern unserer Schule die Existenz anderer Gleichheitszeichen von Dreiecken und die Möglichkeit, diese zu beweisen.

Studienobjekt:

Studieren der Gleichheitszeichen von Dreiecken.

Gegenstand der Studie. Das Dreieck ist eine der Hauptfiguren der Planimetrie.

Untersuchungsmethode:Theoretisch (Studie, Analyse und Synthese), Systemsuche, praktisch (Beweis von Theoremen).

Historische Referenz

Das Dreieck ist eine der zentralen Figuren aller Geometrie.

Bei der Lösung von Problemen werden seine vielfältigen Eigenschaften genutzt.

Die Eigenschaften eines Dreiecks werden in der Praxis häufig genutzt: in der Architektur; bei der Erstellung einer Bauzeichnung, bei der Planung zukünftiger Wohnungen; in der Industrie, bei der Konstruktion verschiedener Teile, bei der Herstellung von Baumaterialien, beim Bau von Schiffen und Flugzeugen; in der Navigation, um die richtige und genaueste Route zu planen; In der Astrologie und Astronomie ist das Dreieck eine sehr bedeutende Figur; Dreiecke machen die Strukturen von Hochspannungsleitungen und Eisenbahnbrücken zuverlässig.

Darüber hinaus gibt es viele andere Bereiche, in denen verschiedene Eigenschaften eines Dreiecks genutzt werden: Zu Beginn einer Billardpartie müssen Sie die Kugeln in Form eines Dreiecks anordnen, hierfür verwenden sie ein spezielles Gerät; Die Platzierung der Kegel beim Bowling erfolgt ebenfalls in Form eines gleichseitigen Dreiecks. Dreiecke werden verwendet, um schöne Parkettböden zu schaffen; Gerät des Pascalschen Dreiecks: Jede Zahl ist gleich der Summe der beiden darüber liegenden Zahlen (kreisen Sie die drei Zahlen mit einem Dreieck ein). Alles ist elementar, aber wie viele Wunder sind darin verborgen! Der Computer übersetzte Pascals Dreieck in die Sprache der Farbe.

Das Thema des Dreiecks lässt sich endlos fortführen.

Es gibt so viele Dreiecke auf der Welt!

Es gibt auch übertragene Bedeutungen dieser Zahl: Beispielsweise basiert die Regel des „goldenen Dreiecks“ auf der Psychologie des Käufers – nachdem der Käufer das Produkt gefunden hat, das er benötigt, eilt er zur Kasse. Die Aufgabe des Verkäufers besteht darin, ihn durch die Platzierung der vom Käufer benötigten Waren an den Eckpunkten eines imaginären Dreiecks länger im Laden zu halten, also den Käufer zu „verankern“. Je größer die Fläche des Dreiecks ist, desto gelungener kann das Ladenlayout bezeichnet werden. In einem Lebensmittelgeschäft sind diese Ankerprodukte Gastronomie, Milchprodukte und Brot. Die hintere Stirnwand der Verkaufsfläche ist der zweitwichtigste Ort und dort empfiehlt es sich am besten, Ankerprodukte zu platzieren – gerade um den Käufer zu zwingen, den gesamten Ladenumfang zu durchqueren.

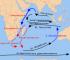
Das bekannte Bermuda-Dreieck ist ein Gebiet im Atlantischen Ozean, in dem angeblich auf mysteriöse Weise Schiffe und Flugzeuge verschwinden. Das Gebiet wird durch Linien von Florida nach Bermuda, weiter nach Puerto Rico und zurück nach Florida über die Bahamas begrenzt.

Daher ist die Untersuchung eines Dreiecks und all seiner Eigenschaften ein sehr relevantes Thema.

Der Zweck dieser Arbeit besteht darin, über die Gleichheitszeichen von Dreiecken zu sprechen, was eine ihrer wichtigsten Eigenschaften ist.

Tests für die Gleichheit von Dreiecken sind Theoreme, anhand derer bewiesen werden kann, dass einigeDreiecke sind gleich.

In der Geometrie werden drei Gleichheitszeichen von Dreiecken verwendet.

Dieses Thema ist praktisch erforscht, da es heute drei Kriterien für die Gleichheit von Dreiecken gibt, die sich mit den entsprechenden Theoremen beweisen lassen.

In der Antike erschien neben der Astronomie auch die Wissenschaft der Trigonometrie. Das Wort „Trigonometrie“ leitet sich vom griechischen „Dreieck“ und „Maß“ ab. Die wörtliche Bedeutung ist „die Wissenschaft vom Messen von Dreiecken“.

Mit gespannten Seilen von 3, 4 und 5 Einheiten Länge erreichten ägyptische Priester beim Bau von Tempeln usw. rechte Winkel.

Die Kunst, Objekte auf einer Ebene darzustellen, hat seit der Antike die Aufmerksamkeit der Menschen auf sich gezogen; Menschen haben verschiedene Ornamente, Pflanzen und Tiere auf Steine, Wände, Gefäße und andere Haushaltsgegenstände gemalt. Man wollte sicherstellen, dass das Bild die natürliche Form des Objekts korrekt widerspiegelt.

Die auf der Beziehungs- und Proportionstheorie basierende Lehre von der Ähnlichkeit von Figuren entstand im antiken Griechenland im 5.-4. Jahrhundert v. Chr. und existiert und entwickelt sich auch heute noch. So gibt es zum Beispiel viele Kinderspielzeuge, die denen der Erwachsenenwelt ähneln, Schuhe und Kleidung des gleichen Stils sind in verschiedenen Größen erhältlich. Diese Beispiele lassen sich weiter fortsetzen. Letztendlich sind alle Menschen einander ähnlich und Gott hat sie, wie die Bibel sagt, nach seinem eigenen Bild und Gleichnis geschaffen.

Tests auf Gleichheit von Dreiecken haben in der Geometrie seit langem eine große Bedeutung, da sich der Beweis zahlreicher Theoreme auf den Nachweis der Gleichheit bestimmter Dreiecke reduzierte. Bereits die Pythagoräer waren damit beschäftigt, die Zeichen der Gleichheit von Dreiecken zu beweisen. Laut Proklos schreibt Eudemus von Rhodos Thales von Milet einen Beweis für die Gleichheit zweier Dreiecke mit gleichen Seiten und zwei angrenzenden Winkeln zu (das zweite Zeichen der Gleichheit von Dreiecken).

Thales nutzte diesen Satz, um die Entfernung vom Ufer zu Seeschiffen zu bestimmen.Es ist nicht genau bekannt, mit welcher Methode Thales dies tat.

Zeichen der Gleichheit von Dreiecken.

Beginnen wir mit einer Definition. Die Dreiecke ABC und A1B1C1 heißen gleich, wenn sie durch Überlappung kombiniert werden können.

Ein Dreieck besteht aus sechs Elementen: drei Winkeln und drei Seiten.

Dies wirft die Frage auf: „Wie viele Dreieckselemente muss man am wenigsten nehmen, um die Gleichheit zweier Dreiecke festzustellen?“

Wir werden nicht in der Lage sein, die Gleichheit zweier Dreiecke anhand eines Elements festzustellen, da unbekannt ist: „Werden die übrigen Elemente gleich sein?“

Es ist auch unmöglich, die Gleichheit zweier Dreiecke anhand zweier Elemente festzustellen, da Informationen zur Feststellung der Gleichheit fehlen.

Es ist möglich, die Gleichheit zweier Dreiecke anhand von drei Elementen festzustellen. Dies wirft jedoch die Frage auf: „Welche genauen drei Elemente müssen benannt werden, um die Gleichheit der Dreiecke festzustellen?“

Beim Studium dieser Ausgabe habe ich Schullehrbücher zur Geometrie verschiedener Autoren sowie Wörterbücher und Nachschlagewerke durchgesehen. In Lehrbüchern für die siebte Klasse werden nur drei Kriterien für die Gleichheit von Dreiecken zum Studium vorgeschlagen.

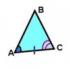
Θ1 Zeichen : Wenn zwei Seiten und der Winkel zwischen ihnen eines Dreiecks jeweils gleich zwei Seiten und der Winkel zwischen ihnen eines anderen Dreiecks sind, dann sind solche Dreiecke kongruent. Abb.1

Nachweisen. Betrachten Sie Dreiecke ABC und A 1 B 1 C 1 , (Abb. 1) für die AB = A 1 B 1, AC = A 1 C 1 ∠ A = ∠ A 1 . Beweisen wir, dass ΔABC = ΔA 1 B 1 C 1 .

Da ∠A = ∠A 1 , dann kann das Dreieck ABC dem Dreieck A überlagert werden 1 B 1 C 1 so dass Scheitelpunkt A mit Scheitelpunkt A zusammenfällt 1 und die Seiten AB und AC überlappen jeweils die Strahlen A 1 B 1 und A 1 C 1 . Da AB = A 1 B 1, AC = A 1 C 1 , dann wird Seite AB an Seite A ausgerichtet 1 in 1 und Seite AC ist mit Seite A 1 C 1 ; insbesondere fallen die Punkte B und B zusammen 1, C und C 1 . Daher fallen die Seiten BC und B zusammen 1 C 1 . Also Dreiecke ABC und A 1 B 1 C 1 sind völlig kompatibel, also gleich.

Und so wurde im alten Ägypten das erste Gleichheitszeichen der Dreiecke verwendet (auf zwei Seiten und den Winkel zwischen ihnen), Thales von Milet gilt auch als ihr Schöpfer, um die Höhe der Pyramide zu messen: Stellen Sie sich vor, wir stehen vor einer riesigen Pyramide, wie können wir ihre Höhe messen? Schließlich kann man daran keine Messgeräte befestigen! Und hier kommt Thales von Milet das erste Zeichen der Gleichheit der Dreiecke zu Hilfe: Er wartete, bis sein Schatten genau mit seiner Höhe übereinstimmte, wendete den Satz an und stellte fest, dass die Höhe der Pyramide gleich ihrem Schatten ist (Abb. 2).

Reis. 2

Θ2 Zeichen: Wenn eine Seite und zwei benachbarte Winkel eines Dreiecks jeweils gleich einer Seite und zwei benachbarten Winkeln eines anderen Dreiecks sind, dann sind solche Dreiecke kongruent.

Beweis: Wenn in △ABC und △A 1 B 1 C 1 Es treten folgende Gleichungen AB=A auf 1 B 1, ∠BAC=∠B 1 A 1 C 1, ∠АВС= ∠А 1 B 1 C 1 . Legen wir die Dreiecke A übereinander 1 B 1 C 1 und ABC, so dass gleiche Seiten AB und A zusammenfallen 1 in 1 und die angrenzenden Ecken. Wie im vorherigen Beispiel bereits besprochen, ggf. Dreieck A 1 B 1 C 1 Sie können es „umdrehen und auf die andere Seite legen“. Die Dreiecke fallen zusammen und können daher als gleich betrachtet werden.

Θ3 Zeichen : Wenn drei Seiten eines Dreiecks jeweils gleich drei Seiten eines anderen Dreiecks sind, dann sind solche Dreiecke kongruent. Beweis: Sei für △ABC und △A 1 B 1 C 1 Gleichungen A gelten 1 B 1 =AB, B 1 C 1 =BC, C 1 A 1 =SA. Verschieben wir Dreieck A 1 B 1 C 1 also die Seite A 1 in 1 fällt mit der Seite AB und dem Scheitelpunkt B zusammen 1 und B, A 1 und A werden zusammenfallen. Nehmen Sie einen Kreis mit Mittelpunkt A und Radius AC und einen zweiten Kreis mit Mittelpunkt B und Radius BC. Diese Kreise schneiden sich an zwei Punkten, die symmetrisch zum Segment AB sind: Punkt C und Punkt C 2 . Das bedeutet, dass C1 nach dem Verschieben des Dreiecks A1B1C1 entweder mit den Punkten C oder C2 zusammenfallen muss. In jedem Fall bedeutet dies die Gleichheit △ABC=△A 1 B 1 C 1 , da Dreiecke △ABC=△ABC 2 sind gleich (schließlich sind diese Dreiecke symmetrisch bezüglich der Strecke AB.

Diese Eigenschaft – die Steifigkeit eines Dreiecks – wird in der Praxis häufig genutzt. Um die Stange in vertikaler Position zu sichern, wird eine Stütze darauf angebracht; Das gleiche Prinzip wird bei der Montage der Halterung angewendet.

Die Eigenschaft der Dreieckssteifigkeit wird in der Praxis häufig beim Bau von Eisenkonstruktionen genutzt.

Aus dem dritten Kriterium für die Gleichheit von Dreiecken folgt, dass ein Dreieck eine starre Figur ist. Denn: Wir können uns zwei Lamellen vorstellen, deren beide Enden mit einem Nagel befestigt sind. Dieses Design ist nicht starr, aber durch Bewegen oder Spreizen der freien Enden der Lamellen können wir den Winkel zwischen ihnen ändern. Nehmen wir nun eine weitere Latte und befestigen deren Enden mit den freien Enden der ersten beiden Latten. Die resultierende Struktur – ein Dreieck – wird bereits starr sein. Es ist unmöglich, zwei beliebige Seiten zu verschieben oder auseinander zu bewegen, d. h. keine einzige Ecke kann verändert werden. Wenn dies möglich wäre, würden wir tatsächlich ein neues Dreieck erhalten, das nicht dem ursprünglichen entspricht. Dies ist jedoch unmöglich, da das neue Dreieck im dritten gleich dem ursprünglichen sein muss

Im Nachschlagewerk über Elementarmathematik von M. Ya. habe ich ein weiteres Zeichen gefunden.

Θ4 Zeichen: Wenn zwei Seiten und der Winkel gegenüber dem größeren eines Dreiecks jeweils gleich zwei Seiten und der Winkel gegenüber dem größeren eines anderen Dreiecks sind, dann sind solche Dreiecke kongruent.

Ich werde dieses Zeichen beweisen.

Gegeben : ΔABC , ΔA1B1C1 , AB=A1B1,AC=A1C1,∠ B= ∠ B1

Beweisen Sie: ΔABC=A1B1C1.

Ordnen wir die Dreiecke wie in Abbildung 1 an. Verbinden wir B und B1, dann ΔАВВ1

Gleichschenklig bedeutet∠ 1= ∠ 2. ∠ 3= ∠ 4 als Reste gleicher Winkel.

Wir erhalten ΔВСВ1 – gleichschenklig, also ВС=В1С1. ΔАВС = ΔА1В1С1 auf drei Seiten.

Auch im Schulkurs werden 4 Gleichheitszeichen rechtwinkliger Dreiecke besprochen:

Θ1 . Sind die Schenkel eines rechtwinkligen Dreiecks entsprechend gleich den Schenkeln eines anderen, dann sind solche Dreiecke kongruent.

Θ2 . Wenn der Schenkel und der angrenzende spitze Winkel eines rechtwinkligen Dreiecks jeweils gleich dem Schenkel und dem angrenzenden spitzen Winkel eines anderen sind, dann sind solche Dreiecke kongruent.

Θ3 . Wenn die Hypotenuse und der spitze Winkel eines rechtwinkligen Dreiecks jeweils gleich der Hypotenuse und dem spitzen Winkel eines anderen sind, dann sind solche Dreiecke kongruent.

Θ4 . Wenn die Hypotenuse und der Schenkel eines rechtwinkligen Dreiecks jeweils gleich der Hypotenuse und dem Schenkel eines anderen sind, dann sind solche Dreiecke kongruent.

Ich habe die theoretischen Grundlagen für die Kriterien für die Gleichheit von Dreiecken gelöst, indem ich weitere Komponenten zu den Seiten und Winkeln hinzugefügt habe, die in den klassischen Tests für die Gleichheit von Dreiecken verwendet werden: Winkelhalbierende, Mediane und Höhe.

Nicht standardmäßige Kriterien für die Kongruenz von Dreiecken.

1) Auf zwei Seiten und die Höhe auf einer davon.

Gegeben: AB=A1B1 , BC=B1C1 , AK=A1K1 ,

Beweisen Sie: ΔABC= ΔA1B1C1.

Beweis: ΔABK=ΔA1B1K1 durch Hypotenuse und Bein also∠ B= ∠ B1 und erhalten Sie ΔABC= ΔA1B1C1 gemäß dem ersten Vorzeichen.

2) Auf zwei Seiten und einem Mittelstreifen zu einer von ihnen

Gegeben: AB=A1B1, BC=B1C1, AK=A1K1, AK und A1K1 sind Mediane.

Beweisen Sie: ΔABC= ΔA1B1C1.

Beweis: ΔABK=ΔA1B1K1 auf drei Seiten, was bedeutet∠ B= ∠ B1 und ΔABC= ΔA1B1C1 entsprechend dem ersten Vorzeichen.

3) Entlang zweier Seiten und einer Höhe, die von der dritten Ecke aus gezeichnet wird.

Gegeben: ∠ B= ∠ B1 , ∠ C= ∠ C1 , AK=A1K1 .

Beweisen Sie: ΔABC= ΔA1B1C1.

Beweis: ΔABK=ΔA1B1K1 entlang des Schenkels und des spitzen Winkels, was BK=B1K1 bedeutet,

ΔACK=ΔA1C1K1 nach Schenkel und spitzem Winkel, was KC=K1C1 und daher BC=B1C1 und ΔABC= ΔA1B1C1 nach dem zweiten Vorzeichen bedeutet.

4) Entlang einer Seite und zwei Höhen, die aus den an diese Seite angrenzenden Winkeln gezogen werden.

Gegeben: AC=A1C1, SM=C1M1, AK=A1K1.

Beweisen Sie: ΔСC= ΔA1B1C1.

Beweis: ΔAMC= ΔA1М1C1 entlang des Beins und der Hypotenuse, was bedeutet∠ EIN= ∠ A1 und ΔAКC= ΔA1К1C1 entlang des Beins und der Hypotenuse, was bedeutet∠ C= ∠ C1.

Also ΔABC= ΔA1B1C1 gemäß dem zweiten Kriterium.

5) Auf zwei Seiten und die Höhe auf der dritten Seite gezeichnet.

Gegeben: AB=A1B1,BC=B1C1,BK=B1K1.

Beweisen Sie: ΔABC= ΔA1B1C1.

Nachweisen: ΔABK=ΔA1B1K1 auf der Hypotenuse und dem Bein, was AK=A1K1 bedeutet,

ΔBКC= ΔB1К1C1 entlang des Beins und der Hypotenuse, was KC=K1C1 bedeutet.

Also ist ΔABC= ΔA1B1C1 auf drei Seiten.

6) Entlang der Seite, einer der an diese Seite angrenzenden Winkel und die Winkelhalbierende dieses Winkels.

Gegeben: AC=A1C1, AK=A1K1,∠ A ∠ A1.

Beweisen Sie: ΔABC= ΔA1B1C1.

Beweis: ΔКАС=ΔК1А1С1 nach dem ersten Vorzeichen, das heißt∠ C= ∠ C1,

ΔABC= ΔA1B1C1 gemäß der zweiten Charakteristik.

7) Durch zwei Höhen und den Winkel, aus dem eine der Höhen gezeichnet wird.

Gegeben: SM=S1M1, AK=A1K1, ∠ A ∠ A1.

Beweisen Sie: ΔABC= ΔA1B1C1.

Beweis: ΔAMC= ΔA1М1C1 am Bein und spitzen Winkel, ΔКАС=ΔК1А1С1 am Bein und Hypotenuse, ΔABC= ΔA1B1C1 am zweiten Vorzeichen.

Abschluss.

Bei der Recherche habe ich herausgefunden, dass neben den drei Hauptzeichen der Gleichheit von Dreiecken noch viele andere angegeben werden können. Ich habe die Gleichheit von Dreiecken formuliert und bewiesen, basierend auf dem Median, der Höhe und der Winkelhalbierenden des Dreiecks in Kombination mit den Seiten und Winkeln des Dreiecks, wobei ich mich an das Vorhandensein von drei Elementen hielt. Jetzt kann ich den Schülern unserer Schule sagen, dass es andere Anzeichen dafür gibt, dass Dreiecke gleich sind. Dies wird es Schulabsolventen ermöglichen, die Ergebnisse meiner Forschung zur Vorbereitung auf das Einheitliche Staatsexamen und das Einheitliche Staatsexamen anzuwenden und geometrische Probleme mithilfe dieser Funktionen einfach zu lösen.

Das Ergebnis meiner Recherche: Mehrere Kriterien für die Gleichheit von Dreiecken, die im Schulgeometriekurs nicht untersucht werden, sind nachgewiesen.

Referenzliste

1. Vygodsky M.Ya. Handbuch der Elementarmathematik.
2. Geometrie. Klassen 7-9: Lehrbuch. Für die Allgemeinbildung Institutionen/L.S.Atanasyan, V.F.Butuzov, S.B. Kadomtsev et al. – 19. Auflage. – M.: Bildung, 2009.
3. Pogorelov A.V. Geometrie: Lehrbuch. Für die Klassen 7-9. Allgemeinbildung Institutionen. – 3. Auflage. – M.: Bildung, 2002.
4. . Enzyklopädie „Avanta“ in Mathematik, Moskau, 2004.
5. 2. Wikipedia ist eine freie Enzyklopädie.
6. 3. Glazer G.I. „Geschichte der Mathematik in der Schule“, Moskau, Prosveshchenie, 1982.
7. 4. Guseva T.M. Ähnlichkeitszeichen von Dreiecken. - Moskau, 1. September, Beilage „Mathematik“, 1999, Nr. 28
8. 5. Pogorelov A.V. „Geometrie Klassen 7-9“Moskau, Bildung, 2003

Anhang 1

1. Wie viele Zeichen glauben Sie, dass Dreiecke gleich sind?

A) 3 B) mehr als drei C) weniger als drei

2. Möchten Sie neue Zeichen für die Kongruenz von Dreiecken lernen?

A) ja B) nein

Zwei Dreiecke heißen kongruent, wenn sie durch Überlappung zusammengebracht werden können. Abbildung 1 zeigt gleiche Dreiecke ABC und A 1 B 1 C 1. Jedes dieser Dreiecke kann übereinander gelegt werden, so dass sie vollständig kompatibel sind, d. h. ihre Eckpunkte und Seiten passen paarweise zusammen. Es ist klar, dass die Winkel dieser Dreiecke auch paarweise übereinstimmen werden.

Wenn also zwei Dreiecke kongruent sind, dann sind die Elemente (d. h. Seiten und Winkel) eines Dreiecks jeweils gleich den Elementen des anderen Dreiecks. Beachten Sie, dass in gleichen Dreiecken gegen entsprechend gleiche Seiten(d. h. Überlappung bei Überlagerung) gleiche Winkel liegen und zurück: Gleiche Seiten liegen sich gegenüber bzw. gleiche Winkel.

So liegen beispielsweise in den in Abbildung 1 gezeigten gleichen Dreiecken ABC und A 1 B 1 C 1 gegenüberliegende gleiche Seiten AB und A 1 B 1 jeweils gleiche Winkel C und C 1. Wir bezeichnen die Gleichheit der Dreiecke ABC und A 1 B 1 C 1 wie folgt: Δ ABC = Δ A 1 B 1 C 1. Es stellt sich heraus, dass die Gleichheit zweier Dreiecke durch den Vergleich einiger ihrer Elemente festgestellt werden kann.

Satz 1. Das erste Zeichen der Gleichheit der Dreiecke. Wenn zwei Seiten und der Winkel zwischen ihnen eines Dreiecks jeweils gleich zwei Seiten und der Winkel zwischen ihnen eines anderen Dreiecks sind, dann sind solche Dreiecke kongruent (Abb. 2).

Nachweisen. Betrachten Sie die Dreiecke ABC und A 1 B 1 C 1, in denen AB = A 1 B 1, AC = A 1 C 1 ∠ A = ∠ A 1 (siehe Abb. 2). Beweisen wir, dass Δ ABC = Δ A 1 B 1 C 1 .

Da ∠ A = ∠ A 1, kann das Dreieck ABC dem Dreieck A 1 B 1 C 1 so überlagert werden, dass der Scheitelpunkt A mit dem Scheitelpunkt A 1 ausgerichtet ist und die Seiten AB und AC jeweils den Strahlen A 1 B 1 und A 1 überlagert werden C 1 . Da AB = A 1 B 1, AC = A 1 C 1, dann wird Seite AB mit Seite A 1 B 1 und Seite AC mit Seite A 1 C 1 ausgerichtet; insbesondere fallen die Punkte B und B 1, C und C 1 zusammen. Folglich fallen die Seiten BC und B 1 C 1 zusammen. Die Dreiecke ABC und A 1 B 1 C 1 sind also vollständig kompatibel, das heißt, sie sind gleich.

Satz 2 wird auf ähnliche Weise mit der Superpositionsmethode bewiesen.

Satz 2. Das zweite Zeichen der Gleichheit der Dreiecke. Wenn eine Seite und zwei benachbarte Winkel eines Dreiecks jeweils gleich der Seite und zwei benachbarte Winkel eines anderen Dreiecks sind, dann sind solche Dreiecke kongruent (Abb. 34).

Kommentar. Basierend auf Satz 2 wird Satz 3 aufgestellt.

Satz 3. Die Summe zweier beliebiger Innenwinkel eines Dreiecks beträgt weniger als 180°.

Satz 4 folgt aus dem letzten Satz.

Satz 4. Ein Außenwinkel eines Dreiecks ist größer als jeder Innenwinkel, der nicht daran angrenzt.

Satz 5. Das dritte Zeichen der Gleichheit der Dreiecke. Wenn drei Seiten eines Dreiecks jeweils gleich drei Seiten eines anderen Dreiecks sind, dann sind solche Dreiecke kongruent ().

Beispiel 1. In den Dreiecken ABC und DEF (Abb. 4)

∠ A = ∠ E, AB = 20 cm, AC = 18 cm, DE = 18 cm, EF = 20 cm. Vergleichen Sie die Dreiecke ABC und DEF. Welcher Winkel im Dreieck DEF ist gleich Winkel B?

Lösung. Diese Dreiecke sind nach dem ersten Vorzeichen gleich. Der Winkel F des Dreiecks DEF ist gleich dem Winkel B des Dreiecks ABC, da diese Winkel jeweils gegenüber den gleichen Seiten DE und AC liegen.

Beispiel 2. Die Segmente AB und CD (Abb. 5) schneiden sich im Punkt O, der jeweils in der Mitte liegt. Wie lang ist das Segment BD, wenn das Segment AC 6 m beträgt?

Lösung. Die Dreiecke AOC und BSB sind gleich (gemäß dem ersten Kriterium): ∠ AOC = ∠ BSB (vertikal), AO = OB, CO = OD (nach Bedingung).
Aus der Gleichheit dieser Dreiecke folgt, dass ihre Seiten gleich sind, d.h. AC = BD. Da aber gemäß der Bedingung AC = 6 m ist, dann ist BD = 6 m.