Trigonometrische Ungleichungen. Trigonometrische Ungleichungen und ihre Lösungen Lösung doppelter trigonometrischer Ungleichungen

Bildungsministerium der Republik Belarus

Bildungseinrichtung

„Staatliche Universität Gomel

benannt nach Francysk Skaryna"

Fakultät für Mathematik

Abteilung für Algebra und Geometrie

Zur Verteidigung geeignet

Kopf Abteilung Shemetkov L.A.

Trigonometrische Gleichungen und Ungleichungen

Kursarbeit

Testamentsvollstrecker:

Studentengruppe M-51

CM. Gorski

Wissenschaftlicher Berater

Alter Dozent

V.G. Safonow

Homel 2008

EINLEITUNG

GRUNDLEGENDE METHODEN ZUM LÖSEN VON TRIGONOMETRISCHEN GLEICHUNGEN

Faktorisierung

Lösen von Gleichungen durch Umwandeln des Produkts trigonometrischer Funktionen in eine Summe

Lösen von Gleichungen mit Formeln mit drei Argumenten

Multiplikation mit einer trigonometrischen Funktion

NICHT STANDARD-TRIGONOMETRISCHE GLEICHUNGEN

TRIGONOMETRISCHE UNGLEICHHEITEN

AUSWAHL DER WURZELN

AUFGABEN ZUR SELBSTSTÄNDIGEN LÖSUNG

FAZIT

LISTE DER VERWENDETEN QUELLEN

In der Antike entstand die Trigonometrie im Zusammenhang mit den Bedürfnissen der Astronomie, Vermessung und Konstruktion, das heißt, sie war rein geometrischer Natur und wurde hauptsächlich dargestellt<<исчисление хорд>>. Im Laufe der Zeit begannen sich einige analytische Punkte darin einzumischen. In der ersten Hälfte des 18. Jahrhunderts gab es eine scharfe Wende, nach der die Trigonometrie eine neue Richtung einschlug und sich in Richtung mathematischer Analyse verlagerte. Zu dieser Zeit begann man, trigonometrische Abhängigkeiten als Funktionen zu betrachten.

Trigonometrische Gleichungen sind eines der schwierigsten Themen im Schulmathematikunterricht. Trigonometrische Gleichungen entstehen beim Lösen von Problemen in Planimetrie, Festkörpergeometrie, Astronomie, Physik und anderen Bereichen. Trigonometrische Gleichungen und Ungleichungen gehören von Jahr zu Jahr zu den Aufgaben des zentralen Testens.

Der wichtigste Unterschied zwischen trigonometrischen und algebraischen Gleichungen besteht darin, dass algebraische Gleichungen eine endliche Anzahl von Wurzeln haben, während trigonometrische Gleichungen eine unendliche Anzahl haben, was die Auswahl von Wurzeln stark erschwert. Eine weitere Besonderheit trigonometrischer Gleichungen ist die nicht eindeutige Schreibweise der Antwort.

Diese Diplomarbeit widmet sich Methoden zur Lösung trigonometrischer Gleichungen und Ungleichungen.

Die Diplomarbeit besteht aus 6 Abschnitten.

Der erste Abschnitt enthält die grundlegenden theoretischen Informationen: die Definition und Eigenschaften von trigonometrischen und inversen trigonometrischen Funktionen; Wertetabelle trigonometrischer Funktionen für einige Argumente; Ausdruck trigonometrischer Funktionen in Form anderer trigonometrischer Funktionen, was sehr wichtig ist, um trigonometrische Ausdrücke umzuwandeln, insbesondere solche, die inverse trigonometrische Funktionen enthalten; zusätzlich zu den aus dem Schulunterricht bekannten trigonometrischen Grundformeln werden Formeln angegeben, die Ausdrücke mit inversen trigonometrischen Funktionen vereinfachen.

Der zweite Abschnitt umreißt die wichtigsten Methoden zum Lösen trigonometrischer Gleichungen. Es werden die Lösung elementarer trigonometrischer Gleichungen, die Methode des Faktorisierens und Methoden zum Reduzieren trigonometrischer Gleichungen auf algebraische Gleichungen betrachtet. Angesichts der Tatsache, dass die Lösungen trigonometrischer Gleichungen auf verschiedene Arten geschrieben werden können und die Form dieser Lösungen es einem nicht erlaubt, sofort festzustellen, ob diese Lösungen gleich oder unterschiedlich sind, was möglich ist<<сбить с толку>> Beim Lösen von Tests wird ein allgemeines Schema zum Lösen trigonometrischer Gleichungen betrachtet und die Transformation von Gruppen allgemeiner Lösungen trigonometrischer Gleichungen im Detail betrachtet.

Der dritte Abschnitt befasst sich mit nicht standardmäßigen trigonometrischen Gleichungen, deren Lösungen auf dem funktionalen Ansatz basieren.

Der vierte Abschnitt beschäftigt sich mit trigonometrischen Ungleichungen. Methoden zur Lösung elementarer trigonometrischer Ungleichungen werden detailliert betrachtet, sowohl auf einem Einheitskreis als auch mit einer grafischen Methode. Beschrieben wird das Lösen von nicht-elementaren trigonometrischen Ungleichungen durch elementare Ungleichungen und die den Schulkindern bereits bekannte Methode der Intervalle.

Der fünfte Abschnitt präsentiert die schwierigsten Aufgaben: wenn es notwendig ist, nicht nur eine trigonometrische Gleichung zu lösen, sondern auch Wurzeln aus den gefundenen Wurzeln auszuwählen, die eine Bedingung erfüllen. In diesem Abschnitt finden Sie Lösungen zu typischen Aufgaben bei der Auswahl von Wurzeln. Die notwendigen theoretischen Informationen für die Wahl der Wurzeln werden gegeben: die Zerlegung der Menge der ganzen Zahlen in sich nicht schneidende Teilmengen, die Lösung von Gleichungen in ganzen Zahlen (diophantisch).

Der sechste Abschnitt stellt Aufgaben zur eigenständigen Lösung dar, die in Form eines Tests gestaltet sind. Die 20 Testaufgaben listen die schwierigsten Aufgaben auf, die beim zentralisierten Testen auftreten können.

Elementare trigonometrische Gleichungen

Elementare trigonometrische Gleichungen sind Gleichungen der Form , wobei eine der trigonometrischen Funktionen ist: , , , .

Elementare trigonometrische Gleichungen haben unendlich viele Wurzeln. Beispielsweise erfüllen die folgenden Werte die Gleichung: , , , usw. Die allgemeine Formel, mit der alle Wurzeln der Gleichung gefunden werden, wobei , ist:

Dabei kann es sich um beliebige ganzzahlige Werte handeln, von denen jeder einer bestimmten Wurzel der Gleichung entspricht; in dieser Formel (wie auch in anderen Formeln, mit denen elementare trigonometrische Gleichungen gelöst werden) heißt Parameter. Sie schreiben normalerweise auf und betonen damit, dass der Parameter beliebige ganzzahlige Werte annehmen kann.

Lösungen der Gleichung , wobei , werden durch die Formel gefunden

Die Gleichung wird durch Anwendung der Formel gelöst

und die Gleichung --- gemäß der Formel

Beachten wir besonders einige Spezialfälle elementarer trigonometrischer Gleichungen, bei denen die Lösung ohne Verwendung allgemeiner Formeln geschrieben werden kann:

Beim Lösen trigonometrischer Gleichungen spielt die Periode trigonometrischer Funktionen eine wichtige Rolle. Daher präsentieren wir zwei nützliche Theoreme:

Satz Wenn --- die Hauptperiode der Funktion ist, dann ist die Zahl die Hauptperiode der Funktion.

Die Perioden der Funktionen und heißen kommensurabel, falls es natürliche Zahlen gibt und , dass .

Satz Wenn periodische Funktionen und , ein entsprechendes und haben, dann haben sie eine gemeinsame Periode, nämlich die Periode der Funktionen , , .

Der Satz sagt aus, was die Periode der Funktion ist , , , und ist nicht unbedingt die Hauptperiode. Zum Beispiel ist die Hauptperiode der Funktionen und --- , und die Hauptperiode ihres Produkts ist --- .

Einführung eines Hilfsarguments

Die Standardmethode zum Konvertieren von Ausdrücken des Formulars ist der folgende Trick: Lassen Sie --- den durch die Gleichheiten gegebenen Winkel , . Für jeden gibt es einen solchen Winkel. Auf diese Weise . Wenn , oder , , , sonst .

Schema zum Lösen trigonometrischer Gleichungen

Das Hauptschema, von dem wir uns beim Lösen trigonometrischer Gleichungen leiten lassen, lautet wie folgt:

die Lösung der gegebenen Gleichung wird auf die Lösung elementarer Gleichungen reduziert. Lösungen --- Transformationen, Faktorisierungen, Ersetzen von Unbekannten. Der Leitgedanke ist, die Wurzeln nicht zu verlieren. Das bedeutet, dass wir beim Übergang zur nächsten Gleichung (Gleichungen) keine Angst vor dem Auftreten zusätzlicher (fremder) Wurzeln haben, sondern uns nur darum kümmern, dass jede nachfolgende Gleichung unserer "Kette" (oder eines Satzes von Gleichungen im Fall von Verzweigung) ist eine Folge der vorherigen. Eine mögliche Methode zur Auswahl von Wurzeln ist das Überprüfen. Wir stellen gleich fest, dass bei trigonometrischen Gleichungen die mit der Wahl der Wurzeln verbundenen Schwierigkeiten bei der Überprüfung im Vergleich zu algebraischen Gleichungen in der Regel stark zunehmen. Schließlich muss man die aus unendlich vielen Mitgliedern bestehende Serie prüfen.

Besonders hervorzuheben ist die Änderung von Unbekannten beim Lösen trigonometrischer Gleichungen. In den meisten Fällen erhält man nach der notwendigen Ersetzung eine algebraische Gleichung. Darüber hinaus sind Gleichungen nicht so selten, die zwar trigonometrisch erscheinen, aber im Wesentlichen nicht trigonometrisch sind, da bereits nach dem ersten Schritt - Änderungen von Variablen - algebraische werden und die Rückkehr zur Trigonometrie erst dann erfolgt Phase der Lösung elementarer trigonometrischer Gleichungen.

Erinnern Sie sich noch einmal: Das Ersetzen des Unbekannten sollte so schnell wie möglich erfolgen, die resultierende Gleichung nach dem Ersetzen muss bis zum Ende gelöst werden, einschließlich der Stufe der Wurzelauswahl, und erst dann kehrt sie zum ursprünglichen Unbekannten zurück.

Eines der Merkmale trigonometrischer Gleichungen ist, dass die Antwort in vielen Fällen auf verschiedene Weise geschrieben werden kann. Sogar um die Gleichung zu lösen Die Antwort kann wie folgt geschrieben werden:

1) in Form von zwei Serien: , , ;

2) in Standardform, die eine Vereinigung der obigen Reihen ist: , ;

3) weil , dann kann die Antwort geschrieben werden als , . (Außerdem bedeutet das Vorhandensein des Parameters , , oder im Antwortdatensatz automatisch, dass dieser Parameter alle möglichen ganzzahligen Werte annimmt. Ausnahmen werden festgelegt.)

Offensichtlich schöpfen die drei aufgeführten Fälle nicht alle Möglichkeiten aus, um die Antwort auf die betrachtete Gleichung zu schreiben (es gibt unendlich viele davon).

Zum Beispiel für . Daher können wir in den ersten beiden Fällen if durch ersetzen .

Normalerweise wird die Antwort auf der Grundlage von Absatz 2 geschrieben. Es ist nützlich, sich an die folgende Empfehlung zu erinnern: Wenn die Arbeit nicht mit der Lösung der Gleichung endet, ist es dennoch erforderlich, eine Studie durchzuführen, die Auswahl der Wurzeln die bequemste Form der Aufzeichnung ist in Absatz 1 angegeben. (Eine ähnliche Empfehlung sollte für die Gleichung gegeben werden.)

Betrachten wir ein Beispiel, das das Gesagte veranschaulicht.

Beispiel Löse die Gleichung.

Lösung. Der offensichtlichste ist der folgende Weg. Diese Gleichung teilt sich in zwei: und . Wenn wir jede von ihnen lösen und die erhaltenen Antworten kombinieren, finden wir .

Ein anderer Weg. Da also Ersetzen von und durch die Reduktionsformeln. Nach geringfügigen Transformationen erhalten wir , woher .

Auf den ersten Blick hat die zweite Formel keine besonderen Vorteile gegenüber der ersten. Wenn wir jedoch zum Beispiel nehmen, dann stellt sich heraus, dass , d.h. die Gleichung hat eine Lösung, während uns der erste Weg zur Antwort führt . Gleichheit „sehen“ und beweisen nicht so einfach.

Antworten. .

Transformation und Vereinigung von Gruppen allgemeiner Lösungen trigonometrischer Gleichungen

Wir betrachten eine arithmetische Folge, die sich in beide Richtungen unendlich erstreckt. Die Mitglieder dieser Progression können in zwei Gruppen von Mitgliedern unterteilt werden, die sich rechts und links von einem Mitglied befinden, das als zentrales oder null-Mitglied der Progression bezeichnet wird.

Wenn wir einen der Terme der unendlichen Progression mit einer Nullzahl fixieren, müssen wir für alle verbleibenden Terme eine doppelte Nummerierung durchführen: positiv für die Terme rechts und negativ für die Terme links von Null.

Im allgemeinen Fall, wenn die Differenz der Progression der Nullterm ist, lautet die Formel für jeden (ten) Term der unendlichen arithmetischen Progression:

Formeltransformationen für jedes Mitglied einer unendlichen arithmetischen Folge

1. Wenn wir die Differenz der Progression zum Nullterm addieren oder subtrahieren, dann ändert sich die Progression hiervon nicht, sondern es verschiebt sich nur der Nullterm, d.h. die Nummerierung der Mitglieder ändert sich.

2. Wird der Koeffizient einer Variablen mit multipliziert, so ergibt sich nur eine Permutation der rechten und linken Mitgliedergruppe.

3. Wenn aufeinanderfolgende Mitglieder einer unendlichen Progression

zum Beispiel , , , ..., , um die zentralen Terme von Progressionen mit demselben Unterschied gleich zu machen:

dann drücken die Progression und die Progressionsreihe dieselben Zahlen aus.

Beispiel Die Zeile kann durch die folgenden drei Zeilen ersetzt werden: , , .

4. Wenn unendliche Progressionen mit derselben Differenz Zahlen als Zentralglieder haben, die eine arithmetische Progression mit einer Differenz bilden, dann können diese Reihen durch eine Progression mit einer Differenz ersetzt werden, und zwar mit einem Zentralglied, das gleich einem der Zentralglieder dieser Reihen ist Progressionen, d.h. wenn

dann werden diese Progressionen zu einer kombiniert:

Beispiel , , , werden beide zu einer Gruppe zusammengefasst, da .

Um Gruppen mit gemeinsamen Lösungen in Gruppen ohne gemeinsame Lösungen umzuwandeln, werden diese Gruppen in Gruppen mit einem gemeinsamen Punkt zerlegt, und dann versuchen wir, die resultierenden Gruppen zu kombinieren, wobei wir Wiederholungen ausschließen.

Faktorisierung

Die Faktorisierungsmethode lautet wie folgt: if

dann jede Lösung der Gleichung

ist die Lösung des Gleichungssystems

Die umgekehrte Aussage ist im Allgemeinen falsch: Nicht jede Lösung der Menge ist eine Lösung der Gleichung. Dies liegt daran, dass die Lösungen einzelner Gleichungen nicht im Definitionsbereich der Funktion enthalten sein dürfen.

Beispiel Löse die Gleichung.

Lösung. Unter Verwendung der grundlegenden trigonometrischen Identität stellen wir die Gleichung in der Form dar

Antworten. ; .

Umwandlung der Summe trigonometrischer Funktionen in ein Produkt

Beispiel löse die Gleichung .

Lösung. Wenden wir die Formel an, erhalten wir eine äquivalente Gleichung

Antworten. .

Beispiel Löse die Gleichung.

Lösung. In diesem Fall sollten Sie vor der Anwendung der Formeln für die Summe trigonometrischer Funktionen die Reduktionsformel verwenden . Als Ergebnis erhalten wir eine äquivalente Gleichung

Antworten. , .

Lösen von Gleichungen durch Umwandeln des Produkts trigonometrischer Funktionen in eine Summe

Beim Lösen einer Reihe von Gleichungen werden Formeln verwendet.

Beispiel löse die Gleichung

Lösung.

Antworten. , .

Beispiel Löse die Gleichung.

Lösung. Durch Anwendung der Formel erhalten wir eine äquivalente Gleichung:

Antworten. .

Lösen von Gleichungen mit Reduktionsformeln

Beim Lösen verschiedenster trigonometrischer Gleichungen spielen Formeln eine Schlüsselrolle.

Beispiel Löse die Gleichung.

Lösung. Durch Anwendung der Formel erhalten wir eine äquivalente Gleichung.

Antworten. ; .

Lösen von Gleichungen mit Formeln mit drei Argumenten

Beispiel Löse die Gleichung.

Lösung. Wir wenden die Formel an, wir erhalten die Gleichung

Antworten. ; .

Beispiel löse die Gleichung .

Lösung. Wenden wir die Formeln zum Absenken des Grades an, erhalten wir: . Bei der Bewerbung erhalten wir:

Antworten. ; .

Gleichheit gleichnamiger trigonometrischer Funktionen

Beispiel Löse die Gleichung.

Lösung.

Antworten. , .

Beispiel löse die Gleichung .

Lösung. Lassen Sie uns die Gleichung umwandeln.

Antworten. .

Beispiel Es ist bekannt, dass und die Gleichung erfüllen

Finden Sie die Summe.

Lösung. Aus der Gleichung folgt, dass

Antworten. .

Betrachten Sie Summen der Form

Diese Summen können in ein Produkt umgewandelt werden, indem man sie multipliziert und durch dividiert, dann erhalten wir

Diese Technik kann verwendet werden, um einige trigonometrische Gleichungen zu lösen, aber es sollte bedacht werden, dass als Ergebnis fremde Wurzeln auftreten können. Hier ist eine Verallgemeinerung dieser Formeln:

Beispiel Löse die Gleichung.

Lösung. Es ist ersichtlich, dass die Menge eine Lösung der ursprünglichen Gleichung ist. Daher führt das Multiplizieren der linken und rechten Seite der Gleichung mit nicht zum Auftreten zusätzlicher Wurzeln.

Wir haben .

Antworten. ; .

Beispiel Löse die Gleichung.

Lösung. Wir multiplizieren die linke und rechte Seite der Gleichung mit und wenden die Formeln an, um das Produkt trigonometrischer Funktionen in eine Summe umzuwandeln, und erhalten

Diese Gleichung entspricht dem Satz von zwei Gleichungen und , woher und .

Da die Wurzeln der Gleichung nicht die Wurzeln der Gleichung sind, sollten die resultierenden Lösungssätze ausgeschlossen werden. Also in der Menge müssen Sie ausschließen.

Antworten. und , .

Beispiel löse die Gleichung .

Lösung. Lassen Sie uns den Ausdruck umwandeln:

Die Gleichung wird in der Form geschrieben:

Antworten. .

Reduktion trigonometrischer Gleichungen auf algebraische

Reduzieren auf quadratisch

Wenn die Gleichung aussieht

dann bringt die Ersetzung es zu einem Quadrat, weil () und.

Wenn anstelle des Begriffs steht, dann wird der erforderliche Ersatz sein.

Die gleichung

reduziert sich auf die quadratische Gleichung

Präsentation als . Es ist leicht zu überprüfen, für welche , keine Wurzeln der Gleichung sind, und durch die Änderung von , wird die Gleichung auf eine quadratische reduziert.

Beispiel Löse die Gleichung.

Lösung. Verschieben Sie es auf die linke Seite, ersetzen Sie es durch , und drücken Sie es durch und aus.

Nach Vereinfachungen erhalten wir: . Dividieren Sie Term für Term durch , führen Sie die Substitution durch :

Zurück zu , finden wir .

Gleichungen homogen bezüglich ,

Betrachten Sie eine Gleichung der Form

wobei , , , ..., , reelle Zahlen sind. In jedem Term auf der linken Seite der Gleichung sind die Grade der Monome gleich, d. h. die Summe der Grade von Sinus und Cosinus ist gleich und gleich. Eine solche Gleichung heißt homogen relativ zu und , und die Nummer wird angerufen Homogenitätsindikator .

Es ist klar, dass wenn dann die Gleichung die Form annehmen wird:

deren Lösungen die Werte sind, für die , also die Zahlen , . Die zweite Gleichung, in Klammern geschrieben, ist ebenfalls homogen, aber die Grade sind um 1 niedriger.

Wenn , dann sind diese Zahlen nicht die Wurzeln der Gleichung.

Wenn wir bekommen: , und die linke Seite von Gleichung (1) nimmt den Wert an.

Für , und können also beide Seiten der Gleichung durch geteilt werden. Als Ergebnis erhalten wir die Gleichung:

was durch Substitution leicht auf die algebraische reduziert werden kann:

Homogene Gleichungen mit Homogenitätsindex 1. Bei haben wir die Gleichung .

Wenn , dann ist diese Gleichung äquivalent zur Gleichung , , woher , .

Beispiel Löse die Gleichung.

Lösung. Diese Gleichung ist homogen ersten Grades. Wenn wir beide Teile durch dividieren, erhalten wir: , , , .

Antworten. .

Beispiel Bei erhalten wir eine homogene Gleichung der Form

Lösung.

Wenn , dann dividieren wir beide Seiten der Gleichung durch , erhalten wir die Gleichung , die durch Substitution leicht auf ein Quadrat reduziert werden kann: . Wenn ein , dann hat die Gleichung echte Wurzeln , . Die ursprüngliche Gleichung hat zwei Gruppen von Lösungen: , , .

Wenn ein , dann hat die Gleichung keine Lösungen.

Beispiel Löse die Gleichung.

Lösung. Diese Gleichung ist homogen zweiten Grades. Dividieren Sie beide Seiten der Gleichung durch , erhalten wir: . Lassen Sie dann , , . , , ; , , .

Antworten. .

Die Gleichung wird auf eine Gleichung der Form reduziert

Dazu genügt es, die Identität zu verwenden

Insbesondere reduziert sich die Gleichung auf eine homogene, wenn sie durch ersetzt wird , dann erhalten wir die äquivalente Gleichung:

Beispiel Löse die Gleichung.

Lösung. Lassen Sie uns die Gleichung in eine homogene umwandeln:

Teilen Sie beide Seiten der Gleichung durch , erhalten wir die Gleichung:

Sei , dann kommen wir zur quadratischen Gleichung: , , , , .

Antworten. .

Beispiel Löse die Gleichung.

Lösung. Lassen Sie uns beide Seiten der Gleichung quadrieren, vorausgesetzt, sie haben positive Werte: , ,

Lass , dann bekommen wir , , .

Antworten. .

Mit Identitäten gelöste Gleichungen

Es ist nützlich, die folgenden Formeln zu kennen:

Beispiel Löse die Gleichung.

Lösung. Mit bekommen wir

Antworten.

Wir bieten nicht die Formeln selbst, sondern den Weg, sie abzuleiten:

Folglich,

Ebenfalls, .

Beispiel löse die Gleichung .

Lösung. Lassen Sie uns den Ausdruck umwandeln:

Die Gleichung wird in der Form geschrieben:

Nehmen wir . , . Folglich

Antworten. .

Universelle trigonometrische Substitution

Trigonometrische Gleichung der Form

wobei --- eine rationale Funktion mit Hilfe von Formeln -- , sowie mit Hilfe von Formeln -- in Bezug auf die Argumente , , , , auf eine rationale Gleichung reduziert werden kann, wonach die Gleichung auf eine reduziert werden kann algebraische rationale Gleichung in Bezug auf die Verwendung der Formeln der universellen trigonometrischen Substitution

Es ist zu beachten, dass die Verwendung von Formeln zu einer Verengung der ODZ der ursprünglichen Gleichung führen kann, da sie an den Punkten nicht definiert ist, sodass in solchen Fällen überprüft werden muss, ob die Winkel die Wurzeln der ursprünglichen Gleichung sind .

Beispiel Löse die Gleichung.

Lösung. Je nach Aufgabe. Wenn wir die Formeln anwenden und die Substitution vornehmen, erhalten wir

woher und deshalb.

Gleichungen der Form

Gleichungen der Form , wobei ein Polynom ist, werden durch Ändern der Unbekannten gelöst

Beispiel Löse die Gleichung.

Lösung. Wenn wir die Substitution vornehmen und das berücksichtigen, erhalten wir

wo , . --- fremde Wurzel, weil . Gleichung Wurzeln sind .

Nutzung eingeschränkter Funktionen

In der Praxis des zentralisierten Testens ist es nicht ungewöhnlich, auf Gleichungen zu stoßen, deren Lösung auf der Beschränktheit der Funktionen und basiert. Zum Beispiel:

Beispiel Löse die Gleichung.

Lösung. Da , , dann überschreitet die linke Seite nicht und ist gleich , wenn

Um die Werte zu finden, die beiden Gleichungen genügen, gehen wir wie folgt vor. Wir lösen einen von ihnen und wählen dann unter den gefundenen Werten diejenigen aus, die den anderen erfüllen.

Beginnen wir mit dem zweiten: , . Dann , .

Es ist klar, dass nur für gerade Zahlen .

Antworten. .

Eine andere Idee wird durch Lösen der folgenden Gleichung realisiert:

Beispiel löse die Gleichung .

Lösung. Nutzen wir die Eigenschaft der Exponentialfunktion: , .

Wenn wir diese Ungleichungen Term für Term addieren, haben wir:

Daher ist die linke Seite dieser Gleichung genau dann gleich, wenn die beiden Gleichheiten gelten:

d.h. es kann die Werte , , , oder es kann die Werte , annehmen.

Antworten. , .

Beispiel löse die Gleichung .

Lösung., . Folglich, .

Antworten. .

Beispiel löse die Gleichung

Lösung. Bezeichnen Sie , dann aus der Definition der inversen trigonometrischen Funktion, die wir haben und .

Da folgt die Ungleichung aus der Gleichung, d.h. . Seit und , dann und . Allerdings und deshalb.

Wenn und dann. Da es vorher festgestellt wurde , dann .

Antworten. , .

Beispiel löse die Gleichung

Lösung. Der Bereich gültiger Werte der Gleichung ist .

Zeigen wir zunächst die Funktion

Für alle kann es nur positive Werte annehmen.

Stellen wir die Funktion wie folgt dar: .

Seitdem also, d. h. .

Um also die Ungleichung zu beweisen, muss man das zeigen . Dazu würfeln wir dann beide Teile dieser Ungleichung

Die resultierende numerische Ungleichung weist darauf hin, dass . Wenn wir das zusätzlich berücksichtigen, dann ist die linke Seite der Gleichung nicht negativ.

Betrachten Sie nun die rechte Seite der Gleichung.

Als , dann

Das ist jedoch bekannt . Daraus folgt, dass d.h. die rechte Seite der Gleichung überschreitet nicht . Es wurde zuvor bewiesen, dass die linke Seite der Gleichung nicht negativ ist, daher kann Gleichheit in nur dann bestehen, wenn beide Teile gleich sind, und dies ist nur für möglich.

Antworten. .

Beispiel löse die Gleichung

Lösung. Bezeichne und . Wenden wir die Cauchy-Bunyakovsky-Ungleichung an, erhalten wir . Daraus folgt das . Auf der anderen Seite gibt es . Daher hat die Gleichung keine Wurzeln.

Antworten. .

Beispiel Löse die Gleichung:

Lösung. Schreiben wir die Gleichung in der Form um:

Antworten. .

Funktionale Methoden zur Lösung trigonometrischer und kombinierter Gleichungen

Nicht jede Gleichung als Ergebnis von Transformationen kann auf eine Gleichung der einen oder anderen Standardform reduziert werden, für die es ein bestimmtes Lösungsverfahren gibt. In solchen Fällen erweist es sich als nützlich, solche Eigenschaften der Funktionen und als Monotonie, Beschränktheit, Gleichmäßigkeit, Periodizität usw. zu verwenden. Wenn also eine der Funktionen abnimmt und die zweite im Intervall zunimmt, dann wenn die Gleichung eine Wurzel auf diesem Intervall hat, ist diese Wurzel eindeutig und kann dann beispielsweise durch Auswahl gefunden werden. Wenn die Funktion nach oben beschränkt ist, und , und die Funktion nach unten beschränkt ist, und , dann ist die Gleichung äquivalent zum Gleichungssystem

Beispiel löse die Gleichung

Lösung. Wir transformieren die ursprüngliche Gleichung in die Form

und löse es als Quadrat bezüglich . Dann bekommen wir

Lösen wir die erste Mengengleichung. Unter Berücksichtigung der Beschränktheit der Funktion kommen wir zu dem Schluss, dass die Gleichung nur auf dem Intervall wurzeln kann. In diesem Intervall steigt die Funktion und die Funktion sinkt. Wenn diese Gleichung also eine Wurzel hat, dann ist sie eindeutig. Wir finden durch Auswahl.

Antworten. .

Beispiel löse die Gleichung

Lösung. Lassen Sie , und , dann kann die ursprüngliche Gleichung als Funktionsgleichung geschrieben werden . Da die Funktion ungerade ist, dann . In diesem Fall erhalten wir die Gleichung

Da , und auf monoton ist, ist die Gleichung äquivalent zur Gleichung , d.h. , die eine einzige Wurzel hat .

Antworten. .

Beispiel löse die Gleichung .

Lösung. Basierend auf dem Satz über die Ableitung einer komplexen Funktion ist klar, dass die Funktion fallend (Funktion fallend, steigend, fallend). Daraus wird deutlich, dass die Funktion definiert auf , abnehmend. Daher hat diese Gleichung höchstens eine Wurzel. Als , dann

Antworten. .

Beispiel Löse die Gleichung.

Lösung. Betrachten Sie die Gleichung in drei Intervallen.

a) Lassen Sie . Dann ist auf dieser Menge die ursprüngliche Gleichung äquivalent zur Gleichung . Das hat keine Lösungen für das Intervall, da , , a . Auf dem Intervall hat die ursprüngliche Gleichung auch keine Wurzeln, weil , a .

b) Lassen Sie . Dann ist auf dieser Menge die ursprüngliche Gleichung äquivalent zur Gleichung

deren Wurzeln auf dem Intervall sind die Zahlen , , , .

c) Lassen Sie . Dann ist auf dieser Menge die ursprüngliche Gleichung äquivalent zur Gleichung

Was keine Lösungen für das Intervall hat, da , aber . Die Gleichung hat auch keine Lösungen im Intervall, da , , a .

Antworten. , , , .

Symmetrie-Methode

Es ist zweckmäßig, die Symmetriemethode zu verwenden, wenn die Aufgabenstellung die Anforderung enthält, dass die Lösung einer Gleichung, Ungleichung, eines Systems usw. eindeutig sein muss. oder eine genaue Angabe der Anzahl der Lösungen. In diesem Fall sollte jede Symmetrie der gegebenen Ausdrücke erkannt werden.

Dabei ist auch die Vielfalt der möglichen Symmetriearten zu berücksichtigen.

Ebenso wichtig ist die strikte Einhaltung logischer Stufen beim symmetrischen Denken.

Normalerweise erlaubt uns die Symmetrie, nur die notwendigen Bedingungen festzulegen, und dann müssen wir ihre Hinlänglichkeit überprüfen.

Beispiel Finden Sie alle Werte des Parameters, für die die Gleichung eine eindeutige Lösung hat.

Lösung. Beachten Sie, dass und gerade Funktionen sind, also ist die linke Seite der Gleichung eine gerade Funktion.

Wenn es also eine Lösung für eine Gleichung gibt, dann gibt es auch eine Lösung für die Gleichung. Wenn die einzige Lösung der Gleichung ist, dann notwendig , .

Lassen Sie uns auswählen möglich Werte, die die Wurzel der Gleichung sein müssen.

Wir stellen sofort fest, dass andere Werte die Bedingung des Problems nicht erfüllen können.

Es ist aber noch nicht bekannt, ob alle Ausgewählten tatsächlich die Bedingung des Problems erfüllen.

Angemessenheit.

1) , die Gleichung nimmt die Form an .

2) , die Gleichung nimmt die Form an:

Offensichtlich für alle und . Daher ist die letzte Gleichung äquivalent zu dem System:

Damit haben wir bewiesen, dass für die Gleichung eine eindeutige Lösung hat.

Antworten. .

Lösung mit Funktionserkundung

Beispiel Beweisen Sie, dass alle Lösungen der Gleichung

Ganze Zahlen.

Lösung. Die Hauptperiode der ursprünglichen Gleichung ist . Daher untersuchen wir diese Gleichung zuerst auf dem Segment .

Lassen Sie uns die Gleichung in die Form umwandeln:

Mit Hilfe eines Rechners erhalten wir:

Wenn , dann erhalten wir aus den vorherigen Gleichungen:

Lösen wir die resultierende Gleichung, erhalten wir: .

Die durchgeführten Berechnungen bieten die Möglichkeit anzunehmen, dass die Wurzeln der zum Intervall gehörenden Gleichung , und sind.

Eine direkte Überprüfung bestätigt diese Hypothese. Damit ist bewiesen, dass die Wurzeln der Gleichung nur ganze Zahlen sind , .

Beispiel Löse die Gleichung .

Lösung. Finde die Hauptperiode der Gleichung. Die Hauptperiode der Funktion ist . Die Hauptperiode der Funktion ist . Das kleinste gemeinsame Vielfache der Zahlen und ist gleich . Daher ist die Hauptperiode der Gleichung . Lassen .

Offensichtlich ist eine Lösung der Gleichung. Im Intervall. Die Funktion ist negativ. Daher sollten andere Nullstellen der Gleichung nur auf den Intervallen x und gesucht werden.

Mit Hilfe eines Mikrorechners finden wir zunächst die Näherungswerte der Wurzeln der Gleichung. Dazu erstellen wir eine Tabelle mit Funktionswerten in Intervallen und ; d.h. auf den Intervallen und .

0	0	202,5	0,85355342
3	-0,00080306	207	0,6893642
6	-0,00119426	210	0,57635189
9	-0,00261932	213	0,4614465
12	-0,00448897	216	0,34549155
15	-0,00667995	219	0,22934931
18	-0,00903692	222	0,1138931
21	-0,01137519	225	0,00000002
24	-0,01312438	228	-0,11145712
27	-0,01512438	231	-0,21961736
30	-0,01604446	234	-0,32363903
33	-0,01597149	237	-0,42270819
36	-0,01462203	240	-0,5160445
39	-0,01170562	243	-0,60290965
42	-0,00692866	246	-0,65261345
45	0,00000002	249	-0,75452006
48	0,00936458	252	-0,81805397
51	0,02143757	255	-0,87270535
54	0,03647455	258	-0,91803444
57	0,0547098	261	-0,95367586
60	0,07635185	264	-0,97934187
63	0,10157893	267	-0,99482505
66	0,1305352	270	-1
67,5	0,14644661

Die folgenden Hypothesen sind aus der Tabelle leicht ersichtlich: Die Wurzeln der zum Segment gehörenden Gleichung sind Zahlen: ; ; . Eine direkte Überprüfung bestätigt diese Hypothese.

Antworten. ; ; .

Lösen trigonometrischer Ungleichungen mit dem Einheitskreis

Beim Lösen trigonometrischer Ungleichungen der Form , wobei eine der trigonometrischen Funktionen ist, ist es zweckmäßig, einen trigonometrischen Kreis zu verwenden, um die Lösung der Ungleichung am deutlichsten darzustellen und die Antwort aufzuschreiben. Die Hauptmethode zum Lösen trigonometrischer Ungleichungen besteht darin, sie auf die einfachsten Ungleichungen des Typs zu reduzieren. Schauen wir uns ein Beispiel an, wie solche Ungleichungen gelöst werden können.

Beispiel Löse die Ungleichung.

Lösung. Lassen Sie uns einen trigonometrischen Kreis zeichnen und darauf die Punkte markieren, für die die Ordinate größer als ist.

Für die Lösung dieser Ungleichung wird sein. Es ist auch klar, dass, wenn sich eine Zahl von einer Zahl aus dem angegebenen Intervall um unterscheidet, es auch nicht weniger als sein wird. Daher müssen Sie an den Enden des gefundenen Segments der Lösung nur hinzufügen. Schließlich erhalten wir, dass die Lösungen der ursprünglichen Ungleichung alle sein werden .

Antworten. .

Um Ungleichungen mit Tangens und Kotangens zu lösen, ist das Konzept einer Linie aus Tangenten und Kotangens nützlich. Dies sind die Linien bzw. (in der Abbildung (1) und (2)), die den trigonometrischen Kreis berühren.

Es ist leicht zu sehen, dass, wenn Sie einen Strahl mit Ursprung am Ursprung bauen und einen Winkel mit der positiven Richtung der Abszissenachse bilden, die Länge des Segments vom Punkt bis zum Schnittpunkt dieses Strahls mit der Linie von Tangens ist genau gleich dem Tangens des Winkels, den dieser Strahl mit der Abszissenachse bildet. Eine ähnliche Beobachtung gilt für den Kotangens.

Beispiel Löse die Ungleichung.

Lösung. Bezeichne , dann nimmt die Ungleichung die einfachste Form an: . Stellen Sie sich ein Intervall mit einer Länge vor, die gleich der kleinsten positiven Periode (LPP) der Tangente ist. Auf diesem Segment stellen wir unter Verwendung der Tangentenlinie fest, dass . Wir erinnern uns jetzt, was hinzugefügt werden muss, da das RPE der Funktion . So, . Zurück zur Variablen bekommen wir das .

Antworten. .

Es ist bequem, Ungleichungen mit inversen trigonometrischen Funktionen zu lösen, indem man Graphen von inversen trigonometrischen Funktionen verwendet. Lassen Sie uns anhand eines Beispiels zeigen, wie das geht.

Lösen trigonometrischer Ungleichungen mit einer grafischen Methode

Beachten Sie, dass wenn --- eine periodische Funktion ist, es zur Lösung der Ungleichung notwendig ist, ihre Lösungen auf einem Segment zu finden, dessen Länge gleich der Periode der Funktion ist. Alle Lösungen der ursprünglichen Ungleichung bestehen aus den gefundenen Werten sowie allen, die sich von den gefundenen durch eine beliebige ganzzahlige Anzahl von Perioden der Funktion unterscheiden.

Betrachten Sie die Lösung der Ungleichung ().

Denn dann hat die Ungleichung keine Lösungen für . Wenn , dann ist die Menge der Lösungen der Ungleichung die Menge aller reellen Zahlen.

Lassen . Die Sinusfunktion hat die kleinste positive Periode, daher kann die Ungleichung zuerst auf einem Segment der Länge gelöst werden, beispielsweise auf einem Segment. Wir bauen Graphen von Funktionen und (). sind gegeben durch Ungleichungen der Form: und, woher,

In diesem Artikel wurden Methoden zum Lösen trigonometrischer Gleichungen und Ungleichungen, sowohl auf einfachstem als auch auf olympischem Niveau, betrachtet. Die Hauptmethoden zum Lösen trigonometrischer Gleichungen und Ungleichungen wurden betrachtet, sowohl spezifische – nur für trigonometrische Gleichungen und Ungleichungen charakteristische – als auch allgemeine funktionale Methoden zum Lösen von Gleichungen und Ungleichungen, wie sie auf trigonometrische Gleichungen angewendet werden.

Die Diplomarbeit vermittelt grundlegende theoretische Informationen: Definition und Eigenschaften von trigonometrischen und inversen trigonometrischen Funktionen; Ausdruck trigonometrischer Funktionen in Form anderer trigonometrischer Funktionen, was sehr wichtig ist, um trigonometrische Ausdrücke umzuwandeln, insbesondere solche, die inverse trigonometrische Funktionen enthalten; zusätzlich zu den aus dem Schulunterricht bekannten trigonometrischen Grundformeln werden Formeln angegeben, die Ausdrücke mit inversen trigonometrischen Funktionen vereinfachen. Es werden die Lösung elementarer trigonometrischer Gleichungen, die Methode des Faktorisierens und Methoden zum Reduzieren trigonometrischer Gleichungen auf algebraische Gleichungen betrachtet. Angesichts der Tatsache, dass die Lösungen trigonometrischer Gleichungen auf verschiedene Arten geschrieben werden können und die Form dieser Lösungen es nicht erlaubt, sofort festzustellen, ob diese Lösungen gleich oder unterschiedlich sind, wird ein allgemeines Schema zum Lösen trigonometrischer Gleichungen betrachtet und die Transformation von Gruppen allgemeiner Lösungen trigonometrischer Gleichungen wird ausführlich betrachtet. Methoden zur Lösung elementarer trigonometrischer Ungleichungen werden detailliert betrachtet, sowohl auf einem Einheitskreis als auch mit einer grafischen Methode. Beschrieben wird das Lösen von nicht-elementaren trigonometrischen Ungleichungen durch elementare Ungleichungen und die den Schulkindern bereits bekannte Methode der Intervalle. Die Lösungen typischer Aufgaben zur Auswahl von Wurzeln werden angegeben. Die notwendigen theoretischen Informationen für die Wahl der Wurzeln werden gegeben: die Zerlegung der Menge der ganzen Zahlen in sich nicht schneidende Teilmengen, die Lösung von Gleichungen in ganzen Zahlen (diophantisch).

Die Ergebnisse dieser Abschlussarbeit können als Unterrichtsmaterial bei der Erstellung von Hausarbeiten und Abschlussarbeiten, bei der Vorbereitung von Wahlfächern für Schüler sowie bei der Vorbereitung von Studenten auf Aufnahmeprüfungen und zentrale Tests verwendet werden.

Vygodsky Ya.Ya., Handbuch der Elementarmathematik. /Vygodsky Ya.Ya. --- M.: Nauka, 1970.

Igudisman O., Mathematik bei der mündlichen Prüfung / Igudisman O. --- M.: Irispresse, Rolf, 2001.

Azarov A.I., Gleichungen / Azarov A.I., Gladun O.M., Fedosenko V.S. --- Minsk: Trivium, 1994.

Litvinenko V. N., Workshop zur Elementarmathematik / Litvinenko V. N. --- M .: Bildung, 1991.

Sharygin I.F., Wahlfach Mathematik: Problemlösung / Sharygin I.F., Golubev V.I. --- M.: Aufklärung, 1991.

Bardushkin V., Trigonometrische Gleichungen. Auswahl der Wurzeln / V. Barduschkin, A. Prokofjew.// Mathematik, Nr. 12, 2005 p. 23--27.

Vasilevsky A.B., Aufgaben für außerschulische Arbeit in Mathematik / Vasilevsky A.B. --- Mn.: Volks-Asveta. 1988. --- 176s.

Sapunov P. I., Transformation und Vereinigung von Gruppen allgemeiner Lösungen trigonometrischer Gleichungen / Sapunov P. I. // Mathematische Bildung, Ausgabe Nr. 3, 1935.

Borodin P., Trigonometrie. Materialien der Aufnahmeprüfungen an der Staatlichen Universität Moskau [Text] / P. Borodin, V. Galkin, V. Panferov, I. Sergeev, V. Tarasov // Mathematik Nr. 1, 2005 p. 36--48.

Samusenko A.V., Mathematik: Typische Fehler von Bewerbern: Referenzhandbuch / Samusenko A.V., Kazachenok V.V. --- Minsk: Higher School, 1991.

Azarov A.I., Funktionale und grafische Methoden zur Lösung von Prüfungsproblemen / Azarov A.I., Barvenov S.A., --- Minsk: Aversev, 2004.

Lösung der einfachsten trigonometrischen Gleichungen

Erinnern wir uns zunächst an die Formeln zur Lösung der einfachsten trigonometrischen Gleichungen.

1. $sinx=a$

1. $cosx=a$

1. $tgx=a$

1. $ctgx=a$

Lösung der einfachsten trigonometrischen Ungleichungen.

Um die einfachsten trigonometrischen Ungleichungen zu lösen, müssen wir zuerst die entsprechende Gleichung lösen und dann mithilfe des trigonometrischen Kreises eine Lösung für die Ungleichung finden. Betrachten Sie die Lösungen der einfachsten trigonometrischen Ungleichungen anhand von Beispielen.

Beispiel 1

$sinx\ge \frac(1)(2)$

Finden Sie eine Lösung für die trigonometrische Ungleichung $sinx=\frac(1)(2)$

\ \

Abbildung 1. Lösung der Ungleichung $sinx\ge \frac(1)(2)$.

Da die Ungleichung ein „größer als oder gleich“-Zeichen hat, liegt die Lösung auf dem oberen Kreisbogen (bezogen auf die Lösung der Gleichung).

Antwort: $\left[\frac(\pi )(6)+2\pi n,\frac(5\pi )(6)+2\pi n\right]$.

Beispiel 2

Finden Sie eine Lösung für die trigonometrische Ungleichung $cosx=\frac(\sqrt(3))(2)$

\ \

Notieren Sie die Lösung auf dem trigonometrischen Kreis

Da die Ungleichung ein „kleiner als“-Zeichen hat, liegt die Lösung auf dem (bezogen auf die Lösung der Gleichung) links liegenden Kreisbogen.

Antwort: $\left(\frac(\pi )(6)+2\pi n,\frac(11\pi )(6)+2\pi n\right)$.

Beispiel 3

$tgx\le \frac(\sqrt(3))(3)$

Finden Sie eine Lösung für die trigonometrische Ungleichung $tgx=\frac(\sqrt(3))(3)$

\ \

Auch hier brauchen wir einen Definitionsbereich. Wie wir uns erinnern, ist die Tangensfunktion $x\ne \frac(\pi )(2)+\pi n,n\in Z$

Notieren Sie die Lösung auf dem trigonometrischen Kreis

Abbildung 3. Lösung der Ungleichung $tgx\le \frac(\sqrt(3))(3)$.

Da die Ungleichung ein „kleiner oder gleich“-Zeichen hat, liegt die Lösung auf den in Abbildung 3 blau markierten Bögen des Kreises.

Antwort: $\ \left(-\frac(\pi )(2)+2\pi n\right.,\left.\frac(\pi )(6)+2\pi n\right]\cup \left (\frac(\pi )(2)+2\pi n,\right.\left.\frac(7\pi )(6)+2\pi n\right]$

Beispiel 4

Finden Sie eine Lösung für die trigonometrische Ungleichung $ctgx=\sqrt(3)$

\ \

Auch hier brauchen wir einen Definitionsbereich. Wie wir uns erinnern, ist die Tangensfunktion $x\ne \pi n,n\in Z$

Notieren Sie die Lösung auf dem trigonometrischen Kreis

Abbildung 4. Lösung der Ungleichung $ctgx\le \sqrt(3)$.

Da die Ungleichung ein „größer als“-Zeichen hat, liegt die Lösung auf den in Abbildung 4 blau markierten Bögen des Kreises.

Antwort: $\ \left(2\pi n,\frac(\pi )(6)+2\pi n\right)\cup \left(\pi +2\pi n,\frac(7\pi )( 6)+2\pi n\right)$

DEFINITION

Trigonometrische Ungleichungen sind Ungleichungen, die eine Variable unter dem Vorzeichen einer trigonometrischen Funktion enthalten.

Lösen trigonometrischer Ungleichungen

Die Lösung trigonometrischer Ungleichungen läuft oft darauf hinaus, die einfachsten trigonometrischen Ungleichungen der Form zu lösen: \(\ \sin x a \), \(\ \cos x > a \), \(\ \operatorname(tg) x > a \ ), \(\ \ Operatorname(ctg) x > a \), \(\ \sin x \leq a \), \(\ \cos x \leq a \), \(\ \operatorname(tg) x \ leq a \), \ (\ \operatorname(ctg) x \leq a \), \(\ \sin x \geq a \), \(\ \cos \geq a \), \(\ \operatorname(tg ) x \geq a \ ), \(\ \operatorname(tg) x \geq a \)

Die einfachsten trigonometrischen Ungleichungen werden grafisch oder mit einem trigonometrischen Einheitskreis gelöst.

Per Definition ist der Sinus des Winkels \(\ \alpha \) die Ordinate des Punktes \(\ P_(\alpha)(x, y) \) des Einheitskreises (Abb. 1), und der Kosinus ist die Abszisse dieses Punktes. Diese Tatsache nutzt man aus, um die einfachsten trigonometrischen Ungleichungen mit Cosinus und Sinus unter Verwendung des Einheitskreises zu lösen.

Beispiele zur Lösung trigonometrischer Ungleichungen

Übung

Löse die Ungleichung \(\ \sin x \leq \frac(\sqrt(3))(2) \)

Gelöst

Da \(\ \left|\frac(\sqrt(3))(2)\right| , hat diese Ungleichung eine Lösung und kann auf zwei Arten gelöst werden

Erster Weg. Lösen wir diese Ungleichung grafisch. Dazu konstruieren wir im selben Koordinatensystem einen Graphen aus dem Sinus \(\ y=\sin x \) (Abb. 2) und der Geraden \(\ y=\frac(\sqrt(3))( 2) \)

Wählen wir die Intervalle aus, in denen sich die Sinuskurve unter dem Graphen der Geraden \(\ y=\frac(\sqrt(3))(2) \) befindet. Finden Sie die Abszissen \(\ x_(1) \) und \(\ x_(2) \) der Schnittpunkte dieser Graphen: \(\ x_(1)=\pi-\arcsin \frac(\sqrt(3 ))(2 )=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_(2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\ frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)

Wir haben das Intervall \(\ \left[-\frac(4 \pi)(3) ; \frac(\pi)(3)\right] \) erhalten, aber da die Funktion \(\ y=\sin x \) periodisch ist und eine Periode \(\ 2 \pi \) hat, dann ist die Antwort die Vereinigung von Intervallen: \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+ 2 \pi k\right] \), \(\ k \in Z \)

Der zweite Weg. Konstruiere einen Einheitskreis und eine Gerade \(\ y=\frac(\sqrt(3))(2) \) , bezeichne ihre Schnittpunkte \(\ P_(x_(1)) \) und \(\ P_(x_ (2 )) \) (Abb. 3). Die Lösung der ursprünglichen Ungleichung ist die Menge der Ordinatenpunkte, die kleiner sind als \(\ \frac(\sqrt(3))(2) \) . Lassen Sie uns den Wert von \(\ \boldsymbol(I)_(1) \) und \(\ \boldsymbol(I)_(2) \) finden, indem wir gegen den Uhrzeigersinn gehen, \(\ x_(1) Abb. 3

\(\ x_(1)=\pi-\arcsin \frac(\sqrt(3))(2)=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_ (2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)

Unter Berücksichtigung der Periodizität der Sinusfunktion erhalten wir schließlich die Intervalle \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+2 \ pi\right] \), \(\k\in Z\)

Antwort\(\ x \in\left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+2 \pi\right] \), \(\ k \in Z\)

Übung

Lösen Sie die Ungleichung \(\ \sin x>2 \)

Lösung

Der Sinus ist eine beschränkte Funktion: \(\ |\sin x| \leq 1 \) , und die rechte Seite dieser Ungleichung ist größer als eins, also gibt es keine Lösungen.

Antwort: Es gibt keine Lösungen.

Übung

Lösen Sie die Ungleichung \(\ \cos x>\frac(1)(2) \)

Lösung

Diese Ungleichung kann auf zwei Arten gelöst werden: grafisch und mit einem Einheitskreis. Betrachten wir jede der Methoden.

Erster Weg. Lassen Sie uns in einem Koordinatensystem die Funktionen darstellen, die den linken und rechten Teil der Ungleichung beschreiben, also \(\ y=\cos x \) und \(\ y=\frac(1)(2) \) . Wählen wir die Intervalle aus, in denen der Graph der Kosinusfunktion \(\ y=\cos x \) über dem Graph der Geraden \(\ y=\frac(1)(2) \) liegt (Abb. 4 ).

Finden Sie die Abszissen der Punkte \(\ \boldsymbol(x)_(1) \) und \(\ x_(2) \) - die Schnittpunkte der Graphen der Funktionen \(\ y=\cos x \ ) und \(\ y=\frac (1)(2) \) , die die Enden eines der Intervalle sind, für die die angegebene Ungleichung gilt. \(\ x_(1)=-\arccos \frac(1)(2)=-\frac(\pi)(3) \); \(\ x_(1)=\arccos \frac(1)(2)=\frac(\pi)(3) \)

Wenn man bedenkt, dass der Kosinus eine periodische Funktion mit einer Periode \(\ 2 \pi \) ist, ist die Antwort der Wert \(\ x \) aus den Intervallen \(\ \left(-\frac(\pi)(3 )+2 \pi k ; \frac(\pi)(3)+2 \pi k\right) \), \(\ k \in Z \)

Der zweite Weg. Konstruieren wir einen Einheitskreis und eine Gerade \(\ x=\frac(1)(2) \) (da die x-Achse den Kosinussen auf dem Einheitskreis entspricht). Seien \(\ P_(x_(1)) \) und \(\ P_(x_(2)) \) (Abb. 5) die Schnittpunkte der Geraden und des Einheitskreises. Die Lösung der ursprünglichen Gleichung ist die Menge der Abszissenpunkte, die kleiner als \(\ \frac(1)(2) \) sind. Finden Sie den Wert von \(\ x_(1) \) und \(\ 2 \) , indem Sie eine Schaltung gegen den Uhrzeigersinn machen, so dass \(\ x_(1) Unter Berücksichtigung der Periodizität des Kosinus erhalten wir schließlich die Intervalle \( \ \left(-\frac (\pi)(3)+2 \pi k ;\frac(\pi)(3)+2 \pi k\right) \),\(\ k \in Z \)

Antwort: \(\ x \in\left(-\frac(\pi)(3)+2 \pi k ; \frac(\pi)(3)+2 \pi k\right) \), \(\ k\in Z\)

Übung

Lösen Sie die Ungleichung \(\ \operatorname(ctg) x \leq-\frac(\sqrt(3))(3) \)

Lösung

Lassen Sie uns Graphen der Funktionen \(\ y=\operatorname(ctg) x \), \(\ y=-\frac(\sqrt(3))(3) \) in einem Koordinatensystem zeichnen

Wählen wir die Intervalle aus, in denen der Graph der Funktion \(\ y=\operatorname(ctg) x \) nicht höher ist als der Graph der Geraden \(\ y=-\frac(\sqrt(3))(3 ) \) (Abb. 6) .

Suchen Sie die Abszisse des Punktes \(\ x_(0) \) , der das Ende eines der Intervalle ist, in denen die Ungleichung \(\ x_(0)=\operatorname(arcctg)\left(-\frac(\ sqrt(3))( 3)\right)=\pi-\operatorname(arcctg)\left(\frac(\sqrt(3))(3)\right)=\pi-\frac(\pi)(3 )=\frac(2\pi)(3)\)

Das andere Ende dieser Lücke ist der Punkt \(\ \pi \) , und die Funktion \(\ y=\operatorname(ctg) x \) ist an diesem Punkt undefiniert. Eine der Lösungen dieser Ungleichung ist also das Intervall \(\ \frac(2 \pi)(3) \leq x

Antwort: \(\ x \in\left[\frac(2 \pi)(3)+\pi k ; \pi+\pi k\right) \), \(\ k \in Z \)

Trigonometrische Ungleichungen mit komplexem Argument

Trigonometrische Ungleichungen mit einem komplexen Argument können durch Substitution auf die einfachsten trigonometrischen Ungleichungen reduziert werden. Nach dem Lösen wird die umgekehrte Substitution durchgeführt und die ursprüngliche Unbekannte ausgedrückt.

Übung

Löse die Ungleichung \(\ 2 \cos \left(2 x+100^(\circ)\right) \leq-1 \)

Lösung

Drücken Sie den Kosinus auf der rechten Seite dieser Ungleichung aus: \(\ \cos \left(2 x+100^(\circ)\right) \leq-\frac(1)(2) \)

Wir führen die Ersetzung \(\ t=2 x+100^(\circ) \) durch, wonach diese Ungleichung in die einfachste Ungleichung \(\ \cos t \leq-\frac(1)(2) \ )

Lösen wir es mit dem Einheitskreis. Konstruieren wir einen Einheitskreis und eine Gerade \(\ x=-\frac(1)(2) \) . Als Schnittpunkte der Geraden und des Einheitskreises bezeichnen wir \(\ P_(1) \) und \(\ P_(2) \) (Abb. 7).

Die Lösung der ursprünglichen Ungleichung ist die Menge der Abszissenpunkte, die höchstens \(\ -\frac(1)(2) \) sind. Der Punkt \(\ P_(1) \) entspricht dem Winkel \(\ 120^(\circ) \) , und der Punkt \(\ P_(2) \) . Bei gegebener Kosinusperiode erhalten wir also \(\ 120^(\circ)+360^(\circ) \cdot n \leq t \leq 240^(\circ)+360^(\circ) \cdot n \ ) , \(\ n \in Z \)

Wir machen die umgekehrte Substitution \(\ t=2 x+100^(\circ) 120^(\circ)+360^(\circ) \cdot n \leq 2 x+100^(\circ) \leq 240^ (\ circ)+360^(\circ) \cdot n \), \(\ n \in Z \)

Wir drücken \(\ \mathbf(x) \) aus, dazu subtrahieren wir zuerst \(\ 100^(\circ) 120^(\circ)-100^(\circ)+360^(\circ) \ cdot n \leq 2 x+100^(\circ)-100^(\circ) \leq 240^(\circ)-100^(\circ)+360^(\circ) \cdot n \), \( \ n\in Z\); \(\ 20^(\circ)+360^(\circ) \cdot n \leq 2 x \leq 140^(\circ)+360^(\circ) \cdot n \), \(\ n \in Z\)

und dann dividiere durch 2 \(\ \frac(20^(\circ)+360^(\circ) \cdot n)(2) \leq \frac(2 x)(2) \leq \frac(140^). (\circ)+360^(\circ) \cdot n)(2) \), \(\ n \in Z \); \(\ 10^(\circ)+180^(\circ) \cdot n \leq x \leq 70^(\circ)+180^(\circ) \cdot n \), \(\ n \in Z \)

Antwort\(\ x \in\left(10^(\circ)+180^(\circ) \cdot n ; 10^(\circ)+180^(\circ) \cdot n\right) \), \ (\ x \in\left(10^(\circ)+180^(\circ) \cdot n ; 10^(\circ)+180^(\circ) \cdot n\right) \)

Doppelte trigonometrische Ungleichungen

Übung

Lösen Sie die doppelte trigonometrische Ungleichung \(\ \frac(1)(2)

Lösung

Führen wir die Ersetzung \(\ t=\frac(x)(2) \) ein, dann nimmt die ursprüngliche Ungleichung die Form \(\ \frac(1)(2) an

Lösen wir es mit dem Einheitskreis. Da die Ordinatenachse dem Sinus auf dem Einheitskreis entspricht, wählen wir darauf die Ordinatenmenge aus, die größer als \(\ x=\frac(1)(2) \) und kleiner oder gleich \(\ \frac(\sqrt(2))(2 ) \) . In Abbildung 8 befinden sich diese Punkte auf den Bögen \(\ P_(t_(1)) \), \(\ P_(t_(2)) \) und \(\ P_(t_(3)) \) , \( \ P_(t_(4)) \) . Lassen Sie uns den Wert \(\ t_(1) \), \(\ t_(2) \), \(\ t_(3) \), \(\ t_(4) \) finden und eine Tour gegen den Uhrzeigersinn machen, und \ (\ t_(1) \(\ t_(3)=\pi-\arcsin \frac(\sqrt(2))(2)=\pi-\frac(\pi)(4)=\frac(3 \ pi)(4) \); \(\ t_(4)=\pi-\arcsin \frac(1)(2)=\pi-\frac(\pi)(6)=\frac(5 \pi ) (6)\)

Somit erhalten wir zwei Intervalle, die sich unter Berücksichtigung der Periodizität der Sinusfunktion wie folgt schreiben lassen: \(\ \frac(\pi)(6)+2 \pi k \leq t \frac(\pi) (4)+2 \pi k \quad \frac(3 \pi)(4)+2 \pi k leq \frac(x)(2) \frac(\pi)(4)+2 \pi k \) , \(\ \frac(3 \pi)(4)+2 \pi k Express \(\ \mathbf( x) \), dazu multiplizieren wir alle Seiten beider Ungleichungen mit 2, wir erhalten \(\ \frac (\pi)(3)+4 \pi k \leq x

Antwort\(\ x \in\left(\frac(\pi)(3)+4 \pi k ; \frac(\pi)(2)+4 \pi k\right] \cup\left[\frac( 3 \pi)(2)+4 \pi k ; \frac(5 \pi)(3)+4 \pi k\right) \), \(\ k \in Z \)

METHODEN ZUR LÖSUNG TRIGONOMETRISCHER UNGLEICHHEITEN

Relevanz. In der Vergangenheit haben trigonometrische Gleichungen und Ungleichungen einen besonderen Platz im Schullehrplan eingenommen. Wir können sagen, dass die Trigonometrie einer der wichtigsten Bereiche des Schulunterrichts und der gesamten mathematischen Wissenschaft im Allgemeinen ist.

Trigonometrische Gleichungen und Ungleichungen nehmen einen der zentralen Plätze in einem Mathematikkurs der Oberstufe ein, sowohl in Bezug auf den Inhalt des Unterrichtsmaterials als auch auf die Methoden der pädagogischen und kognitiven Aktivität, die während des Studiums gebildet und zur Lösung eines großen Problems angewendet werden können und sollten Reihe von Problemen theoretischer und angewandter Art. .

Die Lösung trigonometrischer Gleichungen und Ungleichungen schafft die Voraussetzungen für die Systematisierung des studentischen Wissens in Bezug auf alle Lehrmaterialien der Trigonometrie (z. B. die Eigenschaften trigonometrischer Funktionen, Methoden zur Transformation trigonometrischer Ausdrücke usw.) und ermöglicht es, effektive Verbindungen herzustellen das untersuchte Material in Algebra (Gleichungen, Äquivalenz von Gleichungen, Ungleichungen, identische Transformationen von algebraischen Ausdrücken usw.).

Mit anderen Worten bedeutet die Betrachtung von Methoden zur Lösung trigonometrischer Gleichungen und Ungleichungen eine Art Übertragung dieser Fähigkeiten auf einen neuen Inhalt.

Die Bedeutung der Theorie und ihre zahlreichen Anwendungen belegen die Aktualität des gewählten Themas. Dies wiederum ermöglicht es Ihnen, Ziele, Ziele und Forschungsgegenstand der Studienleistungen festzulegen.

Zweck der Studie: Verallgemeinern Sie die verfügbaren Arten trigonometrischer Ungleichungen, grundlegende und spezielle Methoden zu ihrer Lösung, wählen Sie eine Reihe von Aufgaben zur Lösung trigonometrischer Ungleichungen durch Schulkinder aus.

Forschungsschwerpunkte:

1. Systematisieren Sie das Material auf der Grundlage der Analyse der verfügbaren Literatur zum Forschungsthema.

2. Geben Sie eine Reihe von Aufgaben, die notwendig sind, um das Thema "Trigonometrische Ungleichungen" zu festigen.

Studienobjekt sind trigonometrische Ungleichungen im Schulmathematikunterricht.

Gegenstand der Studie: Arten trigonometrischer Ungleichungen und Methoden zu ihrer Lösung.

Theoretische Bedeutung ist, das Material zu organisieren.

Praktische Bedeutung: Anwendung theoretischen Wissens bei der Lösung von Problemen; Analyse der wichtigsten häufig anzutreffenden Methoden zur Lösung trigonometrischer Ungleichungen.

Forschungsmethoden : Analyse der wissenschaftlichen Literatur, Synthese und Verallgemeinerung des erworbenen Wissens, Analyse der Problemlösung, Suche nach optimalen Methoden zur Lösung von Ungleichungen.

§eines. Arten von trigonometrischen Ungleichungen und grundlegende Methoden zu ihrer Lösung

1.1. Die einfachsten trigonometrischen Ungleichungen

Zwei trigonometrische Ausdrücke, die durch ein Zeichen oder > verbunden sind, heißen trigonometrische Ungleichungen.

Eine trigonometrische Ungleichung zu lösen bedeutet, eine Reihe von Werten der in der Ungleichung enthaltenen Unbekannten zu finden, unter denen die Ungleichung erfüllt ist.

Der Hauptteil der trigonometrischen Ungleichungen wird gelöst, indem man sie auf die Lösung der einfachsten reduziert:

Dies kann eine Methode der Faktorisierung, Änderung der Variablen (
,
usw.), wo zuerst die übliche Ungleichung gelöst wird und dann die Ungleichung der Form
usw. oder auf andere Weise.

Die einfachsten Ungleichungen werden auf zwei Arten gelöst: mit dem Einheitskreis oder grafisch.

Lassenf(x  ist eine der grundlegenden trigonometrischen Funktionen. Um die Ungleichung zu lösen
es genügt, seine Lösung in einer Periode zu finden, d.h. auf jedem Segment, dessen Länge gleich der Periode der Funktion istf  x  . Dann wird die Lösung der ursprünglichen Ungleichung gefundenx , sowie diejenigen Werte, die sich von denen unterscheiden, die durch eine beliebige ganzzahlige Anzahl von Perioden der Funktion gefunden werden. In diesem Fall ist es zweckmäßig, die grafische Methode zu verwenden.

Lassen Sie uns ein Beispiel für einen Algorithmus zum Lösen von Ungleichungen geben
(
) und
.

Algorithmus zur Lösung der Ungleichung
(
).

1. Formulieren Sie die Definition des Sinus einer Zahlx auf dem Einheitskreis.

3. Markieren Sie auf der y-Achse einen Punkt mit der Koordinatea .

4. Ziehen Sie durch diesen Punkt eine Linie parallel zur OX-Achse und markieren Sie deren Schnittpunkte mit dem Kreis.

5. Wählen Sie einen Kreisbogen aus, dessen alle Punkte eine kleinere Ordinate als habena .

6. Geben Sie die Richtung der Überbrückung an (gegen den Uhrzeigersinn) und schreiben Sie das Ergebnis auf, indem Sie die Periode der Funktion an die Enden des Intervalls addieren2πn ,
.

Algorithmus zur Lösung der Ungleichung
.

1. Formulieren Sie die Definition des Tangens einer Zahlx auf dem Einheitskreis.

2. Zeichnen Sie einen Einheitskreis.

3. Zeichnen Sie eine Tangentenlinie und markieren Sie darauf einen Punkt mit einer Ordinatea .

4. Verbinden Sie diesen Punkt mit dem Ursprung und markieren Sie den Schnittpunkt der resultierenden Strecke mit dem Einheitskreis.

5. Wählen Sie einen Kreisbogen aus, dessen alle Punkte eine Ordinate auf der Tangentenlinie haben, die kleiner als ista .

6. Geben Sie die Richtung des Durchlaufs an und schreiben Sie die Antwort unter Berücksichtigung des Funktionsumfangs mit einem Punkt aufPn ,
(Die Zahl auf der linken Seite des Datensatzes ist immer kleiner als die Zahl auf der rechten Seite).

Grafische Interpretation von Lösungen zu den einfachsten Gleichungen und Formeln zum Lösen von Ungleichungen in allgemeiner Form sind im Anhang (Anhänge 1 und 2) angegeben.

Beispiel 1 Löse die Ungleichung
.

Zeichnen Sie eine Linie auf dem Einheitskreis
, die den Kreis an den Punkten A und B schneidet.

Alle Wertej auf dem Intervall NM mehr erfüllen alle Punkte des Bogens AMB diese Ungleichung. Bei allen Drehwinkeln groß , aber kleiner ,
nimmt Werte größer als an (aber nicht mehr als eine).

Abb.1

Somit wird die Lösung der Ungleichung alle Werte im Intervall sein
, d.h.
. Um alle Lösungen dieser Ungleichung zu erhalten, genügt es, an den Enden dieses Intervalls zu addieren
, wo
, d.h.
,
. Beachten Sie, dass die Werte
und
sind die Wurzeln der Gleichung
,

diese.
;
.

Antworten:
,
.

1.2. Grafische Methode

In der Praxis ist oft ein grafisches Verfahren zum Lösen trigonometrischer Ungleichungen sinnvoll. Betrachten Sie das Wesen der Methode am Beispiel der Ungleichung
:

1. Wenn das Argument komplex ist (anders alsX ), dann ersetzen wir es durcht .

2. Wir bauen in einer KoordinatenebenetoOy Funktionsgraphen
und
.

3. Wir finden solchezwei benachbarte Schnittpunkte von Graphen, zwischen denensinusförmiggelegenOben gerade
. Finde die Abszissen dieser Punkte.

4. Schreiben Sie eine doppelte Ungleichung für das Argumentt , unter Berücksichtigung der Kosinusperiode (t zwischen den gefundenen Abszissen liegen).

5. Führen Sie eine umgekehrte Substitution durch (kehren Sie zum ursprünglichen Argument zurück) und drücken Sie den Wert ausX aus einer doppelten Ungleichung schreiben wir die Antwort als numerisches Intervall.

Beispiel 2 Lösen Sie die Ungleichung: .

Beim Lösen von Ungleichungen mit einer grafischen Methode ist es notwendig, Funktionsgraphen so genau wie möglich zu erstellen. Transformieren wir die Ungleichung in die Form:

Konstruieren wir Graphen von Funktionen in einem Koordinatensystem
und
(Abb. 2).

Abb.2

Funktionsgraphen schneiden sich in einem PunktABER mit Koordinaten
;
. Zwischen
Diagrammpunkte
unterhalb der Diagrammpunkte
. Und wann
Funktionswerte sind gleich. Deshalb
bei
.

Antworten:
.

1.3. Algebraische Methode

Nicht selten lässt sich die ursprüngliche trigonometrische Ungleichung durch eine gut gewählte Substitution auf eine algebraische (rationale oder irrationale) Ungleichung zurückführen. Bei dieser Methode wird die Ungleichung transformiert, eine Substitution eingeführt oder eine Variable ersetzt.

Betrachten wir die Anwendung dieser Methode auf konkrete Beispiele.

Beispiel 3 Reduktion auf die einfachste Form
.

(Abb. 3)

Abb. 3

,
.

Antworten:
,

Beispiel 4 Lösen Sie die Ungleichung:

ODZ:
,
.

Verwenden von Formeln:
,

wir schreiben die Ungleichung in der Form:
.

Oder, vorausgesetzt
nach einfachen Transformationen erhalten wir

,

,

.

Lösen wir die letzte Ungleichung nach der Intervallmethode, erhalten wir:

Abb.4

, beziehungsweise
. Dann von Abb. 4 folgt
, wo
.

Abb.5

Antworten:
,
.

1.4. Abstandsmethode

Das allgemeine Schema zum Lösen trigonometrischer Ungleichungen nach der Intervallmethode:

Faktorisiere mit trigonometrischen Formeln.

Finden Sie Haltepunkte und Nullstellen der Funktion und setzen Sie sie auf den Kreis.

Nimm irgendeinen PunktZu (aber nicht früher gefunden) und finden Sie das Zeichen des Produkts heraus. Wenn das Produkt positiv ist, setzen Sie einen Punkt außerhalb des Einheitskreises auf den Strahl, der dem Winkel entspricht. Andernfalls platzieren Sie den Punkt innerhalb des Kreises.

Kommt ein Punkt gerade oft vor, nennen wir ihn einen Punkt gerader Multiplizität, kommt er ungerade oft vor, nennen wir ihn einen Punkt ungerader Multiplizität. Zeichnen Sie Bögen wie folgt: Beginnen Sie an einem PunktZu , wenn der nächste Punkt eine ungerade Multiplizität hat, dann schneidet der Bogen den Kreis an diesem Punkt, aber wenn der Punkt eine gerade Multiplizität hat, dann schneidet er sich nicht.

Bögen hinter einem Kreis sind positive Lücken; innerhalb des Kreises befinden sich negative Intervalle.

Beispiel 5 Löse die Ungleichung

,
.

Punkte der ersten Serie:
.

Punkte der zweiten Serie:
.

Jeder Punkt kommt ungerade oft vor, d. h. alle Punkte haben eine ungerade Multiplizität.

Finden Sie das Zeichen des Produkts unter heraus
: . Wir markieren alle Punkte auf dem Einheitskreis (Abb. 6):

Reis. 6

Antworten:
,
;
,
;
,
.

Beispiel 6 . Löse die Ungleichung.

Lösung:

Lassen Sie uns die Nullstellen des Ausdrucks finden .

Erhaltenäm :

,
;

,
;

,
;

,
;

Auf dem Einheitskreis ReihenwerteX 1 durch Punkte dargestellt
. SerieX 2 gibt Punkte
. Eine SerieX 3 Wir bekommen zwei Punkte
. Endlich eine SerieX 4 wird Punkte darstellen
. Wir setzen alle diese Punkte auf den Einheitskreis und geben in Klammern neben jeder ihrer Vielfachheit an.

Lassen Sie nun die Nummer wird gleich sein. Wir schätzen nach dem Zeichen:

Also der PunktEIN sollte auf dem Strahl gewählt werden, der den Winkel bildet mit StrahlOh, außerhalb des Einheitskreises. (Beachten Sie, dass der HilfsstrahlÖ EIN es muss nicht im Bild gezeigt werden. PunktEIN ungefähr ausgewählt.)

Nun zur SacheEIN Wir zeichnen nacheinander eine wellenförmige durchgehende Linie zu allen markierten Punkten. Und an den Punkten
Unsere Linie geht von einer Region zur anderen: Wenn sie außerhalb des Einheitskreises war, dann geht sie hinein. Annäherung an den Punkt , kehrt die Linie in den inneren Bereich zurück, da die Multiplizität dieses Punktes gerade ist. Ähnlich an der Stelle (bei gerader Multiplizität) muss die Linie nach außen gedreht werden. Also haben wir ein bestimmtes Bild gezeichnet, das in Abb. 7. Es hilft, die gewünschten Bereiche auf dem Einheitskreis zu markieren. Sie sind mit einem „+“ gekennzeichnet.

Abb.7

Endgültige Antwort:

Notiz. Wenn die Wellenlinie nach dem Durchlaufen aller auf dem Einheitskreis markierten Punkte nicht zum Punkt zurückgeführt werden kannEIN , ohne den Kreis an einer „illegalen“ Stelle zu kreuzen, bedeutet dies, dass bei der Lösung ein Fehler gemacht wurde, nämlich eine ungerade Anzahl von Wurzeln weggelassen wurde.

Antworten: .

§2. Eine Reihe von Aufgaben zur Lösung trigonometrischer Ungleichungen

Bei der Entwicklung der Fähigkeit von Schulkindern, trigonometrische Ungleichungen zu lösen, können auch 3 Stufen unterschieden werden.

1. vorbereitend,

2. Bildung von Fähigkeiten zur Lösung der einfachsten trigonometrischen Ungleichungen;

3. Einführung trigonometrischer Ungleichungen anderer Art.

Der Zweck der Vorbereitungsphase besteht darin, dass Schulkinder die Fähigkeit entwickeln müssen, einen trigonometrischen Kreis oder ein trigonometrisches Diagramm zu verwenden, um Ungleichungen zu lösen, nämlich:

Fähigkeit, einfache Ungleichungen der Form zu lösen
,
,
,
, Verwenden der Eigenschaften der Sinus- und Kosinusfunktionen;

Fähigkeit, doppelte Ungleichungen für Bögen eines numerischen Kreises oder für Bögen von Graphen von Funktionen zu machen;

Fähigkeit, verschiedene Transformationen trigonometrischer Ausdrücke durchzuführen.

Es wird empfohlen, diese Phase in den Prozess der Systematisierung des Wissens der Schüler über die Eigenschaften trigonometrischer Funktionen aufzunehmen. Das Hauptmittel können Aufgaben sein, die den Schülern angeboten und entweder unter Anleitung eines Lehrers oder unabhängig durchgeführt werden, sowie Fähigkeiten, die beim Lösen trigonometrischer Gleichungen erworben wurden.

Hier sind Beispiele für solche Aufgaben:

1 . Markieren Sie einen Punkt auf dem Einheitskreis , wenn

.

2. In welchem ​​Viertel der Koordinatenebene liegt der Punkt , wenn gleich:

3. Markieren Sie Punkte auf dem trigonometrischen Kreis , wenn:

4. Bringen Sie den Ausdruck auf trigonometrische FunktionenichViertel.

a)
, b)
, in)

5. Angesichts des Lichtbogens MR.M - Mitteichviertel,R - MitteIIQuartal. Beschränken Sie den Wert einer Variablent for: (bilde eine doppelte Ungleichung) a) arc MP; b) RM-Bögen.

6. Schreiben Sie eine doppelte Ungleichung für die ausgewählten Abschnitte des Diagramms:

Reis. eines

7. Ungleichungen lösen
,
,
,
.

8. Ausdruck umwandeln .

In der zweiten Phase des Lernens zum Lösen trigonometrischer Ungleichungen können wir die folgenden Empfehlungen in Bezug auf die Methodik zum Organisieren von Schüleraktivitäten anbieten. Gleichzeitig ist es notwendig, sich auf die Fähigkeiten der Schüler zu konzentrieren, mit einem trigonometrischen Kreis oder einem Graphen zu arbeiten, die während der Lösung der einfachsten trigonometrischen Gleichungen gebildet werden.

Erstens ist es möglich, die Zweckmäßigkeit zu begründen, ein allgemeines Verfahren zum Lösen der einfachsten trigonometrischen Ungleichungen zu erhalten, indem man sich beispielsweise auf eine Ungleichung der Form bezieht
. Mit den in der Vorbereitungsphase erworbenen Kenntnissen und Fähigkeiten bringen die Studierenden die vorgeschlagene Ungleichung in die Form
, kann es aber schwierig finden, eine Reihe von Lösungen für die resultierende Ungleichung zu finden, da Es ist unmöglich, es nur mit den Eigenschaften der Sinusfunktion zu lösen. Diese Schwierigkeit kann umgangen werden, indem auf die entsprechende Abbildung (Lösung der Gleichung grafisch oder mit Einheitskreis) verwiesen wird.

Zweitens sollte der Lehrer die Aufmerksamkeit der Schüler auf verschiedene Möglichkeiten zur Lösung der Aufgabe lenken und ein geeignetes Beispiel für die Lösung der Ungleichung sowohl grafisch als auch mit einem trigonometrischen Kreis geben.

Betrachten Sie solche Optionen zur Lösung der Ungleichung
.

1. Lösen der Ungleichung mit dem Einheitskreis.

In der ersten Lektion zum Lösen trigonometrischer Ungleichungen bieten wir den Schülern einen detaillierten Lösungsalgorithmus an, der in einer schrittweisen Präsentation alle grundlegenden Fähigkeiten widerspiegelt, die zum Lösen der Ungleichung erforderlich sind.

Schritt 1.Zeichnen Sie einen Einheitskreis, markieren Sie einen Punkt auf der y-Achse und ziehe eine gerade Linie durch sie parallel zur x-Achse. Diese Linie schneidet den Einheitskreis an zwei Punkten. Jeder dieser Punkte stellt Zahlen dar, deren Sinus gleich ist .

Schritt 2Diese gerade Linie teilte den Kreis in zwei Bögen. Lassen Sie uns diejenige herausgreifen, auf der Zahlen angezeigt werden, die einen Sinus größer als haben . Dieser Bogen befindet sich naturgemäß oberhalb der eingezeichneten Geraden.

Reis. 2

Schritt 3Wählen wir eines der Enden des markierten Bogens. Schreiben wir eine der Zahlen auf, die durch diesen Punkt des Einheitskreises repräsentiert wird .

Schritt 4Um eine Nummer zu wählen, die dem zweiten Ende des ausgewählten Bogens entspricht, "übergeben" wir diesen Bogen vom benannten Ende zum anderen. Gleichzeitig erinnern wir uns daran, dass die Zahlen, die wir passieren, zunehmen, wenn wir uns gegen den Uhrzeigersinn bewegen (wenn wir uns in die entgegengesetzte Richtung bewegen, würden die Zahlen abnehmen). Schreiben wir die Zahl auf, die auf dem Einheitskreis am zweiten Ende des markierten Bogens abgebildet ist .

So sehen wir, dass die Ungleichheit
die Zahlen erfüllen, für die die Ungleichung
. Wir haben die Ungleichung für Zahlen gelöst, die auf derselben Periode der Sinusfunktion liegen. Daher können alle Lösungen der Ungleichung geschrieben werden als

Die Schüler sollten gebeten werden, die Figur sorgfältig zu betrachten und herauszufinden, warum alle Lösungen für die Ungleichung
kann in das Formular geschrieben werden
,
.

Reis. 3

Die Aufmerksamkeit der Schüler muss darauf gelenkt werden, dass wir beim Lösen von Ungleichungen für die Kosinusfunktion eine gerade Linie parallel zur y-Achse zeichnen.

Grafischer Weg, um die Ungleichung zu lösen.

Erstellen von Diagrammen
und
, da
.

Reis. vier

Dann schreiben wir die Gleichung
und seine Entscheidung
,
,
, mit Formeln gefunden
,
,
.

(Gebenn Werte 0, 1, 2 finden wir drei Wurzeln der zusammengesetzten Gleichung). Werte
sind drei aufeinanderfolgende Abszissen der Schnittpunkte der Graphen
und
. Natürlich immer im Intervall
die Ungleichheit
, und im Intervall
- Ungleichheit
. Wir interessieren uns für den ersten Fall, und wenn wir dann an den Enden dieses Intervalls eine Zahl hinzufügen, die ein Vielfaches der Sinusperiode ist, erhalten wir eine Lösung der Ungleichung
als:
,
.

Reis. 5

Zusammenfassen. Um die Ungleichung zu lösen
, müssen Sie die entsprechende Gleichung schreiben und lösen. Finden Sie aus der resultierenden Formel die Wurzeln und , und schreiben Sie die Antwort der Ungleichung in der Form: ,
.

Drittens wird die Tatsache über die Menge der Wurzeln der entsprechenden trigonometrischen Ungleichung sehr deutlich bestätigt, wenn man sie graphisch löst.

Reis. 6

Es ist notwendig, den Schülern zu zeigen, dass die Spule, die die Lösung der Ungleichung ist, sich durch dasselbe Intervall wiederholt, das gleich der Periode der trigonometrischen Funktion ist. Eine ähnliche Darstellung kannst du dir auch für den Graphen der Sinusfunktion vorstellen.

Viertens ist es ratsam, Arbeiten zur Aktualisierung der Methoden der Schüler zur Umrechnung der Summe (Differenz) trigonometrischer Funktionen in ein Produkt durchzuführen, um die Aufmerksamkeit der Schüler auf die Rolle dieser Techniken bei der Lösung trigonometrischer Ungleichungen zu lenken.

Eine solche Arbeit kann durch die selbstständige Erfüllung der vom Lehrer vorgeschlagenen Aufgaben durch die Schüler organisiert werden, unter denen wir die folgenden hervorheben:

Fünftens müssen die Schüler aufgefordert werden, die Lösung jeder einfachen trigonometrischen Ungleichung mithilfe eines Diagramms oder eines trigonometrischen Kreises zu veranschaulichen. Achten Sie unbedingt auf seine Zweckmäßigkeit, insbesondere auf die Verwendung eines Kreises, da beim Lösen trigonometrischer Ungleichungen die entsprechende Abbildung als sehr bequemes Mittel dient, um die Lösungsmenge einer bestimmten Ungleichung zu fixieren.

Das Kennenlernen von Schülern mit Methoden zur Lösung trigonometrischer Ungleichungen, die nicht die einfachsten sind, sollte nach folgendem Schema erfolgen: Bezug auf eine bestimmte trigonometrische Ungleichung Bezug auf die entsprechende trigonometrische Gleichung Gemeinsame Suche (Lehrer - Schüler) nach einer Lösung Unabhängiger Transfer der gefundenen Technik auf andere Ungleichungen des gleichen Typs.

Um das Wissen der Schüler über Trigonometrie zu systematisieren, empfehlen wir, solche Ungleichungen gezielt auszuwählen, deren Lösung verschiedene Transformationen erfordert, die im Lösungsprozess implementiert werden können, um die Aufmerksamkeit der Schüler auf ihre Merkmale zu lenken.

Als solche produktiven Ungleichheiten können wir beispielsweise Folgendes vorschlagen:

Abschließend geben wir ein Beispiel für eine Reihe von Problemen zur Lösung trigonometrischer Ungleichungen.

1. Lösen Sie die Ungleichungen:

2. Lösen Sie die Ungleichungen: 3. Finde alle Lösungen von Ungleichungen: 4. Finde alle Lösungen von Ungleichungen:

a)
, erfüllt die Bedingung
;

b)
, erfüllt die Bedingung
.

5. Finde alle Lösungen von Ungleichungen:

a) ;

b) ;

in)
;

G)
;

e)
.

6. Lösen Sie die Ungleichungen:

a) ;

b) ;

in) ;

G)
;

e) ;

e) ;

und)
.

7. Lösen Sie die Ungleichungen:

a)
;

b) ;

in) ;

G) .

8. Lösen Sie die Ungleichungen:

a) ;

b) ;

in) ;

G)
;

e)
;

e) ;

und)
;

h) .

Es ist ratsam, die Aufgaben 6 und 7 Schülern anzubieten, die Mathematik auf fortgeschrittenem Niveau studieren, Aufgabe 8 - Schülern in Klassen mit vertieftem Mathematikstudium.

§3. Spezielle Methoden zur Lösung trigonometrischer Ungleichungen

Spezielle Methoden zum Lösen trigonometrischer Gleichungen - also solche Methoden, die nur zum Lösen trigonometrischer Gleichungen verwendet werden können. Diese Methoden basieren auf der Verwendung der Eigenschaften trigonometrischer Funktionen sowie auf der Verwendung verschiedener trigonometrischer Formeln und Identitäten.

3.1. Sektormethode

Betrachten Sie die Sektormethode zur Lösung trigonometrischer Ungleichungen. Lösung von Ungleichungen der Form

, woP ( x ) undQ ( x ) - rationale trigonometrische Funktionen (Sinus, Cosinus, Tangens und Kotangens werden rational eingegeben), ähnlich wie bei der Lösung rationaler Ungleichungen. Es ist bequem, rationale Ungleichungen mit der Methode der Intervalle auf der reellen Achse zu lösen. Sein Analogon bei der Lösung rationaler trigonometrischer Ungleichungen ist die Methode der Sektoren in einem trigonometrischen Kreis, zSünde undcos (
) oder ein trigonometrischer Halbkreis fürtgx undctgx (
).

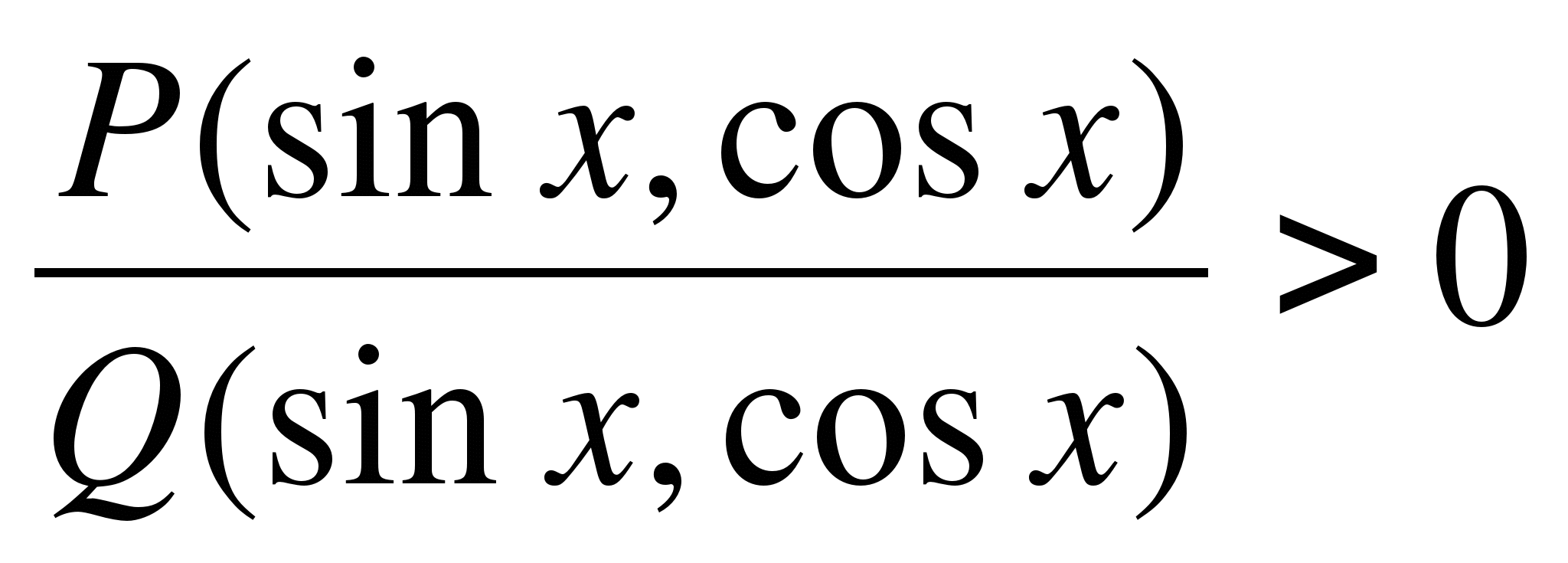
Bei der Intervallmethode besteht jeder lineare Faktor aus Zähler und Nenner der Form
Punkt auf der Zahlenachse , und beim Passieren dieses Punktes
ändert das Vorzeichen. Bei der Sektormethode ist jeder Multiplikator der Form
, wo
- eine der FunktionenSünde odercos und
, in einem trigonometrischen Kreis entsprechen zwei Winkel und
, die den Kreis in zwei Sektoren teilen. Beim Durchfahren und Funktion
ändert das Vorzeichen.

Folgendes ist zu beachten:

a) Multiplikatoren der Form
und
, wo
, Vorzeichen für alle Werte beibehalten . Solche Multiplikatoren des Zählers und Nenners werden verworfen und ändern sich (if
) für jede solche Zurückweisung wird das Ungleichheitszeichen umgekehrt.

b) Multiplikatoren der Form
und
werden ebenfalls verworfen. Wenn dies außerdem Faktoren des Nenners sind, werden Ungleichungen der Form zum äquivalenten Ungleichungssystem hinzugefügt
und
. Wenn dies Faktoren des Zählers sind, dann entsprechen sie im äquivalenten Nebenbedingungssystem den Ungleichungen
und
bei strikter anfänglicher Ungleichheit und Gleichheit
und
im Fall einer nicht strengen Anfangsungleichung. Beim Ablegen des Multiplikators
oder
das Ungleichheitszeichen wird umgekehrt.

Beispiel 1 Ungleichungen lösen: a)
, b)
. wir haben eine Funktion, b). Lösen Sie die Ungleichung, die wir haben

3.2. Methode des konzentrischen Kreises

Diese Methode ist analog zur Methode der parallelen numerischen Achsen beim Lösen von Systemen rationaler Ungleichungen.

Betrachten Sie ein Beispiel für ein System von Ungleichheiten.

Beispiel 5 Lösen Sie ein System einfacher trigonometrischer Ungleichungen

Zuerst lösen wir jede Ungleichung separat (Abbildung 5). In der oberen rechten Ecke der Abbildung geben wir an, für welches Argument der trigonometrische Kreis betrachtet wird.

Abb.5

Als nächstes bauen wir ein System aus konzentrischen Kreisen für das ArgumentX . Wir zeichnen einen Kreis und schattieren ihn nach der Lösung der ersten Ungleichung, dann zeichnen wir einen Kreis mit größerem Radius und schattieren ihn nach der Lösung der zweiten, dann bauen wir einen Kreis für die dritte Ungleichung und einen Grundkreis . Wir ziehen Strahlen von der Mitte des Systems durch die Enden der Bögen, so dass sie alle Kreise schneiden. Wir bilden eine Lösung auf dem Grundkreis (Abbildung 6).

Abb.6

Antworten:
,
.

Fazit

Alle Ziele der Kursarbeit wurden erfüllt. Das theoretische Material wird systematisiert: Die wichtigsten Arten trigonometrischer Ungleichungen und die wichtigsten Methoden zu ihrer Lösung (grafisch, algebraisch, Methode der Intervalle, Sektoren und die Methode der konzentrischen Kreise) werden angegeben. Für jede Methode wurde ein Beispiel zur Lösung einer Ungleichung gegeben. Auf den theoretischen Teil folgte der praktische Teil. Es enthält eine Reihe von Aufgaben zur Lösung trigonometrischer Ungleichungen.

Diese Studienarbeit kann von den Studierenden für selbstständiges Arbeiten genutzt werden. Die Schüler können den Grad der Assimilation dieses Themas überprüfen und die Ausführung von Aufgaben unterschiedlicher Komplexität üben.

Nachdem wir die einschlägige Literatur zu diesem Thema durchgearbeitet haben, können wir offensichtlich feststellen, dass die Fähigkeit und Fertigkeiten zum Lösen trigonometrischer Ungleichungen im Schulkurs der Algebra und der Beginn der Analysis sehr wichtig sind, deren Entwicklung erhebliche Anstrengungen von Seiten erfordert der Mathematiklehrer.

Daher wird diese Arbeit für Mathematiklehrer nützlich sein, da sie es ermöglicht, die Ausbildung von Schülern zum Thema "Trigonometrische Ungleichungen" effektiv zu organisieren.

Das Studium kann durch Erweiterung auf die Abschlussqualifikationsarbeit fortgesetzt werden.

Verzeichnis der verwendeten Literatur

Bogomolov, N.V. Aufgabensammlung der Mathematik [Text] / N.V. Bogomolow. – M.: Trappe, 2009. – 206 S.

Vygodsky, M. Ya. Handbuch der Elementarmathematik [Text] / M.Ya. Wygodski. – M.: Trappe, 2006. – 509 S.

Zhurbenko, L.N. Mathematik in Beispielen und Aufgaben [Text] / L.N. Zhurbenko. – M.: Infra-M, 2009. – 373 S.

Ivanov, O.A. Elementare Mathematik für Schüler, Studenten und Lehrer [Text] / O.A. Iwanow. – M.: MTsNMO, 2009. – 384 p.

Karp, A. P. Aufgaben in Algebra und die Anfänge der Analysis zur Organisation der Abschlusswiederholung und Zertifizierung in der 11. Klasse [Text] / A.P. Karpfen. – M.: Aufklärung, 2005. – 79 S.

Kulanin, E.D. 3000 Konkurrenzprobleme in der Mathematik [Text] / E.D. Kulanin. – M.: Irispresse, 2007. – 624 S.

Leibson, K.L. Sammlung praktischer Aufgaben in Mathematik [Text] / K.L. Leibson. – M.: Trappe, 2010. – 182 S.

Ellenbogen, V.V. Probleme mit Parametern und deren Lösung. Trigonometrie: Gleichungen, Ungleichungen, Systeme. Klasse 10 [Text] / V.V. Ellbogen. – M.: ARKTI, 2008. – 64 S.

Manova, A.N. Mathe. Express-Tutor zur Vorbereitung auf die Prüfung: Konto. Zulage [Text] / A.N. Manova. - Rostow am Don: Phönix, 2012. - 541 p.

Mordkovich, A.G. Algebra und Beginn der mathematischen Analyse. 10-11 Klassen. Lehrbuch für Studierende von Bildungseinrichtungen [Text] / A.G. Mordkowitsch. – M.: Irispresse, 2009. – 201 p.

Novikov, A.I. Trigonometrische Funktionen, Gleichungen und Ungleichungen [Text] / A.I. Novikov. - M.: FIZMATLIT, 2010. - 260 S.

Oganesyan, V.A. Methoden des Mathematikunterrichts in der Sekundarstufe: Allgemeine Methodik. Proz. Zuschuss für Physikstudenten. - Matte. Fälschung. päd. Kamerad. [Text] / V.A. Oganesjan. – M.: Aufklärung, 2006. – 368 S.

Olechnik, S.N. Gleichungen und Ungleichungen. Nicht standardmäßige Lösungsmethoden [Text] / S.N. Olechnik. - M.: Verlag Factorial, 1997. - 219 p.

Sevryukov, P.F. Trigonometrische, exponentielle und logarithmische Gleichungen und Ungleichungen [Text] / P.F. Sevryukov. – M.: Volksbildung, 2008. – 352 S.

Sergejew, I. N. VERWENDUNG: 1000 Aufgaben mit Antworten und Lösungen in Mathematik. Alle Aufgaben der Gruppe C [Text] / I.N. Sergejew. – M.: Klausur, 2012. – 301 S.

Sobolev, A.B. Elementare Mathematik [Text] / A.B. Sobolev. - Jekaterinburg: GOU VPO USTU-UPI, 2005. - 81 p.

Fenko, L.M. Die Methode der Intervalle beim Lösen von Ungleichungen und beim Studium von Funktionen [Text] / L.M. Fenko. – M.: Trappe, 2005. – 124 S.

Friedman, L.M. Theoretische Grundlagen der Methodik des Mathematikunterrichts [Text] / L.M. Friedmann. - M .: Buchhaus "LIBROKOM", 2009. - 248 p.

Anhang 1

Grafische Interpretation von Lösungen für die einfachsten Ungleichungen

Reis. eines

Reis. 2

Abb. 3

Abb.4

Abb.5

Abb.6

Abb.7

Abb.8

Anlage 2

Lösungen für die einfachsten Ungleichungen