On the youtube channel of our site, to keep abreast of all the new video lessons.

To begin with, let's recall the basic formulas of degrees and their properties.

Product of a number a happens to itself n times, we can write this expression as a a ... a = a n

1.a 0 = 1 (a ≠ 0)

3.a n a m = a n + m

4. (a n) m = a nm

5.a n b n = (ab) n

7.a n / a m = a n - m

Power or exponential equations- these are equations in which the variables are in powers (or exponents), and the base is a number.

Examples of exponential equations:

V this example the number 6 is the base, it always stands at the bottom, and the variable x degree or indicator.

Here are some more examples of exponential equations.
2 x * 5 = 10
16 x - 4 x - 6 = 0

Now let's look at how the exponential equations are solved?

Let's take a simple equation:

2 x = 2 3

Such an example can be solved even in the mind. It can be seen that x = 3. After all, in order for the left and right sides to be equal, you need to put the number 3 instead of x.
Now let's see how this solution needs to be formalized:

2 x = 2 3
x = 3

In order to solve such an equation, we removed identical grounds(that is, deuces) and wrote down what was left, these are degrees. We got the desired answer.

Now let's summarize our decision.

Algorithm for solving the exponential equation:
1. Need to check the same whether the equation has bases on the right and left. If the grounds are not the same, we are looking for options to solve this example.
2. After the bases are the same, equate degree and solve the resulting new equation.

Now let's solve a few examples:

Let's start simple.

The bases on the left and right sides are equal to the number 2, which means we can discard the base and equate their degrees.

x + 2 = 4 This is the simplest equation.
x = 4 - 2
x = 2
Answer: x = 2

In the following example, you can see that the bases are different, they are 3 and 9.

3 3x - 9x + 8 = 0

To begin with, we transfer the nine to the right side, we get:

Now you need to make the same bases. We know that 9 = 3 2. Let's use the formula of degrees (a n) m = a nm.

3 3x = (3 2) x + 8

We get 9 x + 8 = (3 2) x + 8 = 3 2x + 16

3 3x = 3 2x + 16 now you can see that in the left and right side the bases are the same and equal to the three, which means we can discard them and equate the degrees.

3x = 2x + 16 got the simplest equation
3x - 2x = 16
x = 16
Answer: x = 16.

See the following example:

2 2x + 4 - 10 4 x = 2 4

First of all, we look at the bases, bases are different two and four. And we need them to be the same. Convert the four by the formula (a n) m = a nm.

4 x = (2 2) x = 2 2x

And we also use one formula a n a m = a n + m:

2 2x + 4 = 2 2x 2 4

Add to the equation:

2 2x 2 4 - 10 2 2x = 24

We have brought the example to the same grounds. But we are hindered by other numbers 10 and 24. What to do with them? If you look closely, you can see that on the left side we repeat 2 2x, here is the answer - 2 2x we can take out of the brackets:

2 2x (2 4 - 10) = 24

Let's calculate the expression in brackets:

2 4 — 10 = 16 — 10 = 6

Divide the whole equation by 6:

Let's imagine 4 = 2 2:

2 2x = 2 2 bases are the same, we discard them and equate the powers.
2x = 2 we get the simplest equation. We divide it by 2 we get
x = 1
Answer: x = 1.

Let's solve the equation:

9 x - 12 * 3 x + 27 = 0

Let's transform:
9 x = (3 2) x = 3 2x

We get the equation:
3 2x - 12 3x +27 = 0

Our bases are the same equal to 3. In this example, you can see that the first three has a degree twice (2x) than the second (just x). In this case, you can solve replacement method... Replace the number with the smallest degree:

Then 3 2x = (3x) 2 = t 2

Replace all powers with x in the equation with t:

t 2 - 12t + 27 = 0
We get quadratic equation... We solve through the discriminant, we get:
D = 144-108 = 36
t 1 = 9
t 2 = 3

Returning to the variable x.

We take t 1:
t 1 = 9 = 3 x

That is,

3 x = 9
3 x = 3 2
x 1 = 2

Found one root. We are looking for the second, from t 2:
t 2 = 3 = 3 x
3 x = 3 1
x 2 = 1
Answer: x 1 = 2; x 2 = 1.

On the site you can ask questions of interest in the HELP TO SOLVE section, we will definitely answer you.

Join the group

I. Work n factors, each of which is equal to a called n-th power of the number a and denoted an.

Examples. Write the work in the form of a degree.

1) mmmm; 2) aaabb; 3) 5 · 5 · 5 · 5 · ccc; 4) ppkk + pppk-ppkkk.

Solution.

1) mmmm = m 4, since, by the definition of the degree, the product of four factors, each of which is equal to m, will the fourth power of m.

2) aaabb = a 3 b 2; 3) 5 · 5 · 5 · 5 · ccc = 5 4 s 3; 4) ppkk + pppk-ppkkk = p 2 k 2 + p 3 k-p 2 k 3.

II. The action by which the product of several equal factors is found is called exponentiation. The number that is raised to a power is called the base of the power. The number that shows the degree to which the base is raised is called the exponent. So, an- degree, a- the base of the degree, n- exponent. For example:

2 3 — this is the degree. Number 2 - the base of the power, the exponent is 3 ... Degree value 2 3 equals 8, because 2 3 = 2 2 2 = 8.

Examples. Write the following expressions without exponent.

5) 4 3; 6) a 3 b 2 c 3; 7) a 3 -b 3; 8) 2a 4 + 3b 2.

Solution.

5) 4 3 = 4 4 4 ; 6) a 3 b 2 c 3 = aaabbccc; 7) a 3 -b 3 = aaa-bbb; 8) 2a 4 + 3b 2 = 2aaaa + 3bb.

III. a 0 = 1 Any number (other than zero) to the zero degree is equal to one. For example, 25 0 = 1.
IV. a 1 = aAny number is in the first degree equal to itself.

V. a m∙ a n= a m + n When multiplying degrees with the same bases, the base is left the same, and the indicators add up.

Examples. Simplify:

9) a · a 3 · a 7; 10) b 0 + b 2 · b 3; 11) c 2 s 0 s s 4.

Solution.

9) a a 3 a 7= a 1 + 3 + 7 = a 11; 10) b 0 + b 2 b 3 = 1 + b 2 + 3 = 1 + b 5;

11) c 2 c 0 c c 4 = 1 c 2 c c 4 = c 2 + 1 + 4 = c 7 .

Vi. a m: a n= a m - nWhen dividing degrees with the same bases, the base is left the same, and the exponent of the divisor is subtracted from the exponent of the dividend.

Examples. Simplify:

12) a 8: a 3; 13) m 11: m 4; 14) 5 6: 5 4.

12) a 8: a 3= a 8-3 = a 5; 13) m 11: m 4= m 11-4 = m 7; fourteen ) 5 6:5 4 = 5 2 = 5 5 = 25.

Vii. (a m) n= a mn When raising a power to a power, the base is left the same, and the indicators are multiplied.

Examples. Simplify:

15) (a 3) 4; 16) (c 5) 2.

15) (a 3) 4= a 3 4 = a 12; 16) (c 5) 2= c 5 2 = c 10.

note, that, since the product does not change from the permutation of the factors, then:

15) (a 3) 4 = (a 4) 3; 16) (c 5) 2 = (c 2) 5.

VI II... (a ∙ b) n = a n ∙ b n When raising a product to a power, each of the factors is raised to this power.

Examples. Simplify:

17) (2a 2) 5; 18) 0.2 6 5 6; 19) 0.25 2 40 2.

Solution.

17) (2a 2) 5= 2 5 · a 2 · 5 = 32a 10; 18) 0.2 6 5 6= (0.2 5) 6 = 1 6 = 1;

19) 0.25 2 40 2= (0.25 40) 2 = 10 2 = 100.

IX. When raising to a power fraction, both the numerator and denominator of the fraction are raised to this power.

Examples. Simplify:

Solution.

Page 1 of 1 1

One of the main characteristics in algebra, and indeed in all mathematics, is the degree. Of course, in the 21st century, all calculations can be carried out on an online calculator, but it is better for the development of brains to learn how to do it yourself.

In this article, we will consider the most important questions regarding this definition. Namely, we will understand what it is in general and what are its main functions, what are the properties in mathematics.

Let's look at examples of how the calculation looks like, what are the basic formulas. Let's analyze the main types of quantities and how they differ from other functions.

Let's understand how to solve various problems using this value. Let's show with examples how to raise to zero, irrational, negative, etc.

Exponentiation calculator online

What is the degree of a number

What is meant by the expression "raise a number to a power"?

The power n of the number a is the product of factors of a value n times in a row.

Mathematically, it looks like this:

a n = a * a * a *… a n.

For example:

• 2 3 = 2 in the third step. = 2 * 2 * 2 = 8;
• 4 2 = 4 in step. two = 4 * 4 = 16;
• 5 4 = 5 in step. four = 5 * 5 * 5 * 5 = 625;
• 10 5 = 10 in 5 steps. = 10 * 10 * 10 * 10 * 10 = 100000;
• 10 4 = 10 in 4 steps. = 10 * 10 * 10 * 10 = 10000.

Below will be a table of squares and cubes from 1 to 10.

Grade table from 1 to 10

Below will be the results of the construction natural numbers in positive degrees - "from 1 to 100".

Ch-lo	2nd article	3rd article
1	1	1
2	4	8
3	9	27
4	16	64
5	25	125
6	36	216
7	49	343
8	64	512
9	81	279
10	100	1000

Power properties

What is typical for such mathematical function? Let's consider the basic properties.

Scientists have established the following signs characteristic of all degrees:

• a n * a m = (a) (n + m);
• a n: a m = (a) (n-m);
• (a b) m = (a) (b * m).

Let's check with examples:

2 3 * 2 2 = 8 * 4 = 32.On the other hand 2 5 = 2 * 2 * 2 * 2 * 2 = 32.

Similarly: 2 3: 2 2 = 8/4 = 2. Otherwise 2 3-2 = 2 1 = 2.

(2 3) 2 = 8 2 = 64. And if it is different? 2 6 = 2 * 2 * 2 * 2 * 2 * 2 = 32 * 2 = 64.

As you can see, the rules work.

But what about with addition and subtraction? It's simple. First, the exponentiation is performed, and only then the addition and subtraction.

Let's see some examples:

• 3 3 + 2 4 = 27 + 16 = 43;
• 5 2 - 3 2 = 25 - 9 = 16. Please note: the rule will not work if you subtract first: (5 - 3) 2 = 2 2 = 4.

But in this case, you must first calculate the addition, since there are actions in parentheses: (5 + 3) 3 = 8 3 = 512.

How to produce calculations in more difficult cases ? The procedure is the same:

• if there are brackets - you need to start with them;
• then exponentiation;
• then perform the actions of multiplication, division;
• after addition, subtraction.

There is specific properties, typical not for all degrees:

1. The nth root of the number a to the power of m will be written as: a m / n.
2. When raising a fraction to a power: both the numerator and its denominator are subject to this procedure.
3. When raising the product of different numbers to a power, the expression will correspond to the product of these numbers to a given power. That is: (a * b) n = a n * b n.
4. When raising a number to a negative step., You need to divide 1 by a number in the same st-no, but with a "+" sign.
5. If the denominator of the fraction is in a negative power, then this expression will be equal to the product of the numerator and the denominator in the positive power.
6. Any number in degree 0 = 1, and in step. 1 = to yourself.

These rules are important in individual cases, we will consider them in more detail below.

Degree with negative exponent

What to do when the degree is minus, i.e. when the exponent is negative?

Based on properties 4 and 5(see point above), it turns out:

A (- n) = 1 / A n, 5 (-2) = 1/5 2 = 1/25.

And vice versa:

1 / A (- n) = A n, 1/2 (-3) = 2 3 = 8.

And if a fraction?

(A / B) (- n) = (B / A) n, (3/5) (-2) = (5/3) 2 = 25/9.

Degree with natural exponent

It is understood as a degree with indicators equal to integers.

Things to remember:

A 0 = 1, 1 0 = 1; 2 0 = 1; 3.15 0 = 1; (-4) 0 = 1 ... etc.

A 1 = A, 1 1 = 1; 2 1 = 2; 3 1 = 3 ... etc.

In addition, if (-a) 2 n +2, n = 0, 1, 2 ... then the result will be with a "+" sign. If a negative number is raised to an odd power, then vice versa.

General properties, and all the specific features described above, are also characteristic of them.

Fractional degree

This view can be written by the scheme: A m / n. It reads as: n-th root of the number A to the m power.

You can do whatever you want with a fractional exponent: shorten, decompose, raise to a different degree, etc.

Irrational grade

Let α be an irrational number and A ˃ 0.

To understand the essence of a degree with such an indicator, consider different possible cases:

• A = 1. The result will be equal to 1. Since there is an axiom - 1 in all degrees is equal to one;

А r 1 ˂ А α ˂ А r 2, r 1 ˂ r 2 - rational numbers;

• 0˂А˂1.

In this case, on the contrary: А r 2 ˂ А α ˂ А r 1 under the same conditions as in the second paragraph.

For example, the exponent is π. It is rational.

r 1 - in this case is equal to 3;

r 2 - will be equal to 4.

Then, for A = 1, 1 π = 1.

A = 2, then 2 3 ˂ 2 π ˂ 2 4, 8 ˂ 2 π ˂ 16.

А = 1/2, then (½) 4 ˂ (½) π ˂ (½) 3, 1/16 ˂ (½) π ˂ 1/8.

These degrees are characterized by all the mathematical operations and specific properties described above.

Conclusion

To summarize - what are these values ​​for, what is the advantage of such functions? Of course, first of all, they simplify the life of mathematicians and programmers when solving examples, since they allow you to minimize calculations, reduce algorithms, systematize data, and much more.

Where else can this knowledge be useful? In any working profession: medicine, pharmacology, dentistry, construction, engineering, engineering, design, etc.

Expressions, expression conversion

Power expressions (expressions with powers) and their conversion

In this article, we will talk about converting power expressions. First, we will focus on the transformations that are performed with expressions of any kind, including those with exponential expressions, such as expanding parentheses, casting similar terms. And then we will analyze the transformations inherent precisely in expressions with powers: working with the base and exponent, using the properties of degrees, etc.

Page navigation.

What are exponential expressions?

The term "exponential expressions" is practically not found in school textbooks of mathematics, but it appears quite often in collections of problems, especially those designed to prepare for the exam and OGE, for example,. After analyzing the tasks in which it is required to perform any actions with exponential expressions, it becomes clear that expres- sions are understood as expressions containing degrees in their records. Therefore, for yourself, you can accept the following definition:

Definition.

Power expressions Are expressions containing degrees.

Let us give examples of exponential expressions... Moreover, we will represent them according to how the development of views on occurs from a degree with a natural indicator to a degree with a real indicator.

As you know, first there is an acquaintance with the power of a number with a natural exponent, at this stage the first simplest power expressions of the type 3 2, 7 5 +1, (2 + 1) 5, (−0,1) 4, 3 a 2 −a + a 2, x 3−1, (a 2) 3, etc.

A little later, the power of a number with an integer exponent is studied, which leads to the appearance of power expressions with negative integer powers, like the following: 3 −2, , a −2 + 2 b −3 + c 2.

In high school, they return to degrees again. There, a degree with a rational exponent is introduced, which entails the appearance of the corresponding power expressions: , , etc. Finally, degrees with irrational indicators and expressions containing them are considered:,.

The matter is not limited to the listed power expressions: the variable penetrates further into the exponent, and, for example, such expressions 2 x 2 +1 or ... And after acquaintance with, expressions with powers and logarithms begin to occur, for example, x 2 · lgx −5 · x lgx.

So, we figured out the question of what are exponential expressions. Next, we will learn how to transform them.

Basic types of transformations of power expressions

With exponential expressions, you can perform any of the basic identical transformations of expressions. For example, you can expand parentheses, replace numeric expressions with their values, provide similar terms, etc. Naturally, in this case it is necessary to follow the accepted procedure for performing actions. Here are some examples.

Example.

Evaluate the value of the exponential expression 2 3 · (4 2 −12).

Solution.

According to the order of performing the actions, we first perform the actions in brackets. There, firstly, we replace the power of 4 2 with its value 16 (see if necessary), and secondly, we calculate the difference 16−12 = 4. We have 2 3 (4 2 −12) = 2 3 (16−12) = 2 3 4.

In the resulting expression, replace the power 2 3 with its value 8, after which we calculate the product 8 4 = 32. This is the desired value.

So, 2 3 (4 2 −12) = 2 3 (16−12) = 2 3 4 = 8 4 = 32.

Answer:

2 3 (4 2 −12) = 32.

Example.

Simplify Power Expressions 3 a 4 b −7 −1 + 2 a 4 b −7.

Solution.

Obviously, this expression contains similar terms 3 · a 4 · b −7 and 2 · a 4 · b −7, and we can bring them:.

Answer:

3 a 4 b −7 −1 + 2 a 4 b −7 = 5 a 4 b −7 −1.

Example.

Imagine an expression with powers as a product.

Solution.

To cope with the task, the representation of the number 9 in the form of a power of 3 2 and the subsequent use of the formula for abbreviated multiplication is the difference of squares:

Answer:

There are also a number identical transformations, inherent in power expressions. Then we will analyze them.

Working with base and exponent

There are degrees, the base and / or exponent of which are not just numbers or variables, but some expressions. As an example, we give the records (2 + 0.37) 5-3.7 and (a (a + 1) -a 2) 2 (x + 1).

When working with such expressions, you can replace both the expression based on the degree and the expression in the exponent with an identically equal expression on the ODZ of its variables. In other words, we can, according to the rules known to us, separately transform the base of the degree, and separately - the exponent. It is clear that as a result of this transformation, an expression will be obtained that is identically equal to the original one.

Such transformations allow us to simplify expressions with powers or achieve other goals we need. For example, in the above exponential expression (2 + 0.3 · 7) 5-3.7, you can perform actions with the numbers in the base and exponent, which will allow you to go to the power 4.1 1.3. And after expanding the parentheses and reducing similar terms in the base of the degree (a (a + 1) −a 2) 2 (x + 1), we get a power expression of a simpler form a 2

Using power properties

One of the main tools for converting expres- sions with powers is equalities, reflecting. Let us recall the main ones. For any positive numbers a and b and arbitrary real numbers r and s, the following power properties are true:

• a r a s = a r + s;
• a r: a s = a r − s;
• (a b) r = a r b r;
• (a: b) r = a r: b r;
• (a r) s = a r s.

Note that for natural, integer, and also positive exponents, the restrictions on the numbers a and b may not be so strict. For example, for natural numbers m and n, the equality a m a n = a m + n is true not only for positive a, but also for negative ones, and for a = 0.

At school, the main attention when transforming power expressions is focused precisely on the ability to choose a suitable property and apply it correctly. In this case, the bases of degrees are usually positive, which allows using the properties of degrees without restrictions. The same applies to the transformation of expressions containing variables in the bases of degrees - the range of admissible values ​​of variables is usually such that the bases take only positive values ​​on it, which allows you to freely use the properties of degrees. In general, you need to constantly ask yourself whether it is possible in this case apply any property of degrees, because inaccurate use of properties can lead to a narrowing of the ODV and other troubles. These points are discussed in detail and with examples in the article on conversion of expressions using degree properties. Here we restrict ourselves to a few simple examples.

Example.

Imagine the expression a 2.5 · (a 2) −3: a −5.5 as a power with base a.

Solution.

First, we transform the second factor (a 2) −3 by the property of raising a power to a power: (a 2) −3 = a 2 (−3) = a −6... The original exponential expression will then take the form a 2.5 · a −6: a −5.5. Obviously, it remains to use the properties of multiplication and division of powers with the same base, we have
a 2.5 a -6: a -5.5 =
a 2.5-6: a -5.5 = a -3.5: a -5.5 =
a −3.5 - (- 5.5) = a 2.

Answer:

a 2.5 (a 2) −3: a −5.5 = a 2.

Power properties are used both from left to right and from right to left when transforming exponential expressions.

Example.

Find the value of the exponential expression.

Solution.

Equality (a b) r = a r b r, applied from right to left, allows you to go from the original expression to the product of the form and further. And when multiplying degrees with the same bases, the indicators add up: .

It was possible to perform the transformation of the original expression in another way:

Answer:

.

Example.

Given the exponential expression a 1.5 −a 0.5 −6, enter the new variable t = a 0.5.

Solution.

The degree a 1.5 can be represented as a 0.5 · 3 and further, based on the property of the degree to the degree (a r) s = a r · s, applied from right to left, transform it to the form (a 0.5) 3. Thus, a 1.5 −a 0.5 −6 = (a 0.5) 3 −a 0.5 −6... Now it is easy to introduce a new variable t = a 0.5, we get t 3 −t − 6.

Answer:

t 3 −t − 6.

Converting fractions containing powers

Power expressions can contain fractions with powers or be such fractions. Any of the basic transformations of fractions that are inherent in fractions of any kind are fully applicable to such fractions. That is, fractions that contain powers can be canceled, reduced to a new denominator, worked separately with their numerator and separately with the denominator, etc. To illustrate the spoken words, consider the solutions of several examples.

Example.

Simplify exponential expression .

Solution.

This exponential expression is a fraction. Let's work with its numerator and denominator. In the numerator, we open the brackets and simplify the expression obtained after that, using the properties of the powers, and in the denominator we give similar terms:

And we also change the sign of the denominator by placing a minus in front of the fraction: .

Answer:

.

The reduction of fractions containing powers to a new denominator is carried out similarly to the reduction of rational fractions to a new denominator. In this case, an additional factor is also found and the numerator and denominator of the fraction are multiplied by it. When performing this action, it is worth remembering that reduction to a new denominator can lead to a narrowing of the ODV. To prevent this from happening, it is necessary that the additional factor does not vanish for any values ​​of the variables from the ODZ variables for the original expression.

Example.

Reduce fractions to a new denominator: a) to the denominator a, b) to the denominator.

Solution.

a) In this case, it is quite easy to figure out what additional factor helps to achieve desired result... This is a factor of a 0.3, since a 0.7 · a 0.3 = a 0.7 + 0.3 = a. Note that on the range of permissible values ​​of the variable a (this is the set of all positive real numbers) the degree a 0.3 does not vanish, therefore, we have the right to multiply the numerator and denominator of the given fraction by this additional factor:

b) Looking more closely at the denominator, you can find that

and multiplying this expression by will give the sum of the cubes and, that is,. And this is the new denominator to which we need to reduce the original fraction.

This is how we found an additional factor. On the range of valid values ​​of the variables x and y, the expression does not vanish, therefore, we can multiply the numerator and denominator of the fraction by it:

Answer:

a) , b) .

The abbreviation of fractions containing powers is also nothing new: the numerator and denominator are represented as a number of factors, and the same factors of the numerator and denominator are canceled.

Example.

Reduce the fraction: a) , b).

Solution.

a) First, the numerator and denominator can be reduced by the numbers 30 and 45, which is 15. Also, obviously, one can perform a reduction by x 0.5 +1 and by ... Here's what we have:

b) In this case, the same factors in the numerator and denominator are not immediately visible. To get them, you will have to perform preliminary transformations. In this case, they consist in factoring the denominator into factors according to the formula for the difference of squares:

Answer:

a)

b) .

Reducing fractions to a new denominator and reducing fractions is mainly used to perform actions with fractions. Actions are performed according to known rules. When adding (subtracting) fractions, they are reduced to common denominator, after which the numerators are added (subtracted), and the denominator remains the same. The result is a fraction, the numerator of which is the product of the numerators, and the denominator is the product of the denominators. Division by a fraction is multiplication by the inverse of the fraction.

Example.

Follow the steps .

Solution.

First, we subtract the fractions in parentheses. To do this, we bring them to a common denominator, which is , after which we subtract the numerators:

Now we multiply the fractions:

Obviously, it is possible to cancel by a power of x 1/2, after which we have .

You can also simplify the exponential expression in the denominator by using the difference of squares formula: .

Answer:

Example.

Simplify exponential expression .

Solution.

Obviously, this fraction can be canceled by (x 2.7 +1) 2, this gives the fraction ... It is clear that something else needs to be done with the degrees of x. To do this, we transform the resulting fraction into a product. This gives us the opportunity to use the property of dividing degrees with the same bases: ... And at the end of the process, we pass from the last product to a fraction.

Answer:

.

And we also add that it is possible and in many cases desirable to transfer multipliers with negative exponents from the numerator to the denominator or from the denominator to the numerator, changing the sign of the exponent. Such transformations often simplify further actions. For example, an exponential expression can be replaced with.

Converting expressions with roots and powers

Often in expressions in which some transformations are required, along with powers with fractional exponents, roots are also present. To transform such an expression to the desired form, in most cases it is enough to go only to the roots or only to the powers. But since it is more convenient to work with degrees, they usually go from roots to degrees. However, it is advisable to carry out such a transition when the ODV of variables for the original expression allows you to replace the roots with powers without the need to refer to the module or split the ODV into several intervals (we discussed in detail in the article the transition from roots to powers and back. a degree with an irrational indicator is introduced, which makes it possible to talk about a degree with an arbitrary real indicator. exponential function , which is analytically set by the degree, at the base of which is the number, and in the indicator - the variable. So we are faced with exponential expressions containing numbers in the base of the degree, and in the exponent - expressions with variables, and naturally there is a need to perform transformations of such expressions.

It should be said that the transformation of expressions of this type usually has to be performed when solving exponential equations and exponential inequalities and these conversions are pretty simple. In the overwhelming majority of cases, they are based on the properties of the degree and are mainly aimed at introducing a new variable in the future. We can demonstrate them by the equation 5 2 x + 1 −3 5 x 7 x −14 7 2 x − 1 = 0.

First, the degrees in which the sum of a variable (or expressions with variables) and a number is found are replaced by products. This applies to the first and last terms of the expression on the left side:
5 2 x 5 1 −3 5 x 7 x −14 7 2 x 7 −1 = 0,
5 5 2 x −3 5 x 7 x −2 7 2 x = 0.

Further, both sides of the equality are divided by the expression 7 2 x, which takes only positive values ​​on the ODZ of the variable x for the original equation (this is a standard technique for solving equations of this kind, we are not talking about it now, so focus on the subsequent transformations of expressions with powers ):

Fractions with powers are now canceled, which gives .

Finally, the ratio of degrees with the same exponents is replaced by the degrees of relations, which leads to the equation which is equivalent ... The performed transformations allow us to introduce a new variable, which reduces the solution of the original exponential equation to the solution of the quadratic equation

I. V. Boykov, L. D. Romanova Collection of tasks for preparing for the exam. Part 1. Penza 2003.

Sections: Maths

Lesson type: lesson in generalization and systematization of knowledge

Goals:

teaching- repeat the definition of the degree, the rules for multiplying and dividing degrees, raising a degree to a power, consolidate the ability to solve examples containing degrees,

developing- development logical thinking students, interest in the studied material,

educating- fostering a responsible attitude towards learning, a culture of communication, a sense of collectivism.

Equipment: computer, multimedia projector, interactive whiteboard, presentation “Degrees” for oral counting, cards with assignments, handouts.

Lesson plan:

Organizing time.

Repeating rules

Verbal counting.

Historical reference.

Work at the blackboard.

Physical education.

Work on an interactive whiteboard.

Independent work.

Homework.

Summing up the lesson.

During the classes

I. Organizational moment

Communication of the topic and objectives of the lesson.

In the previous lessons, you discovered wonderful world degrees, learned to multiply and divide degrees, raise them to a degree. Today we must consolidate the knowledge gained by solving examples.

II. Repeating rules(orally)

1. Give a definition of a degree with a natural indicator? (By the power of the number a with a natural exponent greater than 1 is called the product n factors, each of which is equal to a.)
2. How to multiply two degrees? (To multiply degrees with the same bases, you must leave the base the same, and add the exponents.)
3. How do you divide a degree by a degree? (To divide powers with the same bases, you must leave the base the same, and subtract the indicators.)
4. How to raise a work to a power? (To raise a product to a power, each factor must be raised to this power)
5. How to raise a degree to a degree? (To raise a power to a power, you must leave the base the same, and multiply the indicators)

III. Verbal counting(by multimedia)

IV. Historical reference

All tasks are from the Ahmes papyrus, which was written about 1650 BC. NS. related to the practice of construction, demarcation of land plots, etc. The tasks are grouped by topic. For the most part, these are tasks for finding the areas of a triangle, quadrangles and a circle, various actions with integers and fractions, proportional division, finding ratios, there is also raising to different powers, solving equations of the first and second degrees with one unknown.

There is no explanation or proof whatsoever. The desired result is either given directly, or a short algorithm for its calculation is given. This way of presentation, typical for the science of countries the ancient East, suggests that mathematics there developed through generalizations and guesses that do not form any general theory. However, the papyrus contains a number of evidence that Egyptian mathematicians knew how to root and exponentiate, solve equations, and even possessed the rudiments of algebra.

V. Working at the blackboard

Find the meaning of the expression in a rational way:

Calculate the value of the expression:



Vi. Physical education

6. for eyes
7. for the neck
8. for hands
9. for the torso
10. for legs

Vii. Solving problems(shown on an interactive whiteboard)

Is the root of the equation a positive number?

xn - i1abbnckbmcl9fb.xn - p1ai

Formulas for degrees and roots.

Power formulas are used in the process of reducing and simplifying complex expressions, in solving equations and inequalities.

Number c is an n-th power of the number a when:



Operations with degrees.

1. Multiplying degrees with the same base, their indicators add up:

2. In the division of degrees with the same base, their indicators are subtracted:



3. The degree of the product of 2 or more factors is equal to the product of the degrees of these factors:

(abc ...) n = a n b n c n ...

4. The power of a fraction is equal to the ratio of the powers of the dividend and the divisor:

5. Raising a degree to a degree, the exponents are multiplied:

Each of the above formula is true from left to right and vice versa.

Root operations.

1. The root of the product of several factors is equal to the product of the roots of these factors:

2. Root from relationship is equal to the ratio dividend and divisor of roots:



3. When raising a root to a power, it is enough to raise the root number to this power:



4. If you increase the degree of the root in n once and at the same time build in n-th power of the root number, then the root value will not change:



5. If you reduce the degree of the root in n once and at the same time extract the root n-th power of the radical number, then the value of the root will not change:



The power of a number with a non-positive (integer) exponent is defined as a unit divided by the power of the same number with an exponent equal to the absolute value of the non-positive exponent:



Formula a m : a n = a m - n can be used not only for m > n, but also at m 4: a 7 = a 4 - 7 = a -3.

So that the formula a m : a n = a m - n became fair when m = n, the presence of the zero degree is needed.

The power of any nonzero number with zero exponent equals one.

To erect a real number a to the degree m / n, you need to extract the root n-Th degree of m-th power of this number a:



Degree formulas.

6. a — n = - division of degrees;

7. - division of degrees;

8.a 1 / n = ;

Degrees rule of action with degrees

1. The degree of the product of two or more factors is equal to the product of the degrees of these factors (with the same exponent):

(abc ...) n = a n b n c n ...

Example 1. (7 2 10) 2 = 7 2 2 2 10 2 = 49 4 100 = 19600. Example 2. (x 2 –a 2) 3 = [(x + a) (x - a)] 3 = ( x + a) 3 (x - a) 3

In practical terms, the reverse conversion is more important:

a n b n c n… = (abc…) n

those. the product of the same powers of several quantities is equal to the same degree of the product of these quantities.

Example 3. Example 4. (a + b) 2 (a 2 - ab + b 2) 2 = [(a + b) (a 2 - ab + b 2)] 2 = (a 3 + b 3) 2

2. The power of the quotient (fraction) is equal to the quotient of dividing the same power of the divisor by the same power of the divisor:

Example 5. Example 6.

Reverse conversion: Example 7. ... Example 8. .

3. When multiplying degrees with the same bases, the exponents are added:

Example 9.2 2 2 5 = 2 2 + 5 = 2 7 = 128. Example 10. (a - 4c + x) 2 (a - 4c + x) 3 = (a - 4c + x) 5.

4. When dividing degrees with the same bases, the exponent of the divisor is subtracted from the exponent of the dividend

Example 11.12 5:12 3 = 12 5-3 = 12 2 = 144. Example 12 (x-y) 3: (x-y) 2 = x-y.

5. When raising a degree to a power, the exponents are multiplied:

Example 13. (2 3) 2 = 2 6 = 64. Example 14.

www.maths.yfa1.ru

Degrees and roots

Operations with powers and roots. Degree with negative ,

zero and fractional indicator. About expressions that don't make sense.

Operations with degrees.

1. When multiplying degrees with the same base, their indicators are added:

a m · a n = a m + n.

2. When dividing degrees with the same base, their indicators deducted .



3. The degree of the product of two or more factors is equal to the product of the degrees of these factors.

4. The degree of the ratio (fraction) is equal to the ratio of the degrees of the dividend (numerator) and divisor (denominator):

(a / b) n = a n / b n.

5. When raising a degree to a degree, their indicators are multiplied:

All of the above formulas are read and executed in both directions from left to right and vice versa.

EXAMPLE (2 · 3 · 5/15) ² = 2 ² 3 ² 5 ² / 15 ² = 900/225 = 4 .

Root operations. In all the formulas below, the symbol means arithmetic root(the radical expression is positive).

1. The root of the product of several factors is equal to the product of the roots of these factors:

2. The root of the ratio is equal to the ratio of the roots of the dividend and the divisor:



3. When raising a root to a power, it is enough to raise to this power root number:



4. If we increase the degree of the root by m times and at the same time raise the radical number to the m-th power, then the value of the root will not change:



5. If we reduce the degree of the root by m times and at the same time extract the root of the m -th degree from the radical number, then the value of the root will not change:




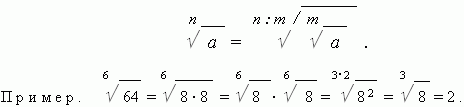
Expansion of the concept of degree. Until now, we have considered degrees only with a natural exponent; but actions with powers and roots can also lead to negative, zero and fractional indicators. All these degree indicators require additional definition.

Degree with negative exponent. The power of a number with a negative (integer) exponent is defined as a unit divided by the power of the same number with an exponent equal to the absolute value of a negative exponent:



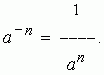
Now the formula a m : a n = a m - n can be used not only for m greater than n, but also at m less than n .

EXAMPLE a 4: a 7 = a 4 — 7 = a — 3 .

If we want the formula a m : a n = a m — n was fair when m = n, we need a definition of the zero degree.

Zero grade. The power of any nonzero number with exponent zero is 1.

EXAMPLE 2 0 = 1, ( – 5) 0 = 1, (– 3 / 5) 0 = 1.

Fractional exponent. In order to raise a real number a to the power of m / n, you need to extract the n-th root of the m-th power of this number a:



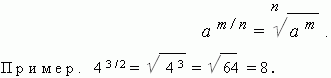
About expressions that don't make sense. There are several such expressions.

where a ≠ 0 , does not exist.

Indeed, assuming that x- some number, then in accordance with the definition of the division operation we have: a = 0· x, i.e. a= 0, which contradicts the condition: a ≠ 0

— any number.

Indeed, if we assume that this expression is equal to some number x, then, according to the definition of the division operation, we have: 0 = 0 x... But this equality holds for any number x, as required.

0 0 — any number.



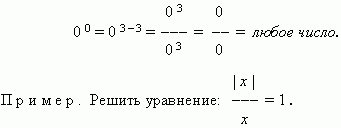
Solution. Consider three main cases:

1) x = 0 – this value does not satisfy the given equation

2) at x> 0 we get: x / x= 1, i.e. 1 = 1, whence it follows that

what x- any number; but taking into account that in

our case x> 0, the answer is x > 0 ;

Degree properties

We remind you that this lesson understands power properties with natural indicators and zero. Rational degrees and their properties will be covered in the 8th grade lessons.

A natural exponent has several important properties that make it easier to calculate in exponent examples.

Property number 1
Product of degrees

When multiplying degrees with the same bases, the base remains unchanged, and the exponents are added.

a m · a n = a m + n, where "a" is any number, and "m", "n" are any natural numbers.

This property of degrees also affects the product of three or more degrees.

• Simplify the expression.
  b b 2 b 3 b 4 b 5 = b 1 + 2 + 3 + 4 + 5 = b 15
• Present as a degree.
  6 15 36 = 6 15 6 2 = 6 15 6 2 = 6 17
• Present as a degree.
  (0.8) 3 (0.8) 12 = (0.8) 3 + 12 = (0.8) 15

Please note that in the specified property, it was only about the multiplication of powers with the same bases.... It does not apply to their addition.

You cannot replace the amount (3 3 + 3 2) with 3 5. This is understandable if
count (3 3 + 3 2) = (27 + 9) = 36, and 3 5 = 243

Property number 2
Private degrees

When dividing degrees with the same bases, the base remains unchanged, and the exponent of the divisor is subtracted from the exponent of the dividend.

• Write the quotient as a degree
  (2b) 5: (2b) 3 = (2b) 5 - 3 = (2b) 2
• Calculate.

11 3 - 2 4 2 - 1 = 11 4 = 44
Example. Solve the equation. We use the property of private degrees.
3 8: t = 3 4

Answer: t = 3 4 = 81

Using properties # 1 and # 2, you can easily simplify expressions and perform calculations.

Example. Simplify the expression.
4 5m + 6 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 - 4m - 3 = 4 2m + 5

Example. Find the value of an expression using the properties of the degree.

2 11 − 5 = 2 6 = 64

Please note that property 2 was only about dividing degrees with the same bases.

You cannot replace the difference (4 3 −4 2) with 4 1. This is understandable if we calculate (4 3 −4 2) = (64 - 16) = 48, and 4 1 = 4

Property number 3
Exponentiation

When raising a degree to a power, the base of the degree remains unchanged, and the exponents are multiplied.

(a n) m = a n · m, where "a" is any number, and "m", "n" are any natural numbers.

Example.
(a 4) 6 = a 4 6 = a 24

Example. Represent 3 20 as a power with base 3 2.

By the property of raising a power to a power it is known that when raised to a power, the indicators are multiplied, which means:

Properties 4
Degree of work

When raising a power to a power of a product, each factor is raised to this power and the results are multiplied.

(a · b) n = a n · b n, where “a”, “b” are any rational numbers; "N" is any natural number.

• Example 1.
  (6 a 2 b 3 s) 2 = 6 2 a 2 2 b 3 2 s 1 2 = 36 a 4 b 6 s 2
• Example 2.
  (−x 2 y) 6 = ((−1) 6 x 2 6 y 1 6) = x 12 y 6

Note that property # 4, like other degree properties, is applied in reverse order.

(a n b n) = (a b) n

That is, in order to multiply degrees with the same indicators, you can multiply the bases, and the exponent can be left unchanged.

• Example. Calculate.
  2 4 5 4 = (2 5) 4 = 10 4 = 10,000
• Example. Calculate.
  0.5 16 2 16 = (0.5 2) 16 = 1

In more complex examples, there may be cases when multiplication and division must be performed over degrees with different bases and different exponents. In this case, we advise you to proceed as follows.

For example, 4 5 3 2 = 4 3 4 2 3 2 = 4 3 (4 3) 2 = 64 12 2 = 64 144 = 9216

An example of raising to a decimal power.

4 21 (−0.25) 20 = 4 4 20 (−0.25) 20 = 4 (4 (−0.25)) 20 = 4 (−1) 20 = 4 1 = 4

Properties 5
Degree of quotient (fraction)

To raise a quotient to a power, you can raise a separate dividend and a divisor to this power, and divide the first result by the second.

(a: b) n = a n: b n, where “a”, “b” are any rational numbers, b ≠ 0, n is any natural number.

• Example. Present the expression in the form of private degrees.
  (5: 3) 12 = 5 12: 3 12

We remind you that the quotient can be represented as a fraction. Therefore, we will dwell on the topic of raising a fraction to a power in more detail on the next page.