نابرابری های مثلثاتی نابرابری های مثلثاتی و راه حل های آنها چگونه نامعادله های مثلثاتی دوگانه را حل کنیم
وزارت آموزش و پرورش جمهوری بلاروس
موسسه تحصیلی
"دانشگاه ایالتی گومل
به نام فرانسیسک اسکارینا"
دانشکده ریاضی
گروه جبر و هندسه
واجد شرایط دفاع
سر بخش Shemetkov L.A.
معادلات و نابرابری های مثلثاتی
کار دوره
مجری:
گروه دانشجویی M-51
سانتی متر. گورسکی
مشاور علمی
استاد ارشد
V.G. سافونوف
گومل 2008
مقدمه
روشهای اساسی برای حل معادلات مثلثاتی
فاکتورسازی
حل معادلات با تبدیل حاصل ضرب توابع مثلثاتی به مجموع
حل معادلات با استفاده از فرمول های استدلال سه گانه
ضرب در یک تابع مثلثاتی
معادلات مثلثاتی غیر استاندارد
نابرابری های مثلثاتی
انتخاب ریشه ها
وظایف برای راه حل مستقل
نتیجه
فهرست منابع مورد استفاده
در دوران باستان، مثلثات در ارتباط با نیازهای نجوم، نقشه برداری و ساخت و ساز پدید آمد، یعنی ماهیت آن کاملاً هندسی بود و عمدتاً نشان داده می شد.<<исчисление хорд>> با گذشت زمان، برخی از نکات تحلیلی شروع به تلاقی در آن کردند. در نیمه اول قرن هجدهم چرخشی شدیدی رخ داد که پس از آن مثلثات مسیر جدیدی را در پیش گرفت و به سمت تحلیل ریاضی رفت. در این زمان بود که وابستگی های مثلثاتی به عنوان توابع در نظر گرفته شدند.
معادلات مثلثاتی یکی از سخت ترین مباحث درس ریاضی مدرسه است. معادلات مثلثاتی هنگام حل مسائل در پلان سنجی، هندسه جامد، نجوم، فیزیک و سایر زمینه ها بوجود می آیند. معادلات مثلثاتی و نابرابری از سال به سال در میان وظایف آزمون متمرکز یافت می شود.
مهمترین تفاوت معادلات مثلثاتی و جبری این است که معادلات جبری تعداد ریشه های محدودی دارند، در حالی که معادلات مثلثاتی دارای تعداد بی نهایت هستند که انتخاب ریشه ها را بسیار پیچیده می کند. یکی دیگر از ویژگی های معادلات مثلثاتی، فرم غیر منحصر به فرد نوشتن پاسخ است.
این پایان نامه به روش های حل معادلات مثلثاتی و نامساوی اختصاص دارد.
کار دیپلم از 6 بخش تشکیل شده است.
بخش اول شامل اطلاعات نظری اساسی است: تعریف و ویژگی‌های توابع مثلثاتی و مثلثاتی معکوس. جدول مقادیر توابع مثلثاتی برای برخی از آرگومان ها؛ بیان توابع مثلثاتی بر حسب سایر توابع مثلثاتی، که برای تبدیل عبارات مثلثاتی، به ویژه آنهایی که حاوی توابع مثلثاتی معکوس هستند، بسیار مهم است. علاوه بر فرمول های مثلثاتی پایه، که از دوره مدرسه به خوبی شناخته شده است، فرمول هایی ارائه شده است که عبارات حاوی توابع مثلثاتی معکوس را ساده می کند.
بخش دوم به تشریح روش های اصلی برای حل معادلات مثلثاتی می پردازد. حل معادلات مثلثاتی ابتدایی، روش فاکتورگیری، روشهای کاهش معادلات مثلثاتی به جبری در نظر گرفته شده است. با توجه به اینکه جواب های معادلات مثلثاتی را می توان به روش های مختلفی نوشت و شکل این جواب ها اجازه نمی دهد که بلافاصله مشخص شود که آیا این جواب ها یکسان هستند یا متفاوت، که می تواند<<сбить с толку>> هنگام حل تست ها، یک طرح کلی برای حل معادلات مثلثاتی در نظر گرفته می شود و تبدیل گروه های راه حل های کلی معادلات مثلثاتی با جزئیات در نظر گرفته می شود.
بخش سوم به معادلات مثلثاتی غیر استاندارد می پردازد که راه حل های آن بر اساس رویکرد تابعی است.
بخش چهارم به نابرابری های مثلثاتی می پردازد. روشهای حل نابرابری‌های مثلثاتی ابتدایی، هم بر روی دایره واحد و هم با روش گرافیکی، به تفصیل در نظر گرفته شده‌اند. فرآیند حل نابرابری‌های مثلثاتی غیر ابتدایی از طریق نابرابری‌های ابتدایی و روش فواصل که قبلاً برای دانش‌آموزان شناخته شده بود، شرح داده می‌شود.
بخش پنجم دشوارترین کارها را ارائه می دهد: زمانی که نه تنها باید یک معادله مثلثاتی را حل کرد، بلکه ریشه هایی را از ریشه های یافت شده انتخاب کرد که شرایطی را برآورده می کند. این بخش راه حل هایی برای کارهای معمولی برای انتخاب ریشه ها ارائه می دهد. اطلاعات نظری لازم برای انتخاب ریشه ها آورده شده است: تقسیم مجموعه اعداد صحیح به زیر مجموعه های غیر متقاطع، حل معادلات در اعداد صحیح (دیوفانتین).
بخش ششم وظایفی را برای حل مستقل ارائه می دهد که در قالب یک آزمون طراحی شده است. 20 کار آزمون سخت ترین کارهایی را که می توان در آزمون متمرکز با آنها مواجه شد فهرست می کند.
معادلات مثلثاتی ابتدایی
معادلات مثلثاتی ابتدایی معادلاتی از فرم هستند که در آن یکی از توابع مثلثاتی وجود دارد: , , , .
معادلات مثلثاتی ابتدایی ریشه های بی نهایت زیادی دارند. به عنوان مثال، مقادیر زیر معادله را برآورده می کند: , , , و غیره. فرمول کلی که با آن تمام ریشه های معادله پیدا می شود، که در آن، عبارت است از:
در اینجا می تواند هر مقدار صحیح را بگیرد، هر یک از آنها با ریشه خاصی از معادله مطابقت دارد. در این فرمول (و همچنین در فرمول های دیگری که معادلات مثلثاتی ابتدایی حل می شوند) نامیده می شود. پارامتر. آنها معمولاً یادداشت می کنند و در نتیجه تأکید می کنند که پارامتر می تواند هر مقدار صحیح را بگیرد.
راه حل های معادله، که در آن، با فرمول پیدا می شود
معادله با استفاده از فرمول حل می شود
و معادله --- طبق فرمول
اجازه دهید به ویژه به برخی از موارد خاص معادلات مثلثاتی ابتدایی توجه کنیم، زمانی که راه حل را می توان بدون استفاده از فرمول های کلی نوشت:
هنگام حل معادلات مثلثاتی، دوره توابع مثلثاتی نقش مهمی ایفا می کند. بنابراین، ما دو قضیه مفید ارائه می دهیم:
قضیه اگر --- دوره اصلی تابع باشد، آنگاه عدد دوره اصلی تابع است.
دوره های توابع و در صورت وجود اعداد طبیعی قابل مقایسه نامیده می شوند، که .
قضیه اگر توابع تناوبی و , دارای تناسب و , باشند , دوره مشترک دارند که دوره توابع , , , .
این قضیه می گوید دوره تابع , , , چیست و لزوما دوره اصلی نیست. به عنوان مثال، دوره اصلی توابع و --- است و دوره اصلی محصول آنها --- است.
معرفی یک استدلال کمکی
روش استاندارد تبدیل عبارات فرم 
ترفند زیر است: اجازه دهید --- زاویه داده شده توسط تساوی 
, 
. برای هر و چنین زاویه ای وجود دارد. به این ترتیب. اگر , یا , , , در غیر این صورت .
طرحی برای حل معادلات مثلثاتی
طرح اصلی که هنگام حل معادلات مثلثاتی از آن راهنمایی خواهیم کرد به شرح زیر است:
حل معادله داده شده به حل معادلات ابتدایی تقلیل می یابد. راه حل --- تبدیل ها، فاکتورسازی ها، جایگزینی مجهولات. اصل راهنما این است که ریشه ها را از دست ندهیم. این بدان معنی است که هنگام حرکت به معادله (معادلات) بعدی، از ظهور ریشه های اضافی (خارجی) نمی ترسیم، بلکه فقط اهمیت می دهیم که هر معادله بعدی از "زنجیره" خود (یا مجموعه ای از معادلات در مورد انشعاب) پیامد قبلی است. یکی از روش های ممکن برای انتخاب ریشه ها بررسی است. ما فوراً متذکر می شویم که در مورد معادلات مثلثاتی ، معمولاً مشکلات مربوط به انتخاب ریشه ها با تأیید در مقایسه با معادلات جبری به شدت افزایش می یابد. پس از همه، شما باید سری، متشکل از تعداد نامتناهی از اعضا را بررسی کنید.
باید به تغییر مجهولات در حل معادلات مثلثاتی اشاره کرد. در اغلب موارد پس از جایگزینی لازم، یک معادله جبری به دست می آید. علاوه بر این، معادلات چندان نادر نیستند، که اگرچه از نظر ظاهر مثلثاتی هستند، اما اساساً چنین نیستند، زیرا قبلاً پس از اولین مرحله --- تغییرات متغیرها --- به جبری تبدیل می شوند و بازگشت به مثلثات فقط در مرحله حل معادلات مثلثاتی ابتدایی
یک بار دیگر به یاد بیاورید: جایگزینی مجهول باید در اسرع وقت انجام شود، معادله حاصل پس از جایگزینی باید تا انتها حل شود، از جمله مرحله انتخاب ریشه ها، و تنها پس از آن به مجهول اصلی باز می گردد.
یکی از ویژگی های معادلات مثلثاتی این است که پاسخ را در بسیاری از موارد می توان به روش های مختلفی نوشت. حتی برای حل معادله 
پاسخ را می توان اینگونه نوشت:
1) در قالب دو سری: 
, , ;
2) به شکل استاندارد که ترکیبی از سری فوق است: ;
3) از آن زمان 
، سپس پاسخ را می توان به صورت زیر نوشت 
، . (به‌علاوه، وجود پارامتر، یا در رکورد پاسخ به‌طور خودکار به این معنی است که این پارامتر تمام مقادیر صحیح ممکن را می‌گیرد. استثنائاتی قید می‌شود.)
بدیهی است که سه مورد ذکر شده تمامی امکانات را برای نوشتن پاسخ معادله مورد بررسی تمام نمی کند (بی نهایت تعداد آنها وجود دارد).
به عنوان مثال، برای 
. بنابراین، در دو مورد اول، اگر، می توانیم با را جایگزین کنیم .
معمولاً پاسخ بر اساس بند 2 نوشته می شود. یادآوری توصیه زیر مفید است: اگر کار با حل معادله به پایان نرسید، باز هم باید یک مطالعه انجام شود، انتخاب ریشه ها، سپس راحت ترین شکل ضبط در بند 1 نشان داده شده است. (توصیه مشابهی باید برای معادله داده شود.)
بیایید مثالی را در نظر بگیریم که آنچه گفته شد را نشان می دهد.
مثال معادله را حل کنید.
راه حل.واضح ترین روش زیر است. این معادله به دو قسمت تقسیم می شود: و. با حل هر یک از آنها و ترکیب پاسخ های به دست آمده به .
یک راه دیگر.پس از آن، جایگزینی و با فرمول های کاهش. پس از دگرگونی های جزئی، از کجا می گیریم 
.
در نگاه اول، فرمول دوم هیچ مزیت خاصی نسبت به فرمول اول ندارد. با این حال، اگر به عنوان مثال، را بگیریم، معلوم می شود که، i.e. معادله یک راه حل دارد، در حالی که راه اول ما را به پاسخ می رساند 
. «ببینید» و برابری را ثابت کنید 
نه چندان آسان
پاسخ. .
تبدیل و اتحاد گروه های جواب های کلی معادلات مثلثاتی
ما یک پیشروی حسابی را در نظر خواهیم گرفت که به طور نامحدود در هر دو جهت گسترش می یابد. اعضای این پیشروی را می توان به دو گروه از اعضا تقسیم کرد که در سمت راست و چپ برخی از اعضا قرار دارند که به آنها عضو مرکزی یا صفر پیشرفت می گویند.
با ثابت کردن یکی از شرایط پیشرفت نامتناهی با یک عدد صفر، باید برای تمام عبارت‌های باقی‌مانده یک شماره‌گذاری مضاعف انجام دهیم: مثبت برای عبارت‌های واقع در سمت راست، و منفی برای عبارت‌های واقع در سمت چپ صفر.
در حالت کلی، اگر اختلاف پیشروی عدد صفر باشد، فرمول هر (امین) ترم پیشروی حسابی نامتناهی است:
تبدیل فرمول برای هر عضو یک پیشرفت حسابی نامحدود
1. اگر تفاضل پیشرفت را به جمله صفر اضافه یا کم کنیم، پیشرفت از این تغییر نمی کند، بلکه فقط جمله صفر حرکت می کند، یعنی. شماره اعضا تغییر خواهد کرد
2. اگر ضریب یک متغیر در ضرب شود، آنگاه این تنها به جایگشت گروه های راست و چپ اعضا منجر می شود.
3. اگر اعضای متوالی یک پیشروی بی نهایت
به عنوان مثال،،،، ...،، برای ساختن شرایط مرکزی پیشرفت ها با همان تفاوت برابر با:
سپس پیشرفت و سری پیشرفت ها اعداد یکسانی را بیان می کنند.
مثال سطر را می توان با سه ردیف زیر جایگزین کرد: , , .
4. اگر پیشروی های نامتناهی با اختلاف یکسان دارای اعدادی به عنوان اعضای مرکزی باشند که یک پیشروی حسابی را با اختلاف تشکیل می دهند، می توان این سری ها را با یک پیشرفت با اختلاف و با عضو مرکزی برابر با هر یک از اعضای مرکزی آنها جایگزین کرد. پیشرفت ها، یعنی اگر
سپس این پیشرفت ها در یکی ترکیب می شوند:
مثال
، ، ، ، هر دو در یک گروه ترکیب می شوند ، زیرا 
.
برای تبدیل گروه‌هایی که راه‌حل‌های مشترک دارند به گروه‌هایی که راه‌حل‌های مشترک ندارند، این گروه‌ها به گروه‌هایی با دوره مشترک تجزیه می‌شوند و سپس سعی می‌کنیم گروه‌های حاصل را به استثنای موارد تکراری ترکیب کنیم.
فاکتورسازی
روش فاکتورسازی به شرح زیر است: اگر
سپس هر حل معادله
حل مجموعه معادلات است
عبارت معکوس، به طور کلی، نادرست است: هر راه حلی از مجموعه، راه حل معادله نیست. این به دلیل این واقعیت است که راه حل های معادلات فردی ممکن است در محدوده تعریف تابع قرار نگیرند.
مثال معادله را حل کنید.
راه حل.با استفاده از هویت مثلثاتی پایه، معادله را به شکل نمایش می دهیم
پاسخ.
; 
.
تبدیل مجموع توابع مثلثاتی به یک محصول
مثال
معادله را حل کنید 
.
راه حل.ما فرمول را اعمال می کنیم، یک معادله معادل به دست می آوریم
پاسخ. .
مثال معادله را حل کنید.
راه حل.در این حالت، قبل از اعمال فرمول های مجموع توابع مثلثاتی، باید از فرمول کاهش استفاده کنید. 
. در نتیجه یک معادله معادل بدست می آوریم
پاسخ.
, 
.
حل معادلات با تبدیل حاصل ضرب توابع مثلثاتی به مجموع
هنگام حل تعدادی از معادلات، از فرمول استفاده می شود.
مثال معادله را حل کنید
راه حل.
پاسخ. , .
مثال معادله را حل کنید.
راه حل.با استفاده از فرمول، یک معادله معادل بدست می آوریم:
پاسخ. .
حل معادلات با استفاده از فرمول های کاهش
هنگام حل طیف گسترده ای از معادلات مثلثاتی، فرمول ها نقش کلیدی ایفا می کنند.
مثال معادله را حل کنید.
راه حل.با استفاده از فرمول، معادله ای معادل به دست می آوریم.
پاسخ. ; .
حل معادلات با استفاده از فرمول های استدلال سه گانه
مثال معادله را حل کنید.
راه حل.ما فرمول را اعمال می کنیم، معادله را بدست می آوریم
پاسخ. ; .
مثال
معادله را حل کنید 
.
راه حل.با اعمال فرمول های کاهش درجه، به دست می آوریم: 
. با درخواست دریافت می کنیم:
پاسخ. ; .
تساوی توابع مثلثاتی به همین نام
مثال معادله را حل کنید.
راه حل.
پاسخ. , .
مثال
معادله را حل کنید 
.
راه حل.بیایید معادله را تبدیل کنیم.
پاسخ. .
مثال معلوم است که و ارضای معادله
جمع را بیابید
راه حل.از معادله بر می آید که
پاسخ. .
مجموع فرم را در نظر بگیرید
این مجموع را می توان با ضرب و تقسیم آنها به یک محصول تبدیل کرد، سپس به دست می آوریم
از این تکنیک می توان برای حل برخی از معادلات مثلثاتی استفاده کرد، اما باید در نظر داشت که در نتیجه ممکن است ریشه های خارجی ظاهر شوند. در اینجا تعمیم این فرمول ها آمده است:
مثال معادله را حل کنید.
راه حل.مشاهده می شود که مجموعه راه حلی برای معادله اصلی است. بنابراین، ضرب کردن سمت چپ و راست معادله در منجر به ظهور ریشه های اضافی نمی شود.
ما داریم 
.
پاسخ. ; .
مثال معادله را حل کنید.
راه حل.سمت چپ و راست معادله را در ضرب می کنیم و با استفاده از فرمول تبدیل حاصل ضرب توابع مثلثاتی به مجموع به دست می آوریم.
این معادله معادل مجموعه دو معادله و , wherece و .
از آنجایی که ریشه های معادله ریشه های معادله نیستند، پس از مجموعه راه حل های حاصل باید حذف شوند. بنابراین در مجموعه باید حذف کنید.
پاسخ.و , .
مثال
معادله را حل کنید 
.
راه حل.بیایید عبارت را تبدیل کنیم:
معادله به شکل زیر نوشته خواهد شد:
پاسخ. .
کاهش معادلات مثلثاتی به معادلات جبری
تقلیل به مربع
اگر معادله به نظر می رسد
سپس جایگزینی آن را به یک مربع می رساند، زیرا 
() و.
اگر به جای عبارت وجود داشته باشد، جایگزین مورد نیاز خواهد بود.
معادله
به معادله درجه دوم کاهش می یابد
ارائه به عنوان 
. به راحتی می توان مواردی را که برای آنها ریشه معادله نیست بررسی کرد و با ایجاد تغییر معادله به یک معادله درجه دوم کاهش می یابد.
مثال معادله را حل کنید.
راه حل.بیایید آن را به سمت چپ منتقل کنیم، آن را با، و از طریق و بیان کنیم.
پس از ساده سازی ها به دست می آید: . عبارت را به عبارت تقسیم کنید و جایگزین کنید:
با بازگشت به، پیدا می کنیم 
.
معادلات همگن با توجه به
معادله ای از فرم را در نظر بگیرید
که در آن،،،، ...، اعداد حقیقی هستند. در هر جمله در سمت چپ معادله، درجات تک جمله ها برابر است، یعنی مجموع درجات سینوس و کسینوس یکسان و برابر است. چنین معادله ای نامیده می شود همگننسبت به و، و عدد نامیده می شود شاخص همگنی .
واضح است که اگر، پس معادله به شکل زیر خواهد بود:
که راه حل های آن مقادیری هستند که برای آنها، یعنی اعداد، . معادله دوم که در پرانتز نوشته شده است نیز همگن است، اما درجه ها 1 کمتر است.
اگر، پس این اعداد ریشه معادله نیستند.
وقتی به دست می آوریم: ، و سمت چپ معادله (1) مقدار .
بنابراین، برای، و، بنابراین، هر دو طرف معادله را می توان بر تقسیم کرد. در نتیجه معادله را بدست می آوریم:
که با جایگزینی به راحتی به جبری تقلیل می یابد:
معادلات همگن با شاخص همگنی 1. در , ما معادله .
اگر , پس این معادله معادل معادله , , wherece , است.
مثال معادله را حل کنید.
راه حل.این معادله از درجه اول همگن است. با تقسیم هر دو قسمت آن بر می گیریم: , , , .
پاسخ. .
مثال در یک معادله همگن از فرم به دست می آوریم
راه حل.
اگر هر دو طرف معادله را بر تقسیم کنیم، معادله را بدست می آوریم 
، که به راحتی می توان با جایگزینی به مربع کاهش داد: 
. اگر یک 
، سپس معادله دارای ریشه های واقعی است، . معادله اصلی دو گروه راه حل خواهد داشت: , , .
اگر یک 
، پس معادله هیچ راه حلی ندارد.
مثال معادله را حل کنید.
راه حل.این معادله از درجه دوم همگن است. دو طرف معادله را بر تقسیم کنیم، بدست می آوریم: . اجازه دهید پس از آن . , , ; , , .
پاسخ.
.
معادله به یک معادله از فرم کاهش می یابد
برای این کار استفاده از هویت کافی است 
به طور خاص، اگر معادله جایگزین شود، به یک معادله همگن کاهش می یابد 
، سپس معادله معادل را بدست می آوریم:
مثال معادله را حل کنید.
راه حل.بیایید معادله را به یک معادله تبدیل کنیم:
دو طرف معادله را تقسیم بر 
، معادله را بدست می آوریم:
اجازه دهید، سپس به معادله درجه دوم می رسیم: 
, , 
, 
, .
پاسخ.
.
مثال معادله را حل کنید.
راه حل.بیایید هر دو طرف معادله را مربع کنیم، با توجه به اینکه مقادیر مثبت دارند:
بگذار، سپس می گیریم 
, , .
پاسخ. .
معادلات حل شده با استفاده از هویت 
دانستن فرمول های زیر مفید است:
مثال معادله را حل کنید.
راه حل.با استفاده از، دریافت می کنیم
پاسخ.
ما نه خود فرمول ها، بلکه روشی را برای استخراج آنها پیشنهاد می کنیم:
در نتیجه،
به همین ترتیب، .
مثال
معادله را حل کنید 
.
راه حل.بیایید عبارت را تبدیل کنیم:
معادله به شکل زیر نوشته خواهد شد:
گرفتن، می گیریم. ، . در نتیجه
پاسخ. .
جایگزینی مثلثاتی جهانی
معادله مثلثاتی فرم
که در آن --- یک تابع گویا با کمک فرمولها -- و همچنین با کمک فرمولها -- را می توان به یک معادله گویا با توجه به آرگومانهای , , , , پس از آن معادله را به یک کاهش داد . معادله منطقی جبری با توجه به استفاده از فرمول های جایگزینی مثلثاتی جهانی
لازم به ذکر است که استفاده از فرمول ها می تواند منجر به باریک شدن ODZ معادله اصلی شود، زیرا در نقاط تعریف نشده است، بنابراین در چنین مواردی باید بررسی شود که آیا زاویه ها ریشه معادله اصلی هستند یا خیر. .
مثال معادله را حل کنید.
راه حل.با توجه به وظیفه. با اعمال فرمول ها و انجام جایگزینی، به دست می آوریم
از کجا و بنابراین، .
معادلات فرم
معادلات شکل که در آن چند جمله ای است با تغییر مجهولات حل می شود
مثال معادله را حل کنید.
راه حل.با انجام تعویض و در نظر گرفتن آن، دریافت می کنیم
جایی که ، . --- ریشه خارجی، زیرا . ریشه های معادله 
هستند .
استفاده از توابع محدود
در عمل تست متمرکز، مواجهه با معادلاتی که حل آنها بر اساس مرزبندی توابع و . مثلا:
مثال معادله را حل کنید.
راه حل.از آنجایی که ، ، پس سمت چپ تجاوز نمی کند و برابر است با اگر
برای یافتن مقادیری که هر دو معادله را برآورده می کنند، به صورت زیر عمل می کنیم. یکی از آنها را حل می کنیم، سپس از بین مقادیر یافت شده، مواردی را انتخاب می کنیم که دیگری را برآورده می کند.
بیایید با دومی شروع کنیم: , . سپس ، 
.
واضح است که فقط برای اعداد زوج خواهد بود.
پاسخ. .
ایده دیگری با حل معادله زیر محقق می شود:
مثال
معادله را حل کنید 
.
راه حل.بیایید از ویژگی تابع نمایی استفاده کنیم: 
.
با اضافه کردن این نابرابری ها به صورت ترم، داریم:
بنابراین، سمت چپ این معادله برابر است اگر و تنها در صورتی که دو برابری برقرار باشد:
یعنی می تواند مقادیر،،،، یا می تواند مقادیر، را بگیرد.
پاسخ. , .
مثال
معادله را حل کنید 
.
راه حل.، . در نتیجه، 
.
پاسخ. .
مثال معادله را حل کنید
راه حل.نشان دهید، سپس از تعریف تابع مثلثاتی معکوس داریم 
و 
.
از آنجایی که، نابرابری از معادله به دست می آید، یعنی. . از زمان و پس از آن و . با این حال، و بنابراین.
اگر و پس . از آنجایی که قبلا ثابت شده بود که پس .
پاسخ. , .
مثال معادله را حل کنید
راه حل.محدوده مقادیر معتبر معادله است.
اجازه دهید ابتدا نشان دهیم که تابع
برای هر کدام، فقط می تواند ارزش های مثبت داشته باشد.
بیایید تابع را به صورت زیر نمایش دهیم: .
از آن زمان به بعد، یعنی 
.
بنابراین، برای اثبات نابرابری، نشان دادن آن ضروری است 
. برای این منظور، هر دو قسمت این نابرابری را مکعب می کنیم
نابرابری عددی حاصل نشان می دهد که . اگر این را هم در نظر بگیریم، سمت چپ معادله غیر منفی است.
اکنون سمت راست معادله را در نظر بگیرید.
زیرا 
، سپس
با این حال، مشخص است که 
. از اینجا نتیجه می گیرد که، یعنی. سمت راست معادله از . قبلا ثابت شده بود که سمت چپ معادله غیر منفی است، بنابراین تساوی در تنها در صورتی می تواند باشد که هر دو قسمت آن برابر باشند و این فقط برای .
پاسخ. .
مثال معادله را حل کنید
راه حل.نشان دادن و 
. با اعمال نابرابری کوشی-بونیاکوفسکی، به دست می آوریم. از این رو نتیجه می شود که 
. از سوی دیگر وجود دارد 
. بنابراین معادله ریشه ندارد.
پاسخ. .
مثال معادله را حل کنید:
راه حل.بیایید معادله را به شکل زیر بازنویسی کنیم:
پاسخ. .
روش های تابعی برای حل معادلات مثلثاتی و ترکیبی
هر معادله ای در نتیجه تبدیل ها را نمی توان به معادله ای از یک فرم استاندارد کاهش داد که روش حل خاصی برای آن وجود دارد. در چنین مواردی، استفاده از خواص توابع مانند یکنواختی، کران، یکنواختی، تناوب و غیره مفید است. بنابراین، اگر یکی از توابع کاهش یابد، و دومی در بازه افزایش یابد، اگر معادله باشد. یک ریشه در این فاصله دارد، این ریشه منحصر به فرد است، و سپس، برای مثال، می توان آن را با انتخاب پیدا کرد. اگر تابع از بالا محدود شود، و، و تابع از پایین محدود شود، و، پس معادله معادل سیستم معادلات است.
مثال معادله را حل کنید
راه حل.معادله اصلی را به شکل تبدیل می کنیم
و آن را به صورت مربع با توجه به . سپس می گیریم
بیایید معادله مجموعه اول را حل کنیم. با در نظر گرفتن کران تابع , به این نتیجه می رسیم که معادله فقط روی بازه می تواند ریشه داشته باشد . در این بازه، تابع افزایش می یابد و تابع 
کاهش می دهد. بنابراین، اگر این معادله ریشه داشته باشد، منحصر به فرد است. ما با انتخاب پیدا می کنیم.
پاسخ. .
مثال معادله را حل کنید
راه حل.اجازه دهید، و 
، سپس معادله اصلی را می توان به عنوان یک معادله تابعی نوشت. از آنجایی که تابع فرد است، پس . در این صورت معادله را بدست می آوریم
از آنجایی که و یکنواخت است، معادله معادل معادله است، i.e. 
، که دارای یک ریشه است.
پاسخ. .
مثال
معادله را حل کنید 
.
راه حل.بر اساس قضیه مشتق تابع مختلط، واضح است که تابع 
کاهش (عملکرد کاهش، افزایش، کاهش). از اینجا مشخص است که تابع 
تعریف شده در، در حال کاهش. بنابراین این معادله حداکثر یک ریشه دارد. زیرا 
، سپس
پاسخ. .
مثال معادله را حل کنید.
راه حل.معادله را در سه بازه در نظر بگیرید.
الف) اجازه دهید. سپس در این مجموعه معادله اصلی معادل معادله است. که هیچ راه حلی در فاصله زمانی ندارد 
، ، آ . در بازه، معادله اصلی نیز ریشه ندارد، زیرا 
، آ .
ب) اجازه دهید. سپس در این مجموعه معادله اصلی معادل معادله است
که ریشه های آن در بازه عبارتند از اعداد , , , .
ج) اجازه دهید. سپس در این مجموعه معادله اصلی معادل معادله است
که هیچ راه حلی در بازه زمانی ندارد، اما . معادله همچنین هیچ راه حلی در بازه ندارد، زیرا ، ، آ .
پاسخ. , , , .
روش تقارن
استفاده از روش تقارن زمانی مناسب است که فرمول کار شامل این نیاز باشد که حل یک معادله، نابرابری، سیستم و غیره منحصر به فرد باشد. یا نشانی دقیق از تعداد راه حل ها. در این حالت، هر گونه تقارن عبارات داده شده باید شناسایی شود.
همچنین لازم است تنوع انواع مختلف تقارن ممکن را در نظر گرفت.
رعایت دقیق مراحل منطقی در استدلال با تقارن به همان اندازه مهم است.
معمولاً تقارن به ما امکان می دهد فقط شرایط لازم را ایجاد کنیم و سپس باید کفایت آنها را بررسی کنیم.
مثال تمام مقادیر پارامتری را که معادله یک راه حل منحصر به فرد برای آن دارد، بیابید.
راه حل.توجه داشته باشید که و توابع زوج هستند، بنابراین سمت چپ معادله یک تابع زوج است.
بنابراین اگر برای یک معادله راه حلی وجود داشته باشد، برای معادله نیز راه حلی وجود دارد. اگر تنها راه حل معادله است، پس لازم است , .
بیایید انتخاب کنیم ممکن استمقادیر، که مستلزم آن است که ریشه معادله باشد.
بلافاصله توجه می کنیم که مقادیر دیگر نمی توانند شرایط مشکل را برآورده کنند.
اما هنوز مشخص نیست که آیا همه افراد انتخاب شده واقعاً شرایط مشکل را برآورده می کنند یا خیر.
کفایت.
1) ، معادله شکل خواهد گرفت 
.
2) معادله به شکل زیر خواهد بود:
بدیهی است که برای همه و 
. بنابراین، آخرین معادله معادل سیستم است:
بنابراین، ما ثابت کردیم که معادله یک راه حل منحصر به فرد دارد.
پاسخ. .
راه حل با کاوش تابع
مثال ثابت کنید که تمام راه حل های معادله
تمام اعداد.
راه حل.دوره اصلی معادله اصلی است. بنابراین، ابتدا این معادله را بر روی قطعه مورد مطالعه قرار می دهیم.
بیایید معادله را به شکل تبدیل کنیم:
با کمک ماشین حساب به دست می آوریم:
اگر، پس از برابری های قبلی به دست می آوریم:
با حل معادله به دست می آوریم: .
محاسبات انجام شده فرصتی را فراهم می کند تا فرض کنیم که ریشه های معادله متعلق به بازه، و.
تأیید مستقیم این فرضیه را تأیید می کند. بنابراین، ثابت می شود که ریشه های معادله فقط اعداد صحیح هستند، .
مثال
معادله را حل کنید 
.
راه حل.دوره اصلی معادله را پیدا کنید. دوره اصلی تابع است. دوره اصلی تابع است. کمترین مضرب مشترک اعداد و برابر است با . بنابراین، دوره اصلی معادله است. اجازه دهید .
بدیهی است که راه حلی برای معادله است. در فاصله زمانی. تابع منفی است. بنابراین، ریشه های دیگر معادله را فقط باید در بازه های x و .
با کمک یک ریز حساب، ابتدا مقادیر تقریبی ریشه های معادله را پیدا می کنیم. برای انجام این کار، جدولی از مقادیر تابع را جمع آوری می کنیم 
در فواصل زمانی و ; یعنی در فواصل و .
| 0 | 0 | 202,5 | 0,85355342 |
| 3 | -0,00080306 | 207 | 0,6893642 |
| 6 | -0,00119426 | 210 | 0,57635189 |
| 9 | -0,00261932 | 213 | 0,4614465 |
| 12 | -0,00448897 | 216 | 0,34549155 |
| 15 | -0,00667995 | 219 | 0,22934931 |
| 18 | -0,00903692 | 222 | 0,1138931 |
| 21 | -0,01137519 | 225 | 0,00000002 |
| 24 | -0,01312438 | 228 | -0,11145712 |
| 27 | -0,01512438 | 231 | -0,21961736 |
| 30 | -0,01604446 | 234 | -0,32363903 |
| 33 | -0,01597149 | 237 | -0,42270819 |
| 36 | -0,01462203 | 240 | -0,5160445 |
| 39 | -0,01170562 | 243 | -0,60290965 |
| 42 | -0,00692866 | 246 | -0,65261345 |
| 45 | 0,00000002 | 249 | -0,75452006 |
| 48 | 0,00936458 | 252 | -0,81805397 |
| 51 | 0,02143757 | 255 | -0,87270535 |
| 54 | 0,03647455 | 258 | -0,91803444 |
| 57 | 0,0547098 | 261 | -0,95367586 |
| 60 | 0,07635185 | 264 | -0,97934187 |
| 63 | 0,10157893 | 267 | -0,99482505 |
| 66 | 0,1305352 | 270 | -1 |
| 67,5 | 0,14644661 |
فرضیه های زیر به راحتی از جدول قابل مشاهده است: ریشه های معادله متعلق به بخش اعداد هستند: ; ; . تأیید مستقیم این فرضیه را تأیید می کند.
پاسخ.
; 
; .
حل نامساوی مثلثاتی با استفاده از دایره واحد
هنگام حل نابرابری های مثلثاتی شکل، جایی که یکی از توابع مثلثاتی است، استفاده از یک دایره مثلثاتی راحت است تا جواب نابرابری را به وضوح نشان داده و پاسخ را یادداشت کنید. روش اصلی برای حل نابرابری های مثلثاتی کاهش آنها به ساده ترین نابرابری های نوع است. بیایید به مثالی از نحوه حل چنین نابرابری هایی نگاه کنیم.
مثال نابرابری را حل کنید.
راه حل.بیایید یک دایره مثلثاتی رسم کنیم و نقاطی را که مختصات آنها بزرگتر از .
برای حل این نابرابری خواهد بود. همچنین واضح است که اگر عددی با عددی از فاصله مشخص شده با عددی متفاوت باشد، آنگاه نیز کمتر از عدد نخواهد بود. بنابراین، به انتهای بخش یافت شده راه حل، فقط باید اضافه کنید. در نهایت، دریافتیم که راه حل های نابرابری اصلی همه خواهد بود 
.
پاسخ.
.
برای حل نابرابری‌های مماس و هم‌تانژانت، مفهوم خط مماس و کوتانژانت مفید است. اینها خطوط هستند و به ترتیب (در شکل (1) و (2)) دایره مثلثاتی را لمس می کنند.
به راحتی می توان فهمید که اگر یک پرتو با مبدأ در مبدأ بسازید و زاویه ای با جهت مثبت محور آبسیسا ایجاد کنید، سپس طول قطعه از نقطه تا نقطه تلاقی این پرتو با خط مماس دقیقاً برابر با مماس زاویه ای است که این پرتو با محور آبسیسا می سازد. مشاهدات مشابهی برای کوتانژانت وجود دارد.
مثال نابرابری را حل کنید.
راه حل.نشان دهید، سپس نابرابری به شکل ساده ترین شکل خواهد بود: . فاصله ای با طولی برابر با کمترین دوره مثبت (LPP) مماس در نظر بگیرید. در این پاره، با استفاده از خط مماس ها، آن را مشخص می کنیم. اکنون آنچه را که باید اضافه شود به خاطر می آوریم، زیرا RPE تابع . بنابراین، 
. با بازگشت به متغیر، آن را دریافت می کنیم.
پاسخ.
.
حل نابرابری ها با توابع مثلثاتی معکوس با استفاده از نمودارهای توابع مثلثاتی معکوس راحت است. بیایید با یک مثال نشان دهیم که چگونه این کار انجام می شود.
حل نابرابری های مثلثاتی با روش گرافیکی
توجه داشته باشید که اگر --- یک تابع تناوبی است، برای حل نابرابری، باید جواب های آن را در قسمتی که طول آن برابر با دوره تابع است، پیدا کنید. همه راه‌حل‌های نابرابری اصلی شامل مقادیر یافت شده و همچنین همه آنهایی هستند که با هر عدد صحیحی از دوره‌های تابع با آنها متفاوت هستند.
حل نابرابری () را در نظر بگیرید.
از آنجایی که نابرابری هیچ راه حلی برای . اگر، پس مجموعه راه حل های نابرابری مجموعه ای از تمام اعداد واقعی است.
اجازه دهید . تابع سینوس دارای کوچکترین دوره مثبت است، بنابراین نابرابری را می توان ابتدا در یک پاره طول، به عنوان مثال، در یک پاره حل کرد. ما نمودارهایی از توابع و () می سازیم. توسط نابرابری های شکل داده می شود: و، از کجا،
در این مقاله روش‌هایی برای حل معادلات و نابرابری‌های مثلثاتی، چه در سطح ساده‌ترین و چه در سطح المپیاد، در نظر گرفته شد. روشهای اصلی برای حل معادلات و نامساوی مثلثاتی، هم خاص --- مشخصه فقط برای معادلات مثلثاتی و نابرابری‌ها - و هم روشهای تابعی عمومی برای حل معادلات و نامساوی‌ها، همانطور که برای معادلات مثلثاتی اعمال می‌شود، در نظر گرفته شد.
این پایان نامه اطلاعات نظری اساسی را ارائه می دهد: تعریف و ویژگی های توابع مثلثاتی و مثلثاتی معکوس. بیان توابع مثلثاتی بر حسب سایر توابع مثلثاتی، که برای تبدیل عبارات مثلثاتی، به ویژه آنهایی که حاوی توابع مثلثاتی معکوس هستند، بسیار مهم است. علاوه بر فرمول های مثلثاتی پایه، که از دوره مدرسه به خوبی شناخته شده است، فرمول هایی ارائه شده است که عبارات حاوی توابع مثلثاتی معکوس را ساده می کند. حل معادلات مثلثاتی ابتدایی، روش فاکتورگیری، روشهای کاهش معادلات مثلثاتی به جبری در نظر گرفته شده است. با توجه به اینکه جواب های معادلات مثلثاتی را می توان به روش های مختلفی نوشت و شکل این جواب ها اجازه نمی دهد بلافاصله مشخص شود که آیا این جواب ها یکسان یا متفاوت هستند، طرحی کلی برای حل معادلات مثلثاتی در نظر گرفته شده است. تبدیل گروه های راه حل های کلی معادلات مثلثاتی با جزئیات در نظر گرفته شده است. روشهای حل نابرابری‌های مثلثاتی ابتدایی، هم بر روی دایره واحد و هم با روش گرافیکی، به تفصیل در نظر گرفته شده‌اند. فرآیند حل نابرابری‌های مثلثاتی غیر ابتدایی از طریق نابرابری‌های ابتدایی و روش فواصل که قبلاً برای دانش‌آموزان شناخته شده بود، شرح داده می‌شود. راه حل های کارهای معمولی برای انتخاب ریشه ها ارائه شده است. اطلاعات نظری لازم برای انتخاب ریشه ها آورده شده است: تقسیم مجموعه اعداد صحیح به زیر مجموعه های غیر متقاطع، حل معادلات در اعداد صحیح (دیوفانتین).
نتایج این کار پایان نامه می تواند به عنوان مواد آموزشی در تهیه ترم و پایان نامه، در تهیه دروس انتخابی برای دانش آموزان و همچنین کار در آماده سازی دانش آموزان برای کنکور و آزمون متمرکز استفاده شود.
Vygodsky Ya.Ya.، کتابچه راهنمای ریاضیات ابتدایی. /ویگودسکی یا.یا. --- M.: Nauka، 1970.
Igudisman O.، ریاضیات در امتحان شفاهی / Igudisman O. --- M.: Iris press, Rolf, 2001.
Azarov A.I., معادلات / Azarov A.I., Gladun O.M., Fedosenko V.S. --- مینسک: Trivium، 1994.
Litvinenko V.N.، کارگاه آموزشی ریاضیات ابتدایی / Litvinenko V.N. --- M.: آموزش، 1991.
شاریگین I.F.، دوره اختیاری در ریاضیات: حل مسئله / Sharygin I.F., Golubev V.I. --- م.: روشنگری، 1991.
باردوشکین وی.، معادلات مثلثاتی. انتخاب ریشه / V. باردوشکین، آ. پروکوفیف.// ریاضیات، شماره 12، 2005 ص. 23--27.
Vasilevsky A.B.، تکالیف برای کارهای فوق برنامه در ریاضیات / Vasilevsky A.B. --- Mn.: مردم Asveta. 1988. --- 176s.
Sapunov P. I.، تبدیل و اتحاد گروه های راه حل های کلی معادلات مثلثاتی / Sapunov P. I. // آموزش ریاضی، شماره 3، 1935.
بورودین پ.، مثلثات. مواد امتحانات ورودی در دانشگاه دولتی مسکو [متن] / P. Borodin, V. Galkin, V. Panferov, I. Sergeev, V. Tarasov // ریاضیات شماره 1, 2005 ص. 36--48.
Samusenko A.V.، ریاضیات: اشتباهات معمول متقاضیان: راهنمای مرجع / Samusenko A.V.، Kazachenok V.V. --- مینسک: مدرسه عالی، 1991.
Azarov A.I.، روش های کاربردی و گرافیکی برای حل مسائل معاینه / Azarov A.I.، Barvenov S.A.، --- Minsk: Aversev، 2004.
حل ساده ترین معادلات مثلثاتی
ابتدا بیایید فرمول های حل ساده ترین معادلات مثلثاتی را یادآوری کنیم.
- $sinx=a$
- $cosx=a$
- $tgx=a$
- $ctgx=a$
حل ساده ترین نابرابری های مثلثاتی.
برای حل ساده ترین نابرابری های مثلثاتی ابتدا باید معادله مربوطه را حل کنیم و سپس با استفاده از دایره مثلثاتی راه حلی برای نامساوی پیدا کنیم. حل ساده ترین نابرابری های مثلثاتی را با مثال در نظر بگیرید.
مثال 1
$sinx\ge \frac(1)(2)$
راه حلی برای نابرابری مثلثاتی $sinx=\frac(1)(2)$ پیدا کنید
\ \
شکل 1. حل نابرابری $sinx\ge \frac(1)(2)$.
از آنجایی که نابرابری دارای علامت "بزرگتر یا مساوی" است، راه حل در قوس بالایی دایره قرار دارد (با توجه به حل معادله).
پاسخ: $\left[\frac(\pi )(6)+2\pi n,\frac(5\pi )(6)+2\pi n\pi n]$.
مثال 2
راه حلی برای نابرابری مثلثاتی پیدا کنید $cosx=\frac(\sqrt(3))(2)$
\ \
به جواب روی دایره مثلثاتی توجه کنید
از آنجایی که نابرابری دارای علامت "کمتر از" است، راه حل بر روی کمان دایره واقع در سمت چپ قرار دارد (با توجه به حل معادله).
پاسخ: $\left(\frac(\pi )(6)+2\pi n,\frac(11\pi )(6)+2\pi n\pi n)$.
مثال 3
$tgx\le \frac(\sqrt(3))(3)$
راه حلی برای نابرابری مثلثاتی پیدا کنید $tgx=\frac(\sqrt(3))(3)$
\ \
در اینجا ما همچنین به یک دامنه تعریف نیاز داریم. همانطور که به یاد داریم، تابع مماس $x\ne \frac(\pi )(2)+\pi n,n\در Z$
به جواب روی دایره مثلثاتی توجه کنید
شکل 3. حل نابرابری $tgx\le \frac(\sqrt(3))(3)$.
از آنجایی که نابرابری دارای علامت "کمتر یا مساوی" است، راه حل روی کمان های دایره ای است که در شکل 3 با رنگ آبی مشخص شده اند.
پاسخ: $\ \left(-\frac(\pi )(2)+2\pi n\right.,\left.\frac(\pi )(6)+2\pi n\right]\cup \چپ (\frac(\pi )(2)+2\pi n،\راست.\چپ.\frac(7\pi )(6)+2\pi n\راست]$
مثال 4
راه حلی برای نابرابری مثلثاتی $ctgx=\sqrt(3)$ پیدا کنید
\ \
در اینجا ما همچنین به یک دامنه تعریف نیاز داریم. همانطور که به یاد داریم، تابع مماس $x\ne \pi n,n\ در Z$
به جواب روی دایره مثلثاتی توجه کنید
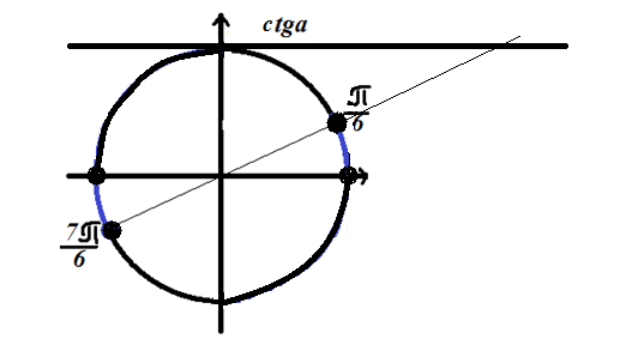
شکل 4. راه حل برای نابرابری $ctgx\le \sqrt(3)$.
از آنجایی که نابرابری دارای علامت "بیشتر از" است، راه حل روی کمان های دایره ای است که در شکل 4 با رنگ آبی مشخص شده اند.
پاسخ: $\ \left(2\pi n,\frac(\pi )(6)+2\pi n\راست)\cup \left(\pi +2\pi n,\frac(7\pi )( 6)+2\pi n\راست)$
تعریف
نابرابری های مثلثاتی نابرابری هایی هستند که دارای یک متغیر تحت علامت یک تابع مثلثاتی هستند.
حل نابرابری های مثلثاتی
حل نابرابری‌های مثلثاتی اغلب به حل ساده‌ترین نابرابری‌های مثلثاتی می‌رسد: \(\ \sin x a \), \(\ \cos x > a \), \(\ \operatorname(tg) x > a \ )، \(\ \ نام اپراتور(ctg) x > a \)، \(\ \sin x \leq a \)، \(\ \cos x \leq a \)، \(\ \نام اپراتور(tg) x \ leq a \)، \ (\ \ نام اپراتور (ctg) x \leq a \)، \(\ \sin x \geq a \)، \(\ \cos \geq a \)، \(\ \ نام اپراتور (tg ) x \geq a \ ), \(\ \نام اپراتور(tg) x \geq a \)
ساده ترین نابرابری های مثلثاتی به صورت گرافیکی یا با استفاده از دایره مثلثاتی واحد حل می شوند.
طبق تعریف، سینوس زاویه \(\ \alpha \) مختص نقطه \(\ P_(\alpha)(x, y) \) دایره واحد است (شکل 1) و کسینوس برابر است ابسیسا این نقطه این واقعیت در حل ساده ترین نابرابری های مثلثاتی با کسینوس و سینوس با استفاده از دایره واحد استفاده می شود.
نمونه هایی از حل نابرابری های مثلثاتی
حل نابرابری \(\ \sin x \leq \frac(\sqrt(3))(2) \)
از آنجایی که \(\ \left|\frac(\sqrt(3))(2)\right| این نابرابری راه حل دارد و به دو صورت قابل حل است.
راه اول بیایید این نابرابری را به صورت گرافیکی حل کنیم. برای انجام این کار، در همان سیستم مختصات، نموداری از سینوس \(\ y=\sin x \) (شکل 2) و خط مستقیم \(\ y=\frac(\sqrt(3)) را می سازیم. 2) \)
بیایید فواصلی را انتخاب کنیم که سینوسی در زیر نمودار خط مستقیم \(\ y=\frac(\sqrt(3))(2) \) قرار دارد. ابسیساهای \(\ x_(1) \) و \(\ x_(2) \) نقاط تقاطع این نمودارها را پیدا کنید: \(\ x_(1)=\pi-\arcsin \frac(\sqrt(3 ))(2)=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_(2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\ frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)
بازه \(\ \left[-\frac(4 \pi)(3) ; \frac(\pi)(3)\right] \) را دریافت کردیم اما از آنجایی که تابع \(\ y=\sin x \) تناوبی است و دارای نقطه \(\ 2 \pi \) است، سپس پاسخ اتحاد فواصل است: \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+ 2 \pi k\راست] \)، \(\ k \in Z \)
راه دوم. یک دایره واحد و یک خط \(\ y=\frac(\sqrt(3))(2) \) بسازید، نقاط تقاطع آنها را مشخص کنید \(\ P_(x_(1)) \) و \(\ P_(x_ (2)) \) (شکل 3). راه حل نابرابری اصلی مجموعه ای از نقاط ارتینی خواهد بود که کمتر از \(\ \frac(\sqrt(3))(2) \) هستند. بیایید مقدار \(\ \boldsymbol(I)_(1) \) و \(\ \boldsymbol(I)_(2) \) را با حرکت در خلاف جهت عقربه‌های ساعت پیدا کنیم، \(\ x_(1) شکل 3
\(\ x_(1)=\pi-\arcsin \frac(\sqrt(3))(2)=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_ (2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)
با در نظر گرفتن تناوب تابع سینوس، در نهایت بازه های \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+2 \ را بدست می آوریم. pi\right] \), \(\k\in Z\)
حل نابرابری \(\ \sin x>2 \)
سینوس یک تابع محدود است: \(\ |\sin x| \leq 1 \) و سمت راست این نابرابری بزرگتر از یک است، بنابراین هیچ راه حلی وجود ندارد.
حل نابرابری \(\ \cos x>\frac(1)(2) \)
این نابرابری را می توان به دو صورت حل کرد: گرافیکی و با استفاده از دایره واحد. بیایید هر یک از روش ها را در نظر بگیریم.
راه اول بیایید در یک سیستم مختصات توابعی را که قسمت‌های چپ و راست نابرابری را توصیف می‌کنند، نشان دهیم، یعنی \(\ y=\cos x \) و \(\ y=\frac(1)(2) \) . اجازه دهید بازه هایی را انتخاب کنیم که نمودار تابع کسینوس \(\ y=\cos x \) در بالای نمودار خط مستقیم \(\ y=\frac(1)(2) \) قرار دارد (شکل 4) ).
ابسیساهای نقاط \(\ \boldsymbol(x)_(1) \) و \(\ x_(2) \) را پیدا کنید - نقاط تقاطع نمودارهای توابع \(\ y=\cos x \ ) و \(\ y=\frac (1)(2) \) که انتهای یکی از بازه هایی هستند که نابرابری نشان داده شده در آن برقرار است. \(\ x_(1)=-\arccos \frac(1)(2)=-\frac(\pi)(3) \); \(\ x_(1)=\arccos \frac(1)(2)=\frac(\pi)(3) \)
با توجه به اینکه کسینوس یک تابع تناوبی است، با نقطه \(\ 2 \pi \) ، پاسخ مقدار \(\ x \) از بازه‌های \(\ \left(-\frac(\pi) (3) است. )+2 \pi k ؛ \frac(\pi)(3)+2 \pi k\راست) \), \(\ k \in Z \)
راه دوم. بیایید یک دایره واحد و یک خط مستقیم \(\ x=\frac(1)(2) \) بسازیم (زیرا محور x با کسینوسهای روی دایره واحد مطابقت دارد). اجازه دهید \(\ P_(x_(1)) \) و \(\ P_(x_(2)) \) (شکل 5) نقاط تلاقی خط و دایره واحد باشند. راه حل معادله اصلی مجموعه ای از نقاط ابسیسا خواهد بود که کمتر از \(\ \frac(1)(2) \) هستند. مقدار \(\ x_(1) \) و \(\ 2 \) را پیدا کنید، یک مدار خلاف جهت عقربه های ساعت ایجاد کنید تا \(\ x_(1) با در نظر گرفتن تناوب کسینوس، در نهایت بازه های \( را بدست آوریم. \ \left(-\frac (\pi)(3)+2 \pi k ;\frac(\pi)(3)+2 \pi k\راست) \),\(\ k \in Z \)
حل نابرابری \(\ \operatorname(ctg) x \leq-\frac(\sqrt(3))(3) \)
بیایید نمودارهای توابع \(\ y=\ نام عامل(ctg) x \), \(\ y=-\frac(\sqrt(3)) (3) \) را در یک سیستم مختصات رسم کنیم.
بیایید فواصل زمانی را انتخاب کنیم که نمودار تابع \(\ y=\operatorname(ctg) x \) از نمودار خط مستقیم \(\ y=-\frac(\sqrt(3))(3) بالاتر نباشد. ) \) (شکل 6) .
ابسیسا نقطه \(\ x_(0) \) را پیدا کنید که انتهای یکی از بازه هایی است که در آن نابرابری \(\ x_(0)=\operatorname(arcctg)\left(-\frac(\ sqrt(3))( 3)\right)=\pi-\operatorname(arcctg)\left(\frac(\sqrt(3))(3)\right)=\pi-\frac(\pi)(3 )=\frac(2 \pi)(3) \)
انتهای دیگر این شکاف نقطه \(\ \pi \) است و تابع \(\ y=\operatorname(ctg) x\) در این نقطه تعریف نشده است. بنابراین، یکی از راه حل های این نابرابری بازه \(\ \frac(2 \pi)(3) \leq x است.
نابرابری های مثلثاتی با استدلال مختلط
نابرابری های مثلثاتی با یک آرگومان پیچیده را می توان با استفاده از یک جایگزین به ساده ترین نابرابری های مثلثاتی کاهش داد. پس از حل آن، جایگزینی معکوس انجام می شود و مجهول اصلی بیان می شود.
حل نابرابری \(\ 2 \cos \left(2 x+100^(\circ)\right) \leq-1 \)
کسینوس سمت راست این نابرابری را بیان کنید: \(\ \cos \left(2 x+100^(\circ)\right) \leq-\frac(1)(2) \)
ما جایگزین \(\ t=2 x+100^(\circ) \) را انجام می دهیم، پس از آن این نابرابری به ساده ترین نابرابری تبدیل می شود \(\ \cos t \leq-\frac(1)(2) \ )
بیایید آن را با استفاده از دایره واحد حل کنیم. بیایید یک دایره واحد و یک خط \(\ x=-\frac(1)(2) \) بسازیم. اجازه دهید \(\ P_(1) \) و \(\ P_(2) \) را به عنوان نقاط تقاطع خط و دایره واحد نشان دهیم (شکل 7).
راه حل نابرابری اصلی مجموعه ای از نقاط ابسیسا خواهد بود که حداکثر \(\ -\frac(1)(2) \) هستند. نقطه \(\ P_(1) \) مربوط به زاویه \(\ 120^(\circ) \) و نقطه \(\ P_(2) \) است. بنابراین، با توجه به دوره کسینوس، \(\ 120^(\circ)+360^(\circ) \cdot n \leq t \leq 240^(\circ)+360^(\circ) \cdot n \ بدست می آوریم ) ، \(\ n \در Z \)
جانشینی معکوس را انجام می دهیم \(\ t=2 x+100^(\circ) 120^(\circ)+360^(\circ) \cdot n \leq 2 x+100^(\circ) \leq 240^ (\ circ)+360^(\circ) \cdot n \)، \(\ n \in Z \)
\(\ \mathbf(x) \) را بیان می کنیم، برای این کار ابتدا \(\ 100^(\circ) 120^(\circ)-100^(\circ)+360^(\circ) \ cdot را کم کنید n \leq 2 x+100^(\circ)-100^(\circ) \leq 240^(\circ)-100^(\circ)+360^(\circ) \cdot n \), \(\ n\در Z\); \(\ 20^(\circ)+360^(\circ) \cdot n \leq 2 x \leq 140^(\circ)+360^(\circ) \cdot n \), \(\ n \in Z\)
و سپس بر 2 تقسیم کنید \(\ \frac(20^(\circ)+360^(\circ) \cdot n)(2) \leq \frac(2 x)(2) \leq \frac(140^ (\circ)+360^(\circ) \cdot n)(2) \), \(\ n \in Z \); \(\ 10^(\circ)+180^(\circ) \cdot n \leq x \leq 70^(\circ)+180^(\circ) \cdot n \), \(\ n \in Z \)
نابرابری های مثلثاتی دوگانه
حل نابرابری مثلثاتی مضاعف \(\ \frac(1)(2)
اجازه دهید جایگزین \(\ t=\frac(x)(2) \) را معرفی کنیم، سپس نابرابری اصلی به شکل \(\ \frac(1)(2) خواهد بود.
بیایید آن را با استفاده از دایره واحد حل کنیم. از آنجایی که محور ارتجاعی منطبق بر سینوس روی دایره واحد است، مجموعه اردیناتی را که بزرگتر از \(\ x=\frac(1)(2) \) و کوچکتر یا مساوی \(\) هستند را بر روی آن انتخاب می کنیم. \frac(\sqrt(2))(2) \) . در شکل 8، این نقاط روی کمان های \(\ P_(t_(1)) \)، \(\ P_(t_(2)) \) و \(\ P_(t_(3)) \) قرار خواهند گرفت. ، \( \ P_(t_(4)) \) . بیایید مقدار \(\ t_(1) \), \(\ t_(2) \), \(\ t_(3) \), \(\ t_(4) \) را پیدا کنیم، یک تور در خلاف جهت عقربه های ساعت انجام دهیم، و \ (\ t_(1) \(\ t_(3)=\pi-\arcsin \frac(\sqrt(2))(2)=\pi-\frac(\pi)(4)=\frac(3 \ pi)(4) \)؛ \(\ t_(4)=\pi-\arcsin \frac(1)(2)=\pi-\frac(\pi)(6)=\frac(5 \pi ) (6)\)
بنابراین، دو بازه به دست می آوریم که با در نظر گرفتن تناوب تابع سینوس، می توان آنها را به صورت زیر نوشت: \(\ \frac(\pi)(6)+2 \pi k \leq t \frac(\pi) (4)+2 \ pi k \quad \frac(3 \pi)(4)+2 \pi k leq \frac(x)(2) \frac(\pi)(4)+2 \pi k \) , \(\ \frac(3 \pi)(4)+2 \pi k Express \(\ \mathbf(x) \)، برای این کار تمام ضلع هر دو نامساوی را در 2 ضرب می کنیم، \(\ \frac را بدست می آوریم (\pi)(3)+4 \pi k \leq x
روشهای حل نابرابری‌های مثلثاتی
ارتباط. از نظر تاریخی معادلات و نابرابری های مثلثاتی جایگاه ویژه ای در برنامه درسی مدارس داشته اند. می توان گفت که مثلثات یکی از مهم ترین بخش های درس مدرسه و به طور کلی تمام علوم ریاضی است.
معادلات و نابرابری های مثلثاتی، هم از نظر محتوای مطالب آموزشی و هم از نظر روش های فعالیت آموزشی و شناختی که می تواند و باید در حین مطالعه شکل بگیرد و برای حل یک مشکل بزرگ به کار رود، یکی از مکان های اصلی درس ریاضی دبیرستان را اشغال می کند. تعدادی از مسائل با ماهیت نظری و کاربردی.
حل معادلات و نابرابری های مثلثاتی پیش نیازهایی را برای نظام مند کردن دانش دانش آموزان مرتبط با کلیه مطالب آموزشی در مثلثات (به عنوان مثال، ویژگی های توابع مثلثاتی، روش های تبدیل عبارات مثلثاتی و غیره) ایجاد می کند و امکان برقراری ارتباط موثر با مطالب مورد مطالعه در جبر (معادلات، معادلات معادلات، نابرابری ها، تبدیل های یکسان عبارات جبری و غیره).
به عبارت دیگر، در نظر گرفتن روش‌هایی برای حل معادلات و نابرابری‌های مثلثاتی مستلزم نوعی انتقال این مهارت‌ها به محتوای جدید است.
اهمیت تئوری و کاربردهای متعدد آن دلیلی بر ارتباط موضوع انتخابی است. این به نوبه خود به شما امکان می دهد اهداف، اهداف و موضوع تحقیق کار دوره را تعیین کنید.
هدف مطالعه: تعمیم انواع موجود نابرابری های مثلثاتی، روش های اساسی و ویژه برای حل آنها، انتخاب مجموعه ای از وظایف برای حل نابرابری های مثلثاتی توسط دانش آموزان مدرسه.
اهداف پژوهش:
1. بر اساس تجزیه و تحلیل ادبیات موجود در مورد موضوع تحقیق، مطالب را نظام مند کنید.
2. مجموعه ای از وظایف لازم برای ادغام مبحث "نابرابری های مثلثاتی" را ارائه دهید.
موضوع مطالعه نابرابری های مثلثاتی در درس ریاضی مدرسه هستند.
موضوع مطالعه: انواع نابرابری های مثلثاتی و روش های حل آنها.
اهمیت نظری سازماندهی مطالب است.
اهمیت عملی: استفاده از دانش نظری در حل مسائل؛ تجزیه و تحلیل روش های اصلی که اغلب برای حل نابرابری های مثلثاتی با آن مواجه می شوند.
روش های پژوهش : تجزیه و تحلیل ادبیات علمی، سنتز و تعمیم دانش کسب شده، تجزیه و تحلیل حل مسئله، جستجوی روش های بهینه برای حل نابرابری ها.
§یک. انواع نابرابری های مثلثاتی و روش های اساسی حل آنها
1.1. ساده ترین نابرابری های مثلثاتی
دو عبارت مثلثاتی که با علامت یا > به هم متصل می شوند، نامساوی مثلثاتی نامیده می شوند.
حل یک نابرابری مثلثاتی به معنای یافتن مجموعه ای از مقادیر مجهولات موجود در نابرابری است که تحت آن نابرابری برآورده می شود.
بخش اصلی نابرابری های مثلثاتی با کاهش آنها به حل ساده ترین آنها حل می شود:
این ممکن است یک روش فاکتورسازی، تغییر متغیر ( 
, 
و غیره)، که در آن ابتدا نابرابری معمول و سپس نابرابری شکل حل می شود 
و غیره یا راه های دیگر
ساده ترین نابرابری ها به دو روش حل می شوند: با استفاده از دایره واحد یا به صورت گرافیکی.
اجازه دهیدf(x
یکی از توابع مثلثاتی اساسی است. برای حل نابرابری 
برای یافتن راه حل آن در یک دوره کافی است، یعنی. روی هر قطعه ای که طول آن برابر با دوره تابع باشدf
ایکس
. سپس راه حل نابرابری اصلی همه پیدا خواهد شدایکس
و همچنین مقادیری که با مقادیری که با هر عدد صحیحی از دوره های تابع پیدا می شوند متفاوت هستند. در این مورد، استفاده از روش گرافیکی راحت است.
اجازه دهید مثالی از الگوریتمی برای حل نابرابری ها ارائه دهیم 
(
) و 
.
الگوریتم حل نابرابری (
).
1. تعریف سینوس یک عدد را فرموله کنیدایکس روی دایره واحد
3. در محور y یک نقطه را با مختصات مشخص کنیدآ .
4. از این نقطه خطی موازی با محور OX رسم کنید و نقاط تلاقی آن را با دایره مشخص کنید.
5. یک کمان از دایره ای را انتخاب کنید که همه نقاط آن دارای مختصات کمتر ازآ .
6. جهت بای پس (در خلاف جهت عقربه های ساعت) را مشخص کنید و با اضافه کردن دوره تابع به انتهای بازه، پاسخ را یادداشت کنید.2πn
,
.
الگوریتم حل نابرابری .
1. تعریف مماس یک عدد را فرموله کنیدایکس روی دایره واحد
2. یک دایره واحد رسم کنید.
3. خطی از مماس ها را رسم کنید و نقطه ای را روی آن با ترتیب مشخص کنیدآ .
4. این نقطه را به مبدأ متصل کرده و نقطه تلاقی قطعه حاصل را با دایره واحد مشخص کنید.
5. یک کمان دایره ای را انتخاب کنید که همه نقاط آن دارای یک مختصات روی خط مماس کمتر ازآ .
6. جهت پیمایش را مشخص کنید و پاسخ را با در نظر گرفتن دامنه تابع، با اضافه کردن نقطه یادداشت کنید.pn
,
(عدد سمت چپ رکورد همیشه کمتر از عدد سمت راست است).
تفسیر گرافیکی راه حل های ساده ترین معادلات و فرمول های حل نابرابری ها به صورت کلی در پیوست آورده شده است (پیوست های 1 و 2).
مثال 1
نابرابری را حل کنید 
.
روی دایره واحد یک خط بکشید 
، که دایره را در نقاط A و B قطع می کند.
همه ارزش هاy
در بازه NM بیشتر
، تمام نقاط کمان AMB این نابرابری را برآورده می کنند. در تمام زوایای چرخش، بزرگ 
، اما کوچکتر 
,
ارزش های بیشتر از
(اما نه بیشتر از یک).
عکس. 1
بنابراین، حل نابرابری تمام مقادیر در بازه خواهد بود 
، یعنی 
. برای به دست آوردن تمام راه حل های این نابرابری، کافی است به انتهای این بازه اضافه کنید 
، جایی که 
، یعنی 
,
.
توجه داشته باشید که مقادیر 
و 
ریشه های معادله هستند 
,
آن ها 
;
.
پاسخ: 
, .
1.2. روش گرافیکی
در عمل، یک روش گرافیکی برای حل نابرابری های مثلثاتی اغلب مفید است. ماهیت روش را در مثال نابرابری در نظر بگیرید 
:
1. اگر آرگومان پیچیده باشد (متفاوت ازایکس ، سپس آن را جایگزین می کنیمتی .
2. ما در یک هواپیما مختصات می سازیمtoOy
نمودارهای تابع 
و 
.
3. چنین می یابیمدو نقطه مجاور از تقاطع نمودارها، بین آنسینوسیواقع شده استدر بالا
سر راست . ابسیساهای این نقاط را بیابید.
4. یک نابرابری مضاعف برای استدلال بنویسیدتی با در نظر گرفتن دوره کسینوس (تی بین ابسیساهای یافت شده خواهد بود).
5. یک جایگزین معکوس انجام دهید (به آرگومان اصلی برگردید) و مقدار را بیان کنیدایکس از یک نامساوی مضاعف، پاسخ را به صورت فاصله عددی می نویسیم.
مثال 2 حل نابرابری: .
هنگام حل نابرابری ها با یک روش گرافیکی، لازم است نمودارهایی از توابع را تا حد امکان دقیق بسازید. بیایید نابرابری را به شکل تبدیل کنیم:
اجازه دهید نمودارهای توابع را در یک سیستم مختصات بسازیم 
و 
(شکل 2).
شکل 2
نمودارهای تابع در یک نقطه قطع می شوندولی
با مختصات 
; 
. در بین 
نقاط نمودار 
زیر نقاط نمودار 
. و وقتی که مقادیر تابع یکسان است. از همین رو در 
.
پاسخ: 
.
1.3. روش جبری
اغلب، نابرابری مثلثاتی اصلی، با یک جایگزینی خوب انتخاب شده، می تواند به یک نابرابری جبری (عقلانی یا غیرمنطقی) کاهش یابد. این روش شامل تبدیل نابرابری، معرفی یک جایگزین یا جایگزینی یک متغیر است.
بیایید کاربرد این روش را در نمونه های خاص در نظر بگیریم.
مثال 3
کاهش به ساده ترین شکل 
.
(شکل 3)
شکل 3
, 
.
پاسخ: 
,
مثال 4 حل نابرابری:
ODZ: 
, 
.
استفاده از فرمول ها: 
, 
نابرابری را به شکل زیر می نویسیم: 
.
یا با فرض 
پس از تحولات ساده به دست می آوریم
,
,
.
با حل آخرین نابرابری به روش بازه ای به دست می آوریم:
شکل 4
، به ترتیب 
. سپس از شکل 4 به دنبال دارد 
، جایی که 
.
شکل 5
پاسخ: 
, 
.
1.4. روش فاصله گذاری
طرح کلی برای حل نابرابری های مثلثاتی به روش بازه:
با استفاده از فرمول های مثلثاتی فاکتورسازی کنید.
نقاط شکست و صفر تابع را پیدا کنید، آنها را روی دایره قرار دهید.
هر نکته ای را در نظر بگیریدبه (اما قبلا پیدا نشد) و نشانه محصول را پیدا کنید. اگر حاصلضرب مثبت است، نقطه ای خارج از دایره واحد روی پرتو مربوط به زاویه قرار دهید. در غیر این صورت نقطه را داخل دایره قرار دهید.
اگر یک نقطه چند بار زوج اتفاق بیفتد، آن را یک نقطه چندتایی زوج و اگر یک عدد فرد باشد، آن را یک نقطه چندتایی فرد می نامیم. کمان ها را به صورت زیر بکشید: از یک نقطه شروع کنیدبه ، اگر نقطه بعدی دارای تعدد فرد باشد، آنگاه کمان دایره را در این نقطه قطع می کند، اما اگر نقطه دارای تعدد زوج باشد، آن را قطع نمی کند.
قوس های پشت یک دایره شکاف های مثبت هستند. در داخل دایره شکاف های منفی وجود دارد.
مثال 5 نابرابری را حل کنید
, 
.
نکات سری اول: 
.
نکات سری دوم: 
.
هر نقطه به تعداد فرد رخ می دهد، یعنی همه نقاط دارای تعدد فرد.
علامت محصول را در 
: . تمام نقاط دایره واحد را علامت گذاری می کنیم (شکل 6):
برنج. 6
پاسخ: 
, 
; 
, 
; 
, 
.
مثال 6 . نابرابری را حل کنید.
راه حل:
بیایید صفرهای عبارت را پیدا کنیم .
گرفتنaeمتر :
,
;
, 
;
, 
;
, 
;
در دایره واحد، مقادیر سریایکس
1
با نقطه نشان داده شده است 
. سلسلهایکس
2
امتیاز می دهد 
. یک سریایکس
3
دو امتیاز می گیریم 
. بالاخره یه سریایکس
4
نشان دهنده امتیاز خواهد بود 
. همه این نقاط را روی دایره واحد قرار می دهیم و در پرانتز در کنار هر یک از کثرت آن را نشان می دهیم.
حالا عدد را بگذارید 
برابر خواهد بود. با علامت تخمین می زنیم:
بنابراین نکتهآ
باید بر روی پرتو تشکیل دهنده زاویه انتخاب شود 
با پرتواوه،
خارج از دایره واحد (توجه داشته باشید که تیر کمکیO
آ
لازم نیست در تصویر نشان داده شود. نقطهآ
تقریباً انتخاب شده است.)
حالا از نقطهآ
یک خط پیوسته مواج به صورت متوالی به تمام نقاط مشخص شده رسم می کنیم. و در نقاط خط ما از یک منطقه به منطقه دیگر منتقل می شود: اگر خارج از دایره واحد بود، به آن منتقل می شود. نزدیک شدن به نقطه 
، خط به ناحیه داخلی برمی گردد، زیرا تعدد این نقطه زوج است. به طور مشابه در نقطه 
(با تعدد زوج) خط باید به ناحیه بیرونی چرخانده شود. بنابراین، ما یک تصویر مشخص را که در شکل نشان داده شده است ترسیم کردیم. 7. به برجسته کردن مناطق مورد نظر در دایره واحد کمک می کند. آنها با "+" مشخص شده اند.
شکل 7
جواب نهایی:
توجه داشته باشید. اگر خط مواج پس از عبور از تمام نقاط مشخص شده روی دایره واحد، قابل بازگشت به نقطه نیستآ , بدون عبور از دایره در یک مکان "غیرقانونی"، این بدان معنی است که یک خطا در راه حل رخ داده است، یعنی تعداد عجیبی از ریشه ها حذف شده است.
پاسخ: .
§2. مجموعه ای از وظایف برای حل نابرابری های مثلثاتی
در روند توسعه توانایی دانش آموزان مدرسه برای حل نابرابری های مثلثاتی، 3 مرحله نیز قابل تشخیص است.
1. مقدماتی،
2. شکل گیری مهارت برای حل ساده ترین نابرابری های مثلثاتی.
3. معرفی نابرابری های مثلثاتی از انواع دیگر.
هدف از مرحله مقدماتی این است که در دانش آموزان مدرسه باید توانایی استفاده از دایره یا نمودار مثلثاتی برای حل نابرابری ها شکل گیرد، یعنی:
توانایی حل نابرابری های ساده فرم ,
, ,
,
استفاده از خواص توابع سینوس و کسینوس؛
امکان ایجاد نابرابری های دوگانه برای کمان های یک دایره عددی یا برای کمان های نمودار توابع.
توانایی انجام تبدیل های مختلف عبارات مثلثاتی.
اجرای این مرحله در فرآیند نظام‌مندسازی دانش دانش‌آموزان در مورد ویژگی‌های توابع مثلثاتی توصیه می‌شود. ابزار اصلی می تواند وظایفی باشد که به دانش آموزان ارائه می شود و تحت هدایت معلم یا به طور مستقل انجام می شود و همچنین مهارت هایی که در حل معادلات مثلثاتی به دست می آید.
در اینجا نمونه هایی از این وظایف آورده شده است:
1
. یک نقطه روی دایره واحد علامت بزنید 
، اگر
.
2.
نقطه در کدام چهارم صفحه مختصات قرار دارد ، اگر 
برابر است با: 
3.
نقاطی را روی دایره مثلثاتی علامت بزنید ، اگر:
4. عبارت را به توابع مثلثاتی بیاوریدمنچهارم.
آ) 
,
ب) 
,
که در) 
5. با توجه به قوس MR.م - وسطمنسه ماهه ام،آر - وسطIIسه ماهه ام مقدار یک متغیر را محدود کنیدتی برای: (یک نابرابری مضاعف بنویسید) الف) قوس MP; ب) قوس های RM.
6. یک نابرابری مضاعف برای بخش های انتخاب شده از نمودار بنویسید:
برنج. یکی
7.
حل نابرابری ها 
, 
, 
, 
.
8. تبدیل عبارت .
در مرحله دوم یادگیری حل نابرابری های مثلثاتی، می توان توصیه های زیر را در رابطه با روش شناسی سازماندهی فعالیت های دانش آموزان ارائه داد. در عین حال باید روی مهارت دانش آموزان برای کار با دایره مثلثاتی یا نمودار که در حین حل ساده ترین معادلات مثلثاتی تشکیل می شود، تمرکز کرد.
ابتدا، می توان با مراجعه به عنوان مثال به نامساوی شکل، مصلحت دستیابی به یک روش کلی برای حل ساده ترین نابرابری های مثلثاتی را برانگیخت. 
.
دانش آموزان با استفاده از دانش و مهارت های کسب شده در مرحله مقدماتی، نابرابری پیشنهادی را به شکلی درمی آورند. 
، اما ممکن است یافتن مجموعه ای از راه حل ها برای نابرابری حاصل دشوار باشد، زیرا حل آن فقط با استفاده از ویژگی های تابع سینوس غیرممکن است. با مراجعه به تصویر مناسب (حل معادله به صورت گرافیکی یا با استفاده از دایره واحد) می توان از این مشکل جلوگیری کرد.
ثانیاً معلم باید توجه دانش‌آموزان را به روشهای مختلف تکمیل تکلیف جلب کند، مثال مناسبی از حل نابرابری هم به صورت گرافیکی و هم با استفاده از دایره مثلثاتی ارائه دهد.
چنین گزینه هایی را برای حل نابرابری در نظر بگیرید .
1. حل نابرابری با استفاده از دایره واحد.
در درس اول در مورد حل نابرابری های مثلثاتی، ما یک الگوریتم حل دقیق را به دانش آموزان ارائه می دهیم که در یک ارائه گام به گام تمام مهارت های اساسی لازم برای حل نابرابری را منعکس می کند.
مرحله 1.یک دایره واحد رسم کنید، یک نقطه روی محور y علامت بزنید 
و یک خط مستقیم از آن به موازات محور x رسم کنید. این خط دایره واحد را در دو نقطه قطع می کند. هر یک از این نقاط اعدادی را نشان می دهد که سینوس آنها برابر است .
گام 2این خط مستقیم دایره را به دو قوس تقسیم می کرد. بیایید اعدادی را که سینوس آنها بزرگتر از آن نمایش داده شده است را مشخص کنیم . طبیعتاً این قوس بالای خط مستقیم کشیده شده قرار دارد.
برنج. 2
مرحله 3بیایید یکی از انتهای قوس مشخص شده را انتخاب کنیم. بیایید یکی از اعدادی را که با این نقطه از دایره واحد نمایش داده می شود، یادداشت کنیم 
.
مرحله 4برای انتخاب یک عدد مربوط به انتهای دوم کمان انتخاب شده، در امتداد این کمان از انتهای نامگذاری شده به انتهای دیگر "گذر" می کنیم. در عین حال، به یاد می آوریم که هنگام حرکت در خلاف جهت عقربه های ساعت، اعدادی که از آنها عبور می کنیم افزایش می یابد (هنگامی که در جهت مخالف حرکت می کنیم، اعداد کاهش می یابد). بیایید عددی را که روی دایره واحد در انتهای دوم قوس مشخص شده نشان داده شده است بنویسیم 
.
بنابراین، ما می بینیم که نابرابری اعدادی را که برای آنها نابرابری وجود دارد برآورده کنید 
. ما نابرابری اعداد واقع در همان دوره تابع سینوس را حل کردیم. بنابراین، تمام راه حل های نابرابری را می توان به صورت نوشتاری نوشت 
باید از دانش آموزان خواسته شود که شکل را با دقت در نظر بگیرند و دلیل همه راه حل های نابرابری را دریابند را می توان در قالب نوشت 
, 
.
برنج. 3
توجه دانش آموزان به این نکته ضروری است که هنگام حل نامساوی برای تابع کسینوس، یک خط مستقیم به موازات محور y رسم می کنیم.
روش گرافیکی برای حل نابرابری
نمودارهای ساختمان 
و 
، با توجه به اینکه 
.
برنج. چهار
سپس معادله را می نویسیم 
و تصمیم او 
, 
, 
، با استفاده از فرمول ها پیدا شد 
, 
, 
.
(دادنn
مقادیر 0، 1، 2، سه ریشه معادله تشکیل شده را پیدا می کنیم). ارزش های 
سه ابسیسا متوالی از نقاط تقاطع نمودارها هستند و . بدیهی است، همیشه در فاصله زمانی 
نابرابری 
، و در فاصله زمانی 
- نابرابری 
. ما به حالت اول علاقه مندیم و سپس با جمع کردن عددی که مضربی از دوره سینوس است به انتهای این بازه، راه حلی برای نابرابری به دست می آوریم. مانند: 
, .
برنج. 5
خلاصه کنید. برای حل نابرابری ، باید معادله مربوطه را بنویسید و آن را حل کنید. از فرمول به دست آمده ریشه ها را پیدا کنید 
و 
و جواب نامساوی را به شکل زیر بنویسید: , .
ثالثاً، این واقعیت در مورد مجموعه ریشه های نابرابری مثلثاتی مربوطه هنگام حل گرافیکی آن به وضوح تأیید می شود.
برنج. 6
لازم است به دانش‌آموزان نشان داده شود که سیم‌پیچ که راه‌حل نابرابری است، در همان بازه برابر با دوره تابع مثلثاتی تکرار می‌شود. همچنین می توانید تصویر مشابهی را برای نمودار تابع سینوس در نظر بگیرید.
چهارم، توصیه می شود برای به روز رسانی روش های دانش آموزان برای تبدیل مجموع (تفاوت) توابع مثلثاتی به یک محصول، کار انجام شود تا توجه دانش آموزان مدرسه ای به نقش این تکنیک ها در حل نابرابری های مثلثاتی جلب شود.
چنین کاری را می توان از طریق انجام مستقل تکالیف پیشنهادی معلم توسط دانش آموزان سازماندهی کرد که در میان آنها موارد زیر را برجسته می کنیم:
پنجم، دانش‌آموزان باید حل هر نابرابری مثلثاتی ساده را با استفاده از نمودار یا دایره مثلثاتی نشان دهند. حتما به مصلحت آن، به ویژه استفاده از دایره توجه کنید، زیرا هنگام حل نابرابری های مثلثاتی، تصویر مربوطه به عنوان وسیله ای بسیار مناسب برای رفع مجموعه راه حل ها برای یک نابرابری معین عمل می کند.
آشنایی دانش‌آموزان با روشهای حل نابرابری‌های مثلثاتی، که ساده‌ترین نیستند، باید طبق طرح زیر انجام شود: اشاره به یک نابرابری مثلثاتی خاص با مراجعه به جستجوی مشترک معادله مثلثاتی مربوطه (معلم - دانش‌آموز) برای انتقال مستقل راه‌حل. از روش یافت شده به نابرابری های دیگر از همان نوع.
به منظور نظام‌مند کردن دانش دانش‌آموزان از مثلثات، توصیه می‌کنیم به طور خاص چنین نابرابری‌هایی را انتخاب کنید که حل آن مستلزم تبدیل‌های مختلفی است که می‌توان در فرآیند حل آن اعمال کرد و توجه دانش‌آموزان را بر ویژگی‌های آنها متمرکز کرد.
به عنوان چنین نابرابری های مولد، می توانیم به عنوان مثال موارد زیر را پیشنهاد کنیم:
در پایان، ما یک مثال از مجموعه ای از مسائل را برای حل نابرابری های مثلثاتی ارائه می دهیم.
1- نابرابری ها را حل کنید:
2- نابرابری ها را حل کنید: 3. همه راه حل های نابرابری ها را بیابید: 4. همه راه حل های نابرابری ها را بیابید:آ) 
، ارضای شرط 
;
ب) 
، ارضای شرط 
.
5. همه راه حل های نابرابری ها را بیابید:
آ) ;
ب) ;
که در) 
;
ز) 
;
ه) 
.
6- نابرابری ها را حل کنید:
آ) ;
ب) ;
که در) ؛
ز) 
;
ه)؛
ه)؛
و) 
.
7- نابرابری ها را حل کنید:
آ) 
;
ب) ;
که در) ؛
ز) .
8- نابرابری ها را حل کنید:
آ) ;
ب) ;
که در) ؛
ز) 
;
ه) 
;
ه)؛
و) 
;
ح) .
توصیه می شود وظایف 6 و 7 را به دانش آموزانی که ریاضیات را در سطح پیشرفته مطالعه می کنند، ارائه دهید، وظیفه 8 - به دانش آموزان در کلاس هایی با مطالعه عمیق ریاضیات.
§3. روش های ویژه برای حل نابرابری های مثلثاتی
روش های ویژه برای حل معادلات مثلثاتی - یعنی روش هایی که فقط برای حل معادلات مثلثاتی قابل استفاده هستند. این روش ها بر اساس استفاده از ویژگی های توابع مثلثاتی و همچنین استفاده از فرمول ها و هویت های مثلثاتی مختلف است.
3.1. روش بخش
روش بخش را برای حل نابرابری های مثلثاتی در نظر بگیرید. حل نابرابری های فرم 
، جایی کهپ
(
ایکس
)
وس
(
ایکس
)
- توابع مثلثاتی گویا (سینوس ها، کسینوس ها، مماس ها و کوتانژانت ها به طور منطقی وارد آنها می شوند)، مشابه حل نابرابری های گویا. حل نابرابری های گویا با روش فواصل روی محور واقعی راحت است. آنالوگ آن در حل نابرابری های مثلثاتی گویا روش بخش ها در یک دایره مثلثاتی است.سینکس
وcosx
(
) یا یک نیم دایره مثلثاتی برایtgx
وctgx
(
).
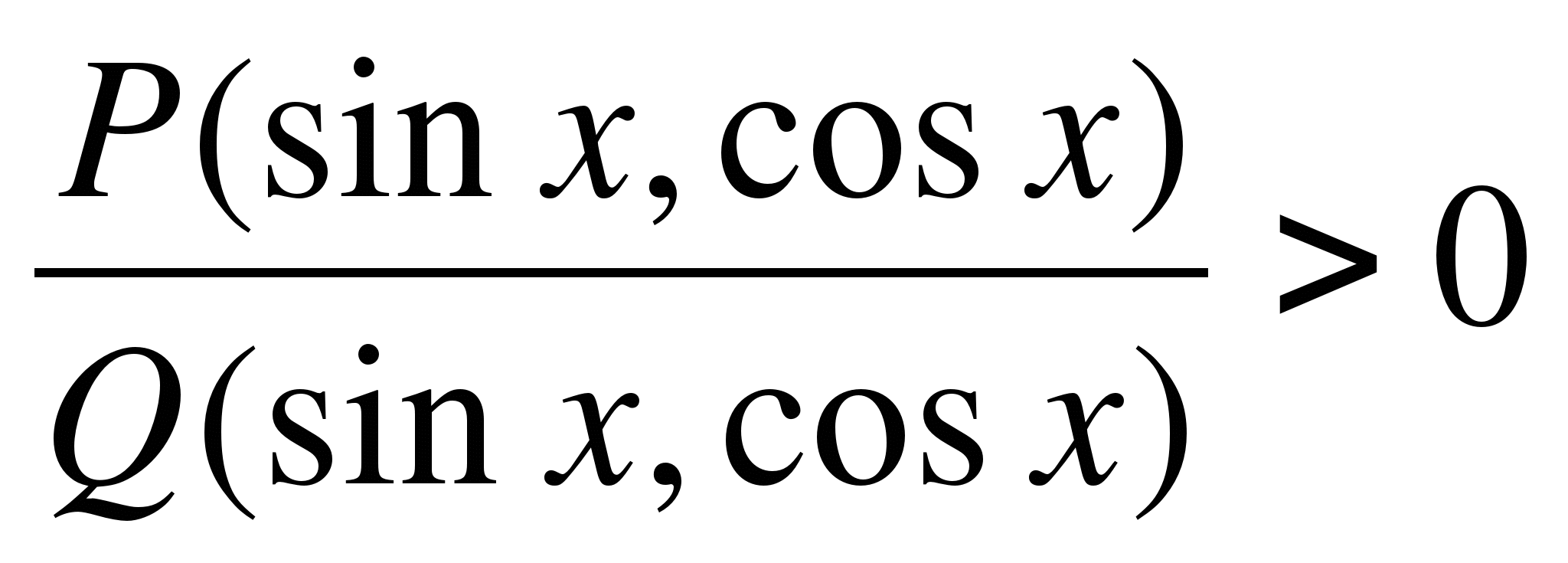
در روش بازه، هر ضریب خطی صورت و مخرج صورت 
نقطه روی محور اعداد 
، و هنگام عبور از این نقطه علامت را تغییر می دهد در روش سکتور هر ضریب فرم 
، جایی که 
- یکی از توابعسینکس
یاcosx
و 
، در یک دایره مثلثاتی دو زاویه وجود دارد 
و 
، که دایره را به دو بخش تقسیم می کند. هنگام عبور از و عملکرد علامت را تغییر می دهد
موارد زیر را باید به خاطر بسپارید:
الف) ضرب کننده های فرم 
و 
، جایی که 
، علامت را برای همه مقادیر حفظ کنید 
. چنین ضرب کننده های صورت و مخرج کنار گذاشته می شوند و تغییر می کنند (اگر 
) برای هر رد، علامت نابرابری معکوس می شود.
ب) ضرب کننده های فرم 
و 
نیز دور ریخته می شوند. علاوه بر این، اگر اینها عوامل مخرج هستند، نابرابری های شکل به سیستم معادل نابرابری ها اضافه می شوند. 
و 
. اگر اینها فاکتورهای شمارنده باشند، در سیستم معادل قیود آنها با نابرابری ها مطابقت دارند. و در مورد نابرابری اولیه شدید و برابری 
و 
در مورد یک نابرابری اولیه غیر دقیق. هنگام انداختن ضریب 
یا 
علامت نابرابری معکوس شده است.
مثال 1
حل نابرابری ها: الف) 
، ب) 
.
ما یک تابع داریم، b). نابرابری را که داریم حل کنید
3.2. روش دایره متحدالمرکز
این روش مشابه روش محورهای عددی موازی در حل سیستم های نابرابری های گویا است.
نمونه ای از سیستم نابرابری ها را در نظر بگیرید.
مثال 5
حل یک سیستم از نابرابری های مثلثاتی ساده 
ابتدا هر نابرابری را جداگانه حل می کنیم (شکل 5). در گوشه سمت راست بالای شکل نشان خواهیم داد که دایره مثلثاتی برای کدام آرگومان در نظر گرفته شده است.
شکل 5
در مرحله بعد، سیستمی از دایره های متحدالمرکز برای استدلال می سازیمایکس . دایره ای رسم می کنیم و با توجه به حل نامعادله اول سایه می زنیم، سپس دایره ای به شعاع بزرگتر می کشیم و با توجه به حل دومی روی آن سایه می زنیم، سپس برای نابرابری سوم دایره ای و دایره پایه می سازیم. . پرتوهایی را از مرکز سیستم از انتهای کمان ها می کشیم به طوری که همه دایره ها را قطع می کنند. روی دایره پایه یک محلول تشکیل می دهیم (شکل 6).
شکل 6
پاسخ:
, 
.
نتیجه
تمام اهداف دوره تکمیل شد. مطالب نظری سیستماتیک شده است: انواع اصلی نابرابری های مثلثاتی و روش های اصلی حل آنها (گرافیک، جبری، روش فواصل، بخش ها و روش دایره های متحدالمرکز) ارائه شده است. برای هر روش یک مثال از حل یک نابرابری آورده شده است. بخش تئوری با بخش عملی دنبال شد. این شامل مجموعه ای از وظایف برای حل نابرابری های مثلثاتی است.
این درس می تواند توسط دانش آموزان برای کار مستقل استفاده شود. دانش آموزان می توانند سطح جذب این موضوع را بررسی کنند، در انجام وظایف با پیچیدگی های مختلف تمرین کنند.
بدیهی است که پس از بررسی ادبیات مربوطه در این زمینه، می‌توان نتیجه گرفت که توانایی و مهارت حل نابرابری‌های مثلثاتی در درس جبر مدرسه و شروع تجزیه و تحلیل بسیار مهم است که توسعه آن نیازمند تلاش قابل توجهی است. معلم ریاضی
بنابراین، این کار برای معلمان ریاضی مفید خواهد بود، زیرا امکان سازماندهی موثر آموزش دانش آموزان در موضوع "نابرابری های مثلثاتی" را فراهم می کند.
مطالعه را می توان با گسترش آن به کار مقدماتی نهایی ادامه داد.
فهرست ادبیات استفاده شده
بوگومولوف، N.V. مجموعه مسائل ریاضی [متن] / N.V. بوگومولوف. – M.: Bustard, 2009. – 206 p.
ویگودسکی، ام.یا. کتاب راهنمای ریاضیات ابتدایی [متن] / م.یا. ویگودسکی – M.: Bustard, 2006. – 509 p.
ژوربنکو، ال.ن. ریاضیات در مثال ها و وظایف [متن] / L.N. ژوربنکو. – M.: Infra-M, 2009. – 373 p.
ایوانف، O.A. ریاضیات ابتدایی برای دانش آموزان، دانش آموزان و معلمان [متن] / O.A. ایوانف - M.: MTsNMO، 2009. - 384 ص.
کارپ، A.P. وظایف جبر و آغاز تجزیه و تحلیل برای سازماندهی تکرار و گواهی نهایی در پایه یازدهم [متن] / A.P. کپور. - م.: روشنگری، 2005. - 79 ص.
کولانین، ای.د. 3000 مسئله رقابتی در ریاضیات [متن] / E.D. کولانین. – م.: Iris-press, 2007. – 624 p.
لیبسون، K.L. مجموعه کارهای عملی در ریاضیات [متن] / K.L. لیبسون. - M.: Bustard, 2010. - 182 p.
آرنج، V.V. مشکلات پارامترها و راه حل آنها. مثلثات: معادلات، نامساوی ها، سیستم ها. درجه 10 [متن] / V.V. آرنج. – م.: آرکتی، 2008. – 64 ص.
مانووا، A.N. ریاضی. معلم اکسپرس برای آماده شدن برای امتحان: حساب. کمک هزینه [متن] / A.N. مانووا. - Rostov-on-Don: Phoenix, 2012. - 541 p.
موردکوویچ، A.G. جبر و شروع تحلیل ریاضی. پایه های 10-11. کتاب درسی برای دانش آموزان مؤسسات آموزشی [متن] / A.G. موردکوویچ. - M.: Iris-press, 2009. - 201 p.
نوویکوف، A.I. توابع مثلثاتی، معادلات و نامساوی [متن] / A.I. نوویکوف. - M.: FIZMATLIT، 2010. - 260 p.
اوگانسیان، V.A. روش های تدریس ریاضی در دوره متوسطه: روش شناسی عمومی. Proc. کمک هزینه برای دانشجویان فیزیک - حصیر جعلی Ped در رفیق [متن] / V.A. اوگانسیان. - م.: روشنگری، 2006. - 368 ص.
اولچنیک، اس.ن. معادلات و نابرابری ها روش های حل غیر استاندارد [متن] / S.N. اولخنیک. - م .: انتشارات فاکتوریل، 1376. - 219 ص.
سوریوکوف، پی.ف. معادلات و نابرابری های مثلثاتی، نمایی و لگاریتمی [متن] / P.F. سوریوکوف – م.: آموزش ملی، 1387. – 352 ص.
سرگیف، I.N. استفاده: 1000 کار با پاسخ و راه حل در ریاضیات. تمام وظایف گروه C [متن] / I.N. سرگئیف – م.: امتحان، 2012. – 301 ص.
سوبولف، A.B. ریاضیات ابتدایی [متن] / A.B. سوبولف. - یکاترینبورگ: GOU VPO USTU-UPI، 2005. - 81 p.
فنکو، ال.ام. روش فواصل در حل نامساوی ها و مطالعه توابع [متن] / L.M. فنکو. – M.: Bustard, 2005. – 124 p.
فریدمن، ال.ام. مبانی نظری روش شناسی تدریس ریاضی [متن] / L.M. فریدمن - م .: کتاب خانه "LIBROKOM"، 2009. - 248 ص.
پیوست 1
تفسیر گرافیکی راه حل های ساده ترین نابرابری ها
برنج. یکی
برنج. 2
شکل 3
شکل 4
شکل 5
شکل 6
شکل 7
شکل 8
پیوست 2
راه حل های ساده ترین نابرابری ها
