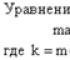کار عملی شماره 2

"تابع دیفرانسیل"

هدف درس: حل مثال ها و مسائل مربوط به این موضوع را یاد بگیرید.

سوالات تئوری (پایه):

1. استفاده از مشتقات برای مطالعه توابع در امتداد.

2. دیفرانسیل یک تابع، معنای هندسی و فیزیکی آن.

3. دیفرانسیل کامل یک تابع از چندین متغیر.

4. حالت بدن به عنوان تابعی از متغیرهای زیادی.

5. محاسبات تقریبی.

6. یافتن مشتقات جزئی و دیفرانسیل کل.

7. نمونه هایی از کاربرد این مفاهیم در فارماکوکینتیک، میکروبیولوژی و غیره.

(آماده سازی خود)

1. پاسخ به سؤالات در مورد موضوع درس.

2. حل مثال

مثال ها

دیفرانسیل توابع زیر را بیابید:

1)	2)	3)
4)	5)	6)
7)	8)	9)
10)	11)	12)
13)	14)	15)
16)	17)	18)
19)	20)

استفاده از مشتقات برای مطالعه توابع

شرط افزایش تابع y = f(x) در بازه [a, b]

شرط کاهش تابع y=f(x) در قطعه [a, b]

شرط حداکثر تابع y=f(x) در x=a

f"(a)=0 و f"" (a)<0

اگر در x=a مشتقات f"(a) = 0 و f"(a) = 0 باشد، باید f"(x) را در مجاورت نقطه x = a مطالعه کرد. تابع y=f( x) در x=a دارای حداکثر است، اگر در هنگام عبور از نقطه x = a، مشتق f"(x) علامت "+" را به "-" تغییر دهد، در مورد حداقل - از "-" به "+" اگر f"(x) هنگام عبور از نقطه x = a علامت را تغییر ندهد، در این مرحله تابع هیچ اکسترومی ندارد.

دیفرانسیل عملکرد

دیفرانسیل یک متغیر مستقل برابر است با افزایش آن:

دیفرانسیل تابع y=f(x)

دیفرانسیل مجموع (تفاوت) دو تابع y=u±v

دیفرانسیل حاصل ضرب دو تابع y=uv

دیفرانسیل ضریب دو تابع y=u/v

dy=(vdu-udv)/v 2

افزایش تابع

Δy = f(x + Δx) - f(x) ≈ dy ≈ f"(x) Δx

جایی که Δx: - افزایش آرگومان.

محاسبه تقریبی مقدار تابع:

f(x + Δx) ≈ f(x) + f"(x) Δx

کاربرد دیفرانسیل در محاسبات تقریبی

دیفرانسیل برای محاسبه خطاهای مطلق و نسبی در اندازه گیری های غیرمستقیم u = f(x, y, z.) استفاده می شود. خطای مطلق نتیجه اندازه گیری

du≈Δu≈|du/dx|Δx+|du/dy|Δy+|du/dz|Δz+…

خطای نسبی نتیجه اندازه گیری

du/u≈Δu/u≈(|du/dx|Δx+|du/dy|Δy+|du/dz|Δz+…)/u

تابع دیفرانسیل.

دیفرانسیل یک تابع به عنوان بخش اصلی افزایش یک تابع و.ارتباط نزدیک با مفهوم مشتق، مفهوم دیفرانسیل یک تابع است. اجازه دهید تابع f(x)برای مقادیر داده شده پیوسته است ایکسو مشتق دارد

D f/Dx = f¢(x) + a(Dx)، از آنجا که افزایش تابع است Df = f¢(x)Dx + a(Dx)Dx،جایی که a (Dx) ® 0در Dх ® 0. اجازه دهید ترتیب بینهایت کوچک را تعیین کنیم f¢(x)Dx Dx:

بنابراین، بی نهایت کوچک f¢(x)Dxو Dxهمان مرتبه کوچکی را دارند، یعنی f¢(x)Dx = O.

اجازه دهید ترتیب بینهایت کوچک را تعیین کنیم a(Dх)Dхنسبت به بی نهایت کوچک Dx:

بنابراین، بی نهایت کوچک a(Dх)Dхدرجه کوچکی بالاتری نسبت به بی نهایت کوچک دارد Dx، به این معنا که a(Dx)Dx = o.

بنابراین، افزایش بی نهایت کوچک Dfتابع متمایز را می توان در قالب دو عبارت نشان داد: بی نهایت کوچک f¢(x)Dxاز همان مرتبه کوچکی با Dxو بی نهایت کوچک a(Dх)Dхدرجه کوچکی بالاتر در مقایسه با بی نهایت کوچک Dxاین بدان معناست که در برابری Df=f¢(x)Dx + a(Dx)Dxدر Dx® 0عبارت دوم به صفر "سریعتر" از جمله اول تمایل دارد a(Dx)Dx = o.

ترم اول f¢(x)Dx،خطی نسبت به Dx، تماس گرفت تابع دیفرانسیل f(x) در نقطه ایکسو نشان دهند دویا df("de igrek" یا "de ef" را بخوانید). بنابراین،

dy = df = f¢(x)Dx.

معنای تحلیلی دیفرانسیلاین است که دیفرانسیل یک تابع بخش اصلی افزایش تابع است Df، خطی با توجه به افزایش آرگومان Dx. دیفرانسیل یک تابع با افزایش یک تابع به میزان بی نهایت کوچکتر از مرتبه کوچکی متفاوت است. Dx. واقعا، Df=f¢(x)Dx + a(Dx)Dxیا Df = df + a(Dx)Dx . دیفرانسیل آرگومان dxبرابر با افزایش آن است Dx: dx=Dx.

مثال.مقدار دیفرانسیل یک تابع را محاسبه کنید f(x) = x 3 + 2x،چه زمانی ایکساز 1 تا 1.1 متغیر است.

راه حل.بیایید یک عبارت کلی برای دیفرانسیل این تابع پیدا کنیم:

جایگزینی مقادیر dx=Dx=1.1–1=0.1و x = 1در آخرین فرمول، مقدار مورد نظر دیفرانسیل را دریافت می کنیم: df½ x=1; = 0,5.

مشتقات جزئی و دیفرانسیل.

مشتقات جزئی مرتبه اول. مشتق جزئی مرتبه اول تابع z = f(x,y ) با استدلال ایکسدر نقطه مورد نظر (x;y)حد نامیده می شود

اگر وجود داشته باشد.

مشتق جزئی یک تابع z = f(x, y)با استدلال ایکسبا یکی از نمادهای زیر نشان داده می شود:

به طور مشابه، مشتق جزئی با توجه به دربا فرمول مشخص و تعریف می شود:

از آنجایی که مشتق جزئی مشتق معمولی تابع یک آرگومان است، محاسبه آن دشوار نیست. برای انجام این کار، باید از تمام قوانین تمایز در نظر گرفته شده استفاده کنید، و در هر مورد در نظر بگیرید که کدام یک از آرگومان ها به عنوان "عدد ثابت" و کدام یک به عنوان "متغیر تمایز" عمل می کند.

اظهار نظر.برای پیدا کردن مشتق جزئی، برای مثال، با توجه به آرگومان x – df/dx، کافی است مشتق معمولی تابع را پیدا کنیم f(x,y)در نظر گرفتن دومی تابعی از یک آرگومان ایکس، آ در- ثابت؛ برای پیدا کردن df/dy- برعکس

مثال.مقادیر مشتقات جزئی یک تابع را بیابید f(x,y) = 2x 2 + y 2در نقطه P(1;2).

راه حل.با احتساب f(x,y)تابع یک آرگومان ایکسو با استفاده از قواعد تمایز، متوجه می شویم

در نقطه P(1;2)ارزش مشتق

با در نظر گرفتن f(x;y) تابعی از یک آرگومان y، متوجه می شویم

در نقطه P(1;2)ارزش مشتق

وظیفه برای کار مستقل دانش آموز:

دیفرانسیل توابع زیر را بیابید:

مشکلات زیر را حل کنید:

1. اگر ضلع آن 0.01 سانتی متر کاهش یابد، مساحت مربع با ضلع x=10 سانتی متر چقدر کاهش می یابد؟

2. معادله حرکت بدن داده می شود: y=t 3 /2+2t 2 که s بر حسب متر بیان می شود، t بر حسب ثانیه است. مسیر s پیموده شده توسط بدن را در t=1.92 ثانیه از ابتدای حرکت پیدا کنید.

ادبیات

1. Lobotskaya N.L. مبانی ریاضیات عالی - M.: "مدرسه عالی", 1978.C198-226.

2. بیلی N. ریاضیات در زیست شناسی و پزشکی. مطابق. از انگلیسی م.: "میر"، 1970.

3. Remizov A.N.، Isakova N.Kh.، Maksina L.G. مجموعه مسائل در فیزیک پزشکی و بیولوژیکی - م.: "دبیرستان"، 1366. ص16-20.

مشتقات جزئی یک تابع از دو متغیر.
مفهوم و مثال هایی از راه حل ها

در این درس به آشنایی خود با عملکرد دو متغیر ادامه می دهیم و شاید رایج ترین کار موضوعی - یافتن - را در نظر بگیریم. مشتقات جزئی مرتبه اول و دوم و همچنین دیفرانسیل کل تابع. دانشجویان پاره وقت معمولاً در ترم دوم در سال اول با مشتقات جزئی مواجه می شوند. علاوه بر این، طبق مشاهدات من، وظیفه یافتن مشتقات جزئی تقریباً همیشه در امتحان ظاهر می شود.

برای مطالعه موثر مطالب زیر، شما لازم استبتواند مشتقات "معمولی" توابع یک متغیر را کم و بیش با اطمینان پیدا کند. شما می توانید یاد بگیرید که چگونه مشتقات را به درستی در دروس مدیریت کنید چگونه مشتق را پیدا کنیم؟و مشتق تابع مختلط. ما همچنین به جدولی از مشتقات توابع ابتدایی و قوانین تمایز نیاز خواهیم داشت؛ اگر به صورت چاپی در دسترس باشد، راحت تر است. می توانید مطالب مرجع را در صفحه دریافت کنید فرمول ها و جداول ریاضی.

بیایید به سرعت مفهوم تابع دو متغیر را تکرار کنیم، سعی می کنم خودم را به حداقل حداقل محدود کنم. تابعی از دو متغیر معمولاً به صورت نوشته می‌شود و متغیرها فراخوانی می‌شوند متغیرهای مستقلیا استدلال ها.

مثال: – تابع دو متغیر.

گاهی اوقات از نماد استفاده می شود. همچنین وظایفی وجود دارد که به جای حرف از حرف استفاده می شود.

از نقطه نظر هندسی، تابعی از دو متغیر اغلب نمایانگر یک سطح در فضای سه بعدی (صفحه، استوانه، کره، سهمی، هایپربولوئید و غیره) است. اما، در واقع، این بیشتر هندسه تحلیلی است، و در دستور کار ما تجزیه و تحلیل ریاضی است، که استاد دانشگاه من هرگز اجازه نداد آن را حذف کنم و "نقطه قوت" من است.

بیایید به مسئله یافتن مشتقات جزئی مرتبه اول و دوم برویم. من یک خبر خوب برای کسانی دارم که چند فنجان قهوه نوشیده اند و در حال تنظیم مطالب فوق العاده دشوار هستند: مشتقات جزئی تقریباً مشابه مشتقات "معمولی" یک تابع از یک متغیر هستند.

برای مشتقات جزئی، تمام قوانین تمایز و جدول مشتقات توابع ابتدایی معتبر است. تنها چند تفاوت کوچک وجود دارد که در حال حاضر با آنها آشنا خواهیم شد:

...بله اتفاقا برای این تاپیک ایجاد کردم کتاب پی دی اف کوچک، که به شما امکان می دهد فقط در چند ساعت "دندان های خود را وارد کنید". اما با استفاده از سایت، مطمئناً همان نتیجه را خواهید گرفت - فقط شاید کمی کندتر:

مثال 1

مشتقات جزئی مرتبه اول و دوم تابع را پیدا کنید

ابتدا، بیایید مشتقات جزئی مرتبه اول را پیدا کنیم. دو تا از آنها موجود است.

تعیین ها:
یا - مشتق جزئی با توجه به "x"
یا - مشتق جزئی با توجه به "y"

بیا شروع کنیم با . وقتی مشتق جزئی را با توجه به "x" پیدا می کنیم، متغیر یک ثابت در نظر گرفته می شود (عدد ثابت).

نظرات در مورد اقدامات انجام شده:

(1) اولین کاری که هنگام یافتن مشتق جزئی انجام می دهیم نتیجه گیری است همهعملکرد در براکت های زیر پرایم با زیرنویس.

توجه، مهم!ما مشترکین را در طول فرآیند حل از دست نمی دهیم. در این مورد، اگر در جایی بدون سکته مغزی بکشید، حداقل معلم می تواند آن را در کنار تکلیف قرار دهد (فوراً بخشی از نقطه را به دلیل بی توجهی گاز بگیرد).

(2) ما از قوانین تمایز استفاده می کنیم ، . برای مثال ساده ای مانند این، هر دو قانون را می توان به راحتی در یک مرحله اعمال کرد. به عبارت اول توجه کنید: از آنجا که ثابت در نظر گرفته می شود و هر ثابتی را می توان از علامت مشتق خارج کرد، سپس آن را از داخل پرانتز قرار می دهیم. یعنی در این شرایط بهتر از یک عدد معمولی نیست. حالا بیایید به اصطلاح سوم نگاه کنیم: در اینجا، برعکس، چیزی برای خارج کردن وجود ندارد. از آنجایی که ثابت است، ثابت است، و از این نظر بهتر از جمله آخر - "هفت" نیست.

(3) از مشتقات جدولی و .

(4) بیایید پاسخ را ساده کنیم، یا، همانطور که دوست دارم بگویم، پاسخ را «ترکیب کنیم».

اکنون . وقتی مشتق جزئی را با توجه به "y" پیدا می کنیم، متغیر را پیدا می کنیمثابت در نظر گرفته می شود (عدد ثابت).

(1) ما از قوانین تمایز یکسانی استفاده می کنیم ، . در جمله اول ثابت را از علامت مشتق خارج می کنیم، در جمله دوم نمی توانیم چیزی را خارج کنیم زیرا از قبل ثابت است.

(2) از جدول مشتقات توابع ابتدایی استفاده می کنیم. بیایید از نظر ذهنی تمام "X"های جدول را به "I's" تغییر دهیم. یعنی این جدول برای (و در واقع تقریباً برای هر حرفی) به یک اندازه معتبر است. به طور خاص، فرمول هایی که ما استفاده می کنیم به این شکل هستند: و.

منظور از مشتقات جزئی چیست؟

در اصل، مشتقات جزئی مرتبه 1 شبیه هستند مشتق "معمولی".:

- این کارکرد، که مشخصه نرخ تغییربه ترتیب در جهت محورها و محورها عمل می کند. بنابراین، برای مثال، تابع شیب‌های "سربالایی" و "شیب" را مشخص می‌کند سطوحدر جهت محور آبسیسا، و تابع به ما در مورد "تسکین" همان سطح در جهت محور ارتین می گوید.

! توجه داشته باشید : در اینجا منظور ما جهت هایی است که موازیمحورهای مختصات.

برای درک بهتر، اجازه دهید یک نقطه خاص از صفحه را در نظر بگیریم و مقدار تابع ("ارتفاع") را در آن محاسبه کنیم:
– و حالا تصور کنید که اینجا هستید (روی سطح).

بیایید مشتق جزئی را با توجه به "x" در یک نقطه مشخص محاسبه کنیم:

علامت منفی مشتق "X" به ما می گوید در حال کاهشدر نقطه ای در جهت محور آبسیسا عمل می کند. به عبارت دیگر، اگر ما یک کوچک، کوچک (بی نهایت کوچک)به سمت نوک محور قدم بردارید (موازی با این محور)، سپس از شیب سطح پایین می رویم.

اکنون ماهیت "زمین" را در جهت محور ترتیب می یابیم:

مشتق با توجه به "y" مثبت است، بنابراین، در نقطه ای در جهت محور تابع افزایش. به بیان ساده، اینجا منتظر یک صعود سربالایی هستیم.

علاوه بر این، مشتق جزئی در یک نقطه مشخص می کند نرخ تغییردر جهت مربوطه عمل می کند. هر چه مقدار حاصل بیشتر باشد مدول- هر چه سطح شیب دارتر باشد و بالعکس هرچه به صفر نزدیکتر باشد سطح صاف تر است. بنابراین، در مثال ما، "شیب" در جهت محور آبسیسا تندتر از "کوه" در جهت محور ترتیب است.

اما این دو مسیر خصوصی بود. کاملاً واضح است که از نقطه‌ای که در آن هستیم، (و به طور کلی از هر نقطه از یک سطح مشخص)می توانیم در مسیر دیگری حرکت کنیم. بنابراین، علاقه به ایجاد یک "نقشه ناوبری" کلی وجود دارد که ما را در مورد "چشم انداز" سطح آگاه کند. در صورت امکاندر هر نقطه دامنه تعریف این تابعدر تمام مسیرهای موجود من در مورد این و چیزهای جالب دیگر در یکی از درس های بعدی صحبت خواهم کرد، اما فعلا اجازه دهید به جنبه فنی موضوع برگردیم.

اجازه دهید قوانین ابتدایی کاربردی را سیستماتیک کنیم:

1) هنگامی که ما با توجه به متمایز می کنیم، متغیر یک ثابت در نظر گرفته می شود.

2) هنگامی که تمایز بر اساس انجام می شود، سپس یک ثابت در نظر گرفته می شود.

3) قوانین و جدول مشتقات توابع ابتدایی برای هر متغیر (یا هر متغیر دیگری) که توسط آن تمایز انجام می شود معتبر و قابل اجرا است.

مرحله دو. مشتقات جزئی مرتبه دوم را پیدا می کنیم. چهار عدد از آن وجود دارد.

تعیین ها:
یا - مشتق دوم با توجه به "x"
یا - مشتق دوم با توجه به "y"
یا - مختلطمشتق "x توسط igr"
یا - مختلطمشتق از "Y"

در مورد مشتق دوم هیچ مشکلی وجود ندارد. به زبان ساده، مشتق دوم مشتق مشتق اول است.

برای راحتی، مشتقات جزئی مرتبه اول را که قبلاً پیدا شده اند بازنویسی می کنم:

ابتدا، بیایید مشتقات مختلط را پیدا کنیم:

همانطور که می بینید، همه چیز ساده است: مشتق جزئی را می گیریم و دوباره آن را متمایز می کنیم، اما در این مورد - این بار با توجه به "Y".

به همین ترتیب:

در مثال های عملی، می توانید بر برابری زیر تمرکز کنید:

بنابراین، از طریق مشتقات مرکب مرتبه دوم، بررسی اینکه آیا مشتقات جزئی مرتبه اول را به درستی پیدا کرده‌ایم بسیار راحت است.

مشتق دوم را با توجه به "x" بیابید.
بدون اختراع، بیایید آن را بگیریم و دوباره آن را با "x" متمایز کنید:

به همین ترتیب:

لازم به ذکر است که هنگام یافتن باید نشان دهید افزایش توجه، زیرا هیچ برابری معجزه آسایی برای تأیید آنها وجود ندارد.

مشتقات دوم نیز کاربردهای عملی گسترده ای پیدا می کنند، به ویژه، آنها در مسئله یافتن استفاده می شوند حداکثر یک تابع از دو متغیر. اما هر چیزی زمان خودش را دارد:

مثال 2

مشتقات جزئی مرتبه اول تابع را در نقطه محاسبه کنید. مشتقات مرتبه دوم را پیدا کنید.

این مثالی است که خودتان می توانید آن را حل کنید (پاسخ در انتهای درس). اگر در تشخیص ریشه ها مشکل دارید، به درس برگردید چگونه مشتق را پیدا کنیم؟به طور کلی، به زودی یاد خواهید گرفت که چنین مشتقاتی را "در حال پرواز" پیدا کنید.

بیایید در مثال های پیچیده تر بهتر شویم:

مثال 3

آن را بررسی کنید. دیفرانسیل کل مرتبه اول را بنویسید.

راه حل: مشتقات جزئی مرتبه اول را بیابید:

به زیرنویس دقت کنید: در کنار X ممنوع نیست داخل پرانتز بنویسید که ثابت است. این یادداشت می تواند برای مبتدیان بسیار مفید باشد تا راه حل را آسان تر کند.

نظرات بیشتر:

(1) همه ثابت ها را فراتر از علامت مشتق حرکت می دهیم. در این حالت، و، و بنابراین، حاصلضرب آنها یک عدد ثابت در نظر گرفته می شود.

(2) فراموش نکنید که چگونه ریشه ها را به درستی متمایز کنید.

(1) ما همه ثابت ها را از علامت مشتق خارج می کنیم؛ در این حالت، ثابت است.

(2) در زیر عدد اول، حاصل ضرب دو تابع باقی مانده است، بنابراین، باید از قانون برای متمایز کردن محصول استفاده کنیم. .

(3) فراموش نکنید که این یک تابع پیچیده است (البته ساده ترین تابع). ما از قانون مربوطه استفاده می کنیم: .

اکنون مشتقات مخلوط مرتبه دوم را می یابیم:

این بدان معنی است که تمام محاسبات به درستی انجام شده است.

بیایید دیفرانسیل کل را بنویسیم. در زمینه تکلیف مورد بررسی، معنی ندارد که بگوییم تفاضل کل یک تابع از دو متغیر چقدر است. مهم است که این تفاوت بسیار اغلب در مسائل عملی نوشته شود.

دیفرانسیل کل مرتبه اولتابع دو متغیر به شکل زیر است:

در این مورد:

یعنی فقط باید احمقانه مشتقات جزئی مرتبه اول پیدا شده را در فرمول جایگزین کنید. در این شرایط و موارد مشابه، بهتر است علائم دیفرانسیل را در اعداد بنویسید:

و با توجه به درخواست های مکرر خوانندگان، دیفرانسیل کامل مرتبه دوم.

به نظر می رسد این است:

بیایید مشتقات "یک حرفی" مرتبه دوم را با دقت پیدا کنیم:

و "هیولا" را یادداشت کنید، مربع ها، حاصلضرب را با دقت "چسب کنید" و فراموش نکنید که مشتق مخلوط را دو برابر کنید:

اگر چیزی دشوار به نظر می رسد، اشکالی ندارد؛ همیشه می توانید بعداً، پس از تسلط بر تکنیک تمایز، به مشتقات بازگردید:

مثال 4

مشتقات جزئی مرتبه اول یک تابع را پیدا کنید . آن را بررسی کنید. دیفرانسیل کل مرتبه اول را بنویسید.

بیایید به یک سری مثال با توابع پیچیده نگاه کنیم:

مثال 5

مشتقات جزئی مرتبه اول تابع را پیدا کنید.

راه حل:

مثال 6

مشتقات جزئی مرتبه اول یک تابع را پیدا کنید .
دیفرانسیل کل را بنویسید.

این مثالی است که خودتان می توانید آن را حل کنید (پاسخ در انتهای درس). من راه حل کاملی به شما نمی دهم زیرا بسیار ساده است.

اغلب، همه قوانین فوق به صورت ترکیبی اعمال می شوند.

مثال 7

مشتقات جزئی مرتبه اول یک تابع را پیدا کنید .

(1) از قانون برای افتراق جمع استفاده می کنیم

(2) جمله اول در این مورد ثابت در نظر گرفته می شود، زیرا چیزی در عبارت که به "x" وابسته باشد وجود ندارد - فقط "y". می دانید، وقتی کسر را می توان به صفر تبدیل کرد، همیشه خوب است). برای ترم دوم، قانون تمایز محصول را اعمال می کنیم. به هر حال، از این نظر، اگر به جای آن یک تابع داده می شد، هیچ چیز تغییر نمی کرد - نکته مهم اینجاست محصول دو تابع، که هر کدام به این بستگی دارد "ایکس"و بنابراین، باید از قانون تمایز محصول استفاده کنید. برای عبارت سوم، قانون تمایز یک تابع پیچیده را اعمال می کنیم.

(1) اولین جمله در صورت و مخرج حاوی "Y" است، بنابراین، باید از قانون برای افتراق ضرایب استفاده کنید: . جمله دوم فقط به "x" بستگی دارد، به این معنی که ثابت در نظر گرفته می شود و به صفر تبدیل می شود. برای ترم سوم از قانون تمایز یک تابع پیچیده استفاده می کنیم.

برای آن دسته از خوانندگانی که با شجاعت تقریباً به پایان درس رسیدند، برای تسکین یک جوک قدیمی مخماتوف به شما می گویم:

یک روز یک مشتق شیطانی در فضای توابع ظاهر شد و شروع به متمایز کردن همه کرد. همه توابع در همه جهات پراکنده هستند، هیچ کس نمی خواهد تبدیل شود! و تنها یک تابع فرار نمی کند. مشتق به او نزدیک می شود و می پرسد:

- چرا از من فرار نمی کنی؟

- ها. اما من اهمیتی نمی دهم، زیرا من "e به توان X" هستم و شما هیچ کاری با من نخواهید کرد!

که مشتق شیطانی با لبخندی موذیانه پاسخ می دهد:

- این جایی است که شما اشتباه می کنید، من شما را با "Y" متمایز می کنم، بنابراین شما باید یک صفر باشید.

هر کسی که این لطیفه را فهمیده است، حداقل تا سطح "C" به مشتقات تسلط دارد).

مثال 8

مشتقات جزئی مرتبه اول یک تابع را پیدا کنید .

این یک مثال برای شماست که خودتان آن را حل کنید. حل کامل و مثال مسئله در انتهای درس آمده است.

خوب، این تقریباً تمام است. در نهایت، نمی توانم از دوستداران ریاضیات با یک مثال دیگر لذت نبرم. این حتی در مورد آماتورها نیست، هر کس سطح متفاوتی از آمادگی ریاضی دارد - افرادی (و نه چندان نادر) وجود دارند که دوست دارند با کارهای دشوارتر رقابت کنند. اگرچه آخرین مثال در این درس آنقدر پیچیده نیست که از نظر محاسباتی دست و پا گیر است.

برای ساده‌تر کردن ضبط و ارائه مطالب، خود را به توابع دو متغیر محدود می‌کنیم. هر چیزی که در ادامه می آید برای توابع هر تعداد متغیر نیز صادق است.

تعریف. مشتق جزئیکارکرد z = f(x، y) توسط متغیر مستقل ایکسمشتق نامیده می شود

ثابت محاسبه می شود در.

مشتق جزئی با توجه به یک متغیر به طور مشابه تعیین می شود در.

برای مشتقات جزئی، قوانین و فرمول های معمول تمایز معتبر است.

تعریف.حاصلضرب مشتق جزئی و افزایش استدلال ایکس(y) نامیده می شود دیفرانسیل جزئیتوسط متغیر ایکس(در) توابع دو متغیر z = f(x، y) (سمبل: ):

اگر تحت دیفرانسیل متغیر مستقل باشد dx(دو) افزایش را درک کنید ایکس(در) آن

برای عملکرد z = f(x، y) معنی هندسی مشتقات فرکانس آن را دریابیم و .

نکته را در نظر بگیرید، نکته پ 0 (ایکس 0 ,y 0 , z 0) روی سطح z = f(ایکس,در) و منحنی L، که با برش سطح با صفحه بدست می آید y = y 0 . این منحنی را می توان به عنوان نمودار یک تابع از یک متغیر مشاهده کرد z = f(x، y) در هواپیما y = y 0 . اگر در نقطه نگه داشته شود آر 0 (ایکس 0 ، y 0 ، z 0) مماس بر منحنی L، سپس با توجه به معنای هندسی مشتق تابع یک متغیر ، جایی که آ – زاویه ای که توسط یک مماس با جهت مثبت محور تشکیل می شود اوه.

یا: اجازه دهید به طور مشابه متغیر دیگری را اصلاح کنیم، یعنی. اجازه دهید سطح را برش دهیم z = f(x، y) سطح x = x 0 . سپس تابع

z = f(ایکس 0 ، y) را می توان تابعی از یک متغیر در نظر گرفت در:

جایی که ب- زاویه تشکیل شده توسط مماس در نقطه م 0 (ایکس 0 ، y 0) با جهت محور مثبت اوه(شکل 1.2).

برنج. 1.2. تصویری از معنای هندسی مشتقات جزئی

مثال 1.6.یک تابع داده شده است z = x 2 – 3xy - 4در 2 - x + 2y + 1. پیدا کردن و .

راه حل.با توجه به دربه عنوان یک ثابت، دریافت می کنیم

با احتساب ایکسثابت، ما پیدا می کنیم

سخنرانی 3 FNP، مشتقات جزئی، دیفرانسیل

مهمترین چیزی که در سخنرانی گذشته یاد گرفتیم چیست؟

ما با آرگومان فضای اقلیدسی فهمیدیم که تابع چند متغیر چیست. ما مطالعه کردیم که محدودیت و تداوم برای چنین تابعی چیست

در این سخنرانی چه خواهیم آموخت؟

در ادامه مطالعه خود در مورد FNP ها، مشتقات جزئی و دیفرانسیل های این توابع را مطالعه خواهیم کرد. بیایید یاد بگیریم که چگونه معادله یک صفحه مماس و یک نرمال به یک سطح را بنویسیم.

مشتق جزئی، دیفرانسیل کامل FNP. ارتباط بین تمایز پذیری یک تابع و وجود مشتقات جزئی

برای تابعی از یک متغیر واقعی، پس از مطالعه مباحث «حدود» و «تداوم» (مقدمه ای بر حساب دیفرانسیل و انتگرال)، مشتقات و دیفرانسیل های تابع مورد مطالعه قرار گرفت. بیایید به بررسی سوالات مشابه برای توابع چندین متغیر ادامه دهیم. توجه داشته باشید که اگر همه آرگومان‌ها به جز یکی در FNP ثابت باشند، آنگاه FNP تابعی از یک آرگومان تولید می‌کند که می‌توان برای آن افزایش، دیفرانسیل و مشتق در نظر گرفت. ما آنها را به ترتیب افزایش جزئی، دیفرانسیل جزئی و مشتق جزئی می نامیم. بیایید به سراغ تعاریف دقیق برویم.

تعریف 10. اجازه دهید تابعی از متغیرها در کجا داده شود - عنصر فضای اقلیدسی و افزایش متناظر آرگومان ها، ,…, . وقتی مقادیر را افزایش جزئی تابع می نامند. افزایش کل یک تابع مقدار است.

به عنوان مثال، برای یک تابع از دو متغیر، که در آن یک نقطه در صفحه و، افزایش متناظر آرگومان ها، افزایش جزئی خواهد بود، . در این حالت، مقدار افزایش کل یک تابع از دو متغیر است.

تعریف 11. مشتق جزئی تابعی از متغیرها بیش از یک متغیر، حد نسبت افزایش جزئی یک تابع بر روی این متغیر به افزایش آرگومان مربوطه در زمانی که به 0 میل می کند است.

اجازه دهید تعریف 11 را به عنوان یک فرمول بنویسیم یا به صورت گسترش یافته (2) برای تابعی از دو متغیر، تعریف 11 به شکل فرمول نوشته می شود , . از منظر عملی، این تعریف به این معنی است که هنگام محاسبه مشتق جزئی با توجه به یک متغیر، همه متغیرهای دیگر ثابت هستند و این تابع را تابعی از یک متغیر انتخاب شده در نظر می گیریم. مشتق معمولی با توجه به این متغیر گرفته می شود.

مثال 4. برای تابعی که در آن، مشتقات جزئی و نقطه ای که هر دو مشتق جزئی برابر با 0 هستند را پیدا کنید.

راه حل . بیایید مشتقات جزئی را محاسبه کنیم، و سیستم را به شکل بنویسید راه حل این سیستم دو نقطه و .

حال بیایید در نظر بگیریم که چگونه مفهوم دیفرانسیل به FNP تعمیم می یابد. به یاد بیاورید که تابع یک متغیر اگر افزایش آن به شکل نمایش داده شود، متمایز نامیده می شود ، در این حالت کمیت جزء اصلی افزایش تابع است و دیفرانسیل آن نامیده می شود. کمیت تابعی از , دارای خاصیت است که در مقایسه با تابعی بی نهایت کوچک است . تابع یک متغیر در یک نقطه قابل تمایز است اگر و فقط در صورتی که مشتق در آن نقطه داشته باشد. در این حالت، ثابت و برابر با این مشتق است، یعنی فرمول برای دیفرانسیل معتبر است. .

اگر یک افزایش جزئی از FNP در نظر گرفته شود، آنگاه تنها یکی از آرگومان ها تغییر می کند و این افزایش جزئی را می توان به عنوان افزایش تابعی از یک متغیر در نظر گرفت، یعنی همان نظریه کار می کند. بنابراین، شرط تمایز اگر و فقط در صورت وجود مشتق جزئی برقرار است، در این صورت دیفرانسیل جزئی با داده می شود .

دیفرانسیل کل تابعی از چند متغیر چقدر است؟

تعریف 12. تابع متغیر در یک نقطه متمایز نامیده می شود ، اگر افزایش آن به شکل نمایش داده شود. در این حالت قسمت اصلی افزایش را دیفرانسیل FNP می نامند.

بنابراین، دیفرانسیل FNP مقدار است. بگذارید منظورمان از کمیت را روشن کنیم ، که در مقایسه با افزایش آرگومان ها آن را بی نهایت کوچک می نامیم . این تابعی است که دارای این ویژگی است که اگر همه افزایش ها به جز یک برابر با 0 باشند، برابری درست است. . در اصل این به این معنی است = = + +…+ .

شرایط تمایزپذیری یک FNP و شرایط وجود مشتقات جزئی این تابع چگونه با یکدیگر مرتبط هستند؟

قضیه 1. اگر تابعی از متغیرها در یک نقطه قابل تفکیک باشد ، سپس دارای مشتقات جزئی نسبت به همه متغیرها در این نقطه و همزمان است.

اثبات. برابری را برای و به شکل می نویسیم و دو طرف برابری حاصل را بر تقسیم کنید. در برابری حاصل، به سمت حد در حرکت می کنیم. در نتیجه برابری لازم را بدست می آوریم. قضیه ثابت شده است.

نتیجه. دیفرانسیل یک تابع از متغیرها با استفاده از فرمول محاسبه می شود . (3)

در مثال 4، دیفرانسیل تابع برابر بود. توجه داشته باشید که همان دیفرانسیل در نقطه برابر است با . اما اگر آن را در یک نقطه با افزایش محاسبه کنیم، آنگاه دیفرانسیل برابر با . توجه داشته باشید که مقدار دقیق تابع داده شده در نقطه است برابر است، اما همین مقدار، تقریباً با استفاده از دیفرانسیل 1 محاسبه می شود، برابر است با. می بینیم که با جایگزین کردن افزایش یک تابع با دیفرانسیل آن، می توانیم مقادیر تابع را تقریباً محاسبه کنیم.

آیا تابعی از چندین متغیر در یک نقطه قابل تمایز خواهد بود اگر در این نقطه مشتقات جزئی داشته باشد؟ بر خلاف تابع یک متغیر، پاسخ این سوال منفی است. فرمول دقیق رابطه با قضیه زیر ارائه شده است.

قضیه 2. اگر تابعی از متغیرها در یک نقطه باشد مشتقات جزئی پیوسته با توجه به همه متغیرها وجود دارد، سپس تابع در این نقطه قابل تمایز است.

مانند . فقط یک متغیر در هر براکت تغییر می کند، بنابراین می توانیم فرمول افزایش محدود لاگرانژ را در هر دو اعمال کنیم. ماهیت این فرمول این است که برای یک تابع متمایز پیوسته از یک متغیر، تفاوت بین مقادیر تابع در دو نقطه برابر است با مقدار مشتق در یک نقطه میانی، ضرب در فاصله بین نقاط. با اعمال این فرمول برای هر یک از براکت ها، دریافت می کنیم. با توجه به تداوم مشتقات جزئی، مشتق در یک نقطه و مشتق در یک نقطه با مشتقات در یک نقطه با مقادیر متفاوت هستند و با گرایش به 0 به عنوان، تمایل به 0. اما پس از آن، بدیهی است، . قضیه ثابت شده است. ، و مختصات. بررسی کنید که این نقطه به سطح تعلق دارد. معادله صفحه مماس و معادله نرمال به سطح را در نقطه نشان داده شده بنویسید.

راه حل. واقعا، . در آخرین سخنرانی، ما قبلاً دیفرانسیل این تابع را در یک نقطه دلخواه محاسبه کردیم؛ در یک نقطه معین برابر است با . در نتیجه، معادله صفحه مماس به شکل یا، و معادله نرمال - به شکل نوشته می شود. .

هر مشتق جزئی (توسط ایکسو توسط y) یک تابع از دو متغیر مشتق معمولی یک تابع از یک متغیر برای مقدار ثابت متغیر دیگر است:

(جایی که y= ثابت)،

(جایی که ایکس= ثابت).

بنابراین، مشتقات جزئی با استفاده از محاسبه می شوند فرمول ها و قوانین برای محاسبه مشتقات توابع یک متغیر، در حالی که متغیر دیگر ثابت را در نظر می گیریم.

اگر نیازی به تجزیه و تحلیل مثال ها و حداقل تئوری لازم برای این کار ندارید، بلکه فقط به یک راه حل برای مشکل خود نیاز دارید، به ادامه مطلب بروید ماشین حساب مشتق جزئی آنلاین .

اگر تمرکز کردن برای ردیابی جایی که ثابت در تابع است دشوار است، در حل پیش‌نویس مثال، به جای متغیری با مقدار ثابت، می‌توانید هر عددی را جایگزین کنید - سپس می‌توانید به سرعت مشتق جزئی را به عنوان محاسبه کنید. مشتق معمولی تابع یک متغیر. فقط باید به یاد داشته باشید که هنگام اتمام طراحی نهایی، ثابت (متغیر با مقدار ثابت) را به جای خود برگردانید.

ویژگی مشتقات جزئی که در بالا توضیح داده شد از تعریف مشتق جزئی که ممکن است در سؤالات امتحان ظاهر شود، ناشی می شود. بنابراین برای آشنایی با تعریف زیر می توانید مرجع نظری را باز کنید.

مفهوم تداوم عملکرد z= f(ایکس, y) در یک نقطه مشابه این مفهوم برای تابعی از یک متغیر تعریف شده است.

تابع z = f(ایکس, y) در یک نقطه اگر پیوسته نامیده می شود

تفاوت (2) را افزایش کل تابع می گویند z(در نتیجه افزایش هر دو آرگومان به دست می آید).

اجازه دهید تابع داده شود z= f(ایکس, y) و دوره

اگر تابع تغییر کند zزمانی اتفاق می افتد که فقط یکی از آرگومان ها تغییر کند، برای مثال، ایکس، با مقدار ثابتی از آرگومان دیگر y، سپس تابع یک افزایش دریافت می کند

افزایش جزئی تابع نامیده می شود f(ایکس, y) توسط ایکس.

در نظر گرفتن تغییر تابع zبسته به تغییر تنها یکی از آرگومان ها، به طور موثر به تابعی از یک متغیر تغییر می کنیم.

اگر حد محدودی وجود دارد

سپس مشتق جزئی تابع نامیده می شود f(ایکس, y) با استدلال ایکسو با یکی از نمادها نشان داده می شود

(4)

افزایش جزئی به طور مشابه تعیین می شود zتوسط y:

و مشتق جزئی f(ایکس, y) توسط y:

(6)

مثال 1.

راه حل. مشتق جزئی را با توجه به متغیر "x" پیدا می کنیم:

(yدرست شد)؛

مشتق جزئی را با توجه به متغیر "y" پیدا می کنیم:

(ایکسدرست شد).

همانطور که می بینید، فرقی نمی کند که تا چه حد متغیر ثابت باشد: در این مورد صرفاً یک عدد معین است که عاملی (مانند مشتق معمولی) متغیر است که با آن مشتق جزئی را پیدا می کنیم. . اگر متغیر ثابت در متغیری که مشتق جزئی را با آن می‌یابیم ضرب نشود، این ثابت تنها، بدون توجه به اینکه تا چه حد، مانند مشتق معمولی، از بین می‌رود.

مثال 2.یک تابع داده شده است

مشتقات جزئی را بیابید

(با X) و (توسط Y) و مقادیر آنها را در نقطه محاسبه کنید آ (1; 2).

راه حل. در ثابت yمشتق جمله اول به عنوان مشتق تابع توان یافت می شود ( جدول توابع مشتق یک متغیر):

.

در ثابت ایکسمشتق جمله اول به عنوان مشتق تابع نمایی و دومی - به عنوان مشتق یک ثابت است:

حال بیایید مقادیر این مشتقات جزئی را در نقطه محاسبه کنیم آ (1; 2):

می توانید راه حل مشکلات مشتق جزئی را در اینجا بررسی کنید ماشین حساب مشتق جزئی آنلاین .

مثال 3.مشتقات جزئی یک تابع را بیابید

راه حل. در یک مرحله پیدا می کنیم

(y ایکسگویی که برهان سینوس 5 است ایکس: به همین ترتیب، 5 قبل از علامت تابع ظاهر می شود).

(ایکسثابت است و در این مورد یک ضریب در است y).

می توانید راه حل مشکلات مشتق جزئی را در اینجا بررسی کنید ماشین حساب مشتق جزئی آنلاین .

مشتقات جزئی یک تابع از سه یا چند متغیر به طور مشابه تعریف می شوند.

اگر هر مجموعه از مقادیر ( ایکس; y; ...; تی) متغیرهای مستقل از مجموعه Dمربوط به یک مقدار خاص است تواز بسیاری E، آن توتابعی از متغیرها نامیده می شود ایکس, y, ..., تیو نشان دهند تو= f(ایکس, y, ..., تی).

برای توابع سه یا چند متغیر، هیچ تفسیر هندسی وجود ندارد.

مشتقات جزئی تابعی از چندین متغیر نیز با این فرض که فقط یکی از متغیرهای مستقل تغییر می کند، تعیین و محاسبه می شود، در حالی که بقیه ثابت هستند.

مثال 4.مشتقات جزئی یک تابع را بیابید

.

راه حل. yو zدرست شد:

ایکسو zدرست شد:

ایکسو yدرست شد:

خودتان مشتقات جزئی را پیدا کنید و سپس به راه حل ها نگاه کنید

مثال 5.

مثال 6.مشتقات جزئی یک تابع را بیابید.

مشتق جزئی تابعی از چندین متغیر یکسان است معنای مکانیکی همان مشتق تابع یک متغیر است، نرخ تغییر تابع نسبت به تغییر در یکی از آرگومان ها است.

مثال 8.مقدار کمی جریان پمسافران راه آهن را می توان با تابع بیان کرد

جایی که پ- تعداد مسافران، ن- تعداد ساکنان نقاط خبرنگار، آر- فاصله بین نقاط

مشتق جزئی یک تابع پتوسط آر، برابر

نشان می دهد که کاهش جریان مسافر با مجذور فاصله بین نقاط متناظر با همان تعداد ساکنین در نقاط نسبت معکوس دارد.

مشتق جزئی پتوسط ن، برابر

نشان می دهد که افزایش جریان مسافر متناسب با دو برابر تعداد ساکنان سکونتگاه ها در فاصله یکسان بین نقاط است.

می توانید راه حل مشکلات مشتق جزئی را در اینجا بررسی کنید ماشین حساب مشتق جزئی آنلاین .

دیفرانسیل کامل

حاصل ضرب یک مشتق جزئی و افزایش متغیر مستقل مربوطه را دیفرانسیل جزئی می گویند. دیفرانسیل های جزئی به صورت زیر نشان داده می شوند:

مجموع دیفرانسیل های جزئی برای همه متغیرهای مستقل، دیفرانسیل کل را نشان می دهد. برای تابعی از دو متغیر مستقل، دیفرانسیل کل با برابری بیان می شود

(7)

مثال 9.دیفرانسیل کامل یک تابع را پیدا کنید

راه حل. نتیجه استفاده از فرمول (7):

تابعی که در هر نقطه از یک دامنه معین دارای دیفرانسیل کلی باشد در آن حوزه قابل تمایز است.

دیفرانسیل کل را خودتان پیدا کنید و سپس به راه حل نگاه کنید

همانطور که در مورد یک تابع از یک متغیر، تمایزپذیری یک تابع در یک حوزه معین، مستلزم تداوم آن در این حوزه است، اما نه برعکس.

اجازه دهید بدون اثبات یک شرط کافی برای تمایزپذیری یک تابع را فرموله کنیم.

قضیه.اگر تابع z= f(ایکس, y) مشتقات جزئی پیوسته دارد

در یک منطقه معین، آنگاه در این ناحیه قابل تمایز است و دیفرانسیل آن با فرمول (7) بیان می شود.

می توان نشان داد که همانطور که در مورد تابعی از یک متغیر، دیفرانسیل تابع قسمت خطی اصلی افزایش تابع است، در مورد تابعی از چندین متغیر، دیفرانسیل کل اصلی، خطی با توجه به افزایش متغیرهای مستقل، بخشی از افزایش کل تابع.

برای تابعی از دو متغیر، افزایش کل تابع دارای شکل است

(8)

که در آن α و β در و بی نهایت کوچک هستند.

مشتقات جزئی مرتبه بالاتر

مشتقات و توابع جزئی f(ایکس, y) خود برخی از توابع متغیرهای مشابه هستند و به نوبه خود می توانند مشتقاتی نسبت به متغیرهای مختلف داشته باشند که به آنها مشتقات جزئی مرتبه بالاتر می گویند.