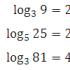대수가 있는 예와 시험에 대한 해. 로그 방정식 풀기

로그란 무엇입니까?

주목!
추가로 있습니다
특별 섹션 555의 자료.
강하게 "별로..."
그리고 "매우 ..."하는 사람들을 위해)

로그란 무엇입니까? 로그를 푸는 방법? 이러한 질문은 많은 졸업생을 혼란스럽게 합니다. 전통적으로 로그 주제는 복잡하고 이해하기 어렵고 무서운 것으로 간주됩니다. 특히 - 로그가 있는 방정식.

이것은 절대 사실이 아닙니다. 전적으로! 안 믿어? 괜찮아. 이제 약 10~20분 동안:

1. 이해하다 로그란 무엇인가.

2. 지수 방정식의 전체 클래스를 푸는 방법을 배웁니다. 당신이 그들에 대해 들어 본 적이 없더라도.

3. 단순 로그를 계산하는 방법을 배웁니다.

또한 이를 위해서는 곱셈표와 숫자가 거듭제곱되는 방법만 알면 됩니다.

나는 당신이 의심하는 것을 느낍니다 ... 글쎄, 시간을 지키십시오! 가다!

먼저 마음속으로 다음 방정식을 풉니다.

이 사이트가 마음에 드신다면...

그건 그렇고, 나는 당신을 위해 몇 가지 더 흥미로운 사이트를 가지고 있습니다.)

예제 해결을 연습하고 레벨을 확인할 수 있습니다. 즉각적인 검증으로 테스트합니다. 학습 - 관심을 가지고!)

함수와 파생어를 알 수 있습니다.

귀하의 개인 정보는 우리에게 중요합니다. 이러한 이유로 당사는 귀하의 정보를 사용하고 저장하는 방법을 설명하는 개인정보 보호정책을 개발했습니다. 개인 정보 보호 정책을 읽고 질문이 있으면 알려주십시오.

개인정보의 수집 및 이용

개인정보란 특정 개인을 식별하거나 연락할 수 있는 데이터를 말합니다.

귀하는 당사에 연락할 때 언제든지 귀하의 개인 정보를 제공하도록 요청할 수 있습니다.

다음은 우리가 수집할 수 있는 개인 정보 유형과 그러한 정보를 사용하는 방법의 몇 가지 예입니다.

수집하는 개인 정보:

사이트에서 신청서를 제출하면 이름, 전화번호, 이메일 주소 등 다양한 정보를 수집할 수 있습니다.

당사가 귀하의 개인 정보를 사용하는 방법:

수집한 개인 정보를 통해 당사는 귀하에게 연락하고 고유한 제안, 프로모션 및 기타 이벤트 및 예정된 이벤트에 대해 알릴 수 있습니다.
때때로 당사는 귀하에게 중요한 통지 및 커뮤니케이션을 보내기 위해 귀하의 개인 정보를 사용할 수 있습니다.
우리는 또한 우리가 제공하는 서비스를 개선하고 서비스에 대한 권장 사항을 제공하기 위해 감사, 데이터 분석 및 다양한 연구 수행과 같은 내부 목적으로 개인 정보를 사용할 수 있습니다.
귀하가 경품 추첨, 콘테스트 또는 유사한 인센티브에 참여하는 경우 당사는 귀하가 제공한 정보를 사용하여 그러한 프로그램을 관리할 수 있습니다.

제3자에 대한 공개

당사는 귀하로부터 받은 정보를 제3자에게 공개하지 않습니다.

예외:

필요한 경우 - 법률, 사법 명령에 따라, 법적 절차에서 및/또는 러시아 연방 영토에 있는 국가 기관의 공개 요청 또는 요청에 따라 - 귀하의 개인 정보를 공개하십시오. 또한 보안, 법 집행 또는 기타 공익상의 이유로 그러한 공개가 필요하거나 적절하다고 판단하는 경우 귀하에 대한 정보를 공개할 수 있습니다.
조직 개편, 합병 또는 매각의 경우, 당사는 수집한 개인 정보를 해당 제3자 승계인에게 양도할 수 있습니다.

개인정보 보호

우리는 관리, 기술 및 물리적 예방 조치를 취하여 손실, 도난 및 오용뿐만 아니라 무단 액세스, 공개, 변경 및 파괴로부터 귀하의 개인 정보를 보호합니다.

회사 수준에서 개인 정보 보호

귀하의 개인 정보를 안전하게 보호하기 위해 당사는 개인 정보 보호 및 보안 관행을 직원에게 알리고 개인 정보 보호 관행을 엄격하게 시행합니다.

로그 표현식, 예제 솔루션. 이 기사에서는 로그 풀이와 관련된 문제를 고려할 것입니다. 작업은 표현의 가치를 찾는 문제를 제기합니다. 로그의 개념은 많은 작업에서 사용되며 그 의미를 이해하는 것이 매우 중요합니다. USE의 경우 로그는 방정식 풀기, 응용 문제 및 함수 연구와 관련된 작업에 사용됩니다.

다음은 로그의 의미를 이해하기 위한 예입니다.

기본 로그 항등:

항상 기억해야 하는 로그의 속성:

*곱의 로그는 요인의 로그의 합과 같습니다.

* * *

* 몫의 대수(분수)는 요인의 대수의 차와 같습니다.

* * *

* 차수의 로그는 지수와 밑의 로그의 곱과 같습니다.

* * *

*새로운 기지로의 전환

* * *

더 많은 속성:

* * *

로그를 계산하는 것은 지수의 속성을 사용하는 것과 밀접한 관련이 있습니다.

그 중 일부를 나열합니다.

이 속성의 본질은 분자를 분모로 또는 그 반대로 전달할 때 지수의 부호가 반대 방향으로 변경된다는 것입니다. 예를 들어:

이 속성의 결과:

* * *

거듭제곱을 거듭제곱할 때 밑은 그대로 유지되지만 지수는 곱해집니다.

* * *

보시다시피, 로그의 개념 자체는 간단합니다. 가장 중요한 것은 특정 기술을 제공하는 좋은 연습이 필요하다는 것입니다. 물론 공식에 대한 지식은 필수입니다. 기본 로그 변환 기술이 형성되지 않으면 간단한 작업을 해결할 때 쉽게 실수 할 수 있습니다.

연습하고 수학 코스에서 가장 간단한 예제를 먼저 풀고 더 복잡한 예제로 넘어갑니다. 앞으로 나는 "추한"로그가 어떻게 해결되는지 확실히 보여줄 것입니다. 시험에는 그러한 로그가 없지만 관심이 있습니다. 놓치지 마세요!

그게 다야! 행운을 빕니다!

감사합니다. Alexander Krutitskikh

추신 : 소셜 네트워크에서 사이트에 대해 알려 주시면 감사하겠습니다.

이 비디오 자습서에서는 근을 찾을 뿐만 아니라 주어진 세그먼트에 있는 근도 선택해야 하는 다소 심각한 로그 방정식을 푸는 방법을 살펴봅니다.

작업 C1. 방정식을 풉니다. 구간에 속하는 이 방정식의 모든 근을 찾으십시오.

로그 방정식에 대한 참고 사항

그런데 해가 거듭될수록 그런 고민을 하는 학생들이 저에게 찾아옵니다. 어려운 방정식, 그러나 동시에 그들은 이해할 수 없습니다. 어디서 시작하고 로그에 접근하는 방법은 무엇입니까? 이러한 문제는 강하고 잘 준비된 학생에게도 발생할 수 있습니다.

결과적으로 많은 사람들이 이 주제를 두려워하기 시작하거나 스스로를 바보로 생각하기 시작합니다. 따라서 기억하십시오. 그러한 방정식을 풀 수 없다고 해서 당신이 어리석은 것은 아닙니다. 예를 들어 이 방정식을 거의 구두로 다룰 수 있기 때문입니다.

로그 2 x = 4

그렇지 않다면 당신은 지금 이 글을 읽지 않았을 것입니다. 왜냐하면 당신은 더 간단하고 일상적인 일에 바빴기 때문입니다. 물론, 이제 누군가는 이의를 제기할 것입니다. "이 가장 단순한 방정식이 우리의 건강한 설계와 무슨 관련이 있습니까?" 나는 대답합니다. 모든 대수 방정식은 아무리 복잡해도 결국에는 간단하고 구두로 해결된 구조로 귀결됩니다.

물론 복잡한 대수 방정식에서 탬버린과 함께 춤을 추거나 선택의 도움으로가 아니라 명확하고 오래 정의 된 규칙에 따라 더 간단한 것으로 이동해야합니다. 대수 표현식 변환 규칙. 그것들을 알면 수학 시험에서 가장 복잡한 방정식조차도 쉽게 알아낼 수 있습니다.

그리고 오늘 수업에서 이야기할 규칙은 바로 이 규칙에 관한 것입니다. 가다!

문제 C1의 로그 방정식 풀기

방정식을 풀자:

우선, 대수 방정식과 관련하여 우리는 주요 전술을 기억합니다. 말하자면 대수 방정식을 푸는 기본 규칙입니다. 다음으로 구성됩니다.

정규 형식 정리. 어떤 로그 방정식이든, 그것이 무엇을 포함하든, 어떤 로그가 있든, 밑이 무엇이든, c 자체에 무엇이 있든 상관없이 그것을 다음 형식의 방정식으로 가져와야 합니다.

log a f (x ) = log a g (x )

방정식을 보면 즉시 두 가지 문제가 있음을 알 수 있습니다.

왼쪽에 우리는 두 숫자의 합, 그 중 하나는 전혀 로그가 아닙니다.
오른쪽에는 상당한 로그가 있지만 그 밑에는 근이 있습니다. 그리고 왼쪽의 로그는 단 2, 즉 왼쪽과 오른쪽 로그의 밑이 다릅니다.

그래서 우리는 우리의 방정식을 그것과 구분하는 문제 목록을 만들었습니다. 정준 방정식, 해결 과정에서 대수 방정식을 줄여야합니다. 따라서 이 단계에서 방정식을 푸는 것은 위에서 설명한 두 가지 문제를 제거하는 것으로 요약됩니다.

모든 대수 방정식은 정규 형식으로 축소하면 빠르고 쉽게 풀 수 있습니다.

로그와 곱의 로그의 합

순서대로 진행합시다. 먼저 왼쪽에 서 있는 구조를 처리해 보겠습니다. 두 로그의 합에 대해 무엇을 말할 수 있습니까? 멋진 공식을 기억합시다.

log a f(x) + log a g(x) = log a f(x) g(x)

그러나 우리의 경우 첫 번째 항이 로그가 아니라는 점을 고려해 볼 가치가 있습니다. 따라서 단위를 밑수 2에 대한 로그로 표시해야 합니다(즉, 밑수 2에 대한 로그가 왼쪽에 있기 때문에 2). 그것을 하는 방법? 다시 한 번 멋진 공식을 기억하십시오.

a = 로그 b b a

여기서 이해해야 합니다. "모든 밑수 b"라고 할 때 b는 여전히 임의의 숫자가 될 수 없음을 의미합니다. 로그에 숫자를 삽입하면 특정 숫자가 즉시 그 위에 겹쳐집니다. 제한, 즉: 로그의 밑은 0보다 커야 하고 1과 같지 않아야 합니다. 그렇지 않으면 로그는 단순히 의미가 없습니다. 다음과 같이 작성해 보겠습니다.

0 < b ≠ 1

우리의 경우에 어떤 일이 일어나는지 봅시다.

1 = 로그 2 2 1 = 로그 2 2

이제 이 사실을 염두에 두고 전체 방정식을 다시 작성해 보겠습니다. 그리고 즉시 다른 규칙을 적용합니다. 로그의 합은 인수의 곱의 로그와 같습니다. 결과적으로 다음을 얻습니다.

새로운 방정식이 있습니다. 보시다시피, 이미 우리가 추구하는 표준 정렬에 훨씬 더 가깝습니다. 그러나 한 가지 문제가 있습니다. 두 번째 점의 형태로 작성했습니다. 왼쪽과 오른쪽에 있는 로그, 다른 근거. 다음 단계로 넘어갑시다.

로그에서 거듭제곱을 취하는 규칙

따라서 왼쪽의 로그는 밑이 2이고 오른쪽의 로그는 밑이 근입니다. 그러나 로그의 인수에서 밑수를 제곱할 수 있다는 것을 기억한다면 이것도 문제가 되지 않습니다. 다음 규칙 중 하나를 작성해 보겠습니다.

로그 a b n = n 로그 a b

인간의 언어로 번역: 로그의 밑에서 차수를 빼서 인자로 앞에 놓을 수 있습니다. 숫자 n은 로그에서 "이동"하여 앞에 있는 계수가 되었습니다.

로그의 밑에서 힘을 빼는 것도 좋습니다. 다음과 같이 표시됩니다.

즉, 로그 인수에서 거듭제곱을 빼면 이 거듭제곱도 로그 앞에 인수로 쓰여지지만 숫자가 아닌 1/k의 역수로 쓰여집니다.

하지만 그게 다가 아닙니다! 이 두 공식을 결합하여 다음 공식을 만들 수 있습니다.

지수가 로그의 밑수와 인수 모두에 있는 경우 밑수와 인수 모두에서 지수를 한 번에 제거하여 시간을 절약하고 계산을 단순화할 수 있습니다. 이 경우 인수(우리의 경우 이것은 계수 n)에 있었던 것은 분자에 있습니다. 밑면의 차수 k는 분모로 갈 것입니다.

그리고 로그를 동일한 밑수로 줄이기 위해 이제 사용할 수 있는 공식이 바로 이 공식입니다.

우선, 우리는 다소 아름다운 기초를 선택할 것입니다. 분명히, 베이스의 듀스는 루트보다 작업하기가 훨씬 더 즐겁습니다. 두 번째 로그를 밑으로 2를 적용해 보겠습니다. 이 로그를 별도로 작성해 보겠습니다.

여기서 무엇을 할 수 있습니까? 합리적인 지수로 거듭제곱 공식을 기억하십시오. 다시 말해, 근거를 지수가 있는 거듭제곱으로 쓸 수 있습니다. 그런 다음 인수와 로그의 밑에서 1/2의 거듭 제곱을 제거합니다. 로그 앞에 있는 분자와 분모의 계수에서 2를 줄입니다.

마지막으로 새로운 계수를 고려하여 원래 방정식을 다시 작성합니다.

로그 2 2(9x 2 + 5) = 로그 2(8x 4 + 14)

정규 로그 방정식을 얻었습니다. 왼쪽과 오른쪽 모두 동일한 밑수 2의 로그가 있습니다. 이러한 로그 외에도 왼쪽이나 오른쪽에 계수나 항이 없습니다.

결과적으로, 우리는 로그의 부호를 제거할 수 있습니다. 물론 정의의 영역을 고려합니다. 하지만 그 전에 다시 돌아가서 분수에 대해 약간 설명하겠습니다.

분수를 분수로 나누기: 추가 고려 사항

모든 학생이 올바른 로그 앞에 있는 요소가 어디서 와서 어디로 가는지 이해하는 것은 아닙니다. 다시 적어 봅시다.

분수가 무엇인지 이해합시다. 글을 쓰자:

이제 분수 나누기 규칙을 기억합니다. 1/2로 나누려면 역 분수를 곱해야 합니다.

물론 추가 계산의 편의를 위해 듀스를 2/1로 쓸 수 있습니다. 이것이 바로 솔루션 프로세스에서 두 번째 계수로 관찰되는 것입니다.

이제 모든 사람들이 두 번째 계수가 어디에서 왔는지 이해하기를 바랍니다. 그래서 우리는 정식 대수 방정식을 푸는 데 직접 이동합니다.

로그 부호 없애기

이제 로그를 제거하고 다음 식을 남길 수 있음을 상기시킵니다.

2(9x2 + 5) = 8x4 + 14

왼쪽의 괄호를 확장해 보겠습니다. 우리는 다음을 얻습니다.

18x2 + 10 = 8x4 + 14

왼쪽에서 오른쪽으로 모든 것을 이동합시다.

8x4 + 14 - 18x2 - 10 = 0

우리는 유사한 것을 제공하고 다음을 얻습니다.

8x4 - 18x2 + 4 = 0

이 방정식의 양변을 2로 나누어 계수를 단순화하면 다음을 얻을 수 있습니다.

4x4 - 9x2 + 2 = 0

우리 앞에는 평소 이차 방정식, 그리고 그것의 근은 판별식으로 쉽게 계산됩니다. 판별식을 작성해 보겠습니다.

D \u003d 81-4 4 2 \u003d 81-32 \u003d 49

좋아, 판별자는 "아름답다"고 그 근은 7입니다. 그게 다야, 우리는 X 자체를 고려합니다. 그러나이 경우 근은 x가 아니라 x 2가 됩니다. 왜냐하면 우리는 이차 방정식을 가지고 있기 때문입니다. 따라서 우리의 옵션은 다음과 같습니다.

참고: 우리는 뿌리를 추출했으므로 두 가지 답변이 있을 것입니다. 정사각형 - 짝수 기능. 그리고 2의 루트만 쓰면 두 번째 루트를 잃게 됩니다.

이제 이차 방정식의 두 번째 근을 그립니다.

다시, 우리는 방정식의 양변에 산술 제곱근을 취하고 두 개의 근을 얻습니다. 그러나 다음 사항을 기억하십시오.

로그의 인수를 정규 형식으로 단순히 동일시하는 것만으로는 충분하지 않습니다. 범위를 기억하십시오!

총 4개의 루트가 있습니다. 그들 모두는 실제로 우리의 원래 방정식에 대한 솔루션입니다. 살펴보세요: 원래의 대수 방정식에서 대수 내부는 9x 2 + 5(이 함수는 항상 양수) 또는 8x 4 + 14입니다. 이 역시 항상 양수입니다. 따라서 로그의 정의 영역은 어떤 근을 얻든 상관없이 모든 경우에 충족되며, 이는 4개의 근이 모두 우리 방정식의 해임을 의미합니다.

좋습니다. 이제 문제의 두 번째 부분으로 넘어가겠습니다.

세그먼트에서 로그 방정식의 근 선택

우리는 간격 [−1; 8/9]. 우리는 우리의 뿌리로 돌아가서 이제 그들의 선택을 수행할 것입니다. 우선 좌표축을 그리고 그 위에 세그먼트의 끝을 표시할 것을 제안합니다.

두 점 모두 음영 처리됩니다. 저것들. 문제의 조건에 따라 음영 부분에 관심이 있습니다. 이제 뿌리를 다루겠습니다.

불합리한 뿌리

비합리적인 뿌리부터 시작합시다. 참고로 8/9< 9/9 = 1. С другой стороны, корень из двух явно больше единицы. Следовательно, наши корни будут находиться на отрезке в таком положении:

이로부터 2의 근은 우리가 관심을 갖는 부분에 속하지 않는다는 결론이 나옵니다. 유사하게, 우리는 음수 루트를 얻습니다. 그것은 -1보다 작습니다. 즉, 관심 세그먼트의 왼쪽에 있습니다.

합리적인 뿌리

두 개의 근이 남아 있습니다. x = 1/2 및 x = −1/2입니다. 세그먼트의 왼쪽 끝(-1)은 음수이고 오른쪽 끝(8/9)은 양수입니다. 따라서 이 끝 사이 어딘가에 숫자 0이 있습니다. 루트 x = −1/2는 −1과 0 사이입니다. 최종 답변에 포함될 것입니다. 루트 x = 1/2로 동일한 작업을 수행합니다. 이 루트는 또한 고려 중인 세그먼트에 있습니다.

숫자 8/9가 1/2보다 큰지 확인하는 것은 매우 쉽습니다. 이 숫자를 서로 빼자.

분수 7/18 > 0을 얻었습니다. 정의에 따르면 8/9 > 1/2입니다.

좌표축에 적절한 근을 표시해 보겠습니다.

최종 답은 1/2와 −1/2의 두 근입니다.

무리수 비교: 보편적인 알고리즘

결론적으로 나는 다시 한번 무리수들로 돌아가고 싶다. 그들의 예를 사용하여 이제 수학에서 합리적인 양과 비합리적인 양을 비교하는 방법을 볼 것입니다. 우선, 그들 사이에 틱 V가 있습니다. "더"또는 "덜"기호가 있지만 우리는 그것이 어느 방향으로 향하고 있는지 아직 모릅니다. 글을 쓰자:

왜 비교 알고리즘이 필요합니까? 사실이 문제에서 우리는 매우 운이 좋았습니다. 해결 과정에서 분리 번호 1이 발생했으며 이에 대해 확실히 말할 수 있습니다.

그러나 이동 중에 항상 그러한 숫자를 볼 수 있는 것은 아닙니다. 따라서 직접 수치를 직접 비교하려고 합니다.

어떻게 완료되었나요? 우리는 일반적인 불평등과 동일하게 수행합니다.

첫째, 어딘가에 음의 계수가 있다면 불평등의 양쪽에 -1을 곱합니다. 물론 기호 변경. 그러한 틱 V는 그러한 - Λ로 변경될 것입니다.
그러나 우리의 경우 양쪽이 이미 긍정적이므로 아무것도 변경할 필요가 없습니다. 정말 필요한 것은 정사각형 양쪽라디칼을 제거하기 위해.

무리한 숫자를 비교할 때 이동 중에 분리 요소를 선택할 수 없는 경우 "이마에서"와 같은 비교를 수행하는 것이 좋습니다. 이를 일반적인 불평등으로 설명합니다.

풀면 다음과 같습니다.

이제 모두 쉽게 비교할 수 있습니다. 사실은 64/81< 81/81 = 1 < 2. На основании той цепочки преобразований мы заключаем, что 64/81 < 2 и, следовательно, корень больше 8/9.

그게 다야, 우리는 모든 숫자가 숫자 라인 x에 정확하고 실제로 있어야 할 순서대로 정확하게 표시되어 있다는 엄격한 증거를 받았습니다. 아무도 그러한 결정에 대해 불평하지 않을 것이므로 기억하십시오. 구분 번호(우리의 경우에는 1)가 즉시 표시되지 않으면 위의 구성을 자유롭게 작성하고 곱하고 제곱하고 결국에는 아름다운 불평등을 얻을 것입니다. 이 부등식으로부터 어느 수가 더 크고 어느 것이 더 작은지 정확히 명확해질 것입니다.

우리의 문제로 돌아가서, 우리가 방정식을 풀 때 맨 처음에 한 일에 다시 한 번 주의를 기울이고 싶습니다. 즉, 우리는 원래의 대수 방정식을 자세히 살펴보고 다음과 같이 줄이려고 했습니다. 정식대수 방정식. 왼쪽과 오른쪽에 로그만 있는 경우 - 추가 항, 앞에 계수 등은 없습니다. 밑수 a 또는 b에 대한 두 개의 로그, 즉 다른 로그와 동일한 로그가 필요하지 않습니다.

또한 로그의 밑도 동일해야 합니다. 동시에 방정식이 올바르게 구성되면 기본 로그 변환(로그의 합, 숫자를 로그로 변환 등)을 사용하여 이 방정식을 표준 방정식으로 줄입니다.

그러므로 이제부터는 "이마에서" 바로 풀리지 않는 대수방정식을 보았을 때 길을 잃거나 답을 찾으려 해서는 안 됩니다. 다음 단계를 따르면 충분합니다.

모든 자유 요소를 로그로 가져옵니다.
그런 다음 이러한 로그를 추가하십시오.
결과 구성에서 모든 로그는 동일한 밑수로 이어집니다.

결과적으로 8-9 학년 자료에서 기초 대수학 수단으로 풀 수 있는 간단한 방정식을 얻게 됩니다. 일반적으로 내 사이트로 이동하여 대수 풀이를 연습하고 나처럼 대수 방정식을 풀고 나보다 잘 풉니다. 그게 다야. Pavel Berdov가 함께했습니다. 곧 봐요!

아시다시피 표현식에 거듭제곱을 곱할 때 지수는 항상 더합니다(a b * a c = a b + c). 이 수학 법칙은 아르키메데스에 의해 파생되었으며 나중에 8세기에 수학자 Virasen이 정수 표시기 테이블을 만들었습니다. 로그의 추가 발견에 기여한 것은 바로 그들이었습니다. 이 함수를 사용하는 예는 번거로운 곱셈을 단순한 덧셈으로 단순화해야 하는 거의 모든 곳에서 찾을 수 있습니다. 이 기사를 읽는 데 10분을 할애하면 로그가 무엇인지, 로그를 사용하는 방법에 대해 설명합니다. 간단하고 접근 가능한 언어.

수학에서의 정의

로그는 다음 형식의 표현입니다. log ab=c, 즉, 밑수 "a"에 의한 음수가 아닌 숫자(즉, 양수) "b"의 로그는 "c"의 거듭제곱으로 간주됩니다. , 기본 "a"를 올려야 하므로 결국 "b" 값을 얻습니다. 예를 사용하여 로그를 분석해 보겠습니다. log 2 8이라는 표현식이 있다고 가정해 보겠습니다. 답을 찾는 방법은 무엇입니까? 그것은 매우 간단합니다. 2에서 필요한 정도까지 8이 되는 정도를 찾아야 합니다. 마음속으로 몇 가지 계산을 하고 나면 숫자 3이 나옵니다! 그리고 옳습니다. 왜냐하면 2의 3승은 답에 숫자 8을 주기 때문입니다.

로그의 종류

많은 학생과 학생들에게 이 주제는 복잡하고 이해할 수 없는 것처럼 보이지만 사실 로그는 그렇게 무섭지 않습니다. 가장 중요한 것은 일반적인 의미를 이해하고 속성과 일부 규칙을 기억하는 것입니다. 로그 표현식에는 세 가지 다른 종류가 있습니다.

자연 로그 ln a, 여기서 밑은 오일러 수(e = 2.7)입니다.
밑이 10인 소수점 이하 자릿수 a.
밑수 a>1에 대한 임의의 숫자 b의 로그.

각각은 단순화, 축소 및 로그 정리를 사용하여 하나의 로그로의 후속 축소를 포함하는 표준 방식으로 해결됩니다. 로그의 올바른 값을 얻으려면 결정의 속성과 작업 순서를 기억해야 합니다.

규칙 및 일부 제한 사항

수학에는 공리로 받아 들여지는 몇 가지 규칙 제한이 있습니다. 즉, 토론의 대상이 아니며 사실입니다. 예를 들어, 숫자를 0으로 나누는 것은 불가능하며, 음수에서 짝수의 근을 추출하는 것도 불가능합니다. 로그에도 고유한 규칙이 있으므로 길고 방대한 로그 표현식을 사용하여 작업하는 방법을 쉽게 배울 수 있습니다.

밑수 "a"는 항상 0보다 커야 하고 동시에 1이 아니어야 합니다. 그렇지 않으면 "1"과 "0"이 어느 정도 항상 값과 같기 때문에 표현식은 의미를 잃습니다.
a > 0, b > 0이면 "c"가 0보다 커야 합니다.

로그를 푸는 방법?

예를 들어, 방정식 10 x \u003d 100에 대한 답을 찾는 작업이 주어지면 매우 쉽습니다. 100이 되는 숫자 10을 올려서 그러한 거듭제곱을 선택해야 합니다. 물론 이것은 10 2입니다. \u003d 100.

이제 이 식을 로그 식으로 표현해 보겠습니다. 로그 10 100 = 2를 얻습니다. 로그를 풀 때 모든 작업은 실제로 주어진 숫자를 얻기 위해 로그의 밑이 입력되어야 하는 정도를 찾는 데 수렴합니다.

미지수의 값을 정확하게 결정하려면 도 표로 작업하는 방법을 배워야 합니다. 다음과 같이 보입니다.

보시다시피 일부 지수는 구구단에 대한 기술적 마인드와 지식이 있으면 직관적으로 추측할 수 있습니다. 그러나 더 큰 값은 검정력 테이블이 필요합니다. 복잡한 수학 주제에 대해 전혀 이해하지 못하는 사람들도 사용할 수 있습니다. 왼쪽 열은 숫자(밑수 a)를 포함하고 숫자의 맨 위 행은 숫자 a가 올라간 c의 거듭제곱 값입니다. 셀의 교차점에서 답인 숫자 값이 결정됩니다(a c = b). 예를 들어 숫자가 10인 첫 번째 셀을 제곱하면 두 셀의 교차점에 표시된 값 100을 얻습니다. 모든 것이 너무 간단하고 쉬워서 가장 진정한 인본주의자라도 이해할 수 있습니다!

방정식과 부등식

특정 조건에서 지수는 로그임이 밝혀졌습니다. 따라서 모든 수학적 수치 표현은 대수 방정식으로 쓸 수 있습니다. 예를 들어, 3 4 =81은 밑이 3인 4(log 3 81 = 4)에 대한 81의 로그로 작성할 수 있습니다. 음의 거듭제곱에 대한 규칙은 동일합니다. 2 -5 = 1/32 로그로 작성하면 로그 2(1/32) = -5가 됩니다. 수학에서 가장 흥미로운 부분 중 하나는 "로그"라는 주제입니다. 속성을 연구한 직후에 방정식의 예와 솔루션을 조금 더 낮게 고려할 것입니다. 이제 부등식의 모양과 부등식을 방정식과 구별하는 방법을 살펴보겠습니다.

다음 형식의 식이 제공됩니다. log 2(x-1) > 3 - 알 수 없는 값 "x"가 로그 부호 아래 있으므로 로그 부등식입니다. 그리고 또한 표현에서 두 개의 양이 비교됩니다. 밑수 2에서 원하는 숫자의 로그는 숫자 3보다 큽니다.

대수 방정식과 부등식의 가장 중요한 차이점은 대수가 있는 방정식(예: 2 x = √9의 대수)은 답에 하나 이상의 특정 숫자 값을 의미하는 반면 부등식을 풀 때 두 범위 모두 허용 가능한 값과 이 기능을 깨는 점. 결과적으로 답은 방정식의 답에서와 같이 개별 숫자의 단순한 집합이 아니라 연속적인 일련 또는 숫자 집합입니다.

로그에 대한 기본 정리

로그 값을 찾는 기본 작업을 해결할 때 해당 속성을 알 수 없을 수 있습니다. 그러나 대수 방정식이나 부등식에 관해서는 우선 대수의 모든 기본 속성을 명확하게 이해하고 실제로 적용할 필요가 있습니다. 방정식의 예는 나중에 알게 될 것이므로 먼저 각 속성을 더 자세히 분석해 보겠습니다.

기본 ID는 logaB =B와 같습니다. 0보다 크고 1이 아니며 B가 0보다 큰 경우에만 적용됩니다.
제품의 로그는 다음 공식으로 나타낼 수 있습니다. log d (s 1 * s 2) = log d s 1 + log d s 2 이 경우 전제 조건은 d, s 1 및 s 2 > 0입니다. ≠1. 예제와 솔루션을 사용하여 이 로그 공식에 대한 증명을 제공할 수 있습니다. log 를 1 = f 1 로 하고 log 2 = f 2 라고 하면 a f1 = s 1 , a f2 = s 2 가 됩니다. s 1 *s 2 = a f1 *a f2 = a f1+f2(차수 속성 ), 그리고 더 나아가 정의에 의해: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log as 2, 이것은 증명되어야 했습니다.
몫의 로그는 다음과 같습니다. log a (s 1 / s 2) = log a s 1 - log a s 2.
공식 형태의 정리는 다음과 같은 형식을 취합니다. log a q b n = n/q log a b.

이 공식을 "로그 차수의 속성"이라고 합니다. 그것은 일반 학위의 속성과 유사하며 모든 수학이 규칙적인 가정에 기초하기 때문에 놀라운 일이 아닙니다. 증거를 봅시다.

a b \u003d t를 기록하면 a t \u003d b가 됩니다. 두 부분을 모두 m 거듭제곱하면: a tn = b n ;

그러나 a tn = (a q) nt/q = b n 이므로 log a q b n = (n*t)/t이므로 log a q b n = n/q log a b입니다. 정리가 증명되었습니다.

문제와 불평등의 예

로그 문제의 가장 일반적인 유형은 방정식과 부등식의 예입니다. 거의 모든 문제집에서 찾을 수 있으며 수학 시험의 필수 부분에도 포함되어 있습니다. 대학에 입학하거나 수학 입학 시험에 합격하려면 그러한 과제를 올바르게 푸는 방법을 알아야 합니다.

불행히도 로그의 미지의 값을 풀고 결정하기 위한 단일 계획이나 계획은 없지만 특정 규칙은 각 수학적 부등식 또는 로그 방정식에 적용될 수 있습니다. 먼저 그 표현을 일반형으로 단순화할 수 있는지 축소할 수 있는지 알아보아야 합니다. 속성을 올바르게 사용하면 긴 대수 표현식을 단순화할 수 있습니다. 빨리 그들을 알아봅시다.

로그 방정식을 풀 때 어떤 종류의 로그가 우리 앞에 있는지 결정하는 것이 필요합니다. 식의 예에는 자연 로그 또는 소수가 포함될 수 있습니다.

다음은 ln100, ln1026의 예입니다. 그들의 솔루션은 밑수 10이 각각 100과 1026이 되는 정도를 결정해야 한다는 사실로 귀결됩니다. 자연 로그 솔루션의 경우 로그 항등식 또는 해당 속성을 적용해야 합니다. 다양한 유형의 로그 문제를 푸는 예를 살펴보겠습니다.

로그 공식을 사용하는 방법: 예제 및 솔루션 포함

따라서 대수에 대한 주요 정리를 사용하는 예를 살펴 보겠습니다.

곱의 로그 속성은 숫자 b의 큰 값을 더 간단한 요소로 분해해야 하는 작업에서 사용할 수 있습니다. 예를 들어, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512입니다. 답은 9입니다.
log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1.5 - 보시다시피 로그 차수의 네 번째 속성을 적용하여 복잡하고 풀 수 없는 표현식을 언뜻 보기에 풀 수 있었습니다. 밑을 인수분해한 다음 로그 부호에서 지수 값을 취하기만 하면 됩니다.

시험의 과제

대수는 입학 시험, 특히 통합 국가 시험(모든 학교 졸업생을 위한 국가 시험)에서 많은 대수 문제에서 자주 발견됩니다. 일반적으로 이러한 작업은 파트 A(시험의 가장 쉬운 테스트 부분)뿐만 아니라 파트 C(가장 어렵고 방대한 작업)에도 있습니다. 이 시험은 "자연 로그"라는 주제에 대한 정확하고 완벽한 지식을 의미합니다.

예제와 문제 해결은 시험의 공식 버전에서 가져옵니다. 그러한 작업이 어떻게 해결되는지 봅시다.

주어진 로그 2(2x-1) = 4. 솔루션:
식을 다시 작성하여 log 2 (2x-1) = 2 2 , 대수 정의에 따라 2x-1 = 2 4 , 따라서 2x = 17을 얻습니다. x = 8.5.

솔루션이 번거롭거나 혼동되지 않도록 모든 로그는 동일한 밑수로 줄이는 것이 가장 좋습니다.
대수 부호 아래의 식은 모두 양수로 나타내므로 대수 부호 아래에 있는 식의 지수를 밑수로 뺄 때 대수 아래에 남아 있는 식은 양수여야 합니다.