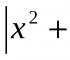Jaka jest waga pozycji w systemie liczbowym. Co to jest system liczbowy? Jakie systemy liczbowe są używane przez ekspertów do komunikacji z komputerem?

Znajomość z Liściem

Wynalazca Listik wynalazł urządzenie do przesyłania liczb. Jego urządzenie przesyłało wiadomości w postaci łańcucha krótkich i długich sygnałów. W swoich notatkach Listik oznaczył krótki sygnał cyfrą „0”, a długi cyfrą „1”. Przy przekazywaniu liczb używał następującego kodu dla każdej cyfry:

Cyfra 12, składająca się z cyfr 1 i 2, ulotka zapisała do transmisji w następujący sposób:

Urządzenie przesłało tę wiadomość w łańcuchu takich sygnałów: trzy krótkie, jeden długi, dwa krótkie, jeden długi i jeden krótki.

Liczba 77 według systemu Listika została zakodowana w następujący sposób:

Kodowanie informacji

Kodowanie to tłumaczenie informacji na formę dogodną do przesyłania lub przechowywania.

Na przykład teksty są kodowane za pomocą liter i znaków interpunkcyjnych. Co więcej, jeden i ten sam rekord można zakodować na różne sposoby: po rosyjsku, po angielsku, po chińsku ...

Liczby są kodowane za pomocą cyfr. Liczby, do których jesteśmy przyzwyczajeni, nazywają się liczbami arabskimi. Czasami używane są cyfry rzymskie. W takim przypadku zmienia się sposób kodowania informacji. Na przykład 12 i XII to różne sposoby zapisania tej samej liczby.

Muzyka może być kodowana za pomocą znaków specjalnych - nut. Znaki drogowe to zakodowane komunikaty dla kierowców i pieszych za pomocą piktogramów.

Produkty w sklepie oznaczone są kodem kreskowym, który zawiera informacje o produkcie i jego producencie.

Kod kreskowy to ciąg czarno-białych pasków, który koduje informacje w formie łatwej do odczytania przez urządzenia techniczne. Dodatkowo pod kodem kreskowym można umieścić kod w postaci ciągu cyfr.

Informacje są zawsze przechowywane i przesyłane w formie kodów. Nie możesz po prostu przechowywać informacji bez nośnika. W ten sam sposób niemożliwe jest przechowywanie i przesyłanie samej informacji: zawsze ma ona jakąś formę, to znaczy jest zaszyfrowana.

Kodowanie binarne

Kodowanie binarne to kodowanie informacji za pomocą zer i jedynek. Ten sposób prezentowania informacji okazał się bardzo wygodny dla technologii komputerowych.

Chodzi o to, że komputery są zbudowane na elementach, które mogą znajdować się w dwóch możliwych stanach. Jeden taki stan jest oznaczony liczbą 0, drugi liczbą 1.

Przykładem urządzenia binarnego jest zwykła żarówka. Może znajdować się w jednym z dwóch stanów: włączony (stan 1) lub wyłączony (stan 0).

Możesz budować pamięć elektryczną na żarówkach i przechowywać w niej np. liczby za pomocą kodu binarnego Leaf.

Do przechowywania każdej cyfry dziesiętnej potrzebne są cztery żarówki. Tak możesz zapamiętać numer 6:

Ustaw przełączniki w żądanej pozycji - i chodźmy na herbatę! Jeśli prąd nie zostanie wyłączony, informacje zostaną zapisane.

Żarówki oczywiście nie nadają się do produkcji komputerów: są duże, szybko się wypalają, są drogie (w końcu są ich miliony) i mocno nagrzewają środowisko.

W nowoczesnych komputerach jako element pamięci stosuje się urządzenie elektroniczne, tranzystor.

Tranzystor może przepuszczać prąd przez siebie (stan 1) lub nie (stan 0).

Był czas, kiedy każdy tranzystor był produkowany osobno i miał znaczne rozmiary.

Teraz tranzystory, podobnie jak inne elementy elektroniczne, wykonuje się w sposób podobny do drukowania zdjęć. Jeden mikroukład wielkości paznokcia można „odcisnąć” kilka milionów tranzystorów.

Kod, którego Listik używał do kodowania wiadomości, jest w rzeczywistości używany do pracy z liczbami w komputerze.

Przy kodowaniu binarnym nie musisz w ogóle patrzeć na tę tabelę, ale pamiętaj o prostej zasadzie tłumaczenia kodu binarnego na cyfrę dziesiętną.

Ten w kodzie na pierwszym miejscu po prawej podaje numer
lo 1, na drugim - 2, na trzecim - 4, na czwartym - 8. Aby uzyskać cyfrę dziesiętną, liczby są dodawane. Na przykład kod „0101” jest tłumaczony na cyfrę 5 (suma liczb 4 i 1).

Ta sama zasada może być również użyta do dekodowania. Na przykład cyfra 6 jest zapisana jako suma cyfr 4 i 2, co oznacza, że jej kod będzie „0110”.

Tabliczka z liczbami zapisanymi w systemie liczbowym używanym w starożytnym Babilonie. Około 1700 pne Rozszyfrowany w 1945 roku.

Systemy liczbowe

Kod liścia i kodowanie liczb

Poprzednia lekcja pokazała, jak pisać liczby za pomocą zer i jedynek. Koduje ulotkę każda cyfra numer cztery dwójkowy oznaki.

Tak więc liczba 102 w kodzie Leaf jest zapisywana za pomocą 12 znaków binarnych:

Kody ulotek osobno każda z 10 cyfr i używa do tego 4 cyfr binarnych. Ale cztery znaki binarne mogą zakodować nie 10, ale 16 wartości:

Okazuje się, że 6 kodów liściowych (czyli ponad połowa z 10) jest zmarnowanych!

Czy można kodować bardziej ekonomicznie?

Możesz, jeśli kodujesz nie liczby(z czego liczba jest zbierana) i natychmiast liczby! Tak więc liczbę 102, przy tej metodzie kodowania, można zapisać nie dwunastoma, ale tylko siedmioma cyframi binarnymi (zapisujemy 5 cyfr):

To kodowanie zostanie omówione w tym samouczku. Ale zacznijmy w kolejności.

System liczb dziesiętnych

Jak wiecie, liczby są zbudowane z liczb, a liczb jest tylko dziesięć, oto one:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Jak można pisać duże liczby z zaledwie dziesięcioma cyframi? Zobaczymy to teraz, ale najpierw zapamiętaj definicję:

Sposób pisania liczb nazywa się system liczbowy.

Słowo naukowe martwy rachunek, zgodne ze słowem „obliczanie” już oznacza „sposób pisania liczb”. Matematykom wydawało się jednak, że zdanie… notacja brzmi lepiej. Nieważne, opanujemy ten dwuwyrazowy termin! Teraz zajmijmy się tym system liczbowy, do którego są przyzwyczajeni.

Spójrz na numer 253. W tym wpisie pierwsza cyfra po prawej (nazywa się najmniej znacząca cyfra) oznacza „trzy jedynki”, pięć oznacza „pięć dziesiątek”, a dwa ( najwyższa cyfra) - "dwieście".

Okazuje się: 253 = 2 · 100 + 5 · 10 + 3 · 1.

Rozmawiamy: „Dwieście pięćdziesiąt trzy”... Oznacza to liczbę uzyskaną przez dodanie:

dwieście (2 100 = dwieście),

pięć tuzinów (5 10 = pięćdziesiąt) i

trzy jednostki (3 1 = trzy).

Widzimy, że wartość cyfry w zapisie liczby zależy od stanowiska w którym znajduje się cyfra. Pozycje cyfr są nazywane inaczej wyładowania liczby.

Najmniej znacząca cyfra oznacza jednostki:

Druga cyfra od prawej oznacza dziesiątki:

Trzecia cyfra od prawej oznacza setki:

Widzimy, że udział cyfry w liczbie wzrasta od prawej do lewej.

Systemy liczbowe, w których udział cyfry w liczbie zależy od stanowiska numery we wpisie nazywają się systemy liczb pozycyjnych.

Znany nam system liczbowy jest pozycyjny, jak widzieliśmy. Zauważ, że w podstawa ma to być liczba 10 - liczba użytych cyfr.

Najmniejsza cyfra oznacza liczbę jednostek w liczbie, druga od prawej – liczbę dziesiątek (1 · 10). Trzeci pokazuje setki (10 10), czwarty pokazuje tysiące (10 100) i tak dalej.

Liczymy jako jednostki, jednostki sumują się do dziesiątek (dziesięć jednostek zastępuje jedna dziesiątka), dziesiątki - na setki (dziesięć dziesiątek zastępuje sto) i tak dalej.

Liczba 10 jest podstawą zwykłego systemu liczbowego, dlatego nazywa się system dziesiętny, lub według systemu liczbowego podstawa 10.

Spójrz jeszcze raz, jak 2789 przekłada się na liczbę.

Liczbę uzyskuje się przez dodanie depozyty zawarte w nim liczby:

Wkład każdej cyfry uzyskuje się przez pomnożenie tej cyfry przez mnożnik zależny od pozycji związany z podstawą systemu.

Mnożniki pozycji są obliczane zgodnie z następującą zasadą:

1. Mnożnik pierwszej (prawej) pozycji to 1 .

2. Mnożnik każdej kolejnej pozycji uzyskuje się przez pomnożenie podstawy układu (liczba 10 ) o współczynnik poprzedniej pozycji.

Mnożniki pozycji będą nazywane wagi pozycji, lub wagi pozycyjne.

Liczba jest równa sumie depozytów. Wkład jest równy iloczynowi figury i wagi pozycyjnej. Waga pierwszej pozycji to 1, druga to 10, trzecia to 100 i tak dalej. Oznacza to, że wagę każdej pozycji (z wyjątkiem pierwszej) uzyskuje się z wagi poprzedniej, mnożąc przez podstawę systemu. Waga pierwszej pozycji jest równa jeden.

Oto jak: mnożyli się, dodawali i nie podejrzewali! Okazuje się, że piszemy liczby w dziesiętna notacja pozycyjna! Dlaczego podstawa naszego systemu jest równa 10? Cóż, to zrozumiałe: w końcu mamy 10 palców, wygodnie jest liczyć, zginając je w kolejności.

Ale dla komputera, jak już wiesz, system binarny jest bardziej znajomy, to znaczy pozycyjna podstawa druga.

System liczb binarnych

W systemie binarnym są tylko dwie cyfry:

Jeżeli w systemie dziesiętnym wagi pozycji uzyskuje się przez pomnożenie przez dziesięć, to w systemie binarnym - przez pomnożenie przez dwa:

Okazuje się: 1011 2 = 1 2 · 4 + 0· 2 · 2 + 1 2 · 1 + 1 1 .

W systemie binarnym uważa się je za jedynki, jedynki sumują się do dwójek (dwa jedynki są zastępowane jedną dwójką), dwójki - czwórki (dwie dwójki są zastępowane jedną czwórką) i tak dalej.

Gdy konieczne jest wyjaśnienie, w jakim systemie jest zapisany numer, podstawa systemu jest przypisywana mu od dołu:

1011 2 - liczba jest zapisana w systemie binarnym.

Konwersja na system dziesiętny nie jest trudna, wystarczy wykonać operacje mnożenia i dodawania:

1011 2 = 1 2 · 4 + 0· 2 · 2 + 1 2 · 1 + 1 1 =

1 8 + 0 4 + 1 2 + 1 1 = 11 10.

Konwersja binarna na dziesiętną

W systemie binarnym wkładem jednego na pierwszym miejscu po prawej jest liczba 1, w drugim - 2, w trzecim - 4, w czwartym - 8 i tak dalej. Wkłady zer są oczywiście równe zeru niezależnie od ich pozycji.

Otrzymujemy następującą zasadę:

Aby przekonwertować z binarnego na dziesiętny, musisz wpisać wagę jego pozycji nad każdą cyfrą binarną i dodać liczby zapisane nad jedynkami.

10111 2 = 16 + 4 + 2 + 1 = 23 10 .

Inny przykład, liczba 100110:

100110 2 = 32 + 4 + 2 = 38 10 .

Konwersja dziesiętna na binarna

Do konwersji z dziesiętnego na binarny użyjemy poprzedniego schematu z wagami pozycji:

Załóżmy, że musisz przetłumaczyć na system binarny liczbę 26. Wybieramy początek liczby binarnej (najbardziej znacząca cyfra) zgodnie ze schematem. 32 to dużo, więc zaczynamy od 16:

Część oryginalnej liczby, a mianowicie 16, jest zakodowana, pozostaje zakodować 26 - 16 = 10. Weź 8 (największą możliwą wagę pozycyjną):

Pozostaje zakodować 10 - 8 = 2. Cztery to dużo. Piszemy do pozycji 0 i bierzemy 2:

Zakodowaliśmy całą liczbę, co oznacza, że ostatnia cyfra powinna wynosić zero:

Okazuje się: 26 10 = 11010 2.

Zasadę konwersji z dziesiętnego na binarny można sformułować w następujący sposób.

Aby lepiej zrozumieć ten algorytm, popracuj na stanowisku testera. Naciśnij przycisk Resetowanie, Wybierz numer. Następnie naciśnij przycisk Początek: zobaczysz, jak Tester krok po kroku wykonuje algorytm konwersji binarnej.

Uwaga: w rekordzie algorytmu zaznaczona jest pozycja, która zostanie wykonana. po naciśnięcie przycisku Początek... Na przykład, jeśli element jest podświetlony „Powtarzaj, aż liczba spadnie do zera”, a następnie po kliknięciu Początek Tester sprawdzi aktualny numer pod kątem równości do zera i zdecyduje, czy kontynuować powtarzanie.

(Wykonaj pracę z Testerem na stronie aplikacji elektronicznej.)

Systemy pozycyjne z innymi podstawami

Wasia uwielbia system dziesiętny, jego komputer jest binarny, a ciekawi matematycy uwielbiają różne systemy liczb pozycyjnych, ponieważ za podstawę można przyjąć dowolną liczbę, a nie tylko 2 lub 10.

Jako przykład weźmy trójskładnikowy system liczbowy.

Trójskładnikowy system liczbowy

Jak można się domyślić, trójskładnikowy system liczbowy wykorzystuje trzy liczby:

W systemie trójskładnikowym uważa się je za jednostki, jedynki dodaje się do trójek (trzy trójki zastępuje jedna trójka), trójki - do dziewiątek (trzy trójki zastępuje jedna dziewiątka) i tak dalej.

Co ciekawe, w 1958 roku pod przewodnictwem N.P. Brusentsov, komputer Setun został stworzony na Moskiewskim Uniwersytecie Państwowym i działał z liczbami nie w systemie binarnym, ale w trójskładnikowym systemie liczbowym! Na zdjęciu pierwszy prototyp „Setun”:

Konwersja z trójnego na dziesiętny

Oznaczmy na diagramie udziały pozycyjne cyfr w trójskładnikowym systemie liczbowym:

Aby przeliczyć na system dziesiętny, dodaj cyfry pomnożone przez ich wagi pozycyjne (pozycje z cyframi zerowymi można oczywiście pominąć):

10212 3 = 1 81 + 2 9 + 1 3 + 2 1 = 104 10 .

W systemie binarnym zrezygnowaliśmy z mnożenia (mnożenie przez 1 nie ma sensu). W systemie trójskładnikowym jest liczba 2, więc musisz podwoić odpowiednie wagi pozycyjne.

Konwersja dziesiętna na potrójną

Niech liczba 196 musi zostać przetłumaczona na system trójkowy.Początek liczby trójkowej wybieramy zgodnie ze schematem. 243 to dużo, więc zaczynamy od 81 i liczby 2 (2 81< 196):

Część oryginalnej liczby, a mianowicie 162 = 2 · 81, jest zakodowana, pozostaje zakodować 196 - 162 = 34. Weź 27 i liczbę 1 (liczba 2 daje 54, czyli za dużo):

Pozostaje zakodować 34 - 1 · 27 = 7. Pozycja z wagą 9 daje za dużo, wpisz w niej 0 i zajmij pozycję z wagą 3 i liczbą 2:

Pozostaje zakodować 7 - 2 · 3 = 1. Jest to dokładnie wartość pozostałej najmniej znaczącej cyfry:

Okazuje się: 196 10 = 21021 3.

Systemy pozycyjne: podstawowe zasady

Sformułujmy ogólne zasady konstruowania liczb w pozycyjnych systemach liczbowych.

Numer jest zapisany cyframi, na przykład:

Aby określić wartość liczby, musisz pomnożyć liczby przez wagi ich pozycji i dodać wyniki.

Pozycje są numerowane od prawej do lewej. Waga pierwszej pozycji to 1.

Waga każdej kolejnej pozycji jest uzyskiwana z wagi poprzedniej poprzez pomnożenie przez podstawę systemu.

Okazuje się, że waga drugiej pozycji jest zawsze równa podstawie systemu.

Baza systemu pokazuje liczbę cyfr, które są używane w danym systemie. Tak więc w systemie o podstawie 10 jest dziesięć cyfr, w systemie o podstawie 5 pięć cyfr.

Spójrzmy na przykład. Jeśli wpis

oznacza liczbę w systemie o podstawie 5, to jest równa

3242 5 = 3 125 + 2 25 + 4 5 + 2 1 = 447 10 .

Ten sam wpis w systemie base 6 oznacza liczbę

3242 6 = 3 216 + 2 36 + 4 6 + 2 1 = 746 10 .

Systemy liczb niepozycyjnych

Pozycyjne systemy liczbowe nie pojawiły się natychmiast, prymitywni ludzie określali liczbę niektórych obiektów jako równą liczbie innych (uważano je za kamyki, patyki, kości).

Stosowano też wygodniejsze metody liczenia: nacięcia na patyku, kreski na kamieniu, węzły na linie.

Czasami współcześni ludzie również używają takiego systemu liczbowego, odnotowując na przykład liczbę dni, które minęły w nacięciach.

To jest przykład niepozycyjny system numerów jednostek: używane do liczenia sam liczba (kamień, kij, kość, kreska, węzeł ...), a wkład tej figury nie zależy od jej miejsca (pozycji), zawsze jest równy jednej jednostce.

Oczywiste jest, że znacznie wygodniej jest używać pozycyjnych systemów liczbowych.

Działania na liczbach

Czynności na liczbach w systemie pozycyjnym o dowolnej podstawie wykonuje się w taki sam sposób, jak w systemie dziesiętnym: opierają się na tablicach dodawania i mnożenia cyfr odpowiednich systemów liczbowych.

Byłoby dziwne, gdyby w różnych systemach trzeba było dodawać, odejmować, mnożyć i dzielić na różne sposoby! Rzeczywiście, we wszystkich systemach liczbowych liczby są konstruowane w ten sam sposób, co oznacza, że działania na nich muszą być wykonywane w ten sam sposób.

Spójrzmy na kilka przykładów.

Dodanie

5 + 7 = 12. W najmniej znaczącym bicie piszemy 2 i dodajemy jedynkę do następnego bitu.

Zbudujmy tabelę dodawania ósemkowego:

Zgodnie z tabelą dodatków 5 + 7 = 14 8. Piszemy 4 w najmniej znaczącej cyfrze i dodajemy jeden do następnej cyfry.

Odejmowanie

Zajmujemy 1 na drugim miejscu i odejmujemy 7 od liczby 15. Podobnie w systemie ósemkowym:

Zajmujemy 1 w drugiej cyfrze i odejmujemy 7 od liczby 15 8. Zgodnie z tabelą dodawania w wierszu 7 znajdujemy liczbę 15. Numer odpowiedniej kolumny daje wynik różnicy - liczbę 6.

Jest to prawdopodobnie wygodne dla pająków
ósemkowy system liczbowy!

Mnożenie

2 7 = 14. Piszemy 4, a 1 idzie do "umysłu" (dodaj do następnej kategorii). 4 · 7 = 28. Piszemy 9 (8 plus 1 z "umysłu") i 2 przenosimy do następnej kategorii.

Zbudujmy tabliczkę mnożenia ósemkowego:

2 7 = 16 8. Piszemy 6, a 1 idzie do „umysłu” (dodaj do następnej kategorii). 4 7 = 34 8. Piszemy 5 (4 plus 1 z "umysłu"), a 3 przenosimy do następnej cyfry.

Podział

3 5< 17 < 4·5, поэтому первая цифра результата - 3. Из 17 вычитаем 5·3 = 15. К разности 2 приписываем цифру 5, получается 25. 25 = 5 ·5. Из 25 вычитаем 25=5·5, получается 0 - деление закончено.

W tabliczce mnożenia w wierszu 5 znajdujemy odpowiednią liczbę 17 8 = 5 3:

Oznacza to, że pierwsza cyfra wyniku to 3. Od 17 8 odejmujemy 17 8 = 5 · 3. Do różnicy 0 przypisujemy ostatnią cyfrę 5. 5 = 5 · 1. Odejmij 5 od 5, okazuje się 0 - dzielenie się skończyło.

Pytania i odpowiedzi

1. Podaj definicję terminu „system liczbowy”.

2. Podaj definicję terminu „system liczb pozycyjnych”.

3. Wyjaśnij zasady konstruowania liczb w zapisie dziesiętnym na przykładzie liczby 548.

4. Jak nazywa się wagę pozycji? Opowiedz nam algorytm obliczania wagi pozycji. Jaka jest waga trzeciej pozycji od prawej w zapisie dziesiętnym liczby? A w systemie binarnym? A w trójce?

5. Co oznacza wyładowanie? Jakie miejsce zajmuje liczba 5 w dziesiętnej liczbie 1532?

6. Co nazywa się wkładem liczb? Jaki jest wkład liczby 7 do 1745 10? A wkład liczby 4 do liczby 1432 5?

7. Podaj definicję terminu „podstawa pozycyjnego systemu liczbowego”. Jak podstawa systemu ma się do liczby cyfr w tym systemie? Ile cyfr jest w pięcioargumentowym systemie liczbowym? A szesnastkowo? A co z systemem bazowym 25?

8. Gdzie jest najmniej znacząca cyfra w rekordzie liczbowym? A najstarszy?

9. Powiedz nam algorytm konwersji liczby binarnej na system liczb dziesiętnych i wykonaj ten algorytm dla liczby 101101 2.

10. Powiedz algorytmowi konwersji liczby dziesiętnej na system liczb binarnych i wykonaj ten algorytm dla liczby 50 10.

11. Jak przekonwertować liczbę z dowolnego systemu liczb pozycyjnego na system dziesiętny? Wyjaśnienie oparte jest na przykładzie systemu z podstawą 4.

Zadania domowe

Wariant 1. Wykonywany bez komputera, „na papierze”

1. Czytaj łamańce językowe, zastępując liczby binarne dziesiętnymi:

Dobrze zjadłem
100001 2 placki z ciastem,
Tak, wszystko z twarogiem.

Było 101000 2 myszy,
Przewieziono 101000 2 grosze,
10 2 myszy są mniejsze
Mieli po 10 2 grosze.

2. Rozwiąż łamigłówki binarne:

3. Wykonaj obliczenia i zapisz odpowiedź w notacji dziesiętnej:

1) 100 2 5 8 =

2) 100 3 + 100 5 =

3) 10 9 10 100 - 10 900 =

4) 33 4 + 44 5 =

5) 15 6 + 51 8 =

4. Przetłumacz podane liczby na wskazane systemy liczbowe:

Opcja 2. Wykonywane na komputerze

1. Zapisz wyrażenie arytmetyczne do rozwiązania następującego problemu i oblicz odpowiedź:

Nasza sprytna Malwina
Dba o Buratino
I kupiłem to dla niego
Czego najbardziej potrzebuje:
10 2 okładki, 11 2 linijki
I za 111 2 ruble naklejki.
Na okładkach - Barmaley,
Cena każdego to 101 2 ruble.
Na linijkach, które kupiłem
101010 wystarczyło 2 ruble.
Ile kosztowały zakupy?
Na refleksję - pół minuty.

2. Spróbuj użyć standardowego programu Kalkulator, aby przekonwertować liczby z wiersza na zwykły zapis dziesiętny ( Widok- Inżynieria, Kosz- binarna reprezentacja liczby, Grudzień- dziesiętna reprezentacja liczby). Użyj Kalkulatora, aby zapisać algorytmy konwersji liczb z binarnego na dziesiętny i odwrotnie, z dziesiętnego na binarny.

Opcja 3. Dla ciekawskich

1. Udowodnij, że wpisanie 10 w dowolnym systemie liczb pozycyjnych oznacza liczbę równą podstawie tego systemu.

2. Określ podstawę systemu liczb pozycyjnych b dla każdej równości:

1) 10 b = 50 10 ;

2) 11 b = 6 10 ;

3) 100 b = 64 10 ;

4) 101 b = 26 10 ;

5) 50 b = 30 10 ;

6) 99 b = 909 10 ;

7) 21 b = 15 6 ;

8) 10 2 b = 100 b ;

9) 12 2 b = 22 b ;

10) 14 b· b = 104 b .

p WYRÓWNAJ = "WYRÓWNAJ"> 3. System liczb szesnastkowych wykorzystuje 16 cyfr. Pierwsze dziesięć cyfr pokrywa się z cyframi systemu dziesiętnego, a ostatnie są oznaczone literami alfabetu łacińskiego:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

	Wartość

Przetłumaczmy na przykład liczbę A8 16 na system dziesiętny:

A8 16 = 10 16 + 8 1 = 168 10 .

W każdym zadaniu znajdź wartość liczby x:

1) 25 16 = x 10 ; 4) 170 10 = x 16 ;

2) AB 16 = x 10 ; 5) 2569 10 = x 16 ;

3) FD 16 = x 10 ; 6) 80 32 = x 16 .

4. Wykonaj następujące zadania.

1) Znajdź wagę trzeciej pozycji w rekordzie liczbowym, jeśli wiadomo, że waga drugiej pozycji wynosi 7. Numeracja pozycji od prawej do lewej.

2) System liczbowy wykorzystuje 5 cyfr. Znajdź wagę czwartej pozycji od prawej w zapisie liczbowym.

3) Liczba jest zapisywana w postaci dwóch jednostek: 11. W jakim systemie liczbowym jest zapisana, jeśli w systemie dziesiętnym jest równa 21?

4) W pewnym systemie liczbowym liczba wygląda jak 100. Ile cyfr używa ten system liczbowy, jeśli w systemie dziesiętnym liczba wynosi 2500?

5) Dwie liczby są zapisywane jako 100, ale w systemach o różnych podstawach. Wiadomo, że podstawa pierwszego systemu jest dwukrotnie większa niż podstawa drugiego. Która liczba jest większa i ile razy?

6) Znajdź podstawę systemu, jeśli wiadomo, że liczba 101 zapisana w tym systemie oznacza liczbę dziesiętną 37.

7) W jakim systemie liczbowym, aby podwoić liczbę, musisz dodać zero po prawej stronie wpisu?

8) Mnożenie przez 10 w systemie dziesiętnym oznacza dodanie zera po prawej stronie liczby. Sformułuj zasadę mnożenia przez 10 b w systemie z bazą b.

5. Sformułuj algorytm konwersji liczby z systemu dziesiętnego na trójskładnikowy.

6. Zbuduj tablice dodawania i mnożenia dla czterokrotnego systemu liczbowego. Korzystając z tych tabel, wykonaj następujące czynności na liczbach w kolumnie (pozostając w systemie liczb czwartorzędowych):

1.a) 1021 4 + 333 4;

b) 3333 4 + 3210 4;

2.a) 321 4 - 123 4;

b) 1000 4 - 323 4;

3. a) 13 4 · 12 4;

b) 302 4 23 4;

4.a) 1123 4:13 4;

b) 112003 4: 101 4.

7. Budować tablice dodawania i mnożenia dla systemu liczb binarnych. Korzystając z tych tabel, wykonaj następujące czynności na liczbach w kolumnie (pozostałe w systemie liczb binarnych):

1.a) 1001 2 + 1010 2;

b) 10111 2 + 1110 2;

2. a) 1110 2 - 101 2;

b) 10000 2 - 111 2;

3. a) 101 2 · 11 2;

b) 1110 2 · 101 2;

4.a) 1000 110 2: 101 2;

b) 100000100 2: 1101 2.

Warsztat

Na stronach aplikacji elektronicznej pracuj z wykonawcą Encoder.

Ćwiczenia zawierają następujące grupy zadań:

Dziesiętny

1. Z binarnego na dziesiętny

2. Od trójnego do dziesiętnego

3. Od pięciu do dziesiętnych

4. Od szesnastkowego do dziesiętnego

Od dziesiętnego

1. Dziesiętny na Binarny

2. Od dziesiętnego do trójnego

3. Od dziesiętnych do pięciu

4. Dziesiętny na Szesnastkowy

Klasa kredytowa 1

2. 1101 2 = ? 10

3. 11101 2 = ? 10

Klasa kredytowa 2

10. 1001 2 = ? 16

Materiały dla nauczycieli

Systemy liczb pozycyjnych

W systemie liczb pozycyjnych liczba jest zapisywana jako łańcuch znaków specjalnych:

za n za n – 1 ... za 2 za 1 (1)

Symbolika ja są nazywane figury... Oznaczają one policzalne ilości porządkowe, począwszy od zera, aż do wartości mniejszej o jedną liczbę. q nazywa podstawa system liczbowy. To znaczy, jeśli q- podstawa, wtedy wartości cyfr leżą w przedziale (w tym granice).

Pozycja cyfry w zapisie liczby (1) nazywa się to pozycja, lub rozładować się.

Uwaga 1. Na tych stronach preferowany jest termin „stanowisko”. Po pierwsze, słowo „pozycja” jest dobrze zgodne z pojęciem „pozycyjny system liczbowy”, a po drugie, termin „waga pozycyjna” lub „waga pozycji” brzmi lepiej, jaśniej i prościej niż „waga bitowa” lub „waga bitowa” . Jednak nauczyciel może i powinien od czasu do czasu przypominać uczniom, że „pozycja” i „ranga” są terminami równoważnymi.

Uwaga 2. Podana w tekstach dla studenta definicja systemu liczb pozycyjnych nie jest do końca dokładna. Sama zależność udziału liczby od pozycji nie wystarczy. Na przykład w systemie liczb rzymskich udział cyfry również zależy od pozycji (liczby IV i VI są różne), ale ten system nie jest pozycyjny. Za dokładną definicję można uznać cały zbiór reguł konstruowania liczby, podany w tym kontekście dla nauczyciela (czyli wraz z faktem zależności pozycyjnej definicja obejmuje: skończoność zbioru cyfr i regułę znalezienie numeru przez jego zapisanie).

Pozycje są numerowane od prawej do lewej. Numer na pierwszej pozycji to młodszy cyfra liczby, w ostatniej - senior.

Każda pozycja jest powiązana z liczbą, którą nazwiemy jej wagą ( pozycja ważenia).

Wagi pozycji wyznaczane są zgodnie z następującą rekurencyjną regułą:

1. Waga najniższej pozycji to 1.

2. Wagę każdej kolejnej pozycji otrzymujemy z wagi poprzedniej, mnożąc przez podstawę systemu.

Zostawiać q- podstawa systemu liczbowego. Następnie reguła obliczania wag pozycyjnych w ja można bardziej zwięźle zapisać jako powtarzającą się formułę:

1. w 1 = 1.

2. w ja = w ja-jeden · q(dla wszystkich ja > 1).

W systemie liczb pozycyjnych rekord

za n za n – 1 ... za 2 za 1 (1)

oznacza numer N, równe sumie iloczynów cyfr przez ich wagi pozycyjne:

N = n· w n + n-jeden · w n–1 + ... + za 2 w 2 + za jeden · w 1 . (2)

Iloczyn cyfry przez jej wagę pozycyjną (tj. ja· w ja) będzie wezwany pozycyjny wkład liczb.

Formuła (2) jest podstawą zasad tłumaczenia liczb z jednego systemu na drugi, zaproponowanych w tekstach dla studenta.

W systemie dziesiętnym liczby są zapisywane przy użyciu dziesięciu znaków arabskich: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Wagi pozycyjne tego systemu to: ..., 1000, 100, 10, 1.

4627 10 = 4 1000 + 6 100 + 2 10 + 7 1.

W systemie binarnym liczby zapisywane są za pomocą dwóch znaków arabskich: 0 i 1. Wagi pozycyjne tego systemu: ..., 256, 128, 64, 32, 16, 8, 4, 2, 1.

Na przykład wpis 10101 jest „odszyfrowany” w ten sposób:

10101 2 = 1 16 + 0 8 + 1 4 + 0 2 + 1 1.

Zauważ, że rekurencyjna reguła obliczania wag implikuje, że w ja = q ja–1 i dlatego notacja (2) jest równoważna notacji tradycyjnej w postaci wielomianu potęgowego:

N = n· q n–1 + n-jeden · q n–2 + ... + za 2 q + za 1 . (3)

Udowodnijmy to przez indukcję. Podstawa indukcyjna w ja= 1 jest sprawdzane bezpośrednio: w 1 = q 0 = 1.

Hipoteza indukcyjna: niech dla niektórych stwierdzenie będzie prawdziwe nie:

w n = q n–1 .

Udowodnijmy, że będzie ona obowiązywać również przez nie + 1.
Oznacza to, że udowodnimy słuszność równości:

wn + 1 = q n.

W rzeczy samej, w n+1 = w n· q(zgodnie z rekurencyjną definicją wagi pozycji), oraz w n = q n-1 przez hipotezę indukcyjną. Wyszło na to, że:

wn + 1 = w n· q = q n-jeden · q = q n.

Udowodnijmy, że dowolna liczba jest reprezentowalna w postaci (1) (Twierdzenie 1) w sposób jednoznaczny (Twierdzenie 2).

Twierdzenie 1 (istnienie). Jakikolwiek numer m można przedstawić w postaci (1) dla dowolnego (1) q > 1.

Dowód. Udowodnijmy to przez indukcję. Dla m = 0
i m= 1 łatwo jest skonstruować wymaganą reprezentację - są to odpowiednio 0 i 1 (dla dowolnego q> 1). Powiedzmy, że udało nam się przedstawić liczbę m w formularzu (1). Następnie znajdujemy reprezentację dla m+ 1. Aby to zrobić, wystarczy przeliczyć sumę

n q n–1 + n-jeden · q n–2 + ... + za 2 q + za 1 + 1 do formy (1).

Jeśli za 1 < (q-1), to żądaną reprezentację uzyskuje się zastępując cyfrę za 1 dnia za " 1 = za 1 + 1.

Jeśli za 1 = (q–1), otrzymujemy przeniesienie jednostki na następną pozycję:

n q n F – 1 + n-jeden · q n–2 + ... + (za 2 + 1) q + 0.

Następnie rozumujemy w podobny sposób. Jeśli za 2 < (q-1), to żądaną reprezentację uzyskuje się zastępując cyfrę za 2 na za " 2 = za 2 + 1. Jeśli za 2 = (q–1), to za 2 zostaje zastąpione przez zero i jeden jest przenoszony na następną pozycję.

Lub na niektórych ja < nie dokończymy budowę, albo dostaniemy rekord 1000...0 - jeden i nie zera po prawej stronie. Dowód jest kompletny.

Przed Twierdzeniem 2 dowodzimy lemat.

Lemat. Wkład każdej niezerowej cyfry w rekordzie (1) przekracza sumę wkładów cyfr znajdujących się po jego prawej stronie.

za n za n – 1 ... za 2 za 1 . (1)

Dowód. Udowodnijmy to dla każdego nie > 1:

n q n–1 > n-jeden · q n–2 + ... + za 2 q+ za 1 .

Liczby ja leżą w przedziale, co oznacza, że wystarczy udowodnić nierówność dla najmniejszej niezerowej cyfry po lewej i maksymalnej cyfry po prawej:

n – 1> ( q-jeden)· q n–2 + ... + (q-jeden)· q + (q–1).

Po prawej stronie wyjmujemy czynnik ( q–1) poza nawiasem:

(q-jeden)· q n–2 + ... + (q-jeden)· q + (q–1) =

= (q-jeden)·( q n–2 + ... + q + 1).

Sumę postępu geometrycznego w ostatnim nawiasie obliczamy według znanego wzoru:

(q-jeden)·( q n–2 + ... + q + 1) =

= (q-jeden)·( q n–1 –1)/(q–1) = q n–1 – 1.

Otrzymujemy oczywistą nierówność, która dowodzi lematu:

qn – 1> q n–1 – 1.

Twierdzenie 2 (unikalność). Liczba w formularzu (1) jest reprezentowana w jedyny sposób.

Dowód. Z lematu wynika, że liczby o różnej liczbie cyfr w zapisie (nieznaczące zera po lewej stronie nie są liczone) nie mogą być równe: liczba o dużej liczbie cyfr jest zawsze większa. Dlatego wystarczy udowodnić, że jeśli ja nie równe b ja dla wszystkich ja od 1 do nie potem zapisuje

za n za n – 1 ... za 2 za 1 (4)

b n b n – 1 ... b 2 b 1 (5)

nie może oznaczać tej samej liczby.

Przejrzyjmy rekordy (4) i (5) od lewej do prawej w poszukiwaniu niedopasowanych cyfr. Niech będzie K i b k Odpuść sobie K – b k = re.

Na k- miejsce w rekordzie, była różnica w re· q k-jeden . Różnicę tę należy zrekompensować wkładami pozycji znajdujących się po prawej stronie. Jest to jednak niemożliwe, ponieważ zgodnie z lematem suma wkładów pozycji znajdujących się po prawej stronie jest zawsze mniejsza niż wkład bieżącej pozycji. Twierdzenie jest udowodnione.

Konwersja na dziesiętny

Aby przetłumaczyć liczby z systemu radix q w systemie dziesiętnym możesz użyć formuły (2), wykonując w niej mnożenie i dodawanie.

N = n· w n + n-jeden · w n–1 + ... + za 2 w 2 + za jeden · w 1 (2)

Przy tłumaczeniu z systemu binarnego w grę wchodzi tylko dodawanie (ponieważ nie można pomnożyć przez 1). W ten sposób otrzymujemy sformułowaną w czytelni regułę tłumaczenia:

Aby przekonwertować z binarnego na dziesiętny, musisz wpisać wagę jego pozycji nad każdą cyfrą binarną i dodać liczby zapisane nad jedynkami.

Na przykład dla numeru 10111 otrzymujemy:

10111 2 = 16 + 4 + 2 + 1 = 23 10

Ogólna zasada transferu z q-ary system na dziesiętny brzmi tak:

Do przeniesienia z q-ary system w systemie dziesiętnym, należy zapisać wagę jego pozycji nad każdą cyfrą i znaleźć sumę iloczynów cyfr przez ich wagi pozycyjne (czyli znaleźć sumę wkładów pozycyjnych).

Na przykład dla numeru 10212 3 otrzymujemy:

Dodajemy liczby pomnożone przez ich wagi pozycyjne (pozycje z cyframi zerowymi można oczywiście pominąć):

10212 3 = 1 81 + 2 9 + 1 3 + 2 1 = 104 10 .

Tłumaczenie na q- osobisty

Aby przekonwertować liczby z dziesiętnych na podstawy q nadal będziemy polegać na wzorze (2):

N = n· w n + n-jeden · w n–1 + ... + za 2 w 2 + za jeden · w 1 . (2)

Algorytm tłumaczenia.

I. Powtarzaj, aż liczba zmieni się na zero:

1. Znajdź pierwszą pozycję po lewej stronie, której waga nie jest większa niż aktualna liczba. Wpisz w pozycję maksymalną możliwą cyfrę, tak aby jej udział pozycyjny (iloczyn cyfry przez wagę) nie przekraczał aktualnej liczby.

2. Zmniejsz aktualną liczbę o wkład zbudowanej pozycji.

II. Wpisz zera na pozycjach nie zajętych przez skonstruowane cyfry.

W każdej pozycji przyjmowana jest maksymalna możliwa cyfra, ponieważ zgodnie z lematem wkładu tej cyfry nie można skompensować cyframi znajdującymi się po prawej stronie. Algorytm zadziała ze względu na udowodnione istnienie (Twierdzenie 1) i jednoznaczność (Twierdzenie 2) reprezentacji liczby w postaci (1).

Dla systemu binarnego otrzymujemy wariant algorytmu podanego w materiale dla ucznia.

Aby przekonwertować na binarny, musisz zbudować szablon z wagami cyfr binarnych:

Liczba jest tłumaczona zgodnie z następującym algorytmem:

I. Powtarzaj, aż liczba zmieni się na zero:

1. Napisz 1 na pierwszej pozycji po lewej stronie, której waga nie jest większa niż aktualna liczba.

2. Zmniejsz aktualną liczbę o wagę zbudowanej jednostki.

II. Wpisz zera na pozycjach niezajętych przez jedynki.

W praktyce ta metoda tłumaczenia okazuje się znacznie prostsza i szybsza niż tradycyjny algorytm ze znajdowaniem reszt.

Przy przeliczaniu z systemu dziesiętnego na system trójkowy należy wziąć pod uwagę zarówno same wagi pozycyjne, jak i ich podwojenie. W celu szybkiego tłumaczenia można zbudować tabelę, której wiersze odpowiadają pozycjom liczb, kolumny liczbom, a komórki udziałom liczby w liczbie, w zależności od jej pozycji w numer rekordu:


pozycja 729
pozycja 243
pozycja 81
pozycja 27
pozycja 9
pozycja 3
pozycja 1

Załóżmy, że wkład liczby 2 na pozycji 243 to liczba 486, a na pozycji 9 to liczba 18.

Aby przełożyć na system trójkowy, należy przeskanować tabelę wiersz po wierszu w poszukiwaniu największej liczby, która nie przekracza aktualnej wartości.

Na przykład przekształćmy liczbę 183 na system trójskładnikowy.Odpowiednia wartość znajduje się w trzecim wierszu i pierwszej kolumnie:


pozycja 729
pozycja 243
pozycja 81
pozycja 27
pozycja 9
pozycja 3
pozycja 1

Stąd liczba trójkowa zaczyna się od cyfry 2:

183 10 = 202?? 3

Dla liczby 21-18 = 3 w tabeli jest dokładne znaczenie, tłumaczenie jest zakończone:

183 10 = 20210 3 .

W przypadku systemów z dużą podstawą odpowiednie tabele będą oczywiście bardziej obszerne. Jako ostatni przykład, zbudujmy tabelę do konwersji na system liczb szesnastkowych:

Niech liczba 4255 zostanie przekonwertowana na system szesnastkowy. Szukamy pierwszej liczby w tabeli (od lewej do prawej, wiersz po wierszu, zaczynając od góry), która okazuje się być nie więcej niż oryginalna liczba 4255:

Otrzymujemy pierwszą cyfrę 1 na pozycji 4096:

Pozostaje zakodować 4255 - 4096 = 159.

Pomiń linię 256 (odpowiednia cyfra będzie wynosić 0), a w linii 16 znajdujemy odpowiednią wartość 144:

Otrzymujemy liczby na pozycjach 256 i 16:

Pozostaje zakodować 159 - 144 = 15. Oczywiste jest, że jest to wartość najmniej znaczącej cyfry:

Okazuje się: 4255 10 = 109F 16.

Działania na liczbach

Sekcja ta została przedstawiona w materiale dla ucznia schematycznie, w celach informacyjnych.

Tematowi można poświęcić osobną, dużą i dość ciekawą lekcję, ale materiału jest już sporo - trudno ogarnąć ogrom!

W prostej, wprowadzającej wersji pokazano, że akcje na liczbach w dowolnym systemie liczbowym są wykonywane w taki sam sposób, jak w systemie dziesiętnym. Dziwne, gdyby było inaczej, bo liczby we wszystkich systemach pozycyjnych budowane są według tych samych reguł, co oznacza, że działania na nich muszą być wykonywane w ten sam sposób.

Ta sekcja jest poparta zadaniami domowymi dla opcji 3. Ćwiczenia te można polecić ciekawskim uczniom jako zadania indywidualne.

Rozdział 4. Arytmetyczne podstawy komputerów

4.1. Co to jest system liczbowy?

Istnieją pozycyjne i niepozycyjne systemy liczbowe.

W niepozycyjnych systemach liczbowych waga cyfry (czyli jej wkład w wartość liczby) nie zależy od jej pozycji w zapisie liczby. Tak więc w systemie rzymskim, w liczbie XXXII (trzydzieści dwa), waga cyfry X w dowolnej pozycji wynosi zaledwie dziesięć.

W systemach liczb pozycyjnych waga każdej cyfry zmienia się w zależności od jej pozycji (pozycji) w sekwencji cyfr reprezentujących liczbę. Na przykład w liczbie 757,7 pierwsza siedem oznacza 7set, druga - 7 jednostek, a trzecia - 7 dziesiątych jednego.

Ten sam zapis liczby 757,7 oznacza wyrażenie skrócone

700 + 50 + 7 + 0,7 = 7 . 10 2 + 5 . 10 1 + 7 . 10 0 + 7 . 10 -1 = 757,7.

Każdy system liczb pozycyjnych charakteryzuje się jego podstawa.

Za podstawę systemu można przyjąć dowolną liczbę naturalną - dwa, trzy, cztery itd. W związku z tym, możliwe niezliczone systemy pozycjonowania: binarny, trójskładnikowy, czwartorzędowy itp. Zapisywanie liczb w każdym z systemów radix q oznacza wyrażenie skrócone

za n-1 q n-1 + a n-2 q n-2 + ... + a 1 q 1 + a 0 q 0 + a -1 q -1 + ... + a -m q -m ,

Gdzie za ja - cyfry; nie i m - odpowiednio liczba cyfr całkowitych i ułamkowych.
Na przykład:

4.2. Jak generowane są liczby całkowite w pozycyjnych systemach liczbowych?

W każdym systemie liczbowym liczby są uporządkowane zgodnie z ich znaczeniem: 1 jest większe od 0, 2 jest większe od 1 itd.

Zwiększenie liczby 1 oznacza zastąpienie jej 2, zwiększenie liczby 2 oznacza zastąpienie jej 3 itd. Promocja wysokiej cyfry(na przykład liczby 9 w systemie dziesiętnym) oznacza zastąpienie go przez 0... W systemie binarnym, który używa tylko dwóch cyfr, 0 i 1, przesunięcie 0 oznacza zastąpienie go 1, a przesunięcie 1 oznacza zastąpienie go 0.

Liczby całkowite w dowolnym systemie liczbowym są generowane za pomocą Zasady konta [44 ]:

Stosując tę zasadę, napiszmy pierwsze dziesięć liczb całkowitych

binarnie: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;

w systemie trójskładnikowym: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;

w systemie pięciokrotnym: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;

ósemkowo: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.

4.3. Jakich systemów numerycznych używają specjaliści do komunikacji z komputerem?

Oprócz systemu dziesiętnego szeroko stosowane są systemy, których podstawą jest liczba całkowita 2, a mianowicie:

dwójkowy(używane są cyfry 0, 1);

ósemkowy(stosowane są numery 0, 1, ..., 7);

szesnastkowy(dla pierwszych liczb całkowitych od zera do dziewięciu stosuje się cyfry 0, 1, ..., 9, a dla kolejnych liczb całkowitych od dziesięciu do piętnastu stosuje się znaki A, B, C, D, E, F jako cyfry).

Warto zapamiętać wpis w tych systemach liczbowych dla pierwszych dwóch dziesiątek liczb całkowitych:

Ze wszystkich systemów liczbowych szczególnie proste i dlatego ciekawy do technicznego wdrożenia w komputerach binarny system liczbowy.

4.4. Dlaczego ludzie używają dziesiętnych, a komputery binarnych?

Ludzie preferują system dziesiętny, prawdopodobnie dlatego, że od czasów starożytnych liczyli palcami, a ludzie mają dziesięć palców na dłoniach i stopach. Nie zawsze i nie wszędzie ludzie używają systemu liczb dziesiętnych. Na przykład w Chinach system pięciokrotnej liczby był używany przez długi czas.

A komputery używają systemu binarnego, ponieważ ma on wiele zalet w porównaniu z innymi systemami:

aby go wdrożyć, potrzebujesz urządzenia techniczne o dwóch stanach ustalonych,(jest prąd - brak prądu, namagnesowany - nienamagnesowany itp.), A nie na przykład z dziesięcioma, jak w systemie dziesiętnym;

prezentacja informacji za pomocą tylko dwóch stanów niezawodnie i przeciwzakłóceniowy;

możliwie Aplikacja do algebry Boole'a wykonywać logiczne przekształcenia informacji;

arytmetyka binarna jest znacznie prostsza niż dziesiętna.

Wadą systemu binarnego jest szybki wzrost liczby cyfr wymagane do pisania liczb.

4.5. Dlaczego komputery używają również systemów liczb ósemkowych i szesnastkowych?

Wygodny dla komputerów system binarny jest niewygodny dla człowieka ze względu na swoją nieporęczność i nietypowe nagrywanie.

Konwersja liczb z dziesiętnych na binarne i odwrotnie jest wykonywana przez maszynę. Jednak, aby profesjonalnie korzystać z komputera, musisz nauczyć się rozumieć maszynę słów. W tym celu opracowano systemy ósemkowe i szesnastkowe.

Liczby w tych systemach czyta się prawie tak samo łatwo jak dziesiętne, wymagają odpowiednio trzech (ósemkowych) i czterech (szesnastkowych) razy mniej cyfr niż w systemie dwójkowym (w końcu liczby 8 i 16 są odpowiednio trzecią i czwarte potęgi liczby 2) ...

Na przykład:

Na przykład,

4.6. Jak przekonwertować liczbę całkowitą z systemu dziesiętnego na dowolny inny system liczb pozycyjnych?

Przykład: Przekształćmy liczbę 75 z systemu dziesiętnego na binarny, ósemkowy i szesnastkowy:

Odpowiedź: 75 10 = 1 001 011 2 = 113 8 = 4B 16.

4.7. Jak przetłumaczyć poprawną liczbę dziesiętną na dowolny inny system liczb pozycyjnych?

Aby przetłumaczyć poprawną liczbę dziesiętnąfa do radixq niezbędnyfa pomnożyć przezq , zapisane w tym samym systemie dziesiętnym, a następnie pomnóż część ułamkową otrzymanego iloczynu przezq, i tak dalej, aż ułamkowa część następnego iloczynu stanie się równa zero lub zostanie osiągnięta wymagana dokładność liczby number fa wq sparowany system. Reprezentacja części ułamkowej liczbyfa w nowym systemie liczbowym pojawi się ciąg całych części otrzymanych prac, pisanych w kolejności ich napływu i przedstawianych jedynką q -numer. Jeśli wymagana dokładność konwersji liczb numberfa jestk miejsc po przecinku, to maksymalny błąd bezwzględny jest równy equalq - (k + 1) / 2.

Przykład. Przekształćmy liczbę 0,36 z systemu dziesiętnego na binarny, ósemkowy i szesnastkowy:

4.8. Jak przekonwertować liczbę z systemu binarnego (ósemkowego, szesnastkowego) na dziesiętny?

Konwersja liczby na system dziesiętnyx nagrane wq -argumentowy system liczbowy (q = 2, 8 lub 16) w postacix q = (a nie za n-1 ... a 0 , a -1 za -2 ... a -m ) q sprowadza się do obliczenia wartości wielomianu

x 10 = a nie q nie + a n-1 q n-1 + ... + a 0 q 0 + a -1 q -1 + a -2 q -2 + ... + a -m q -m

za pomocą arytmetyki dziesiętnej.

Przykłady:

4.9. Tabela podsumowująca tłumaczenia liczb całkowitych z jednego systemu liczbowego na inny

Rozważ tylko te systemy liczbowe, które są używane w komputerach - dziesiętny, binarny, ósemkowy i szesnastkowy. Dla jednoznaczności bierzemy dowolną liczbę dziesiętną, na przykład 46, i dla niej wykonujemy wszystkie możliwe kolejne translacje z jednego systemu liczbowego do drugiego. Kolejność tłumaczeń ustalana jest zgodnie z rysunkiem:

Na tym rysunku zastosowano następujące konwencje:

podstawy systemów liczbowych są napisane w kółko;

strzałki wskazują kierunek tłumaczenia;

liczba obok strzałki oznacza numer seryjny odpowiedniego przykładu w tabeli zbiorczej 4.1.

Na przykład: oznacza tłumaczenie z binarnego na szesnastkowy, które w tabeli ma numer sekwencyjny 6.

Tabela przestawna tłumaczeń liczb całkowitychdwaSekcje- teoria statystyki ... statystyka, Informatyka jako dyscypliny ... KR (elektroniczny wersja wydania). „.... Statystyki mikroekonomiczne PE: Podręcznik. dodatek... - M.: Delo, 2000. ... magazyn. Internet- strony internetowe Rosstat ...

"tworzenie otwartych baz danych zasobów informacyjnych"

Raport

Wydania referencyjne. Bibliograficzny korzyści. Sekcja 1. Publikacje referencyjne ... procedur pojednawczych. Internet-wersja czasopismo zapewnia dostęp do ... URSS / Internet-wynik składa sięzdwa działy: …specjaliści Kancelarii Informatyka i telekomunikacja ...

Notacja to metoda zapisu liczby przy użyciu określonego zestawu znaków specjalnych (liczb).

Notacja:

daje reprezentację zbioru liczb (liczb całkowitych i / lub rzeczywistych);

nadaje każdej liczbie unikalną reprezentację (lub przynajmniej standardową reprezentację);

wyświetla strukturę algebraiczną i arytmetyczną liczby.

Zapisywanie liczby w określonym systemie liczbowym nazywa się kod numeryczny.

Oddzielna pozycja na wyświetlaczu liczby nazywa się rozładować się, co oznacza, że numer pozycji to numer rangi.

Liczba bitów w liczbie nazywa się zgryźliwość i pasuje do jego długości.

Systemy liczbowe są podzielone na pozycyjny i niepozycyjny. Systemy liczb pozycyjnych są podzielone

na jednorodny i mieszany.

system liczb ósemkowych, system liczb szesnastkowych i inne systemy liczbowe.

Tłumaczenie systemów liczbowych. Liczby można tłumaczyć z jednego systemu liczbowego na inny.

Tablica korespondencyjna liczb w różnych systemach liczbowych.