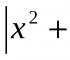Jak znaleźć a1 we wzorze progresji arytmetycznej. odwrotna macierz

Tak więc usługi rozwiązywania macierzy online:

Usługa pracy z macierzami umożliwia wykonywanie elementarnych przekształceń macierzy.
Jeśli masz zadanie do wykonania bardziej złożonej transformacji, to ta usługa powinna być używana jako konstruktor.

Przykład... Podane macierze ZA i b, trzeba znaleźć do = ZA -1 * b + b T,

1. Powinieneś najpierw znaleźć odwrotna macierzA1 = ZA-1, korzystając z usługi wyszukiwania macierzy odwrotnej;
2. Dalej, po znalezieniu matrycy A1 Zrób to mnożenie macierzyA2 = A1 * b korzystanie z usługi mnożenia macierzy;
3. Wykonajmy! transpozycja macierzyA3 = b T (usługa wyszukiwania transponowanej macierzy);
4. I ostatnia rzecz - znajdź sumę macierzy Z = A2 + A3(usługa obliczania sumy macierzy) - i otrzymujemy odpowiedź z najbardziej szczegółowym rozwiązaniem!;

Produkt macierzy

Jest to usługa online w dwa kroki:

• Wprowadź pierwszą macierz czynników ZA
• Wprowadź macierz drugiego czynnika lub wektor kolumnowy b

Mnożenie macierzy-wektora

Mnożenie macierzy przez wektor można znaleźć korzystając z usługi Mnożenie macierzy
(Pierwszym czynnikiem będzie dana macierz, drugim czynnikiem będzie kolumna składająca się z elementów danego wektora)

Jest to usługa online w dwa kroki:

• Wejdź do matrycy ZA, dla którego musisz znaleźć macierz odwrotną
• Uzyskaj odpowiedź ze szczegółowym rozwiązaniem do znalezienia macierzy odwrotnej

Wyznacznik macierzy

Jest to usługa online w jeden krok:

• Wejdź do matrycy ZA, dla którego trzeba znaleźć wyznacznik macierzy

Transpozycja macierzy

Tutaj możesz śledzić algorytm transpozycji macierzy i dowiedzieć się, jak samodzielnie rozwiązywać takie problemy.
To jest usługa online w jeden krok:

• Wejdź do matrycy ZA do transpozycji

Ranga macierzy

Jest to usługa online w jeden krok:

• Wejdź do matrycy ZA, dla którego musisz znaleźć rangę

Wartości własne macierzy i wektory własne macierzy

Jest to usługa online w jeden krok:

• Wejdź do matrycy ZA, dla których trzeba znaleźć wektory własne i wartości własne (wartości własne)

Potęgowanie macierzy

Jest to usługa online w dwa kroki:

• Wejdź do matrycy ZA, którą podniesiesz do potęgi
• Wpisz liczbę całkowitą q- stopień

Macierz $ A ^ (- 1) $ nazywana jest odwrotną względem macierzy kwadratowej $ A $, jeśli warunek $ A ^ (- 1) \ cdot A = A \ cdot A ^ (- 1) = E $ jest spełniony , gdzie $ E $ Jest macierzą jednostkową, której kolejność jest równa kolejności macierzy $ A $.

Macierz niezdegenerowana - macierz, której wyznacznik nie jest równy zero. W związku z tym zdegenerowana macierz to taka, która ma zerowy wyznacznik.

Macierz odwrotna $ A ^ (- 1) $ istnieje wtedy i tylko wtedy, gdy macierz $ A $ jest niezdegenerowana. Jeżeli macierz odwrotna $ A ^ (- 1) $ istnieje, to jest unikalna.

Istnieje kilka sposobów na znalezienie odwrotności macierzy, a przyjrzymy się dwóm z nich. Na tej stronie omówiona zostanie metoda matrycy sprzężonej, która jest uważana za standard na większości kursów matematyki wyższej. W drugiej części omówiono drugą metodę znajdowania macierzy odwrotnej (metoda przekształceń elementarnych), która polega na wykorzystaniu metody Gaussa lub metody Gaussa-Jordana.

Metoda macierzy sprzężonej (sprzężonej)

Niech będzie podana macierz $ A_ (n \ razy n) $. Aby znaleźć odwrotność macierzy $ A ^ (- 1) $, wymagane są trzy kroki:

1. Znajdź wyznacznik macierzy $ A $ i upewnij się, że $ \ Delta A \ neq 0 $, tj. że macierz A jest niezdegenerowana.
2. Uzupełnij algebraiczne $ A_ (ij) $ każdego elementu macierzy $ A $ i zapisz macierz $ A_ (n \ razy n) ^ (*) = \ left (A_ (ij) \ right) $ z znaleziono dopełnienia algebraiczne.
3. Napisz macierz odwrotną, biorąc pod uwagę formułę $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $.

Macierz $ (A ^ (*)) ^ T $ jest często określana jako sprzężona (odwrotna, sprzężona) z macierzą $ A $.

Jeśli rozwiązanie jest wykonywane ręcznie, to pierwsza metoda jest dobra tylko dla macierzy o stosunkowo małych rzędach: druga (), trzecia (), czwarta (). Inne metody służą do znajdowania odwrotności macierzy wyższego rzędu. Na przykład metoda Gaussa, o której mowa w drugiej części.

Przykład 1

Znajdź odwrotność $ A = \ left (\ begin (tablica) (cccc) 5 & -4 & 1 & 0 \\ 12 & -11 & 4 & 0 \\ -5 & 58 & 4 & 0 \\ 3 & - 1 i -9 i 0 \ koniec (tablica) \ prawo) $.

Ponieważ wszystkie elementy czwartej kolumny są równe zeru, to $ \ Delta A = 0 $ (czyli macierz $ A $ jest zdegenerowana). Ponieważ $ \ Delta A = 0 $, macierz odwrotna do macierzy $ A $ nie istnieje.

Odpowiedź: macierz $ A ^ (- 1) $ nie istnieje.

Przykład nr 2

Znajdź odwrotność macierzy $ A = \ left (\ begin (tablica) (cc) -5 & 7 \\ 9 & 8 \ end (array) \ right) $. Czek.

Używamy metody sprzężonej macierzy. Najpierw znajdujemy wyznacznik danej macierzy $ A $:

$$ \ Delta A = \ lewo | \ begin (array) (cc) -5 & 7 \\ 9 & 8 \ end (array) \ right | = -5 \ cdot 8-7 \ cdot 9 = -103. $$

Ponieważ $ \ Delta A \ neq 0 $, to macierz odwrotna istnieje, dlatego będziemy kontynuować rozwiązanie. Znajdowanie dopełnień algebraicznych

\ początek (wyrównany) & A_ (11) = (- 1) ^ 2 \ cdot 8 = 8; \; A_ (12) = (- 1) ^ 3 \ cdot 9 = -9; \\ & A_ (21) = (- 1) ^ 3 \ cdot 7 = -7; \; A_ (22) = (- 1) ^ 4 \ cdot (-5) = - 5. \\ \ koniec (wyrównany)

Tworzymy macierz z dopełnień algebraicznych: $ A ^ (*) = \ left (\ begin (array) (cc) 8 & -9 \\ -7 & -5 \ end (array) \ right) $.

Transponuj wynikową macierz: $ (A ^ (*)) ^ T = \ left (\ begin (array) (cc) 8 & -7 \\ -9 & -5 \ end (array) \ right) $ (wynik macierz jest często nazywana macierzą sprzężoną lub sprzężoną do macierzy $A $). Korzystając ze wzoru $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $, mamy:

$$ A ^ (- 1) = \ frac (1) (- 103) \ cdot \ left (\ begin (tablica) (cc) 8 & -7 \\ -9 & -5 \ end (array) \ right) = \ left (\ begin (tablica) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (tablica) \ right) $$

Tak więc znaleziono odwrotność: $ A ^ (- 1) = \ left (\ begin (tablica) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $. Aby sprawdzić prawdziwość wyniku wystarczy sprawdzić prawdziwość jednej z równości: $ A ^ (- 1) \ cdot A = E $ lub $ A \ cdot A ^ (- 1) = E $. Sprawdźmy równość $ A ^ (- 1) \ cdot A = E $. Aby mniej pracować z ułamkami, podstawimy macierz $ A ^ (- 1) $ nie w postaci $ \ left (\ begin (array) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $, a jako $ - \ frac (1) (103) \ cdot \ left (\ begin (array) (cc) 8 & -7 \\ -9 & -5 \ koniec (tablica ) \ prawo) $:

$$ A ^ (- 1) \ cdot (A) = - \ frac (1) (103) \ cdot \ left (\ begin (tablica) (cc) 8 & -7 \\ -9 & -5 \ end ( array) \ right) \ cdot \ left (\ begin (tablica) (cc) -5 & 7 \\ 9 & 8 \ end (array) \ right) = - \ frac (1) (103) \ cdot \ left ( \ begin (tablica) (cc) -103 & 0 \\ 0 & -103 \ end (array) \ right) = \ left (\ begin (array) (cc) 1 & 0 \\ 0 & 1 \ end (array ) \ prawo) = E $$

Odpowiedź: $ A ^ (- 1) = \ lewo (\ początek (tablica) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ koniec (tablica) \ prawo) $.

Przykład nr 3

Znajdź odwrotność macierzy $ A = \ left (\ begin (tablica) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (array) \ right) $. Czek.

Zacznijmy od obliczenia wyznacznika macierzy $A $. Zatem wyznacznik macierzy $ A $ jest następujący:

$$ \ Delta A = \ lewo | \ begin (tablica) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (tablica) \ right | = 18-36 + 56-12 = 26. $$

Ponieważ $ \ Delta A \ neq 0 $, to macierz odwrotna istnieje, dlatego będziemy kontynuować rozwiązanie. Znajdujemy dopełnienia algebraiczne każdego elementu danej macierzy:

$$ \ begin (wyrównane) & A_ (11) = (- 1) ^ (2) \ cdot \ left | \ begin (tablica) (cc) 9 & 4 \\ 3 & 2 \ end (tablica) \ right | = 6; \; A_ (12) = (- 1) ^ (3) \ cdot \ left | \ begin (tablica) (cc) -4 & 4 \\ 0 & 2 \ end (array) \ right | = 8; \; A_ (13) = (- 1) ^ (4) \ cdot \ left | \ begin (tablica) (cc) -4 & 9 \\ 0 & 3 \ end (array) \ right | = -12; \\ & A_ (21) = (- 1) ^ (3) \ cdot \ left | \ begin (tablica) (cc) 7 & 3 \\ 3 & 2 \ end (array) \ right | = -5; \; A_ (22) = (- 1) ^ (4) \ cdot \ left | \ begin (tablica) (cc) 1 & 3 \\ 0 & 2 \ end (array) \ right | = 2; \; A_ (23) = (- 1) ^ (5) \ cdot \ left | \ begin (tablica) (cc) 1 & 7 \\ 0 & 3 \ end (array) \ right | = -3; \\ & A_ (31) = (- 1) ^ (4) \ cdot \ left | \ begin (tablica) (cc) 7 & 3 \\ 9 & 4 \ end (array) \ right | = 1; \; A_ (32) = (- 1) ^ (5) \ cdot \ left | \ begin (tablica) (cc) 1 & 3 \\ -4 & 4 \ end (array) \ right | = -16; \; A_ (33) = (- 1) ^ (6) \ cdot \ left | \ begin (tablica) (cc) 1 & 7 \\ -4 & 9 \ end (array) \ right | = 37. \ koniec (wyrównany) $$

Komponujemy macierz dopełnień algebraicznych i transponujemy ją:

$$ A ^ * = \ lewo (\ begin (tablica) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37 \ end (tablica) \ right); \; (A ^ *) ^ T = \ lewo (\ początek (tablica) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ end (tablica) \ prawo) ... $$

Używając formuły $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $, otrzymujemy:

$$ A ^ (- 1) = \ frac (1) (26) \ cdot \ left (\ begin (tablica) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37 \ end (tablica) \ right) = \ left (\ begin (tablica) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \ koniec (tablica) \ prawo) $$

Czyli $ A ^ (- 1) = \ lewo (\ początek (tablica) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 i -3/26 i 37/26 \ koniec (tablica) \ prawo) $. Aby sprawdzić prawdziwość wyniku wystarczy sprawdzić prawdziwość jednej z równości: $ A ^ (- 1) \ cdot A = E $ lub $ A \ cdot A ^ (- 1) = E $. Sprawdźmy równość $ A \ cdot A ^ (- 1) = E $. Aby mniej pracować z ułamkami, podstawimy macierz $ A ^ (- 1) $ nie w postaci $ \ left (\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \\ 4 /13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \ end (array) \ right) $ i jako $ \ frac (1) (26) \ cdot \ left ( \ begin (tablica) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ end (array) \ right) $:

$$ A \ cdot (A ^ (- 1)) = \ left (\ begin (tablica) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (tablica) \ prawo) \ cdot \ frac (1) (26) \ cdot \ lewo (\ początek (tablica) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ end (array) \ right) = \ frac (1) (26) \ cdot \ left (\ begin (array) (ccc) 26 & 0 & 0 \\ 0 & 26 & 0 \\ 0 & 0 & 26 \ end (tablica) \ right) = \ left (\ begin (tablica) (ccc) 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end (tablica) \ right) = E $$

Sprawdzenie powiodło się, odwrotność $ A ^ (- 1) $ została znaleziona poprawnie.

Odpowiedź: $ A ^ (- 1) = \ lewo (\ początek (tablica) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 / 13 i -3/26 i 37/26 \ koniec (tablica) \ prawo) $.

Przykład nr 4

Znajdź odwrotność $ A = \ lewo (\ początek (tablica) (cccc) 6 & -5 & 8 & 4 \\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7 \\ -4 & 8 & -8 & -3 \ koniec (tablica) \ prawo) $.

W przypadku macierzy czwartego rzędu znalezienie macierzy odwrotnej przy użyciu uzupełnień algebraicznych jest nieco trudne. Jednak takie przykłady można znaleźć w pracach testowych.

Aby znaleźć odwrotność macierzy, należy najpierw obliczyć wyznacznik macierzy $ A $. Najlepszym sposobem na zrobienie tego w tej sytuacji jest rozszerzenie wyznacznika o wiersz (kolumnę). Wybieramy dowolny wiersz lub kolumnę i znajdujemy algebraiczne dopełnienia każdego elementu wybranego wiersza lub kolumny.

Na przykład dla pierwszej linii otrzymujemy:

$$ A_ (11) = \ left | \ begin (tablica) (ccc) 7 & 5 & 2 \\ 5 & 3 & 7 \\ 8 & -8 & -3 \ end (array) \ right | = 556; \; A_ (12) = - \ lewo | \ początek (tablica) (ccc) 9 & 5 & 2 \\ 7 & 3 & 7 \\ -4 & -8 & -3 \ end (tablica) \ prawo | = -300 ; $$ $$ A_ (13) = \ left | \ begin (tablica) (ccc) 9 & 7 & 2 \\ 7 & 5 & 7 \\ -4 & 8 & -3 \ end (array) \ right | = -536;\; A_ (14) = - \ lewo | \ początek (tablica) (ccc) 9 & 7 & 5 \\ 7 & 5 & 3 \\ -4 & 8 & -8 \ end (tablica) \ prawo | = -112. $$

Wyznacznik macierzy $ A $ jest obliczany według następującego wzoru:

$$ \ Delta (A) = a_ (11) \ cdot A_ (11) + a_ (12) \ cdot A_ (12) + a_ (13) \ cdot A_ (13) + a_ (14) \ cdot A_ (14 ) = 6 \ cdot 556 + (- 5) \ cdot (-300) +8 \ cdot (-536) +4 \ cdot (-112) = 100. $$

$$ \ początek (wyrównany) & A_ (21) = - 77; \; A_ (22) = 50; \; A_ (23) = 87; \; A_ (24) = 4; \\ & A_ (31) = -93; \; A_ (32) = 50; \; A_ (33) = 83; \; A_ (34) = 36; \\ & A_ (41) = 473; \; A_ (42) = - 250 ; \; A_ (43) = - 463; \; A_ (44) = - 96. \ koniec (wyrównany) $$

Algebraiczna Macierz Dopełnień: $ A ^ * = \ left (\ begin (tablica) (cccc) 556 & -300 & -536 & -112 \\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36 \\ 473 & -250 & -463 & -96 \ koniec (tablica) \ prawo) $.

Macierz sprzężona: $ (A ^ *) ^ T = \ left (\ begin (tablica) (cccc) 556 & -77 & -93 & 473 \\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 i -463 \\ -112 i 4 i 36 i -96 \ koniec (tablica) \ prawo) $.

Macierz odwrotna:

$$ A ^ (- 1) = \ frac (1) (100) \ cdot \ left (\ begin (tablica) (cccc) 556 & -77 & -93 & 473 \\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463 \\ -112 & 4 & 36 & -96 \ end (tablica) \ right) = \ left (\ begin (tablica) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28 / 25 i 1/25 i 9/25 i -24/25 \ koniec (tablica) \ prawo) $$

W razie potrzeby sprawdzenie można przeprowadzić w taki sam sposób, jak w poprzednich przykładach.

Odpowiedź: $ A ^ (- 1) = \ lewo (\ początek (tablica) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/25 & 9/25 & -24/25 \ koniec (tablica) \ prawy) $.

W drugiej części zostanie rozważony inny sposób znajdowania macierzy odwrotnej, który polega na wykorzystaniu przekształceń metody Gaussa lub metody Gaussa-Jordana.

Aby rozwiązać układ równań liniowych (3) względem x 1 użyjemy metody Gaussa.

W podobny sposób rozwiązuje się pozostałe układy równań liniowych (2).

Wreszcie grupa wektorów kolumnowych x 1, x 2, ..., x n tworzy odwrotność A-1.

Zauważ, że po znalezieniu macierzy permutacji P 1, P 2, ..., P n-1 i macierze wykluczeń M 1, M 2, ..., M n-1(patrz strona Metoda eliminacji Gaussa) i konstruowanie macierzy

M = M n-1 P n-1 ... M 2 P 2 M 1 P 1,

system (2) można przekształcić do postaci

• Maks. 1 = Ja 1,
• Maks. 2 = Ja 2,
• ......
• Maks. n = Me n.

Stąd są x 1, x 2, ..., x n, z różnymi prawymi stronami Ja 1, Ja 2, ..., Ja n.

Przy obliczaniu macierzy odwrotnej wygodniej jest dodać macierz jednostkową po prawej stronie macierzy pierwotnej i zastosować metodę Gaussa w kierunku do przodu i do tyłu.

Spójrzmy na przykład.

Przykład obliczenia macierzy odwrotnej

Niech będzie wymagane znalezienie macierzy odwrotnej A-1 dla danej macierzy ZA:

Zapiszmy macierz tożsamości po prawej stronie:

Wybieramy element obrotowy „4” (ponieważ jest największy w wartości bezwzględnej) i zmieniamy kolejność pierwszego i trzeciego wiersza:

Zastosuj wyjątek Gaussa dla pierwszej kolumny:

Zamień drugi i trzeci wiersz i zastosuj wykluczenie Gaussa dla drugiej kolumny.

Metody znajdowania macierzy odwrotnej. Rozważ macierz kwadratową

Oznaczamy Δ = det A.

Macierz kwadratowa A nazywa się niezdegenerowany, lub nie w liczbie pojedynczej jeśli jego wyznacznik jest niezerowy, a zdegenerowany, lub specjalny, JeśliΔ = 0.

Macierz kwadratowa B istnieje dla macierzy kwadratowej A tego samego rzędu, jeśli ich iloczyn A B = B A = E, gdzie E jest macierzą jednostkową tego samego rzędu co macierze A i B.

Twierdzenie . Aby macierz A miała macierz odwrotną, konieczne i wystarczające jest, aby jej wyznacznik był niezerowy.

Macierz odwrotna macierzy A, oznaczona przez A- 1, więc B = A - 1 i jest obliczany według wzoru

, (1)

gdzie А i j są algebraicznymi dopełnieniami elementów a i j macierzy A ..

Obliczenie A -1 według wzoru (1) dla macierzy wyższego rzędu jest bardzo pracochłonne, dlatego w praktyce wygodnie jest obliczyć A -1 metodą przekształceń elementarnych (EP). Dowolna nieosobliwa macierz A może zostać zredukowana do macierzy jednostkowej E za pomocą EP tylko kolumn (lub tylko wierszy).Jeśli EF doskonałe nad macierzą A są stosowane w tej samej kolejności do macierzy jednostkowej E, wynikiem jest macierz odwrotna . Wygodnie jest wykonać EP na macierzach A i E w tym samym czasie, pisząc obie macierze obok siebie w jednej linii. Zauważmy ponownie, że przy wyszukiwaniu postaci kanonicznej macierzy w celu znalezienia można skorzystać z przekształceń wierszy i kolumn. Jeśli potrzebujesz znaleźć odwrotność macierzy, w procesie transformacji powinny być używane tylko wiersze lub tylko kolumny.

Przykład 1... Dla matrycy znajdź A -1.

Decyzja.Najpierw znajdujemy wyznacznik macierzy A
stąd macierz odwrotna istnieje i możemy ją znaleźć za pomocą wzoru: , gdzie A i j (i, j = 1,2,3) są algebraicznymi dopełnieniami elementów a i j macierzy pierwotnej.

Skąd .

Przykład 2... Korzystając z metody przekształceń elementarnych, znajdź A -1 dla macierzy: A =.

Decyzja.Do macierzy oryginalnej po prawej stronie przypisujemy macierz jednostkową tego samego rzędu: ... Za pomocą elementarnych przekształceń kolumnowych lewą „połówkę” sprowadzamy do jednostkowej, jednocześnie wykonując dokładnie te same transformacje nad prawą macierzą.
Aby to zrobić, zamieńmy pierwszą i drugą kolumnę: ~ ... Dodaj pierwszą do trzeciej kolumny, a pierwszą pomnożoną przez -2 do drugiej: ... Od pierwszej kolumny odejmujemy drugą podwojoną, a od trzeciej drugą pomnożoną przez 6; ... Dodajmy trzecią kolumnę do pierwszej i drugiej: ... Pomnóżmy ostatnią kolumnę przez -1: ... Macierz kwadratowa uzyskana na prawo od pionowego słupka jest odwrotnością danej macierzy A. Tak więc,
.

Podczas nauki algebry w szkole ogólnokształcącej (klasa 9) jednym z ważnych tematów jest nauka o ciągach liczbowych, które obejmują progresje – geometryczne i arytmetyczne. W tym artykule rozważymy postęp arytmetyczny i przykłady z rozwiązaniami.

Co to jest postęp arytmetyczny?

Aby to zrozumieć, konieczne jest podanie definicji rozważanego postępu, a także podanie podstawowych formuł, które będą dalej wykorzystywane przy rozwiązywaniu problemów.

Postęp arytmetyczny lub algebraiczny to zbiór uporządkowanych liczb wymiernych, z których każdy wyraz różni się od poprzedniego o pewną stałą wartość. Ta wartość nazywana jest różnicą. Oznacza to, że znając dowolny element uporządkowanej serii liczb i różnicę, możesz odtworzyć cały postęp arytmetyczny.

Podajmy przykład. Następny ciąg liczb będzie ciągiem arytmetycznym: 4, 8, 12, 16, ..., ponieważ różnica w tym przypadku wynosi 4 (8 - 4 = 12 - 8 = 16 - 12). Ale zbioru liczb 3, 5, 8, 12, 17 nie można już przypisać do rozważanego rodzaju progresji, ponieważ różnica dla niego nie jest wartością stałą (5 - 3 ≠ 8 - 5 ≠ 12 - 8 ≠ 17 - 12).

Ważne formuły

Podajmy teraz podstawowe wzory, które będą potrzebne do rozwiązywania problemów za pomocą progresji arytmetycznej. Oznaczmy przez n n-ty wyraz ciągu, gdzie n jest liczbą całkowitą. Różnicę oznaczono łacińską literą d. Wtedy poprawne są następujące wyrażenia:

1. Aby określić wartość n-tego członu, odpowiedni jest następujący wzór: a n = (n-1) * d + a 1.
2. Aby określić sumę pierwszych n warunków: S n = (a n + a 1) * n / 2.

Aby zrozumieć wszelkie przykłady postępu arytmetycznego z rozwiązaniem w klasie 9, wystarczy zapamiętać te dwie formuły, ponieważ wszelkie problemy rozważanego typu są zbudowane na ich użyciu. Należy również pamiętać, że różnicę w progresji określa wzór: d = a n - a n-1.

Przykład nr 1: znalezienie nieznanego członka

Podajmy prosty przykład progresji arytmetycznej i formuł, których należy użyć do rozwiązania.

Niech będzie podany ciąg 10, 8, 6, 4, ..., trzeba w nim znaleźć pięć wyrazów.

Z opisu problemu wynika już, że znane są 4 pierwsze terminy. Piąty można zdefiniować na dwa sposoby:

1. Najpierw obliczmy różnicę. Mamy: d = 8 - 10 = -2. Podobnie można było wziąć dowolnych dwóch innych członków stojących obok siebie. Na przykład d = 4 - 6 = -2. Ponieważ wiadomo, że d = a n - a n-1, to d = a 5 - a 4, skąd otrzymujemy: a 5 = a 4 + d. Zastąp znane wartości: a 5 = 4 + (-2) = 2.
2. Druga metoda również wymaga znajomości różnicy rozważanej progresji, więc najpierw musisz ją określić, jak pokazano powyżej (d = -2). Wiedząc, że pierwszy wyraz a 1 = 10, posługujemy się wzorem na liczbę n ciągu. Mamy: a n = (n - 1) * d + a 1 = (n - 1) * (-2) + 10 = 12 - 2 * n. Podstawiając n = 5 w ostatnim wyrażeniu, otrzymujemy: a 5 = 12-2 * 5 = 2.

Jak widać, obie metody rozwiązania doprowadziły do ​​tego samego rezultatu. Zauważ, że w tym przykładzie różnica d progresji jest ujemna. Takie ciągi nazywamy malejącymi, ponieważ każdy kolejny wyraz jest mniejszy od poprzedniego.

Przykład nr 2: Różnica progresji

Teraz trochę skomplikujmy zadanie, podajmy przykład jak

Wiadomo, że w niektórych I semestr jest równy 6, a VII semestr jest równy 18. Trzeba znaleźć różnicę i przywrócić tę kolejność do VII kadencji.

Użyjmy wzoru do wyznaczenia nieznanego wyrazu: a n = (n - 1) * d + a 1. Zastępujemy w nim znane dane z warunku, czyli liczby a 1 i a 7, mamy: 18 = 6 + 6 * d. Z tego wyrażenia możesz łatwo obliczyć różnicę: d = (18 - 6) / 6 = 2. W ten sposób odpowiedzieliśmy na pierwszą część problemu.

Aby odtworzyć sekwencję do 7 wyrazów, powinieneś użyć definicji progresji algebraicznej, czyli a 2 = a 1 + d, a 3 = a 2 + d, i tak dalej. W rezultacie przywracamy całą sekwencję: a 1 = 6, a 2 = 6 + 2 = 8, a 3 = 8 + 2 = 10, a 4 = 10 + 2 = 12, a 5 = 12 + 2 = 14 , a 6 = 14 + 2 = 16, a 7 = 18.

Przykład #3: robienie progresji

Jeszcze bardziej skomplikujmy stan problemu. Teraz trzeba odpowiedzieć na pytanie, jak znaleźć postęp arytmetyczny. Możesz podać następujący przykład: dane dwie liczby, na przykład - 4 i 5. Konieczne jest wykonanie progresji algebraicznej, aby trzy kolejne wyrazy zmieściły się między nimi.

Przed przystąpieniem do rozwiązywania tego problemu konieczne jest zrozumienie, jakie miejsce zajmą dane liczby w przyszłej progresji. Ponieważ będą między nimi jeszcze trzy wyrazy, a 1 = -4 i 5 = 5. Po ustaleniu tego przechodzimy do problemu, który jest podobny do poprzedniego. Ponownie dla n-tego wyrazu używamy wzoru, otrzymujemy: a 5 = a 1 + 4 * d. Skąd: d = (a 5 - a 1) / 4 = (5 - (-4)) / 4 = 2,25. Tutaj nie otrzymaliśmy całkowitej wartości różnicy, ale jest to liczba wymierna, więc wzory na postęp algebraiczny pozostają takie same.

Teraz dodaj znalezioną różnicę do 1 i przywróć brakujące elementy progresji. Otrzymujemy: a 1 = - 4, a 2 = - 4 + 2,25 = - 1,75, a 3 = -1,75 + 2,25 = 0,5, a 4 = 0,5 + 2,25 = 2,75, a 5 = 2,75 + 2,25 = 5, co było zbieżne ze stanem problemu.

Przykład nr 4: pierwszy termin progresji

Podajmy dalej przykłady postępu arytmetycznego z rozwiązaniem. We wszystkich poprzednich problemach znana była pierwsza liczba progresji algebraicznej. Rozważmy teraz problem innego typu: niech podane zostaną dwie liczby, gdzie a 15 = 50 i a 43 = 37. Trzeba znaleźć liczbę, od której zaczyna się ten ciąg.

Stosowane do tej pory formuły zakładają znajomość 1 i d. Nic nie wiadomo o tych liczbach w opisie problemu. Niemniej jednak wypisujemy wyrażenia dla każdego członka, o którym są informacje: a 15 = a 1 + 14 * d i a 43 = a 1 + 42 * d. Otrzymano dwa równania, w których 2 nieznane wielkości (a 1 i d). Oznacza to, że problem sprowadza się do rozwiązania układu równań liniowych.

Najłatwiejszym sposobem rozwiązania tego systemu jest wyrażenie 1 w każdym równaniu, a następnie porównanie otrzymanych wyrażeń. Pierwsze równanie: a 1 = a 15 - 14 * d = 50 - 14 * d; drugie równanie: a 1 = a 43 - 42 * d = 37 - 42 * d. Porównując te wyrażenia, otrzymujemy: 50 - 14 * d = 37 - 42 * d, skąd różnica d = (37 - 50) / (42 - 14) = - 0,464 (podano tylko 3 miejsca po przecinku).

Znając d, możesz użyć dowolnego z dwóch powyższych wyrażeń dla 1. Na przykład pierwszy: a 1 = 50 - 14 * d = 50 - 14 * (-0,464) = 56,496.

Jeśli masz wątpliwości co do wyniku, możesz to sprawdzić, na przykład określić 43 termin progresji, który jest określony w warunku. Otrzymujemy: a 43 = a 1 + 42 * d = 56,496 + 42 * (- 0,464) = 37,008. Mały błąd wynika z faktu, że w obliczeniach zastosowano zaokrąglanie do tysięcznych.

Przykład nr 5: kwota

Spójrzmy teraz na kilka przykładów z rozwiązaniami sumy postępu arytmetycznego.

Niech będzie podany ciąg liczbowy postaci: 1, 2, 3, 4, ...,. Jak obliczyć sumę tych 100 liczb?

Dzięki rozwojowi technologii komputerowej możliwe jest rozwiązanie tego problemu, czyli sekwencyjne sumowanie wszystkich liczb, co komputer zrobi, gdy tylko osoba naciśnie klawisz Enter. Problem można jednak rozwiązać w umyśle, jeśli zwrócimy uwagę, że przedstawiony ciąg liczb jest ciągiem algebraicznym, a jego różnica wynosi 1. Stosując wzór na sumę, otrzymujemy: S n = n * (a 1 + an) / 2 = 100 * (1 + 100) / 2 = 5050.

Ciekawostką jest, że problem ten nazywa się „gaussowskim”, ponieważ na początku XVIII wieku słynny Niemiec, choć miał zaledwie 10 lat, był w stanie rozwiązać go w głowie w kilka sekund. Chłopiec nie znał wzoru na sumę ciągu algebraicznego, ale zauważył, że jeśli dodasz parami liczby na krawędziach ciągu, zawsze otrzymasz jeden wynik, czyli 1 + 100 = 2 + 99 = 3 + 98 = ..., a ponieważ z tych kwot będzie dokładnie 50 (100/2), to aby otrzymać poprawną odpowiedź wystarczy pomnożyć 50 przez 101.

Przykład nr 6: suma członków od n do m

Inny typowy przykład sumy postępu arytmetycznego jest następujący: mając ciąg liczb: 3, 7, 11, 15, ..., musisz znaleźć, jaka będzie suma jego członków od 8 do 14.

Problem rozwiązuje się na dwa sposoby. Pierwsza z nich polega na znalezieniu nieznanych terminów od 8 do 14, a następnie dodaniu ich kolejno. Ponieważ terminów jest niewiele, ta metoda nie jest wystarczająco pracochłonna. Proponuje się jednak rozwiązanie tego problemu drugą metodą, która jest bardziej uniwersalna.

Chodzi o to, aby uzyskać wzór na sumę postępu algebraicznego między wyrazami m i n, gdzie n>m są liczbami całkowitymi. Napiszmy dwa wyrażenia na sumę dla obu przypadków:

1. S m = m * (m + a 1) / 2.
2. S n = n * (a n + a 1) / 2.

Ponieważ n>m jest oczywiste, że suma 2 zawiera pierwszą. Ostatni wniosek oznacza, że ​​jeśli weźmiemy różnicę między tymi sumami i dodamy do niej wyraz a m (w przypadku wzięcia różnicy jest ona odejmowana od sumy S n), to otrzymujemy konieczną odpowiedź na problem. Mamy: S mn = S n - S m + am = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am = a 1 * (n - m) / 2 + an * n / 2 + am * (1- m / 2). W tym wyrażeniu konieczne jest zastąpienie wzorów za n i m. Następnie otrzymujemy: S mn = a 1 * (n - m) / 2 + n * (a 1 + (n - 1) * d) / 2 + (a 1 + (m - 1) * d) * (1 - m / 2) = a 1 * (n - m + 1) + d * n * (n - 1) / 2 + d * (3 * m - m 2 - 2) / 2.

Otrzymany wzór jest nieco kłopotliwy, jednak suma S mn zależy tylko od n, m, a 1 i d. W naszym przypadku a 1 = 3, d = 4, n = 14, m = 8. Podstawiając te liczby, otrzymujemy: S mn = 301.

Jak widać z podanych rozwiązań, wszystkie problemy opierają się na znajomości wyrażenia dla n-tego członu i wzoru na sumę zbioru pierwszych członów. Przed przystąpieniem do rozwiązania któregokolwiek z tych problemów zaleca się uważne przeczytanie stanu, jasne zrozumienie, co należy znaleźć, a dopiero potem przejście do rozwiązania.

Kolejną wskazówką jest dążenie do prostoty, to znaczy, jeśli możesz odpowiedzieć na pytanie bez użycia skomplikowanych obliczeń matematycznych, musisz to zrobić, ponieważ w tym przypadku prawdopodobieństwo popełnienia błędu jest mniejsze. Na przykład w przykładzie ciągu arytmetycznego z rozwiązaniem nr 6 można zatrzymać się na wzorze S mn = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am i przerwać ogólny problem na osobne podzadania (w tym przypadku najpierw znajdź członków an i am).

Jeśli istnieją wątpliwości co do uzyskanego wyniku, zaleca się sprawdzenie go, tak jak to zrobiono w niektórych podanych przykładach. Odkryliśmy, jak znaleźć postęp arytmetyczny. Jeśli się zorientujesz, to nie jest takie trudne.