Tabela wartości funkcji trygonometrycznych kątów. Stopniowa miara kąta
Trygonometria jako nauka wywodzi się ze starożytnego Wschodu. Astronomowie wyprowadzili pierwsze stosunki trygonometryczne w celu stworzenia dokładnego kalendarza i orientacji według gwiazd. Obliczenia te dotyczyły trygonometrii sferycznej, podczas gdy na zajęciach szkolnych badano stosunek boków i kątów płaskiego trójkąta.
Trygonometria to dział matematyki zajmujący się właściwościami funkcji trygonometrycznych oraz zależnościami między bokami i kątami trójkątów.
W okresie rozkwitu kultury i nauki w I tysiącleciu naszej ery wiedza rozprzestrzeniła się ze starożytnego Wschodu do Grecji. Ale główne odkrycia trygonometrii są zasługą ludzi kalifatu arabskiego. W szczególności turkmeński naukowiec al-Marazi wprowadził funkcje takie jak tangens i cotangens oraz opracował pierwsze tabele wartości sinusów, stycznych i cotangensów. Pojęcia sinusa i cosinusa zostały wprowadzone przez indyjskich naukowców. Trygonometrii poświęcano wiele uwagi w pracach tak wielkich postaci starożytności, jak Euklides, Archimedes i Eratostenes.
Podstawowe wielkości trygonometrii
Podstawowe funkcje trygonometryczne argumentu numerycznego to sinus, cosinus, tangens i cotangens. Każdy z nich ma swój własny wykres: sinus, cosinus, tangens i cotangens.
Wzory do obliczania wartości tych wielkości opierają się na twierdzeniu Pitagorasa. Jest to lepiej znane uczniom w sformułowaniu: „Spodnie pitagorejskie są równe we wszystkich kierunkach”, ponieważ dowód przedstawiono na przykładzie trójkąta prostokątnego równoramiennego.
Sinus, cosinus i inne zależności ustalają związek między kątami ostrymi i bokami dowolnego trójkąta prostokątnego. Przedstawmy wzory na obliczenie tych wielkości dla kąta A i prześledźmy zależności pomiędzy funkcjami trygonometrycznymi:

Jak widać, tg i ctg są funkcjami odwrotnymi. Jeśli wyobrazimy sobie nogę a jako iloczyn grzechu A i przeciwprostokątnej c oraz nogę b jako cos A*c, otrzymamy następujące wzory na styczną i kotangę:

Koło trygonometryczne
Graficznie zależność pomiędzy wymienionymi wielkościami można przedstawić w następujący sposób:

Okrąg w tym przypadku reprezentuje wszystkie możliwe wartości kąta α - od 0° do 360°. Jak widać na rysunku, każda funkcja przyjmuje wartość ujemną lub dodatnią w zależności od kąta. Przykładowo sin α będzie miał znak „+”, jeśli α należy do 1. i 2. ćwiartki koła, czyli mieści się w przedziale od 0° do 180°. Dla α od 180° do 360° (III i IV ćwiartka) sin α może mieć tylko wartość ujemną.
Spróbujmy zbudować tablice trygonometryczne dla określonych kątów i dowiedzieć się, co oznaczają wielkości.

Wartości α równe 30°, 45°, 60°, 90°, 180° itd. nazywane są przypadkami specjalnymi. Wartości funkcji trygonometrycznych dla nich są obliczane i prezentowane w formie specjalnych tabel.

Kąty te nie zostały wybrane przypadkowo. Oznaczenie π w tabelach dotyczy radianów. Rad to kąt, pod którym długość łuku koła odpowiada jego promieniowi. Wartość tę wprowadzono w celu ustalenia uniwersalnej zależności, przy obliczaniu w radianach rzeczywista długość promienia w cm nie ma znaczenia.

Kąty w tabelach funkcji trygonometrycznych odpowiadają wartościom radianów:

Nietrudno więc zgadnąć, że 2π to pełny okrąg, czyli 360°.
Własności funkcji trygonometrycznych: sinus i cosinus
Aby rozważyć i porównać podstawowe właściwości sinusa i cosinusa, tangensa i cotangensu, należy narysować ich funkcje. Można tego dokonać w postaci krzywej umiejscowionej w dwuwymiarowym układzie współrzędnych.
Rozważ tabelę porównawczą właściwości sinusa i cosinusa:

| Sinusoida | Cosinus |
|---|---|
| y = grzech x | y = cos x |
| ODZ [-1; 1] | ODZ [-1; 1] |
| sin x = 0, dla x = πk, gdzie k ϵ Z | cos x = 0, dla x = π/2 + πk, gdzie k ϵ Z |
| sin x = 1, dla x = π/2 + 2πk, gdzie k ϵ Z | cos x = 1, przy x = 2πk, gdzie k ϵ Z |
| sin x = - 1, przy x = 3π/2 + 2πk, gdzie k ϵ Z | cos x = - 1, dla x = π + 2πk, gdzie k ϵ Z |
| sin (-x) = - sin x, czyli funkcja jest nieparzysta | cos (-x) = cos x, czyli funkcja jest parzysta |
| funkcja jest okresowa, najmniejszy okres wynosi 2π | |
| sin x › 0, gdzie x należy do 1. i 2. ćwiartki lub od 0° do 180° (2πk, π + 2πk) | cos x › 0, gdzie x należy do ćwiartek I i IV lub od 270° do 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, gdzie x należy do trzeciej i czwartej ćwiartki lub od 180° do 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, gdzie x należy do 2. i 3. ćwiartki lub od 90° do 270° (π/2 + 2πk, 3π/2 + 2πk) |
| wzrosty przedziału [- π/2 + 2πk, π/2 + 2πk] | rośnie w przedziale [-π + 2πk, 2πk] |
| maleje na przedziałach [π/2 + 2πk, 3π/2 + 2πk] | maleje w odstępach czasu |
| pochodna (sin x)’ = cos x | pochodna (cos x)’ = - sin x |
Ustalenie, czy funkcja jest parzysta, czy nie, jest bardzo proste. Wystarczy wyobrazić sobie okrąg trygonometryczny ze znakami wielkości trygonometrycznych i w myślach „złożyć” wykres względem osi OX. Jeśli znaki się pokrywają, funkcja jest parzysta, w przeciwnym razie jest nieparzysta.

Wprowadzenie radianów i wyszczególnienie podstawowych własności fal sinusoidalnych i cosinusoidalnych pozwala przedstawić następujący wzór:

Bardzo łatwo jest sprawdzić poprawność wzoru. Na przykład dla x = π/2 sinus wynosi 1, podobnie jak cosinus x = 0. Sprawdzenie można przeprowadzić, korzystając z tabel lub śledząc krzywe funkcji dla danych wartości.
Właściwości tangentsoid i kotangentsoid
Wykresy funkcji stycznej i cotangens różnią się znacznie od funkcji sinus i cosinus. Wartości tg i ctg są względem siebie odwrotne.


- Y = brązowy x.
- Styczna dąży do wartości y przy x = π/2 + πk, ale nigdy ich nie osiąga.
- Najmniejszy dodatni okres tangentoidy to π.
- Tg (- x) = - tg x, czyli funkcja jest nieparzysta.
- Tg x = 0, dla x = πk.
- Funkcja jest rosnąca.
- Tg x › 0, dla x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, dla x ϵ (— π/2 + πk, πk).
- Pochodna (tg x)’ = 1/cos 2 x.
Rozważ graficzny obraz kotangentoidy poniżej w tekście.

Główne właściwości kotangentoidów:
- Y = łóżeczko x.
- W przeciwieństwie do funkcji sinus i cosinus, w tangentoidzie Y może przyjmować wartości zbioru wszystkich liczb rzeczywistych.
- Kotangentoida dąży do wartości y przy x = πk, ale nigdy ich nie osiąga.
- Najmniejszy dodatni okres kotangentoidy to π.
- Ctg (- x) = - ctg x, czyli funkcja jest nieparzysta.
- Ctg x = 0, dla x = π/2 + πk.
- Funkcja jest malejąca.
- Ctg x › 0, dla x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, dla x ϵ (π/2 + πk, πk).
- Pochodna (ctg x)’ = - 1/sin 2 x Poprawnie
W artykule w pełni zrozumiemy, jak to wygląda tabela wartości trygonometrycznych, sinus, cosinus, tangens i cotangens. Rozważmy podstawowe znaczenie funkcji trygonometrycznych dla kątów 0,30,45,60,90,...,360 stopni. Zobaczmy, jak korzystać z tych tabel przy obliczaniu wartości funkcji trygonometrycznych.
Najpierw spójrzmy tabela cosinusów, sinusów, tangensów i cotangensów pod kątem 0, 30, 45, 60, 90,... stopni. Definicja tych wielkości pozwala nam wyznaczyć wartość funkcji kątów 0 i 90 stopni:
sin 0 0 =0, cos 0 0 = 1. tg 00 = 0, cotangens od 00 będzie nieokreślony
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, tangens od 90 0 będzie niepewny
Jeśli weźmiesz trójkąty prostokątne, których kąty wynoszą od 30 do 90 stopni. Otrzymujemy:
grzech 30 0 = 1/2, cos 30 0 = √3/2, tan 30 0 = √3/3, cos 30 0 = √3
grzech 45 0 = √2/2, cos 45 0 = √2/2, tan 45 0 = 1, cos 45 0 = 1
grzech 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, łóżeczko 60 0 = √3/3
Przedstawmy wszystkie uzyskane wartości w formularzu tablica trygonometryczna:
Tabela sinusów, cosinusów, stycznych i kotangentów!
Jeśli skorzystamy ze wzoru redukcyjnego, nasza tabela powiększy się, dodając wartości dla kątów aż do 360 stopni. Będzie wyglądać tak:

Ponadto, w oparciu o właściwości okresowości, tabelę można zwiększyć, jeśli zastąpimy kąty 0 0 +360 0 *z .... 330 0 +360 0 *z, w którym z jest liczbą całkowitą. W tabeli tej możliwe jest obliczenie wartości wszystkich kątów odpowiadających punktom pojedynczego okręgu.

Przyjrzyjmy się, jak wykorzystać tabelę w rozwiązaniu.
Wszystko jest bardzo proste. Ponieważ potrzebna nam wartość leży w punkcie przecięcia potrzebnych nam komórek. Weźmy na przykład cos kąta 60 stopni, w tabeli będzie to wyglądać następująco:

W końcowej tabeli głównych wartości funkcji trygonometrycznych postępujemy w ten sam sposób. Ale w tej tabeli można dowiedzieć się, ile wynosi tangens pod kątem 1020 stopni, to = -√3 Sprawdźmy 1020 0 = 300 0 +360 0 *2. Znajdźmy to za pomocą tabeli.

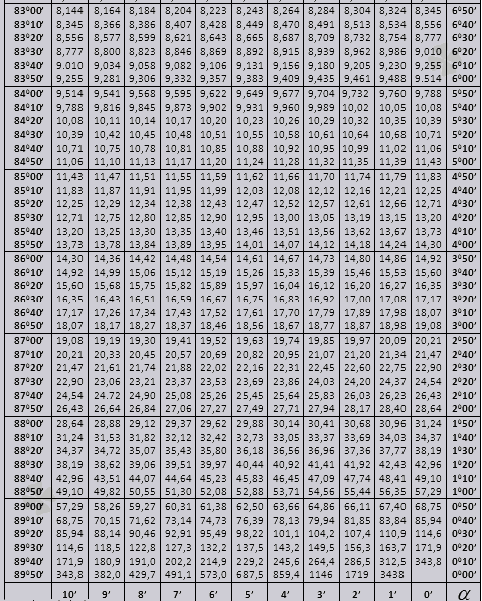
Stół Bradisa. Dla sinusa, cosinusa, tangensa i cotangensa.
Tablice Bradisa podzielone są na kilka części, składających się z tablic cosinusów i sinusów, stycznych i cotangensów - która jest podzielona na dwie części (tg kątów do 90 stopni i ctg małych kątów).
Sinus i cosinus


tg kąta zaczynającego się od 00 kończącego się na 760, ctg kąta rozpoczynającego się od 140 kończącego się na 900.


tg do 900 i ctg małych kątów.
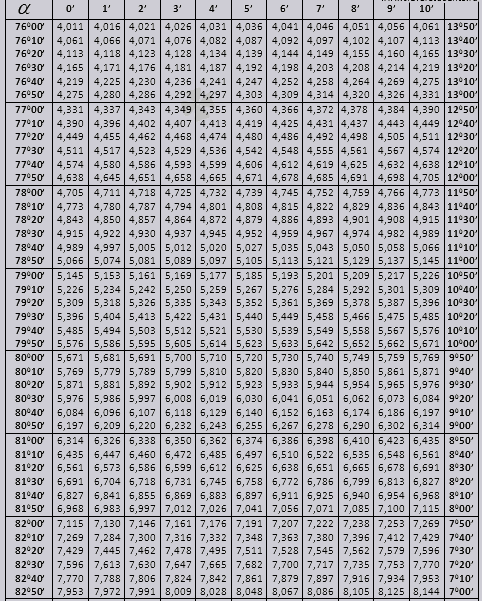
Zastanówmy się, jak używać tabel Bradisa do rozwiązywania problemów.
Znajdźmy oznaczenie sin (oznaczenie w kolumnie po lewej stronie) 42 minuty (oznaczenie w górnym wierszu). Na przecięciu szukamy oznaczenia, it = 0,3040.
Wartości minutowe są wskazywane w odstępie sześciu minut, co zrobić, jeśli potrzebna nam wartość mieści się dokładnie w tym przedziale. Weźmy 44 minuty, ale w tabeli jest ich tylko 42. Za podstawę bierzemy 42 i korzystamy z dodatkowych kolumn po prawej stronie, weźmy drugą poprawkę i dodamy do 0,3040 + 0,0006 otrzymamy 0,3046.
Przy grzechu 47 minutach przyjmujemy za podstawę 48 minut i odejmujemy od niego 1 korektę, tj. 0,3057 - 0,0003 = 0,3054
Obliczając cos, postępujemy podobnie jak grzech, tyle że za podstawę bierzemy dolny rząd tabeli. Na przykład cos 20 0 = 0,9397
Wartości kąta tg do 90 0 i łóżeczka małego kąta są prawidłowe i nie ma w nich żadnych poprawek. Na przykład znajdź tg 78 0 37min = 4,967 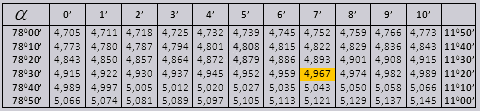
i ctg 20 0 13 min = 25,83 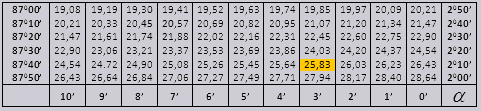
Cóż, przyjrzeliśmy się podstawowym tabelom trygonometrycznym. Mamy nadzieję, że te informacje były dla Ciebie niezwykle przydatne. Jeśli masz jakieś pytania dotyczące stołów, koniecznie napisz je w komentarzach!
Uwaga: Odbojniki ścienne to listwa zderzakowa służąca do ochrony ścian. Kliknij link bezramowe zderzaki ścienne (http://www.spi-polymer.ru/otboyniki/) i dowiedz się więcej.
W V wieku p.n.e. starożytny grecki filozof Zenon z Elei sformułował swoje słynne aporie, z których najsłynniejszą jest aporia „Achilles i żółw”. Oto jak to brzmi:Załóżmy, że Achilles biegnie dziesięć razy szybciej niż żółw i jest o tysiąc kroków za nim. W czasie, jaki potrzebuje Achilles na pokonanie tej odległości, żółw wykona sto kroków w tym samym kierunku. Kiedy Achilles przebiegnie sto kroków, żółw czołga się przez kolejne dziesięć kroków i tak dalej. Proces ten będzie trwał w nieskończoność, Achilles nigdy nie dogoni żółwia.
To rozumowanie stało się logicznym szokiem dla wszystkich kolejnych pokoleń. Arystoteles, Diogenes, Kant, Hegel, Hilbert... Wszyscy oni w ten czy inny sposób rozważali aporię Zenona. Wstrząs był tak silny, że „ ... dyskusje trwają do dziś, w środowisku naukowym nie udało się jeszcze dojść do wspólnej opinii co do istoty paradoksów ... w badaniu tego zagadnienia zaangażowano analizę matematyczną, teorię mnogości, nowe podejścia fizyczne i filozoficzne ; żaden z nich nie stał się ogólnie przyjętym rozwiązaniem problemu...„[Wikipedia, „Aporia Zenona”. Każdy rozumie, że daje się oszukać, ale nikt nie rozumie, na czym to oszustwo polega.
Z matematycznego punktu widzenia Zenon w swoich aporiach wyraźnie pokazał przejście od ilości do. To przejście oznacza zastosowanie, a nie trwałe. O ile rozumiem, aparat matematyczny do stosowania zmiennych jednostek miary albo nie został jeszcze opracowany, albo nie został zastosowany do aporii Zenona. Stosowanie naszej zwykłej logiki prowadzi nas w pułapkę. My, ze względu na bezwładność myślenia, do wartości odwrotności stosujemy stałe jednostki czasu. Z fizycznego punktu widzenia wygląda to na spowolnienie czasu, aż do całkowitego zatrzymania się w momencie, gdy Achilles dogoni żółwia. Jeśli czas się zatrzyma, Achilles nie będzie już w stanie przegonić żółwia.
Jeśli odwrócimy naszą zwykłą logikę, wszystko ułoży się na swoim miejscu. Achilles biegnie ze stałą prędkością. Każdy kolejny odcinek jego ścieżki jest dziesięć razy krótszy od poprzedniego. W związku z tym czas poświęcony na jego pokonanie jest dziesięć razy krótszy niż poprzedni. Jeśli zastosujemy w tej sytuacji koncepcję „nieskończoności”, wówczas słuszne będzie stwierdzenie: „Achilles nieskończenie szybko dogoni żółwia”.
Jak uniknąć tej logicznej pułapki? Pozostań w stałych jednostkach czasu i nie przełączaj się na jednostki odwrotne. W języku Zenona wygląda to tak:
W czasie, jaki zajmie Achillesowi przebiegnięcie tysiąca kroków, żółw wykona sto kroków w tym samym kierunku. W następnym odstępie czasowym, równym pierwszemu, Achilles przebiegnie kolejne tysiąc kroków, a żółw przeczołga się sto kroków. Teraz Achilles jest osiemset kroków przed żółwiem.
Podejście to adekwatnie opisuje rzeczywistość, bez żadnych logicznych paradoksów. Ale to nie jest pełne rozwiązanie problemu. Stwierdzenie Einsteina o nieodpartej prędkości światła jest bardzo podobne do aporii Zenona „Achilles i żółw”. Musimy jeszcze przestudiować, przemyśleć i rozwiązać ten problem. A rozwiązania należy szukać nie w nieskończenie dużych liczbach, ale w jednostkach miary.
Kolejna interesująca aporia Zenona opowiada o lecącej strzałce:
Lecąca strzała jest nieruchoma, ponieważ w każdej chwili jest w spoczynku, a ponieważ jest w spoczynku w każdej chwili, jest zawsze w spoczynku.
W tej aporii paradoks logiczny zostaje przezwyciężony w bardzo prosty sposób - wystarczy wyjaśnić, że w każdym momencie lecąca strzała znajduje się w spoczynku w różnych punktach przestrzeni, co w rzeczywistości jest ruchem. Należy tutaj zwrócić uwagę na jeszcze jedną kwestię. Na podstawie jednego zdjęcia samochodu na drodze nie da się określić ani faktu jego ruchu, ani odległości do niego. Aby ustalić, czy samochód się porusza, potrzebne są dwa zdjęcia wykonane z tego samego punktu w różnych momentach w czasie, ale nie można określić odległości od nich. Aby określić odległość do samochodu, potrzebujesz dwóch zdjęć zrobionych z różnych punktów przestrzeni w tym samym momencie, ale na ich podstawie nie można ustalić faktu ruchu (oczywiście nadal potrzebujesz dodatkowych danych do obliczeń, trygonometria ci pomoże ). To na co chcę zwrócić szczególną uwagę to to, że dwa punkty w czasie i dwa punkty w przestrzeni to różne rzeczy, których nie należy mylić, gdyż dają odmienne możliwości badawcze.
środa, 4 lipca 2018 r
Różnice między zestawem a zestawem wielokrotnym są bardzo dobrze opisane w Wikipedii. Zobaczmy.
Jak widać „w zestawie nie mogą znajdować się dwa identyczne elementy”, ale jeśli w zestawie znajdują się identyczne elementy, taki zbiór nazywa się „multizbiorem”. Rozsądne istoty nigdy nie zrozumieją tak absurdalnej logiki. To jest poziom gadających papug i tresowanych małp, które nie mają inteligencji od słowa „całkowicie”. Matematycy zachowują się jak zwykli trenerzy, wmawiając nam swoje absurdalne pomysły.
Dawno, dawno temu inżynierowie, którzy zbudowali most, pływali łodzią pod mostem podczas testowania mostu. Jeśli most się zawali, przeciętny inżynier zginął pod gruzami swojego dzieła. Jeśli most wytrzymał obciążenie, utalentowany inżynier zbudował inne mosty.
Niezależnie od tego, jak matematycy ukrywają się za zwrotem „pamiętaj, jestem w domu” lub raczej „matematyka bada pojęcia abstrakcyjne”, istnieje jedna pępowina, która nierozerwalnie łączy ich z rzeczywistością. Ta pępowina to pieniądze. Zastosujmy matematyczną teorię mnogości do samych matematyków.
Bardzo dobrze uczyliśmy się matematyki, a teraz siedzimy przy kasie i wypłacamy pensje. Tak więc matematyk przychodzi do nas po swoje pieniądze. Odliczamy mu całą kwotę i układamy ją na naszym stole w różnych stosach, do których wkładamy banknoty o tym samym nominale. Następnie bierzemy po jednym rachunku z każdego stosu i dajemy matematykowi jego „matematyczny zestaw wynagrodzeń”. Wyjaśnijmy matematykowi, że resztę rachunków otrzyma dopiero wtedy, gdy udowodni, że zbiór bez identycznych elementów nie jest równy zbiorowi z identycznymi elementami. Tutaj zaczyna się zabawa.
Przede wszystkim sprawdzi się logika posłów: „Można to zastosować do innych, ale nie do mnie!” Wtedy zaczną nas uspokajać, że banknoty o tym samym nominale mają różne numery banknotów, a co za tym idzie, nie można ich uważać za te same elementy. OK, policzmy pensje w monetach - na monetach nie ma cyfr. Tutaj matematyk zacznie gorączkowo przypominać sobie fizykę: różne monety mają różną ilość brudu, struktura kryształów i układ atomów jest dla każdej monety unikalna...
I teraz mam najciekawsze pytanie: gdzie jest granica, za którą elementy multizbioru zamieniają się w elementy zbioru i odwrotnie? Taka linia nie istnieje – o wszystkim decydują szamani, nauka nawet nie jest bliska kłamstwa.
Popatrz tutaj. Wybieramy stadiony piłkarskie o tej samej powierzchni boiska. Pola pól są takie same - co oznacza, że mamy multizbiór. Ale jeśli spojrzymy na nazwy tych samych stadionów, otrzymamy wiele, ponieważ nazwy są różne. Jak widać, ten sam zbiór elementów jest jednocześnie zbiorem i multizbiorem. Który jest poprawny? I tu matematyk-szaman-sostrzysta wyciąga z rękawa asa atutowego i zaczyna nam opowiadać albo o zestawie, albo o wielokrotności. W każdym razie przekona nas, że ma rację.
Aby zrozumieć, jak współcześni szamani operują teorią mnogości, wiążąc ją z rzeczywistością, wystarczy odpowiedzieć na jedno pytanie: czym różnią się elementy jednego zbioru od elementów innego zbioru? Pokażę ci, bez żadnego „wyobrażalnego jako pojedyncza całość” lub „niewyobrażalnego jako pojedyncza całość”.
Niedziela, 18 marca 2018 r
Suma cyfr liczby to taniec szamanów z tamburynem, który nie ma nic wspólnego z matematyką. Tak, na lekcjach matematyki uczy się nas znajdować sumę cyfr liczby i posługiwać się nią, ale po to są szamani, aby uczyć swoich potomków swoich umiejętności i mądrości, w przeciwnym razie szamani po prostu wymrą.
Czy potrzebujesz dowodu? Otwórz Wikipedię i spróbuj znaleźć stronę „Suma cyfr liczby”. Ona nie istnieje. W matematyce nie ma wzoru, za pomocą którego można by znaleźć sumę cyfr dowolnej liczby. Przecież liczby to symbole graficzne, za pomocą których piszemy liczby, a w języku matematyki zadanie brzmi tak: „Znajdź sumę symboli graficznych reprezentujących dowolną liczbę”. Matematycy nie potrafią rozwiązać tego problemu, ale szamani mogą to zrobić z łatwością.
Zastanówmy się, co i jak zrobić, aby znaleźć sumę cyfr danej liczby. I tak otrzymamy liczbę 12345. Co należy zrobić, aby znaleźć sumę cyfr tej liczby? Rozważmy wszystkie kroki w kolejności.
1. Zapisz numer na kartce papieru. Co my zrobiliśmy? Przekonwertowaliśmy liczbę na graficzny symbol liczbowy. To nie jest operacja matematyczna.
2. Jeden powstały obraz wycinamy na kilka obrazków zawierających indywidualne liczby. Cięcie obrazu nie jest operacją matematyczną.
3. Zamień poszczególne symbole graficzne na liczby. To nie jest operacja matematyczna.
4. Dodaj powstałe liczby. Teraz to jest matematyka.
Suma cyfr liczby 12345 wynosi 15. Są to „kursy krojenia i szycia”, prowadzone przez szamanów, z których korzystają matematycy. Ale to nie wszystko.
Z matematycznego punktu widzenia nie ma znaczenia, w jakim systemie liczbowym zapiszemy liczbę. Zatem w różnych systemach liczbowych suma cyfr tej samej liczby będzie inna. W matematyce system liczbowy jest oznaczony jako indeks dolny po prawej stronie liczby. Przy dużej liczbie 12345, nie chcę oszukiwać głowy, rozważmy liczbę 26 z artykułu o. Zapiszmy tę liczbę w systemie binarnym, ósemkowym, dziesiętnym i szesnastkowym. Nie będziemy patrzeć na każdy krok pod mikroskopem, już to zrobiliśmy. Spójrzmy na wynik.
Jak widać, w różnych systemach liczbowych suma cyfr tej samej liczby jest inna. Wynik ten nie ma nic wspólnego z matematyką. To tak, jakby wyznaczając pole prostokąta w metrach i centymetrach, otrzymałbyś zupełnie inne wyniki.
Zero wygląda tak samo we wszystkich systemach liczbowych i nie ma sumy cyfr. To kolejny argument przemawiający za tym, że. Pytanie do matematyków: jak w matematyce oznacza się coś, co nie jest liczbą? Co, dla matematyków nie istnieje nic poza liczbami? Mogę na to pozwolić szamanom, ale nie naukowcom. Rzeczywistość to nie tylko liczby.
Uzyskany wynik należy uznać za dowód, że systemy liczbowe są jednostkami miary liczb. W końcu nie możemy porównywać liczb o różnych jednostkach miary. Jeśli te same działania z różnymi jednostkami miary tej samej wielkości prowadzą do różnych wyników po ich porównaniu, to nie ma to nic wspólnego z matematyką.
Czym jest prawdziwa matematyka? Dzieje się tak wtedy, gdy wynik operacji matematycznej nie zależy od wielkości liczby, użytej jednostki miary i tego, kto wykonuje tę czynność.
Oh! Czy to nie jest damska toaleta?
- Młoda kobieta! To laboratorium do badania niedefilicznej świętości dusz podczas ich wznoszenia się do nieba! Aureola na górze i strzałka w górę. Jaka inna toaleta?
Kobieta... Aureola na górze i strzałka w dół oznaczają mężczyznę.
Jeśli takie dzieło sztuki projektowej przelatuje Ci przed oczami kilka razy dziennie,
Nic więc dziwnego, że nagle w swoim samochodzie znajdujesz dziwną ikonę:
Osobiście staram się widzieć minus cztery stopnie u osoby robiącej kupę (jeden obrazek) (kompozycja kilku obrazków: znak minus, cyfra cztery, oznaczenie stopni). I nie sądzę, że ta dziewczyna jest głupia, która nie zna fizyki. Ma po prostu silny stereotyp postrzegania obrazów graficznych. A matematycy uczą nas tego cały czas. Oto przykład.
1A nie oznacza „minus cztery stopnie” ani „jeden a”. To jest „kupujący człowiek” lub liczba „dwadzieścia sześć” w zapisie szesnastkowym. Osoby, które stale pracują w tym systemie liczbowym, automatycznie postrzegają cyfrę i literę jako jeden symbol graficzny.
Pojęcia sinus (), cosinus (), tangens (), cotangens () są nierozerwalnie związane z pojęciem kąta. Aby dobrze zrozumieć te, na pierwszy rzut oka złożone, pojęcia (które u wielu uczniów wywołują przerażenie) i upewnić się, że „diabeł nie jest taki straszny, jak go malują”, zacznijmy od bardzo początku i rozumiem pojęcie kąta.
Pojęcie kąta: radian, stopień
Spójrzmy na zdjęcie. Wektor „obrócił się” względem punktu o określoną wartość. Zatem miara tego obrotu względem pozycji początkowej będzie wynosić narożnik.
Co jeszcze musisz wiedzieć o pojęciu kąta? Cóż, oczywiście, jednostki kąta!
Kąt, zarówno w geometrii, jak i trygonometrii, można mierzyć w stopniach i radianach.
Kąt (jeden stopień) to kąt środkowy okręgu oparty na łuku kołowym równym części koła. Zatem całe koło składa się z „kawałków” łuków kołowych lub kąt opisany przez okrąg jest równy.

Oznacza to, że powyższy rysunek pokazuje kąt równy, to znaczy kąt ten opiera się na łuku kołowym wielkości obwodu.
Kąt w radianach to kąt środkowy okręgu oparty na łuku kołowym, którego długość jest równa promieniowi okręgu. Cóż, wpadłeś na to? Jeśli nie, rozwiążmy to na podstawie rysunku.

Zatem rysunek pokazuje kąt równy radianowi, to znaczy kąt ten opiera się na łuku kołowym, którego długość jest równa promieniowi koła (długość jest równa długości lub promień jest równy promieniowi długość łuku). Zatem długość łuku oblicza się ze wzoru:
Gdzie jest kąt środkowy w radianach.
Cóż, wiedząc to, czy możesz odpowiedzieć, ile radianów zawiera się w kącie opisanym przez okrąg? Tak, w tym celu musisz pamiętać wzór na obwód. Tutaj jest:
Cóż, teraz skorelujmy te dwa wzory i przekonajmy się, że kąt opisany przez okrąg jest równy. Oznacza to, że korelując wartość w stopniach i radianach, otrzymamy to. Odpowiednio, . Jak widać, w przeciwieństwie do „stopni”, słowo „radian” zostało pominięte, ponieważ jednostka miary jest zwykle jasna z kontekstu.
Ile jest tam radianów? Zgadza się!
Rozumiem? Następnie napraw to:
Masz trudności? Potem spójrz odpowiedzi:
Trójkąt prostokątny: sinus, cosinus, tangens, cotangens kąta
Opracowaliśmy więc pojęcie kąta. Ale czym jest sinus, cosinus, tangens i cotangens kąta? Rozwiążmy to. Aby to zrobić, pomoże nam trójkąt prostokątny.

Jak nazywają się boki trójkąta prostokątnego? Zgadza się, przeciwprostokątna i nogi: przeciwprostokątna to strona leżąca naprzeciwko kąta prostego (w naszym przykładzie jest to bok); nogami są dwie pozostałe boki i (te sąsiadujące z kątem prostym), a jeśli weźmiemy pod uwagę nogi w odniesieniu do kąta, to noga jest sąsiednią nogą, a noga jest przeciwna. A więc teraz odpowiedzmy na pytanie: czym jest sinus, cosinus, tangens i cotangens kąta?
Sinus kąta- jest to stosunek przeciwnej (odległej) nogi do przeciwprostokątnej.
W naszym trójkącie.
Cosinus kąta- jest to stosunek sąsiedniej (bliskiej) nogi do przeciwprostokątnej.
W naszym trójkącie.
Tangens kąta- jest to stosunek strony przeciwnej (odległej) do strony sąsiedniej (bliskiej).
W naszym trójkącie.
Kotansa kąta- jest to stosunek sąsiedniej (bliskiej) nogi do przeciwnej (dalekiej).
W naszym trójkącie.
Te definicje są konieczne Pamiętać! Aby łatwiej było zapamiętać, na którą nogę podzielić, musisz to jasno zrozumieć tangens I cotangens tylko nogi siedzą, a przeciwprostokątna pojawia się tylko w Zatoka I cosinus. A potem możesz wymyślić łańcuch skojarzeń. Na przykład ten:
Cosinus → dotyk → dotyk → sąsiad;
Cotangens → dotyk → dotyk → sąsiad.
Przede wszystkim trzeba pamiętać, że sinus, cosinus, tangens i cotangens, ponieważ stosunki boków trójkąta nie zależą od długości tych boków (pod tym samym kątem). Nie wierz? Następnie upewnij się, patrząc na zdjęcie:

Rozważmy na przykład cosinus kąta. Z definicji z trójkąta: , ale cosinus kąta możemy obliczyć z trójkąta: . Widzisz, długości boków są różne, ale wartość cosinusa jednego kąta jest taka sama. Zatem wartości sinusa, cosinusa, tangensa i cotangensu zależą wyłącznie od wielkości kąta.
Jeśli rozumiesz definicje, śmiało je skonsoliduj!
Dla trójkąta pokazanego na poniższym rysunku znajdujemy.

No cóż, zrozumiałeś? Następnie spróbuj sam: oblicz to samo dla kąta.
Okrąg jednostkowy (trygonometryczny).
Rozumiejąc pojęcia stopni i radianów, rozważaliśmy okrąg o promieniu równym. Taki okrąg nazywa się pojedynczy. Będzie bardzo przydatny podczas nauki trygonometrii. Dlatego przyjrzyjmy się temu nieco bardziej szczegółowo.

Jak widać, okrąg ten jest zbudowany w kartezjańskim układzie współrzędnych. Promień okręgu jest równy jeden, natomiast środek okręgu leży w początku współrzędnych, początkowe położenie wektora promienia jest ustalone wzdłuż dodatniego kierunku osi (w naszym przykładzie jest to promień).
Każdy punkt na okręgu odpowiada dwóm liczbom: współrzędnej osi i współrzędnej osi. Jakie są te numery współrzędnych? I w ogóle, co one mają wspólnego z poruszanym tematem? Aby to zrobić, musimy pamiętać o rozważanym trójkącie prostokątnym. Na powyższym rysunku widać dwa całe trójkąty prostokątne. Rozważmy trójkąt. Jest prostokątny, ponieważ jest prostopadły do osi.
Czemu równy jest trójkąt? Zgadza się. Ponadto wiemy, że jest to promień okręgu jednostkowego, co oznacza . Podstawmy tę wartość do naszego wzoru na cosinus. Oto, co się dzieje:
Czemu równy jest trójkąt? Ależ oczywiście, ! Zastąp wartość promienia tym wzorem i uzyskaj:
Czy możesz więc powiedzieć, jakie współrzędne ma punkt należący do okręgu? No cóż, nie ma mowy? A co jeśli zdasz sobie z tego sprawę i okażesz się tylko liczbami? Której współrzędnej odpowiada? Cóż, oczywiście, współrzędne! I jakiej współrzędnej to odpowiada? Zgadza się, współrzędne! Zatem kropka.

Czym zatem są i czym się równają? Zgadza się, użyjmy odpowiednich definicji tangensu i cotangensu i otrzymajmy to, a.
A co jeśli kąt będzie większy? Na przykład tak jak na tym obrazku:

Co się zmieniło w tym przykładzie? Rozwiążmy to. Aby to zrobić, zwróćmy się ponownie do trójkąta prostokątnego. Rozważmy trójkąt prostokątny: kąt (w sąsiedztwie kąta). Jakie są wartości sinusa, cosinusa, tangens i cotangens dla kąta? Zgadza się, stosujemy się do odpowiednich definicji funkcji trygonometrycznych:
Cóż, jak widać, wartość sinusa kąta nadal odpowiada współrzędnej; wartość cosinusa kąta - współrzędna; oraz wartości tangensa i cotangensu do odpowiednich stosunków. Zależności te dotyczą zatem dowolnego obrotu wektora promienia.
Wspomniano już, że położenie początkowe wektora promienia leży wzdłuż dodatniego kierunku osi. Do tej pory obracaliśmy ten wektor w kierunku przeciwnym do ruchu wskazówek zegara, ale co się stanie, jeśli obrócimy go w kierunku zgodnym z ruchem wskazówek zegara? Nic nadzwyczajnego, również otrzymasz kąt o określonej wartości, ale tylko on będzie ujemny. Zatem obracając wektor promienia w kierunku przeciwnym do ruchu wskazówek zegara, otrzymujemy kąty dodatnie, a przy obrocie w kierunku zgodnym z ruchem wskazówek zegara - negatywny.
Wiemy więc, że cały obrót wektora promienia wokół okręgu wynosi lub. Czy można obrócić wektor promienia do lub do? Oczywiście, że możesz! Zatem w pierwszym przypadku wektor promienia wykona jeden pełny obrót i zatrzyma się w pozycji lub.
W drugim przypadku wektor promienia wykona trzy pełne obroty i zatrzyma się w pozycji lub.
Zatem z powyższych przykładów możemy wywnioskować, że kąty różniące się lub (gdzie jest dowolną liczbą całkowitą) odpowiadają temu samemu położeniu wektora promienia.
Poniższy rysunek przedstawia kąt. Ten sam obraz odpowiada narożnikowi itp. Listę tę można ciągnąć w nieskończoność. Wszystkie te kąty można zapisać za pomocą ogólnego wzoru lub (gdzie jest dowolną liczbą całkowitą)

Teraz znając definicje podstawowych funkcji trygonometrycznych i korzystając z okręgu jednostkowego spróbuj odpowiedzieć jakie to są wartości:
Oto okrąg jednostkowy, który Ci pomoże:

Masz trudności? Więc rozwiążmy to. Wiemy więc, że:
Stąd wyznaczamy współrzędne punktów odpowiadających pewnym miarom kąta. Cóż, zacznijmy po kolei: kąt w odpowiada punktowi o współrzędnych, zatem:
Nie istnieje;
Dalej, trzymając się tej samej logiki, dowiadujemy się, że rogi odpowiadają odpowiednio punktom o współrzędnych. Wiedząc o tym, łatwo jest określić wartości funkcji trygonometrycznych w odpowiednich punktach. Najpierw spróbuj sam, a potem sprawdź odpowiedzi.
Odpowiedzi:
W ten sposób możemy sporządzić następującą tabelę:

Nie ma potrzeby zapamiętywania wszystkich tych wartości. Wystarczy pamiętać o zgodności współrzędnych punktów na okręgu jednostkowym z wartościami funkcji trygonometrycznych:
Ale wartości funkcji trygonometrycznych kątów w i, podane w poniższej tabeli, trzeba pamiętać:

Nie bój się, teraz pokażemy Ci jeden przykład dość proste do zapamiętania odpowiednich wartości:
Aby skorzystać z tej metody, należy pamiętać o wartościach sinusa dla wszystkich trzech miar kąta (), a także o wartości tangensa kąta. Znając te wartości, dość łatwo jest przywrócić całą tabelę - wartości cosinusów przenoszone są zgodnie ze strzałkami, czyli:
Wiedząc o tym, możesz przywrócić wartości. Licznik „ ” będzie zgodny i mianownik „ ” będzie zgodny. Wartości cotangens są przenoszone zgodnie ze strzałkami wskazanymi na rysunku. Jeśli to zrozumiesz i zapamiętasz diagram ze strzałkami, wystarczy zapamiętać wszystkie wartości z tabeli.
Współrzędne punktu na okręgu
Czy można znaleźć punkt (jego współrzędne) na okręgu, znając współrzędne środka okręgu, jego promień i kąt obrotu?
Oczywiście, że możesz! Wyciągnijmy to ogólny wzór na znalezienie współrzędnych punktu.
Na przykład oto okrąg przed nami:

Wiemy, że punkt jest środkiem okręgu. Promień okręgu jest równy. Konieczne jest znalezienie współrzędnych punktu uzyskanego poprzez obrót punktu o stopnie.
Jak widać na rysunku, współrzędna punktu odpowiada długości odcinka. Długość odcinka odpowiada współrzędnej środka okręgu, czyli jest równa. Długość odcinka można wyrazić korzystając z definicji cosinusa:
Następnie mamy to dla współrzędnej punktu.
Stosując tę samą logikę, znajdujemy wartość współrzędnej y punktu. Zatem,
Ogólnie rzecz biorąc, współrzędne punktów określają wzory:
Współrzędne środka okręgu,
Promień okręgu,
Kąt obrotu promienia wektora.
Jak widać, dla rozważanego okręgu jednostkowego wzory te są znacznie zmniejszone, ponieważ współrzędne środka są równe zeru, a promień jest równy jeden:
Cóż, wypróbujmy te formuły, ćwicząc znajdowanie punktów na okręgu?
1. Znajdź współrzędne punktu na okręgu jednostkowym uzyskanym poprzez obrót punktu.
2. Znajdź współrzędne punktu na okręgu jednostkowym uzyskanym poprzez obrót punktu.
3. Znajdź współrzędne punktu na okręgu jednostkowym uzyskanym poprzez obrót punktu.
4. Punkt jest środkiem okręgu. Promień okręgu jest równy. Konieczne jest znalezienie współrzędnych punktu uzyskanego poprzez obrót początkowego wektora promienia o.
5. Punkt jest środkiem okręgu. Promień okręgu jest równy. Konieczne jest znalezienie współrzędnych punktu uzyskanego poprzez obrót początkowego wektora promienia o.
Masz problem ze znalezieniem współrzędnych punktu na okręgu?
Rozwiąż te pięć przykładów (lub bądź dobry w ich rozwiązywaniu), a nauczysz się je znajdować!
PODSUMOWANIE I PODSTAWOWE FORMUŁY
Sinus kąta to stosunek przeciwnej (dalekiej) nogi do przeciwprostokątnej.
Cosinus kąta to stosunek sąsiedniej (bliskiej) nogi do przeciwprostokątnej.
Tangens kąta to stosunek strony przeciwnej (dalekiej) do strony sąsiedniej (bliskiej).
Cotangens kąta to stosunek sąsiedniej (bliskiej) strony do przeciwnej (dalekiej) strony.
No cóż, temat się skończył. Jeśli czytasz te słowa, oznacza to, że jesteś bardzo fajny.
Bo tylko 5% ludzi jest w stanie samodzielnie coś opanować. A jeśli przeczytasz do końca, to jesteś w tych 5%!
Teraz najważniejsza rzecz.
Zrozumiełeś teorię na ten temat. I powtarzam, to... to jest po prostu super! Już jesteś lepszy od zdecydowanej większości Twoich rówieśników.
Problem w tym, że to może nie wystarczyć...
Po co?
Za pomyślne zdanie egzaminu Unified State Exam, za rozpoczęcie studiów z ograniczonym budżetem i, CO NAJWAŻNIEJSZE, za całe życie.
Nie będę Cię do niczego przekonywał, powiem tylko jedno...
Ludzie, którzy otrzymali dobre wykształcenie, zarabiają znacznie więcej niż ci, którzy go nie otrzymali. To jest statystyka.
Ale to nie jest najważniejsze.
Najważniejsze, że są BARDZIEJ SZCZĘŚLIWI (są takie badania). Być może dlatego, że otwiera się przed nimi o wiele więcej możliwości i życie staje się jaśniejsze? nie wiem...
Ale pomyśl samodzielnie...
Czego potrzeba, aby na egzaminie Unified State Exam wypaść lepiej od innych i ostatecznie… być szczęśliwszym?
Zdobądź rękę, rozwiązując problemy z tego tematu.
Podczas egzaminu nie będziesz proszony o zadawanie teorii.
Będziesz potrzebować rozwiązywać problemy z czasem.
A jeśli ich nie rozwiązałeś (DUŻO!), na pewno popełnisz gdzieś głupi błąd lub po prostu nie będziesz miał czasu.
To jak w sporcie – trzeba to powtarzać wiele razy, żeby na pewno wygrać.
Znajdź kolekcję gdziekolwiek chcesz, koniecznie z rozwiązaniami, szczegółową analizą i decyduj, decyduj, decyduj!
Możesz skorzystać z naszych zadań (opcjonalnie) i oczywiście je polecamy.
Aby lepiej radzić sobie z naszymi zadaniami, musisz pomóc przedłużyć żywotność podręcznika YouClever, który aktualnie czytasz.
Jak? Istnieją dwie opcje:
- Odblokuj wszystkie ukryte zadania w tym artykule -
- Odblokuj dostęp do wszystkich ukrytych zadań we wszystkich 99 artykułach podręcznika - Kup podręcznik - 499 RUR
Tak, w naszym podręczniku mamy 99 takich artykułów i dostęp do wszystkich zadań oraz wszystkich ukrytych w nich tekstów można od razu otworzyć.
Dostęp do wszystkich ukrytych zadań jest zapewniony przez CAŁY okres istnienia witryny.
Podsumowując...
Jeśli nie podobają Ci się nasze zadania, znajdź inne. Tylko nie poprzestawaj na teorii.
„Rozumiem” i „Umiem rozwiązać” to zupełnie różne umiejętności. Potrzebujesz obu.
Znajdź problemy i rozwiąż je!