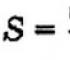Wzór na moduł przemieszczenia ciała w ruchu jednostajnie przyspieszonym. Równanie rzutowania przemieszczeń

Strona 8 z 12

§ 7. Ruch z równomiernie przyspieszonym
ruch prostoliniowy

1. Korzystając z wykresu prędkości w funkcji czasu, możesz uzyskać wzór na poruszanie ciałem ruchem jednostajnym prostoliniowym.

Rysunek 30 przedstawia wykres rzutu prędkości ruchu równomiernego na oś x od czasu. Jeśli w pewnym momencie ustawimy prostopadłą do osi czasu C, wtedy otrzymujemy prostokąt OABC. Powierzchnia tego prostokąta jest równa iloczynowi boków OA oraz OC. Ale długość boku OA jest równe v x i długość boku OC - T, W związku z tym S = v x t. Iloczyn rzutu prędkości na oś x a czas jest równy rzutowi przemieszczenia, tj. s x = v x t.

W ten sposób, rzut przemieszczenia dla jednostajnego ruchu prostoliniowego jest liczbowo równy powierzchni prostokąta ograniczonego osiami współrzędnych, wykresem prędkości i prostopadłą podniesioną do osi czasu.

2. W podobny sposób otrzymujemy wzór na rzut przemieszczenia w ruchu prostoliniowym jednostajnie przyspieszonym. W tym celu korzystamy z wykresu zależności rzutu prędkości na oś x od czasu (ryc. 31). Wybierz mały obszar na wykresie ab i upuść prostopadłe z punktów a oraz b na osi czasu. Jeżeli przedział czasu D T, odpowiadający sekcji płyta CD na osi czasu jest mała, to możemy założyć, że prędkość nie zmienia się w tym czasie i ciało porusza się jednostajnie. W tym przypadku postać taksówkarz niewiele różni się od prostokąta, a jego powierzchnia jest liczbowo równa rzutowi ruchu ciała w czasie odpowiadającym segmentowi płyta CD.

Całą figurę można rozbić na takie paski OABC, a jego pole będzie równe sumie pól wszystkich pasów. Dlatego projekcja ruchu ciała w czasie T liczbowo równa powierzchni trapezu OABC. Z kursu geometrii wiesz, że powierzchnia trapezu jest równa iloczynowi połowy sumy jego podstaw i wysokości: S= (OA + pne)OC.

Jak widać na rysunku 31, OA = v 0x , pne = v x, OC = T. Wynika z tego, że rzut przemieszczenia wyraża się wzorem: s x= (v x + v 0x)T.

Przy jednostajnie przyspieszonym ruchu prostoliniowym prędkość ciała w dowolnym momencie jest równa v x = v 0x + a x t, W związku z tym, s x = (2v 0x + a x t)T.

Stąd:

Aby otrzymać równanie ruchu ciała, do wzoru na rzut przemieszczenia podstawiamy jego wyrażenie przez różnicę współrzędnych s x = x – x 0 .

Otrzymujemy: x – x 0 = v 0x T+ , lub

x = x 0 + v 0x T + .

Zgodnie z równaniem ruchu można w każdej chwili wyznaczyć współrzędną ciała, jeśli znana jest współrzędna początkowa, prędkość początkowa i przyspieszenie ciała.

3. W praktyce często pojawiają się problemy, w których konieczne jest znalezienie przemieszczenia ciała podczas ruchu prostoliniowego jednostajnie przyspieszonego, ale czas ruchu jest nieznany. W takich przypadkach stosuje się inny wzór rzutowania przemieszczeń. Chodźmy po to.

Ze wzoru na rzut prędkości ruchu prostoliniowego jednostajnie przyspieszonego v x = v 0x + a x t wyraźmy czas:

T = .

Podstawiając to wyrażenie do wzoru rzutowania przemieszczeń, otrzymujemy:

s x = v 0x + .

Stąd:

s x = , lub
–= 2a x s x.

Jeżeli początkowa prędkość ciała wynosi zero, to:

2a x s x.

4. Przykład rozwiązania problemu

Narciarz zjeżdża ze zbocza góry ze stanu spoczynku z przyspieszeniem 0,5 m / s 2 w ciągu 20 s, a następnie porusza się po poziomym odcinku, dojeżdżając do przystanku 40 m. Z jakim przyspieszeniem poruszał się po pozioma powierzchnia? Jaka jest długość zbocza góry?

Dany:

Rozwiązanie

v 01 = 0

a 1 = 0,5 m/s 2

T 1 = 20 s

s 2 = 40 m

v 2 = 0

Ruch narciarza składa się z dwóch etapów: w pierwszym etapie, schodząc ze zbocza góry, narciarz porusza się z rosnącą prędkością w wartości bezwzględnej; w drugim etapie, poruszając się po poziomej powierzchni, jego prędkość maleje. Wartości związane z pierwszym etapem ruchu będą zapisywane z indeksem 1, a związane z drugim etapem z indeksem 2.

a 2?

s 1?

Połączymy układ odniesienia z Ziemią, oś x na każdym etapie ruchu skierujmy się w kierunku prędkości narciarza (rys. 32).

Napiszmy równanie na prędkość narciarza pod koniec zjazdu z góry:

v 1 = v 01 + a 1 T 1 .

W rzutach na oś x otrzymujemy: v 1x = a 1x T. Ponieważ rzuty prędkości i przyspieszenia na oś x są dodatnie, moduł prędkości narciarza wynosi: v 1 = a 1 T 1 .

Napiszmy równanie odnoszące się do rzutów prędkości, przyspieszenia i ruchu narciarza w drugiej fazie ruchu:

–= 2a 2x s 2x .

Biorąc pod uwagę, że początkowa prędkość narciarza na tym etapie ruchu jest równa jego końcowej prędkości na pierwszym etapie

v 02 = v 1 , v 2x= 0 otrzymujemy

– = –2a 2 s 2 ; (a 1 T 1) 2 = 2a 2 s 2 .

Stąd a 2 = ;

a 2 == 0,125 m / s 2.

Moduł ruchu narciarza w pierwszej fazie ruchu jest równy długości górskiego stoku. Napiszmy równanie przemieszczenia:

s 1x = v 01x T + .

Stąd długość zbocza góry wynosi s 1 = ;

s 1 == 100 m.

Odpowiedź: a 2 \u003d 0,125 m / s 2; s 1 = 100m.

Pytania do samodzielnego zbadania

1. Jak wynika z wykresu rzutu prędkości jednostajnego ruchu prostoliniowego na oś x

2. Jak wynika z wykresu rzutu prędkości ruchu prostoliniowego jednostajnie przyspieszonego na oś x od czasu do określenia rzutu przemieszczenia ciała?

3. Jakiego wzoru używa się do obliczenia rzutu przemieszczenia ciała podczas ruchu prostoliniowego jednostajnie przyspieszonego?

4. Jakiego wzoru używa się do obliczenia rzutu przemieszczenia ciała poruszającego się jednostajnie przyspieszonym i prostoliniowym, jeśli początkowa prędkość ciała wynosi zero?

Zadanie 7

1. Jaki jest moduł przemieszczenia samochodu w ciągu 2 minut, jeśli w tym czasie jego prędkość zmieniła się z 0 do 72 km/h? Jakie są współrzędne samochodu w tym czasie? T= 2 min? Zakłada się, że początkowa współrzędna wynosi zero.

2. Pociąg porusza się z prędkością początkową 36 km/hi przyspieszeniem 0,5 m/s2. Jakie jest przemieszczenie pociągu w ciągu 20 s i jego współrzędna w tej chwili? T= 20 s, jeśli współrzędna początkowa pociągu wynosi 20 m?

3. Jaki jest ruch rowerzysty przez 5 s po rozpoczęciu hamowania, jeśli jego prędkość początkowa podczas hamowania wynosi 10 m/s, a przyspieszenie 1,2 m/s 2? Jakie są współrzędne rowerzysty w czasie? T= 5 s, jeśli w początkowym momencie był on u początku?

4. Samochód jadący z prędkością 54 km/h zatrzymuje się przy hamowaniu na 15 sekund. Jaki jest moduł przemieszczenia samochodu podczas hamowania?

5. Z dwóch osiedli oddalonych od siebie o 2 km zbliżają się do siebie dwa samochody. Prędkość początkowa jednego samochodu wynosi 10 m/s, a przyspieszenie 0,2 m/s 2 , prędkość początkowa drugiego 15 m/s, a przyspieszenie 0,2 m/s 2 . Określ czas i współrzędne miejsca spotkania samochodów.

Laboratorium #1

Badanie jednostajnie przyspieszone
ruch prostoliniowy

Cel:

nauczyć się mierzyć przyspieszenie w jednostajnie przyspieszonym ruchu prostoliniowym; eksperymentalnie ustalić stosunek torów pokonywanych przez ciało podczas jednostajnie przyspieszonego ruchu prostoliniowego w kolejnych równych odstępach czasu.

Urządzenia i materiały:

zsyp, statyw, metalowa kula, stoper, taśma miernicza, metalowy cylinder.

Porządek pracy

1. Jeden koniec zsypu zamocuj w stopie statywu tak, aby tworzył mały kąt z powierzchnią stołu, na drugim końcu włóż do niego metalowy walec.

2. Zmierz drogi pokonywane przez kulkę w 3 kolejnych odstępach czasu równych 1 s każdy. Można to zrobić na różne sposoby. Na rynnie można nanosić kredą oznaczenia, ustalając pozycję kuli w punktach czasowych równych 1 s, 2 s, 3 s oraz mierzyć odległości s_ między tymi znakami. Możliwe jest wypuszczanie piłki za każdym razem z tej samej wysokości, aby zmierzyć ścieżkę s, minął go najpierw w 1 s, potem w 2 s i w 3 s, a następnie oblicz drogę przebytą przez piłkę w drugiej i trzeciej sekundzie. Zapisz wyniki pomiarów w tabeli 1.

3. Znajdź stosunek drogi przebytej w drugiej sekundzie do drogi przebytej w pierwszej sekundzie oraz drogi przebytej w trzeciej sekundzie do drogi przebytej w pierwszej sekundzie. Wyciągnij wniosek.

4. Zmierz czas, jaki piłka przebyła po rynnie i przebytą przez nią odległość. Oblicz jego przyspieszenie ze wzoru s = .

5. Wykorzystując uzyskaną eksperymentalnie wartość przyspieszenia oblicz drogi, jakie musi pokonać kulka w pierwszej, drugiej i trzeciej sekundzie swojego ruchu. Wyciągnij wniosek.

Tabela 1

numer doświadczenia

Dane eksperymentalne

Wyniki teoretyczne

Czas T , Z

Ścieżka , cm

Czas t , Z

Ścieżka

s, cm

Przyspieszenie a, cm/s2

CzasT, Z

Ścieżka , cm

Prędkość (v) jest wielkością fizyczną, liczbowo równą ścieżce (ścieżkom) przebytej przez ciało w jednostce czasu (t).

Ścieżka

Ścieżka (S) - długość trajektorii, po której poruszało się ciało, jest liczbowo równa iloczynowi prędkości (v) ciała i czasu (t) ruchu.

Czas podróży

Czas ruchu (t) jest równy stosunkowi drogi (S) przebytej przez ciało do prędkości (v) ruchu.

Średnia prędkość

Średnia prędkość (vav) jest równa stosunkowi sumy odcinków ścieżki (s 1 s 2, s 3, ...) przebytej przez ciało do przedziału czasu (t 1 + t 2 + t 3 + ...) dla której ta ścieżka została przebyta.

Średnia prędkość jest stosunkiem długości drogi przebytej przez ciało do czasu, w którym ta droga została przebyta.

Średnia prędkość poruszając się nierówno po linii prostej: jest to stosunek całej ścieżki do całkowitego czasu.

Dwa kolejne etapy z różnymi prędkościami: gdzie

Przy rozwiązywaniu problemów - ile etapów ruchu będzie tak wiele elementów:

Rzuty wektora przemieszczenia na osie współrzędnych

Rzut wektora przemieszczenia na oś OX:

Rzut wektora przemieszczenia na oś OY:

Rzut wektora na oś wynosi zero, jeśli wektor jest prostopadły do osi.

Znaki rzutów przemieszczeń: rzut uważa się za dodatni, jeśli ruch od rzutu początku wektora do rzutu końca następuje w kierunku osi, a ujemny, jeśli jest przeciwny do osi. W tym przykładzie

Moduł ruchu to długość wektora przemieszczenia:

Zgodnie z twierdzeniem Pitagorasa:

Projekcje ruchu i kąta nachylenia

W tym przykładzie:

Równanie współrzędnych (ogólnie):

Wektor promienia- wektor, którego początek pokrywa się z początkiem współrzędnych, a koniec - z pozycją ciała w danym momencie. Rzuty wektora promienia na osie współrzędnych wyznaczają współrzędne ciała w określonym czasie.

Wektor promienia pozwala ustawić położenie punktu materialnego w zadanym system odniesienia:

Ruch prostoliniowy jednostajny - definicja

Ruch prostoliniowy jednostajny- ruch, w którym ciało w równych odstępach czasu wykonuje równe przemieszczenia.

Prędkość w jednostajnym ruchu prostoliniowym. Prędkość jest wektorową wielkością fizyczną, która pokazuje, ile ruchu wykonuje ciało w jednostce czasu.

W formie wektorowej:

W rzutach na oś OX:

Dodatkowe jednostki prędkości:

1 km/h = 1000 m/3600 s,

1 km/s = 1000 m/s,

1 cm/s = 0,01 m/s,

1 m/min =1 m/60 s.

Urządzenie pomiarowe - prędkościomierz - pokazuje moduł prędkości.

Znak rzutu prędkości zależy od kierunku wektora prędkości i osi współrzędnych:

Wykres projekcji prędkości to zależność projekcji prędkości od czasu:

Wykres prędkości dla ruchu jednostajnego prostoliniowego- linia prosta równoległa do osi czasu (1, 2, 3).

Jeśli wykres leży nad osią czasu (.1), to ciało porusza się w kierunku osi OX. Jeśli wykres znajduje się pod osią czasu, to ciało porusza się w kierunku osi OX (2, 3).

Geometryczne znaczenie ruchu.

Przy jednostajnym ruchu prostoliniowym przemieszczenie określa wzór. Ten sam wynik uzyskamy, jeśli policzymy pole powierzchni figury pod wykresem prędkości w osiach. Tak więc, aby określić ścieżkę i moduł przemieszczenia podczas ruchu prostoliniowego, konieczne jest obliczenie obszaru figury pod wykresem prędkości w osiach:

Wykres projekcji przemieszczenia- zależność rzutu przemieszczenia od czasu.

Wykres projekcji przemieszczenia dla jednostajny ruch prostoliniowy- linia prosta wychodząca z początku (1, 2, 3).

Jeżeli linia prosta (1) leży nad osią czasu, to ciało porusza się w kierunku osi OX, a jeśli pod osią (2, 3), to w kierunku osi OX.

Im większa tangens nachylenia (1) wykresu, tym większy moduł prędkości.

Współrzędna działki- zależność współrzędnych ciała od czasu:

Współrzędne wykresu dla ruchu jednostajnego prostoliniowego - linie proste (1, 2, 3).

Jeśli z czasem współrzędna wzrośnie (1, 2), to ciało porusza się w kierunku osi OX; jeśli współrzędna zmniejszy się (3), to ciało porusza się w kierunku przeciwnym do osi OX.

Im większa tangens nachylenia (1), tym większy moduł prędkości.

Jeżeli wykresy współrzędnych dwóch ciał przecinają się, to od punktu przecięcia należy obniżyć prostopadłe do osi czasu i osi współrzędnych.

Względność ruchu mechanicznego

Przez względność rozumiemy zależność czegoś od wyboru układu odniesienia. Na przykład pokój jest względny; względny ruch i względna pozycja ciała.

Zasada sumowania przemieszczeń. Wektorowa suma przemieszczeń

gdzie jest przemieszczenie ciała względem ruchomego układu odniesienia (RFR); - ruch PSO względem ustalonego układu odniesienia (FRS); - ruch ciała względem ustalonego układu odniesienia (FRS).

Dodawanie wektorów:

Dodanie wektorów skierowanych wzdłuż jednej prostej:

Dodawanie wektorów prostopadłych do siebie

Zgodnie z twierdzeniem Pitagorasa

Wyprowadźmy wzór, który można wykorzystać do obliczenia rzutu wektora przemieszczenia ciała poruszającego się po linii prostej i jednostajnie przyspieszonego przez dowolny okres czasu. Aby to zrobić, przejdźmy do rysunku 14. Zarówno na rysunku 14 a, jak i na rysunku 14 b odcinek AC jest wykresem rzutu wektora prędkości ciała poruszającego się ze stałym przyspieszeniem a (przy prędkości początkowej v 0).

Ryż. 14. Rzut wektora przemieszczenia ciała poruszającego się po linii prostej i jednostajnie przyspieszonego jest liczbowo równy powierzchni S pod wykresem

Przypomnijmy, że przy prostoliniowym jednostajnym ruchu ciała rzut wektora przemieszczenia wykonany przez to ciało jest określony przez ten sam wzór, co obszar prostokąta zamkniętego pod wykresem projekcji wektora prędkości (patrz ryc. 6). Dlatego rzut wektora przemieszczenia jest liczbowo równy powierzchni tego prostokąta.

Udowodnijmy, że w przypadku ruchu prostoliniowego jednostajnie przyspieszonego rzut wektora przemieszczenia sx można wyznaczyć tym samym wzorem, co pole powierzchni figury zawartej między wykresem AC, osią Ot i odcinkami OA i BC, czyli w tym przypadku rzut wektora przemieszczenia liczbowo równego powierzchni figury pod wykresem prędkości. Aby to zrobić, na osi Ot (patrz ryc. 14, a) wybieramy mały przedział czasu db. Z punktów d i b rysujemy prostopadłe do osi Ot, aż przecinają się z wykresem rzutu wektora prędkości w punktach a i c.

Zatem przez okres czasu odpowiadający odcinkowi db prędkość ciała zmienia się od v ax do v cx.

Przez wystarczająco krótki czas rzut wektora prędkości zmienia się bardzo nieznacznie. Dlatego ruch ciała w tym okresie niewiele różni się od ruchu jednostajnego, czyli od ruchu ze stałą prędkością.

Na takie paski można podzielić całą powierzchnię figury OASV, która jest trapezem. Dlatego rzut wektora przemieszczenia sx dla przedziału czasu odpowiadającego segmentowi OB jest liczbowo równy powierzchni S trapezu OASV i jest określony tym samym wzorem, co ten obszar.

Zgodnie z zasadą podaną na szkolnych kursach geometrii powierzchnia trapezu jest równa iloczynowi połowy sumy jego podstaw i wysokości. Rysunek 14 b pokazuje, że podstawami trapezu OASV są odcinki OA = v 0x i BC = v x, a wysokość to odcinek OB = t. W związku z tym,

Ponieważ v x \u003d v 0x + a x t, a S \u003d s x, możemy napisać:

W ten sposób uzyskaliśmy wzór na obliczenie rzutu wektora przemieszczenia podczas ruchu jednostajnie przyspieszonego.

Stosując ten sam wzór, rzut wektora przemieszczenia oblicza się również, gdy ciało porusza się ze malejącym modułem prędkości, tylko w tym przypadku wektory prędkości i przyspieszenia będą skierowane w przeciwnych kierunkach, a więc ich rzuty będą miały różne znaki.

pytania

Korzystając z rysunku 14, a udowodnij, że rzut wektora przemieszczenia podczas ruchu jednostajnie przyspieszonego jest liczbowo równy powierzchni figury OASV.
Napisz równanie określające rzut wektora przemieszczenia ciała podczas jego prostoliniowego ruchu jednostajnie przyspieszonego.

Ćwiczenie 7

Strona 8 z 12

§ 7. Ruch z równomiernie przyspieszonym
ruch prostoliniowy

1. Korzystając z wykresu prędkości w funkcji czasu, możesz uzyskać wzór na poruszanie ciałem ruchem jednostajnym prostoliniowym.

Jak widać na rysunku 31, OA = v 0x , pne = v x, OC = T. Wynika z tego, że rzut przemieszczenia wyraża się wzorem: s x= (v x + v 0x)T.

Przy jednostajnie przyspieszonym ruchu prostoliniowym prędkość ciała w dowolnym momencie jest równa v x = v 0x + a x t, W związku z tym, s x = (2v 0x + a x t)T.

Aby otrzymać równanie ruchu ciała, do wzoru na rzut przemieszczenia podstawiamy jego wyrażenie przez różnicę współrzędnych s x = x – x 0 .

Otrzymujemy: x – x 0 = v 0x T+ , lub

x = x 0 + v 0x T + .

Zgodnie z równaniem ruchu można w każdej chwili wyznaczyć współrzędną ciała, jeśli znana jest współrzędna początkowa, prędkość początkowa i przyspieszenie ciała.

Ze wzoru na rzut prędkości ruchu prostoliniowego jednostajnie przyspieszonego v x = v 0x + a x t wyraźmy czas:

Podstawiając to wyrażenie do wzoru rzutowania przemieszczeń, otrzymujemy:

s x = v 0x + .

s x = , lub
–= 2a x s x.

Jeżeli początkowa prędkość ciała wynosi zero, to:

2a x s x.

4. Przykład rozwiązania problemu

Dany:

v 01 = 0

a 1 = 0,5 m/s 2

T 1 = 20 s

s 2 = 40 m

v 2 = 0

a 2?

s 1?

Połączymy układ odniesienia z Ziemią, oś x na każdym etapie ruchu skierujmy się w kierunku prędkości narciarza (rys. 32).

Napiszmy równanie na prędkość narciarza pod koniec zjazdu z góry:

v 1 = v 01 + a 1 T 1 .

W rzutach na oś x otrzymujemy: v 1x = a 1x T. Ponieważ rzuty prędkości i przyspieszenia na oś x są dodatnie, moduł prędkości narciarza wynosi: v 1 = a 1 T 1 .

Napiszmy równanie odnoszące się do rzutów prędkości, przyspieszenia i ruchu narciarza w drugiej fazie ruchu:

–= 2a 2x s 2x .

Biorąc pod uwagę, że początkowa prędkość narciarza na tym etapie ruchu jest równa jego końcowej prędkości na pierwszym etapie

v 02 = v 1 , v 2x= 0 otrzymujemy

– = –2a 2 s 2 ; (a 1 T 1) 2 = 2a 2 s 2 .

Stąd a 2 = ;

a 2 == 0,125 m / s 2.

Moduł ruchu narciarza w pierwszej fazie ruchu jest równy długości górskiego stoku. Napiszmy równanie przemieszczenia:

s 1x = v 01x T + .

Stąd długość zbocza góry wynosi s 1 = ;

s 1 == 100 m.

Odpowiedź: a 2 \u003d 0,125 m / s 2; s 1 = 100m.

Pytania do samodzielnego zbadania

1. Jak wynika z wykresu rzutu prędkości jednostajnego ruchu prostoliniowego na oś x

2. Jak wynika z wykresu rzutu prędkości ruchu prostoliniowego jednostajnie przyspieszonego na oś x od czasu do określenia rzutu przemieszczenia ciała?

3. Jakiego wzoru używa się do obliczenia rzutu przemieszczenia ciała podczas ruchu prostoliniowego jednostajnie przyspieszonego?

4. Jakiego wzoru używa się do obliczenia rzutu przemieszczenia ciała poruszającego się jednostajnie przyspieszonym i prostoliniowym, jeśli początkowa prędkość ciała wynosi zero?

Zadanie 7

4. Samochód jadący z prędkością 54 km/h zatrzymuje się przy hamowaniu na 15 sekund. Jaki jest moduł przemieszczenia samochodu podczas hamowania?

Laboratorium #1

Badanie jednostajnie przyspieszone
ruch prostoliniowy

Cel:

Urządzenia i materiały:

zsyp, statyw, metalowa kula, stoper, taśma miernicza, metalowy cylinder.

Porządek pracy

1. Jeden koniec zsypu zamocuj w stopie statywu tak, aby tworzył mały kąt z powierzchnią stołu, na drugim końcu włóż do niego metalowy walec.

4. Zmierz czas, jaki piłka przebyła po rynnie i przebytą przez nią odległość. Oblicz jego przyspieszenie ze wzoru s = .

5. Wykorzystując uzyskaną eksperymentalnie wartość przyspieszenia oblicz drogi, jakie musi pokonać kulka w pierwszej, drugiej i trzeciej sekundzie swojego ruchu. Wyciągnij wniosek.

Tabela 1

numer doświadczenia

Dane eksperymentalne

Wyniki teoretyczne

Czas T , Z

Ścieżka , cm

Czas t , Z

Ścieżka

s, cm

Przyspieszenie a, cm/s2

CzasT, Z

Ścieżka , cm

Jak, znając drogę hamowania, określić prędkość początkową samochodu, a jak, znając cechy ruchu, takie jak prędkość początkowa, przyspieszenie, czas, określić ruch samochodu? Odpowiedzi uzyskamy po zapoznaniu się z tematem dzisiejszej lekcji: „Przemieszczenie przy ruchu jednostajnie przyspieszonym, zależność współrzędnych od czasu przy ruchu jednostajnie przyspieszonym”

Przy ruchu jednostajnie przyspieszonym wykres wygląda jak linia prosta idąca w górę, ponieważ jego projekcja przyspieszenia jest większa od zera.

Przy jednostajnym ruchu prostoliniowym obszar ten będzie liczbowo równy modułowi rzutu przemieszczenia ciała. Okazuje się, że fakt ten można uogólnić nie tylko na przypadek ruchu jednostajnego, ale także na dowolny ruch, czyli pokazać, że powierzchnia pod wykresem jest liczbowo równa modułowi rzutu przemieszczenia. Odbywa się to ściśle matematycznie, ale użyjemy metody graficznej.

Ryż. 2. Wykres zależności prędkości od czasu przy ruchu jednostajnie przyspieszonym ()

Podzielmy wykres rzutu prędkości od czasu dla ruchu jednostajnie przyspieszonego na małe przedziały czasowe Δt. Załóżmy, że są one tak małe, że na ich długości prędkość praktycznie się nie zmieniała, to znaczy warunkowo zamienimy liniowy wykres zależności na rysunku w drabinę. Na każdym jego etapie wierzymy, że prędkość niewiele się zmieniła. Wyobraź sobie, że robimy odstępy czasu Δt nieskończenie małe. W matematyce mówią: robimy przejście do granic możliwości. W takim przypadku obszar takiej drabiny będzie w nieskończoność ściśle pokrywał się z obszarem trapezu, który jest ograniczony wykresem V x (t). A to oznacza, że dla przypadku ruchu jednostajnie przyspieszonego możemy powiedzieć, że moduł rzutowania przemieszczeń jest liczbowo równy powierzchni ograniczonej wykresem Vx(t): osie odciętej i rzędnej oraz prostopadła opuszczona do osi odciętej, czyli obszar trapezu OABS, który widzimy na ryc. 2.

Problem zmienia się z fizycznego w matematyczny - znalezienie obszaru trapezu. To standardowa sytuacja, kiedy fizycy robią model opisujący dane zjawisko, a potem do gry wchodzi matematyka, która ten model wzbogaca równaniami, prawami - zamieniając model w teorię.

Znajdujemy obszar trapezu: trapez jest prostokątny, ponieważ kąt między osiami wynosi 90 0, trapez dzielimy na dwa kształty - prostokąt i trójkąt. Oczywiście całkowita powierzchnia będzie równa sumie powierzchni tych figur (ryc. 3). Znajdźmy ich obszary: powierzchnia prostokąta jest równa iloczynowi boków, czyli V 0x t, powierzchnia trójkąta prawego będzie równa połowie iloczynu nóg - 1/2AD BD podstawiając wartości rzutowania otrzymujemy: 1/2t (V x - V 0x), a pamiętając prawo zmiany prędkości od czasu ruchem jednostajnie przyspieszonym: V x (t) = V 0x + axt, jest dość oczywiste, że różnica rzutów prędkości jest równa iloczynowi rzutu przyspieszenia ax przez czas t, czyli V x - V 0x = a x t.

Ryż. 3. Określenie obszaru trapezu ( Źródło)

Biorąc pod uwagę fakt, że powierzchnia trapezu jest liczbowo równa modułowi rzutu przemieszczenia, otrzymujemy:

S x (t) \u003d V 0 x t + a x t 2 / 2

Otrzymaliśmy prawo zależności rzutu przemieszczenia od czasu przy ruchu jednostajnie przyspieszonym w postaci skalarnej, w postaci wektorowej będzie to wyglądało tak:

(t) = t + t 2 / 2

Wyprowadźmy jeszcze jeden wzór na rzut przemieszczenia, który nie będzie uwzględniał czasu jako zmiennej. Rozwiązujemy układ równań, wyłączając z niego czas:

S x (t) \u003d V 0 x + a x t 2 / 2

V x (t) \u003d V 0 x + a x t

Wyobraźmy sobie, że nie znamy czasu, wtedy czas wyrazimy z drugiego równania:

t \u003d V x - V 0x / a x

Podstaw otrzymaną wartość do pierwszego równania:

Dostajemy takie kłopotliwe wyrażenie, podliczamy je do kwadratu i podajemy podobne:

Otrzymaliśmy bardzo wygodne wyrażenie rzutowania przemieszczenia dla przypadku, gdy nie znamy czasu ruchu.

Miejmy, że początkowa prędkość samochodu, gdy rozpoczęło się hamowanie, wynosi V 0 \u003d 72 km / h, prędkość końcowa V \u003d 0, przyspieszenie a \u003d 4 m / s 2. Dowiedz się, jaka jest długość drogi hamowania. Przeliczając kilometry na metry i podstawiając wartości do wzoru otrzymujemy, że droga hamowania będzie wynosić:

S x \u003d 0 - 400 (m / s) 2 / -2 4 m / s 2 \u003d 50 m

Przeanalizujmy następujący wzór:

S x \u003d (V 0 x + V x) / 2 t

Rzut ruchu jest połową sumy rzutów prędkości początkowej i końcowej pomnożonej przez czas ruchu. Przypomnij sobie wzór na przemieszczenie dla średniej prędkości

S x \u003d V cf t

W przypadku ruchu jednostajnie przyspieszonego średnia prędkość wyniesie:

V cf \u003d (V 0 + V k) / 2

Zbliżyliśmy się do rozwiązania głównego problemu mechaniki ruchu jednostajnie przyspieszonego, czyli uzyskania prawa, zgodnie z którym współrzędna zmienia się w czasie:

x(t) \u003d x 0 + V 0 x t + a x t 2 / 2

Aby nauczyć się korzystać z tego prawa, przeanalizujemy typowy problem.

Samochód, wychodząc ze stanu spoczynku, uzyskuje przyspieszenie 2 m / s 2. Znajdź odległość przebytą przez samochód w 3 sekundy i w trzeciej sekundzie.

Biorąc pod uwagę: V 0 x = 0

Zapiszmy prawo, zgodnie z którym przemieszczenie zmienia się w czasie o

ruch jednostajnie przyspieszony: S x \u003d V 0 x t + a x t 2 /2. 2 centy

Na pierwsze pytanie problemu możemy odpowiedzieć podłączając dane:

t 1 \u003d 3 c S 1x \u003d a x t 2 / 2 \u003d 2 3 2 / 2 \u003d 9 (m) - to jest ścieżka, która poszła

c samochód w 3 sekundy.

Dowiedz się, jak daleko przebył w 2 sekundy:

S x (2 s) \u003d a x t 2 / 2 \u003d 2 2 2 / 2 \u003d 4 (m)

Więc ty i ja wiemy, że w dwie sekundy samochód przejechał 4 metry.

Teraz, znając te dwie odległości, możemy znaleźć drogę, którą przebył w trzeciej sekundzie:

S 2x \u003d S 1x + S x (2 s) \u003d 9 - 4 \u003d 5 (m)

Ruch jednostajnie przyspieszony nazwany takim ruchem, w którym wektor przyspieszenia pozostaje niezmieniony pod względem wielkości i kierunku. Przykładem takiego ruchu jest ruch kamienia rzuconego pod pewnym kątem do horyzontu (ignorując opór powietrza). W dowolnym punkcie trajektorii przyspieszenie kamienia jest równe przyspieszeniu swobodnego spadania. W ten sposób badanie ruchu jednostajnie przyspieszonego sprowadza się do badania ruchu prostoliniowego jednostajnie przyspieszonego. W przypadku ruchu prostoliniowego wektory prędkości i przyspieszenia są skierowane wzdłuż prostej linii ruchu. Dlatego prędkość i przyspieszenie w rzutach na kierunek ruchu można uznać za wielkości algebraiczne. Przy jednostajnie przyspieszonym ruchu prostoliniowym prędkość ciała określa wzór (1)

W tym wzorze prędkość ciała przy T = 0 (prędkość początkowa ), = const – przyspieszenie. W rzucie na wybraną oś x równanie (1) zostanie zapisane w postaci: (2). Na wykresie projekcji prędkości υ x ( T), ta zależność ma postać linii prostej.

Nachylenie wykresu prędkości można wykorzystać do określenia przyspieszenia a ciało. Odpowiednie konstrukcje są wykonane na ryc. dla wykresu I Przyspieszenie jest liczbowo równe stosunkowi boków trójkąta ABC: .

Im większy kąt β tworzący wykres prędkości z osią czasu, czyli tym większe nachylenie wykresu ( stromość), tym większe przyspieszenie ciała.

Dla wykresu I: υ 0 \u003d -2 m / s, a\u003d 1/2 m / s 2. Dla wykresu II: υ 0 \u003d 3 m / s, a\u003d -1/3 m / s 2.

Wykres prędkości pozwala również na wyznaczenie rzutu przemieszczenia s ciała na pewien czas t. Wyznaczmy mały przedział czasu Δt na osi czasu. Jeśli ten okres czasu jest wystarczająco mały, to zmiana prędkości w tym okresie jest niewielka, to znaczy ruch w tym okresie można uznać za jednostajny z pewną średnią prędkością, która jest równa prędkości chwilowej υ ciało w środku przedziału Δt. Dlatego przemieszczenie Δs w czasie Δt będzie równe Δs = υΔt. To przemieszczenie jest równe obszarowi zacienionemu na ryc. paski. Dzieląc przedział czasu od 0 do pewnego momentu t na małe przedziały Δt, możemy uzyskać, że przemieszczenie s dla danego czasu t przy jednostajnie przyspieszonym ruchu prostoliniowym jest równe powierzchni trapezu ODEF. Odpowiednie konstrukcje są wykonane na ryc. dla harmonogramu II. Czas t wynosi 5,5 s.

(3) - otrzymany wzór pozwala na wyznaczenie przemieszczenia ruchem jednostajnie przyspieszonym, jeśli przyspieszenie nie jest znane.

Jeśli zamienimy wyrażenie na prędkość (2) do równania (3), to otrzymamy (4) - ten wzór służy do zapisania równania ruchu ciała: (5).

Jeśli z równania (2) wyrażmy czas ruchu (6) i podstawimy do równości (3), to

Ta formuła pozwala określić ruch w nieznanym czasie ruchu.

Zastanówmy się, jak obliczany jest rzut wektora przemieszczenia ciała poruszającego się jednostajnie przyspieszonym, jeśli jego prędkość początkowa v 0 jest równa zeru. W tym przypadku równanie

będzie wyglądać tak:

Przepiszmy to równanie, podstawiając do niego zamiast rzutów s x i a x moduły s i a wektorów

przemieszczenie i przyspieszenie. Ponieważ w tym przypadku wektory sua są skierowane w tym samym kierunku, ich rzuty mają te same znaki. Dlatego równanie dla modułów wektorów można zapisać:

Z tego wzoru wynika, że przy ruchu prostoliniowym jednostajnie przyspieszonym bez prędkości początkowej, moduł wektora przemieszczenia jest wprost proporcjonalny do kwadratu przedziału czasu, w którym ten ruch został wykonany. Oznacza to, że wraz ze wzrostem czasu ruchu n razy (liczonym od momentu rozpoczęcia ruchu), ruch wzrasta n 2 razy.

Na przykład, jeśli przez arbitralny czas t 1 od początku ruchu ciało się poruszyło

następnie przez czas t 2 \u003d 2t 1 (liczony od tego samego momentu co t 1) będzie się poruszać

przez czas t n \u003d nt l - przemieszczenie s n \u003d n 2 s l (gdzie n jest liczbą naturalną).

Ta zależność modułu wektora przemieszczenia od czasu podczas ruchu prostoliniowego jednostajnie przyspieszonego bez prędkości początkowej jest wyraźnie odzwierciedlona na rysunku 15, gdzie segmenty OA, OB, OS, OD i OE są modułami wektorów przemieszczenia (s 1, s 2, s 3, s 4 i s 5), popełnionych przez ciało, odpowiednio, dla przedziałów czasu t 1 , t 2 = 2t 1 , t 3 = 3t 1 , t 4 = 4t 1 i t 5 = 5t 1 .

Ryż. 15. Wzorce ruchu jednostajnie przyspieszonego: OA:OB:OC:OD:0E = 1:4:9:16:25; OA:AB:BC:CD:DE = 1:3:5:7:9

Z tej liczby jasno wynika, że

OA:OB:OS:OD:OE = 1:4:9:16:25, (1)

tj. wraz ze wzrostem odstępów czasu liczonych od początku ruchu, o całkowitą liczbę razy w porównaniu z t 1, moduły odpowiednich wektorów przemieszczenia zwiększają się jako szereg kwadratów kolejnych liczb naturalnych.

Rysunek 15 pokazuje inny wzór:

OA:AB:BC:CD:DE = 1:3:5:7:9, (2)

tzn. moduły wektorów przemieszczeń wykonywanych przez ciało w kolejnych równych okresach czasu (z których każdy jest równy t 1) są powiązane jako ciąg kolejnych liczb nieparzystych.

Regularności (1) i (2) są nieodłączne tylko dla ruchu jednostajnie przyspieszonego. Dlatego można je wykorzystać, jeśli konieczne jest określenie, czy ruch jest jednostajnie przyspieszony, czy nie.

Określmy na przykład, czy ruch ślimaka był jednostajnie przyspieszony, który przesunął się o 0,5 cm w pierwszych 20 s ruchu, 1,5 cm w drugiej 20 s i 2,5 cm w trzeciej 20 s.

Aby to zrobić, sprawdźmy, ile razy ruchy wykonane w drugim i trzecim przedziale czasowym są większe niż w pierwszym:

Oznacza to, że 0,5 cm:1,5 cm:2,5 cm = 1:3:5. Ponieważ te stosunki są szeregiem kolejnych liczb nieparzystych, ruch ciała został równomiernie przyspieszony.

W tym przypadku jednostajnie przyspieszony charakter ruchu ujawnił się na podstawie prawidłowości (2).

pytania

Jakich wzorów używa się do obliczenia rzutu i modułu wektora przemieszczenia ciała podczas ruchu jednostajnie przyspieszonego ze stanu spoczynku?
Ile razy moduł wektora przemieszczenia ciała wzrośnie wraz ze wzrostem czasu jego ruchu od spoczynku o n razy?
Napisz, jak moduły wektorów przemieszczenia ciała poruszającego się jednostajnie przyspieszonym ze stanu spoczynku odnoszą się do siebie ze wzrostem czasu jego ruchu o liczbę całkowitą razy w porównaniu do t 1 .
Napisz, jak moduły wektorów przemieszczeń wykonywanych przez ciało w kolejnych równych odstępach czasu odnoszą się do siebie, jeśli ciało to porusza się jednostajnie przyspieszone ze stanu spoczynku.
Jaki jest cel używania regularności (1) i (2)?

Ćwiczenie 8

Pociąg odjeżdżający ze stacji w ciągu pierwszych 20 s porusza się po linii prostej i równomiernie przyspiesza. Wiadomo, że w trzeciej sekundzie od początku ruchu pociąg przejechał 2 m. Wyznacz moduł wektora przemieszczenia wykonanego przez pociąg w pierwszej sekundzie oraz moduł wektora przyspieszenia, z jakim się poruszał.
Samochód poruszający się równomiernie rozpędzony ze stanu spoczynku pokonuje w piątej sekundzie przyspieszenia 6,3 m. Jaką prędkość rozwinął samochód do końca piątej sekundy od rozpoczęcia ruchu?
Przez pierwsze 0,03 s ruchu bez prędkości początkowej jakieś ciało przemieściło się o 2 mm, przez pierwsze 0,06 s - 8 mm, przez pierwsze 0,09 s - 18 mm. Na podstawie prawidłowości (1) udowodnij, że przez wszystkie 0,09 s ciało poruszało się jednostajnie z przyspieszeniem.

Pytania.

1. Jakich wzorów używa się do obliczenia rzutu i modułu wektora przemieszczenia ciała podczas ruchu jednostajnie przyspieszonego ze stanu spoczynku?

2. Ile razy moduł wektora przemieszczenia ciała wzrośnie wraz ze wzrostem czasu jego ruchu od spoczynku o n razy?

3. Napisz, jak moduły wektorów przemieszczeń ciała poruszającego się jednostajnie przyspieszonym ze stanu spoczynku odnoszą się do siebie ze wzrostem czasu jego ruchu o liczbę całkowitą razy w porównaniu z t 1.

4. Napisz, w jaki sposób moduły wektorów przemieszczeń wykonywanych przez ciało w kolejnych równych odstępach czasu odnoszą się do siebie, jeśli ciało to porusza się jednostajnie przyspieszone ze stanu spoczynku.

5. W jakim celu można wykorzystać prawidłowości (3) i (4)?

Wzory (3) i (4) służą do określenia, czy ruch jest jednostajnie przyspieszony, czy nie (patrz str. 33).

Ćwiczenia.

1. Pociąg odjeżdżający ze stacji w ciągu pierwszych 20 s porusza się po linii prostej i równomiernie przyspiesza. Wiadomo, że w trzeciej sekundzie od początku ruchu pociąg przejechał 2 m. Wyznacz moduł wektora przemieszczenia wykonanego przez pociąg w pierwszej sekundzie oraz moduł wektora przyspieszenia, z jakim się poruszał.