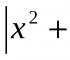Як знайти a1 в арифметичній прогресії формула. зворотна матриця

Отже, сервіси за рішенням матриць онлайн:

Сервіс роботи з матрицями дозволяє виконати елементарні перетворення матриць.
Якщо у Вас стоїть завдання виконати більш складне перетворення, то цим сервісом варто користуватися як конструктором.

приклад. дано матриці Aі B, треба знайти C = A -1 * B + B T,

Вам варто спочатку знайти зворотний матрицюA1 = A-1, скориставшись сервісом по знаходженню оберненої матриці;
Далі, після того, як знайшли матрицю A1виконаємо множення матрицьA2 = A1 * B, Скориставшись сервісом по множенню матриць;
Виконаємо транспонування матриціA3 = B T (сервіс по знаходженню транспонованою матриці);
І останнє - знайдемо суму матриць З = A2 + A3(Сервіс по обчисленню суми матриць) - і отримуємо відповідь з самим докладним рішенням !;

твір матриць

Це он-лайн сервіс в два кроки:

Ввести перший співмножник матрицю A
Ввести другий співмножник матрицю або вектор-стовпець B

Множення матриці на вектор

Множення матриці на вектор можна знайти, скориставшись сервісом множення матриць
(Першим співмножником буде дана матриця, другим співмножником буде стовпець, що складається з елементів даного вектора)

Це он-лайн сервіс в два кроки:

Введіть матрицю A, Для якої потрібно знайти зворотну матрицю
Отримайте відповідь з докладним рішенням по знаходженню оберненої матриці

визначник матриці

Це он-лайн сервіс в один крок:

Введіть матрицю A, Для якої потрібно знайти визначник матриці

транспонування матриці

Тут Ви зможете відстежити алгоритм транспонування матриці і навчитися самому вирішувати подібні завдання.
Це он-лайн сервіс в один крок:

Введіть матрицю A, Яку треба транспонувати

Ранг матриці

Це он-лайн сервіс в один крок:

Введіть матрицю A, Для якої потрібно виконати знаходження рангу

Власні значення матриці і власні вектора матриці

Це он-лайн сервіс в один крок:

Введіть матрицю A, Для якої потрібно знайти власні вектора і власні значення (власні числа)

Зведення матриці в ступінь

Це он-лайн сервіс в два кроки:

Введіть матрицю A, Яку будете підносити до степеня
Ввести ціле число q- ступінь

Матриця $ A ^ (- 1) $ називається зворотної по відношенню до квадратної матриці $ A $, якщо виконана умова $ A ^ (- 1) \ cdot A = A \ cdot A ^ (- 1) = E $, де $ E $ - одинична матриця, порядок якої дорівнює порядку матриці $ A $.

Невироджених матриця - матриця, визначник якої не дорівнює нулю. Відповідно, вироджена матриця - та, у якій дорівнює нулю визначник.

Зворотній матриця $ A ^ (- 1) $ існує тоді і тільки тоді, коли матриця $ A $ - невироджена. Якщо зворотна матриця $ A ^ (- 1) $ існує, то вона єдина.

Є кілька способів знаходження зворотної матриці, і ми розглянемо два з них. На цій сторінці буде розглянуто метод приєднаної матриці, який покладається стандартним в більшості курсів вищої математики. Другий спосіб знаходження оберненої матриці (метод елементарних перетворень), який передбачає використання методу Гаусса або методу Гаусса-Жордана, розглянуто у другій частині.

Метод приєднаної (союзної) матриці

Нехай задана матриця $ A_ (n \ times n) $. Для того, щоб знайти зворотну матрицю $ A ^ (- 1) $, потрібно здійснити три кроки:

Знайти визначник матриці $ A $ і переконатися, що $ \ Delta A \ neq 0 $, тобто що матриця А - невироджена.
Скласти алгебраїчні доповнення $ A_ (ij) $ кожного елемента матриці $ A $ і записати матрицю $ A_ (n \ times n) ^ (*) = \ left (A_ (ij) \ right) $ зі знайдених алгебраїчних доповнень.
Записати зворотну матрицю з урахуванням формули $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $.

Матрицю $ (A ^ (*)) ^ T $ часто називають приєднаної (взаємної, союзної) до матриці $ A $.

Якщо рішення відбувається вручну, то перший спосіб хороший лише для матриць порівняно невеликих порядків: другого (), третього (), четвертого (). Щоб знайти зворотну матрицю для матриці вищого порядку, використовуються інші методи. Наприклад, метод Гаусса, який розглянуто у другій частині.

приклад №1

Знайти матрицю, обернену до матриці $ A = \ left (\ begin (array) (cccc) 5 & -4 & 1 & 0 \\ 12 & -11 & 4 & 0 \\ -5 & 58 & 4 & 0 \\ 3 & - 1 & -9 & 0 \ end (array) \ right) $.

Так як всі елементи четвертого стовпця дорівнюють нулю, то $ \ Delta A = 0 $ (тобто матриця $ A $ є виродження). Так як $ \ Delta A = 0 $, то зворотної матриці до матриці $ A $ не існує.

відповідь: Матриці $ A ^ (- 1) $ не існує.

приклад №2

Знайти матрицю, обернену до матриці $ A = \ left (\ begin (array) (cc) -5 & 7 \\ 9 & 8 \ end (array) \ right) $. Виконати перевірку.

Використовуємо метод приєднаної матриці. Спочатку знайдемо визначник заданої матриці $ A $:

$$ \ Delta A = \ left | \ Begin (array) (cc) -5 & 7 \\ 9 & 8 \ end (array) \ right | = -5 \ cdot 8-7 \ cdot 9 = -103. $$

Так як $ \ Delta A \ neq 0 $, то зворотна матриця існує, тому продовжимо рішення. Знаходимо алгебраїчні доповнення

\ Begin (aligned) & A_ (11) = (- 1) ^ 2 \ cdot 8 = 8; \; A_ (12) = (- 1) ^ 3 \ cdot 9 = -9; \\ & A_ (21) = (- 1) ^ 3 \ cdot 7 = -7; \; A_ (22) = (- 1) ^ 4 \ cdot (-5) = - 5. \\ \ end (aligned)

Складаємо матрицю з алгебраїчних доповнень: $ A ^ (*) = \ left (\ begin (array) (cc) 8 & -9 \\ -7 & -5 \ end (array) \ right) $.

Транспоніруем отриману матрицю: $ (A ^ (*)) ^ T = \ left (\ begin (array) (cc) 8 & -7 \\ -9 & -5 \ end (array) \ right) $ (отримана матриця часто іменується приєднаної або союзної матрицею до матриці $ A $). Використовуючи формулу $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $, маємо:

$$ A ^ (- 1) = \ frac (1) (- 103) \ cdot \ left (\ begin (array) (cc) 8 & -7 \\ -9 & -5 \ end (array) \ right) = \ left (\ begin (array) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $$

Отже, обернена матриця знайдена: $ A ^ (- 1) = \ left (\ begin (array) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $. Щоб перевірити істинність результату, досить перевірити істинність одного з рівності: $ A ^ (- 1) \ cdot A = E $ або $ A \ cdot A ^ (- 1) = E $. Перевіримо виконання рівності $ A ^ (- 1) \ cdot A = E $. Щоб поменше працювати з дробом, будемо підставляти матрицю $ A ^ (- 1) $ не в формі $ \ left (\ begin (array) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $, а у вигляді $ - \ frac (1) (103) \ cdot \ left (\ begin (array) (cc) 8 & -7 \\ -9 & -5 \ end (array ) \ right) $:

$$ A ^ (- 1) \ cdot (A) = - \ frac (1) (103) \ cdot \ left (\ begin (array) (cc) 8 & -7 \\ -9 & -5 \ end ( array) \ right) \ cdot \ left (\ begin (array) (cc) -5 & 7 \\ 9 & 8 \ end (array) \ right) = - \ frac (1) (103) \ cdot \ left ( \ begin (array) (cc) -103 & 0 \\ 0 & -103 \ end (array) \ right) = \ left (\ begin (array) (cc) 1 & 0 \\ 0 & 1 \ end (array ) \ right) = E $$

відповідь: $ A ^ (- 1) = \ left (\ begin (array) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $.

приклад №3

Знайти обернену матрицю для матриці $ A = \ left (\ begin (array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (array) \ right) $. Виконати перевірку.

Почнемо з обчислення визначника матриці $ A $. Отже, визначник матриці $ A $ такий:

$$ \ Delta A = \ left | \ Begin (array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (array) \ right | = 18-36 + 56-12 = 26. $$

Так як $ \ Delta A \ neq 0 $, то зворотна матриця існує, тому продовжимо рішення. Знаходимо алгебраїчні доповнення кожного елемента заданої матриці:

$$ \ begin (aligned) & A_ (11) = (- 1) ^ (2) \ cdot \ left | \ begin (array) (cc) 9 & 4 \\ 3 & 2 \ end (array) \ right | = 6; \; A_ (12) = (- 1) ^ (3) \ cdot \ left | \ begin (array) (cc) -4 & 4 \\ 0 & 2 \ end (array) \ right | = 8; \; A_ (13) = (- 1) ^ (4) \ cdot \ left | \ begin (array) (cc) -4 & 9 \\ 0 & 3 \ end (array) \ right | = -12; \\ & A_ (21) = (- 1) ^ (3) \ cdot \ left | \ begin (array) (cc) 7 & 3 \\ 3 & 2 \ end (array) \ right | = -5; \; A_ (22) = (- 1) ^ (4) \ cdot \ left | \ begin (array) (cc) 1 & 3 \\ 0 & 2 \ end (array) \ right | = 2; \; A_ (23) = (- 1) ^ (5) \ cdot \ left | \ begin (array) (cc) 1 & 7 \\ 0 & 3 \ end (array) \ right | = -3; \\ & A_ (31) = (- 1) ^ (4) \ cdot \ left | \ begin (array) (cc) 7 & 3 \\ 9 & 4 \ end (array) \ right | = 1; \; A_ (32) = (- 1) ^ (5) \ cdot \ left | \ begin (array) (cc) 1 & 3 \\ -4 & 4 \ end (array) \ right | = -16; \; A_ (33) = (- 1) ^ (6) \ cdot \ left | \ begin (array) (cc) 1 & 7 \\ -4 & 9 \ end (array) \ right | = 37. \ End (aligned) $$

Складаємо матрицю з алгебраїчних доповнень і транспоніруем її:

$$ A ^ * = \ left (\ begin (array) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37 \ end (array) \ right); \; (A ^ *) ^ T = \ left (\ begin (array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ end (array) \ right) . $$

Використовуючи формулу $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $, отримаємо:

$$ A ^ (- 1) = \ frac (1) (26) \ cdot \ left (\ begin (array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37 \ end (array) \ right) = \ left (\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \ end (array) \ right) $$

Отже, $ A ^ (- 1) = \ left (\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6/13 & -3/26 & 37/26 \ end (array) \ right) $. Щоб перевірити істинність результату, досить перевірити істинність одного з рівності: $ A ^ (- 1) \ cdot A = E $ або $ A \ cdot A ^ (- 1) = E $. Перевіримо виконання рівності $ A \ cdot A ^ (- 1) = E $. Щоб поменше працювати з дробом, будемо підставляти матрицю $ A ^ (- 1) $ не в формі $ \ left (\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \ end (array) \ right) $, а у вигляді $ \ frac (1) (26) \ cdot \ left ( \ begin (array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ end (array) \ right) $:

$$ A \ cdot (A ^ (- 1)) = \ left (\ begin (array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (array) \ right) \ cdot \ frac (1) (26) \ cdot \ left (\ begin (array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ end (array) \ right) = \ frac (1) (26) \ cdot \ left (\ begin (array) (ccc) 26 & 0 & 0 \\ 0 & 26 & 0 \\ 0 & 0 & 26 \ end (array) \ right) = \ left (\ begin (array) (ccc) 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end (array) \ right) = E $$

Перевірка пройдена успішно, зворотна матриця $ A ^ (- 1) $ знайдена вірно.

відповідь: $ A ^ (- 1) = \ left (\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 / 13 & -3/26 & 37/26 \ end (array) \ right) $.

приклад №4

Знайти матрицю, зворотну матриці $ A = \ left (\ begin (array) (cccc) 6 & -5 & 8 & 4 \\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7 \\ -4 & 8 & -8 & -3 \ end (array) \ right) $.

Для матриці четвертого порядку знаходження оберненої матриці за допомогою алгебраїчних доповнень трохи важко. Однак такі приклади в контрольних роботах зустрічаються.

Щоб знайти зворотну матрицю, для початку потрібно обчислити визначник матриці $ A $. Найкраще в даній ситуації це зробити за допомогою розкладання визначника по рядку (стовпцю). Вибираємо будь-який рядок або стовпець і знаходимо алгебраїчні доповнення кожного елемента обраної рядки або стовпці.

Наприклад, для першого рядка отримаємо:

$$ A_ (11) = \ left | \ begin (array) (ccc) 7 & 5 & 2 \\ 5 & 3 & 7 \\ 8 & -8 & -3 \ end (array) \ right | = 556; \; A_ (12) = - \ left | \ begin (array) (ccc) 9 & 5 & 2 \\ 7 & 3 & 7 \\ -4 & -8 & -3 \ end (array) \ right | = -300 ; $$ $$ A_ (13) = \ left | \ begin (array) (ccc) 9 & 7 & 2 \\ 7 & 5 & 7 \\ -4 & 8 & -3 \ end (array) \ right | = -536; \; A_ (14) = - \ left | \ begin (array) (ccc) 9 & 7 & 5 \\ 7 & 5 & 3 \\ -4 & 8 & -8 \ end (array) \ right | = -112. $$

Визначник матриці $ A $ обчислимо за такою формулою:

$$ \ Delta (A) = a_ (11) \ cdot A_ (11) + a_ (12) \ cdot A_ (12) + a_ (13) \ cdot A_ (13) + a_ (14) \ cdot A_ (14 ) = 6 \ cdot 556 + (- 5) \ cdot (-300) +8 \ cdot (-536) +4 \ cdot (-112) = 100. $$

$$ \ begin (aligned) & A_ (21) = - 77; \; A_ (22) = 50; \; A_ (23) = 87; \; A_ (24) = 4; \\ & A_ (31) = -93; \; A_ (32) = 50; \; A_ (33) = 83; \; A_ (34) = 36; \\ & A_ (41) = 473; \; A_ (42) = - 250 ; \; A_ (43) = - 463; \; A_ (44) = - 96. \ End (aligned) $$

Матриця з алгебраїчних доповнень: $ A ^ * = \ left (\ begin (array) (cccc) 556 & -300 & -536 & -112 \\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36 \\ 473 & -250 & -463 & -96 \ end (array) \ right) $.

Приєднана матриця: $ (A ^ *) ^ T = \ left (\ begin (array) (cccc) 556 & -77 & -93 & 473 \\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463 \\ -112 & 4 & 36 & -96 \ end (array) \ right) $.

Зворотна матриця:

$$ A ^ (- 1) = \ frac (1) (100) \ cdot \ left (\ begin (array) (cccc) 556 & -77 & -93 & 473 \\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463 \\ -112 & 4 & 36 & -96 \ end (array) \ right) = \ left (\ begin (array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28 / 25 & 1/25 & 9/25 & -24/25 \ end (array) \ right) $$

Перевірка, при бажанні, може бути проведена так само, як і в попередніх прикладах.

відповідь: $ A ^ (- 1) = \ left (\ begin (array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/25 & 9/25 & -24/25 \ end (array) \ right) $.

У другій частині буде розглянуто інший спосіб знаходження зворотної матриці, який передбачає використання перетворень методу Гаусса або методу Гаусса-Жордана.

Для вирішення системи лінійних рівнянь (3) щодо x 1скористаємося методом Гаусса.

Аналогічним чином вирішуються інші системи лінійних рівнянь (2).

Нарешті група векторів стовпців x 1, x 2, ..., x nутворює зворотний матрицю A -1.

Зауважимо, що один раз знаходячи матриці перестановок P 1, P 2, ..., P n-1і матриці винятків М 1, М 2, ..., M n-1(Див. Сторінку Метод виключення Гаусса) і побудувавши матрицю

M = M n-1 P n-1 ... M 2 P 2 M 1 P 1,

систему (2) можна перетворити до вигляду

MAx 1 = Me 1,
MAx 2 = Me 2,
......
MAx n = Me n.

Звідси знаходяться x 1, x 2, ..., x n, При різних правих частинах Me 1, Me 2, ..., Me n.

При обчисленні оберненої матриці більш зручно з правого боку вихідної матриці додати одиничну матрицю і застосовувати метод Гаусса в прямому і зворотному напрямках.

Розглянемо це на прикладі.

Приклад обчислення зворотної матриці

Нехай потрібно знайти зворотну матрицю A -1для даної матриці A:

Запишемо з правого боку одиничну матрицю:

Вибираємо провідний елемент "4" (тому що він найбільший за модулем) і переставляємо місцями першу і третю рядки:

Застосовуємо Гаусове виняток для першого стовпця:

Переставляємо другу і третю рядки і застосовуємо Гаусове виняток для другого стовпця.

Способи знаходження оберненої матриці. Розглянемо квадратну матрицю

Позначимо Δ = det A.

Квадратна матриця А називається невироджених,або неособенной, Якщо її визначник відмінний від нуля, і виродження,або особливою, якщоΔ = 0.

Квадратна матриця В є для квадратної матриці А такого ж порядку, якщо їх твір А У = В А = Е, де Е - одинична матриця того ж порядку, що і матриці А і В.

теорема . Для того, щоб матриця А мала зворотний матрицю, необхідно і достатньо, щоб їх визначник був різниться від нуля.

Зворотній матриця матриці А, позначається через А- 1, так що В = А - 1 і обчислюється за формулою

, (1)

де А i j - алгебраїчні доповнення елементів a i j матриці A ..

Обчислення A -1 за формулою (1) для матриць високого порядку дуже занадто багато, тому на практиці буває зручно знаходити A -1 за допомогою методу елементарних перетворень (ЕП). Будь-яку неособенную матрицю А шляхом ЕП тільки стовпців (або тільки рядків) можна привести до одиничної матриці Є. Якщо скоєні над матрицею А ЕП в тому ж порядку застосувати до одиничної матриці Е, то в результаті вийде зворотна матриця. Зручно здійснювати ЕП над матрицями А і Е одночасно, записуючи обидві матриці поруч через риску. Відзначимо ще раз, що при знаходженні канонічного виду матриці з метою знаходження можна користуватися перетвореннями рядків і стовпців. Якщо потрібно знайти зворотну матрицю, в процесі перетворень слід використовувати тільки рядки або тільки стовпці.

приклад 1. для матриці знайти A -1.

Рішення.Знаходимо спочатку детермінант матриці А
значить, зворотна матриця існує і ми її можемо знайти за формулою: , Де А i j (i, j = 1,2,3) - алгебраїчні доповнення елементів а i j вихідної матриці.

Звідки .

приклад 2. Методом елементарних перетворень знайти A -1 для матриці: А =.

Рішення.Приписуємо до вихідної матриці справа одиничну матрицю того ж порядку: . За допомогою елементарних перетворень стовпців наведемо ліву "половину" до одиничної, здійснюючи одночасно точно такі перетворення над правою матрицею.
Для цього поміняємо місцями перший і другий стовпці: ~ . До третього одну додамо перший, а до другого - перший, помножений на -2: . З першого стовпчика віднімемо подвоєний другий, а з третього - помножений на 6 другий; . Додамо третій стовпець до першого і другого: . Помножимо останній рядок на -1: . Отримана праворуч від вертикальної риси квадратна матриця є зворотною матрицею до даної матриці А. Отже,
.

При вивченні алгебри в загальноосвітній школі (9 клас) однією з важливих тем є вивчення числових послідовностей, до яких відносяться прогресії -геометріческая і арифметична. У цій статті розглянемо арифметичну прогресію і приклади з рішеннями.

Що собою являє арифметична прогресія?

Щоб це зрозуміти, необхідно дати визначення розглянутої прогресії, а також привести основні формули, які далі будуть використані при вирішенні завдань.

Арифметична або алгебраїчна прогресія - це такий набір упорядкованих раціональних чисел, кожен член якого відрізняється від попереднього на деяку постійну величину. Ця величина називається різницею. Тобто, знаючи будь-який член упорядкованого ряду чисел і різниця, можна відновити всю арифметичну прогресію.

Наведемо приклад. Наступна послідовність чисел буде прогресією арифметичної: 4, 8, 12, 16, ..., оскільки різниця в цьому випадку дорівнює 4 (8 - 4 = 12 - 8 = 16 - 12). А ось набір чисел 3, 5, 8, 12, 17 вже не можна віднести до даного виду прогресії, оскільки різниця для нього не є постійною величиною (5 - 3 ≠ 8 - 5 ≠ 12 - 8 ≠ 17 - 12).

важливі формули

Наведемо тепер основні формули, які знадобляться для вирішення завдань з використанням арифметичної прогресії. Позначимо символом a n n-й член послідовності, де n - ціле число. Різниця позначимо латинською буквою d. Тоді справедливі такі вирази:

Для визначення значення n-го члена підійде формула: a n = (n-1) * d + a 1.
Для визначення суми перших n доданків: S n = (a n + a 1) * n / 2.

Щоб зрозуміти будь-які приклади арифметичної прогресії з рішенням в 9 класі, досить запам'ятати ці дві формули, оскільки на їх використанні будуються будь-які завдання розглянутого типу. Також слід не забувати, що різниця прогресії визначається за формулою: d = a n - a n-1.

Приклад №1: знаходження невідомого члена

Наведемо простий приклад арифметичній прогресії і формул, які необхідно використовувати для вирішення.

Нехай дана послідовність 10, 8, 6, 4, ..., необхідно в ній знайти п'ять членів.

З умови задачі вже випливає, що перші 4 доданків відомі. П'яте можна визначити двома способами:

Обчислимо для початку різницю. Маємо: d = 8 - 10 = -2. Аналогічним чином можна було взяти будь-які два інших члена, що стоять поруч один з одним. Наприклад, d = 4 - 6 = -2. Оскільки відомо, що d = a n - a n-1, тоді d = a 5 - a 4, звідки отримуємо: a 5 = a 4 + d. Підставляємо відомі значення: a 5 = 4 + (-2) = 2.
Другий спосіб також вимагає знання різниці розглянутої прогресії, тому спочатку потрібно визначити її, як показано вище (d = -2). Знаючи, що перший член a 1 = 10, скористаємося формулою для n числа послідовності. Маємо: a n = (n - 1) * d + a 1 = (n - 1) * (-2) + 10 = 12 - 2 * n. Підставляючи в останній вираз n = 5, отримуємо: a 5 = 12-2 * 5 = 2.

Як видно, обидва способи вирішення привели до одного і того ж результату. Відзначимо, що в цьому прикладі різницю d прогресії є негативною величиною. Такі послідовності називаються убутними, так як кожен наступний член менше попереднього.

Приклад №2: різниця прогресії

Тепер усложним трохи завдання, наведемо приклад, як

Відомо, що в деякій 1-й член дорівнює 6, а 7-й член дорівнює 18. Необхідно знайти різницю і відновити цю послідовність до 7 члена.

Скористаємося формулою для визначення невідомого члена: a n = (n - 1) * d + a 1. Підставами в неї відомі дані з умови, тобто числа a 1 і a 7, маємо: 18 = 6 + 6 * d. З цього виразу можна легко обчислити різницю: d = (18 - 6) / 6 = 2. Таким чином, відповіли на першу частину завдання.

Щоб відновити послідовність до 7 члена, слід скористатися визначенням алгебраїчної прогресії, тобто a 2 = a 1 + d, a 3 = a 2 + d і так далі. В результаті відновлюємо всю послідовність: a 1 = 6, a 2 = 6 + 2 = 8, a 3 = 8 + 2 = 10, a 4 = 10 + 2 = 12, a 5 = 12 + 2 = 14, a 6 = 14 + 2 = 16, a 7 = 18.

Приклад №3: складання прогресії

Ускладнимо ще сильніше умову задачі. Тепер необхідно відповісти на питання, як знаходити арифметичну прогресію. Можна навести такий приклад: дано два числа, наприклад, - 4 і 5. Необхідно скласти прогресію алгебраїчну так, щоб між цими містилося ще три члени.

Перш ніж починати вирішувати цю задачу, необхідно зрозуміти, яке місце займатимуть задані числа в майбутньої прогресії. Оскільки між ними будуть перебувати ще три члени, тоді a 1 = -4 і a 5 = 5. Встановивши це, переходимо до задачі, яка аналогічна попередній. Знову для n-го члена скористаємося формулою, одержимо: a 5 = a 1 + 4 * d. Звідки: d = (a 5 - a 1) / 4 = (5 - (-4)) / 4 = 2,25. Тут отримали не ціле значення різниці, однак воно є раціональним числом, тому формули для алгебраїчної прогресії залишаються тими ж самими.

Тепер додамо знайдену різницю до a 1 і відновимо відсутні члени прогресії. Отримуємо: a 1 = - 4, a 2 = - 4 + 2,25 = - 1,75, a 3 = -1,75 + 2,25 = 0,5, a 4 = 0,5 + 2,25 = 2,75, a 5 = 2,75 + 2,25 = 5, що збіглося з умовою завдання.

Приклад №4: перший член прогресії

Продовжимо наводити приклади арифметичної прогресії з рішенням. У всіх попередніх завданнях було відомо перше число алгебраїчної прогресії. Тепер розглянемо задачу іншого типу: нехай дано два числа, де a 15 = 50 і a 43 = 37. Необхідно знайти, з якого числа починається ця послідовність.

Формули, якими користувалися до теперішнього часу, припускають знання a 1 і d. В умові задачі про ці числа нічого невідомо. Проте випишемо вираження для кожного члена, про яку є інформація: a 15 = a 1 + 14 * d і a 43 = a 1 + 42 * d. Отримали два рівняння, в яких 2 невідомі величини (a 1 і d). Це означає, що завдання зводиться до вирішення системи лінійних рівнянь.

Зазначену систему найпростіше вирішити, якщо висловити в кожному рівнянні a 1, а потім порівняти отримані вирази. Перше рівняння: a 1 = a 15 - 14 * d = 50 - 14 * d; друге рівняння: a 1 = a 43 - 42 * d = 37 - 42 * d. Прирівнюючи ці вирази, отримаємо: 50 - 14 * d = 37 - 42 * d, звідки різниця d = (37 - 50) / (42 - 14) = - 0,464 (наведені лише 3 знаки точності після коми).

Знаючи d, можна скористатися будь-яким з 2 наведених вище виразів для a 1. Наприклад, першим: a 1 = 50 - 14 * d = 50 - 14 * (- 0,464) = 56,496.

Якщо виникають сумніви в отриманому результаті, можна його перевірити, наприклад, визначити 43 член прогресії, який заданий в умові. Отримаємо: a 43 = a 1 + 42 * d = 56,496 + 42 * (- 0,464) = 37,008. Невелика похибка пов'язана з тим, що при обчисленнях використовувалося округлення до тисячних часток.

Приклад №5: сума

Тепер розглянемо кілька прикладів з рішеннями на суму арифметичної прогресії.

Нехай дана числова прогресія такого вигляду: 1, 2, 3, 4, ...,. Як розрахувати суму 100 цих чисел?

Завдяки розвитку комп'ютерних технологій можна цю задачу вирішити, тобто послідовно скласти всі числа, що обчислювальна машина зробить відразу ж, як тільки людина натисне клавішу Enter. Однак завдання можна вирішити в розумі, якщо звернути увагу, що представлений ряд чисел є прогресією алгебраїчної, причому її різниця дорівнює 1. Застосовуючи формулу для суми, отримуємо: S n = n * (a 1 + an) / 2 = 100 * (1 + 100) / 2 = 5050.

Цікаво відзначити, що ця задача носить назву "гаусом", оскільки на початку XVIII століття знаменитий німецький ще будучи у віці всього 10 років, зміг розв'язати цю проблему в розумі за кілька секунд. Хлопчик не знав формули для суми алгебри прогресії, але він зауважив, що якщо складати попарно числа, що знаходяться на краях послідовності, то виходить завжди один результат, тобто 1 + 100 = 2 + 99 = 3 + 98 = ..., а оскільки витрат на пальне буде рівно 50 (100/2), то для отримання правильної відповіді досить помножити 50 на 101.

Приклад №6: сума членів від n до m

Ще одним типовим прикладом суми арифметичної прогресії є наступний: дана така чисел ряд: 3, 7, 11, 15, ..., потрібно знайти, чому дорівнює сума його членів з 8 по 14.

Завдання вирішується двома способами. Перший з них передбачає знаходження невідомих членів з 8 по 14, а потім їх послідовне підсумовування. Оскільки доданків трохи, то такий спосіб не є досить трудомістким. Проте пропонується вирішити цю задачу другим методом, який є більш універсальним.

Ідея полягає в отриманні формули для суми алгебри прогресії між членами m і n, де n> m - цілі числа. Випишемо для обох випадків два вирази для суми:

S m = m * (a m + a 1) / 2.
S n = n * (a n + a 1) / 2.

Оскільки n> m, то очевидно, що 2 сума включає в себе першу. Останнє умовивід означає, що якщо взяти різницю між цими сумами, і додати до неї член a m (в разі взяття різниці він віднімається від суми S n), то отримаємо необхідний відповідь на завдання. Маємо: S mn = S n - S m + am = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am = a 1 * (n - m) / 2 + an * n / 2 + am * (1 m / 2). В цей вислів необхідно підставити формули для a n і a m. Тоді отримаємо: S mn = a 1 * (n - m) / 2 + n * (a 1 + (n - 1) * d) / 2 + (a 1 + (m - 1) * d) * (1 - m / 2) = a 1 * (n - m + 1) + d * n * (n - 1) / 2 + d * (3 * m - m 2 - 2) / 2.

Отримана формула є дещо громіздкою, проте сума S mn залежить тільки від n, m, a 1 і d. У нашому випадку a 1 = 3, d = 4, n = 14, m = 8. Підставляючи ці числа, отримаємо: S mn = 301.

Як видно з наведених рішень, все завдання грунтуються на знанні вираження для n-го члена і формули для суми набору перших доданків. Перед тим як приступити до вирішення будь-якої з цих завдань, рекомендується уважно прочитати умову, ясно зрозуміти, що потрібно знайти, і лише потім приступати до вирішення.

Ще одна порада полягає в прагненні до простоти, тобто якщо можна відповісти на запитання, чи не застосовуючи складні математичні викладки, то необхідно чинити саме так, оскільки в цьому випадку ймовірність припуститися помилки менше. Наприклад, в прикладі арифметичної прогресії з рішенням №6 можна було б зупинитися на формулі S mn = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am, і розбити загальну задачу на окремі підзадачі (в даному випадку спочатку знайти члени an і am).

Якщо виникають сумніви в отриманому результаті, то рекомендується його перевіряти, як це було зроблено в деяких наведених прикладах. Як знаходити арифметичну прогресію, з'ясували. Якщо розібратися, то це не так складно.