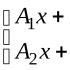Umumiylik va borliqning miqdor ko‘rsatkichlari. Kvantorlar Predikatlar mantiqiy formulasining ma'nosi
1. Kvantorlar.
2. Universal kvantor.
3. Mavjudlik kvantori.
4. Predikat mantiqiy formula haqida tushuncha. Formula ma'nosi
predikativ mantiq.
5. Predikatlar mantiqining ekvivalent formulalari.
Miqdor ko'rsatkichi haqida tushuncha
Kvantor - (lotincha kvant - qancha), mantiqiymiqdoriy operatsiya
ifoda nazarda tutilgan ob'ektlar maydoni,
foydalanish natijasida olingan.
Oddiy til bilan aytganda, bunday xususiyatlarning tashuvchilari
kabi so'zlar "hamma", "har bir", "ba'zi",
"mavjud",
"mavjud",
"har qanday",
"har qanday",
"yagona", "bir nechta", "cheksiz ko'p",
"cheklangan son", shuningdek, barcha miqdoriy
raqamlar.
Predikat uchun amallar
Predikatlar uchun ikkita yangisi kiritiladitaklif mantiqiy operatsiyalari bilan solishtirganda:
umumiy miqdor ko'rsatkichi
mavjudlik kvantifikatori
Umumiy miqdor ko'rsatkichi
P(x) ga aniqlangan unar predikat bo'lsinmavzu to'plami M.
ga mos keladigan universal bayonot
P(x) predikati uchun quyidagi gap deyiladi:
“M to‘plamining har bir elementi qanoatlantiradi
predikat P(x)"
yoki
"har bir x uchun predikat bajariladi"
Bu bayonot - (x)P(x) bilan belgilanadi.
Agar (x)P(x) bayoni rost deb hisoblanadi
P(x) predikati bir xilda to'g'ri va noto'g'ri
aks holda.
Umumiy miqdor ko'rsatkichi
X belgisi kvantlashtiruvchi deyiladix o'zgaruvchisi, u quyidagicha o'qiladi:
"barcha x uchun"
"har bir x uchun"
"har qanday x uchun"
umumiylik
(x)P(x) ifodasi: “barcha x, P(x) uchun” yoki
"har bir x, P (x) uchun".
Masalan, x(x=x) haqiqiy universaldir
bayonot va x(x>2) noto'g'ri universaldir
bayonot.
chekli to'plam (a1,a2,...am), keyin:
P(x) P(a1) P(a2) ... P(am)
Umumiy miqdor ko'rsatkichi
Shunday qilib, umumiy kvantifikatoroperator deb tushunish mumkin
miqdoriy qo‘shma gaplar
o'zgaruvchan.
Mavjudlik kvantifikatori
Ekzistensialbayonot,
muvofiq
predikat
P(x),
chaqirdi
"M to'plamining elementi mavjud,
qoniqarli
predikat
P(x)",
qaysi
x P(x) bilan belgilanadi va agar rost deb hisoblanadi
P(x) predikati qanoatlansa bo'ladi, lekin aks holda yolg'on
hol.
X belgisi ekzistensial kvant deb ataladi va
bu miqdor ko'rsatkichi oldidan kelgan x ifodasi
x o'zgaruvchisi quyidagicha o'qiladi:
"X shunday mavjudki ..."
"ba'zi x uchun, ..."
Mavjudlik kvantifikatori
MASALANx(x>2) – haqiqiy ekzistensial bayonot
x(x=x+1) - noto'g'ri ekzistensial bayonot.
Agar P(x) -da aniqlangan unar predikat bo'lsa
chekli to'plam (a1,a2,...am), keyin
P(x) P(a1) P(a2) ... P(am)
Mavjudlik kvantifikatori
Shunday qilib, miqdor ko'rsatkichimavjudligi deb tushunish mumkin
tomonidan ajratish operatori
miqdoriy o'zgaruvchi.
10. Misollar
Formula yozuvlari va ularning og'zaki ifodalariga misollar:x(x 2 1 (x 1)(x 1)) Hamma x uchun predikat bajariladi...
x(x0)
tengsizlik...
x(x0)
Barcha x uchun, adolatli ....
y (5 y 5)
5+y=5 bo'ladigan y mavjud
y(y 2 y 1 0)
Hamma y uchun predikat qanoatlantiriladi
y(y 2 y 1 0)
Siz bor ....
x(x x)
Ba'zi x uchun, to'g'ri
3
2
11. Predikatlar mantiqining formulalari
Predikatlar mantiqi quyidagi simvolizmga ega:P, q, r, ... belgilar qabul qiluvchi taklif o‘zgaruvchilari
ikkita qiymat: 1 - rost, 0 - noto'g'ri.
Mavzu o'zgaruvchilari - x, y, z, …, ishlaydi
ba'zi M to'plamidagi qiymatlar;
x0, y0, z0 - mavzu konstantalari, ya'ni mavzuning qiymatlari
o'zgaruvchilar.
P(·), Q(·), F(·), … - bir o‘rinli predikativ o‘zgaruvchilar;
Q(·,·,…,·), R(·,·, …,·) n-o‘rinli predikativ o‘zgaruvchilardir.
P0(·), Q0(·,·, …,·) doimiy predikatlarning belgilaridir.
Mantiqiy amallarning belgilari: , .
Kvantor amallarining belgilari: x, x.
Yordamchi belgilar: qavs, vergul.
12. Predikatlar mantiqining formulalari
Agar mavzu o'zgaruvchisi bo'lsa, erkin deyiladimiqdor ko'rsatkichiga darhol ergashmaydi va unga kiritilmaydi
bu o'zgaruvchi bo'yicha kvantifikatorning qamrovi, qolganlari
o'zgaruvchilar,
kirish qutisi
V
formula
chaqiriladi
ulangan.
y z (P(x,y) P(y,z))
Predikat mantiqining formulalari quyidagilardir:
Har bir predikat harfi va predikat harfi bilan
keyin qavs ichida mavzu o'zgaruvchilari.
F G, F G, G, F G, F G, (y)F shaklidagi ifodalar,
(y)G, bu erda F va G predikat mantiqiy formulalar, o'zgaruvchi
aql.
13. Predikatlar mantiqining formulalari
Har bir gap ham oʻzgaruvchan, hamdoimiy, formuladir (elementar).
Va
Agar F(·,·, …,·) n-ar predikatli o‘zgaruvchi bo‘lsa
yoki doimiy predikat va x1, x2,…, xn ob'ektivdir
o'zgaruvchilar yoki mavzu konstantalari (yo'q
albatta, hammasi bir-biridan farq qiladi), keyin F(x1, x2,…, xn) bo'ladi
formula. Ushbu formula elementar deb ataladi, in
uning mavzu o'zgaruvchilari bepul, emas
bog‘langan miqdor ko‘rsatkichlari.
14. Predikatlar mantiqining formulalari
Agar A va B formulalar bo'lsa va ular bir xil bo'lsamavzu o'zgaruvchisi ulardan birida emas
bog'langan va boshqasida erkin, keyin A B so'zlari,
A B, A B formulalardir. Ushbu formulalarda ular
asl formulalarda bo'lgan o'zgaruvchilar
ozod va ozod bo'lganlar
bog‘langan, bog‘langan.
Agar A formula bo'lsa, u holda A formula va belgidir
A formuladan o'tishda mavzu o'zgaruvchilari
A formulasi o'zgarmaydi.
15. Predikatlar mantiqining formulalari
Agar A(x) sub'ekt bo'lgan formula bo'lsax o'zgaruvchisi erkin kiradi, keyin xA(x) va so'zlari
xA(x) formulalar, bundan tashqari, mavzu
o'zgaruvchi ularga bog'langan bo'ladi.
Nomlanganlardan boshqa har bir so'z
oldingi paragraflardagi formulalar mavjud emas
formula.
16. Predikatlar mantiqining formulalari
Masalan, agar P(x) va Q(x,y) bitta vaqo'sh predikatlar, q, r esa o'zgaruvchilardir
ifodalar, keyin formulalar ifodalar bo'ladi:
q, P(x), P(x) Q(x , y), xP(x) xQ(x, y), (Q(x, y) q) r
0
Masalan, so'z formula emas: xQ(x, y) P(x)
Bu erda formuladan beri 3-bandning sharti buziladi
xQ(x,y) x o'zgaruvchisi bog'langan va formulada ko'rinadi
P(x) o'zgaruvchisi x erkin kiradi.
Predikat mantiqiy formulasining ta'rifidan ko'rinib turibdiki
Har bir taklif algebra formulasi
predikatlar mantiq formulasi.
17. Predikat formulasining talqini
Predikatlar hisoblash formulasini talqin qilishqaysi to'plamlarning instantsiyasi deyiladi
mavzu o'zgaruvchilari qiymatlarni oladi va
spetsifikatsiya
munosabatlar
Va
muvofiq
har bir predikat harfi uchun haqiqat to'plami.
18. Predikatlar hisoblash formulalari
xuddi shundayrost da
har qanday
talqinlar,
bular.
universal amal qiladi
xuddi shunday
yolg'on
da
har qanday
talqinlar,
bular.
bahsli
mumkin
(formulalar,
haqiqat
qaysi bog'liq
dan
talqinlar)
19. Predikat mantiq formulasining ma'nosi
Misol sifatida formulani ko'rib chiqingy z (P(x, y) P(y, z))
Formulada ikki o'rinli P(x, y) predikati aniqlangan
MxM o'rnating, bu erda M=(0,1,2,…,n,…), ya'ni. MxM=NxN.
Formula o'zgaruvchan predikat P(x,y), sub'ektni o'z ichiga oladi
x,y,z o'zgaruvchilari, ulardan ikkitasi y va z kvantlar bilan bog'langan,
va x bepul.
Keling, olamiz
orqasida
xos
ma'nosi
predikat
P(x,y)
sobit predikat P0(x,y): “x
U holda x0=5 dan kichik y qiymatlari uchun P0(x0,y) predikati
“noto‘g‘ri” qiymatini va qachon P(x,y) P(y,z) implikatsiyasini oladi
all z M qiymatini qabul qiladi "to'g'ri", ya'ni. bayonot
"to'g'ri" ma'nosiga ega.
20. Predikatlar mantiqining ekvivalent formulalari
Ta'rif 1.M domenidagi ekvivalent, agar ular qabul qilsalar
kiritilgan barcha qiymatlar uchun bir xil mantiqiy qiymatlar
M maydoniga tayinlangan o'zgaruvchilardan.
Ta'rif 2.
Ikkita predikatli mantiqiy formulalar A va B deyiladi
har qanday sohada ekvivalent bo'lsa, ekvivalent.
21. Predikatlar mantiqining ekvivalent formulalari
A(x) va B(x) o‘zgaruvchan predikatlar, C esa o‘zgaruvchi bo‘lsinbayonot (yoki x ni o'z ichiga olmaydi formula). Keyin ular bor
quyidagi ekvivalentlarni joylashtiring:
22. Predikatlar mantiqining ekvivalent formulalari
MisolOna(x,y) predikati x ning y ning onasi ekanligini bildiradi.
Keyin y xMother(x,y) har bir odamda borligini bildiradi
ona, bu to'g'ri gap.
x yOna(x,y) barcha odamlarning onasi borligini bildiradi
haqiqatga bog'liq bo'lgan yana bir bayonotdir
y olishi mumkin bo'lgan qiymatlar to'plami: agar u
ko'p aka-uka va opa-singillar, keyin bu haqiqat, aks holda
bu yolg'on bo'lsa.
Shunday qilib, universal kvantlarni qayta tartibga solish va
mavjudligi iboraning ma'nosi va ma'nosini o'zgartirishi mumkin.
23. Mantiqiy amallar qonunlari (predikatlar mantiqining umumiy amaldagi formulalari)
24. Mashq qilish
Quyidagi formulalarning inkorini toping25. Mashq qilish
VaMashq qilish
Ekvivalentligini isbotlang
x(A(x) B(x)) xA(x) xB(x)
A(x) va B(x) predikatlar bir xil yolg‘on bo‘lsin. Keyin bo'ladi
noto'g'ri va predikat A(x) B(x)
x(A(x) B(x))
Bunday holda, bayonotlar yolg'on bo'ladi
xA(x) xB(x)
Predikatlardan kamida bittasi (masalan, A(x)) bo'lmasin
xuddi shunday yolg'on. Keyin u bir xil yolg'on va bo'lmaydi
predikat A(x) B(x)
Bunda xA(x) x(A(x) B(x)) mulohazalari to'g'ri bo'ladi
Bu asl formulalar ham to'g'ri bo'lishini anglatadi
Shuning uchun: x(A(x) B(x)) xA(x) xB(x)
26.
O'z-o'zidanMaterialni batafsil o'rganish uchun
Biz o'zimiz o'qiymiz:
DARSLIK: “Matematik mantiq va nazariya
algoritmlar",
muallif Igoshin V.I.
157-164-betlar
165-178-betlar
178-183-betlar
27.
Uy vazifasiEkvivalentligini isbotlang
C xA(x) x(C A(x))
Formulaning umumiy asosli ekanligini isbotlang
A V (P(x) Q(x)) xP(x) xQ(x)
Formulaning mos kelmasligini isbotlang
A x((F (x) F (x)) (F (x) F (x)))
Predikatning funktsional tabiati boshqa kontseptsiyani kiritishni talab qiladi - miqdor ko'rsatkichi. (kvant – lotincha “qancha”) Kvantlovchi amallarni konyunksiya va dis’yunksiya amallarini chekli va cheksiz hududlarda umumlashtirish sifatida ko‘rish mumkin.
Umumiy miqdor ko'rsatkichi (hamma, hamma, hamma, har qanday (barchasi - "hamma")). Tegishli og'zaki ifoda quyidagicha eshitiladi:
"Har bir x P(x) uchun to'g'ri." Formuladagi o'zgaruvchining paydo bo'lishi, agar o'zgaruvchi kvant belgisidan so'ng darhol yoki o'zgaruvchi paydo bo'lgan kvant belgisi doirasida joylashgan bo'lsa, bog'lanishi mumkin. Boshqa barcha hodisalar erkindir, P(x) dan x(Px) yoki (Px) ga oʻtish x oʻzgaruvchisini bogʻlash yoki x oʻzgaruvchisiga (yoki P predikatiga) kvant biriktirish yoki x oʻzgaruvchining miqdoriy aniqlash deb ataladi. Miqdor ko'rsatkichi biriktirilgan o'zgaruvchi deyiladi bog'liq, bog'liq bo'lmagan kvantlash o'zgaruvchisi deyiladi ozod.
Masalan, P(x) predikatidagi x o’zgaruvchisi erkin deyiladi (x M ning istalgani), P(x) bayonida x o’zgaruvchisi bog’langan o’zgaruvchi deyiladi.
Ekvivalentlik to‘g‘ri: P(x 1)P(x 2)…P(x n),
P(x) – to‘plamda aniqlangan predikat M=(x 1,x 2 ...x 4)
Mavjudlik kvantifikatori(mavjud - "mavjud bo'lmoq"). Tegishli og'zaki ibora: "P(x) to'g'ri bo'lgan x bor." xP(x) bayonoti endi x ga bog'liq emas, x o'zgaruvchisi kvant bilan bog'langan.
Ekvivalentlik adolatli:
xP(x) = P(x 1)P(x 2)…P(x n), bu yerda
P(x) - M=(x 1 ,x 2 …x n ) to‘plamda aniqlangan predikat.
Umumiy kvant va ekzistensial miqdor ko'rsatkichi dual deyiladi, ba'zan kvant belgisi ishlatiladi! - "mavjud va bundan tashqari, faqat bitta."
Ko'rinib turibdiki, xP(x) bayoni faqat P(x) bir xil to'g'ri predikat bo'lgan yagona holatda to'g'ri bo'ladi, P(x) esa bir xil yolg'on predikat bo'lgandagina bayonot noto'g'ri bo'ladi.
Kvantor amallari ko'p joyli predikatlarga ham tegishli. X o‘zgaruvchisiga nisbatan P(x,y) predikatiga kvantlovchi amalni qo‘llash ikki o‘rinli P(x,y) predikati bilan bir o‘rinli xP(x,y) yoki xP() predikatini moslashtiradi. x,y), y ga qarab va x dan mustaqil.
Ikki o'rinli predikatga siz ikkala o'zgaruvchiga ham kvantlash amallarini qo'llashingiz mumkin. Keyin biz sakkizta bayonotni olamiz:
1. P(x,y); 2. P(x,y);
3. P(x,y); 4. P(x,y);
5. P(x,y); 6. P(x,y);
7. P(x,y); 8. P(x,y)
3-misol. Kvantorlarni predikatga qo'shishning mumkin bo'lgan variantlarini ko'rib chiqing P(x,y) – “x tomonidan bo'linadi y”, natural sonlar to'plamida aniqlangan (nolsiz) N. Qabul qilingan bayonotlarning og'zaki formulalarini bering va ularning haqiqatini aniqlang.
Miqdorlarni biriktirish operatsiyasi quyidagi formulalarga olib keladi:
“Har qanday ikkita natural son uchun biri ikkinchisiga boʻlinadi” (yoki 1) barcha natural sonlar istalgan natural songa boʻlinadi; 2) har qanday natural son har qanday natural sonning boʻluvchisi) yolgʻon;
“Ikkita natural son borki, birinchisi ikkinchisiga boʻlinadi” (1. “bir necha y soniga boʻlinadigan x natural soni bor”; 2. “y natural soni bor, u ning boʻluvchisi boʻladi” iboralari. ba'zi natural sonlar x") rost;
“Har qanday natural songa boʻlinadigan natural son bor” degan gap notoʻgʻri;
“Har bir natural son uchun birinchiga boʻlinadigan natural son mavjud” (yoki har bir natural son uchun dividend bor) toʻgʻri;
“Har bir natural son x uchun u boʻlinadigan natural y soni mavjud” (yoki “har bir natural son uchun boʻluvchi bor”) gapi toʻgʻri;
“Har bir natural sonning bo‘luvchisi bo‘lgan natural son bor” degan gap to‘g‘ri (bunday bo‘luvchi bitta).
Umumiy holatda, kvantlarning tartibini o'zgartirish bayonotning ma'nosini va uning mantiqiy ma'nosini o'zgartiradi, ya'ni. masalan, P(x,y) va P(x,y) gaplar boshqacha.
P(x,y) predikati x y ning onasi ekanligini bildirsin, u holda P(x,y) har bir odamning onasi borligini bildiradi - haqiqiy gap. P(x,y) barcha odamlarning onasi borligini bildiradi. Ushbu bayonotning haqiqati siz olishi mumkin bo'lgan qiymatlar to'plamiga bog'liq: agar u birodarlar to'plami bo'lsa, u to'g'ri, aks holda u noto'g'ri. Shunday qilib, umumbashariylik va mavjudlik miqdoriy ko'rsatkichlarini qayta tartibga solish ifodaning ma'nosi va ma'nosini o'zgartirishi mumkin.
a) boshlang'ich belgini (yoki) teskari belgi bilan almashtiring
b) predikatning qolgan qismidan oldin belgi qo'ying
Operator qaysi yordamida k.-l haqida. alohida ob'ekt bunday ob'ektlarning to'plami (to'plami) haqidagi bayonotga aylantiriladi.
Mantiqda ikkita asosiy kod qo'llaniladi: umumiylik kodi "V" va mavjudlik kodi "E". Tabiiy tilda jamoa tushunchasining uzoq semantik analoglari "hamma", "har qanday", "hamma" so'zlari; K. mavjudligining semantik analoglari - "ba'zi", "mavjud" so'zlari. K ma’lumotlar yordamida x ob’ekt P ga xos bo‘lgan P(x) tipidagi har qanday atributiv ko‘rinish VxP(x) tipidagi va ZxP(x) tipidagi tegishli kvant ko‘rsatkichiga aylantirilishi mumkin. Tarkibida “VxP(x)” miqdoriy formulasining o‘zi “hamma x uchun P(x) bor”, “ExP(x)” formulasi esa “ba’zi x uchun P(x) bor” deb o‘qiladi. VxP(x) ko'rinishdagi bayonot to'g'ri bo'ladi, agar har qanday x ning P xossasi bo'lsa; va agar hech bo'lmaganda bitta x ning P xossasi bo'lmasa, noto'g'ri bo'ladi. Xuddi shunday, ZxP(x) ko'rinishdagi bayonot, agar kamida bitta x P xossaga ega bo'lsa, to'g'ri bo'ladi; va agar x ning P xossasi bo'lmasa, noto'g'ri.
“VxP(x)”, “ExP(x)” elementar kvant formulalariga asoslanib, boshqa murakkabroq miqdorlovchi formulalar tuzilishi mumkin. Bunday formulalar orasidagi mantiqiy munosabatlar predikat mantiqida o'rganiladi. Xususan, “ZxP(x)” formulasi mantiqiy jihatdan “) VxQUANTITOR| P(x)” va “VxP(x)” formulasi “) Ex) P(x)” formulasiga ekvivalent, bu yerda “)” inkorlardir.
Yashirin shaklda mantiqlar allaqachon Aristotel tomonidan qo'llanilgan, ammo qat'iy substantiv va rasmiy ma'noda ular birinchi marta G. Frege mantig'iga kiritilgan.
Falsafa: Ensiklopedik lug'at. - M .: Gardariki. A.A. tomonidan tahrirlangan. Ivina. 2004 .
(dan lat. kvant - qancha), faqat bitta erkin o'zgaruvchini o'z ichiga olgan formulalarga qo'llaniladigan predikat mantiqiy operatori beradi (bayonot). Belgisi bilan belgilangan K. jamoalari mavjud (dan Ingliz hammasi - hammasi), va K. mavjudligi (mavjuddan - mavjud bo'lmoq): xP(x) izohlanadi (sm. talqini)"barcha x uchun P xossaga ega" kabi va xP(x) - "xususiyatga ega bo'lgan x mavjudmi?(x)" kabi. Agar (koinot) chekli bo‘lsa, xP(x) barcha P formulalar birikmasiga ekvivalent bo‘ladi (A), bu erda a - mavzu sohasining elementi. Xuddi shunday, xP(x) shaklning barcha formulalarining diszyunksiyasiga ekvivalentmi? (A). Agar mavzu maydoni cheksiz bo'lsa, u holda xP (x) va xP(x) mos ravishda cheksiz va diszyunksiya sifatida talqin qilinishi mumkin. Koʻp joyli predikatlar mantigʻida K.ga kirish (ya'ni yagona bo'lmagan) predikatlar hisobining aniqlanmasligiga olib keladi. Umumiylik va mavjudlik tamoyillari bilan taklif mantiqining mantiqiy bog`lovchilari o`rtasidagi turli munosabatlar predikatlar hisobida rasmiylashtiriladi.
Falsafiy ensiklopedik lug'at. - M.: Sovet Entsiklopediyasi. Ch. muharrir: L. F. Ilyichev, P. N. Fedoseev, S. M. Kovalev, V. G. Panov. 1983 .
(lot. quantumdan - qancha) - mantiqiy. operator mantiqiy uchun qo'llaniladi. ifodalar va miqdorlarni berish. K.ni qoʻllash natijasida olingan narsalarni oʻz ichiga oluvchi obʼyektlar sohasining (baʼzan predikatlar sohasining) xarakteristikasi. Qanday mantiqiy Umumiy, xususiy va individual mulohazalarning shakllarini ifodalash uchun taklif mantiqining vositalari etarli emas; printsiplarni kiritish orqali taklif mantiqini kengaytirish orqali olingan predikat mantiqida bunday hukmlar ifodalanadi. Shunday qilib, masalan, to'rtta asosiy. urf-odatlarni hukm qilish shakllari. “Hammasi A B”, “A yo‘q B”, “A ba’zi A B” va “Ba’zi A B emas” mantiqlarini yozish mumkin (agar Aristotel mantig‘ining A ning bo‘sh emasligi haqidagi taxmin qilingan talabini e’tiborsiz qoldirsak). umumiy mulohazalarda) quyidagi tarzda izohlangan simvolizmdan foydalangan holda: ∀(x) (A (x) ⊃ B (x)), ∀(x) (A (x) ⊃ B(x)), ∃(x) (A) (x ) & B (x)) va ∃ (x) (A (x) & B (x)). Kirish K. uni rasmiylashtirilgan mantiqiy tarzda yozish imkonini beradi. tabiatning ifoda tili. miqdorlarni o'z ichiga olgan tillar. k.-l ning xususiyatlari. mavzu yoki predikat sohalari. Tabiiy holatda Tillarda bunday xususiyatlarning tashuvchilari deyiladi. miqdoriy so'zlar, xususan, miqdorlarni o'z ichiga oladi. sonlar, olmoshlar “hamma”, “har biri”, “baʼzi”, feʼl “mavjud”, “har qanday”, “har bir”, “yakka” sifatlari, “cheksiz koʻp” qoʻshimchalari va boshqalar. Ma’lum bo‘lishicha, barcha aytilgan kvant so‘zlarni formalizmda ifodalash. tillar va mantiq Hisoblashda eng ko'p ishlatiladigan ikkitasi etarli. K.: K. umumiylik (yoki umumiylik), odatda ∀ belgisi bilan belgilanadi (teskari A harfi - inglizcha “barcha”, nemischa “alle” soʻzining bosh harfi va boshqalar) va K. borliq, odatda belgilanadi. ∃ belgisi bo'yicha (teskari E harfi inglizcha "exist", nemischa "existieren" so'zining bosh harfi va boshqalar); miqdor belgisidagi ∀ va ∃ belgilaridan keyin ma’lum alifbodagi harf qo‘yiladi, bu o‘zgaruvchi deb ataladi, bu odatda kvant belgisining bir qismi sifatida qabul qilinadi: ∀x, ∀y, ∀ F, ∃x, ∃a va boshqalar. K. umumiyligi uchun quyidagi belgilar ham qoʻllaniladi:
K. mavjudligi uchun:

K. qoʻllanilgan ifodadan oldin K. belgisi qoʻyiladi (K.ni qoʻllash amali koʻpincha miqdorlashtirish deb ataladi); bu ibora qavslar ichiga olingan (agar bu noaniqlikka olib kelmasa, ko'pincha olib tashlanadi). Umumiy printsipni o'z ichiga olgan ∀x (A (x)) ifodasi "Barcha x uchun A (x) haqiqatdir" yoki "Har bir x uchun A (x) to'g'ri"; Mavjudlik K.ni oʻz ichiga olgan ∃x (A(x)) ifodasi “A(x) boʻlgan x bor”, yoki “Baʼzi x uchun A(x) toʻgʻri” deb oʻqiladi. Bu ikkala holatda ham, umuman olganda, A(x) ifodasi aslida x o'zgaruvchisiga bog'liq deb hisoblanmaydi (u umuman o'zgaruvchini o'z ichiga olmaydi, ya'ni ma'lum bir bayonotni bildirishi mumkin; bu holda u emas. ushbu bayonotning ma'nosini o'zgartiring). Biroq, asosiy K.ning maqsadi kvantlashtiruvchi oʻzgaruvchiga bogʻliq boʻlgan ifodadan olingan gaplar yoki hech boʻlmaganda ochiq (ochiq) formula boʻlgan bu ifoda bogʻliq boʻlgan oʻzgaruvchilar sonining kamayishidir (Qarang: Yopiq formula). Masalan, (y>0&z>0&x=y-z) ifoda uchta o'zgaruvchini (x, y va z) o'z ichiga oladi va k.-l bo'lganda gapga (to'g'ri yoki noto'g'ri) aylanadi. def. bu o'zgaruvchilarni ularning qiymatlari oralig'idan ma'lum ob'ektlar nomlari bilan almashtirish. ∃ z(y>0&z>0&x = y-z) ifodasi faqat ikkita o'zgaruvchiga (x va y) va ∃y∃z (y>0&z>0& &x = y –z) - bitta x ga bog'liq. Oxirgi formula, shuning uchun ma'lum bir xususiyatni (bir joyni) ifodalaydi. Nihoyat, ∃x∃u∃z (y>0&z>0&x=y–z) formulasi toʻliq aniqlanganni ifodalaydi. bayonot.
Dr. Tarkibida K. boʻlgan formulalarga misollar: 1) ∀x(x>0); 2) ∃x(x>0); 3) ∀x (2+2=5); 4) ∃x (2+2=4); 5) ∀x (x = x)& (x+2=y); 6) x ∃y - formulaning ularning o'ng tomonidagi qismlari va formulaning ta'sir doirasi (x = z⊃x ≠ 0) Formula belgisida yoki formulada ma'lum bir o'zgaruvchining paydo bo'lishi. Ushbu o'zgaruvchini o'z ichiga olgan formulaning ta'sir doirasi , formuladagi o'zgaruvchining bog'langan hodisasi deb ataladi.Boshqa hollarda o'zgaruvchining paydo bo'lishi erkin deyiladi. Xuddi shu o'zgaruvchining ma'lum bir formulada bir joyda paydo bo'lishi mumkin. bog'langan shakl va boshqa joyda - bo'sh joyda.Bu, masalan, 5-formula: undagi x o'zgaruvchining dastlabki uchta (chapdan sanab) kelishi bog'langan, oxirgisi erkin. Ba'zan ular o'zgaruvchining ushbu formuladagi barcha hodisalari bog'langan bo'lsa, berilgan formulada bog'langanligini aytishadi. Matematika va mantiqda erkin o'zgaruvchini o'z ichiga olgan har qanday iborani (norasmiy yondashuvda) ko'rib chiqish mumkin, chunki so'zning odatiy ma'nosida u (ifoda) ushbu o'zgaruvchining turli qiymatlariga bog'liq; ushbu o'zgaruvchiga turli xil ma'nolarni berish orqali (ya'ni, uning barcha erkin hodisalarini ushbu o'zgaruvchining qiymatlari oralig'iga kiruvchi ma'lum bir ob'ekt nomi bilan almashtirish), biz ushbu iboraning qiymatiga qarab turli xil (umuman aytganda) ma'nolarini olamiz. o'zgaruvchining, ya'ni. o'rniga almashtirilgan doimiydan. Bog'langan o'zgaruvchilarga kelsak, ularni qamrab oluvchi iboralar aslida ularga bog'liq emas. Masalan, y ga (uning tarkibiga erkin kiritilgan) qarab ∃x(x = 2y) ifoda ∃z(z = 2y), ∃u(u = 2y) va hokazo ifodalarga ekvivalentdir. Bu mantiqiy ularga kiritilgan bog'liq o'zgaruvchilardan ifodalar deb atalmish topilgan. Dep.da taxmin qilingan yoki chiqarilgan tegishli o'zgaruvchilar nomini o'zgartirish qoidasi. mantiqiy hisob (qarang O'zgaruvchan, Predikatlar hisobi).
K. maʼnosining yuqoridagi talqini mantiqiy mazmun bilan bogʻliq. nazariyalar. To'g'ri hisob-kitoblarga kelsak. ma'no (rasmiy tizimlar deb ataladi), unda ularda u yoki bu hisobning "ma'nosi" haqida gapirishning hech qanday ma'nosi yo'q, bu erda oddiygina hisobning ma'lum bir belgisi. Hisoblashning ma'nosi (ma'nosi) haqidagi savol to'liq hisob-kitoblarni talqin qilish sohasiga tegishli. K.ni qoʻllashda kamida uchta talqin haqida gapirish mumkin: klassik, intuitivist va konstruktiv, mantiq va matematikadagi borliq va universallikning turli tushunchalariga mos keladi (qarang Intuisionizm, Konstruktiv mantiq). Klassik va intuitiv (konstruktiv) predikatlar hisobida, asliyat yoki formulalar isbotlanishi kerak bo'lgan formulani o'z ichiga olgan hollarda xulosa chiqarish usullari bir xil predikat hisobi bilan tavsiflanadi. miqdorni aniqlash postulatlari, masalan. Bernaysning postulatlari.
Umumiylik va mavjudlik tamoyillari mantiqda qo'llaniladigan tamoyillar turlarini tugatmaydi.Kengaytirilgan tamoyillar deyiladi. ∀xP(x)A(x) yoki ∃xQ(x)A(x) koʻrinishdagi cheklangan kvant tenglamalari, bunda x miqdoriy oʻzgaruvchining oʻzgarish diapazoni baʼzi maxsus oʻzgarishlar bilan “cheklangan”. predikat P(x) (yoki Q(x)). Cheklangan K. izlar yordamida umumiylik va borliq K. ga keltiriladi. ekvivalentlar: ∀xP(x)A(x) QUANTITOR ∀x(P(x) ⊃A(x)) va ∃xQ(x)A(x) QUANTITOR ∃x(Q(x)&A(x)). Koʻp qoʻllaniladigan yagonalik K.si ∃!xA(x) (“oʻziga xos x borki, A(x)”) ham, masalan, umumiylik va borliq K. orqali ifodalanadi. shunday: xA(x) QUANTITOR ∃xA(x)& ∀y∀z(A(y)&A(z)⊃y=z).
Cheklangan hisoblash tushunchasiga kirmaydigan hisoblarning boshqa turlari ham qo‘llaniladi.Bu ∃xnA(x) ko‘rinishdagi “raqamli” hisoblardir (“A(x) ning aniq n xil x bor”), hisoblashning intuitivistik mantiqida foydalaniladi.“kvazi-mavjudlik” ∃ xA(x), yoki (“A(x) kabi x mavjud emasligi haqiqat emas”); t.zr bilan. klassik “kvazimavjudlik” Q. mantigʻida borliq Q.sidan farqi yoʻq, intuisionistik mantiqda A( ga teng boʻlgan x ni topish algoritmining mavjudligi haqida hech narsa aytilmagan ∃xA(x) jumlasi. x), haqiqatda bunday x va K ning faqat “kvazi”sini tasdiqlaydi. ∃x∞A(x) cheksizligi (“A(x) kabi cheksiz ko'p x bor”). Cheksizlik tamoyillari va sonli terminlarni o'z ichiga olgan iboralar umumiylik va mavjudlik shartlari yordamida ham yozilishi mumkin. Kengaytirilgan predikat hisobida koeffitsientlar nafaqat mavzu o'zgaruvchilari, balki predikat o'zgaruvchilari tomonidan ham olinadi, ya'ni. ∃F∀xF(x), ∀F∃u(F(y)) va boshqalar ko’rinishdagi formulalar ko’rib chiqiladi.
Lit.: Gilbert D. va Ackerman V., Nazariy mantiq asoslari, trans. Ingliz tilidan, M., 1947, p. 81-108; Tarski A., Deduktiv fanlar mantiqi va metodologiyasiga kirish, trans. ingliz tilidan, M., 1948, haqida. 36-42, 100-102, 120-23; Kleene S.K., Metamatematikaga kirish, trans. ingliz tilidan, M., 1957, p. 72-80, 130-38; Cherkov A., Matematik mantiqqa kirish, trans. Ingliz tilidan, 1-jild, bet. 42–48; Kuznetsov A.V., Algoritmning mantiqiy konturlari, standartlashtirilgan rus tilidan axborot-mantiqiy tilga tarjimasi, in: Axborotni qayta ishlash, mashina tarjimasi va matnni avtomatik o'qish bo'yicha konferentsiyadagi ma'ruza tezislari, M., 1961; Mostowski A., Kvanterlarni umumlashtirish to'g'risida, "Fundam. math.", 1957, t. 44, № 1, b. 12–36; Hailperin T., Cheklangan miqdoriy aniqlash nazariyasi, I–II, "J. Symb. Logic", 1957, v. 22, № 1, bet. 19–35, № 2, b. 113–29.
Yu. Gastev. Moskva.
Falsafiy entsiklopediya. 5 jildda - M.: Sovet Entsiklopediyasi. F. V. Konstantinov tomonidan tahrirlangan. 1960-1970 .
Sinonimlar:
Boshqa lug'atlarda "QUANTITOR" nima ekanligini ko'ring:
Ism, sinonimlar soni: 1 operator (24) ASIS sinonim lug'ati. V.N. Trishin. 2013… Sinonim lug'at
miqdor ko'rsatkichi- - Telekommunikatsiya mavzulari, asosiy tushunchalar EN kvanti... Texnik tarjimon uchun qo'llanma
Miqdor ko'rsatkichi - predikatning haqiqat sohasini cheklaydigan va bayon yaratuvchi mantiqiy amallarning umumiy nomi. Eng tez-tez eslatib o'tilgan: Umumjahonlikning kvantifikatori (belgisi: , o'qiladi: “hamma uchun...”, “har biri uchun...” yoki “har bir...” ... Vikipediya
P(x) predikatining haqiqat sohasini tavsiflovchi bayonotni tuzish uchun P(x) predikatidan foydalanadigan mantiqiy amallarning umumiy nomi. Matematikada Mantiqda umumbashariylik va borliqning miqdoriy ko‘rsatkichi eng ko‘p qo‘llaniladi.Izoh degani... ... Matematik entsiklopediya
Miqdor ko'rsatkichi- (lotin kvantidan qancha) matematik mantiqning ma'lum operatsiyalarini belgilash uchun ishlatiladigan belgi, shu bilan birga ... ifodasi olingan ob'ektlar maydonining miqdoriy tavsifini beruvchi mantiqiy operatsiya. Zamonaviy tabiatshunoslikning boshlanishi
Predikatlar uchun bizga ma'lum bo'lgan mantiqiy amallardan tashqari ikkita yangi: mavjudlik va umumiylik kvantlarini biriktirish amali kiritiladi.
"Barcha uchun X"(har kim uchun X, har biriga X) deyiladi umumiy miqdor ko'rsatkichi va belgilanadi X.
Bayonotda "bor X"(ba'zilar uchun X, kamida bittasi uchun X, shunga o'xshash narsa bor X) deyiladi mavjudlik kvantifikatori va belgilanadi X.
"Yagona va bitta" bayonoti X"(bir ma'no uchun X) deyiladi yagonalik kvantifikatori : ! X.
Masalan: "Barcha butalar o'simliklardir." Ushbu bayonotda umumiy miqdor ko'rsatkichi ("barchasi") mavjud. Bayonotda "ko'p sonli raqamlar mavjud 5 "ekzistensial kvantifikatorni o'z ichiga oladi ("mavjud").
Ko'p joyli predikatdan gap olish uchun har bir o'zgaruvchini kvantlar bilan bog'lash kerak. Masalan, Agar P(x;y) demak, ikki o‘rinli predikatdir (xX) (yY) P(x; y)- bayonot.
Agar har bir o‘zgaruvchi kvant bilan bog‘lanmagan bo‘lsa, unda olingan narsa gap emas, balki kvant bilan bog‘lanmagan o‘zgaruvchiga bog‘liq predikat bo‘ladi. Demak, agar predikatdan oldin P(x;y) miqdor ko'rsatkichini qo'ying y, keyin predikatni olamiz (yY) P(x; y), o'zgaruvchiga qarab X.
Quyidagi gaplardan qaysi biri gap, qaysi biri predikat ekanligini aniqlaymiz: a) shunday bor X, Nima x+y = 2;
b) har qanday uchun X Va da tenglik mavjud x + y = y + x.
Yechim: Keling, ushbu gaplarning mantiqiy tuzilishini aniqlaymiz.
a) "Bunday narsa bor" jumlasi X, Nima x + y = 2” shaklida yozilishi mumkin (xR) x + y = 2. Faqat x o‘zgaruvchisi kvant bilan bog‘langanligi sababli, ikki o‘zgaruvchili so‘z yuritilayotgan gap predikatdir.
b) Taklif “har qanday uchun X Va da yuzaga keladi x + y = y + x” shaklida yozilishi mumkin : (xR) (yR) x + y = y + x, Qayerda ikkala o'zgaruvchi ham bog'liq. Shuning uchun bu jumla bayonotdir.
Agar formuladagi biron bir ob'ektiv o'zgaruvchi kvant bilan bog'lanmagan bo'lsa, u deyiladi erkin o'zgaruvchilar.
Masalan: (x) xy=uh. Mana o'zgaruvchi da hech qanday kvant bilan bog'lanmaydi, shuning uchun u erkindir. Berilgan bayonotning haqiqati unga bog'liq emas.
Miqdor ko'rsatkichlari (x) (x) deyiladi ikkilik bir-biriga, bir-birini, o'zaro.
Xuddi shu nomdagi kvantlar almashtirilishi mumkin, bu gapning haqiqatiga ta'sir qilmaydi.
Masalan: (y) (x) x + y = 5. Bu bayonot ham xuddi shunday ma'nosi, nima va (x) (y) x + y = 5.
Bir-biriga o'xshamaydigan kvantlar uchun tartibning o'zgarishi bayonotning haqiqatini o'zgartirishga olib kelishi mumkin.
Masalan: (x) (y) x<у , ya'ni. har qanday raqam uchun X ko'proq bor da- haqiqiy bayonot.
Keling, miqdor ko'rsatkichlarini almashtiramiz: (x) (y) x
Miqdor ko'rsatkichlarini joriy qilish bilan bog'liq holda quyidagilarni e'tiborga olish kerak:
1. Predikat mantiqiy formulasi bir xil ob'ektiv o'zgaruvchini o'z ichiga olmaydi, u formulaning bir qismida bog'langan va boshqa qismida erkin bo'ladi.
2. Bir xil o‘zgaruvchi bir-biriga qo‘sh bo‘lgan kvantlovchilar mintaqasida bo‘la olmaydi.
Ushbu shartlarning buzilishi deyiladi o'zgaruvchan to'qnashuv.
Kvantorli gapning haqiqat qiymati qanday aniqlanadi?
Gapni umumiy miqdor ko‘rsatkichi bilan isbotlash qiymatlarning har birini almashtirishda ishonch hosil qilishingiz kerak X predikatga aylanadi P(x) ikkinchisi haqiqiy bayonotga aylanadi. Agar X to'plam chekli bo'lsa, u holda bu barcha holatlarni sanab o'tish orqali amalga oshirilishi mumkin; agar X to'plam cheksiz bo'lsa, u holda umumiy shaklda fikr yuritish kerak.
Bayonot (x) P(x) agar bunday qiymatni belgilash mumkin bo'lsa, noto'g'ri AX, qaysi vaqtda P(x) yolg'on bayonotga aylanadi R(a). Shunung uchun, gapni umumiy miqdor belgisi bilan rad etish Bunga misol keltirish kifoya.
Bayonot (x) P(x) rost, agar bunday qiymatni belgilash mumkin bo'lsa AX, qaysi vaqtda P(x) haqiqiy bayonotga aylanadi R(a). Shuning uchun, tartibda gapning to‘g‘riligini miqdor ko‘rsatkichi bilan tasdiqlang mavjudlik , misol keltirish va shu bilan isbotlash kifoya.
Uchun bayonotning yolg'onligini tekshirish miqdor ko'rsatkichi bilan mavjudlik (x) P(x), har birining yolg'onligini tekshirish kerak P(x), P(x), …, P(x). Agar to'plam X Albatta, bu qo'pol kuch bilan amalga oshirilishi mumkin. Agar ko'p bo'lsa X cheksiz, keyin umumiy shaklda fikr yuritish kerak.
Misollar.
1. “Raqamlar orasidan” haqiqat qiymatini toping. 1, 2, 3, 4 tub son bor."
Yechim: Bayonot ekzistensial kvantifikatorni o'z ichiga oladi va shuning uchun bayonotlarning diszyunksiyasi sifatida ifodalanishi mumkin: " 1 - tub raqam" yoki " 2 - tub raqam" yoki " 3 - tub raqam" yoki " 4 - Bosh raqam". Dizyunksiyaning haqiqatini isbotlash uchun kamida bitta bayonotning haqiqati etarli, masalan, " 3 to'g'ri bo'lgan tub sondir. Shuning uchun, asl bayonot ham to'g'ri.
2. Har qanday kvadrat to'rtburchak ekanligini isbotlaylik.
Yechim: Bayonotda umumiy miqdor ko'rsatkichi mavjud. Shuning uchun uni birlashma sifatida taqdim etish mumkin: "kvadrat - to'rtburchak" va "kvadrat - to'rtburchak" va "kvadrat - to'rtburchak" va boshqalar. Bu gaplarning hammasi to‘g‘ri bo‘lgani uchun bu gaplarning bog‘lovchisi ham to‘g‘ri bo‘ladi, demak, asl gap ham to‘g‘ri bo‘ladi.
3. “Har qanday uchburchak teng yonlidir”. Bu yolg'on bayonot. Buni tekshirish uchun teng yonli bo'lmagan uchburchakni chizish kifoya.a
Miqdor ko‘rsatkichlari bilan gapning inkorini yasash zarur:
1) umumiylik miqdor ko‘rsatkichini borlik miqdor ko‘rsatkichi bilan, mavjudlik miqdorini umumiylik ko‘rsatkichi bilan almashtiring;
2) predikatni uning inkori bilan almashtiring.
Misol. Keling, quyidagi bayonotlar uchun inkorni shakllantiramiz:
a) to'plamning barcha elementlari Z tekis; b) ba'zi fe'llar "nima qilish kerak?" Degan savolga javob beradi.
Yechim: a) Umumiylik miqdor ko‘rsatkichini borlik miqdor ko‘rsatkichi bilan, ifodasini esa inkor bilan almashtiramiz: to‘plamning ayrim elementlari. Z g'alati.
b) Borliq sonlovchisini umumiylik sonlovchisi bilan, ifodasini esa inkor bilan almashtiraylik: barcha fe’llar “nima qilish kerak?” degan savolga javob bermaydi.
Predikat (lat. praedicatum- aytilgan, aytib o'tilgan, aytilgan) - kamida bitta o'zgaruvchi mavjud bo'lgan har qanday matematik bayonot. Predikat birinchi tartibli mantiqda asosiy tadqiqot ob'ekti hisoblanadi.
Predikat - bu o'zgaruvchilarning ruxsat etilgan qiymatlari uchun mantiqiy o'zgaruvchilarga ega ifoda.
Ifodalar: x > 5, x > y – predikatlar.
Predikat ( n-mahalliy yoki n-ary) - bu to'plamda aniqlangan qiymatlar to'plami (0,1) (yoki "noto'g'ri" va "to'g'ri") bo'lgan funksiya. Shunday qilib, to'plam elementlarining har bir to'plami M"to'g'ri" yoki "noto'g'ri" sifatida tavsiflanadi.
Predikat matematik munosabat bilan bog'lanishi mumkin: agar n-ka munosabatga mansub bo`lsa, unda predikat unga 1 ni qaytaradi.Xususan, unar predikat ma'lum to`plamga a'zolik munosabatini belgilaydi.
Predikat birinchi va yuqori tartibli mantiq elementlaridan biridir. Ikkinchi tartibli mantiqdan boshlab, kvantlar formulalardagi predikatlarga joylashtirilishi mumkin.
Predikat deyiladi xuddi shunday haqiqat va yozing:
agar argumentlar to'plamida u 1 qiymatini oladi.
Predikat deyiladi xuddi shunday yolg'on va yozing:
agar argumentlar to'plamida u 0 qiymatini oladi.
Predikat deyiladi mumkin, agar u kamida bitta argumentlar to'plamida 1 qiymatini qabul qilsa.
Predikatlar faqat ikkita ma'noga ega bo'lganligi sababli, ular uchun mantiqiy algebraning barcha amallari qo'llaniladi, masalan: inkor, implikatsiya, konyunksiya, dis'yunksiya va boshqalar.
Kvantor - predikatning haqiqat sohasini cheklovchi mantiqiy amallarning umumiy nomi. Eng tez-tez tilga olinadi:
Universal kvantifikator(belgilash: o'qiydi: "hamma uchun ...", "hamma uchun ..." yoki "har bir ...", "har qanday ...", "har qanday ... uchun").
Mavjudlik kvantifikatori(belgilash: , o'qiydi: "mavjud ..." yoki "topiladi ...").
Misollar
belgilaylik P(x) predikat " x 5 ga bo'linadi." Umumiy kvantdan foydalanib, biz quyidagi bayonotlarni rasmiy ravishda yozishimiz mumkin (albatta, noto'g'ri):
har qanday natural son 5 ga bo'linadi;
har bir natural son 5 ga karrali;
barcha natural sonlar 5 ga karrali;
quyida bayon qilinganidek:
![]() .
.
Quyidagi (allaqachon to'g'ri) bayonotlar ekzistensial kvantdan foydalanadi:
5 ga karrali natural sonlar mavjud;
5 ga karrali natural son mavjud;
kamida bitta natural son 5 ga bo'linadi.
Ularning rasmiy belgilari:
![]() .Tushunchaga kirish
.Tushunchaga kirish
X tub sonlar to‘plamida P(x) predikati berilgan bo‘lsin: “X tub son toqdir”. Keling, ushbu predikat oldiga "har qanday" so'zini qo'yaylik. Biz "har qanday tub son x toq" degan noto'g'ri bayonotni olamiz (bu bayonot noto'g'ri, chunki 2 - tub son).
Berilgan P(x) predikati oldiga “mavjud” so‘zini qo‘yib, “Toq bo‘lgan x tub son bor” degan to‘g‘ri gapni olamiz (masalan, x = 3).
Shunday qilib, predikat oldiga mantiqda kvantlovchilar deb ataladigan "hamma narsa", "mavjud" va hokazo so'zlarni qo'yish orqali predikatni gapga aylantirishingiz mumkin.
Matematik mantiqda kvantifikatorlar
Bayonot o'zgaruvchining diapazoni degan ma'noni anglatadi x predikatning haqiqat sohasiga kiritilgan P(x).
(“(x) ning barcha qiymatlari uchun bayonot to‘g‘ri.”)
Bayonot predikatning haqiqat sohasini bildiradi P(x) bo'sh emas.
(“Bayonot to‘g‘ri bo‘lgan (x) mavjud”).
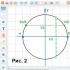
31-savol Grafik va uning elementlari. Asosiy tushunchalar. Hodisa, ko‘plik, halqa, tutashlik. Grafik turlari. Grafikdagi marshrut va uning uzunligi. Yo'nalishlarning tasnifi. Yo'naltirilgan va yo'naltirilmagan grafiklarning qo'shnilik matritsalari.
Matematik grafiklar nazariyasida va informatikada grafik - bu bo'sh bo'lmagan cho'qqilar to'plami va juft cho'qqilar to'plamidir.
Ob'ektlar grafikning cho'qqilari yoki tugunlari, ulanishlar esa yoylar yoki qirralar sifatida ifodalanadi. Turli xil qo'llash sohalari uchun grafiklar turlari yo'nalishda, ulanishlar soni bo'yicha cheklovlarda va cho'qqilar yoki qirralar haqida qo'shimcha ma'lumotlarda farq qilishi mumkin.
Grafikdagi yo'l (yoki zanjir) - bu cho'qqilarning chekli ketma-ketligi bo'lib, unda har bir cho'qqi (oxirgisidan tashqari) uchlari ketma-ketligidagi keyingisiga chekka bilan bog'langan.
Digrafdagi yo'naltirilgan yo'l uchlarning chekli ketma-ketligidir v i, buning uchun barcha juftliklar ( v i,v i+ 1) (yo'naltirilgan) qirralardir.
Tsikl - bu birinchi va oxirgi uchlari mos keladigan yo'l. Bunday holda, yo'lning (yoki tsiklning) uzunligi uning tarkibiy qismlarining sonidir qovurg'alar. E'tibor bering, agar cho'qqilar u Va v ba'zi bir chekkaning uchlari, keyin bu ta'rifga ko'ra, ketma-ketlik ( u,v,u) sikldir. Bunday "degenerativ" holatlarning oldini olish uchun quyidagi tushunchalar kiritiladi.
Yo'l (yoki tsikl) agar uning qirralari takrorlanmasa, oddiy deyiladi; oddiy bo'lsa va uning uchlari takrorlanmasa elementar. Buni ko'rish oson:
Ikki cho'qqini bog'laydigan har bir yo'lda bir xil ikkita cho'qqini bog'laydigan elementar yo'l mavjud.
Har qanday oddiy boshlang'ich bo'lmagan yo'lda elementar mavjud tsikl.
Har qanday oddiy ba'zi bir cho'qqi (yoki chekka) orqali o'tuvchi tsikli o'z ichiga oladi boshlang'ich bir xil cho'qqi (yoki chekka) orqali o'tadigan (sub-) tsikl.
Loop elementar sikldir.
Grafik yoki yo'naltirilmagan grafik G tartiblangan juftlikdir G: = (V,E
V
E bu chekkalar deb ataladigan juftliklar to'plami (yo'naltirilmagan grafik bo'lsa, tartibsiz).
V(va shuning uchun E, aks holda u ko'p to'plam bo'lar edi) odatda chekli to'plamlar hisoblanadi. Cheklangan grafiklar uchun olingan ko'plab yaxshi natijalar to'g'ri emas (yoki qandaydir tarzda farqlanadi). cheksiz grafiklar. Buning sababi shundaki, cheksiz to'plamlar holatida bir qator mulohazalar noto'g'ri bo'ladi.
Grafikning uchlari va qirralari grafik elementlari deb ham ataladi, grafikdagi uchlari soni | V| - tartib, qirralarning soni | E| - grafik hajmi.
Cho'qqilar u Va v chekka uchlari (yoki oddiygina uchlari) deb ataladi e = {u,v). Bir chekka, o'z navbatida, bu cho'qqilarni bog'laydi. Xuddi shu qirraning ikkita uchi qo'shni deyiladi.
Ikki qirraning umumiy uchi bo'lsa, qo'shni deyiladi.
Ikki chekka, agar ularning oxirgi uchlari to'plami mos kelsa, ko'p sonli deb ataladi.
Agar uning uchlari bir-biriga to'g'ri kelsa, chekka pastadir deb ataladi, ya'ni e = {v,v}.
daraja daraja V cho'qqilari V unga tushgan qirralarning sonini chaqiring (bu holda, looplar ikki marta hisoblanadi).
Agar cho'qqi biron bir chekkaning oxiri bo'lmasa, u izolyatsiya qilingan deyiladi; osilgan (yoki barg), agar u aniq bir chekkaning oxiri bo'lsa.
Yo'naltirilgan grafik (qisqartirilgan digraf) G tartiblangan juftlikdir G: = (V,A), ular uchun quyidagi shartlar bajariladi:
V cho'qqilar yoki tugunlarning bo'sh bo'lmagan to'plamidir,
A bu yoylar yoki yo'naltirilgan qirralar deb ataladigan (tartibli) aniq juftliklar to'plamidir.
yoy tartiblangan juft uchlaridir (v, w), uchi qayerda v boshlanishi deb ataladi va w- yoyning oxiri. Aytishimiz mumkinki, yoy yuqoridan olib boradi v tepaga w.
Aralash grafik
Aralash grafik G ba'zi qirralari yo'naltirilishi mumkin bo'lgan va ba'zilari yo'naltirilmagan bo'lishi mumkin bo'lgan grafikdir. Buyurtma qilingan uchlik sifatida yozilgan G: = (V,E,A), Qayerda V, E Va A yuqoridagi kabi aniqlangan.
Yo'naltirilgan va yo'naltirilmagan grafiklar aralash grafiklarning maxsus holatlaridir.
Izomorf grafiklar (?)
Grafik G grafikga izomorf deyiladi H, agar bijection mavjud bo'lsa f grafik uchlari to'plamidan G grafikning cho'qqilari to'plamiga H, quyidagi xususiyatga ega: agar grafikda bo'lsa G cho'qqidan chekka bor A tepaga B, keyin grafikda H f(A) tepaga f(B) va aksincha - agar grafikda bo'lsa H cho'qqidan chekka bor A tepaga B, keyin grafikda G tepadan chekka bo'lishi kerak f − 1 (A) tepaga f − 1 (B). Yo'naltirilgan grafik bo'lsa, bu ikkilanish chekka yo'nalishini ham saqlab qolishi kerak. Og'irlangan grafik bo'lsa, bijeksiyon chekka og'irligini ham saqlab turishi kerak.
Grafik qo'shnilik matritsasi G chekli sonli uchlari bilan n(1 dan boshlab raqamlangan n) kvadrat matritsadir A hajmi n, unda element qiymati a ij dan qirralarning soniga teng i grafikning th cho'qqisi j- cho'qqi.
Ba'zan, ayniqsa, yo'naltirilmagan grafikda, pastadir (chet i th cho'qqisining o'ziga) ikkita chekka, ya'ni diagonal elementning qiymati hisoblanadi. a ii bu holda atrofida aylanalar sonining ikki barobariga teng i th cho'qqisi.
Oddiy grafikning qo'shnilik matritsasi (ko'chadan yoki bir nechta qirralardan iborat) ikkilik matritsa bo'lib, asosiy diagonalda nollarni o'z ichiga oladi.
32-savol Funktsiya. Topshiriq berish usullari. Funksiyalarning tasnifi. Asosiy elementar funksiyalar va ularning grafiklari. Funksiyalarning tarkibi. Elementar funksiyalar.
Funktsiya - bu to'plam elementlari orasidagi munosabatni aks ettiruvchi matematik tushuncha. Aytishimiz mumkinki, funktsiya bu "qonun" bo'lib, unga ko'ra bitta to'plamning har bir elementi (deb ataladi ta'rif sohasi ) boshqa to'plamning biron bir elementi bilan yozishmalarga qo'yiladi (deb ataladi qiymatlar diapazoni ).
Funktsiyaning matematik kontseptsiyasi bir miqdor boshqa miqdorning qiymatini qanday to'liq aniqlashi haqidagi intuitiv fikrni ifodalaydi. Shunday qilib, o'zgaruvchining qiymati x ifoda ma’nosini o‘ziga xos tarzda belgilaydi x 2 va oyning qiymati undan keyingi oyning qiymatini yagona tarzda belgilaydi, shuningdek, har qanday odamni boshqa odam bilan - uning otasi bilan solishtirish mumkin. Xuddi shunday, ba'zi bir oldindan ishlab chiqilgan algoritm turli xil kirish ma'lumotlariga asoslangan holda ma'lum bir chiqish ma'lumotlarini ishlab chiqaradi.
Funktsiyani belgilash usullari
Analitik usul
Funksiya - ma'lum shartlarni qanoatlantiradigan ikkilik munosabat bo'lgan matematik ob'ekt. Funktsiya to'g'ridan-to'g'ri tartiblangan juftliklar to'plami sifatida ko'rsatilishi mumkin, masalan: funktsiya mavjud. Biroq, bu usul cheksiz to'plamlardagi funktsiyalar uchun mutlaqo mos kelmaydi (ular odatiy real funktsiyalar: quvvat, chiziqli, eksponensial, logarifmik va boshqalar).
Funktsiyani belgilash uchun quyidagi ifodadan foydalaning: . Bunda, x funktsiyani aniqlash sohasi bo'ylab ishlaydigan o'zgaruvchidir va y- qiymatlar diapazoni. Ushbu yozuv to'plamlar elementlari o'rtasida funktsional munosabat mavjudligini ko'rsatadi. X Va y har qanday tabiatdagi ob'ektlarning har qanday to'plamidan o'tishi mumkin. Bu raqamlar, vektorlar, matritsalar, olmalar, kamalak ranglari bo'lishi mumkin. Keling, misol bilan tushuntiramiz:
To'plam bo'lsin olma, samolyot, nok, stul va ko'p odam, lokomotiv, kvadrat. f funksiyani quyidagicha aniqlaymiz: (olma, odam), (samolyot, lokomotiv), (nok, kvadrat), (stul, odam). Agar to‘plam bo‘ylab o‘tuvchi x o‘zgaruvchini va to‘plam bo‘ylab o‘tuvchi y o‘zgaruvchini kiritsak, belgilangan funksiya analitik tarzda quyidagicha ko‘rsatilishi mumkin: .
Raqamli funktsiyalar ham xuddi shunday belgilanishi mumkin. Masalan: bu erda x haqiqiy sonlar to'plamidan o'tadi va ba'zi f funktsiyasini belgilaydi. Bu ifodaning o'zi funktsiya emasligini tushunish muhimdir. Ob'ekt sifatida funktsiya (tartibli juftliklar) to'plamidir. Va bu ifoda ob'ekt sifatida ikkita o'zgaruvchining tengligidir. Bu funktsiyani belgilaydi, lekin bitta emas.
Biroq, matematikaning ko‘pgina bo‘limlarida funksiyaning o‘zini ham, uni aniqlovchi analitik ifodani ham f(x) bilan belgilash mumkin. Bu sintaktik konventsiya nihoyatda qulay va asosli.
Grafik usul
Raqamli funksiyalarni grafik yordamida ham aniqlash mumkin. n ta o‘zgaruvchining real funksiyasi bo‘lsin.
Haqiqiy sonlar maydoni ustidagi ba'zi (n+1) o'lchovli chiziqli fazoni ko'rib chiqaylik (funksiya haqiqiy bo'lgani uchun). Keling, ushbu bo'shliqda har qanday asosni () tanlaymiz. Funktsiyaning har bir nuqtasi vektor bilan bog'langan: . Shunday qilib, biz belgilangan qoida bo'yicha berilgan funktsiyaning nuqtalariga mos keladigan chiziqli fazo vektorlari to'plamiga ega bo'lamiz. Tegishli affin fazoning nuqtalari ma'lum bir sirt hosil qiladi.
Agar erkin geometrik vektorlarning (yo‘naltirilgan segmentlarning) Evklid fazosini chiziqli fazo sifatida olsak va f funksiya argumentlari soni 2 dan oshmasa, ko‘rsatilgan nuqtalar to‘plamini chizma (grafik) ko‘rinishida vizual tasvirlash mumkin. ). Agar qo'shimcha ravishda asl asos ortonormal bo'lsa, biz funktsiya grafigining "maktab" ta'rifini olamiz.
3 yoki undan ko'p argumentli funktsiyalar uchun bu vakillik insonning ko'p o'lchovli bo'shliqlarning geometrik sezgisi yo'qligi sababli qo'llanilmaydi.
Biroq, bunday funktsiyalar uchun vizual yarim geometrik tasvirni topish mumkin (masalan, nuqtaning to'rtinchi koordinatasining har bir qiymati grafikdagi ma'lum bir rang bilan bog'lanishi mumkin).
Proportsional miqdorlar. Agar o'zgaruvchilar y Va x to'g'ridan-to'g'ri proportsionaldir
y = k x,

Qayerda k- doimiy qiymat ( proportsionallik omili).
Jadval to'g'ridan-to'g'ri proportsionallik– koordinatalar boshi orqali o‘tuvchi va o‘q bilan chiziq hosil qiluvchi to‘g‘ri chiziq X tangensi teng bo'lgan burchak k: sarg'ish = k(8-rasm). Shuning uchun proportsionallik koeffitsienti ham deyiladi qiyalik. 8-rasmda uchta grafik ko'rsatilgan k = 1/3, k= 1 va k = 3 .
Chiziqli funksiya. Agar o'zgaruvchilar y Va x 1-darajali tenglama bilan bog'langan:
A x + B y = C ,
bu erda raqamlarning kamida bittasi A yoki B nolga teng bo'lmasa, bu funksional bog'liqlikning grafigi to'g'ri chiziq. Agar C= 0, keyin u koordinatadan o'tadi, aks holda u o'tmaydi. Turli kombinatsiyalar uchun chiziqli funktsiyalarning grafiklari A,B,C 9-rasmda ko'rsatilgan.

Teskari proportsionallik. Agar o'zgaruvchilar y Va x teskari proportsionaldir, u holda ular orasidagi funksional munosabat tenglama bilan ifodalanadi:
y = k / x,
Qayerda k- doimiy qiymat.
 Teskari proportsional grafik - giperbola(10-rasm). Bu egri chiziqning ikkita novdasi bor. Giperbolalar dumaloq konus tekislik bilan kesishganda olinadi (konus kesimlari uchun "Stereometriya" bobidagi "Konus" bo'limiga qarang). 10-rasmda ko'rsatilganidek, giperbola nuqtalari koordinatalarining ko'paytmasi doimiy qiymat bo'lib, bizning misolimizda 1 ga teng. Umumiy holatda bu qiymat ga teng. k, bu giperbola tenglamasidan kelib chiqadi: xy = k.
Teskari proportsional grafik - giperbola(10-rasm). Bu egri chiziqning ikkita novdasi bor. Giperbolalar dumaloq konus tekislik bilan kesishganda olinadi (konus kesimlari uchun "Stereometriya" bobidagi "Konus" bo'limiga qarang). 10-rasmda ko'rsatilganidek, giperbola nuqtalari koordinatalarining ko'paytmasi doimiy qiymat bo'lib, bizning misolimizda 1 ga teng. Umumiy holatda bu qiymat ga teng. k, bu giperbola tenglamasidan kelib chiqadi: xy = k.
Giperbolaning asosiy xususiyatlari va xususiyatlari:
x 0, diapazon: y 0 ;
Funktsiya monotonik (kamayuvchi) da x< 0va da x> 0, lekin emas
tanaffus nuqtasi tufayli monotonik umumiy x = 0);
Cheklanmagan funksiya, bir nuqtada uzluksiz x= 0, toq, davriy bo'lmagan;
- Funktsiyada nol yo'q.
Kvadrat funksiya. Bu funksiya: y = bolta 2 + bx + c, Qayerda a, b, c- doimiy, a b=c= 0 va y = bolta 2. Ushbu funktsiyaning grafigi kvadrat parabola - OY, deb ataladi parabolaning o'qi.Nuqta O parabolaning tepasi.

Kvadrat funksiya. Bu funksiya: y = bolta 2 + bx + c, Qayerda a, b, c- doimiy, a 0. Eng oddiy holatda bizda: b=c= 0 va y = bolta 2. Ushbu funktsiyaning grafigi kvadrat parabola - koordinatalarning kelib chiqishidan o'tuvchi egri chiziq (11-rasm). Har bir parabolaning simmetriya o'qi bor OY, deb ataladi parabolaning o'qi.Nuqta O parabolaning uning o'qi bilan kesishishi deyiladi parabolaning tepasi.
Funksiya grafigi y = bolta 2 + bx + c- shuningdek, bir xil turdagi kvadrat parabola y = bolta 2, lekin uning cho'qqisi boshlang'ichda emas, balki koordinatali nuqtada yotadi:

Kvadrat parabolaning koordinatalar tizimidagi shakli va joylashishi butunlay ikkita parametrga bog'liq: koeffitsient a da x 2 va diskriminant D:D=b 2 – 4ac. Bu xususiyatlar kvadrat tenglamaning ildizlarini tahlil qilishdan kelib chiqadi ("Algebra" bo'limidagi tegishli bo'limga qarang). Kvadrat parabola uchun barcha mumkin bo'lgan turli holatlar 12-rasmda ko'rsatilgan.
 Kvadrat parabolaning asosiy xarakteristikalari va xossalari:
Kvadrat parabolaning asosiy xarakteristikalari va xossalari:
Funktsiya doirasi: < x+ (ya’ni. x R) va hudud
qiymatlar: … (Iltimos, bu savolga o'zingiz javob bering!);
Butun funktsiya monotonik emas, balki tepaning o'ng yoki chap tomonida joylashgan
o'zini monoton kabi tutadi;
Funktsiya cheklanmagan, hamma joyda, hatto qachon ham davom etadi b = c = 0,
va davriy bo'lmagan;
- da D< 0 не имеет нулей.
 Eksponensial funktsiya. Funktsiya y = a x, Qayerda a- musbat doimiy son deyiladi eksponensial funktsiya.Dalil x qabul qiladi har qanday haqiqiy qiymatlar; funksiyalar qiymat sifatida qabul qilinadi faqat ijobiy raqamlar, chunki aks holda bizda ko'p qiymatli funksiya mavjud. Ha, funksiya y = 81x da bor x= 1/4 to'rt xil qiymat: y = 3, y = 3, y = 3 i Va y = 3 i(Iltimos, tekshiring!). Lekin biz faqat funktsiyaning qiymati sifatida qaraymiz y= 3. uchun ko'rsatkichli funktsiyaning grafiklari a= 2 va a= 1/2 17-rasmda keltirilgan. Ular (0, 1) nuqtadan o'tadilar. Da a= 1 bizda o'qga parallel bo'lgan to'g'ri chiziqning grafigi mavjud X, ya'ni. funksiya 1 ga teng doimiy qiymatga aylanadi. Qachon a> 1 bo'lsa, eksponensial funktsiya ortadi va 0 bo'lsa< a < 1 – убывает. Основные характеристики и свойства показательной функции:
Eksponensial funktsiya. Funktsiya y = a x, Qayerda a- musbat doimiy son deyiladi eksponensial funktsiya.Dalil x qabul qiladi har qanday haqiqiy qiymatlar; funksiyalar qiymat sifatida qabul qilinadi faqat ijobiy raqamlar, chunki aks holda bizda ko'p qiymatli funksiya mavjud. Ha, funksiya y = 81x da bor x= 1/4 to'rt xil qiymat: y = 3, y = 3, y = 3 i Va y = 3 i(Iltimos, tekshiring!). Lekin biz faqat funktsiyaning qiymati sifatida qaraymiz y= 3. uchun ko'rsatkichli funktsiyaning grafiklari a= 2 va a= 1/2 17-rasmda keltirilgan. Ular (0, 1) nuqtadan o'tadilar. Da a= 1 bizda o'qga parallel bo'lgan to'g'ri chiziqning grafigi mavjud X, ya'ni. funksiya 1 ga teng doimiy qiymatga aylanadi. Qachon a> 1 bo'lsa, eksponensial funktsiya ortadi va 0 bo'lsa< a < 1 – убывает. Основные характеристики и свойства показательной функции:
Funktsiya doirasi: < x+ (ya’ni. x R);
diapazon: y> 0 ;
Funktsiya monotonik: u bilan ortadi a> 1 va 0 da kamayadi< a < 1;
- Funktsiyada nol yo'q.
 Logarifmik funktsiya. Funktsiya y=log a x, Qayerda a– 1 ga teng bo‘lmagan doimiy musbat son deyiladi logarifmik. Bu funktsiya ko'rsatkichli funktsiyaga teskari funktsiyadir; uning grafigini (18-rasm) ko’rsatkichli funksiya grafigini 1-koordinata burchagi bissektrisasi atrofida aylantirib olish mumkin.
Logarifmik funktsiya. Funktsiya y=log a x, Qayerda a– 1 ga teng bo‘lmagan doimiy musbat son deyiladi logarifmik. Bu funktsiya ko'rsatkichli funktsiyaga teskari funktsiyadir; uning grafigini (18-rasm) ko’rsatkichli funksiya grafigini 1-koordinata burchagi bissektrisasi atrofida aylantirib olish mumkin.
Logarifmik funktsiyaning asosiy xarakteristikalari va xossalari:
Funktsiya doirasi: x> 0 va qiymatlar diapazoni: < y+
(ya'ni y R);
Bu monotonik funktsiya: u kabi ortadi a> 1 va 0 da kamayadi< a < 1;
Funktsiya cheksiz, hamma joyda uzluksiz, davriy emas;
Funktsiya bitta nolga ega: x = 1.
Trigonometrik funktsiyalar. Trigonometrik funktsiyalarni qurishda biz foydalanamiz radian burchaklar o'lchovi.Keyin funktsiya y= gunoh x grafik bilan ifodalanadi (19-rasm). Bu egri chiziq deyiladi sinusoid.

Funksiya grafigi y=cos x 20-rasmda keltirilgan; bu ham grafikni siljitish natijasida hosil bo'ladigan sinus to'lqinidir y= gunoh x eksa bo'ylab X2 tomonidan chapga

Ushbu grafiklardan ushbu funktsiyalarning xarakteristikalari va xususiyatlari aniq:
Domen: < x+ qiymatlar diapazoni: 1 y +1;
Bu funksiyalar davriydir: ularning davri 2;
Cheklangan funksiyalar (| y| , hamma joyda uzluksiz, monoton emas, balki
deb atalgan monotonlik intervallari, ular ichida joylashgan
o'zini monotonik funktsiyalar kabi tuting (19-rasm va 20-rasmdagi grafiklarga qarang);
Funktsiyalar cheksiz sonli nolga ega (batafsil ma'lumot uchun bo'limga qarang).
"Trigonometrik tenglamalar").
Funksiya grafiklari y= sarg'ish x Va y= krovat x mos ravishda 21-rasm va 22-rasmda ko'rsatilgan.

Grafiklardan ko'rinib turibdiki, bu funktsiyalar: davriy (ularning davri ,
cheksiz, odatda monotonik emas, lekin monotonlik intervallariga ega
(qaysi biri?), uzluksiz (bu funksiyalar qanday uzilish nuqtalariga ega?). Mintaqa
Ushbu funktsiyalarning ta'riflari va qiymatlari diapazoni:
Funksiyalar y= Arsin x(23-rasm) va y= Arccos x(24-rasm) ko'p qiymatli, cheksiz; ularning ta'rif sohasi va qiymatlar diapazoni mos ravishda: 1 x+1 va < y+ . Ushbu funktsiyalar ko'p qiymatli bo'lgani uchun, qilmang
Boshlang'ich matematikada ko'rib chiqiladigan, ularning asosiy qiymatlari teskari trigonometrik funktsiyalar sifatida qabul qilinadi: y= arksin x Va y= arkkos x; ularning grafiklari 23-rasmda va 24-rasmda qalin chiziqlar bilan ajratilgan.
Funksiyalar y= arksin x Va y= arkkos x quyidagi xususiyatlar va xususiyatlarga ega:
Ikkala funksiya ham bir xil ta'rif sohasiga ega: 1 x +1 ;
ularning qiymat diapazoni: /2 y/2 uchun y= arksin x va 0 y Uchun y= arkkos x;
(y= arksin x- funktsiyani oshirish; y= arkkos x - kamayadi);
Har bir funksiya bitta nolga ega ( x funktsiya uchun = 0 y= arksin x Va
x funktsiya uchun = 1 y= arkkos x).

Funksiyalar y= Arktan x(25-rasm) va y= Arkko x(26-rasm) - ko'p qiymatli, cheksiz funktsiyalar; ularning ta'rif sohasi: x+ . Ularning asosiy ma'nolari y= arktan x Va y= arkkot x teskari trigonometrik funksiyalar sifatida qaraladi; ularning grafiklari 25-rasmda va 26-rasmda qalin novdalar bilan ajratilgan.
Funksiyalar y= arktan x Va y= arkkot x quyidagi xususiyatlar va xususiyatlarga ega:
Ikkala funksiya ham bir xil ta'rif sohasiga ega: x + ;
ularning qiymat diapazoni: /2<y < /2 для y= arktan x va 0< y < для y= arkkos x;
Funktsiyalar cheklangan, davriy bo'lmagan, doimiy va monotonik
(y= arktan x- funktsiyani oshirish; y= arkkot x - kamayadi);
Faqat funktsiya y= arktan x bitta nolga ega ( x= 0);
funktsiyasi y= arkkot x nolga ega emas.
Funksiyalarning tarkibi
Agar ikkita xarita berilgan bo'lsa va , bu erda , u holda formula bo'yicha berilgan "uchdan oxirigacha xarita" mantiqiy bo'ladi, bu funksiyalar tarkibi deb ataladi va va bilan belgilanadi.

1.30-rasm.Uchdan oxirigacha displey