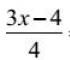Úkoly pro aplikaci Pythagorovy věty. Začněte v Science Doc v Pythagorových větách

Ujistěte se, že zadaný trojúhelník je pravoúhlý, protože Pythagorova věta platí pouze pro pravoúhlé trojúhelníky. V pravoúhlém trojúhelníku má jeden ze tří úhlů vždy 90 stupňů.

• Pravý úhel v pravoúhlém trojúhelníku je označen čtvercem místo křivky, která představuje nepravé úhly.

Označte strany trojúhelníku. Označte nohy jako "a" a "b" (nohy jsou strany protínající se v pravém úhlu) a přeponu jako "c" (přepona je největší strana pravoúhlého trojúhelníku, která leží naproti pravému úhlu).

Určete, kterou stranu trojúhelníku chcete najít. Pythagorova věta umožňuje najít libovolnou stranu pravoúhlého trojúhelníku (pokud jsou známy další dvě strany). Určete, kterou stranu (a, b, c) je třeba najít.

• Pokud je například přepona rovna 5 a přepona rovná 3. V tomto případě musíte najít druhou větev. K tomuto příkladu se vrátíme později.
• Pokud jsou další dvě strany neznámé, je nutné najít délku jedné z neznámých stran, aby bylo možné aplikovat Pythagorovu větu. K tomu použijte základní goniometrické funkce (pokud je vám zadána hodnota jednoho z nepravých úhlů).

Nahraďte ve vzorci a 2 + b 2 \u003d c 2 hodnoty, které vám byly přiděleny (nebo hodnoty, které jste našli). Pamatujte, že a a b jsou nohy a c je přepona.

• V našem příkladu napište: 3² + b² = 5².

Umocněte každou známou stranu. Nebo ponechte exponenty – čísla můžete odmocnit později.

• V našem příkladu napište: 9 + b² = 25.

Izolujte neznámou stranu na jedné straně rovnice. Chcete-li to provést, přeneste známé hodnoty na druhou stranu rovnice. Pokud najdete přeponu, tak v Pythagorově větě je již izolována na jedné straně rovnice (není tedy třeba nic dělat).

• V našem příkladu přesuňte 9 na pravou stranu rovnice, abyste izolovali neznámou b². Získáte b² = 16.

Vezměte druhou odmocninu obou stran rovnice. V této fázi je na jedné straně rovnice neznámá (druhá mocniny) a na druhé straně průsečík (číslo).

• V našem příkladu je b² = 16. Vezměte druhou odmocninu obou stran rovnice a získejte b = 4. Druhá větev je tedy 4 .

Používejte Pythagorovu větu v každodenním životě, protože ji lze použít ve velkém množství praktických situací. K tomu se naučte rozpoznávat pravoúhlé trojúhelníky v každodenním životě – v každé situaci, kdy se dva předměty (nebo čáry) protínají v pravém úhlu a třetí předmět (nebo čára) spojuje (diagonálně) vrcholy prvních dvou předmětů (resp. čáry), můžete použít Pythagorovu větu k nalezení neznámé strany (pokud jsou známy další dvě strany).

• Příklad: Daný žebřík opřený o budovu. Spodní část schodiště je 5 metrů od paty zdi. Vrchol schodiště je 20 metrů od země (po zdi). Jaká je délka žebříku?
  • "5 metrů od základny zdi" znamená, že a = 5; "je 20 metrů od země" znamená, že b = 20 (to znamená, že máte dvě nohy pravoúhlého trojúhelníku, protože stěna budovy a povrch Země se protínají v pravém úhlu). Délka žebříku je délka přepony, která není známa.
    • a² + b² = c²
    • (5)² + (20)² = c²
    • 25 + 400 = c²
    • 425 = c²
    • c = √425
    • c = 20,6. Tedy přibližná délka schodů je 20,6 metru.

Kdo se zajímá o historii Pythagorovy věty, která je probírána ve školních osnovách, bude zvědavý i na takovou skutečnost, jakou byla v roce 1940 vydána kniha se třemi sty sedmdesáti důkazy této zdánlivě jednoduché věty. Ale zaujalo mysl mnoha matematiků a filozofů různých epoch. V Guinessově knize rekordů je zapsána jako věta s maximálním počtem důkazů.

Historie Pythagorovy věty

Věta spojená se jménem Pythagoras byla známá dlouho před narozením velkého filozofa. Takže v Egyptě při stavbě staveb byl před pěti tisíci lety vzat v úvahu poměr stran pravoúhlého trojúhelníku. Babylonské texty zmiňují stejný poměr stran pravoúhlého trojúhelníku 1200 let před narozením Pythagora.

Nabízí se otázka, proč pak příběh říká – vznik Pythagorovy věty patří jemu? Odpověď může být jen jedna – dokázal poměr stran v trojúhelníku. Udělal to, co před staletími nedělali ti, kteří jednoduše používali poměr stran a přeponu, stanovenou zkušeností.

Ze života Pythagora

Budoucí velký vědec, matematik, filozof se narodil na ostrově Samos v roce 570 před naším letopočtem. V historických dokumentech se zachovaly informace o otci Pythagora, který byl řezbářem drahokamů, ale o jeho matce nejsou žádné informace. O narozeném chlapci říkali, že je to vynikající dítě, které od dětství projevovalo vášeň pro hudbu a poezii. Historici připisují Hermodamanta a Pherekida ze Syrosu učitelům mladého Pythagora. První uvedl chlapce do světa Múz a druhý, jako filozof a zakladatel italské filozofické školy, nasměroval pohled mladého muže k logu.

Ve věku 22 let (548 př. n. l.) odešel Pythagoras do Naucratis studovat jazyk a náboženství Egypťanů. Jeho cesta dále vedla v Memphisu, kde díky kněžím, kteří prošli jejich důmyslnými testy, pochopil egyptskou geometrii, což možná přimělo zvídavého mladíka k prokázání Pythagorovy věty. Historie později přiřadí toto jméno teorému.

Zajat babylonským králem

Na cestě domů do Hellas je Pythagoras zajat babylonským králem. Ale pobyt v zajetí prospěl zvídavé mysli začínajícího matematika, musel se hodně učit. V těch letech byla matematika v Babylonu skutečně rozvinutější než v Egyptě. Strávil dvanáct let studiem matematiky, geometrie a magie. A možná to byla babylonská geometrie, která se podílela na důkazu poměru stran trojúhelníku a na historii objevu věty. Pythagoras na to měl dostatek znalostí a času. Ale že se to stalo v Babylonu, neexistuje žádné dokumentární potvrzení ani vyvrácení.

V roce 530 př.n.l Pythagoras prchá ze zajetí do své vlasti, kde žije na dvoře tyrana Polykrata v postavení polootroka. Takový život Pythagorovi nevyhovuje a odejde do jeskyní na Samosu a poté se vydá na jih Itálie, kde se v té době nacházela řecká kolonie Croton.

Tajný mnišský řád

Na základě této kolonie zorganizoval Pythagoras tajný mnišský řád, který byl náboženským spolkem a vědeckou společností zároveň. Tato společnost měla svou chartu, která hovořila o dodržování zvláštního způsobu života.

Pythagoras tvrdil, že aby člověk porozuměl Bohu, musí znát takové vědy, jako je algebra a geometrie, znát astronomii a rozumět hudbě. Výzkumná práce se omezila na poznání mystické stránky čísel a filozofie. Je třeba poznamenat, že principy, které v té době hlásal Pythagoras, mají v současné době smysl při napodobování.

Mnoho objevů, které učinili Pythagorovi žáci, bylo připisováno jemu. Přesto je zkrátka historie vzniku Pythagorovy věty tehdejšími starověkými historiky a životopisci přímo spojena se jménem tohoto filozofa, myslitele a matematika.

Pythagorovo učení

Možná, že myšlenka spojení věty se jménem Pythagoras byla vyvolána prohlášením historiků velkého Řeka, že v notoricky známém trojúhelníku s nohami a přeponami jsou zašifrovány všechny jevy našeho života. A tento trojúhelník je „klíčem“ k vyřešení všech problémů, které se objeví. Velký filozof řekl, že bychom měli vidět trojúhelník, pak můžeme předpokládat, že problém je ze dvou třetin vyřešen.

Pythagoras vyprávěl o svém učení pouze svým studentům ústně, aniž by si dělal poznámky, držel to v tajnosti. Učení největšího filozofa se bohužel do dnešních dnů nedochovalo. Něco z toho uniklo, ale nelze říci, nakolik je pravda a nakolik nepravda na tom, co se stalo známým. Ani s historií Pythagorovy věty není vše jisté. Historici matematiky pochybují o autorství Pythagora, podle jejich názoru byl teorém používán mnoho století před jeho narozením.

Pythagorova věta

Může se to zdát zvláštní, ale neexistují žádná historická fakta o důkazu věty samotným Pythagorem – ani v archivech, ani v žádných jiných zdrojích. V moderní verzi se věří, že nepatří nikomu jinému než samotnému Euklidovi.

Existují důkazy o jednom z největších historiků matematiky Moritzi Cantorovi, který objevil na papyru uloženém v berlínském muzeu, sepsaném Egypťany kolem roku 2300 před naším letopočtem. E. rovnost, která zní: 3² + 4² = 5².

Krátce z historie Pythagorovy věty

Formulace věty z euklidovských „počátků“ v překladu zní stejně jako v moderní interpretaci. V jeho čtení není nic nového: čtverec strany protilehlé pravému úhlu se rovná součtu čtverců stran sousedících s pravým úhlem. Skutečnost, že starověké civilizace Indie a Číny používaly teorém, potvrzuje pojednání Zhou Bi Suan Jin. Obsahuje informace o egyptském trojúhelníku, který popisuje poměr stran jako 3:4:5.

Neméně zajímavá je další čínská matematická kniha „Chu-pei“, která zmiňuje i pythagorejský trojúhelník s vysvětlením a kresbami, které se shodují s kresbami hinduistické geometrie Baškary. O trojúhelníku samotném kniha říká, že pokud lze pravý úhel rozložit na jeho jednotlivé části, pak čára, která spojuje konce stran, bude rovna pěti, pokud je základna tři a výška je čtyři.

Indické pojednání „Sulva Sutra“, pocházející asi ze 7.–5. století před naším letopočtem. e., vypráví o konstrukci pravého úhlu pomocí egyptského trojúhelníku.

Důkaz věty

Ve středověku považovali studenti dokazování teorému za příliš obtížné. Slabí studenti se učili věty nazpaměť, aniž by rozuměli významu důkazu. V tomto ohledu se jim dostalo přezdívky „osli“, protože Pythagorova věta pro ně byla nepřekonatelnou překážkou jako most pro osla. Ve středověku studenti přišli s hravým veršem na téma této věty.

Chcete-li Pythagorovu větu nejsnazším způsobem dokázat, měli byste jednoduše změřit její strany, aniž byste v důkazu používali koncept oblastí. Délka strany naproti pravému úhlu je c a k ní přiléhající a a b, výsledkem je rovnice: a 2 + b 2 \u003d c 2. Toto tvrzení, jak je uvedeno výše, je ověřeno měřením délek stran pravoúhlého trojúhelníku.

Pokud začneme důkaz věty uvažováním plochy obdélníků postavených na stranách trojúhelníku, můžeme určit plochu celého obrázku. Bude se rovnat ploše čtverce se stranou (a + b) a na druhé straně součtu ploch čtyř trojúhelníků a vnitřního čtverce.

(a + b) 2 = 4 x ab/2 + c2;

a2 + 2ab + b2;

c 2 = a 2 + b 2 , což mělo být prokázáno.

Praktický význam Pythagorovy věty spočívá v tom, že ji lze použít k nalezení délek segmentů bez jejich měření. Při stavbě konstrukcí se počítají vzdálenosti, umístění podpěr a nosníků, určují se těžiště. Pythagorova věta se také uplatňuje ve všech moderních technologiích. Na větu nezapomněli ani při tvorbě filmů ve 3D-6D rozměrech, kde se kromě obvyklých 3 hodnot zohledňuje výška, délka, šířka, čas, vůně a chuť. Ptáte se, jak souvisí chutě a vůně s teorémem? Vše je velmi jednoduché – při promítání filmu je potřeba spočítat, kde a co voní a chutě v hledišti režírovat.

Je to jen začátek. Na zvídavé mysli čeká neomezený prostor pro objevování a vytváření nových technologií.

Pythagoras je řecký vědec, který žil asi před 2500 lety (564-473 př.nl).

Nechť je dán pravoúhlý trojúhelník, jehož strany A, b a s(obr. 267).

Po jeho stranách postavíme čtverce. Plochy těchto čtverců jsou resp A 2 , b 2 a s 2. Pojďme to dokázat s 2 = a 2 +b 2 .

Sestrojme dva čtverce MKOR a M'K'O'R' (obr. 268, 269), přičemž za stranu každého z nich vezmeme úsečku rovnající se součtu ramen pravoúhlého trojúhelníku ABC.

Po dokončení konstrukcí znázorněných na obrázcích 268 a 269 v těchto čtvercích uvidíme, že čtverec MKOR je rozdělen na dva čtverce s plochami A 2 a b 2 a čtyři stejné pravoúhlé trojúhelníky, z nichž každý se rovná pravoúhlému trojúhelníku ABC. Čtverec M'K'O'R' je rozdělen na čtyřúhelník (na obrázku 269 je vystínován) a čtyři pravoúhlé trojúhelníky, z nichž každý je roven trojúhelníku ABC. Stínovaný čtyřúhelník je čtverec, protože jeho strany jsou stejné (každá je rovna přeponě trojúhelníku ABC, tj. s), a úhly jsou přímky ∠1 + ∠2 = 90°, odkud ∠3 = 90°).

Součet ploch čtverců postavených na nohách (na obrázku 268 jsou tyto čtverce stínované) se tedy rovná ploše čtverce MKOR bez součtu ploch čtyř stejných trojúhelníků a ploše ​čtverec postavený na přeponě (na obrázku 269 je tento čtverec rovněž zastíněn) se rovná ploše čtverce M'K'O'R', rovné čtverci MKOR, bez součtu ploch čtyři podobné trojúhelníky. Proto se plocha čtverce postaveného na přeponě pravoúhlého trojúhelníku rovná součtu ploch čtverců postavených na nohách.

Dostáváme vzorec s 2 = a 2 +b 2, kde s- přepona, A a b- nohy pravoúhlého trojúhelníku.

Pythagorova věta se dá shrnout takto:

Druhá mocnina přepony pravoúhlého trojúhelníku se rovná součtu čtverců nohou.

Ze vzorce s 2 = a 2 +b 2 můžete získat následující vzorce:

A 2 = s 2 - b 2 ;

b 2 = s 2 - A 2 .

Tyto vzorce lze použít k nalezení neznámé strany pravoúhlého trojúhelníku, která má dvě jeho strany.

Například:

a) jsou-li dány nohy A= 4 cm, b\u003d 3 cm, pak můžete najít přeponu ( s):

s 2 = a 2 +b 2, tzn. s 2 = 42 + 32; s 2 = 25, odkud s= √25 = 5(cm);

b) je-li dána přepona s= 17 cm a noha A= 8 cm, pak můžete najít jinou nohu ( b):

b 2 = s 2 - A 2, tzn. b 2 = 17 2 - 8 2 ; b 2 = 225, odkud b= √225 = 15 (cm).

Důsledek: Je-li ve dvou pravoúhlých trojúhelníkech ABC a A 1 B 1 C 1 přepona s a s 1 jsou stejné a noha b trojúhelník ABC je větší než noha b 1 trojúhelník A 1 B 1 C 1,

pak nohu A trojúhelník ABC je menší než noha A 1 trojúhelník A 1 B 1 C 1 .

Na základě Pythagorovy věty skutečně dostáváme:

A 2 = s 2 - b 2 ,

A 1 2 = s 1 2 - b 1 2

V psaných vzorcích jsou minuendy stejné a subtrahend v prvním vzorci je větší než subtrahend ve druhém vzorci, proto je první rozdíl menší než druhý,

tj. A 2 a 12. Kde A a 1.

1

Shapovalová L.A. (stanice Egorlykskaya, MBOU ESOSH č. 11)

1. Glazer G.I. Dějiny matematiky ve škole VII - VIII ročníky, příručka pro učitele, - M: Education, 1982.

2. Dempan I.Ya., Vilenkin N.Ya. Příručka „Za stránkami učebnice matematiky“ pro žáky 5.–6. – M.: Osvícení, 1989.

3. Zenkevič I.G. „Estetika lekce matematiky“. – M.: Osvícení, 1981.

4. Litzman V. Pythagorova věta. - M., 1960.

5. Vološinov A.V. "Pythagoras". - M., 1993.

6. Pichurin L.F. „Za stránkami učebnice algebry“ . - M., 1990.

7. Zemljakov A.N. "Geometrie v 10. třídě." - M., 1986.

8. Noviny "Matematika" 17/1996.

9. Noviny "Matematika" 3/1997.

10. Antonov N.P., Vygodskii M.Ya., Nikitin V.V., Sankin A.I. „Sbírka úloh v elementární matematice“. - M., 1963.

11. Dorofeev G.V., Potapov M.K., Rozov N.Kh. "Matematická příručka". - M., 1973.

12. Shchetnikov A.I. „Pythagorejská doktrína počtu a velikosti“. - Novosibirsk, 1997.

13. „Reálná čísla. Iracionální výrazy» Třída 8. Tomsk University Press. – Tomsk, 1997.

14. Atanasyan M.S. "Geometrie" ročník 7-9. – M.: Osvícení, 1991.

15. URL: www.moypifagor.narod.ru/

16. URL: http://www.zaitseva-irina.ru/html/f1103454849.html.

V tomto akademickém roce jsem se seznámil se zajímavou větou, známou, jak se ukázalo, z dávných dob:

"Čtverec postavený na přeponě pravoúhlého trojúhelníku se rovná součtu čtverců postavených na nohách."

Obvykle se objev tohoto tvrzení připisuje starověkému řeckému filozofovi a matematikovi Pythagorovi (VI. století před naším letopočtem). Ale studium starověkých rukopisů ukázalo, že tento výrok byl znám dávno před narozením Pythagora.

Přemýšlel jsem, proč je v tomto případě spojen se jménem Pythagoras.

Relevance tématu: Pythagorova věta má velký význam: používá se v geometrii doslova na každém kroku. Věřím, že Pythagorova díla jsou stále aktuální, protože kamkoli se podíváme, všude můžeme vidět plody jeho skvělých myšlenek, vtělených do různých odvětví moderního života.

Účelem mého výzkumu bylo: zjistit, kdo byl Pythagoras a jaký vztah má k této větě.

Při studiu historie věty jsem se rozhodl zjistit:

Existují další důkazy této věty?

Jaký význam má tato věta v životě lidí?

Jakou roli sehrál Pythagoras ve vývoji matematiky?

Z životopisu Pythagora

Pythagoras ze Samosu je velký řecký vědec. Jeho sláva je spojena se jménem Pythagorovy věty. Ačkoli nyní již víme, že tato věta byla známa ve starověkém Babylóně 1200 let před Pythagorem a v Egyptě 2000 let před ním byl znám pravoúhlý trojúhelník se stranami 3, 4, 5, stále ji nazýváme jménem tohoto starověkého vědec.

O životě Pythagora není s jistotou známo téměř nic, ale s jeho jménem je spojeno velké množství legend.

Pythagoras se narodil v roce 570 př. n. l. na ostrově Samos.

Pythagoras měl hezký vzhled, nosil dlouhé vousy a na hlavě zlatý diadém. Pythagoras není jméno, ale přezdívka, kterou filozof dostal za to, že vždy mluvil správně a přesvědčivě, jako řecký orákulum. (Pythagoras - "přesvědčovací řeč").

V roce 550 př. n. l. se Pythagoras rozhodne a odejde do Egypta. Před Pythagorem se tedy otevírá neznámá země a neznámá kultura. Pythagoras byl v této zemi velmi ohromen a překvapen a po několika pozorováních života Egypťanů si Pythagoras uvědomil, že cesta k poznání, chráněná kastou kněží, vede přes náboženství.

Po jedenácti letech studia v Egyptě odchází Pythagoras do své vlasti, kde po cestě padá do babylonského zajetí. Tam se seznamuje s babylonskou vědou, která byla rozvinutější než egyptská. Babyloňané uměli řešit lineární, kvadratické a některé typy kubických rovnic. Po útěku ze zajetí nemohl dlouho zůstat ve své vlasti kvůli atmosféře násilí a tyranie, která tam vládla. Rozhodl se přestěhovat do Crotonu (řecká kolonie v severní Itálii).

Právě v Krotónu začíná nejslavnější období v životě Pythagora. Tam založil něco jako nábožensko-etické bratrstvo nebo tajný mnišský řád, jehož členové byli povinni vést tzv. pythagorejský způsob života.

Pythagoras a Pythagorejci

Pythagoras zorganizoval v řecké kolonii na jihu Apeninského poloostrova náboženské a etické bratrstvo, například mnišský řád, který se později nazýval Pythagorejská unie. Členové svazu museli dodržovat určité zásady: za prvé usilovat o to, aby bylo krásné a slavné, za druhé být užitečné a za třetí usilovat o vysoké potěšení.

Systém morálních a etických pravidel, který Pythagoras odkázal svým žákům, byl zkompilován do jakéhosi mravního kodexu pythagorejských „Zlatých veršů“, které byly velmi populární v době antiky, středověku a renesance.

Pythagorejský systém studií se skládal ze tří částí:

Učení o číslech - aritmetika,

Učení o figurách - geometrie,

Učení o stavbě vesmíru - astronomie.

Vzdělávací systém stanovený Pythagorem přetrval po mnoho staletí.

Pythagorova škola udělala mnoho pro to, aby dala geometrii charakter vědy. Hlavním rysem Pythagorovy metody byla kombinace geometrie s aritmetikou.

Pythagoras se hodně zabýval proporcemi a průběhy a pravděpodobně i podobností obrazců, protože se zasloužil o vyřešení problému: „Sestavte třetí, velikostně stejné jako jeden z dat a podobné druhému, na základě dán dvěma číslicemi."

Pythagoras a jeho studenti představili koncept polygonálních, přátelských, dokonalých čísel a studovali jejich vlastnosti. Aritmetika jako způsob počítání Pythagora nezajímala a hrdě prohlásil, že „aritmetiku staví nad zájmy obchodníka“.

Členové Pythagorejské unie byli obyvateli mnoha měst v Řecku.

Pythagorejci do své společnosti přijímali i ženy. Unie vzkvétala více než dvacet let a poté začalo pronásledování jejích členů, mnoho studentů bylo zabito.

O smrti samotného Pythagora kolovalo mnoho různých legend. Ale učení Pythagora a jeho žáků žilo dál.

Z historie vzniku Pythagorovy věty

V současné době je známo, že tuto větu neobjevil Pythagoras. Někteří se však domnívají, že to byl Pythagoras, kdo jako první podal úplný důkaz, zatímco jiní mu tuto zásluhu upírají. Někteří připisují Pythagorovi důkaz, který Euklides podává v první knize svých Živlů. Na druhou stranu Proclus tvrdí, že důkaz v Elementech má na svědomí sám Euclid. Jak vidíme, historie matematiky nemá téměř žádné spolehlivé konkrétní údaje o životě Pythagora a jeho matematické činnosti.

Historický přehled Pythagorovy věty začněme starověkou Čínou. Zde přitahuje zvláštní pozornost matematická kniha Chu-pei. Tato esej říká toto o pythagorejském trojúhelníku se stranami 3, 4 a 5:

"Pokud se pravý úhel rozloží na jednotlivé části, pak čára spojující konce jeho stran bude 5, když základna je 3 a výška je 4."

Je velmi snadné reprodukovat jejich způsob konstrukce. Vezměte lano o délce 12 m a přivažte ho k němu podél barevného pruhu ve vzdálenosti 3 m. z jednoho konce a 4 metry od druhého. Mezi stranami o délce 3 a 4 metry bude uzavřen pravý úhel.

Geometrie mezi hinduisty byla úzce spjata s kultem. Je vysoce pravděpodobné, že věta o druhé mocnině přepony byla známa již v Indii kolem 8. století před naším letopočtem. Spolu s čistě rituálními předpisy existují díla geometricky teologické povahy. V těchto spisech, pocházejících ze 4. nebo 5. století před naším letopočtem, se setkáváme s konstrukcí pravého úhlu pomocí trojúhelníku o stranách 15, 36, 39.

Ve středověku definovala Pythagorova věta hranici, když ne největší možné, tak alespoň dobrých matematických znalostí. Charakteristická kresba Pythagorovy věty, kterou dnes někdy školáci proměňují například v cylindr oblečený v róbě profesora nebo muže, byla v tehdejší době často používána jako symbol matematiky.

Na závěr uvádíme různé formulace Pythagorovy věty přeložené z řečtiny, latiny a němčiny.

Euklidova věta zní (doslovný překlad):

"V pravoúhlém trojúhelníku se čtverec strany překrývající pravý úhel rovná čtvercům na stranách, které svírají pravý úhel."

Jak vidíte, v různých zemích a různých jazycích existují různé verze formulace známé věty. Byly vytvořeny v různých dobách a v různých jazycích a odrážejí podstatu jednoho matematického vzorce, jehož důkaz má také několik možností.

Pět způsobů, jak dokázat Pythagorovu větu

starověké čínské důkazy

Na staré čínské kresbě jsou čtyři stejné pravoúhlé trojúhelníky s nohami a, b a přeponou c naskládány tak, že jejich vnější obrys tvoří čtverec se stranou a + b a vnitřní tvoří čtverec se stranou c, postavený na přepona

a2 + 2ab + b2 = c2 + 2ab

Důkaz od J. Gardfielda (1882)

Uspořádejme dva stejné pravoúhlé trojúhelníky tak, aby noha jednoho z nich byla pokračováním druhého.

Plocha uvažovaného lichoběžníku se zjistí jako součin poloviny součtu základen a výšky

Na druhé straně se plocha lichoběžníku rovná součtu ploch získaných trojúhelníků:

Porovnáním těchto výrazů dostaneme:

Důkaz je jednoduchý

Tento důkaz získáme v nejjednodušším případě rovnoramenného pravoúhlého trojúhelníku.

Pravděpodobně u něj tato věta začala.

Opravdu, stačí se podívat na dlaždice rovnoramenných pravoúhlých trojúhelníků, abychom viděli, že teorém je pravdivý.

Například pro trojúhelník ABC: čtverec postavený na přeponě AC obsahuje 4 počáteční trojúhelníky a čtverce postavené na nohách obsahují dva. Věta byla prokázána.

Důkaz starověkých hinduistů

Čtverec se stranou (a + b) lze rozdělit na části buď jako na obr. 12. a, nebo jako na Obr. 12b. Je zřejmé, že díly 1, 2, 3, 4 jsou na obou obrázcích stejné. A pokud se rovní odečítají od rovných (ploch), pak rovní zůstanou, tzn. c2 = a2 + b2.

Euklidův důkaz

Po dvě tisíciletí byl nejčastějším důkazem Pythagorovy věty, kterou vynalezl Euklides. Je umístěn v jeho slavné knize "Začátky".

Euklides snížil výšku BH od vrcholu pravého úhlu k přeponě a dokázal, že jeho prodloužení rozděluje čtverec dokončený na přeponě na dva obdélníky, jejichž plochy se rovnají plochám odpovídajících čtverců postavených na nohách.

Kresba použitá v důkazu této věty se vtipně nazývá „Pythagorejské kalhoty“. Dlouhou dobu byl považován za jeden ze symbolů matematické vědy.

Aplikace Pythagorovy věty

Význam Pythagorovy věty spočívá v tom, že z ní nebo s její pomocí lze odvodit většinu geometrických vět a vyřešit mnoho problémů. Praktický význam Pythagorovy věty a její inverzní věty navíc spočívá v tom, že je lze použít k nalezení délek segmentů bez měření samotných segmentů. To jakoby otevírá cestu z přímky do roviny, z roviny do objemového prostoru a dále. Právě z tohoto důvodu je Pythagorova věta tak důležitá pro lidstvo, které se snaží objevovat další dimenze a vytvářet technologie v těchto dimenzích.

Závěr

Pythagorova věta je tak slavná, že je těžké si představit člověka, který o ní neslyšel. Zjistil jsem, že existuje několik způsobů, jak dokázat Pythagorovu větu. Prostudoval jsem řadu historických a matematických zdrojů včetně informací na internetu a uvědomil jsem si, že Pythagorova věta je zajímavá nejen svou historií, ale také tím, že zaujímá důležité místo v životě a vědě. Svědčí o tom různé interpretace textu této věty, které jsem v tomto příspěvku uvedl, a způsoby jejího dokazování.

Pythagorova věta je tedy jednou z hlavních a dalo by se říci nejdůležitější věty geometrie. Jeho význam spočívá v tom, že z něj nebo s jeho pomocí lze odvodit většinu geometrických vět. Pythagorova věta je pozoruhodná také tím, že sama o sobě není vůbec samozřejmá. Vlastnosti rovnoramenného trojúhelníku jsou například vidět přímo na výkresu. Ale bez ohledu na to, jak moc se díváte na pravoúhlý trojúhelník, nikdy neuvidíte, že mezi jeho stranami existuje jednoduchý vztah: c2 = a2 + b2. K prokázání se proto často používá vizualizace. Předností Pythagora bylo, že podal úplný vědecký důkaz této věty. Zajímavá je osobnost samotného vědce, jehož paměť není touto větou náhodou uchována. Pythagoras je skvělý řečník, učitel a vychovatel, organizátor své školy, zaměřené na harmonii hudby a čísel, dobro a spravedlnost, znalosti a zdravý životní styl. Může dobře sloužit jako příklad pro nás, vzdálené potomky.

Bibliografický odkaz

Tumanová S.V. NĚKOLIK ZPŮSOBŮ, JAK DOKÁZAT PYTHAGOROVU VĚTU // Začněte ve vědě. - 2016. - č. 2. - S. 91-95;
URL: http://science-start.ru/ru/article/view?id=44 (datum přístupu: 28.02.2020).

Podle van der Waerdena je velmi pravděpodobné, že poměr v obecné podobě byl znám již v Babylonu kolem 18. století před naším letopočtem. E.

Přibližně 400 let před naším letopočtem. e., podle Proclus, Plato dal metodu pro nalezení Pythagorean trojice, kombinovat algebru a geometrii. Kolem roku 300 př.n.l. E. v "Prvcích" Euklida se objevil nejstarší axiomatický důkaz Pythagorovy věty.

Formulace

Hlavní formulace obsahuje algebraické operace - v pravoúhlém trojúhelníku, jehož délky jsou stejné a (\displaystyle a) a b (\displaystyle b), a délka přepony je c (\displaystyle c), vztah je splněn:

.

Je také možná ekvivalentní geometrická formulace, která se uchýlí k pojmu plocha číslo: v pravoúhlém trojúhelníku se plocha čtverce postaveného na přeponě rovná součtu ploch čtverců postavených na nohách. V této podobě je věta formulována v Euklidově Principia.

Inverzní Pythagorova věta- tvrzení o pravoúhlosti libovolného trojúhelníku, jehož délky stran souvisí vztahem a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)). V důsledku toho pro jakoukoli trojici kladných čísel a (\displaystyle a), b (\displaystyle b) a c (\displaystyle c), takové, že a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)), existuje pravoúhlý trojúhelník s nohami a (\displaystyle a) a b (\displaystyle b) a přepona c (\displaystyle c).

Důkaz

Ve vědecké literatuře bylo zaznamenáno nejméně 400 důkazů Pythagorovy věty, což je vysvětleno jak základní hodnotou pro geometrii, tak elementaritou výsledku. Hlavní směry důkazů jsou: algebraické použití poměrů prvků trojúhelník (takový je např. oblíbená podobnostní metoda), plošná metoda, existují i ​​různé exotické důkazy (např. pomocí diferenciálních rovnic).

Prostřednictvím podobných trojúhelníků

Euklidův klasický důkaz si klade za cíl stanovit rovnost ploch mezi obdélníky vytvořenými disekcí čtverce nad přeponou s výškou z pravého úhlu se čtverci nad nohama.

Konstrukce použitá pro důkaz je následující: pro pravoúhlý trojúhelník s pravým úhlem C (\displaystyle C), čtverce nad nohama a a čtverce nad přeponou A B I K (\displaystyle ABIK) výška se staví CH (\displaystyle CH) a paprsek, který v něm pokračuje s (\displaystyle s), rozdělující čtverec nad přeponou na dva obdélníky a . Důkaz je zaměřen na stanovení rovnosti ploch obdélníku A H J K (\displaystyle AHJK) se čtvercem přes nohu A C (\displaystyle AC); obdobným způsobem se stanoví rovnost ploch druhého obdélníku, což je čtverec nad přeponou, a obdélníku nad druhým ramenem.

Rovnost ploch obdélníku A H J K (\displaystyle AHJK) a A C E D (\displaystyle ACED) vytvořený pomocí kongruence trojúhelníků △ A C K ​​​​(\displaystyle \triangle ACK) a △ A B D (\displaystyle \triangle ABD), přičemž plocha každého z nich se rovná polovině plochy čtverců A H J K (\displaystyle AHJK) a A C E D (\displaystyle ACED) respektive ve spojení s následující vlastností: plocha trojúhelníku se rovná polovině plochy obdélníku, pokud mají postavy společnou stranu, a výška trojúhelníku ke společné straně je druhá strana obdélník. Shoda trojúhelníků vyplývá z rovnosti dvou stran (stran čtverců) a úhlu mezi nimi (složeného z pravého úhlu a úhlu v A (\displaystyle A).

Důkaz tedy prokazuje, že plocha čtverce nad přeponou se skládá z obdélníků A H J K (\displaystyle AHJK) a B H J I (\displaystyle BHJI), se rovná součtu ploch čtverců nad nohama.

Důkaz Leonarda da Vinciho

Plošná metoda zahrnuje také důkaz nalezený Leonardem da Vincim. Nechť existuje pravoúhlý trojúhelník △ A B C (\displaystyle \triangle ABC) pravý úhel C (\displaystyle C) a čtverce A C E D (\displaystyle ACED), B C F G (\displaystyle BCFG) a A B H J (\displaystyle ABHJ)(viz obrázek). V tomto důkazu na straně H J (\displaystyle HJ) posledně jmenovaný trojúhelník je konstruován směrem ven, shodný △ A B C (\displaystyle \triangle ABC) se navíc odráží jak vzhledem k přeponě, tak vzhledem k výšce k ní (tj. J I = B C (\displaystyle JI=BC) a H I = AC (\displaystyle HI=AC)). Rovný C I (\displaystyle CI) rozdělí čtverec postavený na přeponě na dvě stejné části, protože trojúhelníky △ A B C (\displaystyle \triangle ABC) a △ J H I (\displaystyle \triangle JHI) ve stavebnictví jsou si rovni. Důkaz stanoví kongruenci čtyřúhelníků C A J I (\displaystyle CAJI) a D A B G (\displaystyle DABG), přičemž plocha každého z nich se na jedné straně rovná součtu poloviny ploch čtverců na nohách a plochy původního trojúhelníku, na druhé straně polovině plochy čtverec na přeponě plus plocha původního trojúhelníku. Celkově se polovina součtu ploch čtverců nad nohama rovná polovině plochy čtverce nad přeponou, což je ekvivalentní geometrické formulaci Pythagorovy věty.

Důkaz infinitezimální metodou

Existuje několik důkazů pomocí techniky diferenciálních rovnic. Zejména Hardymu je připisován důkaz pomocí nekonečně malých přírůstků nohou a (\displaystyle a) a b (\displaystyle b) a přepona c (\displaystyle c) a zachování podobnosti s původním obdélníkem, to znamená zajištění následujících diferenciálních vztahů:

d a d c = c a (\displaystyle (\frac (da)(dc))=(\frac (c)(a))), d b d c = c b (\displaystyle (\frac (db)(dc))=(\frac (c)(b))).

Metodou separace proměnných je z nich odvozena diferenciální rovnice c d c = a d a + b d b (\displaystyle c\ dc=a\,da+b\,db), jehož integrace dává vztah c 2 = a 2 + b 2 + C o n s t (\displaystyle c^(2)=a^(2)+b^(2)+\mathrm (Const) ). Aplikace počátečních podmínek a = b = c = 0 (\displaystyle a=b=c=0) definuje konstantu jako 0, což má za následek tvrzení věty.

Kvadratická závislost v konečném vzorci se objevuje v důsledku lineární úměrnosti mezi stranami trojúhelníku a přírůstky, zatímco součet je způsoben nezávislými příspěvky přírůstku různých větví.

Variace a zobecnění

Podobné geometrické tvary na třech stranách

Důležité geometrické zobecnění Pythagorovy věty podal Euklides v „Počátcích“ a přesunul se od ploch čtverců na stranách k plochám libovolných podobných geometrických obrazců: součet ploch takových obrazců postavených na nohách bude rovná ploše postavy podobné jim, postavené na přeponě.

Hlavní myšlenkou tohoto zobecnění je, že plocha takového geometrického útvaru je úměrná čtverci libovolného z jeho lineárních rozměrů a zejména druhé mocnině délky kterékoli strany. Proto u podobných čísel s plochami A (\displaystyle A), B (\displaystyle B) a C (\displaystyle C) postavené na nohách s délkami a (\displaystyle a) a b (\displaystyle b) a přepona c (\displaystyle c) podle toho existuje vztah:

A a 2 = B b 2 = C c 2 ⇒ A + B = a 2 c 2 C + b 2 c 2 C (\displaystyle (\frac (A)(a^(2)))=(\frac (B )(b^(2)))=(\frac (C)(c^(2))\,\Šipka doprava \,A+B=(\frac (a^(2))(c^(2) ))C+(\frac (b^(2))(c^(2)))C).

Jelikož podle Pythagorovy věty a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)), pak je hotovo.

Pokud je navíc možné bez použití Pythagorovy věty dokázat, že pro plochy tří podobných geometrických útvarů na stranách pravoúhlého trojúhelníku platí vztah A + B = C (\displaystyle A+B=C), pak pomocí opaku důkazu Euklidova zobecnění můžeme odvodit důkaz Pythagorovy věty. Například, když na přeponě sestrojíme pravoúhlý trojúhelník shodný s počáteční s plochou C (\displaystyle C), a na nohách - dva podobné pravoúhlé trojúhelníky s plochami A (\displaystyle A) a B (\displaystyle B), pak se ukáže, že trojúhelníky na nohách jsou vytvořeny jako výsledek dělení počátečního trojúhelníku jeho výškou, to znamená, že součet dvou menších oblastí trojúhelníků se rovná ploše třetího, tedy A + B = C (\displaystyle A+B=C) a použitím vztahu pro podobná čísla je odvozena Pythagorova věta.

Kosinová věta

Pythagorova věta je speciálním případem obecnější kosinové věty, která dává do souvislosti délky stran v libovolném trojúhelníku:

a 2 + b 2 − 2 a b cos ⁡ θ = c 2 (\displaystyle a^(2)+b^(2)-2ab\cos (\theta )=c^(2)),

kde je úhel mezi stranami a (\displaystyle a) a b (\displaystyle b). Pokud je úhel 90°, pak cos ⁡ θ = 0 (\displaystyle \cos \theta =0) a vzorec se zjednoduší na obvyklou Pythagorovu větu.

Libovolný trojúhelník

Existuje zobecnění Pythagorovy věty na libovolný trojúhelník, který funguje pouze na základě poměru délek stran a předpokládá se, že jej poprvé zavedl sabiánský astronom Sabit ibn Kurra. V něm, pro libovolný trojúhelník se stranami, rovnoramenný trojúhelník se základnou na straně c (\displaystyle c), vrchol se shoduje s vrcholem původního trojúhelníku, naproti straně c (\displaystyle c) a úhly na základně rovné úhlu θ (\displaystyle \theta ) opačná strana c (\displaystyle c). Výsledkem jsou dva trojúhelníky, podobné tomu původnímu: první se stranami a (\displaystyle a), boční strana vepsaného rovnoramenného trojúhelníku daleko od něj a r (\displaystyle r)- boční díly c (\displaystyle c); druhý je k němu ze strany symetrický b (\displaystyle b) s partou s (\displaystyle s)- příslušná část strany c (\displaystyle c). V důsledku toho je vztah splněn:

a 2 + b 2 = c (r + s) (\displaystyle a^(2)+b^(2)=c(r+s)),

který degeneruje do Pythagorovy věty at θ = π / 2 (\displaystyle \theta =\pi /2). Poměr je důsledkem podobnosti vytvořených trojúhelníků:

c a = a r , c b = b s ⇒ c r + c s = a 2 + b 2 (\displaystyle (\frac (c)(a))=(\frac (a)(r)),\,(\frac (c) (b))=(\frac (b)(s))\,\Šipka doprava \,cr+cs=a^(2)+b^(2)).

Pappusova oblastní věta

Neeuklidovská geometrie

Pythagorova věta je odvozena z axiomů euklidovské geometrie a pro neeuklidovskou geometrii je neplatná – naplnění Pythagorovy věty se rovná postulátu euklidovského paralelismu.

V neeuklidovské geometrii bude vztah mezi stranami pravoúhlého trojúhelníku nutně ve formě odlišné od Pythagorovy věty. Například ve sférické geometrii mají všechny tři strany pravoúhlého trojúhelníku, který váže oktant jednotkové koule, délku π / 2 (\displaystyle \pi /2), což je v rozporu s Pythagorovou větou.

Navíc Pythagorova věta platí v hyperbolické a eliptické geometrii, pokud je požadavek, aby trojúhelník byl pravoúhlý, nahrazen podmínkou, že součet dvou úhlů trojúhelníku se musí rovnat třetímu.

sférická geometrie

Pro libovolný pravoúhlý trojúhelník na kouli s poloměrem R (\displaystyle R)(například pokud je úhel v trojúhelníku pravý) se stranami a , b , c (\displaystyle a,b,c) vztah mezi stranami je:

cos ⁡ (c R) = cos ⁡ (a R) ⋅ cos ⁡ (b R) (\displaystyle \cos \left((\frac (c)(R))\right)=\cos \left((\frac (a)(R))\right)\cdot \cos \left((\frac (b)(R))\right)).

Tuto rovnost lze odvodit jako speciální případ sférického kosinusového teorému, který platí pro všechny sférické trojúhelníky:

cos ⁡ (c R) = cos ⁡ (a R) ⋅ cos ⁡ (b R) + sin ⁡ (a R) ⋅ sin ⁡ (b R) ⋅ cos ⁡ γ (\displaystyle \cos \left((\frac ( c)(R))\right)=\cos \left((\frac (a)(R))\right)\cdot \cos \left((\frac (b)(R))\right)+\ sin \left((\frac (a)(R))\right)\cdot \sin \left((\frac (b)(R))\right)\cdot \cos \gamma ). ch ⁡ c = ch ⁡ a ⋅ ch ⁡ b (\displaystyle \operatorname (ch) c=\operatorname (ch) a\cdot \operatorname (ch) b),

kde ch (\displaystyle \operatorname (ch) )- hyperbolický kosin. Tento vzorec je speciálním případem hyperbolické kosinové věty, která platí pro všechny trojúhelníky:

ch ⁡ c = ch ⁡ a ⋅ ch ⁡ b − sh ⁡ a ⋅ sh ⁡ b ⋅ cos ⁡ γ (\displaystyle \operatorname (ch) c=\operatorname (ch) a\cdot \operatorname (ch) b-\operatorname (sh) a\cdot \operatorname (sh) b\cdot \cos \gamma ),

kde γ (\displaystyle \gamma )- úhel, jehož vrchol je opačný ke straně c (\displaystyle c).

Použití Taylorovy řady pro hyperbolický kosinus ( ch ⁡ x ≈ 1 + x 2 / 2 (\displaystyle \operatorname (ch) x\cca 1+x^(2)/2)) lze ukázat, že pokud se hyperbolický trojúhelník zmenšuje (tedy kdy a (\displaystyle a), b (\displaystyle b) a c (\displaystyle c) inklinují k nule), pak se hyperbolické vztahy v pravoúhlém trojúhelníku blíží vztahu klasické Pythagorovy věty.

aplikace

Vzdálenost ve dvourozměrných pravoúhlých systémech

Nejdůležitější aplikací Pythagorovy věty je určení vzdálenosti mezi dvěma body v pravoúhlém systému souřadnicích: vzdálenost s (\displaystyle s) mezi body se souřadnicemi (a , b) (\displaystyle (a,b)) a (c, d) (\displaystyle (c,d)) rovná se:

s = (a − c) 2 + (b − d) 2 (\displaystyle s=(\sqrt ((a-c)^(2)+(b-d)^(2)))).

Pro komplexní čísla poskytuje Pythagorova věta přirozený vzorec pro nalezení modulového komplexního čísla – např. z = x + y i (\displaystyle z=x+yi) rovná se délce