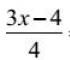Definice jednočlenu: související pojmy, příklady. Definice jednočlenu, související pojmy, příklady Standardní forma jednočlenného pravidla s příkladem

1. Celočíselný kladný koeficient. Mějme monomial +5a, protože kladné číslo +5 je považováno za stejné jako aritmetické číslo 5, pak

5a = a ∙ 5 = a + a + a + a + a.

Také +7xy² = xy² ∙ 7 = xy² + xy² + xy² + xy² + xy² + xy² + xy²; +3a³ = a³ ∙ 3 = a³ + a³ + a³; +2abc = abc ∙ 2 = abc + abc a tak dále.

Na základě těchto příkladů můžeme stanovit, že kladný celočíselný koeficient ukazuje, kolikrát se doslovný faktor (nebo: součin doslovných faktorů) monočlenu opakuje s termem.

Člověk by si na to měl zvyknout do té míry, že se v představě hned objeví, že třeba v mnohočlenu

3a + 4a² + 5a³

záležitost se redukuje na skutečnost, že nejprve se a² opakuje 3krát jako termín, poté se a³ opakuje 4krát jako termín a poté se a 5krát opakuje jako termín.

Také: 2a + 3b + c = a + a + b + b + b + c
x³ + 2xy² + 3y³ = x³ + xy² + xy² + y³ + y³ + y³ atd.

2. Kladný zlomkový koeficient. Mějme jednočlenný +a. Protože kladné číslo + se shoduje s aritmetickým číslem, pak +a = a ∙ , což znamená: potřebujete vzít tři čtvrtiny čísla a, tzn.

Tedy: zlomkový kladný koeficient ukazuje, kolikrát a jaká část doslovného násobitele monomiálu se v členu opakuje.

Polynom by mělo být snadno reprezentováno jako:

atd.

3. Záporný koeficient. Když známe násobení relativních čísel, můžeme snadno zjistit, že například (+5) ∙ (–3) = (–5) ∙ (+3) nebo (–5) ∙ (–3) = (+5) ∙ (+ 3) nebo obecně a ∙ (–3) = (–a) ∙ (+3); také a ∙ (–) = (–a) ∙ (+) atd.

Pokud tedy vezmeme monočlen se záporným koeficientem, například –3a, pak

–3a = a ∙ (–3) = (–a) ∙ (+3) = (–a) ∙ 3 = – a – a – a (–a se bere jako člen 3x).

Z těchto příkladů vidíme, že záporný koeficient ukazuje, kolikrát se písmenná část jednočlenu nebo jeho určitý zlomek, braný se znaménkem mínus, opakuje u daného členu.

Monomiály jsou jedním z hlavních typů výrazů studovaných v rámci kurzu školní algebry. V tomto článku vám řekneme, co to jsou výrazy, definujeme jejich standardní formu a ukážeme příklady a také se budeme zabývat souvisejícími pojmy, jako je stupeň monomiálu a jeho koeficient.

Co je to monomial

Školní učebnice obvykle uvádějí následující definici tohoto pojmu:

Definice 1

Monomery zahrnujíčísla, proměnné a také jejich stupně s přirozeným ukazatelem a různé druhy výrobků z nich tvořených.

Na základě této definice můžeme uvést příklady takových výrazů. Takže všechna čísla 2 , 8 , 3004 , 0 , - 4 , - 6 , 0 , 78 , 1 4 , - 4 3 7 budou odkazovat na jednočleny. Všechny proměnné, například x, a, b, p, q, t, y, z budou také podle definice monočleny. Patří sem také mocniny proměnných a čísel, například 6 3 , (− 7 , 41) 7 , x 2 a t 15, stejně jako výrazy jako 65 x , 9 (− 7) x y 3 6 , x x y 3 x y 2 z atd. Vezměte prosím na vědomí, že monočlen může obsahovat jedno číslo nebo proměnnou nebo několik a mohou být zmíněny několikrát jako součást jednoho polynomu.

Takové typy čísel, jako jsou celá čísla, racionální, přirozená čísla, také patří k monočlenům. Zde můžete také zahrnout reálná a komplexní čísla. Takže výrazy jako 2 + 3 i x z 4 , 2 x , 2 π x 3 budou také monočleny.

Jaký je standardní tvar jednočlenu a jak na něj převést výraz

Pro usnadnění práce jsou všechny monomiály nejprve zredukovány na speciální formu, nazývanou standardní. Pojďme být konkrétní, co to znamená.

Definice 2

Standardní forma monomiálu nazývají to takovou formou, ve které je součinem číselného faktoru a přirozených mocnin různých proměnných. Číselný faktor, nazývaný také monomiální koeficient, se obvykle zapisuje nejprve z levé strany.

Pro názornost vybereme několik monočlenů standardního tvaru: 6 (jedná se o monočlen bez proměnných), 4 · a , − 9 · x 2 · y 3 , 2 3 5 · x 7 . Patří sem i výraz x y(zde bude koeficient roven 1), − x 3(zde je koeficient - 1).

Nyní uvádíme příklady monomií, které je třeba uvést do standardní formy: 4 a 2 a 3(zde musíte zkombinovat stejné proměnné), 5 x (− 1) 3 y 2(zde je třeba kombinovat číselné faktory vlevo).

Obvykle v případě, kdy má monomial několik proměnných zapsaných písmeny, jsou faktory písmen zapsány v abecedním pořadí. Například preferovaný záznam 6 a b 4 c z 2, jak b 4 6 a z 2 c. Pořadí se však může lišit, pokud to vyžaduje účel výpočtu.

Jakýkoli monomiál lze zredukovat na standardní formu. Chcete-li to provést, musíte provést všechny potřebné identické transformace.

Pojem stupně monomiálu

Velmi důležitý je doprovodný pojem stupně monomiálu. Zapišme si definici tohoto pojmu.

Definice 3

Stupeň monomiálu, zapsaný ve standardním tvaru, je součtem exponentů všech proměnných, které jsou zahrnuty v jeho záznamu. Pokud v něm není jediná proměnná a samotný monomial se liší od 0, pak bude jeho stupeň nula.

Uveďme příklady stupňů monomiálu.

Příklad 1

Monomial a má tedy stupeň 1, protože a = a 1 . Pokud máme jednočlenný 7 , pak bude mít nulový stupeň, protože nemá žádné proměnné a je odlišný od 0 . A tady je záznam 7 a 2 x y 3 a 2 bude monomiál 8. stupně, protože součet exponentů všech stupňů proměnných v něm zahrnutých bude roven 8: 2 + 1 + 3 + 2 = 8 .

Standardizovaný monočlen a původní polynom budou mít stejný stupeň.

Příklad 2

Ukážeme si, jak vypočítat stupeň monomiálu 3 x 2 y 3 x (− 2) x 5 y. Ve standardním tvaru může být zapsán jako − 6 x 8 y 4. Vypočítáme stupeň: 8 + 4 = 12 . Stupeň původního polynomu je tedy také roven 12 .

Pojem monomiální koeficient

Pokud máme standardizovaný monomial, který obsahuje alespoň jednu proměnnou, pak o něm mluvíme jako o součinu s jedním číselným faktorem. Tento faktor se nazývá číselný koeficient nebo monomiální koeficient. Zapišme si definici.

Definice 4

Koeficient jednočlenu se nazývá číselný faktor monočlenu redukovaný do standardního tvaru.

Vezměte si například koeficienty různých monomií.

Příklad 3

Tedy ve výrazu 8 a 3 koeficient bude číslo 8 a in (− 2, 3) x y z budou − 2 , 3 .

Zvláštní pozornost je třeba věnovat koeficientům rovným jedné a mínus jedné. Zpravidla nejsou výslovně uvedeny. Předpokládá se, že v monomiálu standardního tvaru, ve kterém není žádný číselný faktor, je koeficient 1, například ve výrazech a, x z 3, a t x, protože je lze považovat za 1 a, x z 3 - tak jako 1 x z 3 atd.

Podobně v monočlenech, které nemají číselný faktor a začínají znaménkem mínus, můžeme uvažovat koeficient - 1.

Příklad 4

Například výrazy − x, − x 3 y z 3 budou mít takový koeficient, protože je lze reprezentovat jako − x = (− 1) x, − x 3 y z 3 = (− 1) x 3 y z 3 atd.

Pokud monomiál nemá vůbec jediný doslovný faktor, pak lze i v tomto případě mluvit o koeficientu. Koeficienty takových jednočlenných čísel budou tato čísla sama. Takže například koeficient monomiálu 9 se bude rovnat 9.

Pokud si všimnete chyby v textu, zvýrazněte ji a stiskněte Ctrl+Enter

Lekce na téma: "Standardní forma monomiálu. Definice. Příklady"

Doplňkové materiály
Vážení uživatelé, nezapomeňte zanechat své komentáře, zpětnou vazbu, návrhy. Všechny materiály jsou kontrolovány antivirovým programem.

Výukové pomůcky a simulátory v internetovém obchodě "Integral" pro 7. ročník
Elektronická učebnice "Srozumitelná geometrie" pro ročníky 7-9
Multimediální studijní příručka "Geometrie za 10 minut" pro ročníky 7-9

Monomiální. Definice

Monomiální je matematický výraz, který je součinem prvočísla a jedné nebo více proměnných.

Monomiály zahrnují všechna čísla, proměnné, jejich mocniny s přirozeným exponentem:
42; 3; 0; 62; 2 3; b3; ax4; 4x3; 5a2; 12xyz 3.

Poměrně často je obtížné určit, zda daný matematický výraz odkazuje na jednočlen nebo ne. Například $\frac(4a^3)(5)$. Je to monomiální nebo ne? Abychom na tuto otázku odpověděli, musíme výraz zjednodušit, tzn. reprezentují ve tvaru: $\frac(4)(5)*а^3$.
S jistotou můžeme říci, že tento výraz je jednočlenný.

Standardní forma monomiálu

Při výpočtu je žádoucí uvést monomiál do standardního tvaru. Toto je nejkratší a nejsrozumitelnější zápis monomiálu.

Pořadí uvedení monomiálu do standardního tvaru je následující:
1. Vynásobte koeficienty monomiálu (nebo číselné faktory) a výsledek dejte na první místo.
2. Vyberte všechny stupně se stejným základem písmen a vynásobte je.
3. Opakujte bod 2 pro všechny proměnné.

Příklady.
I. Zmenšete daný monomiál $3x^2zy^3*5y^2z^4$ na standardní tvar.

Rozhodnutí.
1. Vynásobte koeficienty monomiálu $15x^2y^3z * y^2z^4$.
2. Nyní uveďme podobné výrazy $15х^2y^5z^5$.

II. Převeďte daný monomial $5a^2b^3 * \frac(2)(7)a^3b^2c$ do standardního tvaru.

Rozhodnutí.
1. Vynásobte koeficienty monomiálu $\frac(10)(7)a^2b^3*a^3b^2c$.
2. Nyní uveďme podobné výrazy $\frac(10)(7)a^5b^5c$.

Monomiální je výraz, který je součinem dvou nebo více faktorů, z nichž každý je číslo vyjádřené písmenem, číslicemi nebo mocninou (s nezáporným exponentem celého čísla):

2A, A 3 X, 4abc, -7X

Protože součin identických faktorů lze zapsat jako stupeň, pak jeden stupeň (s nezáporným celočíselným exponentem) je také monomiální:

(-4) 3 , X 5 ,

Vzhledem k tomu, že číslo (celé nebo zlomkové), vyjádřené písmenem nebo čísly, lze zapsat jako součin tohoto čísla jedničkou, pak každé jednotlivé číslo lze také považovat za jednočlenné:

X, 16, -A,

Standardní forma monomiálu

Standardní forma monomiálu- jedná se o jednočlen, který má pouze jeden číselný činitel, který je nutné zapsat na prvním místě. Všechny proměnné jsou v abecedním pořadí a jsou obsaženy v monomiálu pouze jednou.

Čísla, proměnné a stupně proměnných také odkazují na monočleny standardního tvaru:

7, b, X 3 , -5b 3 z 2 - monomily standardního tvaru.

Číselný faktor monomiálu standardního tvaru se nazývá monomiální koeficient. Monomiální koeficienty rovné 1 a -1 se obvykle nezapisují.

Pokud v monomiálu standardního tvaru není žádný číselný faktor, pak se předpokládá, že koeficient monomiálu je 1:

X 3 = 1 X 3

Pokud ve standardním tvaru monomial není žádný číselný faktor a předchází mu znaménko mínus, pak se předpokládá, že koeficient monomiálu je -1:

-X 3 = -1 X 3

Redukce monomiálu na standardní tvar

K převedení monomiálu do standardního tvaru potřebujete:

1. Vynásobte číselné faktory, pokud jich je několik. Zvyšte číselný faktor na mocninu, pokud má exponent. Na první místo dejte násobitel čísel.
2. Vynásobte všechny identické proměnné tak, aby se každá proměnná v monomiálu vyskytla pouze jednou.
3. Uspořádejte proměnné za číselným faktorem v abecedním pořadí.

Příklad. Vyjádřete jednočlen ve standardním tvaru:

a) 3 yx 2 (-2) y 5 X; b) 6 před naším letopočtem 0,5 ab 3

Rozhodnutí:

a) 3 yx 2 (-2) y 5 X= 3 (-2) X 2 Xyy 5 = -6X 3 y 6
b) 6 před naším letopočtem 0,5 ab 3 = 6 0,5 abb 3 C = 3ab 4 C

Stupeň monomiálu

Stupeň monomiálu je součet exponentů všech písmen v něm.

Pokud je jednočlen číslo, to znamená, že neobsahuje proměnné, pak se jeho stupeň považuje za rovný nule. Například:

5, -7, 21 - jednočleny nula stupňů.

Proto, abyste našli stupeň monomiálu, musíte určit exponent každého z písmen v něm obsažených a tyto exponenty sečíst. Pokud exponent písmene není zadán, pak je roven jedné.

Příklady:

Tak jak se máš X exponent není specifikován, to znamená, že je roven 1. Monomial neobsahuje další proměnné, to znamená, že jeho stupeň je roven 1.

Monomial obsahuje pouze jednu proměnnou ve druhém stupni, což znamená, že stupeň tohoto monomiálu je 2.

3) ab 3 C 2 d

Indikátor A je roven 1, indikátor b- 3, indikátor C- 2, indikátor d- 1. Stupeň tohoto monomiálu se rovná součtu těchto ukazatelů.

Stupeň monomiálu

Pro monomial existuje pojem jeho stupně. Pojďme zjistit, co to je.

Definice.

Stupeň monomiálu standardní forma je součet exponentů všech proměnných zahrnutých v jeho záznamu; pokud v monomiálním záznamu nejsou žádné proměnné a je odlišný od nuly, pak se jeho stupeň považuje za nulový; číslo nula je považováno za jednočlenný, jehož stupeň není definován.

Definice stupně jednočlenu nám umožňuje uvést příklady. Stupeň monomiálu a je roven jedné, protože a je a 1 . Stupeň monomiálu 5 je nulový, protože je nenulový a jeho zápis neobsahuje žádné proměnné. A součin 7·a 2 ·x·y 3 ·a 2 je monočlen osmého stupně, protože součet exponentů všech proměnných a, x a y je 2+1+3+2=8.

Mimochodem, stupeň monomiálu nezapsaného ve standardní formě se rovná stupni odpovídajícího standardního tvaru monomial. Abychom ilustrovali, co bylo řečeno, vypočítáme stupeň monomiálu 3 x 2 y 3 x (−2) x 5 y. Tento jednočlen ve standardním tvaru má tvar −6·x 8 ·y 4 , jeho stupeň je 8+4=12 . Stupeň původního monomiálu je tedy 12 .

Monomiální koeficient

Monomial ve standardním tvaru, který má ve svém zápisu alespoň jednu proměnnou, je součin s jediným číselným faktorem - číselným koeficientem. Tento koeficient se nazývá monomiální koeficient. Uveďme výše uvedené úvahy do podoby definice.

Definice.

Monomiální koeficient je číselný faktor monomiálu zapsaný ve standardním tvaru.

Nyní můžeme uvést příklady koeficientů různých monočlenů. Číslo 5 je z definice koeficientem jednočlenu 5 a 3, podobně i jednočlen (−2,3) x y z má koeficient −2,3 .

Zvláštní pozornost si zaslouží koeficienty monočlenů rovné 1 a −1. Jde o to, že v záznamu obvykle nejsou výslovně uvedeny. Předpokládá se, že koeficient monomiálů standardní formy, které nemají ve svém zápisu číselný faktor, je roven jedné. Například monočleny a , x z 3 , at x atd. mají koeficient 1, protože a lze považovat za 1 a, x z 3 za 1 x z 3 atd.

Stejně tak koeficient monočlenů, jejichž zápisy ve standardním tvaru nemají číselný faktor a začínají znaménkem mínus, se považuje za mínus jedna. Například monočleny −x , −x 3 y z 3 atd. mít koeficient −1 , protože −x=(−1) x , −x 3 y z 3 =(−1) x 3 y z 3 atd.

Mimochodem, pojem koeficient jednočlenu je často označován jako monomiály standardního tvaru, což jsou čísla bez abecedních faktorů. Koeficienty takových jednočlenných čísel jsou považovány za tato čísla. Takže například koeficient monomiálu 7 je považován za rovný 7.

Bibliografie.

• Algebra: učebnice pro 7 buněk. obecné vzdělání instituce / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; vyd. S. A. Teljakovskij. - 17. vyd. - M. : Vzdělávání, 2008. - 240 s. : nemocný. - ISBN 978-5-09-019315-3.
• Mordkovich A.G. Algebra. 7. třída. Ve 14 hodin 1. část. Učebnice pro studenty vzdělávacích institucí / A. G. Mordkovich. - 17. vyd., dodat. - M.: Mnemozina, 2013. - 175 s.: ill. ISBN 978-5-346-02432-3.
• Gusev V. A., Mordkovich A. G. Matematika (příručka pro uchazeče o technické školy): Proc. příspěvek.- M.; Vyšší škola, 1984.-351 s., ill.