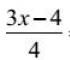Jak najít x0 v derivaci. Najděte hodnotu derivace funkce v bodě x0

Příklad 1

Odkaz: Následující způsoby zápisu funkce jsou ekvivalentní: V některých úlohách je vhodné označit funkci jako „player“ a v některých jako „ef from x“.

Nejprve najdeme derivaci:

Příklad 2

Vypočítejte derivaci funkce v bodě

, , plně funkční studium atd.

Příklad 3

Vypočítejte derivaci funkce v bodě . Nejprve najdeme derivaci:

No, to je úplně jiná věc. Vypočítejte hodnotu derivace v bodě:

V případě, že nerozumíte, jak byla derivace nalezena, vraťte se k prvním dvěma lekcím tématu. Pokud se vyskytnou potíže (nedorozumění) s arkus tangentou a jejími významy, nutně studovat metodický materiál Grafy a vlastnosti elementárních funkcí- úplně poslední odstavec. Protože arctangentů pro studentský věk je stále dost.

Příklad 4

Vypočítejte derivaci funkce v bodě .

Rovnice tečny ke grafu funkce

Chcete-li upevnit předchozí odstavec, zvažte problém nalezení tečny k funkční grafika v tomto bodě. S tímto úkolem jsme se setkali ve škole a nachází se i v kurzu vyšší matematiky.

Zvažte "demonstrační" elementární příklad.

Napište rovnici pro tečnu ke grafu funkce v bodě s úsečkou. Okamžitě dám hotové grafické řešení problému (v praxi to ve většině případů není nutné):

Přesná definice tečny je dána pomocí definice derivace funkce, ale zatím si osvojíme technickou část problematiky. Téměř každý jistě intuitivně chápe, co je to tečna. Pokud vysvětlíte "na prstech", pak tečna ke grafu funkce je rovný, který se týká grafu funkce v jediný směřovat. V tomto případě jsou všechny blízké body přímky umístěny co nejblíže grafu funkce.

V našem případě: v , se tečna (standardní zápis) dotýká grafu funkce v jediném bodě.

A naším úkolem je najít rovnici přímky.

Derivace funkce v bodě

Jak najít derivaci funkce v bodě? Z formulace plynou dva zřejmé body tohoto úkolu:

1) Je nutné najít derivaci.

2) Je nutné vypočítat hodnotu derivace v daném bodě.

Příklad 1

Vypočítejte derivaci funkce v bodě

Nápověda: Následující způsoby zápisu funkce jsou ekvivalentní:


V některých úlohách je vhodné označit funkci jako „player“ a v některých jako „ef from x“.

Nejprve najdeme derivaci:

Doufám, že mnozí se již přizpůsobili, aby našli takové deriváty ústně.

Ve druhém kroku vypočítáme hodnotu derivace v bodě:

Malý příklad zahřátí pro nezávislé řešení:

Příklad 2

Vypočítejte derivaci funkce v bodě

Úplné řešení a odpověď na konci lekce.

Potřeba najít derivaci v bodě vyvstává v následujících úlohách: sestrojení tečny ke grafu funkce (další odstavec), studium funkce pro extrém , studium funkce pro inflexi grafu , plně funkční studium atd.

Zvažovaný úkol se však nachází v kontrolních dokumentech a sám o sobě. A zpravidla je v takových případech funkce dána poměrně složitě. V tomto ohledu zvažte další dva příklady.

Příklad 3

Vypočítejte derivaci funkce v bodě .
Nejprve najdeme derivaci:

Derivace je v zásadě nalezena a požadovaná hodnota může být nahrazena. Ale vlastně se mi do ničeho nechce. Výraz je velmi dlouhý a hodnota "x" je zlomková. Proto se snažíme naši derivaci co nejvíce zjednodušit. V tomto případě zkusme zredukovat poslední tři pojmy na společného jmenovatele: v bodě .

Toto je příklad typu „udělej si sám“.

Jak zjistit hodnotu derivace funkce F(x) v bodě Ho? Jak to obecně řešit?

Pokud je zadán vzorec, najděte derivaci a místo X dosaďte X-nula. počet
Pokud mluvíme o b-8 USE, grafu, pak musíte najít tečnu úhlu (ostrého nebo tupého), která tvoří tečnu k ose X (pomocí mentální konstrukce pravoúhlého trojúhelníku a určení tangens úhel)

Timur Adilkhodzhaev

Nejprve se musíte rozhodnout pro znamení. Pokud je bod x0 ve spodní části souřadnicové roviny, pak znaménko v odpovědi bude mínus, a pokud je vyšší, pak +.
Za druhé, musíte vědět, co je tange v obdélníkovém obdélníku. A to je poměr protilehlé strany (nohy) k sousední straně (také noha). Na malbě je obvykle několik černých skvrn. Z těchto značek vytvoříte pravoúhlý trojúhelník a najdete tange.

Jak zjistit hodnotu derivace funkce f x v bodě x0?

neexistuje žádná konkrétní otázka - před 3 lety

V obecném případě, abychom v kterémkoli bodě našli hodnotu derivace funkce vzhledem k nějaké proměnné, je nutné danou funkci vzhledem k této proměnné diferencovat. Ve vašem případě proměnnou X. Ve výsledném výrazu dosaďte místo X hodnotu x do bodu, pro který potřebujete najít hodnotu derivace, tzn. ve vašem případě dosaďte nulu X a vypočítejte výsledný výraz.

No, vaše touha porozumět této problematice si podle mého názoru nepochybně zaslouží +, což dávám s čistým svědomím.

Taková formulace problému nalezení derivace je často kladena za účelem fixace materiálu na geometrický význam derivace. Navrhne se graf určité funkce, zcela libovolný a není dán rovnicí, a je potřeba najít hodnotu derivace (nikoli derivace samotné!) v zadaném bodě X0. K tomu se sestrojí tečna k dané funkci a najdou se body jejího průsečíku se souřadnicovými osami. Potom se rovnice této tečny sestaví ve tvaru y=kx+b.

V této rovnici bude koeficient k a hodnotou derivace. zbývá pouze najít hodnotu koeficientu b. Za tímto účelem najdeme hodnotu y v x \u003d o, nechť se rovná 3 - to je hodnota koeficientu b. Do původní rovnice dosadíme hodnoty X0 a Y0 a najdeme k - naši hodnotu derivace v tomto bodě.

V úloze B9 je uveden graf funkce nebo derivace, ze kterého je třeba určit jednu z následujících veličin:

1. Hodnota derivace v nějakém bodě x 0,
2. Vysoké nebo nízké body (extrémní body),
3. Intervaly rostoucí a klesající funkce (intervaly monotonie).

Funkce a derivace uvedené v tomto problému jsou vždy spojité, což značně zjednodušuje řešení. Přestože úloha patří do sekce matematické analýzy, je zcela v silách i těch nejslabších studentů, protože zde nejsou potřeba žádné hluboké teoretické znalosti.

Pro nalezení hodnoty derivace, extrémních bodů a intervalů monotonie existují jednoduché a univerzální algoritmy – všechny budou probrány níže.

Pečlivě si přečtěte stav problému B9, abyste se nedopustili hloupých chyb: někdy se objeví poměrně objemné texty, ale existuje jen málo důležitých podmínek, které ovlivňují průběh řešení.

Výpočet hodnoty derivátu. Dvoubodová metoda

Pokud je problému dán graf funkce f(x), tečný k tomuto grafu v nějakém bodě x 0 , a je potřeba najít hodnotu derivace v tomto bodě, použije se následující algoritmus:

1. Najděte dva "adekvátní" body na grafu tečny: jejich souřadnice musí být celé číslo. Označme tyto body jako A (x 1 ; y 1) a B (x 2 ; y 2). Zapište si souřadnice správně – to je klíčový bod řešení a jakákoliv chyba zde vede ke špatné odpovědi.
2. Při znalosti souřadnic je snadné vypočítat přírůstek argumentu Δx = x 2 − x 1 a přírůstek funkce Δy = y 2 − y 1 .
3. Nakonec najdeme hodnotu derivace D = Δy/Δx. Jinými slovy, musíte vydělit přírůstek funkce přírůstkem argumentu - a toto bude odpověď.

Ještě jednou podotýkáme: body A a B je třeba hledat přesně na tečně, a nikoli na grafu funkce f(x), jak tomu často bývá. Tečna bude nutně obsahovat alespoň dva takové body, jinak je problém formulován špatně.

Zvažte body A (−3; 2) a B (−1; 6) a najděte přírůstky:
Δx \u003d x 2 - x 1 \u003d -1 - (-3) \u003d 2; Δy \u003d y 2 - y 1 \u003d 6 - 2 \u003d 4.

Nalezneme hodnotu derivace: D = Δy/Δx = 4/2 = 2.

Úkol. Obrázek ukazuje graf funkce y \u003d f (x) a tečnu k ní v bodě s úsečkou x 0. Najděte hodnotu derivace funkce f(x) v bodě x 0 .

Zvažte body A (0; 3) a B (3; 0), najděte přírůstky:
Δx \u003d x 2 - x 1 \u003d 3 - 0 \u003d 3; Δy \u003d y 2 - y 1 \u003d 0 - 3 \u003d -3.

Nyní najdeme hodnotu derivace: D = Δy/Δx = −3/3 = −1.

Úkol. Obrázek ukazuje graf funkce y \u003d f (x) a tečnu k ní v bodě s úsečkou x 0. Najděte hodnotu derivace funkce f(x) v bodě x 0 .

Zvažte body A (0; 2) a B (5; 2) a najděte přírůstky:
Δx \u003d x 2 - x 1 \u003d 5 - 0 \u003d 5; Δy = y2 - y1 = 2 - 2 = 0.

Zbývá najít hodnotu derivace: D = Δy/Δx = 0/5 = 0.

Z posledního příkladu můžeme formulovat pravidlo: je-li tečna rovnoběžná s osou OX, je derivace funkce v bodě dotyku rovna nule. V tomto případě nemusíte ani nic počítat - stačí se podívat na graf.

Výpočet nejvyšších a nejnižších bodů

Někdy se místo grafu funkce v problému B9 uvádí derivační graf a je potřeba najít maximální nebo minimální bod funkce. V tomto scénáři je dvoubodová metoda k ničemu, ale existuje jiný, ještě jednodušší algoritmus. Nejprve si definujme terminologii:

1. Bod x 0 se nazývá maximální bod funkce f(x), pokud v některém okolí tohoto bodu platí následující nerovnost: f(x 0) ≥ f(x).
2. Bod x 0 se nazývá minimální bod funkce f(x), pokud v některém okolí tohoto bodu platí následující nerovnost: f(x 0) ≤ f(x).

K nalezení maximálních a minimálních bodů na grafu derivace stačí provést následující kroky:

1. Překreslete graf derivace a odstraňte všechny nepotřebné informace. Jak ukazuje praxe, další údaje pouze narušují rozhodnutí. Na souřadnicové ose proto označíme nuly derivace – a je to.
2. Zjistěte znaménka derivace na intervalech mezi nulami. Pokud je pro nějaký bod x 0 známo, že f'(x 0) ≠ 0, pak jsou možné pouze dvě možnosti: f'(x 0) ≥ 0 nebo f'(x 0) ≤ 0. Znaménko derivace je snadno určit z původního výkresu: pokud graf derivace leží nad osou OX, pak f'(x) ≥ 0. Naopak, pokud graf derivace leží pod osou OX, pak f'(x) ≤ 0.
3. Znovu zkontrolujeme nuly a znaménka derivace. Tam, kde se znaménko změní z mínus na plus, je minimální bod. Naopak, pokud se znaménko derivace změní z plus na mínus, jedná se o maximální bod. Počítání se vždy provádí zleva doprava.

Toto schéma funguje pouze pro spojité funkce - v problému B9 žádné jiné nejsou.

Úkol. Obrázek ukazuje graf derivace funkce f(x) definované na segmentu [−5; 5]. Najděte minimální bod funkce f(x) na tomto segmentu.

Zbavme se zbytečných informací - ponecháme pouze hranice [−5; 5] a nuly derivace x = −3 a x = 2,5. Všimněte si také značek:

Je zřejmé, že v bodě x = −3 se znaménko derivace změní z mínus na plus. Toto je minimální bod.

Úkol. Obrázek ukazuje graf derivace funkce f(x) definované na segmentu [−3; 7]. Najděte maximální bod funkce f(x) na tomto segmentu.

Překreslíme graf a ponecháme pouze hranice [−3; 7] a nuly derivace x = −1,7 a x = 5. Všimněte si znamének derivace na výsledném grafu. My máme:

Je zřejmé, že v bodě x = 5 se znaménko derivace změní z plus na mínus - to je maximální bod.

Úkol. Obrázek ukazuje graf derivace funkce f(x) definované na segmentu [−6; 4]. Najděte počet maximálních bodů funkce f(x), které patří do intervalu [−4; 3].

Z podmínek úlohy vyplývá, že stačí uvažovat pouze část grafu ohraničenou úsečkou [−4; 3]. Sestavíme proto nový graf, na kterém vyznačíme pouze hranice [−4; 3] a nuly derivace uvnitř. Konkrétně body x = −3,5 a x = 2. Dostaneme:

Na tomto grafu je pouze jeden maximální bod x = 2. Právě v něm se znaménko derivace mění z plusu na mínus.

Malá poznámka k bodům s neceločíselnými souřadnicemi. Například v minulé úloze byl uvažován bod x = −3,5, ale se stejným úspěchem můžeme vzít x = −3,4. Pokud je problém formulován správně, neměly by takové změny ovlivnit odpověď, protože body „bez trvalého bydliště“ se přímo nepodílejí na řešení problému. Samozřejmě s celočíselnými body takový trik nebude fungovat.

Hledání intervalů nárůstu a poklesu funkce

V takovém problému, jako jsou body maxima a minima, se navrhuje najít oblasti, ve kterých funkce sama roste nebo klesá z grafu derivace. Nejprve si definujme, co jsou vzestupné a sestupné:

1. Funkce f(x) se nazývá rostoucí na segmentu, pokud pro libovolné dva body x 1 a x 2 z tohoto segmentu platí tvrzení: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2). Jinými slovy, čím větší je hodnota argumentu, tím větší je hodnota funkce.
2. Funkce f(x) se nazývá klesající na úsečce, pokud pro libovolné dva body x 1 a x 2 z této úsečky platí: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Tito. větší hodnota argumentu odpovídá menší hodnotě funkce.

Formulujeme dostatečné podmínky pro zvýšení a snížení:

1. Aby spojitá funkce f(x) na segmentu narostla, stačí, aby její derivace uvnitř segmentu byla kladná, tzn. f'(x) ≥ 0.
2. Aby spojitá funkce f(x) na segmentu klesala, stačí, aby její derivace uvnitř segmentu byla záporná, tj. f'(x) ≤ 0.

Tato tvrzení přijímáme bez důkazů. Získáme tak schéma pro nalezení intervalů nárůstu a poklesu, které je v mnoha ohledech podobné algoritmu pro výpočet extrémních bodů:

1. Odstraňte všechny nadbytečné informace. Na původním grafu derivace nás primárně zajímají nuly funkce, proto necháme jen je.
2. Označte znaménka derivace v intervalech mezi nulami. Kde f'(x) ≥ 0, funkce roste, a kde f'(x) ≤ 0, klesá. Pokud má problém omezení na proměnnou x, označíme je navíc v novém grafu.
3. Nyní, když známe chování funkce a omezení, zbývá vypočítat požadovanou hodnotu v úloze.

Úkol. Obrázek ukazuje graf derivace funkce f(x) definované na segmentu [−3; 7,5]. Najděte intervaly klesající funkce f(x). Ve své odpovědi napište součet celých čísel zahrnutých v těchto intervalech.

Jako obvykle překreslíme graf a označíme hranice [−3; 7,5], stejně jako nuly derivace x = −1,5 a x = 5,3. Poté označíme znaménka derivace. My máme:

Protože derivace je záporná na intervalu (− 1,5), jedná se o interval klesající funkce. Zbývá sečíst všechna celá čísla, která jsou uvnitř tohoto intervalu:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Úkol. Obrázek ukazuje graf derivace funkce f(x) definované na segmentu [−10; 4]. Najděte intervaly rostoucí funkce f(x). Ve své odpovědi napište délku největšího z nich.

Zbavme se nadbytečných informací. Ponecháváme pouze hranice [−10; 4] a nuly derivace, které se tentokrát ukázaly jako čtyři: x = −8, x = −6, x = −3 a x = 2. Všimněte si znamének derivace a získejte následující obrázek:

Zajímají nás intervaly rostoucí funkce, tzn. kde f'(x) ≥ 0. V grafu jsou dva takové intervaly: (−8; −6) a (−3; 2). Spočítejme si jejich délku:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.

Protože je potřeba najít délku největšího z intervalů, zapíšeme jako odpověď hodnotu l 2 = 5.