Boolesche Constraint-Methode in der qualitativen Analyse binärer dynamischer Systeme. Qualitative Analyse dynamischer Systeme

KINETIK BIOLOGISCHER PROZESSE

Wie lässt sich die Dynamik biologischer Systeme beschreiben? Zu jedem Zeitpunkt weist ein biologisches System eine Reihe bestimmter Eigenschaften auf. Beispielsweise kann man durch die Beobachtung einer Population einer Art deren Größe, die besetzte Fläche des Territoriums, die verfügbare Nahrungsmenge, die Umgebungstemperatur usw. erfassen. Der Ablauf einer chemischen Reaktion kann durch die Konzentrationen charakterisiert werden der beteiligten Stoffe, Druck, Temperatur und Säuregrad der Umgebung. Die Wertemenge aller Merkmale, die der Forscher zur Beschreibung des Systems gewählt hat, ist der Zustand des Systems zu jedem Zeitpunkt. Beim Erstellen eines Modells werden Variablen und Parameter im angegebenen Satz ausgewählt. Variablen sind solche Größen, deren Änderungen den Forscher primär interessieren, Parameter sind die Bedingungen der „äußeren Umgebung“. Für die ausgewählten Variablen werden Gleichungen zusammengestellt, die die Änderungsmuster im System über die Zeit widerspiegeln. Wenn zum Beispiel ein Modell für das Wachstum einer mikrobiellen Kultur erstellt wird, wird normalerweise ihre Anzahl als Variable und die Reproduktionsrate als Parameter verwendet. Es ist möglich, dass die Temperatur, bei der das Wachstum stattfindet, signifikant ausfällt, dann wird dieser Indikator auch als Parameter in das Modell aufgenommen. Und wenn zum Beispiel die Belüftung immer ausreichend ist und keinen Einfluss auf Wachstumsprozesse hat, dann geht sie gar nicht in das Modell ein. In der Regel bleiben die Parameter während des Experiments unverändert, es ist jedoch anzumerken, dass dies nicht immer der Fall ist.

Es ist möglich, die Dynamik eines biologischen Systems (dh die Änderung seines Zustands im Laufe der Zeit) sowohl mit diskreten als auch mit kontinuierlichen Modellen zu beschreiben. Diskrete Modelle gehen davon aus, dass Zeit eine diskrete Größe ist. Dies entspricht der Aufzeichnung der Werte von Variablen in bestimmten festen Intervallen (z. B. einmal pro Stunde oder einmal im Jahr). In kontinuierlichen Modellen ist eine biologische Variable eine kontinuierliche Funktion der Zeit, die beispielsweise als x(T).

Oft von großer Bedeutung Anfangsbedingungen Modelle - der Zustand des untersuchten Merkmals zum Anfangszeitpunkt, d.h. beim T = 0.

Beim Studium der kontinuierlichen Änderung eines Merkmals x(T) kennen wir möglicherweise Informationen über die Änderungsrate. Diese Information kann allgemein als Differentialgleichung geschrieben werden:

Eine solche formale Notation bedeutet, dass die Änderungsrate eines untersuchten Merkmals eine Funktion der Zeit und der Größe dieses Merkmals ist.

Wenn die rechte Seite einer Differentialgleichung der Form nicht explizit von der Zeit abhängt, d.h. Messe:

dann wird diese Gleichung aufgerufen autonom(Das durch eine solche Gleichung beschriebene System heißt autonom). Der Zustand autonomer Systeme zu jedem Zeitpunkt wird durch einen einzigen Wert charakterisiert - den Wert der Variablen x in dem Augenblick T.

Stellen wir uns eine Frage: Gegeben sei eine Differentialgleichung für x(T), ist es möglich, alle Funktionen zu finden x(T) diese Gleichung erfüllen? Oder: wenn der Anfangswert einer bestimmten Größe bekannt ist (zum Beispiel die Anfangsgröße einer Population, die Konzentration eines Stoffes, die elektrische Leitfähigkeit des Mediums usw.) und Informationen über die Art der Änderung vorliegen Lässt sich mit dieser Variable vorhersagen, welchen Wert sie zu allen nachfolgenden Zeitpunkten haben wird? Die Antwort auf die gestellte Frage lautet wie folgt: Wenn die Anfangsbedingungen für gegeben sind und die Bedingungen des Satzes von Cauchy für die Gleichung erfüllt sind (die in einem bestimmten Bereich gegebene Funktion und ihre partielle Ableitung sind in diesem Bereich stetig), dann dort ist eine eindeutige Lösung der Gleichung, die die gegebenen Anfangsbedingungen erfüllt. (Erinnern Sie sich daran, dass jede stetige Funktion, die eine Differentialgleichung erfüllt, als Lösung dieser Gleichung bezeichnet wird.) Das bedeutet, dass wir das Verhalten eines biologischen Systems eindeutig vorhersagen können, wenn die Eigenschaften seines Anfangszustands bekannt sind und die Modellgleichung die Bedingungen von erfüllt Satz von Cauchy.

Stationärer Zustand. Nachhaltigkeit

Wir betrachten die autonome Differentialgleichung

In einem stationären Zustand ändern sich die Werte der Variablen im System nicht mit der Zeit, dh die Änderungsrate der Werte der Variablen beträgt 0: . Wenn die linke Seite von Gleichung (1.2) gleich Null ist, dann ist auch die rechte gleich Null: . Die Wurzeln dieser algebraischen Gleichung sind stationäre Zustände Differentialgleichung (1.2).

Beispiel1.1: Finden Sie die stationären Zustände der Gleichung.

Lösung: Verschieben wir den Term, der die Ableitung nicht enthält, auf die rechte Seite der Gleichheit: . Per Definition gilt im stationären Zustand die folgende Gleichheit: . Also muss die Gleichheit gelten . Wir lösen die Gleichung:

,

Die Gleichung hat also 3 stationäre Zustände: , .

Biologische Systeme sind ständig verschiedenen äußeren Einflüssen und zahlreichen Schwankungen ausgesetzt. Gleichzeitig haben sie (biologische Systeme) Homöostase, d.h. beständig. In der mathematischen Sprache bedeutet dies, dass die Variablen bei kleinen Abweichungen zu ihren stationären Werten zurückkehren. Wird sich dieses Verhalten eines biologischen Systems in seinem mathematischen Modell widerspiegeln? Sind die stationären Zustände des Modells stabil?

Der stationäre Zustand ist nachhaltig, wenn sich das System bei einer hinreichend kleinen Abweichung von der Gleichgewichtslage niemals weit vom singulären Punkt entfernt. Der stabile Zustand entspricht dem stabilen Modus des Systembetriebs.

Ein Gleichgewichtszustand einer Gleichung ist Lyapunov-stabil, wenn man für alle immer finden kann, dass wenn, dann für alle.

Es gibt eine analytische Methode zur Untersuchung der Stabilität eines stationären Zustands - die Lyapunov-Methode. Um dies zu belegen, erinnern wir uns Taylor-Formel.

Grob gesagt zeigt die Taylor-Formel das Verhalten einer Funktion in der Nähe eines bestimmten Punktes. Eine Funktion habe in einem Punkt aller Ordnungen bis zu Ableitungen n- einschließlich. Dann gilt die Taylor-Formel für:

Wenn wir den Restterm verwerfen, der selbst ein Infinitesimal höherer Ordnung als darstellt, erhalten wir die ungefähre Taylor-Formel:

Die rechte Seite der Näherungsformel wird aufgerufen Taylor-Polynom Funktionen, es wird als bezeichnet.

Beispiel 1.2: Erweitern Sie die Funktion in einer Taylorreihe in der Umgebung eines Punktes bis zur 4. Ordnung.

Lösung: Wir schreiben die Taylorreihe bis zur 4. Ordnung in allgemeiner Form:

Finden Sie die Ableitungen der gegebenen Funktion am Punkt:

,

Ersetzen Sie die erhaltenen Werte in die ursprüngliche Formel:

Eine analytische Methode zur Untersuchung der Stabilität eines stationären Zustands ( Lyapunov-Methode) ist wie folgt. Sei der stationäre Zustand der Gleichung . Stellen wir eine kleine Abweichung der Variablen ein x von seinem stationären Wert: , wobei . Ersetzen Sie den Ausdruck für den Punkt x in die ursprüngliche Gleichung: . Die linke Seite der Gleichung nimmt die Form an: , da im stationären Zustand die Änderungsrate des Wertes der Variablen gleich Null ist: . Wir erweitern die rechte Seite zu einer Taylor-Reihe in der Nähe des stationären Zustands, wobei wir berücksichtigen, dass wir nur den linearen Term auf der rechten Seite der Gleichung belassen:

Erhalten linearisierte Gleichung oder erste Näherungsgleichung. Der Wert ist ein konstanter Wert, bezeichnen Sie ihn ein: . Die allgemeine Lösung der linearisierten Gleichung hat die Form: . Dieser Ausdruck beschreibt das Gesetz, nach dem sich die Abweichung von dem von uns gegebenen stationären Zustand mit der Zeit ändert. Die Abweichung wird mit der Zeit abklingen, d.h. at , wenn der Exponent im Exponenten negativ ist, also . Per Definition wird der stationäre Zustand sein nachhaltig. Wenn dann mit zunehmender Zeit die Abweichung nur noch größer wird, ist der stationäre Zustand instabil. Für den Fall, dass die Gleichung der ersten Näherung die Frage nach der Stabilität des stationären Zustands nicht beantworten kann. Es ist notwendig, Terme höherer Ordnung in der Entwicklung der Taylor-Reihen zu berücksichtigen.

Neben der analytischen Methode zur Untersuchung der Stabilität eines stationären Zustands gibt es auch eine grafische.

Beispiel 1.3. Lassen . Finden Sie die stationären Zustände der Gleichung und bestimmen Sie deren Art der Stabilität anhand des Graphen der Funktion .

Lösung: Lassen Sie uns spezielle Punkte finden:

,

,

Wir bauen einen Graphen der Funktion (Abb. 1.1).

Reis. 1.1. Funktionsgraph (Beispiel 1.3).

Lassen Sie uns anhand des Diagramms bestimmen, ob jeder der gefundenen stationären Zustände stabil ist. Stellen wir eine kleine Abweichung des repräsentativen Punktes vom singulären Punkt nach links ein: . An einem Punkt mit einer Koordinate nimmt die Funktion einen positiven Wert an: oder . Die letzte Ungleichung bedeutet, dass die Koordinate im Laufe der Zeit zunehmen sollte, dh der repräsentative Punkt sollte zum Punkt zurückkehren. Stellen wir nun eine kleine Abweichung des repräsentativen Punktes vom singulären Punkt nach rechts ein: . In diesem Bereich behält die Funktion einen positiven Wert, daher über die Zeit die Koordinate x nimmt ebenfalls zu, das heißt, der repräsentative Punkt wird sich vom Punkt wegbewegen. Somit bringt eine kleine Abweichung das System aus dem stationären Zustand, daher ist der singuläre Punkt per Definition instabil. Eine ähnliche Überlegung führt dazu, dass jede Abweichung vom singulären Punkt mit der Zeit abklingt, der stationäre Zustand stabil ist. Die Abweichung des darstellenden Punktes in irgendeiner Richtung vom stationären Zustand führt zu seiner Entfernung vom Punkt , dies ist ein instabiler stationärer Zustand.

Lösen eines Systems linearer Differentialgleichungen

Wenden wir uns dem Studium von Gleichungssystemen zu, zunächst linear. Im Allgemeinen kann das System linearer Differentialgleichungen dargestellt werden als:

Die Analyse des Gleichungssystems beginnt mit dem Auffinden der stationären Zustände. Für Systeme der Form (1.3) ist der singuläre Punkt eindeutig, seine Koordinaten sind (0,0). Die Ausnahme ist der entartete Fall, in dem die Gleichungen dargestellt werden können als:

(1.3*)

In diesem Fall sind alle Paare, die die Beziehung erfüllen, stationäre Punkte des Systems (1.3*). Insbesondere ist auch für das System (1.3*) der Punkt (0,0) stationär. In der Phasenebene haben wir in diesem Fall eine Gerade mit einem Steigungskoeffizienten, die durch den Ursprung verläuft, wobei jeder Punkt ein singulärer Punkt des Systems (1.3 *) ist (siehe Tabelle 1.1, Punkt 6).

Die Hauptfrage, die durch das Ergebnis der Untersuchung eines Gleichungssystems beantwortet werden sollte, ist, ob der stationäre Zustand des Systems stabil ist und welchen Charakter diese Lösung hat (monoton oder nicht monoton).

Gemeinsame Entscheidung Das System zweier linearer Gleichungen hat die Form:

charakteristische Zahlen kann durch die Koeffizienten linearer Gleichungen wie folgt ausgedrückt werden:

Kennzahlen können 1) reell mit verschiedenen Vorzeichen, 2) reell mit gleichem Vorzeichen, 3) komplex konjugiert und in entarteten Fällen auch 4) rein imaginär, 5) reell übereinstimmend, 6) reell sein, von denen eine (bzw beide) ist gleich Null. Diese Fälle bestimmen die Art des Verhaltens der Lösung eines Systems gewöhnlicher Differentialgleichungen. Die entsprechenden Phasenporträts sind in Tabelle 1.1 dargestellt.

Tabelle 1.1. Arten von stationären Zuständen eines Systems zweier linearer Differentialgleichungen und die dazugehörigen Phasenportraits. Die Pfeile zeigen die Bewegungsrichtung des repräsentativen Punktes

Konstruktion von Phasen- und Kinetikporträts eines Systems zweier linearer Differentialgleichungen

Phasenebene bezeichnet eine Ebene mit Koordinatenachsen, auf denen die Werte von Variablen aufgetragen sind x und j entspricht jeder Punkt der Ebene einem bestimmten Zustand des Systems. Die Menge von Punkten auf der Phasenebene, deren Position den Zuständen des Systems im Prozess der zeitlichen Änderung von Variablen gemäß den gegebenen Gleichungen des untersuchten Systems entspricht, wird genannt Phasenverlauf. Der Satz von Phasentrajektorien für verschiedene Anfangswerte der Variablen gibt ein Porträt des Systems. Gebäude Phasenportrait ermöglicht es Ihnen, Rückschlüsse auf die Art der Änderungen von Variablen zu ziehen x und j ohne die analytischen Lösungen des ursprünglichen Gleichungssystems zu kennen.

Betrachten Sie ein System linearer Differentialgleichungen:

Die Konstruktion des Phasenporträts beginnt mit der Konstruktion Hauptisoklinen(Eine Isokline ist eine Linie, durch die die durch die Gleichung bestimmte Steigung der Phasenkurve (Trajektorie) konstant bleibt). Bei einem System aus zwei linearen Differentialgleichungen sind dies immer Geraden, die durch den Ursprung gehen. Die gleichung Isoklinen horizontaler Tangenten: . Gleichung der Isokline vertikaler Tangenten: . Zur weiteren Konstruktion des Phasenportraits ist es sinnvoll, eine Isokline aus schräg verlaufenden Tangenten zu konstruieren. Um die entsprechende Isoklinengleichung zu finden, muss die Gleichung gelöst werden . Sie können auch die Isoklinen von Tangenten anderer Winkel finden, indem Sie die ungefähren Werte der Tangenten der Winkel verwenden. Auch die Beantwortung der Frage, unter welchem ​​Winkel die Phasentrajektorien die Koordinatenachsen schneiden sollen, kann bei der Konstruktion des Phasenportraits helfen. Dazu in der Isoklinengleichung wir ersetzen die entsprechenden Gleichungen (um den Schnittwinkel mit der OY-Achse zu bestimmen) und (um den Schnittwinkel mit der OX-Achse zu bestimmen).

Beispiel 1.4. Bestimmen Sie die Art des singulären Punktes des linearen Gleichungssystems:

Erstellen Sie ein Phasen- und kinetisches Porträt des Systems.

Lösung: Die singulären Punktkoordinaten sind (0,0). Die Koeffizienten der linearen Gleichungen sind: , , , . Definieren wir die Art des stationären Zustands (siehe Abschnitt Kennziffern):

Die charakteristischen Wurzeln sind also imaginär: Der singuläre Punkt des betrachteten linearen Systems hat also den Zentrumstyp (Abb. 1.2a).

Gleichung der Isokline der horizontalen Tangente: , Gleichung der Isokline der vertikalen Tangente: . Unter einem Winkel von 45° schneiden die Trajektorien des Systems eine Gerade .

Nach der Erstellung des Phasenporträts ist es notwendig, die Bewegungsrichtung entlang der gefundenen Trajektorien zu bestimmen. Dies kann auf folgende Weise erfolgen. Nehmen Sie einen beliebigen Punkt auf einer beliebigen Bahn. Zum Beispiel auf der Isokline von horizontalen Tangenten (1,1). Setzen wir die Koordinaten dieses Punktes in das Gleichungssystem ein. Wir erhalten Ausdrücke für die Änderungsraten von Variablen x,j An diesem Punkt:

Die erhaltenen Werte zeigen, dass die Änderungsrate der Variablen x- negativ, das heißt, sein Wert sollte abnehmen, und die Variable jändert sich nicht. Wir markieren die empfangene Richtung mit einem Pfeil. Somit ist im betrachteten Beispiel die Bewegung entlang der Phasentrajektorien gegen den Uhrzeigersinn gerichtet. Wenn Sie die Koordinaten verschiedener Punkte in das System einsetzen, können Sie eine "Karte" der Richtungen von Geschwindigkeiten erhalten, die sogenannte Vektorfeld.

Abb. 1.2. Phase (a) und kinetisches (b) Porträt des Systems, Beispiel 1.4

Beachten Sie, dass auf der Isokline der horizontalen Tangente die Variable j auf einer gegebenen Bahn ihren maximalen oder minimalen Wert erreicht. Im Gegenteil, auf der Isokline der vertikalen Tangente ist die Variable x.

Ein kinetisches Porträt des Systems zu erstellen bedeutet, die Abhängigkeit der Werte der Variablen aufzuzeichnen x,j von Zeit. Ein Phasenporträt kann verwendet werden, um ein kinetisches zu erstellen und umgekehrt. Eine Phasenbahn entspricht einem Paar kinetischer Kurven. Wählen wir einen beliebigen Punkt auf dem Phasenportrait auf einer beliebigen Phasentrajektorie. Dies ist der Startpunkt, der der Zeit entspricht. Abhängig von der Bewegungsrichtung im betrachteten System sind die Werte der Variablen x,j entweder verringern oder erhöhen. Die Koordinaten des Startpunkts seien (1,1). Gemäß dem konstruierten Phasenporträt müssen wir ausgehend von diesem Punkt die Koordinaten gegen den Uhrzeigersinn verschieben x und j während sie abnehmen. Im Laufe der Zeit die Koordinate x durchläuft 0, Wert j dabei positiv bleiben. Weitere Koordinaten x und j weiter abnehmen, die Koordinate j geht durch 0 (Wert x während es negativ ist). Wert x erreicht seinen Minimalwert auf der Isokline der vertikalen Tangente und beginnt dann anzusteigen. Wert j erreicht seinen Minimalwert auf der Isokline der horizontalen Tangente (Wert x zu diesem Zeitpunkt ist negativ). Als nächstes und der Wert x, und der Wert j erhöhen und zu den Anfangswerten zurückkehren (Abb. 1.2b).

Untersuchung der Stabilität stationärer Zustände nichtlinearer Systeme zweiter Ordnung

Ein biologisches System sei durch ein System zweier autonomer Differentialgleichungen zweiter Ordnung allgemeiner Form beschrieben:

Die stationären Werte der Systemvariablen werden aus den algebraischen Gleichungen bestimmt:

In der Nachbarschaft jedes stationären Zustandes kann man sich überlegen Erstes Näherungssystem(linearisiertes System), dessen Untersuchung es ermöglichen kann, die Frage nach der Stabilität des singulären Punktes und der Natur der Phasentrajektorien in seiner kleinen Nachbarschaft zu beantworten.

außen

Wir haben , , der Singularpunkt ist rauh. Die charakteristischen Wurzeln des Systems der ersten Näherung sind gleich , beide sind reell und negativ, daher wird das Verhalten der Phasentrajektorien des Systems in der Nähe des singulären Nullpunkts dem Typ eines stabilen Knotens entsprechen.

Automatisierung und Telemechanik, L-1, 2007

RAS B 02.70.-c, 47.ll.-j

© 2007 Yu.S. POPKOV, Dr. tech. Sci. (Institut für Systemanalyse RAS, Moskau)

QUALITATIVE ANALYSE DYNAMISCHER SYSTEME MIT Vd-ENTROPY OPERATOR

Es wird ein Verfahren vorgeschlagen, um die Existenz, Einzigartigkeit und Lokalisierung von singulären Punkten der betrachteten Klasse von DSEE zu untersuchen. Es werden Stabilitätsbedingungen „im Kleinen“ und „im Großen“ geschaffen. Beispiele für die Anwendung der erhaltenen Bedingungen werden angegeben.

1. Einleitung

Viele Probleme der mathematischen Modellierung dynamischer Prozesse lassen sich auf der Grundlage des Konzepts dynamischer Systeme mit einem Entropieoperator (DEOS) lösen. DSEE ist ein dynamisches System, in dem die Nichtlinearität durch das parametrische Problem der Entropiemaximierung beschrieben wird. Feiomoyologisch ist DSEO ein Modell eines Makrosystems mit "langsamer" Selbstreproduktion und "schneller" Ressourcenallokation. Einige Eigenschaften von DSEO wurden in untersucht. Diese Arbeit setzt den Studienzyklus der qualitativen Eigenschaften von DSEOs fort.

Wir betrachten ein dynamisches System mit einem Vd-Entropieoperator:

^ = £(x, y(x)), x e En:

y(x) = a^max(Hv(y) | Ty = u(x), y e E^) > 0.

In diesen Ausdrücken:

C(x, y), u(x) sind stetig differenzierbare Vektorfunktionen;

Entropie

(1.2) Hv (y) = uz 1n as > 0, s = T~m;

T - (r x w)-Matrix mit Elementen ^ 0 hat einen Gesamtrang gleich r;

Die Vektorfunktion u(x) wird als stetig differenzierbar angenommen, die Menge

(1.3) Q = (q: 0<оТ ^ ц ^ а+} С Е+,

wobei a- und a + Vektoren von E+ sind, wobei a- ein Vektor mit kleinen Komponenten ist.

Verwenden der bekannten Darstellung des Entropieoperators in Form von Lagrange-Multiplikatoren. wir transformieren System (1.1) in die folgende Form:

- = £(x, y(z)), x e Kn, y(z) e K?, r e Er+

Uz (r) \u003d az\\ ^, 3 \u003d 1, m-

O(x, z) = Ty(z) = q(x),

wobei rk = exp(-Ak) > 0 die exponentiellen Lagrange-Multiplikatoren sind.

Neben dem DSEE der allgemeinen Form (1.1) betrachten wir nach der Einteilung in .

DSEE mit trennbarer Strömung:

(1-5) ^ = I (x) + Vy (z),

wobei B (n x m)-Matrix;

DSEO mit multiplikativem Fluss:

(1.6) ^ = x ® (a - x ® Xu(r)), ab

wobei W eine (n x m)-Matrix mit nicht negativen Elementen ist, a ein Vektor mit positiven Komponenten ist, ® das Zeichen der koordinatenweisen Multiplikation ist.

Das Ziel dieser Arbeit ist es, die Existenz, Einzigartigkeit und Lokalisierung einzelner Punkte des DSEE und ihre Stabilität zu untersuchen.

2. Singuläre Punkte

2.1. Existenz

Betrachten Sie System (1.4). Die singulären Punkte dieses dynamischen Systems werden durch die folgenden Gleichungen bestimmt:

(2.1) C^(x, y(z))=0, r = TP;

(2.2) uz(r) = a^r^, 3 = T^:

(2.3) bk(r) = ^as r^ = dk(x), k = 1,r.

Betrachten Sie zunächst das Hilfsgleichungssystem:

(2.4) C(q, z) = r, q e R,

wobei die Menge R durch Gleichheit (1.3) definiert ist und C(q, r) eine Vektorfunktion mit Komponenten ist

(2.5) Sk(d, r) = - Ok(r), a-< дк < а+, к =1,г.

Gleichung (2.4) hat für jeden festen Vektor q eine eindeutige Lösung r*, was aus den Eigenschaften des Vg-Entropieoperators folgt (siehe ).

Aus der Definition der Komponenten der Vektorfunktion С(g, z) erfolgt die offensichtliche Abschätzung:

(2.6) C(a+,r)< С(д, г) < С(а-,г), г в Е+. Рассмотрим два уравнения:

Bezeichnen wir die Lösung der ersten Gleichung mit r+ und die zweite - mit r-. Lassen Sie uns definieren

(2.7) C (a+,z) = z, C(a

(2.8) zmax = max z+, zmin = mm zk

und r-dimensionale Vektoren

(2.9) z(zmax, zmax), z(zmin , zmin).

Lemma 2.1. Für alle q G Q (1 . 3) gehören Lösungen z*(q) von Gleichung (2.4) zum Vektor 1 zum Segment

zmin< z*(q) < zmax,

wobei die Vektoren zmin und zmax durch die Ausdrücke (2.7)-(2.9) definiert sind.

Der Beweis des Satzes befindet sich im Anhang. Qq

qk(x) (1.3) für x G Rn, dann haben wir

Folgerung 2.1. Die Bedingungen von Lemma 2.1 seien erfüllt und die Funktionen qk(x) erfüllten die Bedingungen (1.3) für alle ex x G Rn. Dann gehören für alle x G Rm die Lösungen z* von Gleichung (2.3) zum Vektorsegment

zmin< z* < zmax

Kehren wir nun zu den Gleichungen (2.2) zurück. die die Komponenten der Vektorfunktion y(z) bestimmen. Die Elemente seiner Jacobi haben die Form

(2.10) jb aj zk JJ & > 0

für alle z G R+ außer 0 und g. Daher ist die Vektorfunktion y(z) streng monoton steigend. Nach Lemma 2.1 ist sie nach unten und oben beschränkt, d.h. für alle z G Rr (also für alle x G Rn) gehören ihre Werte zur Menge

(2.11) Y = (y: y-< y < y+},

wobei die Komponenten der Vektoren yk, y+ durch die Ausdrücke bestimmt werden:

(2.12) yk = aj y+ = aj znlax, j = h™.

(2.13) bj = Y, tsj, 3 =1,

Betrachten Sie die erste Gleichung in (2.1) und schreiben Sie sie um als:

(2.14) L(x, y) = 0 für alle y e Y ⊂ E^.

Diese Gleichung bestimmt die Abhängigkeit der Variablen x von der zu Y gehörenden Variablen y

we (1.4) reduziert sich auf die Existenz einer durch Gleichung (2.14) definierten impliziten Funktion x(y).

Lemma 2.2. Es seien die folgenden Bedingungen erfüllt:

a) die Vektorfunktion L(x, y) ist stetig in der Menge der Variablen;

b) lim L(x, y) = ±<ж для любого фиксированного у е Y;

c) det J (x, y) = 0 für alle ex x e En für alle festen y e Y.

Dann gibt es eine eindeutige implizite Funktion x*(y), die auf Y definiert ist. In diesem Lemma ist J(x, y) die Jacobi-Funktion mit Elementen

(2.15) Ji,i (x,y) = --i, i,l = l,n.

Der Beweis findet sich im Anhang. Aus den obigen Lemmata folgt

Satz 2.1. Die Bedingungen von Lemmas 2.1 und 2.2 seien erfüllt. Dann gibt es einen eindeutig singulären Punkt der DSEE (1.4) und dementsprechend (1.1).

2.2. Lokalisierung

Unter der Untersuchung der Lokalisierung eines singulären Punktes versteht man die Möglichkeit, das Intervall festzustellen, in dem er sich befindet. Diese Aufgabe ist nicht sehr einfach, aber für einige DSEE-Klassen kann ein solches Intervall eingerichtet werden.

Wenden wir uns der ersten Gruppe von Gleichungen in (2.1) zu und stellen sie in der Form dar

(2.16) L(x,y)=0, y- y y y+,

wobei y- und y+ durch Gleichungen (2.12), (2.13) definiert sind.

Satz 2.2. Die Vektorfunktion L(x,y) sei in beiden Variablen stetig differenzierbar und monoton steigend, d.h.

--> 0, --> 0; i, l = 1, n; j = 1,m. dxi dyj

Dann gehört die Lösung von System (2.16) bezüglich der Variablen x zum Intervall (2.17) xmin x x x xmax,

a) Die Vektoren xmin, xmax haben die Form

Min \u003d ich x 1 xmax \u003d r x t;

\xmin: . .., xminlxmax, . . ., xmax) :

xmin - ^Qin ^ ■ , xmax - ^QaX ^ ;

6) x- und x+ - Komponenten der Lösung der folgenden Gleichungen

(2.19) L(x,y-)=0, L(x,y+) = 0

mit oo m natürlich.

Der Beweis des Satzes befindet sich im Anhang.

3. Nachhaltigkeit von DSEA „im Kleinen“

3.1. DSEE mit trennbarem Fluss Wenden wir uns den DSEE-Gleichungen mit trennbarem Fluss zu und präsentieren sie in der Form:

- \u003d / (x) + Bu (r (x)), x e Kp ab

Y- (r (X)) \u003d azP (X) Y33, 3 \u003d 1, "~ 8 \u003d 1

0(x, r(x)) = Ty(r(x)) = q(x), r e Hr.

Hier gehören die Werte der Komponenten der Vektorfunktion q(x) zur Menge Q (1.3), die (n × w)-Matrix B hat einen Gesamtrang gleich n (n< ш). Вектор-функция / (х) непрерывно дифференцируемая.

Das betrachtete System habe einen singulären Punkt x. Um die Stabilität dieses singulären Punktes "im Kleinen" zu untersuchen, konstruieren wir ein linearisiertes System

wobei A eine (n x n)-Matrix ist, deren Elemente im Punkt x berechnet werden, und der Vektor t = x - x. Nach der ersten Gleichung in (3.1) hat die Matrix des linearisierten Systems

A \u003d 7 (x) + BUg (g) Xx (x), x \u003d g (x),

| 3 \u003d 1, w, k \u003d 1,

Ich k \u003d 1, g, ich \u003d 1, p

Aus (3.1) werden die Elemente der Matrix Yr:dy bestimmt.

"bkzP" 8=1

3, r8 x8, 5 1, r.

Zur Bestimmung der Elemente der Matrix Zx wenden wir uns der letzten Gruppe von Gleichungen in (3.1) zu. B zeigt, dass diese Gleichungen eine implizite Vektorfunktion r(x) definieren, die stetig differenzierbar ist, wenn die Vektorfunktion g(x) stetig differenzierbar ist. Das Jacobi-Zx der Vektorfunktion z(x) ist durch die Gleichung definiert

<Эг (z)Zx(Х) = Qx(Х),

vg (X) \u003d T Ug (X),

ddk, -t-, - "- k \u003d 1, r, ich \u003d 1, n dx \

Aus dieser Gleichung haben wir (3.9) Zx(x) = s-1(z)Qx(x).

Einsetzen dieses Ergebnisses in Gleichheit (3.3). wir bekommen:

A \u003d 1 (x) + P (x), P (x) \u003d VUg (g) [Tg (g)] -1 Qx (x).

Somit nimmt die Gleichung des linearisierten Systems die Form an

(c.i) | = (j+p)e

Hier werden die Elemente der Matrizen J, P an einem singulären Punkt berechnet. Ausreichende Stabilitätsbedingungen „im kleinen“ DSEE (3.1) werden durch folgendes bestimmt

Satz 3.1. Der DSEE (3.1) hat einen singulären Punkt x, der "im Kleinen" stabil ist, wenn die folgenden Bedingungen erfüllt sind:

a) die Matrizen J, P (3.10) des linearisierten Systems (3.11) haben reelle und verschiedene Eigenwerte, und die Matrix J hat den maximalen Eigenwert

Pmax = max Pg > 0,

Wmax = maxUi< 0;

Umax + Ptah<

Aus diesem Satz und der Gleichung (3.10) folgt, dass für singuläre Punkte, für die Qx(x) = 0 und (oder) für X, = 0 und tkj ^ 1 für alle ex k,j gilt, die hinreichenden Bedingungen des Satzes nicht gelten befriedigt.

3.2. DSEE mit multiplikativem Fluss Betrachten Sie Gleichungen (1.6). präsentieren sie in der Form:

X ® (a - x ® Wy(z(x))), x e Rn;

yj(z(x)) = aj ÏZs(x)]isi" j = 1,m;

(ZL2) yj (z(x)) = a^<~"ts

Q(x, z(x)) = Ty(z(x)) = q(x), z e R++.

Systeme. Werde haben:

(3.13)

In diesem Ausdruck ist diag C] eine diagonale Matrix mit positiven Elementen a1,..., an, Yr, Zx sind Matrizen, die durch Gleichheiten (3.4)-(3.7) definiert sind.

Wir stellen die Matrix A in der Form dar

(3.14) A = diag + P(x),

(3.15) P(x) = -2xWYz(z)Zx(x).

Es sei: maxi ai = nmax und wmax ist der maximale Eigenwert der Matrix P(x) (3.15). Dann gilt Satz 3.1 auch für die DSEE (1.6). (3.12).

4. Nachhaltigkeit von DSEA „in the big“

Wenden wir uns den DESO-Gleichungen (1.4) zu, in denen die Werte der Komponenten der Vektorfunktion q(x) zur Menge Q (1.3) gehören. Im betrachteten System gibt es einen singulären Punkt Z, zu dem die Vektoren z(x) = z ^ z-> 0 und

y(x) = y(z) = y > y- > 0.

Führen wir die Abweichungsvektoren £, C, П vom singulären Punkt ein: (4.1) £ = x - x, (= y - y, n = z - z.

ZHEZHERUN A.A., POKROWSKY A.V. - 2009

Einführung

Da das Konzept eines nichtlinearen dynamischen Systems reich genug ist, um ein extrem breites Spektrum von Prozessen abzudecken, bei denen das zukünftige Verhalten des Systems durch die Vergangenheit bestimmt wird, sind die auf diesem Gebiet entwickelten Analysemethoden in einer Vielzahl von Kontexten nützlich.

Die nichtlineare Dynamik gelangt auf mindestens drei Arten in die Literatur. Erstens gibt es Fälle, in denen experimentelle Daten über die zeitliche Änderung einer oder mehrerer Größen gesammelt und mit Techniken analysiert werden, die auf nichtlinearer dynamischer Theorie basieren, mit minimalen Annahmen über die zugrunde liegenden Gleichungen, die den Prozess steuern, der die Daten erzeugt. Das heißt, es ist ein Fall, in dem versucht wird, Korrelationen in den Daten zu finden, die die Entwicklung eines mathematischen Modells leiten können, anstatt zuerst das Modell zu erraten und es dann mit den Daten zu vergleichen.

Zweitens gibt es Fälle, in denen die nichtlineare dynamische Theorie verwendet werden kann, um festzustellen, dass ein vereinfachtes Modell wichtige Merkmale eines bestimmten Systems zeigen sollte, was impliziert, dass das beschreibende Modell über einen weiten Bereich von Parametern erstellt und untersucht werden kann. Dies führt häufig zu Modellen, die sich unter verschiedenen Parametern qualitativ unterschiedlich verhalten und zeigen, dass eine Region ein Verhalten zeigt, das dem im realen System beobachteten Verhalten sehr ähnlich ist. In vielen Fällen reagiert das Verhalten des Modells sehr empfindlich auf Parameteränderungen. Wenn also die Parameter des Modells in einem realen System gemessen werden können, zeigt das Modell bei diesen Werten ein realistisches Verhalten, und man kann sicher sein, dass das Modell erfasst die wesentlichen Merkmale des Systems.

Drittens gibt es Fälle, in denen Modellgleichungen auf der Grundlage detaillierter Beschreibungen bekannter Physik erstellt werden. Numerische Experimente können dann Informationen über Variablen liefern, die physikalischen Experimenten nicht zur Verfügung stehen.

Basierend auf dem zweiten Weg ist diese Arbeit eine Erweiterung meiner vorherigen Arbeit „Nichtlineares dynamisches Modell interdependenter Industrien“ sowie einer anderen Arbeit (Dmitriev, 2015)

Alle notwendigen Definitionen und andere theoretische Informationen, die in der Arbeit benötigt werden, erscheinen im ersten Kapitel nach Bedarf. An dieser Stelle sollen zwei Definitionen gegeben werden, die für die Offenlegung des Forschungsthemas selbst notwendig sind.

Lassen Sie uns zunächst die Systemdynamik definieren. Nach einer der Definitionen ist System Dynamics ein Simulationsmodellierungsansatz, der dank seiner Methoden und Werkzeuge hilft, die Struktur komplexer Systeme und ihre Dynamik zu bewerten (Shterman). Es ist erwähnenswert, dass die Systemdynamik auch eine Modellierungstechnik ist, die verwendet wird, um (in Bezug auf die Genauigkeit) korrekte Computermodelle für komplexe Systeme für ihre zukünftige Verwendung neu zu erstellen, um ein effizienteres Unternehmen / eine effizientere Organisation zu schaffen und Methoden zu verbessern von Interaktion mit diesem System. Der größte Bedarf an Systemdynamik ergibt sich aus der Konfrontation mit langfristigen, strategischen Modellen, und es ist auch erwähnenswert, dass sie ziemlich abstrakt ist.

Apropos nichtlineare Differentialdynamik, wir betrachten ein nichtlineares System, das per Definition ein System ist, bei dem die Änderung des Ergebnisses nicht proportional zur Änderung der Eingangsparameter ist und bei dem die Funktion die beschreibt Abhängigkeit der Zeitänderung und der Position eines Punktes im Raum (Boeing, 2016).

Basierend auf den obigen Definitionen wird deutlich, dass diese Arbeit verschiedene nichtlineare differentielle Systeme betrachten wird, die die Interaktion von Unternehmen beschreiben, sowie darauf aufbauende Simulationsmodelle. Auf dieser Grundlage wird der Zweck der Arbeit festgelegt.

Ziel dieser Arbeit ist es daher, eine qualitative Analyse dynamischer Systeme, die das Zusammenwirken von Unternehmen in erster Näherung beschreiben, durchzuführen und darauf aufbauend ein Simulationsmodell aufzubauen.

Um dieses Ziel zu erreichen, wurden folgende Aufgaben identifiziert:

Bestimmung der Stabilität des Systems.

Aufbau von Phasenportraits.

Integrale Trajektorien von Systemen finden.

Aufbau von Simulationsmodellen.

Jede dieser Aufgaben wird einem der Abschnitte jedes der Kapitel der Arbeit gewidmet.

Aus der Praxis heraus zeigt die Konstruktion grundlegender mathematischer Strukturen, die die Dynamik in verschiedenen physikalischen Systemen und Prozessen effektiv modellieren, dass das entsprechende mathematische Modell in gewissem Maße die Nähe zum untersuchten Original widerspiegelt, wenn seine charakteristischen Merkmale aus den Eigenschaften abgeleitet werden können und Strukturen aus der Art der Bewegung, die die Dynamik des Systems bildet. Bis heute befindet sich die Wirtschaftswissenschaft in einem Stadium ihrer Entwicklung, in dem neue und vielfach nicht standardisierte Methoden und Methoden der physikalischen und mathematischen Modellierung wirtschaftlicher Prozesse besonders effektiv eingesetzt werden. Daraus folgt die Schlussfolgerung über die Notwendigkeit, Modelle zu erstellen, zu studieren und zu bauen, die die wirtschaftliche Situation irgendwie beschreiben können.

Als Grund für die Wahl einer qualitativen statt einer quantitativen Analyse ist anzumerken, dass sich in den allermeisten Fällen die Ergebnisse und Schlussfolgerungen einer qualitativen Analyse dynamischer Systeme als aussagekräftiger erweisen als die Ergebnisse ihrer quantitativen Analyse. In einer solchen Situation ist es angebracht, auf die Aussagen von V.P. Milovanov, in dem er erklärt, dass sie traditionell glauben, dass die Ergebnisse, die bei der Anwendung mathematischer Methoden auf die Analyse realer Objekte erwartet werden, auf ein numerisches Ergebnis reduziert werden sollten. Qualitative Methoden haben in diesem Sinne eine etwas andere Aufgabe. Sie konzentriert sich auf das Erzielen eines Ergebnisses, das die Qualität des Systems beschreibt, auf die Suche nach charakteristischen Merkmalen aller Phänomene als Ganzes, auf die Vorhersage. Natürlich ist es wichtig zu verstehen, wie sich die Nachfrage ändert, wenn sich die Preise für eine bestimmte Art von Waren ändern, aber vergessen Sie nicht, dass es viel wichtiger ist zu verstehen, ob es unter solchen Bedingungen einen Mangel oder einen Überschuss an diesen Waren geben wird (Dmitriev , 2016).

Gegenstand dieser Studie ist die nichtlineare Differential- und Systemdynamik.

Forschungsgegenstand ist dabei die Beschreibung des Interaktionsprozesses zwischen Unternehmen durch nichtlineare Differential- und Systemdynamik.

In Bezug auf die praktische Anwendung des Studiums lohnt es sich, es sofort in zwei Teile zu unterteilen. Nämlich theoretisch, dh eine qualitative Analyse von Systemen, und praktisch, in dem der Aufbau von Simulationsmodellen betrachtet wird.

Der theoretische Teil dieser Studie vermittelt grundlegende Konzepte und Phänomene. Es berücksichtigt einfache Differenzsysteme, wie in den Arbeiten vieler anderer Autoren (Teschl, 2012; Nolte, 2015), ermöglicht aber gleichzeitig die Beschreibung der Interaktion zwischen Unternehmen. Darauf aufbauend können in Zukunft weiterführende Studien durchgeführt werden oder sich mit dem vertraut gemacht werden, was eine qualitative Analyse von Systemen ausmacht.

Der praktische Teil der Arbeit kann zur Erstellung eines Entscheidungsunterstützungssystems genutzt werden. Entscheidungsunterstützungssystem – ein automatisiertes Informationssystem, das darauf abzielt, das Geschäft oder die Entscheidungsfindung in einer Organisation zu unterstützen und es Ihnen ermöglicht, zwischen vielen verschiedenen Alternativen zu wählen (Keen, 1980). Auch wenn die Modelle im Moment nicht sehr genau sind, aber durch die Änderung für ein bestimmtes Unternehmen können Sie genauere Ergebnisse erzielen. Wenn Sie also verschiedene Parameter und Bedingungen ändern, die auf dem Markt auftreten können, können Sie eine Prognose für die Zukunft erhalten und im Voraus eine profitablere Entscheidung treffen.

1. Interaktion von Unternehmen unter den Bedingungen des Mutualismus

Die Arbeit wird zweidimensionale Systeme vorstellen, die im Vergleich zu Systemen höherer Ordnung recht einfach sind, uns aber gleichzeitig erlauben, die Beziehungen zwischen Organisationen aufzuzeigen, die wir brauchen.

Es lohnt sich, die Arbeit mit der Auswahl des Interaktionstyps zu beginnen, der in Zukunft beschrieben wird, da die Systeme, die ihn beschreiben, für jeden der Typen, wenn auch geringfügig, unterschiedlich sind. Abbildung 1.1 zeigt Yujim Odums Klassifikation für Bevölkerungsinteraktion, modifiziert für wirtschaftliche Interaktion (Odum, 1968), auf deren Grundlage wir die Interaktion von Unternehmen weiter betrachten werden.

Abbildung 1.1. Arten der Interaktion zwischen Unternehmen

Anhand von Abbildung 1.1 heben wir 4 Wechselwirkungsarten heraus und stellen für jede von ihnen ein Gleichungssystem vor, das sie basierend auf dem Malthus-Modell (Malthus, 1798) beschreibt. Demnach ist die Wachstumsrate proportional zur aktuellen Häufigkeit der Art, lässt sich also durch folgende Differenzialgleichung beschreiben:

wobei a ein Parameter ist, der vom natürlichen Bevölkerungswachstum abhängt. Es ist auch erwähnenswert, dass in den unten betrachteten Systemen alle Parameter sowie Variablen nicht negative Werte annehmen.

Die Produktion von Rohstoffen ist die Produktion von Produkten, die dem Räuber-Beute-Modell ähnelt. Das Räuber-Beute-Modell, auch als Lotka-Volterra-Modell bekannt, ist ein Paar nichtlinearer Differentialgleichungen erster Ordnung, das die Dynamik eines biologischen Systems mit zwei Arten beschreibt, von denen eine ein Räuber und die andere eine Beute ist (Llibre , 2007). Die Veränderung der Häufigkeit dieser Arten wird durch das folgende Gleichungssystem beschrieben:

(1.2)

wobei - das Wachstum der Produktion des ersten Unternehmens ohne den Einfluss des zweiten charakterisiert (im Fall des Räuber-Beute-Modells das Wachstum der Beutepopulation ohne Räuber),

Es charakterisiert das Wachstum der Produktion des zweiten Unternehmens ohne den Einfluss des ersten (Wachstum der Population von Raubtieren ohne Beute),

Es charakterisiert das Wachstum der Produktion des ersten Unternehmens unter Berücksichtigung des Einflusses des zweiten Unternehmens darauf (eine Zunahme der Anzahl der Beutetiere bei der Interaktion mit Raubtieren).

Es charakterisiert das Produktionswachstum des zweiten Unternehmens unter Berücksichtigung des Einflusses des ersten Unternehmens darauf (eine Zunahme der Anzahl von Raubtieren während ihrer Interaktion mit Opfern).

Zum einen hat das Raubtier, wie aus dem System ersichtlich ist, sowie Odums Klassifizierung, ihre Wechselwirkung einen günstigen Effekt. Andererseits ungünstig. Betrachtet man die wirtschaftlichen Realitäten, so ist das einfachste Analogon, wie aus der Abbildung ersichtlich, der Hersteller und sein Lieferant von Ressourcen, die jeweils dem Raubtier und der Beute entsprechen. Ohne Rohstoffe sinkt die Produktion also exponentiell.

Wettbewerb ist Rivalität zwischen zwei oder mehr (in unserem Fall betrachten wir zweidimensionale Systeme, also nehmen wir genau zwei Arten Wettbewerb) Arten, Wirtschaftsgruppen um Territorien, begrenzte Ressourcen oder andere Werte (Elton, 1968). Änderungen in der Anzahl der Arten oder in unserem Fall der Anzahl der Produkte werden durch das folgende System beschrieben:

(1.3)

In diesem Fall beeinflussen sich Arten oder Unternehmen, die ein Produkt herstellen, gegenseitig nachteilig. Das heißt, in Ermangelung eines Konkurrenten wird das Produktwachstum exponentiell zunehmen.

Kommen wir nun zu einer symbiotischen Interaktion, bei der sich beide Unternehmen gegenseitig positiv beeinflussen. Beginnen wir mit Mutualismus. Mutualismus ist eine Art von Beziehung zwischen verschiedenen Arten, in der jede von den Handlungen der anderen profitiert, und es ist erwähnenswert, dass die Anwesenheit eines Partners eine notwendige Voraussetzung für die Existenz ist (Thompson, 2005). Diese Art von Beziehung wird durch das System beschrieben:

(1.4)

Da die Interaktion zwischen Unternehmen für ihre Existenz notwendig ist, nimmt die Produktion der Güter eines anderen exponentiell ab, wenn das Produkt eines Unternehmens fehlt. Dies ist möglich, wenn Unternehmen schlichtweg keine anderen Beschaffungsalternativen haben.

Betrachten Sie eine andere Art der symbiotischen Interaktion, die Protokooperation. Proto-Kooperation ähnelt Mutualismus, mit der einzigen Ausnahme, dass kein Partner notwendig ist, da es beispielsweise andere Alternativen gibt. Da sie ähnlich sind, sehen ihre Systeme fast identisch aus:

(1.5)

Somit behindert das Fehlen des Produkts eines Unternehmens nicht das Wachstum des Produkts eines anderen Unternehmens.

Natürlich können neben den in den Abschnitten 3 und 4 aufgeführten anderen Arten von symbiotischen Beziehungen festgestellt werden: Kommensalismus und Amensalismus (Hanski, 1999). Aber sie werden nicht weiter erwähnt, da im Kommensalismus einem der Partner seine Interaktion mit dem anderen gleichgültig ist, aber wir betrachten dennoch Fälle, in denen es einen Einfluss gibt. Und Amensalismus wird nicht berücksichtigt, weil aus wirtschaftlicher Sicht solche Beziehungen, wenn ihre Wechselwirkung dem einen schadet und der andere gleichgültig ist, einfach nicht existieren können.

Ausgehend von der gegenseitigen Beeinflussung von Unternehmen, nämlich der Tatsache, dass symbiotische Beziehungen zu einer nachhaltigen Koexistenz von Unternehmen führen, werden in diesem Beitrag nur Fälle von Mutualismus und Proto-Kooperation betrachtet, da in beiden Fällen die Interaktion für alle von Vorteil ist.

Dieses Kapitel widmet sich der Interaktion von Unternehmen unter den Bedingungen des Mutualismus. Es werden zwei Systeme betrachtet, die eine Weiterentwicklung von Systemen nach dem Malthus-Modell sind, nämlich Systeme mit auferlegten Beschränkungen der Produktionssteigerung.

Die Dynamik eines Paares, das wie oben erwähnt durch wechselseitige Beziehungen verbunden ist, kann in erster Näherung durch das System beschrieben werden:

(1.6)

Es ist ersichtlich, dass bei einer großen anfänglichen Produktionsmenge das System unendlich wächst und bei einer kleinen Menge die Produktion abfällt. Hierin liegt die Unrichtigkeit der bilinearen Beschreibung des Effekts, der durch den Mutualismus entsteht. Um zu versuchen, das Bild zu korrigieren, führen wir einen Faktor ein, der der Sättigung eines Raubtiers ähnelt, dh einen Faktor, der die Wachstumsrate der Produktion verringert, wenn sie übermäßig ist. In diesem Fall kommen wir zu folgendem System:

(1.7)

wo ist das Wachstum der Produktion des Produkts des ersten Unternehmens in seiner Wechselwirkung mit dem zweiten unter Berücksichtigung der Sättigung,

Wachstum der Produktion des Produkts des zweiten Unternehmens in seiner Interaktion mit dem ersten unter Berücksichtigung der Sättigung,

Sättigungskoeffizienten.

Somit haben wir zwei Systeme: das malthusianische Wachstumsmodell mit und ohne Sättigung.

1.1 Stabilität von Systemen in erster Näherung

Die Stabilität von Systemen in erster Näherung wird in vielen ausländischen (Hairer, 1993; Bhatia, 2002; Khalil, 2001; Strogatz, 2001 und andere) und russischsprachigen Arbeiten (Akhromeyeva, 1992; Bellman, 1954; Demidovich, 1967; Krasovsky, 1959 und andere), und ihre Definition ist ein grundlegender Schritt zur Analyse der im System ablaufenden Prozesse. Führen Sie dazu die folgenden notwendigen Schritte aus:

Lassen Sie uns Gleichgewichtspunkte finden.

Lassen Sie uns die Jacobi-Matrix des Systems finden.

Finden Sie die Eigenwerte der Jacobi-Matrix.

Wir klassifizieren die Gleichgewichtspunkte nach dem Satz von Lyapunov.

Nachdem wir uns die Schritte angesehen haben, lohnt es sich, näher auf ihre Erklärung einzugehen, daher werde ich Definitionen geben und die Methoden beschreiben, die wir in jedem dieser Schritte verwenden werden.

Der erste Schritt, die Suche nach Gleichgewichtspunkten. Um sie zu finden, setzen wir jede Funktion mit Null gleich. Das heißt, wir lösen das System:

wobei a und b alle Parameter der Gleichung bedeuten.

Der nächste Schritt besteht darin, die Jacobi-Matrix zu finden. In unserem Fall wird dies irgendwann eine 2-mal-2-Matrix mit ersten Ableitungen sein, wie unten gezeigt:

Nachdem wir die ersten beiden Schritte abgeschlossen haben, fahren wir fort, die Wurzeln der folgenden charakteristischen Gleichung zu finden:

Wobei der Punkt den im ersten Schritt gefundenen Gleichgewichtspunkten entspricht.

Nachdem wir und gefunden haben, gehen wir zum vierten Schritt über und verwenden die folgenden Lyapunov-Theoreme (Parks, 1992):

Satz 1: Wenn alle Wurzeln der charakteristischen Gleichung einen negativen Realteil haben, dann ist der Gleichgewichtspunkt, der dem ursprünglichen und dem linearisierten System entspricht, asymptotisch stabil.

Satz 2: Wenn mindestens eine der Wurzeln der charakteristischen Gleichung einen positiven Realteil hat, dann ist der Gleichgewichtspunkt, der dem ursprünglichen und dem linearisierten System entspricht, asymptotisch instabil.

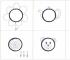
Außerdem lässt sich anhand der in Abbildung 1.2 (Lamar University) dargestellten Aufteilung die Stabilitätsart genauer bestimmen.

Abbildung 1.2. Arten der Stabilität von Gleichgewichtspunkten

Nachdem wir die notwendigen theoretischen Informationen berücksichtigt haben, wenden wir uns der Analyse von Systemen zu.

Betrachten Sie ein System ohne Sättigung:

Es ist sehr einfach und für die Praxis nicht geeignet, da es keine Einschränkungen gibt. Aber als erstes Beispiel kommt eine Systemanalyse in Betracht.

Lassen Sie uns zuerst die Gleichgewichtspunkte finden, indem wir die rechten Seiten der Gleichungen mit Null gleichsetzen. Somit finden wir zwei Gleichgewichtspunkte, nennen wir sie A und B: .

Kombinieren wir den Schritt mit der Suche nach der Jacobi-Matrix, den Wurzeln der charakteristischen Gleichung und der Bestimmung der Stabilitätsart. Da sie elementar sind, bekommen wir sofort die Antwort:

1. An der Stelle , , befindet sich ein stabiler Knoten.

Am Punkt: ... Sattel.

Wie ich bereits geschrieben habe, ist dieses System zu trivial, sodass keine Erklärung erforderlich war.

Lassen Sie uns nun das System von der Sättigung aus analysieren:

(1.9)

Das Auftreten einer Beschränkung der gegenseitigen Sättigung von Produkten durch Unternehmen bringt uns näher an das wirkliche Bild dessen, was passiert, und verkompliziert auch das System geringfügig.

Wie zuvor setzen wir die rechten Teile des Systems gleich Null und lösen das resultierende System. Der Punkt blieb unverändert, aber der andere Punkt enthält in diesem Fall mehr Parameter als zuvor: .

In diesem Fall hat die Jacobi-Matrix folgende Form:

Subtrahiere davon die mit multiplizierte Identitätsmatrix und setze die Determinante der resultierenden Matrix an den Punkten A und B mit Null gleich.

An der Stelle eines ähnlichen frühen Bildes:

stabiler Knoten.

Aber an der Stelle alles ist etwas komplizierter, und obwohl die Mathematik immer noch recht einfach ist, verursacht die Komplexität die Unannehmlichkeit, mit langen wörtlichen Ausdrücken zu arbeiten. Da sich die Werte als ziemlich lang und umständlich niedergeschrieben herausstellen, werden sie nicht angegeben, es reicht zu sagen, dass in diesem Fall wie beim vorherigen System die Art der erhaltenen Stabilität ein Sattel ist.

2 Phasenporträts von Systemen

Die überwiegende Mehrheit der nichtlinearen dynamischen Modelle sind komplexe Differentialgleichungen, die entweder nicht gelöst werden können, oder dies ist eine Art Komplexität. Ein Beispiel ist das System aus dem vorherigen Abschnitt. Trotz der scheinbaren Einfachheit war es keine leichte Aufgabe, die Art der Stabilität am zweiten Gleichgewichtspunkt zu finden (wenn auch nicht aus mathematischer Sicht), und mit einer Zunahme von Parametern, Einschränkungen und Gleichungen, um die Anzahl der interagierenden Unternehmen zu erhöhen die Komplexität wird nur zunehmen. Wenn die Parameter numerische Ausdrücke sind, wird natürlich alles unglaublich einfach, aber dann verliert die Analyse irgendwie jede Bedeutung, weil wir am Ende Gleichgewichtspunkte finden und ihre Stabilitätstypen nur für ein bestimmtes herausfinden können Fall, kein allgemeiner.

In solchen Fällen lohnt es sich, sich an Phasenebene und Phasenportraits zu erinnern. In der angewandten Mathematik, insbesondere im Kontext der nichtlinearen Systemanalyse, ist die Phasenebene eine visuelle Darstellung bestimmter Eigenschaften bestimmter Arten von Differentialgleichungen (Nolte, 2015). Die Koordinatenebene mit Werteachsen beliebiger Variablenpaare, die den Zustand des Systems charakterisieren, ist ein zweidimensionaler Fall eines gemeinsamen n-dimensionalen Phasenraums.

Dank der Phasenebene ist es möglich, das Vorhandensein von Grenzzyklen in Lösungen einer Differentialgleichung grafisch zu bestimmen.

Die Lösungen einer Differentialgleichung sind eine Familie von Funktionen. Grafisch lässt sich dies in der Phasenebene als zweidimensionales Vektorfeld darstellen. In der Ebene werden Vektoren gezeichnet, die Ableitungen an charakteristischen Punkten in Bezug auf einen Parameter darstellen, in unserem Fall in Bezug auf die Zeit, dh (). Mit genügend dieser Pfeile in einem Bereich kann das Verhalten des Systems visualisiert und Grenzzyklen leicht identifiziert werden (Boeing, 2016).

Das Vektorfeld ist ein Phasenporträt, ein bestimmter Pfad entlang der Flusslinie (dh ein Pfad, der immer tangential zu den Vektoren verläuft) ist ein Phasenpfad. Strömungen in einem Vektorfeld geben die zeitliche Veränderung des Systems an, beschrieben durch eine Differentialgleichung (Jordan, 2007).

Es ist erwähnenswert, dass ein Phasenporträt auch ohne Lösen der Differentialgleichung erstellt werden kann und gleichzeitig eine gute Visualisierung viele nützliche Informationen liefern kann. Außerdem gibt es derzeit viele Programme, die bei der Konstruktion von Phasendiagrammen helfen können.

Daher sind Phasenebenen nützlich, um das Verhalten physikalischer Systeme zu visualisieren. Insbesondere oszillierende Systeme, wie das oben bereits erwähnte Räuber-Beute-Modell. In diesen Modellen können sich Phasentrajektorien in Richtung Null "verdrehen", ins Unendliche "aus einer Spirale herausgehen" oder eine neutrale stabile Situation erreichen, die als Zentren bezeichnet wird. Dies ist nützlich, um festzustellen, ob die Dynamik stabil ist oder nicht (Jordan, 2007).

Die in diesem Abschnitt vorgestellten Phasenporträts werden mit WolframAlpha-Tools erstellt oder aus anderen Quellen bereitgestellt. Malthusianisches Wachstumsmodell ohne Sättigung.

Lassen Sie uns ein Phasenporträt des ersten Systems mit drei Sätzen von Parametern erstellen, um ihr Verhalten zu vergleichen. Satz A ((1,1), (1,1)), der als einzelner Satz bezeichnet wird, Satz B ((10,0,1), (2,2)), wenn er ausgewählt wird, erfährt das System eine Spitze Rückgang der Produktion, und die Menge C ((1,10), (1,10)), für die im Gegenteil ein starkes und unbegrenztes Wachstum auftritt. Es ist zu beachten, dass die Werte entlang der Achsen in allen Fällen in den gleichen Intervallen von -10 bis 10 liegen, um Phasendiagramme bequem miteinander vergleichen zu können. Dies gilt natürlich nicht für ein qualitatives Porträt des Systems, dessen Achsen dimensionslos sind.

Abbildung 1.3 Phasenporträt mit Parametern A

Differentialgrenzgleichung des Mutualismus

Abbildung 1.3 oben zeigt die Phasenportraits des Systems für die drei angegebenen Parametersätze sowie das Phasenportrait, das das qualitative Verhalten des Systems beschreibt. Vergessen Sie nicht, dass aus praktischer Sicht das erste Quartal am wichtigsten ist, da die Produktionsmenge, die nur nicht negativ sein kann, unsere Achse ist.

In jeder der Abbildungen ist die Stabilität am Gleichgewichtspunkt (0,0) deutlich sichtbar. Und in der ersten Abbildung macht sich der „Sattelpunkt“ auch am Punkt (1,1) bemerkbar, das heißt, wenn wir die Werte des Parametersatzes in das System einsetzen, dann am Gleichgewichtspunkt B. Wenn sich die Grenzen des Modellbaus ändern, findet sich der Sattelpunkt auch auf anderen Phasenportraits wieder.

Malthusianisches Wachstumsmodell aus Sättigung.

Konstruieren wir Phasendiagramme für das zweite System, in dem es Sättigung gibt, mit drei neuen Sätzen von Parameterwerten. Satz A, ((0,1,15,100), (0,1,15,100)), Satz B ((1,1,0,5), (1, 1,0,5)) und Satz C ((20,1,100), (20,1,100 )).

Abbildung 1.4. Phasenportrait mit Parameter A

Wie Sie sehen können, ist der Punkt (0,0) für jeden Parametersatz gleichgewichtig und auch stabil. Auch in manchen Figuren ist ein Sattelpunkt zu sehen.

Dabei wurden verschiedene Skalen betrachtet, um deutlicher zu machen, dass sich das qualitative Bild auch bei Hinzunahme eines Sättigungsfaktors nicht ändert, dh Sättigung allein nicht ausreicht. Dabei ist zu berücksichtigen, dass Unternehmen in der Praxis Stabilität brauchen, d.h. wenn wir nichtlineare Differentialgleichungen betrachten, dann sind wir am meisten an stabilen Gleichgewichtspunkten interessiert, und in diesen Systemen sind nur Nullpunkte solche Punkte, was bedeutet dass solche mathematischen Modelle eindeutig nicht für Unternehmen geeignet sind. Das bedeutet schließlich, dass Unternehmen nur bei Nullproduktion in einer Stabilität sind, die sich deutlich vom realen Bild der Welt unterscheidet.

In der Mathematik ist eine Integralkurve eine parametrische Kurve, die eine spezifische Lösung einer gewöhnlichen Differentialgleichung oder eines Gleichungssystems darstellt (Lang, 1972). Stellt man die Differentialgleichung als Vektorfeld dar, dann tangieren die entsprechenden Integralkurven das Feld in jedem Punkt.

Integralkurven sind je nach Art und Interpretation der Differentialgleichung oder des Vektorfeldes auch unter anderen Namen bekannt. In der Physik sind Integralkurven für ein elektrisches oder magnetisches Feld als Feldlinien bekannt, und Integralkurven für ein Fluidgeschwindigkeitsfeld sind als Stromlinien bekannt. In dynamischen Systemen werden Integralkurven für eine Differentialgleichung Trajektorien genannt.

Abbildung 1.5. Integrale Kurven

Lösungen eines beliebigen Systems können auch als Gleichungen von Integralkurven betrachtet werden. Offensichtlich ist jede Phasenbahn eine Projektion einer Integralkurve im x,y,t-Raum auf die Phasenebene.

Es gibt mehrere Möglichkeiten, Integralkurven zu konstruieren.

Eine davon ist die Isokline-Methode. Eine Isokline ist eine Kurve, die durch Punkte verläuft, an denen die Steigung der betrachteten Funktion unabhängig von den Anfangsbedingungen immer gleich ist (Hanski, 1999).

Es wird oft als grafische Methode zum Lösen gewöhnlicher Differentialgleichungen verwendet. Beispielsweise sind in einer Gleichung der Form y " = f (x, y) Isoklinen Linien in der (x, y)-Ebene, die man erhält, indem man f (x, y) mit einer Konstanten gleichsetzt. Dies ergibt eine Reihe von Linien ( für verschiedene Konstanten), entlang derer die Kurvenlösungen die gleiche Steigung haben. Durch die Berechnung dieser Steigung für jede Isokline kann das Steigungsfeld visualisiert werden, was es relativ einfach macht, ungefähre Lösungskurven zu zeichnen. Die folgende Abbildung zeigt ein Beispiel für die Verwendung der Isoklinenmethode .

Abbildung 1.6. Isokline-Methode

Diese Methode erfordert keine Computerberechnungen und war in der Vergangenheit sehr beliebt. Jetzt gibt es Softwarelösungen, die Integralkurven auf Computern extrem genau und schnell erstellen. Trotzdem hat sich die Isokline-Methode als gutes Werkzeug zur Untersuchung des Verhaltens von Lösungen bewährt, da sie es erlaubt, die Bereiche des typischen Verhaltens von Integralkurven zu zeigen.

Malthusianisches Wachstumsmodell ohne Sättigung.

Beginnen wir damit, dass es trotz der Existenz verschiedener Konstruktionsmethoden nicht so einfach ist, die Integralkurven eines Gleichungssystems darzustellen. Das zuvor erwähnte Isokline-Verfahren ist nicht geeignet, da es für Differentialgleichungen erster Ordnung funktioniert. Und Software-Tools, die solche Kurven zeichnen können, sind nicht öffentlich zugänglich. Bezahlt wird zum Beispiel Wolfram Mathematica, das dazu in der Lage ist. Daher werden wir versuchen, die Fähigkeiten von Wolfram Alpha so weit wie möglich zu nutzen, dessen Arbeit in verschiedenen Artikeln und Werken beschrieben wird (Orca, 2009). Auch wenn das Bild eindeutig nicht ganz zuverlässig ist, können Sie zumindest die Abhängigkeit in den Ebenen (x, t), (y, t) zeigen. Lassen Sie uns zuerst jede der Gleichungen nach t lösen. Das heißt, wir leiten die Abhängigkeit jeder der Variablen in Bezug auf die Zeit ab. Für dieses System erhalten wir:

(1.10)

(1.11)

Die Gleichungen sind symmetrisch, also betrachten wir nur eine davon, nämlich x(t). Lassen Sie die Konstante gleich 1 sein. In diesem Fall verwenden wir die Plotfunktion.

Abbildung 1.7. Dreidimensionales Modell für Gleichung (1.10)

Malthusianisches Wachstumsmodell aus Sättigung.

Lassen Sie uns dasselbe für das andere Modell tun. Letztendlich erhalten wir zwei Gleichungen, die die Abhängigkeit von Variablen von der Zeit zeigen.

(1.12)

(1.13)

Lassen Sie uns ein dreidimensionales Modell bauen und wieder Linien nivellieren.

Abbildung 1.8. Dreidimensionales Modell für Gleichung (1.12)

Da die Werte der Variablen nicht negativ sind, erhalten wir im Bruch mit dem Exponenten eine negative Zahl. Somit nimmt die Integralkurve mit der Zeit ab.

Zuvor wurde eine Definition der Systemdynamik gegeben, um die Essenz der Arbeit zu verstehen, aber lassen Sie uns jetzt näher darauf eingehen.

Systemdynamik ist eine Methodik und Methode der mathematischen Modellierung zur Bildung, zum Verständnis und zur Diskussion komplexer Probleme, die ursprünglich in den 1950er Jahren von Jay Forrester entwickelt und in seinem Werk (Forrester, 1961) beschrieben wurde.

Systemdynamik ist ein Aspekt der Systemtheorie als Methode zum Verständnis des dynamischen Verhaltens komplexer Systeme. Grundlage der Methode ist die Erkenntnis, dass die Struktur eines jeden Systems aus zahlreichen Beziehungen zwischen seinen Komponenten besteht, die für sein Verhalten oft ebenso wichtig sind wie die einzelnen Komponenten selbst. Beispiele sind die Chaostheorie und die soziale Dynamik, die in den Werken verschiedener Autoren beschrieben werden (Grebogi, 1987; Sontag, 1998; Kuznetsov, 2001; Tabor, 2001). Es wird auch argumentiert, dass, da Ganzheitseigenschaften oft nicht in Elementeigenschaften gefunden werden können, in einigen Fällen das Verhalten des Ganzen nicht durch das Verhalten der Teile erklärt werden kann.

Simulation kann wirklich die volle praktische Bedeutung eines dynamischen Systems zeigen. Obwohl es in Tabellenkalkulationen möglich ist, gibt es viele Softwarepakete, die speziell für diesen Zweck optimiert wurden.

Die Modellierung selbst ist der Prozess der Erstellung und Analyse eines Prototyps eines physikalischen Modells, um seine Leistung in der realen Welt vorherzusagen. Simulationsmodellierung hilft Konstrukteuren und Ingenieuren zu verstehen, unter welchen Bedingungen und in welchen Fällen ein Prozess versagen kann und welchen Belastungen er standhalten kann (Khemdy, 2007). Die Modellierung kann auch dabei helfen, das Verhalten von Fluidströmungen und anderen physikalischen Phänomenen vorherzusagen. Das Modell analysiert die ungefähren Arbeitsbedingungen aufgrund der angewandten Simulationssoftware (Strogalev, 2008).

Einschränkungen der Möglichkeiten der Simulationsmodellierung haben eine gemeinsame Ursache. Die Konstruktion und numerische Berechnung eines exakten Modells garantiert nur dort Erfolg, wo es eine exakte quantitative Theorie gibt, d. h. wenn die Gleichungen, die bestimmte Phänomene beschreiben, bekannt sind und es nur darum geht, diese Gleichungen mit der erforderlichen Genauigkeit zu lösen. In Bereichen, in denen es keine quantitative Theorie gibt, ist die Erstellung eines exakten Modells von begrenztem Wert (Bazykin, 2003).

Die Modellierungsmöglichkeiten sind jedoch nicht unbegrenzt. Dies liegt zunächst daran, dass der Anwendungsbereich des Simulationsmodells schwer einzuschätzen ist, insbesondere der Zeitraum, für den die Prognose mit der erforderlichen Genauigkeit erstellt werden kann (Law, 2006). Hinzu kommt, dass das Simulationsmodell naturgemäß an ein bestimmtes Objekt gebunden ist und beim Versuch, es auf ein anderes, auch ähnliches Objekt anzuwenden, eine radikale Anpassung oder zumindest eine deutliche Modifikation erfordert.

Es gibt einen allgemeinen Grund für das Bestehen von Einschränkungen bei der Simulation. Die Konstruktion und numerische Berechnung eines „exakten“ Modells gelingt nur, wenn eine quantitative Theorie existiert, also nur wenn alle Gleichungen bekannt sind, und sich das Problem nur darauf reduziert, diese Gleichungen mit einer gewissen Genauigkeit zu lösen (Bazykin, 2003).

Aber trotzdem ist die Simulationsmodellierung ein hervorragendes Werkzeug, um dynamische Prozesse zu visualisieren und mit einem mehr oder weniger korrekten Modell Entscheidungen auf der Grundlage seiner Ergebnisse zu treffen.

In dieser Arbeit werden Systemmodelle unter Verwendung der vom AnyLogic-Programm angebotenen Systemdynamik-Tools erstellt.

Malthusianisches Wachstumsmodell ohne Sättigung/

Vor dem Erstellen eines Modells ist es notwendig, die Elemente der Systemdynamik zu betrachten, die wir verwenden werden, und sie mit unserem System in Beziehung zu setzen. Die folgenden Definitionen sind den Hilfeinformationen des Programms AnyLogic entnommen.

Der Antrieb ist das Hauptelement von Systemdynamikdiagrammen. Sie werden verwendet, um Objekte der realen Welt darzustellen, in denen sich bestimmte Ressourcen ansammeln: Geld, Substanzen, eine Anzahl von Personengruppen, einige materielle Objekte usw. Akkumulatoren spiegeln den statischen Zustand des simulierten Systems wider und ihre Werte ändern sich im Laufe der Zeit entsprechend den im System vorhandenen Flüssen. Daraus folgt, dass die Dynamik des Systems durch die Strömungen bestimmt wird. Ströme, die in den Akkumulator eintreten und ihn verlassen, erhöhen oder verringern die Werte des Akkumulators.

Die Strömung ist neben dem erwähnten Antrieb das Hauptelement systemdynamischer Diagramme.

Während die Lagerplätze den statischen Teil des Systems definieren, bestimmen die Flüsse die Änderungsrate der Lagerplätze, also wie sich die Bestände über die Zeit verändern, und damit die Dynamik des Systems.

Der Agent kann Variablen enthalten. Variablen werden typischerweise verwendet, um die sich ändernden Eigenschaften eines Agenten zu modellieren oder um die Ergebnisse des Modells zu speichern. Typischerweise bestehen dynamische Variablen aus Akkumulatorfunktionen.

Der Agent kann Parameter haben. Parameter werden häufig verwendet, um einige der Eigenschaften des modellierten Objekts darzustellen. Sie sind nützlich, wenn Objektinstanzen das gleiche Verhalten wie in der Klasse beschrieben haben, sich aber in einigen Parameterwerten unterscheiden. Es gibt einen klaren Unterschied zwischen Variablen und Parametern. Die Variable stellt den Zustand des Modells dar und kann sich während der Simulation ändern. Der Parameter wird normalerweise verwendet, um Objekte statisch zu beschreiben. Während eines "Durchlaufs" des Modells ist der Parameter normalerweise eine Konstante und wird nur geändert, wenn das Verhalten des Modells neu konfiguriert werden muss.

Ein Link ist ein Element der Systemdynamik, das verwendet wird, um die Beziehung zwischen Elementen eines Flussdiagramms und Akkumulatoren zu bestimmen. Es erstellt nicht automatisch Links, sondern zwingt den Benutzer, sie explizit im grafischen Editor zu zeichnen (es ist jedoch erwähnenswert). dass AnyLogic auch einen Mechanismus zum schnellen Setzen fehlender Links unterstützt). Wenn beispielsweise ein Element von A in der Gleichung oder der Anfangswert von Element B erwähnt wird, müssen Sie diese Elemente zuerst mit einem Link von A nach B verbinden und erst dann den Ausdruck in den Eigenschaften von B eingeben .

Es gibt einige andere Elemente der Systemdynamik, aber sie werden im Verlauf der Arbeit nicht involviert sein, also werden wir sie weglassen.

Betrachten wir zunächst, woraus das Modell des Systems (1.4) bestehen wird.

Zuerst markieren wir sofort zwei Laufwerke, die die Werte der Produktionsmenge jedes Unternehmens enthalten.

Da wir zweitens zwei Terme in jeder Gleichung haben, erhalten wir zwei Flüsse zu jedem der Antriebe, einen eingehenden, den anderen ausgehenden.

Drittens übergeben wir Variablen und Parameter. Es gibt nur zwei Variablen. X und Y, verantwortlich für das Wachstum der Produktion. Wir haben auch vier Optionen.

Viertens muss im Hinblick auf die Verbindungen jeder der Flüsse den in der Flussgleichung enthaltenen Variablen und Parametern zugeordnet werden, und beide Variablen müssen Akkumulatoren zugeordnet werden, um den Wert über die Zeit zu ändern.

Wir werden eine detaillierte Beschreibung des Aufbaus eines Modells als Beispiel für die Arbeit in der AnyLogic-Modellierungsumgebung für das nächste System hinterlassen, da es etwas komplizierter ist und mehr Parameter verwendet, und wir werden sofort mit der Betrachtung der fertigen Version fortfahren System.

Abbildung 1.9 unten zeigt das konstruierte Modell:

Abbildung 1.9. Systemdynamikmodell für System (1.4)

Alle Elemente der Systemdynamik entsprechen den oben beschriebenen, d.h. zwei Laufwerke, vier Streams (zwei eingehende, zwei ausgehende), vier Parameter, zwei dynamische Variablen und notwendige Links.

Die Abbildung zeigt, dass je mehr Produkte, desto stärker sein Wachstum, was zu einem starken Anstieg der Warenanzahl führt, was unserem System entspricht. Aber wie bereits erwähnt, lässt das Fehlen von Beschränkungen für dieses Wachstum die Anwendung dieses Modells in der Praxis nicht zu.

Malthusianisches Wachstumsmodell aus Sättigung/

Lassen Sie uns in Anbetracht dieses Systems näher auf die Konstruktion des Modells eingehen.

Der erste Schritt besteht darin, zwei Laufwerke hinzuzufügen, nennen wir sie X_stock und Y_stock. Weisen wir jedem von ihnen einen Anfangswert gleich 1. Beachten Sie, dass in Abwesenheit von Flüssen nichts in der klassisch gegebenen Speichergleichung ist.

Abbildung 1.10. Erstellen eines Systemmodells (1.9)

Der nächste Schritt ist das Hinzufügen von Threads. Lassen Sie uns mit einem grafischen Editor einen eingehenden und ausgehenden Stream für jedes Laufwerk erstellen. Wir dürfen nicht vergessen, dass eine der Kanten der Strömung im Antrieb sein muss, sonst werden sie nicht verbunden.

Sie können sehen, dass die Gleichung für das Laufwerk automatisch gesetzt wurde, natürlich kann der Benutzer sie selbst schreiben, indem er den „beliebigen“ Gleichungsmodus wählt, aber der einfachste Weg ist, diese Aktion dem Programm zu überlassen.

Unser dritter Schritt besteht darin, sechs Parameter und zwei dynamische Variablen hinzuzufügen. Lassen Sie uns jedem Element einen Namen gemäß seinem wörtlichen Ausdruck im System geben und auch die Anfangswerte der Parameter wie folgt festlegen: e1 = e2 = 1, a12 = a21 = 3, n1 = n2 = 0,2.

Alle Elemente der Gleichungen sind vorhanden, es müssen nur noch die Gleichungen für die Flüsse geschrieben werden, aber dazu müssen Sie zuerst Verbindungen zwischen den Elementen hinzufügen. Beispielsweise muss der für den Begriff verantwortliche Ausgangsstrom mit e1 und x verknüpft werden. Und jede dynamische Variable muss mit ihrer entsprechenden Aktie verknüpft werden (X_Aktie x, Y_Aktie y). Das Erstellen von Links ähnelt dem Hinzufügen von Threads.

Nachdem Sie die erforderlichen Verbindungen erstellt haben, können Sie mit dem Schreiben von Gleichungen für die Flüsse fortfahren, was in der rechten Abbildung dargestellt ist. Sie können natürlich auch in umgekehrter Reihenfolge vorgehen, aber wenn es Verbindungen gibt, erscheinen beim Schreiben von Gleichungen Hinweise zum Ersetzen der erforderlichen Parameter / Variablen, was die Aufgabe in komplexen Modellen erleichtert.

Nachdem Sie alle Schritte abgeschlossen haben, können Sie das Simulationsmodell ausführen und sich das Ergebnis ansehen.

Nachdem wir die Systeme nichtlinearer Differentialgleichungen für die Interaktion von Unternehmen unter den Bedingungen des Mutualismus betrachtet haben, können wir mehrere Schlussfolgerungen ziehen.

Es gibt zwei Zustände des Systems: ein scharfes unbegrenztes Wachstum oder die Tendenz der Produktionsmenge gegen Null. Welchen der beiden Zustände das System einnimmt, hängt von den Parametern ab.

Keines der vorgeschlagenen Modelle, einschließlich des Modells unter Berücksichtigung der Sättigung, ist aufgrund des Fehlens einer stabilen Position ungleich Null sowie der in Absatz 1 beschriebenen Gründe für die praktische Verwendung nicht geeignet.

Im Falle eines Versuchs, diese Art der symbiotischen Interaktion weiter zu untersuchen, um ein von Unternehmen in der Praxis anwendbares Modell zu erstellen, ist es notwendig, das System weiter zu verkomplizieren und neue Parameter einzuführen. Zum Beispiel gibt Bazykin in seinem Buch ein Beispiel für die Dynamik zweier wechselseitiger Populationen mit der Einführung eines zusätzlichen Faktors des intraspezifischen Wettbewerbs. Aufgrund dessen nimmt das System die Form an:

(1.15)

Und in diesem Fall erscheint eine von Null verschiedene stabile Position des Systems, die durch einen „Sattel“ von der Null getrennt ist, was es dem realen Bild des Geschehens näher bringt.

2. Interaktion von Unternehmen unter den Bedingungen der Protokooperation

Alle grundlegenden theoretischen Informationen wurden im vorherigen Kapitel präsentiert, so dass bei der Analyse der in diesem Kapitel betrachteten Modelle die Theorie größtenteils weggelassen wird, mit Ausnahme einiger Punkte, auf die wir im vorherigen Kapitel nicht gestoßen sind Kapitel, und es kann auch zu einer Reduzierung der Berechnungen kommen. Das in diesem Kapitel betrachtete Modell der Interaktion zwischen Organisationen unter Bedingungen der Protokooperation, das aus Systemen von zwei Gleichungen auf der Grundlage des malthusianischen Modells besteht, sieht aus wie System (1.5). Die im vorigen Kapitel analysierten Systeme haben gezeigt, dass es für ihre maximale Annäherung an die bestehenden Modelle notwendig ist, die Systeme zu komplizieren. Basierend auf diesen Erkenntnissen werden wir dem Modell sofort eine Wachstumsbeschränkung hinzufügen. Anders als bei der vorherigen Art der Interaktion, wenn das Wachstum, das nicht von einem anderen Unternehmen abhängt, negativ ist, stehen in diesem Fall alle Zeichen auf positiv, was bedeutet, dass wir ein konstantes Wachstum haben. Um die zuvor beschriebenen Mängel zu vermeiden, werden wir versuchen, sie auf die logistische Gleichung zu beschränken, die auch als Verhulst-Gleichung (Gershenfeld, 1999) bekannt ist und die folgende Form hat:

, (2.1)

wobei P die Populationsgröße ist, r der Parameter ist, der die Wachstumsrate anzeigt, K der Parameter ist, der für die maximal mögliche Populationsgröße verantwortlich ist. Das heißt, die Bevölkerungsgröße (in unserem Fall die Produktion) tendiert im Laufe der Zeit zu einem bestimmten Parameter K.

Diese Gleichung wird dazu beitragen, das ungezügelte Produktionswachstum einzudämmen, das wir bisher gesehen haben. Somit nimmt das System folgende Form an:

(2.2)

Vergessen Sie nicht, dass die Menge der im Lager gelagerten Waren für jedes Unternehmen unterschiedlich ist, sodass die Parameter, die das Wachstum begrenzen, unterschiedlich sind. Nennen wir dieses System "", und in Zukunft werden wir diesen Namen verwenden, wenn wir darüber nachdenken.

Das zweite System, das wir betrachten werden, ist die Weiterentwicklung des Modells mit der Verhulst-Beschränkung. Wie im vorigen Kapitel führen wir eine Sättigungsbeschränkung ein, dann nimmt das System die Form an:

(2.3)

Nun hat jeder der Terme seine eigene Grenze, sodass ohne weitere Analyse ersichtlich ist, dass es kein unbegrenztes Wachstum wie in den Modellen des vorherigen Kapitels geben wird. Und da jeder der Begriffe ein positives Wachstum zeigt, wird die Produktionsmenge nicht auf Null fallen. Nennen wir dieses Modell das „Proto-Operationsmodell mit zwei Beschränkungen“.

Diese beiden Modelle werden in verschiedenen Quellen zu biologischen Populationen diskutiert. Nun werden wir versuchen, die Systeme etwas zu erweitern. Betrachten Sie dazu die folgende Abbildung.

Die Abbildung zeigt beispielhaft die Prozesse zweier Unternehmen: der Stahl- und der Kohleindustrie. In beiden Unternehmen gibt es eine voneinander unabhängige Produktionssteigerung, und es gibt auch eine Produktionssteigerung, die durch ihr Zusammenwirken erzielt wird. Dies haben wir bereits bei früheren Modellen berücksichtigt. Nun lohnt es sich, darauf zu achten, dass Unternehmen nicht nur Produkte herstellen, sondern sie beispielsweise auch an den Markt oder an ein damit interagierendes Unternehmen verkaufen. Jene. Aufgrund logischer Schlussfolgerungen ist ein negatives Wachstum von Unternehmen aufgrund des Verkaufs von Produkten (in der Abbildung sind dafür die Parameter β1 und β2 verantwortlich) sowie aufgrund der Übertragung eines Teils der Produkte an ein anderes Unternehmen erforderlich . Bisher haben wir dies nur mit einem positiven Vorzeichen für ein anderes Unternehmen berücksichtigt, aber nicht berücksichtigt, dass bei der Übertragung von Produkten die Anzahl der Produkte für das erste Unternehmen abnimmt. In diesem Fall erhalten wir das System:

(2.4)

Und wenn über den Begriff gesagt werden kann, dass, wenn in früheren Modellen angegeben wurde, dass , den natürlichen Anstieg charakterisieren und der Parameter negativ sein kann, dann gibt es praktisch keinen Unterschied, dann über den Begriff das kann man nicht sagen. Darüber hinaus ist es in Zukunft bei der Betrachtung eines solchen Systems mit einer ihm auferlegten Beschränkung korrekter, die Begriffe positives und negatives Wachstum zu verwenden, da ihnen in diesem Fall unterschiedliche Beschränkungen auferlegt werden können, was für natürliche unmöglich ist Wachstum. Nennen wir es das „erweiterte Proto-Kooperationsmodell“.

Schließlich ist das vierte betrachtete Modell das erweiterte Proto-Kooperationsmodell mit der zuvor erwähnten logistischen Wachstumsbeschränkung. Und das System für dieses Modell ist wie folgt:

, (2.5)

wo ist die Steigerung der Produktion des ersten Unternehmens, unabhängig vom zweiten, unter Berücksichtigung der logistischen Beschränkungen, - die Produktionssteigerung des ersten Unternehmens in Abhängigkeit von der zweiten unter Berücksichtigung der logistischen Beschränkungen, - die Produktionssteigerung des zweiten Unternehmens unabhängig von der ersten unter Berücksichtigung der logistischen Beschränkungen, - Steigerung der Produktion des zweiten Unternehmens, abhängig vom ersten, unter Berücksichtigung der logistischen Zwänge, - Verbrauch der Waren des ersten Unternehmens, die nicht mit einem anderen verbunden sind, - Verbrauch der Waren des zweiten Unternehmens, die nicht mit einem anderen verbunden sind , - Verbrauch von Gütern der ersten Branche durch die zweite Branche, - Verbrauch von Gütern der zweiten Branche der ersten Branche.

Dieses Modell wird zukünftig als „erweitertes Proto-Betriebsmodell mit logistischer Randbedingung“ bezeichnet.

1 Stabilität von Systemen in erster Näherung

Proto-Operationsmodell mit Verhulst-Einschränkung

Methoden zur Analyse der Stabilität des Systems wurden in einem ähnlichen Abschnitt des vorherigen Kapitels angegeben. Zunächst finden wir Gleichgewichtspunkte. Einer von ihnen ist wie immer Null. Der andere ist ein Punkt mit Koordinaten .

Für den Nullpunkt λ1 = , λ2 = erhalten wir, da beide Parameter nicht negativ sind, einen instabilen Knoten.

Da es wegen der fehlenden Möglichkeit, den Ausdruck abzukürzen, nicht sehr komfortabel ist, mit dem zweiten Punkt zu arbeiten, überlassen wir die Definition der Stabilitätsart den Phasendiagrammen, da sie eindeutig zeigen, ob der Gleichgewichtspunkt stabil ist oder nicht.

Die Analyse dieses Systems ist komplizierter als die des vorherigen, da der Sättigungsfaktor hinzugefügt wird, somit neue Parameter erscheinen und beim Auffinden von Gleichgewichtspunkten aufgrund von nicht eine lineare, sondern eine bilineare Gleichung gelöst werden muss die Variable im Nenner. Daher überlassen wir wie im vorigen Fall die Definition des Stabilitätstyps Phasendiagrammen.

Trotz des Auftretens neuer Parameter sieht der Jacobi am Nullpunkt sowie die Wurzeln der charakteristischen Gleichung ähnlich aus wie das vorherige Modell. Somit entsteht am Nullpunkt ein instabiler Knoten.

Kommen wir zu fortgeschrittenen Modellen. Der erste von ihnen enthält keine Einschränkungen und hat die Form von System (2.4)

Lassen Sie uns eine Änderung der Variablen vornehmen, , und . Neues System:

(2.6)

In diesem Fall erhalten wir zwei Gleichgewichtspunkte, Punkt A(0,0), B(). Punkt B liegt im ersten Quartal, da die Variablen einen nicht negativen Wert haben.

Für den Gleichgewichtspunkt A erhalten wir:

. - instabiler Knoten

. - Sattel,

. - Sattel,

. - stabiler Knoten

Am Punkt B sind die Wurzeln der charakteristischen Gleichung komplexe Zahlen: λ1 = , λ2 = . Wir können die Art der Stabilität nicht anhand der Sätze von Lyapunov bestimmen, also werden wir numerische Simulationen durchführen, die nicht alle möglichen Zustände zeigen, uns aber erlauben, zumindest einige davon herauszufinden.

Abbildung 2.2. Numerische Simulation der Suche nach der Stabilitätsart

Betrachtet man dieses Modell, muss man sich mit Rechenschwierigkeiten auseinandersetzen, da es eine große Anzahl verschiedener Parameter sowie zwei Einschränkungen aufweist.

Ohne auf Einzelheiten der Berechnungen einzugehen, gelangen wir zu den folgenden Gleichgewichtspunkten. Punkt A(0,0) und Punkt B mit folgenden Koordinaten:

(), wobei ein =

Für Punkt A ist die Bestimmung der Stabilitätsart eine triviale Aufgabe. Die Wurzeln der charakteristischen Gleichung sind λ1 = , λ2 = . Somit erhalten wir vier Optionen:

1. λ1 > 0, λ2 > 0 - instabiler Knoten.

2.λ1< 0, λ2 >0 - Sattel.

3. λ1 ​​​​> 0, λ2< 0 - седло.

4.λ1< 0, λ2 < 0 - устойчивый узел.

Apropos Punkt B: Es lohnt sich zuzustimmen, dass das Einsetzen von Abkürzungen in den Ausdruck die Arbeit mit dem Jacobi-Zeichen und das Finden der Wurzeln der charakteristischen Gleichung erschweren wird. Zum Beispiel dauerte die Ausgabe der Wurzeln nach dem Versuch, sie mit WolframAlpha-Computing-Tools zu finden, etwa fünf Zeilen, was es nicht erlaubt, wörtlich mit ihnen zu arbeiten. Bei bereits vorhandenen Parametern scheint es natürlich möglich, schnell einen Gleichgewichtspunkt zu finden, aber dies ist ein Sonderfall, da wir den Gleichgewichtszustand, wenn überhaupt, nur für diese Parameter finden werden, was für die Entscheidung nicht geeignet ist Unterstützungssystem, für das das Modell erstellt werden soll.

Aufgrund der Komplexität der Arbeit mit den Wurzeln der charakteristischen Gleichung konstruieren wir die gegenseitige Anordnung von Null-Isoklinen in Analogie zu dem in Bazykins Arbeit analysierten System (Bazykin, 2003). Dies wird es uns ermöglichen, die möglichen Zustände des Systems zu betrachten und in Zukunft bei der Erstellung von Phasenporträts Gleichgewichtspunkte und Arten ihrer Stabilität zu finden.

Nach einigen Berechnungen nehmen die nullisoklinen Gleichungen die folgende Form an:

(2.7)

Isoklinen haben also die Form von Parabeln.

Abbildung 2.3. Mögliche null-isokline Lage

Insgesamt gibt es vier mögliche Fälle ihrer gegenseitigen Anordnung entsprechend der Anzahl gemeinsamer Punkte zwischen den Parabeln. Jeder von ihnen hat seine eigenen Parametersätze und damit die Phasenporträts des Systems.

2 Phasenporträts von Systemen

Lassen Sie uns ein Phasenporträt des Systems erstellen, sofern dies der Fall ist und die restlichen Parameter sind gleich 1. In diesem Fall ist ein Variablensatz ausreichend, da sich die Qualität nicht ändert.

Wie aus den folgenden Abbildungen ersichtlich ist, ist der Nullpunkt ein instabiler Knoten, und der zweite Punkt, wenn wir die numerischen Werte der Parameter ersetzen, erhalten wir (-1,5, -1,5) - einen Sattel.

Abbildung 2.4. Phasenportrait für das System (2.2)

Da also keine Änderungen auftreten sollten, gibt es für dieses System nur instabile Zustände, was höchstwahrscheinlich auf die Möglichkeit unbegrenzten Wachstums zurückzuführen ist.

Ein Proto-Betriebsmodell mit zwei Einschränkungen.

In diesem System gibt es einen zusätzlichen begrenzenden Faktor, daher müssen die Phasendiagramme vom vorherigen Fall abweichen, wie in der Abbildung zu sehen ist. Der Nullpunkt ist auch ein instabiler Knoten, aber in diesem System erscheint eine stabile Position, nämlich ein stabiler Knoten. Mit diesen Parametern, seinen Koordinaten (5.5,5.5), ist es in der Abbildung dargestellt.

Abbildung 2.5. Phasenportrait für das System (2.3)

Somit ermöglichte die Beschränkung auf jeden Begriff, eine stabile Position des Systems zu erhalten.

Erweitertes Proto-Betriebsmodell.

Lassen Sie uns Phasenporträts für das erweiterte Modell erstellen, aber sofort in seiner modifizierten Form:

Betrachten wir vier Sätze von Parametern, um beispielsweise alle Fälle mit einem Gleichgewichtspunkt von Null zu berücksichtigen und auch die Phasendiagramme der numerischen Simulation zu demonstrieren, die für einen Gleichgewichtspunkt ungleich Null verwendet werden: der Satz A (1, 0,5, 0,5) entspricht dem Zustand , Satz B(1,0,5,-0,5) entspricht setze C(-1.0.5,0.5) und setze D(-1.0.5,-0.5) , also ein stabiler Knoten am Nullpunkt. Die ersten beiden Sätze zeigen die Phasenporträts für die Parameter, die wir in der numerischen Simulation berücksichtigt haben.

Abbildung 2.6. Phasenportrait für System (2.4) mit Parametern А-D.

In den Abbildungen ist auf die Punkte (-1,2) bzw. (1,-2) zu achten, in denen ein „Sattel“ erscheint. Für eine detailliertere Darstellung zeigt die Figur einen anderen Maßstab der Figur mit einem Sattelpunkt (1,-2). In der Figur ist an den Punkten (1,2) und (-1,-2) ein stabiles Zentrum sichtbar. Was den Nullpunkt betrifft, so können wir von Figur zu Figur in den Phasendiagrammen einen instabilen Knoten, einen Sattel, einen Sattel und einen stabilen Knoten klar unterscheiden.

Erweitertes Proto-Kooperationsmodell mit logistischer Einschränkung.

Wie im vorherigen Modell werden wir Phasenporträts für vier Fälle eines Nullpunkts demonstrieren, und wir werden auch versuchen, in diesen Diagrammen Nicht-Null-Lösungen zu notieren. Nehmen Sie dazu die folgenden Parametersätze mit den angegebenen Parametern in der folgenden Reihenfolge (): A (2,1,2,1), B (2,1,1,2), C (1,2,2 ,1) und D (1,2,1,2). Die verbleibenden Parameter für alle Sätze sind wie folgt: , .

In den unten dargestellten Abbildungen kann man die im vorigen Abschnitt beschriebenen vier Gleichgewichtszustände des Nullpunktes für dieses dynamische System beobachten. Und auch in den Figuren die stabile Position eines Punktes mit einer Koordinate ungleich Null.

Abbildung 2.7. Phasenporträt für System (2.5) mit Parametern A-B

3 Integrale Trajektorien von Systemen

Proto-Operationsmodell mit Verhulst-Einschränkung

Wie im vorigen Kapitel lösen wir jede der Differentialgleichungen einzeln und drücken explizit die Abhängigkeit der Variablen vom Zeitparameter aus.

(2.8)

(2.9)

Aus den erhaltenen Gleichungen ist ersichtlich, dass der Wert jeder der Variablen zunimmt, was im dreidimensionalen Modell unten gezeigt wird.

Abbildung 2.8. Dreidimensionales Modell für Gleichung (2.8)

Diese Art von Diagramm ähnelt zunächst dem in Kapitel 1 besprochenen ungesättigten 3D-Malthus-Modell, da es ein ähnlich schnelles Wachstum aufweist, aber später können Sie eine Abnahme der Wachstumsrate sehen, wenn die Ausgabegrenze erreicht wird. Somit ähnelt das endgültige Erscheinungsbild der Integralkurven dem Diagramm der logistischen Gleichung, die verwendet wurde, um einen der Terme einzuschränken.

Ein Proto-Betriebsmodell mit zwei Einschränkungen.

Wir lösen jede der Gleichungen mit Wolfram Alpha Tools. Damit reduziert sich die Abhängigkeit der Funktion x(t) auf folgende Form:

(2.10)

Für die zweite Funktion ist die Situation ähnlich, weshalb wir ihre Lösung weglassen. Numerische Werte erschienen aufgrund des Ersatzes der Parameter durch bestimmte geeignete Werte, was das qualitative Verhalten der Integralkurven nicht beeinflusst. Die folgenden Diagramme zeigen die Verwendung von Wachstumsgrenzen, da das exponentielle Wachstum im Laufe der Zeit logarithmisch wird.

Abbildung 2.9. Dreidimensionales Modell für Gleichung (2.10)

Erweitertes Proto-Betriebsmodell

Fast ähnlich den Modellen mit Gegenseitigkeit. Der einzige Unterschied besteht im schnelleren Wachstum im Vergleich zu diesen Modellen, was aus den folgenden Gleichungen (wenn Sie sich den Grad des Exponenten ansehen) und den Grafiken ersichtlich ist. Die Integralkurve muss die Form eines Exponenten haben.

(2.11)

(2.12)

Erweitertes Proto-Kooperationsmodell mit logistischer Einschränkung

Abhängigkeit x(t) sieht so aus:

Ohne einen Graphen ist es schwierig, das Verhalten der Funktion zu bewerten, also werden wir sie mit den uns bereits bekannten Tools erstellen.

Abbildung 2.10 3D-Modell für Gleichung

Der Wert der Funktion nimmt für nicht kleine Werte einer anderen Variablen ab, was auf das Fehlen von Einschränkungen für den negativen bilinearen Term zurückzuführen ist und ein offensichtliches Ergebnis ist

4 Systemdynamik interagierender Unternehmen

Proto-Operationsmodell mit Verhulst-Einschränkung.

Konstruieren wir System (2.2). Mit den uns bereits bekannten Werkzeugen bauen wir ein Simulationsmodell auf. Dieses Mal wird das Modell, im Gegensatz zu den Mutualistischen Modellen, eine logistische Einschränkung haben.

Abbildung 2.11. Systemdynamikmodell für System (2.2)

Lassen Sie uns das Modell ausführen. In diesem Modell ist es erwähnenswert, dass das Wachstum aus der Beziehung durch nichts begrenzt ist und das Wachstum des Outputs ohne den Einfluss des anderen eine spezifische Begrenzung hat. Betrachtet man den Ausdruck der Logistikfunktion selbst, so sieht man, dass in dem Fall, dass die Variable (Anzahl der Güter) das maximal mögliche Lagervolumen überschreitet, der Term negativ wird. Bei rein logistischer Funktion ist dies nicht möglich, aber bei einem zusätzlichen, immer positiven Wachstumsfaktor ist dies möglich. Und jetzt ist es wichtig zu verstehen, dass die Logistikfunktion mit der Situation eines nicht zu schnellen Wachstums der Anzahl von Produkten fertig wird, zum Beispiel linear. Werfen wir einen Blick auf die Bilder unten.

Abbildung 2.12. Ein Beispiel für den Betrieb des Systemdynamikmodells für System (2.2)

Die linke Abbildung zeigt den 5. Schritt des Programms entsprechend dem vorgeschlagenen Modell. Aber im Moment lohnt es sich, auf die richtige Figur zu achten.

Erstens wurde für einen der eingehenden Streams für Y_stock der Link zu x, ausgedrückt in Form von , entfernt. Dies geschieht, um den Unterschied in der Leistung des Modells mit einem linearen, immer positiven Fluss und einem bilinearen Wachstum zu zeigen, der für X_stock dargestellt wird. Bei linear unbegrenzten Strömen kommt das System nach Überschreiten des Parameters K irgendwann ins Gleichgewicht (in diesem Modell beträgt der Gleichgewichtszustand 200.000 Wareneinheiten). Aber viel früher führt bilineares Wachstum zu einer starken Zunahme der Warenmenge, die ins Unendliche übergeht. Wenn wir sowohl rechts als auch links konstant positive Flüsse bilinear lassen, dann kommt der Wert des Akkumulators bereits bei etwa 20-30 Schritten auf die Differenz von zwei Unendlich.

Auf der Grundlage des oben Gesagten kann mit Sicherheit gesagt werden, dass im Falle einer weiteren Verwendung solcher Modelle ein positives Wachstum begrenzt werden muss.

Ein Proto-Betriebsmodell mit zwei Einschränkungen.

Nachdem wir die Mängel des vorherigen Modells herausgefunden und eine Beschränkung des zweiten Terms durch den Sättigungsfaktor eingeführt haben, werden wir ein neues Modell erstellen und ausführen.

Abbildung 2.13. Modell der Systemdynamik und ein Beispiel seiner Funktionsweise für System (2.3)

Dieses Modell bringt am Ende die lang erwarteten Ergebnisse. Es stellte sich heraus, das Wachstum der Akkumulatorwerte zu begrenzen. Wie aus der rechten Abbildung ersichtlich ist, wird bei beiden Unternehmen das Gleichgewicht mit einem leichten Überschuss an Speichervolumen erreicht.

Erweitertes Proto-Betriebsmodell.

Unter Berücksichtigung der Systemdynamik dieses Modells werden die Möglichkeiten der AnyLogic-Softwareumgebung zur farbenfrohen Visualisierung von Modellen demonstriert. Alle vorherigen Modelle wurden nur unter Verwendung von Elementen der Systemdynamik gebaut. Daher sahen die Modelle selbst unauffällig aus, sie erlaubten es nicht, die Dynamik von Änderungen der Produktionsmenge im Laufe der Zeit zu verfolgen und die Parameter zu ändern, während das Programm lief. Bei der Arbeit mit diesem und den nächsten Modellen werden wir versuchen, eine breitere Palette von Programmfunktionen zu verwenden, um die drei oben genannten Nachteile zu ändern.

Erstens enthält das Programm neben dem Abschnitt „Systemdynamik“ auch die Abschnitte „Bilder“, „3D-Objekte“, die es ermöglichen, das Modell zu diversifizieren, was für seine weitere Präsentation nützlich ist, da es das Modell erstellt „angenehmer“ aussehen.

Zweitens, um die Dynamik von Änderungen in den Werten des Modells zu verfolgen, gibt es einen Abschnitt "Statistiken", in dem Sie Diagramme und verschiedene Datenerfassungstools hinzufügen können, indem Sie sie mit dem Modell verknüpfen.

Drittens, um Parameter und andere Objekte während der Ausführung des Modells zu ändern, gibt es einen Abschnitt "Steuerelemente". Mit den Objekten in diesem Abschnitt können Sie Parameter ändern, während das Modell läuft (z. B. „Schieberegler“), verschiedene Zustände des Objekts auswählen (z. B. „Schalter“) und andere Aktionen ausführen, die die anfänglich angegebenen Daten während der Arbeit ändern .

Das Modell ist geeignet, um die Dynamik von Veränderungen in der Produktion von Unternehmen kennenzulernen, aber das Fehlen von Wachstumsbeschränkungen erlaubt es nicht, es in der Praxis anzuwenden.

Erweitertes Proto-Kooperationsmodell mit logistischer Einschränkung.

Unter Verwendung des bereits vorbereiteten Vorgängermodells werden wir Parameter aus der logistischen Gleichung hinzufügen, um das Wachstum zu begrenzen.

Wir verzichten auf die Konstruktion des Modells, da die vorherigen fünf in der Arbeit vorgestellten Modelle bereits alle notwendigen Werkzeuge und Prinzipien für die Arbeit mit ihnen demonstriert haben. Es ist nur erwähnenswert, dass sein Verhalten dem Proto-Kooperationsmodell mit der Verhulst-Einschränkung ähnlich ist. Jene. der Mangel an Sättigung behindert seine praktische Anwendung.

Nachdem wir die Modelle im Hinblick auf die Proto-Kooperation analysiert haben, definieren wir mehrere Hauptpunkte:

Die in diesem Kapitel betrachteten Modelle sind für die Praxis besser geeignet als wechselseitige, da sie selbst bei zwei Termen stabile Gleichgewichtslagen ungleich Null haben. Ich möchte Sie daran erinnern, dass wir dies in den Modellen des Mutualismus nur durch Hinzufügen eines dritten Begriffs erreichen konnten.

Geeignete Modelle müssen Einschränkungen für jeden der Terme haben, da sonst ein starker Anstieg der bilinearen Faktoren das gesamte Simulationsmodell "zerstört".

Ausgehend von Absatz 2 soll beim Hinzufügen einer Proto-Operation mit der Verhulst-Beschränkung des Sättigungsfaktors zum erweiterten Modell sowie beim Hinzufügen einer niedrigeren kritischen Produktionsmenge das Modell dem realen Zustand so nahe wie möglich kommen. Aber vergessen Sie nicht, dass solche Manipulationen des Systems seine Analyse erschweren.

Fazit

Als Ergebnis der Studie wurden sechs Systeme analysiert, die die Dynamik der Produktion von Unternehmen beschreiben, die sich gegenseitig beeinflussen. Als Ergebnis wurden die Gleichgewichtspunkte und Arten ihrer Stabilität auf eine der folgenden Arten bestimmt: analytisch oder dank der konstruierten Phasenporträts in Fällen, in denen eine analytische Lösung aus irgendeinem Grund nicht möglich ist. Für jedes der Systeme wurden Phasendiagramme sowie dreidimensionale Modelle erstellt, auf denen bei der Projektion integrale Kurven in den Ebenen (x, t), (y, t) erhalten werden können. Anschließend wurden mit der Modellierungsumgebung AnyLogic alle Modelle gebaut und deren Verhaltensoptionen unter bestimmten Parametern betrachtet.

Nach der Analyse der Systeme und dem Aufbau ihrer Simulationsmodelle wird deutlich, dass diese Modelle aufgrund ihrer geringen Genauigkeit und an manchen Stellen nur als Training oder zur Beschreibung makroskopischer Systeme, nicht aber als Entscheidungsunterstützungssystem für einzelne Unternehmen angesehen werden können nicht ganz verlässliche Darstellung der laufenden Prozesse. Vergessen Sie aber auch nicht, dass, egal wie wahr das dynamische System ist, das das Modell beschreibt, jedes Unternehmen / jede Organisation / Branche ihre eigenen Prozesse und Einschränkungen hat, sodass es nicht möglich ist, ein allgemeines Modell zu erstellen und zu beschreiben. In jedem konkreten Fall wird es modifiziert: um komplizierter zu werden oder im Gegenteil, um für die weitere Arbeit vereinfacht zu werden.

Um aus den Schlussfolgerungen für jedes Kapitel eine Schlussfolgerung zu ziehen, lohnt es sich, sich auf die offenbarte Tatsache zu konzentrieren, dass die Einführung von Einschränkungen für jeden der Terme der Gleichung das System zwar komplizierter macht, es Ihnen aber auch ermöglicht, stabile Positionen des Systems zu erkennen. und es näher an das zu bringen, was in der Realität passiert. Und es ist erwähnenswert, dass Proto-Kooperationsmodelle besser zum Studium geeignet sind, da sie stabile Positionen ungleich Null haben, im Gegensatz zu den beiden von uns betrachteten wechselseitigen Modellen.

Somit wurde das Ziel dieser Studie erreicht und die Aufgaben wurden abgeschlossen. In Zukunft wird als Fortsetzung dieser Arbeit ein erweitertes Modell der Interaktion des Typs der Proto-Operation mit drei darauf eingeführten Einschränkungen in Betracht gezogen: Logistik, Sättigungsfaktor, untere kritische Zahl, was die Erstellung einer genaueren ermöglichen sollte Modell für ein Entscheidungsunterstützungssystem sowie ein Modell mit drei Unternehmen. Als Erweiterung der Arbeit können wir neben der Symbiose noch zwei weitere Arten der Interaktion betrachten, die in der Arbeit erwähnt wurden.

Literatur

1. Bhatia Nam Parshad; Szegh Giorgio P. (2002). Stabilitätstheorie dynamischer Systeme. Springer.

2. Blanchard P.; Devaney, R. L.; Hall, GR (2006). Differentialgleichung. London: Thomson. pp. 96-111.

Boeing, G. (2016). Visuelle Analyse nichtlinearer dynamischer Systeme: Chaos, Fraktale, Selbstähnlichkeit und die Grenzen der Vorhersage. Systeme. 4(4):37.

4. Campbell, David K. (2004). Nichtlineare Physik: Frische Verschnaufpause. Natur. 432 (7016): 455-456.

Elton C.S. (1968) Nachdruck. Tierökologie. Großbritannien: William Clowes and Sons Ltd.

7. Forrester Jay W. (1961). Industrielle Dynamik. MIT Press.

8. Gandolfo, Giancarlo (1996). Wirtschaftsdynamik (3. Aufl.). Berlin: Springer. pp. 407-428.

9. Gershenfeld Neil A. (1999). Die Natur der mathematischen Modellierung. Cambridge, Großbritannien: Cambridge University Press.

10 Goodman M. (1989). Studiennotizen in Systemdynamik. Pegasus.

Grebogi C., Ott E. und Yorke J. (1987). Chaos, seltsame Attraktoren und fraktale Beckengrenzen in der nichtlinearen Dynamik. Science 238 (4827), S. 632-638.

12 Haar Ernst; Nørsett Syvert Paul; Wanner, Gerhard (1993), Lösen gewöhnlicher Differentialgleichungen I: Nichtsteife Probleme, Berlin, New York

Hanski I. (1999) Metapopulationsökologie. Oxford University Press, Oxford, S. 43-46.

Hughes-Hallett Deborah; McCallum, William G.; Gleason, Andrew M. (2013). Calculus: Single and Multivariable (6. Aufl.). John Wiley.

15. Llibre J., Valls C. (2007). Globale analytische erste Integrale für das reelle planare Lotka-Volterra-System, J. Math. Phys.

16. Jordan DW; Smith P. (2007). Nichtlineare gewöhnliche Differentialgleichungen: Einführung für Wissenschaftler und Ingenieure (4. Aufl.). Oxford University Press.

Khalil Hassan K. (2001). nichtlineare Systeme. Lehrlingshalle.

Lamar University, Online Math Notes - Phase Plane, P. Dawkins.

Lamar University, Online Math Notes - Systeme von Differentialgleichungen, P. Dawkins.

Lang Serge (1972). Differentialkrümmer. Reading, Mass.-London-Don Mills, Ontario: Addison-Wesley Publishing Co., Inc.

Gesetz Averill M. (2006). Simulationsmodellierung und -analyse mit Expertfit Software. McGraw-Hill-Wissenschaft.

Lazard D. (2009). Dreißig Jahre polynomiales Systemlösen, und jetzt? Zeitschrift für symbolische Berechnung . 44(3):222-231.

24 Lewis Mark D. (2000). Das Versprechen dynamischer Systemansätze für eine integrierte Darstellung der menschlichen Entwicklung. Entwicklung des Kindes. 71(1): 36-43.

25. Malthus T.R. (1798). An Essay on the Principle of Population, im Nachdruck der Oxford World's Classics, S. 61, Ende von Kapitel VII

26. Morecroft-John (2007). Strategische Modellierung und Geschäftsdynamik: Ein Feedback-Systemansatz. John Wiley & Söhne.

27. Nolte D.D. (2015), Einführung in die moderne Dynamik: Chaos, Netzwerke, Raum und Zeit, Oxford University Press.

Einführung 4

A priori Analyse dynamischer Systeme 5

Durchgang eines Zufallssignals durch ein lineares System 5

Entwicklung des Phasenvektors des Systems 7

Entwicklung der Kovarianzmatrix des Phasenvektors des Systems 8

Statistische Linearisierung 8

Erster Weg 9

Zweiter Weg 10

Berechnung der Linearisierungskoeffizienten 10

Mehrdeutigkeit in nichtlinearen Verbindungen 14

Nichtlineare Verbindung durch Feedback abgedeckt 15

Simulation zufälliger Prozesse 16

Formfilter 16

Weißes Rauschen modellieren 17

Schätzung statistischer Eigenschaften dynamischer Systeme nach der Monte-Carlo-Methode 18

Gradgenauigkeit 18

Instationäre dynamische Systeme 20

Stationäre dynamische Systeme 21

A-posteriori-Analyse dynamischer Systeme 22

Kalman-Filter 22

Bewegungsmuster 22

Messmodell 23

Berichtigung 23

Prognose 23

Klasse 23

Verwendung der Kalman-Filterung bei nichtlinearen Problemen 25

Kleinste Quadrate 27

Gebäudeklassen 27

Prognose 29

Anwendung der Methode der kleinsten Quadrate bei nichtlinearen Problemen 29

Konstruktion der Cauchy-Matrix 30

Messmodellierung 30

Numerische Methoden 31

Sonderfunktionen 31

Simulation von Zufallsvariablen 31

Gleichverteilte Zufallsvariablen 31

Gaußsche Zufallsvariablen 32

Zufallsvektoren 33

Integral der Wahrscheinlichkeiten 34

Tschebyscheff-Polynome 36

Integration gewöhnlicher Differentialgleichungen 36

Runge-Kutta-Methoden 36

Genauigkeit der numerischen Integrationsergebnisse 37

Verschachtelter Dorman-Prince 5(4) Ordnung 37

Mehrschrittverfahren 39

Adams-Methoden 39

Integration verzögerter Gleichungen 40

Vergleich der Rechenqualitäten von Methoden 40

Arenstorf-Problem 40

Elliptische Jacobi-Funktionen 41

Zweikörperproblem 41

Van-der-Pol-Gleichung 42

Brüsseler 42

Hängende Zeichenfolge Lagrange-Gleichung 42

Plejaden 42

Eine Erläuterung machen 43

Titelseite 43

Abschnitt "Einführung" 44

Abschnitt "Theorie" 44

Abschnitt "Algorithmus" 44

Abschnitt "Programm" 45

Abschnitt "Ergebnisse" 45

Abschnitt "Schlussfolgerungen" 45

Abschnitt "Verzeichnis der verwendeten Quellen" 45

Bewerbungen 45

Literatur 47

Einführung

Dieses Handbuch enthält Richtlinien zur Bearbeitung von Studienarbeiten zu Studienprojekten und zur Durchführung praktischer Übungen zur Lehrveranstaltung "Grundlagen der statistischen Dynamik".

Ziel des Kursdesigns und der praktischen Übungen ist es, die Technologie der a priori und a posteriori Analyse nichtlinearer dynamischer Systeme unter dem Einfluss zufälliger Störungen zu beherrschen.

A priori Analyse dynamischer Systeme

Statistische Linearisierung

Mit der statistischen Linearisierung können Sie das ursprüngliche nichtlineare dynamische System so transformieren, dass für seine Analyse Methoden, Algorithmen und Beziehungen verwendet werden können, die für lineare Systeme gültig sind.

Dieser Abschnitt widmet sich der Darstellung der Methode der statistischen Linearisierung, basierend auf dem einfachsten Näherungsverfahren, das von Prof. I.E. Kazakov, der es dennoch ermöglicht, Schätzungen der Genauigkeit eines Systems zu konstruieren, das selbst signifikante Nichtlinearitäten mit unstetigen Eigenschaften enthält.

Die statistische Linearisierung besteht darin, die ursprüngliche trägheitslose nichtlineare Abhängigkeit zwischen den Eingabe- und Ausgabeprozessen durch eine solche ungefähre Abhängigkeit zu ersetzen, die in Bezug auf den zentrierten Eingabe-Zufallsprozess linear ist und in Bezug auf die ursprüngliche statistisch äquivalent ist:

Eine Verbindung, die eine solche ungefähre Beziehung zwischen den Eingangs- und Ausgangssignalen hat, wird als äquivalent zu der betrachteten nichtlinearen Verbindung bezeichnet.

Der Wert wird basierend auf der Bedingung der Gleichheit der mathematischen Erwartungen der nichtlinearen und linearisierten Signale ausgewählt und wird als statistische Durchschnittscharakteristik der äquivalenten Verbindung bezeichnet:

,

wo ist die Verteilungsdichte des Eingangssignals .

Für nichtlineare Verbindungen mit ungeraden Eigenschaften, d.h. beim , ist es zweckmäßig, das statistische Merkmal in der Form darzustellen:

ist die mathematische Erwartung des Eingangssignals;
ist der statistische Gewinn des äquivalenten Links in Bezug auf die durchschnittliche Komponente.

Dass. Die äquivalente Abhängigkeit hat in diesem Fall die Form:

Das Merkmal wird als statistischer Gewinn der äquivalenten Verbindung für die zufällige Komponente (Fluktuationen) bezeichnet und wird auf zwei Arten bestimmt.

Erster Weg

Gemäß dem ersten Verfahren der statistischen Linearisierung wird der Koeffizient basierend auf der Bedingung der Gleichheit der Dispersionen des ursprünglichen und des äquivalenten Signals ausgewählt. Dass. zur Berechnung erhalten wir folgende Beziehung:

,

wobei die Varianz der eingegebenen zufälligen Aktion ist.

Das Vorzeichen im Ausdruck for wird durch die Art der Abhängigkeit in der Nähe des Werts des Arguments bestimmt. Steigt sie, dann , und sinkt sie, dann .

Zweiter Weg

Der Wert nach dem zweiten Verfahren wird aus der Bedingung der Minimierung des mittleren quadratischen Linearisierungsfehlers ausgewählt:

Das endgültige Verhältnis zur Berechnung des Koeffizienten nach der zweiten Methode ist:

.

Abschließend stellen wir fest, dass keines der beiden oben betrachteten Linearisierungsverfahren die Gleichheit der Korrelationsfunktionen der Ausgangssignale der nichtlinearen und äquivalenten Verbindungen gewährleistet. Berechnungen zeigen, dass für die Korrelationsfunktion eines nichtlinearen Signals das erste Auswahlverfahren eine obere Schätzung ergibt und das zweite Verfahren eine untere Schätzung, d. h. Fehler bei der Bestimmung der Korrelationsfunktion des nichtlinearen Ausgangssignals haben unterschiedliche Vorzeichen. Prof.. I.E. Kazakov, der Autor der hier beschriebenen Methode, empfiehlt, als resultierenden Linearisierungskoeffizienten die Halbsumme der mit der ersten und zweiten Methode erhaltenen Koeffizienten zu wählen.

Formfilter

Typischerweise werden die Parameter bestimmt, indem die Koeffizienten der Zähler- und Nennerpolynome in der Gleichung gleichgesetzt werden

mit den gleichen Abschlüssen.

Nach der Bestimmung der Übertragungsfunktion des Formungsfilters sieht das resultierende Schema zur Modellierung eines zufälligen Prozesses wie in der Abbildung gezeigt aus.

Die spektrale Dichte des zu modellierenden Prozesses hat beispielsweise die Form:

,

mathematische Erwartung, und weißes Rauschen mit Intensität wird zum Modellieren verwendet, daher hat es eine spektrale Dichteeinheit.

Offensichtlich müssen Zähler und Nenner der gewünschten Übertragungsfunktion die Ordnungen 1 und 2 haben (tatsächlich bildet die Übertragungsfunktion, da sie modulo quadriert ist, einen Quotienten von Polynomen 2. und 4. Grades).

Dass. Die Übertragungsfunktion des Formungsfilters in seiner allgemeinsten Form ist wie folgt:

,

und das Quadrat seines Moduls:

Lassen Sie uns die erhaltenen Verhältnisse gleichsetzen:

Lassen Sie uns die Klammern und auf der rechten Seite der Gleichheit entfernen, wodurch die Koeffizienten bei null Grad gleichgesetzt werden:

,

woraus klar die folgenden Gleichheiten folgen:

; ; ; .

Dass. Das Blockdiagramm der Bildung eines Zufallsprozesses mit gegebenen statistischen Eigenschaften aus weißem Rauschen mit einer Einheitsspektraldichte sieht wie in der Abbildung gezeigt aus, wobei die berechneten Werte der Parameter des Formungsfilters berücksichtigt werden.

Modellierung von weißem Rauschen

Um einen zufälligen Prozess mit gegebenen statistischen Eigenschaften zu simulieren, wird weißes Rauschen als ein zufälliger Eingabeprozess in das Formungsfilter verwendet. Eine exakte Modellierung von weißem Rauschen ist jedoch aufgrund der unendlichen Varianz dieses Zufallsprozesses nicht möglich.

Aus diesem Grund wird als Ersatz für weißes Rauschen, das auf das dynamische System einwirkt, ein Zufallsschrittverfahren verwendet. Das Intervall, in dem die Implementierung eines Zufallsprozesses seinen Wert unverändert beibehält (Schrittweite, Korrelationsintervall), ist ein konstanter Wert. Die Implementierungswerte selbst (Stufenhöhen) sind nach dem Normalgesetz verteilte Zufallsvariablen mit null mathematischer Erwartung und begrenzter Varianz. Die Werte der Prozessparameter - Korrelationsintervall und Dispersion - werden durch die Eigenschaften des dynamischen Systems bestimmt, das von weißem Rauschen beeinflusst wird.

Die Idee des Verfahrens basiert auf der begrenzten Bandbreite jedes realen dynamischen Systems. Jene. Die Verstärkung eines realen dynamischen Systems nimmt ab, wenn die Frequenz des Eingangssignals zunimmt, und daher gibt es eine Frequenz (kleiner als unendlich), für die die Verstärkung des Systems so klein ist, dass sie auf Null gesetzt werden kann. Und dies wiederum bedeutet, dass das Eingangssignal mit einer konstanten, aber durch diese Frequenz begrenzten spektralen Dichte für ein solches System äquivalent zu weißem Rauschen (mit einer konstanten und unendlichen spektralen Dichte) sein wird.

Die Parameter des äquivalenten Zufallsprozesses - das Korrelationsintervall und die Varianz werden wie folgt berechnet:

wobei die empirisch ermittelte Bandbreitengrenze des dynamischen Systems ist.

Schätzungsgenauigkeit

Erwartungsschätzungen

und Streuung

Zufallsvariablen, die auf der Grundlage der Verarbeitung einer begrenzten Stichprobe ihrer Implementierungen , , konstruiert wurden, sind selbst Zufallsvariablen.

Offensichtlich ist die unverzerrte Schätzung umso genauer, je größer die Stichprobengröße der Implementierungen ist, desto näher liegt sie am wahren Wert des geschätzten Parameters. Nachfolgend finden Sie ungefähre Formeln, die auf der Annahme ihrer Normalverteilung basieren. Das symmetrische relative Konfidenzintervall für den der Konfidenzwahrscheinlichkeit entsprechenden Schätzwert wird durch den Wert bestimmt, für den die Beziehung gilt:

,

wo
ist der wahre Wert der mathematischen Erwartung der Zufallsvariablen ,
ist die Standardabweichung der Zufallsvariablen ,
ist das Wahrscheinlichkeitsintegral.

Basierend auf der obigen Beziehung kann die Menge wie folgt bestimmt werden:

,

wo ist die Funktion invers in Bezug auf das Wahrscheinlichkeitsintegral .

Da wir die Streucharakteristik des Schätzwerts nicht genau kennen, verwenden wir dessen Näherungswert, der sich aus dem Schätzwert ergibt:

Dass. Die endgültige Beziehung, die die Genauigkeit der Schätzung der mathematischen Erwartung und die Größe der Stichprobe, für die die Schätzung vorgenommen wird, verbindet, sieht folgendermaßen aus:

.

Dies bedeutet, dass der Wert des Konfidenzintervalls (bei konstantem Wert der Konfidenzwahrscheinlichkeit), der symmetrisch um liegt, ausgedrückt in Bruchteilen der Standardabweichungsschätzung, umgekehrt proportional zur Quadratwurzel des Stichprobenumfangs ist.

Das Konfidenzintervall zur Schätzung der Varianz ist ähnlich definiert:

bis zum Wert , der sich mangels genauerer Angaben näherungsweise aus der Beziehung bestimmen lässt:

Dass. der Wert des symmetrisch zu liegenden Konfidenzintervalls (bei konstantem Wert der Konfidenzwahrscheinlichkeit ), ausgedrückt in seinen Anteilen, ist umgekehrt proportional zur Quadratwurzel des Werts , wobei der Stichprobenumfang ist.

Genauere Formeln zum Erstellen von Konfidenzintervallen von Schätzungen können erhalten werden, indem genaue Informationen über das Verteilungsgesetz einer Zufallsvariablen verwendet werden.

Zum Beispiel für das Gaußsche Verteilungsgesetz die Zufallsvariable

gehorcht dem Studentschen Verteilungsgesetz mit einem Freiheitsgrad und der Zufallsvariablen

nach dem Gesetz auch mit einem Freiheitsgrad verteilt.

Kalman-Filter

Bewegungsmodell

Wie Sie wissen, dient der Kalman-Filter dazu, den Zustandsvektor eines linearen dynamischen Systems zu schätzen, dessen Evolutionsmodell wie folgt geschrieben werden kann:

wo
ist die Cauchy-Matrix, die die Änderung des Zustandsvektors des Systems in seiner eigenen Bewegung (ohne Steuer- und Rauschaktionen) von Zeitpunkt zu Zeitpunkt bestimmt;
ist der Vektor nicht-zufälliger erzwingender Aktionen auf dem System (z. B. Steueraktionen) zum Zeitpunkt;
ist die Matrix des Einflusses von Zwangsmaßnahmen zum Zeitpunkt auf den Zustandsvektor des Systems zum Zeitpunkt ;
ist der Vektor zufälliger unabhängiger zentrierter Aktionen auf dem System zum Zeitpunkt der Zeit;
ist die Matrix des Einflusses zufälliger Einflüsse zum Zeitpunkt auf den Zustandsvektor des Systems zum Zeitpunkt .

Messmodell

Die Schätzung erfolgt auf der Grundlage einer statistischen Verarbeitung von Messergebnissen, linear bezogen auf den Zustandsvektor und verzerrt durch einen additiven unverzerrten Fehler:

wobei eine Matrix ist, die den Zustands- und den Messvektor gleichzeitig verbindet.

Korrektur

Die Grundlage des Kalman-Filters sind die Korrekturverhältnisse, die das Ergebnis der Minimierung der Spur der Kovarianzmatrix der A-Posteriori-Verteilungsdichte der linearen (entlang des Messvektors) Schätzungen des Systemzustandsvektors sind:

Vorhersage

Ergänzung der Korrekturrelationen mit Prognoserelationen basierend auf den linearen Eigenschaften des Systementwicklungsmodells:

wobei die Kovarianzmatrix des Vektors ist, erhalten wir Formeln für den rekurrenten Bayes'schen Algorithmus zur Schätzung des Systemzustandsvektors und seiner Kovarianzmatrix basierend auf einer statistischen Verarbeitung der Messergebnisse.

Auswertung

Offensichtlich ist es zum Implementieren der obigen Beziehungen notwendig, in der Lage zu sein, Matrizen aus dem Evolutionsmodell, eine Matrix aus dem Messmodell sowie Kovarianzmatrizen und für jeden ten Zeitpunkt zu erstellen.

Außerdem ist es zum Initialisieren des Rechenprozesses notwendig, a posteriori oder a priori Schätzwerte des Zustandsvektors und seiner Kovarianzmatrix irgendwie zu bestimmen. Der Begriff "a priori" oder "a posteriori" bedeutet dabei nur die Qualität, in der der Zustandsvektor und seine Kovarianzmatrix im Rechenalgorithmus verwendet werden, und sagt nichts darüber aus, wie sie gewonnen wurden.

Somit wird die Wahl des Verhältnisses, ab dem mit Berechnungen begonnen werden soll, durch die Zeitpunkte bestimmt, denen die anfänglichen Filterbedingungen und der erste Rohmessvektor zugeordnet sind. Wenn die Zeitpunkte zusammenfallen, sollten die Korrekturverhältnisse zuerst angewendet werden, um die Anfangsbedingungen zu verfeinern, wenn nicht, dann sollten die Anfangsbedingungen zuerst bis zum Zeitpunkt des Bindens des ersten Rohmessvektors vorhergesagt werden.

Lassen Sie uns den Kalman-Filteralgorithmus anhand einer Abbildung erläutern.

In der Abbildung sind in den Koordinatenachsen (im Bewegungskanal) mehrere mögliche Trajektorien des Phasenvektors dargestellt:

ist die wahre Entwicklungsbahn des Phasenvektors;
ist die Entwicklung des Phasenvektors, vorhergesagt basierend auf der Verwendung des Bewegungsmodells und einer a-priori-Schätzung des Phasenvektors, bezogen auf die Zeit;
ist die Entwicklung des Phasenvektors, vorhergesagt basierend auf der Verwendung des Bewegungsmodells und einer nachträglichen (genaueren) Schätzung des Phasenvektors, bezogen auf die Zeit

Die Koordinatenachsen , (im Messkanal) zu den Zeitpunkten und zeigen die Messergebnisse und :

,

wo
ist der wahre Wert des Messvektors zum Zeitpunkt ;
ist der zum Zeitpunkt realisierte Vektor der Messfehler.

Um eine Korrektur des a priori Phasenvektors des Systems zu konstruieren, wird die Differenz zwischen dem Messergebnis und dem Wert verwendet, der gemäß dem Messmodell des Problems gemessen würde, wenn der Phasenvektor tatsächlich den Wert angenommen hätte. Als Ergebnis der Anwendung von Korrekturbeziehungen auf A-priori-Schätzungen wird die Schätzung des Phasenvektors des Systems etwas präziser und nimmt den Wert an

Zum jetzigen Zeitpunkt wird das Ergebnis der Prognose als A-priori-Schätzung verwendet auf der durch den Phasenvektor verlaufenden Trajektorie wird wiederum die Messdifferenz gebildet, nach der a posteriori ein noch genauerer Wert berechnet wird usw. solange Messvektoren zu verarbeiten sind oder das Verhalten des Phasenvektors vorhergesagt werden muss.

Methode der kleinsten Quadrate

Dieser Abschnitt stellt die Methode der kleinsten Quadrate vor, die für eine A-posteriori-Analyse dynamischer Systeme angepasst ist.

Noten aufbauen

Für den Fall eines linearen Modells gleicher Maße:

wir haben den folgenden Phasenvektor-Schätzalgorithmus:

.

Für den Fall ungleicher Messungen führen wir die Matrix ein, die Gewichtskoeffizienten auf der Diagonalen enthält. Unter Berücksichtigung der Gewichtskoeffizienten nimmt das vorherige Verhältnis die Form an:

.

Wenn wir die zur Kovarianzmatrix der Messfehler inverse Matrix als Gewichtsmatrix verwenden, dann erhalten wir unter Berücksichtigung der Tatsache:

.

Wie sich aus den obigen Beziehungen ergibt, ist die Grundlage des Verfahrens die Matrix, die den geschätzten Phasenvektor 7 bezogen auf einen bestimmten Zeitpunkt 7 und den Messvektor 7 in Beziehung setzt. Der Vektor hat in der Regel eine Blockstruktur, wobei jeder der Blöcke einem Zeitpunkt zugeordnet ist, der im Allgemeinen nicht mit zusammenfällt.

Die Abbildung zeigt eine mögliche gegenseitige Anordnung der Zeitpunkte, auf die sich die Messungen beziehen, und des Zeitpunkts, auf den sich der Vektor geschätzter Parameter bezieht.

Für jeden Vektor gilt die Beziehung:

, beim .

In der resultierenden Kleinste-Quadrate-Beziehung haben der Vektor und die Matrix also die folgende Struktur:

; .

wo
– bestimmt eine nicht zufällige Zwangswirkung auf das System;
– bestimmt die zufällige Auswirkung auf das System.

Vorhersagebeziehungen verwendet werden, die oben bei der Beschreibung des Kalman-Filteralgorithmus angetroffen wurden:

wobei die Kovarianzmatrix des Vektors ist.

Konstruktion der Cauchy-Matrix

Bei den Problemen der Erstellung von Schätzungen durch Methoden der statistischen Verarbeitung von Messungen tritt häufig das Problem der Erstellung der Cauchy-Matrix auf. Diese Matrix verbindet die Phasenvektoren des Systems, bezogen auf verschiedene Zeitpunkte, in ihrer eigenen Bewegung.

In diesem Abschnitt beschränken wir uns darauf, Fragen im Zusammenhang mit der Konstruktion der Cauchy-Matrix für ein Evolutionsmodell zu betrachten, das als System gewöhnlicher Differentialgleichungen (linear oder nichtlinear) geschrieben ist.

wobei für die in der Nähe der Bezugsbahn konstruierten Proportionalitätsmatrizen folgende Notation verwendet wird , :

; .

Dimensionsmodellierung

Das Problem entsteht, wenn man zB bei der Abschätzung der potentiell erreichbaren Genauigkeit einer Methode in einer Problemstellung keine Messergebnisse hat. In diesem Fall müssen die Messergebnisse simuliert werden. Die Besonderheit der Modellierung der Messergebnisse besteht darin, dass die zu diesem Zweck verwendeten Bewegungs- und Messmodelle möglicherweise nicht mit den Modellen übereinstimmen, die Sie im Laufe der Erstellung von Schätzungen mit der einen oder anderen Filtermethode verwenden werden.

Als Anfangsbedingungen für die Modellierung der Entwicklung des Phasenvektors eines dynamischen Systems sollten die wahren Werte der Koordinaten dieses Vektors verwendet werden. Außer an dieser Stelle sollten die wahren Werte der Koordinaten des Phasenvektors des Systems nirgendwo anders verwendet werden.

Numerische Methoden

Besondere Merkmale

Zufällige Vektoren

Das Problem, dessen Lösung in diesem Unterabschnitt beschrieben wird, besteht darin, einen Vektor korrelierter Gaußscher Zufallsvariablen zu modellieren.

Der zu modellierende Zufallsvektor 7 sei auf der Grundlage der Transformation des Vektors von standardmäßigen unkorrelierten Zufallsvariablen der entsprechenden Dimension wie folgt gebildet: mit einer Genauigkeit von 4 Stellen, auf der Grundlage der Potenzreihenentwicklung des Arguments für seine drei Intervalle.

Bei wird die Summe der asymptotischen Reihe fast gleich 1.