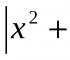How to find a1 in arithmetic progression formula. inverse matrix

So, services for solving matrices online:

The service for working with matrices allows you to perform elementary matrix transformations.
If you have a task to perform a more complex transformation, then this service should be used as a constructor.

Example... Given matrices A and B, need to find C = A -1 * B + B T,

1. You should first find inverse matrixA1 = A-1, using the service for finding the inverse matrix;
2. Further, after finding the matrix A1 do it matrix multiplicationA2 = A1 * B using the matrix multiplication service;
3. Let's execute matrix transposeA3 = B T (service for finding the transposed matrix);
4. And the last thing - find the sum of the matrices FROM = A2 + A3(service for calculating the sum of matrices) - and we get an answer with the most detailed solution !;

Product of matrices

This is an online service in two steps:

• Introduce the first factor matrix A
• Introduce the second factor matrix or column vector B

Matrix-vector multiplication

Multiplication of a matrix by a vector can be found using the service Matrix multiplication
(The first factor will be the given matrix, the second factor will be the column consisting of the elements of the given vector)

This is an online service in two steps:

• Enter the matrix A, for which you need to find the inverse matrix
• Get an answer with a detailed solution for finding the inverse matrix

Determinant of a matrix

This is an online service in one step:

• Enter the matrix A, for which you need to find the determinant of the matrix

Matrix transpose

Here you can track the matrix transposition algorithm and learn how to solve such problems yourself.
This is an online service in one step:

• Enter the matrix A to be transposed

Matrix rank

This is an online service in one step:

• Enter the matrix A, for which you need to find the rank

Matrix eigenvalues ​​and matrix eigenvectors

This is an online service in one step:

• Enter the matrix A, for which you need to find eigenvectors and eigenvalues ​​(eigenvalues)

Exponentiation of a matrix

This is an online service in two steps:

• Enter the matrix A, which you will raise to the power
• Enter an integer q- degree

The matrix $ A ^ (- 1) $ is called inverse with respect to the square matrix $ A $ if the condition $ A ^ (- 1) \ cdot A = A \ cdot A ^ (- 1) = E $ is satisfied, where $ E $ Is the identity matrix, the order of which is equal to the order of the matrix $ A $.

Non-degenerate matrix - a matrix, the determinant of which is not equal to zero. Accordingly, a degenerate matrix is ​​one with zero determinant.

The inverse matrix $ A ^ (- 1) $ exists if and only if the matrix $ A $ is non-degenerate. If the inverse matrix $ A ^ (- 1) $ exists, then it is unique.

There are several ways to find the inverse of a matrix, and we will look at two of them. This page will cover the adjoint matrix method, which is considered standard in most higher mathematics courses. The second method for finding the inverse matrix (the method of elementary transformations), which involves the use of the Gauss method or the Gauss-Jordan method, is discussed in the second part.

The adjoint (adjoint) matrix method

Let the matrix $ A_ (n \ times n) $ be given. In order to find the inverse of the $ A ^ (- 1) $ matrix, three steps are required:

1. Find the determinant of the matrix $ A $ and make sure that $ \ Delta A \ neq 0 $, i.e. that the matrix A is non-degenerate.
2. Make up the algebraic complements $ A_ (ij) $ of each element of the matrix $ A $ and write the matrix $ A_ (n \ times n) ^ (*) = \ left (A_ (ij) \ right) $ from the found algebraic complements.
3. Write the inverse matrix taking into account the formula $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $.

The matrix $ (A ^ (*)) ^ T $ is often referred to as adjoined (reciprocal, adjoint) to the matrix $ A $.

If the solution is done manually, then the first method is good only for matrices of relatively small orders: second (), third (), fourth (). Other methods are used to find the inverse of a higher-order matrix. For example, the Gauss method, which is discussed in the second part.

Example # 1

Find the inverse of $ A = \ left (\ begin (array) (cccc) 5 & -4 & 1 & 0 \\ 12 & -11 & 4 & 0 \\ -5 & 58 & 4 & 0 \\ 3 & - 1 & -9 & 0 \ end (array) \ right) $.

Since all the elements of the fourth column are equal to zero, then $ \ Delta A = 0 $ (that is, the matrix $ A $ is degenerate). Since $ \ Delta A = 0 $, the matrix inverse to the matrix $ A $ does not exist.

Answer: the matrix $ A ^ (- 1) $ does not exist.

Example No. 2

Find the inverse of the matrix $ A = \ left (\ begin (array) (cc) -5 & 7 \\ 9 & 8 \ end (array) \ right) $. Check.

We use the adjoint matrix method. First, we find the determinant of the given matrix $ A $:

$$ \ Delta A = \ left | \ begin (array) (cc) -5 & 7 \\ 9 & 8 \ end (array) \ right | = -5 \ cdot 8-7 \ cdot 9 = -103. $$

Since $ \ Delta A \ neq 0 $, then the inverse matrix exists, therefore we will continue the solution. Finding Algebraic Complements

\ begin (aligned) & A_ (11) = (- 1) ^ 2 \ cdot 8 = 8; \; A_ (12) = (- 1) ^ 3 \ cdot 9 = -9; \\ & A_ (21) = (- 1) ^ 3 \ cdot 7 = -7; \; A_ (22) = (- 1) ^ 4 \ cdot (-5) = - 5. \\ \ end (aligned)

We compose a matrix from algebraic complements: $ A ^ (*) = \ left (\ begin (array) (cc) 8 & -9 \\ -7 & -5 \ end (array) \ right) $.

Transpose the resulting matrix: $ (A ^ (*)) ^ T = \ left (\ begin (array) (cc) 8 & -7 \\ -9 & -5 \ end (array) \ right) $ (the resulting matrix is ​​often referred to as the adjoint or adjoint matrix to the $ A $ matrix). Using the formula $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $, we have:

$$ A ^ (- 1) = \ frac (1) (- 103) \ cdot \ left (\ begin (array) (cc) 8 & -7 \\ -9 & -5 \ end (array) \ right) = \ left (\ begin (array) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $$

So the inverse is found: $ A ^ (- 1) = \ left (\ begin (array) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $. To check the truth of the result, it is enough to check the truth of one of the equalities: $ A ^ (- 1) \ cdot A = E $ or $ A \ cdot A ^ (- 1) = E $. Let us check the equality $ A ^ (- 1) \ cdot A = E $. In order to work less with fractions, we will substitute the matrix $ A ^ (- 1) $ not in the form $ \ left (\ begin (array) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $, and as $ - \ frac (1) (103) \ cdot \ left (\ begin (array) (cc) 8 & -7 \\ -9 & -5 \ end (array ) \ right) $:

$$ A ^ (- 1) \ cdot (A) = - \ frac (1) (103) \ cdot \ left (\ begin (array) (cc) 8 & -7 \\ -9 & -5 \ end ( array) \ right) \ cdot \ left (\ begin (array) (cc) -5 & 7 \\ 9 & 8 \ end (array) \ right) = - \ frac (1) (103) \ cdot \ left ( \ begin (array) (cc) -103 & 0 \\ 0 & -103 \ end (array) \ right) = \ left (\ begin (array) (cc) 1 & 0 \\ 0 & 1 \ end (array ) \ right) = E $$

Answer: $ A ^ (- 1) = \ left (\ begin (array) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $.

Example No. 3

Find the inverse of the matrix $ A = \ left (\ begin (array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (array) \ right) $. Check.

Let's start by calculating the determinant of the matrix $ A $. So, the determinant of the matrix $ A $ is as follows:

$$ \ Delta A = \ left | \ begin (array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (array) \ right | = 18-36 + 56-12 = 26. $$

Since $ \ Delta A \ neq 0 $, then the inverse matrix exists, therefore we will continue the solution. We find the algebraic complements of each element of the given matrix:

$$ \ begin (aligned) & A_ (11) = (- 1) ^ (2) \ cdot \ left | \ begin (array) (cc) 9 & 4 \\ 3 & 2 \ end (array) \ right | = 6; \; A_ (12) = (- 1) ^ (3) \ cdot \ left | \ begin (array) (cc) -4 & 4 \\ 0 & 2 \ end (array) \ right | = 8; \; A_ (13) = (- 1) ^ (4) \ cdot \ left | \ begin (array) (cc) -4 & 9 \\ 0 & 3 \ end (array) \ right | = -12; \\ & A_ (21) = (- 1) ^ (3) \ cdot \ left | \ begin (array) (cc) 7 & 3 \\ 3 & 2 \ end (array) \ right | = -5; \; A_ (22) = (- 1) ^ (4) \ cdot \ left | \ begin (array) (cc) 1 & 3 \\ 0 & 2 \ end (array) \ right | = 2; \; A_ (23) = (- 1) ^ (5) \ cdot \ left | \ begin (array) (cc) 1 & 7 \\ 0 & 3 \ end (array) \ right | = -3; \\ & A_ (31) = (- 1) ^ (4) \ cdot \ left | \ begin (array) (cc) 7 & 3 \\ 9 & 4 \ end (array) \ right | = 1; \; A_ (32) = (- 1) ^ (5) \ cdot \ left | \ begin (array) (cc) 1 & 3 \\ -4 & 4 \ end (array) \ right | = -16; \; A_ (33) = (- 1) ^ (6) \ cdot \ left | \ begin (array) (cc) 1 & 7 \\ -4 & 9 \ end (array) \ right | = 37. \ end (aligned) $$

We compose a matrix of algebraic complements and transpose it:

$$ A ^ * = \ left (\ begin (array) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37 \ end (array) \ right); \; (A ^ *) ^ T = \ left (\ begin (array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ end (array) \ right) ... $$

Using the formula $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $, we get:

$$ A ^ (- 1) = \ frac (1) (26) \ cdot \ left (\ begin (array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37 \ end (array) \ right) = \ left (\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \ end (array) \ right) $$

So $ A ^ (- 1) = \ left (\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6/13 & -3/26 & 37/26 \ end (array) \ right) $. To check the truth of the result, it is enough to check the truth of one of the equalities: $ A ^ (- 1) \ cdot A = E $ or $ A \ cdot A ^ (- 1) = E $. Let us check the equality $ A \ cdot A ^ (- 1) = E $. In order to work less with fractions, we will substitute the matrix $ A ^ (- 1) $ not in the form $ \ left (\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \ end (array) \ right) $, and as $ \ frac (1) (26) \ cdot \ left ( \ begin (array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ end (array) \ right) $:

$$ A \ cdot (A ^ (- 1)) = \ left (\ begin (array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (array) \ right) \ cdot \ frac (1) (26) \ cdot \ left (\ begin (array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ end (array) \ right) = \ frac (1) (26) \ cdot \ left (\ begin (array) (ccc) 26 & 0 & 0 \\ 0 & 26 & 0 \\ 0 & 0 & 26 \ end (array) \ right) = \ left (\ begin (array) (ccc) 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end (array) \ right) = E $$

The check was successful, the inverse $ A ^ (- 1) $ was found correctly.

Answer: $ A ^ (- 1) = \ left (\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 / 13 & -3/26 & 37/26 \ end (array) \ right) $.

Example No. 4

Find the inverse of $ A = \ left (\ begin (array) (cccc) 6 & -5 & 8 & 4 \\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7 \\ -4 & 8 & -8 & -3 \ end (array) \ right) $.

For a fourth-order matrix, finding the inverse matrix using algebraic complements is somewhat difficult. However, such examples are found in test papers.

To find the inverse of a matrix, you first need to calculate the determinant of the matrix $ A $. The best way to do this in this situation is to expand the determinant by row (column). We select any row or column and find the algebraic complements of each element of the selected row or column.

For example, for the first line we get:

$$ A_ (11) = \ left | \ begin (array) (ccc) 7 & 5 & 2 \\ 5 & 3 & 7 \\ 8 & -8 & -3 \ end (array) \ right | = 556; \; A_ (12) = - \ left | \ begin (array) (ccc) 9 & 5 & 2 \\ 7 & 3 & 7 \\ -4 & -8 & -3 \ end (array) \ right | = -300 ; $$ $$ A_ (13) = \ left | \ begin (array) (ccc) 9 & 7 & 2 \\ 7 & 5 & 7 \\ -4 & 8 & -3 \ end (array) \ right | = -536; \; A_ (14) = - \ left | \ begin (array) (ccc) 9 & 7 & 5 \\ 7 & 5 & 3 \\ -4 & 8 & -8 \ end (array) \ right | = -112. $$

The determinant of the matrix $ A $ is calculated by the following formula:

$$ \ Delta (A) = a_ (11) \ cdot A_ (11) + a_ (12) \ cdot A_ (12) + a_ (13) \ cdot A_ (13) + a_ (14) \ cdot A_ (14 ) = 6 \ cdot 556 + (- 5) \ cdot (-300) +8 \ cdot (-536) +4 \ cdot (-112) = 100. $$

$$ \ begin (aligned) & A_ (21) = - 77; \; A_ (22) = 50; \; A_ (23) = 87; \; A_ (24) = 4; \\ & A_ (31) = -93; \; A_ (32) = 50; \; A_ (33) = 83; \; A_ (34) = 36; \\ & A_ (41) = 473; \; A_ (42) = - 250 ; \; A_ (43) = - 463; \; A_ (44) = - 96. \ end (aligned) $$

Algebraic Complement Matrix: $ A ^ * = \ left (\ begin (array) (cccc) 556 & -300 & -536 & -112 \\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36 \\ 473 & -250 & -463 & -96 \ end (array) \ right) $.

Joined matrix: $ (A ^ *) ^ T = \ left (\ begin (array) (cccc) 556 & -77 & -93 & 473 \\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463 \\ -112 & 4 & 36 & -96 \ end (array) \ right) $.

Inverse matrix:

$$ A ^ (- 1) = \ frac (1) (100) \ cdot \ left (\ begin (array) (cccc) 556 & -77 & -93 & 473 \\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463 \\ -112 & 4 & 36 & -96 \ end (array) \ right) = \ left (\ begin (array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28 / 25 & 1/25 & 9/25 & -24/25 \ end (array) \ right) $$

Checking, if desired, can be performed in the same way as in the previous examples.

Answer: $ A ^ (- 1) = \ left (\ begin (array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/25 & 9/25 & -24/25 \ end (array) \ right) $.

In the second part, a different way of finding the inverse matrix will be considered, which involves the use of transformations of the Gauss method or the Gauss-Jordan method.

To solve the system of linear equations (3) with respect to x 1 we will use the Gauss method.

The remaining systems of linear equations (2) are solved in a similar way.

Finally a group of column vectors x 1, x 2, ..., x n forms the inverse A -1.

Note that once finding the permutation matrices P 1, P 2, ..., P n-1 and exclusion matrices M 1, M 2, ..., M n-1(see page Gaussian elimination method) and constructing a matrix

M = M n-1 P n-1 ... M 2 P 2 M 1 P 1,

system (2) can be transformed to the form

• MAx 1 = Me 1,
• MAx 2 = Me 2,
• ......
• MAx n = Me n.

From here are x 1, x 2, ..., x n, with different right-hand sides Me 1, Me 2, ..., Me n.

When calculating the inverse matrix, it is more convenient to add the identity matrix on the right side of the original matrix and apply the Gaussian method in the forward and reverse directions.

Let's look at an example.

An example of calculating the inverse matrix

Let it be required to find the inverse matrix A -1 for a given matrix A:

Let's write the identity matrix on the right side:

We select the pivot element "4" (since it is the largest in absolute value) and rearrange the first and third lines:

Apply the Gaussian exception for the first column:

Swap the second and third rows and apply a Gaussian exclusion for the second column.

Methods for finding the inverse matrix. Consider a square matrix

We denote Δ = det A.

The square matrix A is called non-degenerate, or non-special if its determinant is nonzero, and degenerate or special, if aΔ = 0.

A square matrix B exists for a square matrix A of the same order if their product A B = B A = E, where E is the identity matrix of the same order as the matrices A and B.

Theorem . For the matrix A to have an inverse matrix, it is necessary and sufficient that its determinant be nonzero.

The inverse matrix of the matrix A, denoted by A- 1, so that B = A - 1 and is calculated by the formula

, (1)

where А i j are the algebraic complements of the elements a i j of the matrix A ..

Calculation of A -1 according to formula (1) for high-order matrices is very laborious, therefore in practice it is convenient to find A -1 using the method of elementary transformations (EP). Any nonsingular matrix A can be reduced to the identity matrix E by means of EP of only columns (or only rows). If EPs perfect over the matrix A are applied in the same order to the identity matrix E, then the result is an inverse matrix. It is convenient to perform EP over the matrices A and E at the same time, writing both matrices side by side through a line. Note again that when finding the canonical form of a matrix for the purpose of finding, one can use transformations of rows and columns. If you need to find the inverse of a matrix, you should use only rows or only columns during the transformation.

Example 1... For matrix find A -1.

Decision.We first find the determinant of the matrix A
hence, the inverse matrix exists and we can find it by the formula: , where A i j (i, j = 1,2,3) are the algebraic complements of the elements a i j of the original matrix.

From where .

Example 2... Using the method of elementary transformations, find A -1 for the matrix: A =.

Decision.We assign to the original matrix on the right the identity matrix of the same order: ... With the help of elementary column transformations, we bring the left “half” to the unit one, simultaneously performing exactly the same transformations over the right matrix.
To do this, let's swap the first and second columns: ~ ... Add the first to the third column, and the first multiplied by -2 to the second: ... From the first column we subtract the second doubled, and from the third - the second multiplied by 6; ... Let's add the third column to the first and second: ... Let's multiply the last column by -1: ... The square matrix obtained to the right of the vertical bar is the inverse of the given matrix A. So,
.

When studying algebra in a general education school (grade 9), one of the important topics is the study of numerical sequences, which include progressions - geometric and arithmetic. In this article, we will consider the arithmetic progression and examples with solutions.

What is an arithmetic progression?

To understand this, it is necessary to give a definition of the considered progression, as well as to give the basic formulas that will be further used in solving problems.

An arithmetic or algebraic progression is a set of ordered rational numbers, each term of which differs from the previous one by some constant amount. This value is called the difference. That is, knowing any member of the ordered series of numbers and the difference, you can restore the entire arithmetic progression.

Let's give an example. The following sequence of numbers will be an arithmetic progression: 4, 8, 12, 16, ..., since the difference in this case is 4 (8 - 4 = 12 - 8 = 16 - 12). But the set of numbers 3, 5, 8, 12, 17 can no longer be attributed to the considered type of progression, since the difference for it is not a constant value (5 - 3 ≠ 8 - 5 ≠ 12 - 8 ≠ 17 - 12).

Important formulas

Let us now give the basic formulas that will be needed to solve problems using an arithmetic progression. Let us denote by a n the nth term of the sequence, where n is an integer. The difference is denoted by the Latin letter d. Then the following expressions are valid:

1. To determine the value of the nth term, the formula is suitable: a n = (n-1) * d + a 1.
2. To determine the sum of the first n terms: S n = (a n + a 1) * n / 2.

To understand any examples of arithmetic progression with a solution in grade 9, it is enough to remember these two formulas, since any problems of the type under consideration are built on their use. You should also remember that the difference in progression is determined by the formula: d = a n - a n-1.

Example # 1: finding an unknown member

Let's give a simple example of an arithmetic progression and formulas that must be used to solve.

Let the sequence 10, 8, 6, 4, ... be given, it is necessary to find five terms in it.

It already follows from the problem statement that the first 4 terms are known. The fifth can be defined in two ways:

1. Let's calculate the difference first. We have: d = 8 - 10 = -2. Likewise, one could take any two other members standing next to each other. For example, d = 4 - 6 = -2. Since it is known that d = a n - a n-1, then d = a 5 - a 4, whence we get: a 5 = a 4 + d. Substitute the known values: a 5 = 4 + (-2) = 2.
2. The second method also requires knowing the difference of the considered progression, so first you need to determine it, as shown above (d = -2). Knowing that the first term a 1 = 10, we use the formula for n number of the sequence. We have: a n = (n - 1) * d + a 1 = (n - 1) * (-2) + 10 = 12 - 2 * n. Substituting n = 5 into the last expression, we get: a 5 = 12-2 * 5 = 2.

As you can see, both methods of solution led to the same result. Note that in this example, the difference d of the progression is negative. Such sequences are called decreasing, since each next term is less than the previous one.

Example # 2: Progression Difference

Now let's complicate the task a little, let's give an example how

It is known that in some the 1st term is equal to 6, and the 7th term is equal to 18. It is necessary to find the difference and restore this sequence to the 7th term.

Let's use the formula to determine the unknown term: a n = (n - 1) * d + a 1. We substitute in it the known data from the condition, that is, the numbers a 1 and a 7, we have: 18 = 6 + 6 * d. From this expression, you can easily calculate the difference: d = (18 - 6) / 6 = 2. Thus, we have answered the first part of the problem.

To restore a sequence up to 7 terms, you should use the definition of an algebraic progression, that is, a 2 = a 1 + d, a 3 = a 2 + d, and so on. As a result, we restore the entire sequence: a 1 = 6, a 2 = 6 + 2 = 8, a 3 = 8 + 2 = 10, a 4 = 10 + 2 = 12, a 5 = 12 + 2 = 14, a 6 = 14 + 2 = 16, a 7 = 18.

Example # 3: making a progression

Let us complicate the condition of the problem even more. Now it is necessary to answer the question of how to find the arithmetic progression. You can give the following example: given two numbers, for example - 4 and 5. It is necessary to make an algebraic progression so that three more terms fit between these.

Before starting to solve this problem, it is necessary to understand what place the given numbers will occupy in the future progression. Since there will be three more terms between them, then a 1 = -4 and a 5 = 5. Having established this, we proceed to the problem, which is similar to the previous one. Again, for the nth term, we use the formula, we get: a 5 = a 1 + 4 * d. From where: d = (a 5 - a 1) / 4 = (5 - (-4)) / 4 = 2.25. Here we received not an integer value of the difference, but it is a rational number, so the formulas for the algebraic progression remain the same.

Now add the found difference to a 1 and restore the missing members of the progression. We get: a 1 = - 4, a 2 = - 4 + 2.25 = - 1.75, a 3 = -1.75 + 2.25 = 0.5, a 4 = 0.5 + 2.25 = 2.75, a 5 = 2.75 + 2.25 = 5, which coincided with the condition of the problem.

Example # 4: the first term of the progression

Let's continue to give examples of arithmetic progression with a solution. In all the previous problems, the first number of the algebraic progression was known. Now consider a problem of a different type: let two numbers be given, where a 15 = 50 and a 43 = 37. It is necessary to find the number from which this sequence begins.

The formulas used so far assume knowledge of a 1 and d. Nothing is known about these numbers in the problem statement. Nevertheless, we write out expressions for each member about which there is information: a 15 = a 1 + 14 * d and a 43 = a 1 + 42 * d. Received two equations in which 2 unknown quantities (a 1 and d). This means that the problem is reduced to solving a system of linear equations.

The easiest way to solve this system is to express a 1 in each equation, and then compare the resulting expressions. The first equation: a 1 = a 15 - 14 * d = 50 - 14 * d; second equation: a 1 = a 43 - 42 * d = 37 - 42 * d. Equating these expressions, we get: 50 - 14 * d = 37 - 42 * d, whence the difference d = (37 - 50) / (42 - 14) = - 0.464 (only 3 decimal places are given).

Knowing d, you can use any of the 2 above expressions for a 1. For example, the first: a 1 = 50 - 14 * d = 50 - 14 * (- 0.464) = 56.496.

If you have doubts about the result, you can check it, for example, determine the 43 member of the progression, which is specified in the condition. We get: a 43 = a 1 + 42 * d = 56.496 + 42 * (- 0.464) = 37.008. A small error is due to the fact that the calculations used rounding to thousandths.

Example # 5: amount

Now let's look at some examples with solutions for the sum of an arithmetic progression.

Let a numerical progression of the following form be given: 1, 2, 3, 4, ...,. How do you calculate the sum of these 100 numbers?

Thanks to the development of computer technology, it is possible to solve this problem, that is, to add up all the numbers sequentially, which the computer will do as soon as a person presses the Enter key. However, the problem can be solved in the mind, if we pay attention that the presented series of numbers is an algebraic progression, and its difference is 1. Applying the formula for the sum, we get: S n = n * (a 1 + an) / 2 = 100 * (1 + 100) / 2 = 5050.

It is curious to note that this problem is called "Gaussian", because at the beginning of the 18th century the famous German, while still only 10 years old, was able to solve it in his head in a few seconds. The boy did not know the formula for the sum of an algebraic progression, but he noticed that if you add in pairs the numbers on the edges of the sequence, you always get one result, that is, 1 + 100 = 2 + 99 = 3 + 98 = ..., and since of these amounts will be exactly 50 (100/2), then to get the correct answer, it is enough to multiply 50 by 101.

Example # 6: sum of members from n to m

Another typical example of the sum of an arithmetic progression is the following: given a series of numbers: 3, 7, 11, 15, ..., you need to find what the sum of its members from 8 to 14 will equal.

The problem is solved in two ways. The first of them involves finding unknown terms from 8 to 14, and then their sequential summation. Since there are few terms, this method is not laborious enough. Nevertheless, it is proposed to solve this problem by the second method, which is more universal.

The idea is to obtain a formula for the sum of the algebraic progression between the terms m and n, where n> m are integers. Let us write out two expressions for the sum for both cases:

1. S m = m * (a m + a 1) / 2.
2. S n = n * (a n + a 1) / 2.

Since n> m, it is obvious that the 2 sum includes the first. The last conclusion means that if we take the difference between these sums, and add to it the term a m (in the case of taking the difference, it is subtracted from the sum S n), then we get the necessary answer to the problem. We have: S mn = S n - S m + am = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am = a 1 * (n - m) / 2 + an * n / 2 + am * (1- m / 2). In this expression it is necessary to substitute the formulas for a n and a m. Then we get: S mn = a 1 * (n - m) / 2 + n * (a 1 + (n - 1) * d) / 2 + (a 1 + (m - 1) * d) * (1 - m / 2) = a 1 * (n - m + 1) + d * n * (n - 1) / 2 + d * (3 * m - m 2 - 2) / 2.

The resulting formula is somewhat cumbersome; nevertheless, the sum of S mn depends only on n, m, a 1 and d. In our case, a 1 = 3, d = 4, n = 14, m = 8. Substituting these numbers, we get: S mn = 301.

As can be seen from the solutions given, all problems are based on knowledge of the expression for the nth term and the formula for the sum of the set of the first terms. Before proceeding with the solution of any of these problems, it is recommended to carefully read the condition, clearly understand what is required to be found, and only then proceed to the solution.

Another tip is to strive for simplicity, that is, if you can answer a question without using complex mathematical calculations, then you need to do just that, since in this case the probability of making a mistake is less. For example, in an example of an arithmetic progression with solution # 6, one could stop at the formula S mn = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am, and break the general problem into separate subtasks (in this case, first find the members an and am).

If there are doubts about the result obtained, it is recommended to check it, as it was done in some of the examples given. We figured out how to find the arithmetic progression. If you figure it out, it's not that difficult.