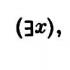Quantifiers of generality and existence. Quantifiers Meaning of predicate logic formula
1. Quantifiers.
2. Universal quantifier.
3. Existence quantifier.
4. The concept of a predicate logic formula. Formula meaning
predicate logic.
5. Equivalent formulas of predicate logic.
The concept of a quantifier
Quantifier - (from Latin quantum - how much), logicalquantitative operation
the area of objects to which the expression refers,
obtained as a result of its use.
In ordinary language, bearers of such characteristics
words like "all", "every", "some",
"exists",
"available",
"any",
"any",
"single", "several", "infinitely many",
"finite number", as well as all quantitative
numerals.
Operations for predicate
For predicates, two new ones are introducedcompared to propositional logic operations:
general quantifier
existence quantifier
General quantifier
Let P(x) be a unary predicate defined onsubject set M.
A universal statement corresponding to
predicate P(x), the following statement is called:
“each element of the set M satisfies
predicate P(x)"
or
“for every x the predicate is satisfied”
This statement is denoted - (x)P(x)
The statement (x)P(x) is considered true if
the predicate P(x) is identically true, and false
otherwise.
General quantifier
The symbol x is called a quantifiervariable x, it is read like this:
"for all x"
"for every x"
"for any x"
commonality in
The expression (x)P(x) reads: “for all x, P(x)”, or
“for every x, P(x).”
For example, x(x=x) is a true universal
statement, and x(x>2) is a false universal
statement.
finite set (a1,a2,…am), then:
P(x) P(a1) P(a2) ... P(am)
General quantifier
Thus, the general quantifiercan be understood as an operator
conjunctions by quantifiable
variable.
Existence quantifier
Existentialstatement,
relevant
predicate
P(x),
called
the statement “there is an element of the set M,
satisfying
predicate
P(x)",
which
is denoted by x P(x) and is considered true if
the predicate P(x) is satisfiable, but otherwise false
case.
The symbol x is called the existential quantifier, and
expression x in which this quantifier is preceded
variable x read like this:
“there exists x such that...”
"for some x, ..."
Existence quantifier
FOR EXAMPLEx(x>2) – true existential statement
x(x=x+1) is a false existential statement.
If P(x) is a unary predicate defined on
finite set (a1,a2,…am), then
P(x) P(a1) P(a2) ... P(am)
Existence quantifier
So the quantifierexistence can be understood as
disjunction operator by
quantified variable.
10. Examples
Examples of formula records and their verbal expressions:x(x 2 1 (x 1)(x 1)) For all x the predicate is satisfied...
x(x0)
inequality...
x(x0)
For all x, fair…..
y (5 y 5)
There is y such that 5+y=5
y(y 2 y 1 0)
For all y the predicate is satisfied
y(y 2 y 1 0)
There is y that….
x(x x)
For some x, true
3
2
11. Formulas of predicate logic
Predicate logic has the following symbolism:Symbols p, q, r, ... are propositional variables that take
two values: 1 - true, 0 - false.
Subject variables – x, y, z, …, which run
values from some set M;
x0, y0, z0 – subject constants, i.e. values of subject
variables.
P(·), Q(·), F(·), … - single-place predicate variables;
Q(·,·,…,·), R(·,·, …,·) are n-place predicate variables.
P0(·), Q0(·,·, …,·) are symbols of constant predicates.
Symbols of logical operations: , .
Symbols of quantifier operations: x, x.
Auxiliary characters: parentheses, commas.
12. Formulas of predicate logic
A subject variable is called free if itdoes not immediately follow the quantifier and is not included in
the scope of the quantifier on this variable, all others
variables,
inbox
V
formula
are called
connected.
y z (P(x,y) P(y,z))
The formulas of predicate logic are:
Each predicate letter and predicate letter with
followed by subject variables in parentheses.
Expressions of the form F G, F G, G, F G, F G, (y)F,
(y)G, where F and G are predicate logic formulas, variable
mind.
13. Formulas of predicate logic
Each utterance is both variable andconstant, is a formula (elementary).
And
If F(·,·, …,·) is an n-ary predicate variable
or a constant predicate, and x1, x2,…, xn are objective
variables or subject constants (not
are necessarily all distinct), then F(x1, x2,…, xn) is
formula. This formula is called elementary, in
its subject variables are free, not
associated quantifiers.
14. Formulas of predicate logic
If A and B are formulas, and such that they are the samethe subject variable is not in one of them
bound, and free in the other, then the words A B,
A B, A B are formulas. In these formulas those
variables that were in the original formulas
free are free, and those who were
connected, are connected.
If A is a formula, then A is a formula, and the character
subject variables in the transition from formula A to
formula A does not change.
15. Formulas of predicate logic
If A(x) is a formula in which the subjectvariable x enters freely, then the words xA(x) and
xA(x) are formulas, moreover, subject
the variable is included in them connected.
Every word other than those named
formulas in the previous paragraphs is not
formula.
16. Formulas of predicate logic
For example, if P(x) and Q(x,y) are single anddouble predicates, and q, r are variables
statements, then the formulas will be expressions:
q, P(x), P(x) Q(x , y), xP(x) xQ(x, y), (Q(x, y) q) r
0
For example, the word is not a formula: xQ(x, y) P(x)
Here the condition of clause 3 is violated, since the formula
xQ(x,y) the variable x appears bound, and in the formula
P(x) variable x enters freely.
From the definition of the predicate logic formula it is clear that
every propositional algebra formula is
formula of predicate logic.
17. Interpretation of the predicate formula
Interpretation of the predicate calculus formulais called the instantiation of sets from which
subject variables take values and
specification
relations
And
relevant
truth sets for each predicate letter.
18. Predicate calculus formulas
identicallytrue at
any
interpretations,
those.
universally valid
identically
false
at
any
interpretations,
those.
controversial
feasible
(formulas,
truth
which depends
from
interpretations)
19. The meaning of the predicate logic formula
As an example, consider the formulay z (P(x, y) P(y, z))
In the formula, the two-place predicate P(x, y) is defined on
set MхM, where M=(0,1,2,…,n,…), i.e. MxM=NxN.
The formula includes the variable predicate P(x,y), subject
variables x,y,z, two of which y and z are connected by quantifiers,
and x is free.
Let's take
behind
specific
meaning
predicate
P(x,y)
fixed predicate P0(x,y): “x
Then for values of y less than x0=5, the predicate P0(x0,y)
takes the value “false”, and the implication P(x,y) P(y,z) when
all z M takes the value “true”, i.e. statement
has the meaning “true”.
20. Equivalent formulas of predicate logic
Definition 1.equivalent on the domain M if they take
the same logical values for all values included in
of the variables assigned to the M area.
Definition 2.
Two predicate logic formulas A and B are called
equivalent if they are equivalent in any area.
21. Equivalent formulas of predicate logic
Let A(x) and B(x) be variable predicates, and C be a variablestatement (or formula not containing x). Then they have
place the following equivalences:
22. Equivalent formulas of predicate logic
ExampleThe predicate Mother(x,y) means that x is the mother of y.
Then y xMother(x,y) means that each person has
mother, is a true statement.
x yMother(x,y) means that there is a mother of all people, which
is another statement whose truth depends on
sets of values that y can take: if it
many brothers and sisters, then it is true, otherwise
case it is false.
Thus, the rearrangement of universal quantifiers and
existence can change the meaning and meaning of an expression.
23. Laws of logical operations (generally valid formulas of predicate logic)
24. Exercise
Find the negation of the following formulas25. Exercise
AndExercise
Prove equivalence
x(A(x) B(x)) xA(x) xB(x)
Let the predicates A(x) and B(x) be identically false. Then it will be
false and the predicate A(x) B(x)
x(A(x) B(x))
In this case the statements will be false
xA(x) xB(x)
Let at least one of the predicates (for example, A(x)) not
identically false. Then it will not be identically false and
predicate A(x) B(x)
In this case, the statements xA(x) x(A(x) B(x)) will be true
This means that the original formulas will also be true
Therefore: x(A(x) B(x)) xA(x) xB(x)
26.
On one's ownFor a more detailed study of the material
we read on our own:
TEXTBOOK: “Mathematical logic and theory
algorithms",
author Igoshin V.I.
Pages 157-164
Pages 165-178
Pages 178-183
27.
HomeworkProve equivalence
C xA(x) x(C A(x))
Prove that the formula is generally valid
A V (P(x) Q(x)) xP(x) xQ(x)
Prove that the formula is inconsistent
A x((F (x) F (x)) (F (x) F (x)))
The functional nature of the predicate entails the introduction of another concept - quantifier. (quantum – from Latin “how much”) Quantifier operations can be considered as a generalization of the operations of conjunction and disjunction in the case of finite and infinite regions.
General quantifier (all, everyone, everyone, any (all – “everyone”)). The corresponding verbal expression sounds like this:
“For every x P(x) is true.” The occurrence of a variable in a formula can be bound if the variable is located either immediately after the quantifier sign, or in the scope of the quantifier after which the variable appears. All other occurrences are free, the transition from P(x) to x(Px) or (Px) is called binding the variable x or attaching a quantifier to the variable x (or to the predicate P) or quantification of the variable x. The variable on which the quantifier is attached is called related, an unrelated quantization variable is called free.
For example, the variable x in the predicate P(x) is called free (x is any of M), in the statement P(x) the variable x is called a bound variable.
The equivalence is true: P(x 1)P(x 2)…P(x n),
P(x) – predicate defined on the set M=(x 1,x 2 ...x 4)
Existence quantifier(exist – “to exist”). The corresponding verbal expression is: “There is an x such that P(x) is true.” The statement xP(x) no longer depends on x, the variable x is connected by a quantifier.
The equivalence is fair:
xP(x) = P(x 1)P(x 2)…P(x n), where
P(x) is a predicate defined on the set M=(x 1 ,x 2 …x n ).
The general quantifier and the existential quantifier are called dual, sometimes the quantifier notation is used! - “there exists, and, moreover, only one.”
It is clear that the statement xP(x) is true only in the unique case when P(x) is an identically true predicate, and the statement is false only when P(x) is an identically false predicate.
Quantifier operations also apply to multiplace predicates. The application of a quantifier operation to the predicate P(x,y) with respect to the variable x puts in correspondence with the two-place predicate P(x,y) the one-place predicate xP(x,y) or xP(x,y), depending on y and independent of x.
To a two-place predicate, you can apply quantifier operations on both variables. Then we get eight statements:
1. P(x,y); 2. P(x,y);
3. P(x,y); 4. P(x,y);
5. P(x,y); 6. P(x,y);
7. P(x,y); 8. P(x,y)
Example 3. Consider possible options for attaching quantifiers to a predicate P(x,y) – “x divided by y”, defined on the set of natural numbers (without zero) N. Give verbal formulations of the received statements and determine their truth.
The operation of attaching quantifiers leads to the following formulas:
Statements “for any two natural numbers, one is divisible by the other” (or 1) all natural numbers are divisible by any natural number; 2) any natural number is a divisor for any natural number) false;
Statements “there are two natural numbers such that the first is divisible by the second” (1. “there is a natural number x that is divisible by some number y”; 2. “there is a natural number y that is a divisor of some natural number numbers x") are true;
The statement “there is a natural number that is divisible by any natural number” is false;
The statement “for every natural number there is a natural number that is divisible by the first” (or for every natural number there is a dividend) is true;
The statement “for every natural number x there is a natural number y by which it is divisible” (or “for every natural number there is a divisor”) is true;
The statement “there is a natural number which is a divisor of every natural number” is true (such a divisor is one).
In the general case, changing the order of quantifiers changes the meaning of the statement and its logical meaning, i.e. for example, the statements P(x,y) and P(x,y) are different.
Let the predicate P(x,y) mean that x is the mother of y, then P(x,y) means that every person has a mother - a true statement. P(x,y) means that there is a mother of all people. The truth of this statement depends on the set of values that y can take: if it is the set of siblings then it is true, otherwise it is false. Thus, rearranging the quantifiers of universality and existence can change the very meaning and meaning of the expression.
a) replace the initial sign (or) with the opposite one
b) put a sign before the rest of the predicate
The operator with the help of which about k.-l. a separate object is transformed into a statement about a collection (set) of such objects.
In logic, two basic codes are used: the code of generality, “V,” and the code of existence, “E.” In natural language, distant semantic analogues of the community concept are the words “all,” “any,” “everyone”; semantic analogues of K. existence are the words “some”, “exists”. With the help of K data, any attributive statement of the type P(x) that an object x is inherent in P can be transformed into a corresponding quantifier statement of the type VxP(x) and the type ZxP(x). In content, the quantifier formula “VxP(x)” itself reads as “for all x there is P(x)”, and the formula “ExP(x)” - as “for some x there is P(x)”. A statement of the form VxP(x) is true if any x has property P; and is false if at least one x does not have the property P. Similarly, a statement of the form ZxP(x) is true if at least one x has the property P; and false if no x has property P.
Based on the elementary quantifier formulas “VxP(x)”, “ExP(x)” other, more complex quantifier formulas can be constructed. The logical relationships between such formulas are studied in predicate logic. In particular, the formula “ZxP(x)” is logically equivalent to the formula “) VxQUANTITOR| P(x)”, and the formula “VxP(x)” is equivalent to the formula “) Eх) P(x)”, where “)” are negations.
In an implicit form, logics were already used by Aristotle, but in a strict substantive and formal sense they were first introduced into the logic of G. Frege.
Philosophy: Encyclopedic Dictionary. - M.: Gardariki. Edited by A.A. Ivina. 2004 .
(from lat. quantum - how much), a predicate logic operator, applied to formulas containing only one free variable gives (statement). There are K. communities, denoted by the symbol (from English all - everything), and K. existence (from exist - to exist): xP(x) is interpreted (cm. Interpretation) as “for all x the property P holds”, and xP(x) - as “there is an x such that the property?(x)” holds. If (universe) is finite, then xP(x) is equivalent to the conjunction of all formulas P (A), where a is an element of the subject area. Similarly, xP(x) is equivalent to the disjunction of all formulas of the form? (A). If the subject area is infinite, then xP (x) and xP(x) can be interpreted as infinite and disjunction respectively. Introduction to K. in the logic of multiplace predicates (i.e. non-single) causes the undecidability of predicate calculus. Various relationships between the principles of generality and existence and the logical connectives of propositional logic are formalized in predicate calculus.
Philosophical encyclopedic dictionary. - M.: Soviet Encyclopedia. Ch. editor: L. F. Ilyichev, P. N. Fedoseev, S. M. Kovalev, V. G. Panov. 1983 .
(from Lat. quantum - how much) - logical. operator applied to logical. expressions and giving quantities. a characteristic of the domain of objects (and sometimes the domain of predicates), which includes what is obtained as a result of the application of K. How logical The means of propositional logic are not enough to express the forms of general, particular, and individual judgments; in predicate logic, obtained by expanding propositional logic by introducing principles, such judgments are expressible. So, for example, four basic. forms of judgments of traditions. logics “All A are B”, “No A is B”, “Some A are B” and “Some A are not B” can be written down (if we ignore the presupposed requirement of Aristotelian logic for the non-emptiness of A in general judgments) using the symbolism explained below as follows: ∀(x) (A (x) ⊃ B (x)), ∀(x) (A (x) ⊃ B(x)), ∃(x) (A (x ) & B (x)) and ∃ (x) (A (x) & B (x)). Introduction K. allows you to write it down in a formalized logical way. language of expression of nature. languages containing quantities. characteristics of k.-l. subject or predicate areas. In natural In languages, the carriers of such characteristics are the so-called. quantifier words, which include, in particular, quantities. numerals, pronouns “all”, “each”, “some”, verb “exists”, adjectives “any”, “every”, “single”, adverbs “infinitely many”, etc. It turns out that to express all the mentioned quantifier words in a formalism. languages and logic In calculus, the two most commonly used are sufficient. K.: K. generality (or in generality), usually denoted by the symbol ∀ (inverted letter A - the initial letter of the English word “all”, German “alle”, etc.), and K. existence, usually denoted by the symbol ∃ (the inverted letter E is the initial letter of the English word “exist”, German “existieren”, etc.); the signs ∀ and ∃ in the notation of a quantorial variable are followed by a letter of a certain alphabet, called a quantifier variable, which is usually considered as part of the notation of a quantorial variable: ∀x, ∀y, ∀F, ∃x, ∃α, etc. For K. generalities the following notations are also used:
for K. existence:

The sign K. is placed before the expression to which K. is applied (the operation of applying K. is often called quantification); this expression is enclosed in parentheses (which are often omitted if this does not lead to ambiguity). The expression ∀x (A (x)) containing the general principle reads as “For all x it is true that A (x)”, or “For every x it is true that A (x)”; The expression ∃x (A(x)) containing the K. of existence is read as “There is x such that A (x)”, or “For some x, A(x) is true.” In both of these cases it is not assumed, generally speaking, that the expression A(x) actually depends on the variable x (it may not contain any variables at all, i.e. it may denote a certain statement; in this case it does not change the meaning of this statement ). However, the main the purpose of K. is statements from an expression that depends on a quantifier variable, or at least a reduction in the number of variables on which this expression, being an open (open) formula (see Closed formula), depends. For example, the expression (y>0&z>0&x=y-z) contains three variables (x, y and z) and becomes a statement (true or false) when k.-l. def. replacing these variables with the names of certain objects from the range of their values. The expression ∃ z(y>0&z>0&x = y-z) depends on only two variables (x and y), and ∃y∃z (y>0&z>0& &x = y –z) - on one x. The last formula expresses, therefore, a certain property (one-place). Finally, the formula ∃х∃у∃z (y>0&z>0&x=y–z) expresses a completely defined statement.
Dr. examples of formulas containing K.: 1) ∀x(x>0); 2) ∃x(x>0); 3) ∀х (2+2=5); 4) ∃x (2+2=4); 5) ∀x (x = x)& (x+2=y); 6) x ∃y are the parts of the formula to the right of them, and the domain of action of a formula (x = z⊃x ≠ 0). The occurrence of a certain variable in the sign of a formula or in the domain of action of a formula containing this variable , is called a bound occurrence of a variable in a formula. In other cases, the occurrence of a variable is called a free one. The same one can appear in a certain formula in one place in a bound form, and in another. place - in a free place. This is, for example, formula 5): the first three (counting from the left) occurrences of the variable x in it are connected, the last one is free. Sometimes they say that a variable is connected in a given formula if all its occurrences in this formula are connected. In mathematics and logic, any expression containing a free variable can be considered (in an informal approach) as it in the usual sense of the word that it (the expression) depends on various values of this variable; by giving this variable different meanings (i.e., replacing all its free occurrences with the name of a certain object belonging to the range of values of this variable), we obtain different (generally speaking) meanings of this expression, depending on the value of the variable, i.e. . from the constant substituted instead. As for bound variables, the expressions that enclose them do not really depend on them. For example, the expression ∃x(x = 2y), depending on y (which is freely included in it), is equivalent to the expressions ∃z(z = 2y), ∃u(u = 2y), etc. This logical expressions from the associated variables included in them are found in the so-called. the rule for renaming related variables, postulated or deduced in dep. logical calculus (see Variable, Predicate calculus).
The above interpretation of the meaning of K. related to the content of logical. theories. As for the calculations in proper. sense (so-called formal systems), then in them it makes no sense at all to talk about the “meaning” of this or that calculus, which here is simply a certain symbol of calculus. The question of the meaning (meaning) of calculus relates entirely to the area of interpretation of calculus. In application to K. we can talk about at least three interpretations: classical, intuitionistic and constructive, corresponding to various concepts of existence and universality in logic and mathematics (see Intuitionism, Constructive logic). Both in classical and intuitionistic (constructive) predicate calculus, methods of inference in cases where the original or formulas to be proved contain a formula are described by the same so-called predicate calculus. quantification postulates, e.g. Bernays' postulates.
The principles of generality and existence do not exhaust the types of principles used in logic. Extensive principles are the so-called. limited quantum equations of the form ∀xP(x)A(x) or ∃xQ(x)A(x), in which the range of change of the quantifier variable x is “limited” by some special predicate P(x) (or Q(x)). Limited K. are reduced to K. of generality and existence with the help of traces. equivalences: ∀xP(x)A(x) QUANTITOR ∀x(P(x) ⊃A(x)) and ∃xQ(x)A(x) QUANTITOR ∃x(Q(x)&A(x)). The often used K. of uniqueness ∃!xA(x) (“there is a unique x such that A(x)”) is also expressed through the K. of generality and existence, for example. so: xA(x) QUANTITOR ∃xA(x)& ∀y∀z(A(y)&A(z)⊃y=z).
Other types of calculations are also used, which are not covered by the concept of limited calculation. These are “numerical” calculations of the form ∃xnA(x) (“there are exactly n different x such that A(x)”), used in intuitionistic logic of calculation. “quasi-existence” ∃ xA(x), or (“it is not true that there does not exist an x such that A(x)”); with t.zr. classic in the logic of the Q. of “quasi-existence” is no different from the Q. of existence, in intuitionistic logic the sentence ∃xA(x), which says nothing about the existence of an algorithm for finding such x that A(x), really asserts only the “quasi” of such x and K. infinity ∃x∞A(x) (“there are infinitely many x such that A(x)”). Expressions containing the principles of infinity and numerical terms can also be written using the terms of generality and existence. In the extended predicate calculus, coefficients are taken not only by subject variables, but also by predicate variables, i.e. formulas of the form ∃F∀xF(x), ∀Ф∃у(Ф(y)), etc. are considered.
Lit.: Gilbert D. and Ackerman V., Fundamentals of Theoretical Logic, trans. from English, M., 1947, p. 81-108; Tarski A., Introduction to logic and methodology of deductive sciences, trans. from English, M., 1948, about. 36-42, 100-102, 120-23; Kleene S.K., Introduction to Metamathematics, trans. from English, M., 1957, p. 72-80, 130-38; Church A., Introduction to Mathematical Logic, trans. from English, vol. 1, p. 42–48; Kuznetsov A.V., Logical contours of the algorithm, translation from the standardized Russian language into the information-logical language, in: Abstracts of reports at the conference on information processing, machine translation and automatic text reading, M., 1961; Mostowski A., On a generalization of quantifiers, "Fundam. math.", 1957, t. 44, No. 1, p. 12–36; Hailperin T., A theory of restricted quantification, I–II, "J. Symb. Logic", 1957, v. 22, No. 1, p. 19–35, No. 2, p. 113–29.
Yu. Gastev. Moscow.
Philosophical Encyclopedia. In 5 volumes - M.: Soviet Encyclopedia. Edited by F. V. Konstantinov. 1960-1970 .
Synonyms:
See what "QUANTITOR" is in other dictionaries:
Noun, number of synonyms: 1 operator (24) ASIS synonym dictionary. V.N. Trishin. 2013… Synonym dictionary
quantifier- - Telecommunications topics, basic concepts EN quantifier... Technical Translator's Guide
Quantifier is a general name for logical operations that limit the domain of truth of a predicate and create a statement. Most often mentioned: Quantifier of universality (designation: , reads: “for all...”, “for each...” or “every...” ... Wikipedia
A general name for logical operations that use the predicate P(x) to construct a statement that characterizes the domain of truth of the predicate P(x). In mathematics In logic, the quantifier of universality and the quantifier of existence are most commonly used. A statement means... ... Mathematical Encyclopedia
Quantifier- (from Latin quantum how much) a symbol used to denote certain operations of mathematical logic, at the same time a logical operation that gives a quantitative characteristic of the field of objects to which the expression obtained in ... ... The beginnings of modern natural science
In addition to the logical operations known to us for predicates, two new ones are introduced: the operation of attaching quantifiers of existence and generality.
"for all X" (for anyone X, for each X) is called general quantifier and is designated X.
The statement "there is X" (for some X, at least for one X, there is something like this X) is called existence quantifier and is designated X.
The statement "there is one and only one" X"(for single meaning X) is called uniqueness quantifier : ! X.
For example: “All shrubs are plants.” This statement contains a general quantifier (“all”). The statement “there are numbers that are multiples of 5 "contains an existential quantifier ("exist").
In order to obtain a statement from a multiplace predicate, it is necessary to connect each variable with quantifiers. For example, If P(x;y) is a two-place predicate, then (xX) (yY) P(x; y)- statement.
If not every variable is connected by a quantifier, then what is obtained is not a statement, but a predicate depending on the variable that is not connected by a quantifier. So, if before the predicate P(x;y) put a quantifier y, then we get the predicate (yY) P(x; y), depending on the variable X.
Let's find out which of the following sentences are statements and which are predicates: a) there is such X, What x+y = 2;
b) for any X And at there is equality x + y = y + x.
Solution: Let’s identify the logical structure of these sentences.
a) The sentence “There is such a thing” X, What x + y = 2" can be written in the form (xR) x + y = 2. Since only the variable x is associated with a quantifier, the sentence in question with two variables is a predicate.
b) Offer “for any X And at occurs x + y = y + x" can be written in the form : (xR) (yR) x + y = y + x, Where both variables are related. Therefore, this sentence is a statement.
If any objective variable in a formula is not associated with a quantifier, then it is called free variables.
For example: (x) xy=uh. Here's the variable at is not bound by any quantifier, so it is free. The truth of a given statement does not depend on it.
Quantifiers (x) (x) are called dual each other.
Quantifiers of the same name can be swapped, which does not affect the truth of the statement.
For example: (y) (x) x + y = 5. This the statement has the same meaning, what and (x) (y) x + y = 5.
For dissimilar quantifiers, a change in order can lead to a change in the truth of the statement.
For example: (x) (y) x<у , i.e. for any number X there are more at- true statement.
Let's swap the quantifiers: (x) (y) x
In connection with the introduction of quantifiers, the following must be taken into account:
1. A predicate logic formula cannot contain the same objective variable, which would be bound in one part of the formula and free in another.
2. The same variable cannot be in the region of quantifiers that are dual to each other.
Violation of these conditions is called variable collision.
How is the truth value of a statement with a quantifier established?
To prove a statement with a general quantifier you need to make sure that when substituting each of the values X into a predicate P(x) the latter turns into a true statement. If the set X is finite, then this can be done by enumerating all cases; if the set X is infinite, then it is necessary to carry out reasoning in a general form.
Statement (x) P(x) false if such a value can be specified AX, at which P(x) turns into a false statement R(a). That's why, to refute a statement with a general quantifier It is enough to give an example.
Statement (x) P(x) true if such a value can be specified AX, at which P(x) turns into a true statement R(a). Therefore, in order verify the truth of a statement with a quantifier existence , it is enough to give an example and thus prove it.
In order to verify the falsity of a statement with quantifier existence (x) P(x), it is necessary to verify the falsity of each P(x), P(x), …, P(x). If the set X Of course, this can be done by brute force. If there are many X infinitely, then it is necessary to carry out reasoning in a general form.
Examples.
1. Find the truth value “among the numbers” 1, 2, 3, 4 there is a prime number."
Solution: The statement contains an existential quantifier and can therefore be represented as a disjunction of statements: “ 1 - prime number" or " 2 - prime number" or " 3 - prime number" or " 4 - Prime number". To prove the truth of a disjunction, the truth of at least one statement is sufficient, for example, “ 3 is a prime number that is true. Therefore, the original statement is also true.
2. Let us prove that any square is a rectangle.
Solution: The statement contains a general quantifier. Therefore, it can be presented as a conjunction: “square - rectangle” and “square - rectangle” and “square - rectangle”, etc. Since all these statements are true, then the conjunction of these statements is true, therefore, the original sentence is true.
3. “Any triangle is isosceles.” This is a false statement. To verify this, it is enough to draw a triangle that is not isosceles.a
To construct the negation of a statement with quantifiers necessary:
1) replace the quantifier of generality with the quantifier of existence, and the quantifier of existence with the quantifier of generality;
2) replace the predicate with its negation.
Example. Let us formulate a negation for the following statements:
a) all elements of the set Z even; b) some verbs answer the question “what to do?”.
Solution: a) Let us replace the quantifier of generality with the quantifier of existence, and its statement with its negation: some elements of the set Z odd.
b) Let us replace the quantifier of existence with a quantifier of generality, and its expression with negation: all verbs do not answer the question “what to do?”
Predicate (lat. praedicatum- stated, mentioned, said) - any mathematical statement in which there is at least one variable. The predicate is the main object of study in first-order logic.
A predicate is an expression with logical variables that make sense for any valid values of these variables.
Expressions: x > 5, x > y – predicates.
Predicate ( n-local, or n-ary) is a function with a set of values (0,1) (or “false” and “true”), defined on the set. Thus, each set of elements of the set M characterized as either "true" or "false".
A predicate can be associated with a mathematical relation: if n-ka belongs to the relation, then the predicate will return 1 on it. In particular, a unary predicate defines the relation of membership to a certain set.
A predicate is one of the elements of logic of the first and higher orders. Starting from second-order logic, quantifiers can be placed on predicates in formulas.
The predicate is called identically true and write:
if on any set of arguments it takes the value 1.
The predicate is called identically false and write:
if on any set of arguments it takes the value 0.
The predicate is called feasible, if it takes the value 1 on at least one set of arguments.
Since predicates take only two meanings, all operations of Boolean algebra are applicable to them, for example: negation, implication, conjunction, disjunction, etc.
Quantifier is a general name for logical operations that limit the domain of truth of a predicate. Most often mentioned:
Universal quantifier(designation: reads: “for everyone...”, “for everyone...” or “every...”, “any...”, “for any...”).
Existence quantifier(designation: , reads: “exists...” or “will be found...”).
Examples
Let's denote P(x) predicate " x divisible by 5." Using the general quantifier, we can formally write the following statements (false, of course):
any natural number is divisible by 5;
every natural number is a multiple of 5;
all natural numbers are multiples of 5;
in the following way:
![]() .
.
The following (already true) statements use the existential quantifier:
there are natural numbers that are multiples of 5;
there is a natural number that is a multiple of 5;
at least one natural number is divisible by 5.
Their formal notation:
![]() .Introduction to the concept
.Introduction to the concept
Let the predicate P(x) be given on the set X of prime numbers: “The prime number x is odd.” Let us substitute the word “any” in front of this predicate. We get the false statement “any prime number x is odd” (this statement is false, since 2 is a prime even number).
Substituting the word “exists” in front of the given predicate P(x), we obtain the true statement “There is a prime number x that is odd” (for example, x = 3).
Thus, you can turn a predicate into a statement by placing in front of the predicate the words “everything”, “exists”, etc., called quantifiers in logic.
Quantifiers in mathematical logic
The statement means that the range of the variable x included in the domain of truth of the predicate P(x).
(“For all values of (x), the statement is true.”)
The statement means that the domain of truth of the predicate P(x) is non-empty.
(“There is an (x) for which the statement is true”).
Question 31 Graph and its elements. Basic concepts. Incidence, multiplicity, loop, contiguity. Types of graphs. The route in the graph and its length. Classification of routes. Adjacency matrices of directed and undirected graphs.
In mathematical graph theory and computer science, a graph is a collection of a non-empty set of vertices and a set of pairs of vertices.
Objects are represented as vertices, or nodes, of a graph, and connections are represented as arcs, or edges. For different application areas, types of graphs may differ in directionality, restrictions on the number of connections, and additional data about vertices or edges.
A path (or chain) in a graph is a finite sequence of vertices in which each vertex (except the last) is connected to the next one in the sequence of vertices by an edge.
A directed path in a digraph is a finite sequence of vertices v i, for which all pairs ( v i,v i+ 1) are (oriented) edges.
A cycle is a path in which the first and last vertices coincide. In this case, the length of a path (or cycle) is the number of its components ribs. Note that if the vertices u And v are the ends of some edge, then according to this definition, the sequence ( u,v,u) is a cycle. To avoid such “degenerate” cases, the following concepts are introduced.
A path (or cycle) is called simple if its edges are not repeated; elementary if it is simple and its vertices are not repeated. It's easy to see that:
Every path connecting two vertices contains an elementary path connecting the same two vertices.
Any simple non-elementary path contains elementary cycle.
Any simple a cycle passing through some vertex (or edge) contains elementary(sub-)cycle passing through the same vertex (or edge).
A loop is an elementary cycle.
Graph or undirected graph G is an ordered pair G: = (V,E
V
E this is a set of pairs (in the case of an undirected graph, unordered) of vertices, called edges.
V(and therefore E, otherwise it would be a multiset) are usually considered finite sets. Many good results obtained for finite graphs are not true (or differ in some way) for infinite graphs. This is because a number of considerations become false in the case of infinite sets.
The vertices and edges of a graph are also called graph elements, the number of vertices in the graph | V| - order, number of edges | E| - the size of the graph.
Peaks u And v are called the terminal vertices (or simply ends) of an edge e = {u,v). An edge, in turn, connects these vertices. Two end vertices of the same edge are called adjacent.
Two edges are said to be adjacent if they have a common end vertex.
Two edges are called multiple if the sets of their end vertices coincide.
An edge is called a loop if its ends coincide, that is e = {v,v}.
degree deg V peaks V call the number of edges incident to it (in this case, the loops are counted twice).
A vertex is said to be isolated if it is not the end of any edge; hanging (or leaf) if it is the end of exactly one edge.
Directed graph (abbreviated digraph) G is an ordered pair G: = (V,A), for which the following conditions are met:
V is a non-empty set of vertices or nodes,
A it is a set of (ordered) pairs of distinct vertices, called arcs or directed edges.
Arc is an ordered pair of vertices (v, w), where is the vertex v called the beginning, and w- the end of the arc. We can say that the arc leads from the top v to the top w.
Mixed graph
Mixed graph G is a graph in which some edges can be directed and some can be undirected. Written as an ordered triple G: = (V,E,A), Where V, E And A defined the same as above.
Directed and undirected graphs are special cases of mixed graphs.
Isomorphic graphs(?)
Graph G is called isomorphic to the graph H, if there is a bijection f from the set of graph vertices G to the set of vertices of the graph H, which has the following property: if in the graph G there is an edge from the vertex A to the top B, then in the graph H f(A) to the top f(B) and vice versa - if in the graph H there is an edge from the vertex A to the top B, then in the graph G there must be an edge from the vertex f − 1 (A) to the top f − 1 (B). In the case of a directed graph, this bijection must also preserve the orientation of the edge. In the case of a weighted graph, the bijection must also preserve the weight of the edge.
Graph adjacency matrix G with a finite number of vertices n(numbered from 1 to n) is a square matrix A size n, in which the element value a ij equal to the number of edges from i th vertex of the graph in j-th peak.
Sometimes, especially in the case of an undirected graph, a loop (an edge from i th vertex into itself) is counted as two edges, that is, the value of the diagonal element a ii in this case equal to twice the number of loops around i th peak.
The adjacency matrix of a simple graph (containing no loops or multiple edges) is a binary matrix and contains zeros on the main diagonal.
Question32 Function. Methods of assignment. Classification of functions. Basic elementary functions and their graphs. Composition of functions. Elementary functions.
Function is a mathematical concept that reflects the relationship between elements of sets. We can say that a function is a “law” according to which each element of one set (called domain of definition ) is put into correspondence with some element of another set (called range of values ).
The mathematical concept of a function expresses the intuitive idea of how one quantity completely determines the value of another quantity. So the value of the variable x uniquely defines the meaning of an expression x 2, and the value of the month uniquely determines the value of the month following it, also any person can be compared with another person - his father. Similarly, some pre-conceived algorithm produces certain output data based on varying input data.
Methods for specifying a function
Analytical method
A function is a mathematical object that is a binary relation that satisfies certain conditions. A function can be specified directly as a set of ordered pairs, for example: there is a function . However, this method is completely unsuitable for functions on infinite sets (which are the usual real functions: power, linear, exponential, logarithmic, etc.).
To specify a function, use the expression: . Wherein, x is a variable that runs through the domain of definition of the function, and y- range of values. This entry indicates the presence of a functional relationship between the elements of sets. X And y can run through any sets of objects of any nature. These can be numbers, vectors, matrices, apples, colors of the rainbow. Let's explain with an example:
Let there be a set apple, plane, pear, chair and many man, locomotive, square. Let's define the function f as follows: (apple, person), (plane, locomotive), (pear, square), (chair, person). If we introduce a variable x running through the set and a variable y running through the set, the specified function can be specified analytically as: .
Numerical functions can be specified similarly. For example: where x runs through the set of real numbers and defines some function f. It is important to understand that the expression itself is not a function. A function as an object is a set of (ordered pairs). And this expression as an object is the equality of two variables. It defines a function, but is not one.
However, in many branches of mathematics, it is possible to denote by f(x) both the function itself and the analytical expression that defines it. This syntactic convention is extremely convenient and justified.
Graphic method
Numerical functions can also be specified using a graph. Let be a real function of n variables.
Let's consider some (n+1)-dimensional linear space over the field of real numbers (since the function is real). Let us choose any basis () in this space. Each point of the function is associated with a vector: . Thus, we will have a set of linear space vectors corresponding to the points of a given function according to the specified rule. The points of the corresponding affine space will form a certain surface.
If we take the Euclidean space of free geometric vectors (directed segments) as a linear space, and the number of arguments of the function f does not exceed 2, the specified set of points can be visually depicted in the form of a drawing (graph). If, in addition, the original basis is taken to be orthonormal, we obtain the “school” definition of the graph of a function.
For functions of 3 arguments or more, this representation is not applicable due to a person’s lack of geometric intuition of multidimensional spaces.
However, for such functions one can come up with a visual semi-geometric representation (for example, each value of the fourth coordinate of a point can be associated with a certain color on the graph)
Proportional quantities. If the variables y And x are directly proportional
y = k x ,

Where k- constant value ( proportionality factor).
Schedule direct proportionality– a straight line passing through the origin of coordinates and forming a line with the axis X angle whose tangent is equal to k: tan = k(Fig. 8). Therefore, the proportionality coefficient is also called slope. Figure 8 shows three graphs for k = 1/3, k= 1 and k = 3 .
Linear function. If the variables y And x are related by the 1st degree equation:
A x + B y = C ,
where at least one of the numbers A or B is not equal to zero, then the graph of this functional dependence is straight line. If C= 0, then it passes through the origin, otherwise it does not. Graphs of linear functions for various combinations A,B,C are shown in Fig.9.

Inverse proportionality. If the variables y And x are inversely proportional, then the functional relationship between them is expressed by the equation:
y = k / x,
Where k- constant value.
 Inverse proportional graph – hyperbola(Fig. 10). This curve has two branches. Hyperbolas are obtained when a circular cone intersects with a plane (for conic sections, see the “Cone” section in the “Stereometry” chapter). As shown in Fig. 10, the product of the coordinates of the hyperbola points is a constant value, in our example equal to 1. In the general case, this value is equal to k, which follows from the hyperbola equation: xy = k.
Inverse proportional graph – hyperbola(Fig. 10). This curve has two branches. Hyperbolas are obtained when a circular cone intersects with a plane (for conic sections, see the “Cone” section in the “Stereometry” chapter). As shown in Fig. 10, the product of the coordinates of the hyperbola points is a constant value, in our example equal to 1. In the general case, this value is equal to k, which follows from the hyperbola equation: xy = k.
Main characteristics and properties of a hyperbola:
x 0, range: y 0 ;
The function is monotonic (decreasing) at x< 0and at x> 0, but not
monotonic overall due to the break point x = 0);
Unbounded function, discontinuous at a point x= 0, odd, non-periodic;
- The function has no zeros.
Quadratic function. This is the function: y = ax 2 + bx + c, Where a, b, c- permanent, a b=c= 0 and y = ax 2. Graph of this function square parabola - OY, which is called the axis of the parabola.Dot O the vertex of the parabola.

Quadratic function. This is the function: y = ax 2 + bx + c, Where a, b, c- permanent, a 0. In the simplest case we have: b=c= 0 and y = ax 2. Graph of this function square parabola - a curve passing through the origin of coordinates (Fig. 11). Every parabola has an axis of symmetry OY, which is called the axis of the parabola.Dot O the intersection of a parabola with its axis is called the vertex of the parabola.
Graph of a function y = ax 2 + bx + c- also a square parabola of the same type as y = ax 2, but its vertex lies not at the origin, but at a point with coordinates:

The shape and location of a square parabola in the coordinate system depends entirely on two parameters: the coefficient a at x 2 and discriminant D:D=b 2 – 4ac. These properties follow from the analysis of the roots of a quadratic equation (see the corresponding section in the chapter “Algebra”). All possible different cases for a square parabola are shown in Fig. 12.
 Main characteristics and properties of a square parabola:
Main characteristics and properties of a square parabola:
Function scope: < x+ (i.e. x R), and the area
values: … (Please answer this question yourself!);
The function as a whole is not monotonic, but to the right or left of the vertex
behaves as monotonous;
The function is unbounded, continuous everywhere, even when b = c = 0,
and non-periodic;
- at D< 0 не имеет нулей.
 Exponential function. Function y = a x, Where a- a positive constant number is called exponential function.Argument x accepts any valid values; functions are considered as values only positive numbers, since otherwise we have a multi-valued function. Yes, the function y = 81x has at x= 1/4 four different values: y = 3, y = 3, y = 3 i And y = 3 i(Check, please!). But we consider as the value of the function only y= 3. Graphs of the exponential function for a= 2 and a= 1/2 are presented in Fig. 17. They pass through the point (0, 1). At a= 1 we have a graph of a straight line parallel to the axis X, i.e. the function turns into a constant value equal to 1. When a> 1 the exponential function increases, and at 0< a < 1 – убывает. Основные характеристики и свойства показательной функции:
Exponential function. Function y = a x, Where a- a positive constant number is called exponential function.Argument x accepts any valid values; functions are considered as values only positive numbers, since otherwise we have a multi-valued function. Yes, the function y = 81x has at x= 1/4 four different values: y = 3, y = 3, y = 3 i And y = 3 i(Check, please!). But we consider as the value of the function only y= 3. Graphs of the exponential function for a= 2 and a= 1/2 are presented in Fig. 17. They pass through the point (0, 1). At a= 1 we have a graph of a straight line parallel to the axis X, i.e. the function turns into a constant value equal to 1. When a> 1 the exponential function increases, and at 0< a < 1 – убывает. Основные характеристики и свойства показательной функции:
Function scope: < x+ (i.e. x R);
range: y> 0 ;
The function is monotonic: it increases with a> 1 and decreases at 0< a < 1;
- The function has no zeros.
 Logarithmic function. Function y= log a x, Where a– a constant positive number not equal to 1 is called logarithmic. This function is the inverse of the exponential function; its graph (Fig. 18) can be obtained by rotating the graph of the exponential function around the bisector of the 1st coordinate angle.
Logarithmic function. Function y= log a x, Where a– a constant positive number not equal to 1 is called logarithmic. This function is the inverse of the exponential function; its graph (Fig. 18) can be obtained by rotating the graph of the exponential function around the bisector of the 1st coordinate angle.
Main characteristics and properties of the logarithmic function:
Function scope: x> 0, and range of values: < y+
(i.e. y R);
This is a monotonic function: it increases as a> 1 and decreases at 0< a < 1;
The function is unlimited, continuous everywhere, non-periodic;
The function has one zero: x = 1.
Trigonometric functions. When constructing trigonometric functions we use radian measure of angles. Then the function y= sin x is represented by a graph (Fig. 19). This curve is called sinusoid.

Graph of a function y=cos x presented in Fig. 20; this is also a sine wave resulting from moving the graph y= sin x along the axis X to the left by 2

From these graphs, the characteristics and properties of these functions are obvious:
Domain: < x+ range of values: 1 y +1;
These functions are periodic: their period is 2;
Limited functions (| y| , continuous everywhere, not monotonic, but
having so-called intervals of monotony, inside which they are
behave like monotonic functions (see graphs in Fig. 19 and Fig. 20);
Functions have an infinite number of zeros (for more details, see section
"Trigonometric Equations").
Function graphs y= tan x And y=cot x are shown in Fig. 21 and Fig. 22, respectively.

From the graphs it is clear that these functions are: periodic (their period ,
unlimited, generally not monotonic, but have intervals of monotonicity
(which ones?), discontinuous (what discontinuity points do these functions have?). Region
definitions and range of values of these functions:
Functions y= Arcin x(Fig.23) and y= Arccos x(Fig. 24) multi-valued, unlimited; their domain of definition and range of values, respectively: 1 x+1 and < y+ . Since these functions are multi-valued, do not
considered in elementary mathematics, their main values are considered as inverse trigonometric functions: y= arcsin x And y= arccos x; their graphs are highlighted in Fig. 23 and Fig. 24 with thick lines.
Functions y= arcsin x And y= arccos x have the following characteristics and properties:
Both functions have the same domain of definition: 1 x +1 ;
their range of values: /2 y/2 for y= arcsin x and 0 y For y= arccos x;
(y= arcsin x– increasing function; y= arccos x – decreasing);
Each function has one zero ( x= 0 for function y= arcsin x And
x= 1 for function y= arccos x).

Functions y= Arctan x(Fig.25) and y= Arccot x(Fig. 26) - multi-valued, unlimited functions; their domain of definition: x+ . Their main meanings y= arctan x And y= arccot x are considered as inverse trigonometric functions; their graphs are highlighted in Fig. 25 and Fig. 26 with bold branches.
Functions y= arctan x And y= arccot x have the following characteristics and properties:
Both functions have the same domain of definition: x + ;
their range of values: /2<y < /2 для y= arctan x and 0< y < для y= arccos x;
Functions are limited, non-periodic, continuous and monotonic
(y= arctan x– increasing function; y= arccot x – decreasing);
Function only y= arctan x has a single zero ( x= 0);
function y= arccot x has no zeros.
Composition of functions
If two maps are given and , where , then the “end-to-end map” from to , given by the formula , makes sense, which is called the composition of functions and and is denoted by .

Fig. 1.30. End-to-end display from to