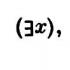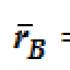Addition of translational and rotational movements. Screw movement

Forward movement,
- rotation around a fixed axis,
- flat movement,
- spherical movement,
- free movement.

Translational motion of a rigid body - this is a movement in which any straight line associated with the body, during its movement, remains parallel to its initial position.

Examples of translational motion: the movement of bicycle pedals relative to its frame, the movement of pistons in the cylinders of an internal combustion engine relative to the cylinders, the movement of Ferris wheel cabins relative to the Earth, etc.

The problem of the kinematics of the translational motion of a rigid body is reduced to the problem of the kinematics of a material point.

Theorem . During translational motion, all points of the body describe identical (coinciding when superimposed) trajectories and at each moment of time have the same velocity and acceleration in magnitude and direction.

Proof.

If you select two points of a rigid body A And IN, then the radius vectors of these points are related by the relation

Point trajectory A is a curve that is specified by the function, and the trajectory of the point B is a curve that is specified by the function. The trajectory of point B is obtained by transferring the trajectory of point A in space along the vector AB, which does not change its magnitude and direction over time (AB = const). Consequently, the trajectories of all points of the rigid body are the same.

Let us differentiate the expression with respect to time

We get

Let us differentiate the speed with respect to time and obtain the expression a B = a A . Consequently, the velocities and accelerations of all points of a rigid body are the same.

To specify the translational motion of a rigid body, it is enough to specify the movement of one of its points

Rotational movement- type of mechanical movement. When a material point rotates, it describes a circle. During the rotational motion of an absolutely rigid body, all its points describe circles located in parallel planes. The centers of all circles lie on the same straight line, perpendicular to the planes of the circles and called the axis of rotation. The axis of rotation can be located inside the body or outside it. The axis of rotation in a given reference system can be either movable or stationary. For example, in the reference frame associated with the Earth, the axis of rotation of the generator rotor at a power plant is stationary.

By choosing certain axes of rotation, you can get complex rotational motion - spherical motion, when the points of the body move along the spheres. When rotating around a fixed axis that does not pass through the center of the body or a rotating material point, the rotational motion is called circular.

Rotation is characterized by angle, measured in degrees or radians, angular velocity (measured in rad/s) and angular acceleration (unit rad/s²).

6. Relationship between angular and linear parameter

To change the radius vector drawn to point A from an arbitrary point O on the axis of rotation of the body, we have . Let us divide both sides of this expression by, taking into account the fact that and , - Euler's formula.

Speed ​​module. Let's find the total acceleration of point A from Euler's formula, using the rule for differentiating the product of two functions or .

Let us determine which term represents normal and which tangential acceleration:

- second term, - first term;

or, reasoning differently: since the axis of rotation is motionless, then - this is ; - .

These projections equal ; ,

A full acceleration module - .

The total acceleration vectors of points of a rigid body lying on the same radius drawn perpendicular to the axis of rotation are parallel to each other, and their modulus increases in proportion to the distance from the axis. The angle characterizes the direction relative to the radius and is equal to

, it does not depend on .

So, linear and angular parameters are related in the following way :

You can carry out the following analogy between translational and rotational types of motion: so, with: , ; at : , .

7. Dynamics. Mass and momentum of a body. Basic laws of dynamics.

Dynamics – this is a branch of mechanics that studies the movement of bodies under the influence of forces applied to them. When studying quantities that are characterized not only by magnitude, but also by direction (for example, speed, acceleration, force, etc.), their vector image is used.

Weight

Weight- a physical quantity that is a measure of the inertia of bodies ( inert mass) and their gravitational properties ( gravitational mass)

Inertia - the compliance of a body to changes in its speed (in magnitude or direction).

Units masses in SI:

Properties of mass:
- additivity: - the mass of the system is equal to the sum of the masses of its individual elements;
- independence from speed;
- constancy of mass for an isolated system of bodies and independence from the processes occurring in them: - law of conservation of mass.

Body impulse

- momentum(according to Newton) ; pulse(modern name).

Classical dynamics in mechanics (the main branch of mechanics) is based on Newton's three laws.

Newton's first law: every material point (body) maintains a state of rest or uniform rectilinear motion until impact from other bodies will not force her to change this state.

The desire of a body to maintain a state of rest or uniform rectilinear motion is called inertia. Therefore, Newton's first law is also called law of inertia.

Mechanical motion is relative, and its nature depends on the frame of reference. Newton's first law is not satisfied in every frame of reference, and those systems in relation to which it is satisfied are called inertial reference systems.

An inertial reference system is a reference system relative to which the material point, free from external influences, either at rest or moving uniformly and in a straight line. Newton's first law states the existence of inertial frames of reference.

It is known from experience that under the same influences, different bodies change the speed of their movement differently, i.e., in other words, they acquire different accelerations. Acceleration depends not only on the magnitude of the impact, but also on the properties of the body itself (its mass).

To describe the influences mentioned in Newton's first law, the concept of force is introduced. Under the influence of forces

bodies either change the speed of movement, i.e., acquire acceleration (dynamic manifestation of forces), or become deformed, i.e., change their shape and size (static manifestation of forces).

At each moment of time, the force is characterized by a numerical value, direction in space and point

applications. So, force - this is a vector quantity, which is a measure of the mechanical impact on a body from other bodies or fields, as a result of which the body acquires acceleration or changes its shape and size.

Newton's second law- the basic law of the dynamics of translational motion - answers the question of how the mechanical motion of a material point (body) changes under the influence of forces applied to it.

If we consider the action of different forces on the same body, it turns out that the acceleration acquired by the body is always proportional to the resultant of the applied forces: .

When the same force acts on bodies with different masses, their acceleration

turn out to be different, namely

Considering that force and acceleration are vector quantities, we can write

The ratio expresses Newton's second law: acceleration acquired by a material point (body), proportional to the force causing it, coincides with it in direction and is inversely proportional to mass

material point (body).

In SI proportionality coefficient To - 1. Then or

Considering that the mass of a material point (body) in classical mechanics is a constant quantity, it can be included in the expression under the derivative sign:

This expression - a more general formulation of Newton's second law: the rate of change of momentum of a material point is equal to the force acting on it. The expression is also called equation of motion of a material point.

If several forces act on a body, then in the formulas under F their resultant is implied

(vector sum of forces).

The SI unit of force is newton (N): 1 N is a force that imparts acceleration 1 to a mass of 1 kg in the direction of the force: 1 N = 1 kg*. Newton's second law is valid only in inertial frames of reference.

The interaction between material points (bodies) is determined Newton's third law: every action of material points (bodies) on each other is in the nature of interaction; the forces with which material points act on each other are always equal in magnitude, oppositely directed and act along the straight line connecting these points: , where - force acting on the first material point from the second; - the force acting on the second material point from the first. These forces are applied to different material points (bodies), always act in pairs and are forces of the same nature.

Newton's third law, like the first two, is valid only in inertial frames of reference.

8. Classification of forces. It's all about strength.

Force is a vector quantity that characterizes the measure of influence on a material point at any point in time from other material objects.

Dimension strength:

,

Resultant of all forces, acting on the point under study, according to superposition principle

Where is the force with which the th body would act on a given point in the absence of other bodies .

Line of action force – a straight line along which the force vector is directed.

Two forces equal in magnitude and oppositely directed– if they, applied to the body, do not cause acceleration.

Types of interactions: gravitational, electromagnetic, strong, weak.

Two manifestations of strength:
- static (deformation of bodies),

Dynamic (change in movement speed).

Classification of forces

- Fundamental forces:
a) gravitational,
b) electric.

- Approximate forces:

a) gravity;

b) friction force;

c) elastic force (elastic force);

d) resistance force.

A) Gravity in the reference frame associated with the Earth,

Reaction force suspension or support is the force with which other bodies act on the body, limiting its movement.

Body weight- the force with which the body acts on a support or suspension.

If the suspension or support is at rest relative to the Earth (or moving without acceleration):

b) Friction force

1) external (occurs at the points of contact of bodies and prevents their relative movement);

Sliding friction (occurs when one body moves forward along the surface of another);

Rolling friction (occurs when one body rolls on the surface of another);

Static friction (occurs when trying to cause movement);

2) internal (occurs when parts of liquid or gas move)

Empirical law for all types of external friction forces:

Where is the normal pressure force pressing the contacting surfaces against each other, is the coefficient of sliding friction (rest, rolling), depending on the nature and condition of the surfaces (roughness, etc.).

V) Elastic force

Where is the radius vector characterizing the displacement of a material point from the equilibrium position, is the coefficient of proportionality. motion with a variable mass.

t rocket mass T, and her speed v, then after time dt T - dm, and the speed will become equal v+dv. dt

Where And -

The second term on the right side is called reactive force Fp. If And opposite v direction, then the rocket accelerates, and if it coincides with v, then it slows down. So we got equation of motion of a body of variable mass , which was first derived by I. B. Meshchersky (1859-1935):

Where - Reactive force, which arises as a result of the action of the attached (separated) mass on the body.

10. Motion of a body with variable mass. Tsiolkovsky's formula.

The movement of some bodies is accompanied by a change in their mass, for example, the mass of a rocket decreases due to the outflow of gases formed during the combustion of fuel, etc. This movement is called motion with variable mass.

Let us derive the equation of motion of a body of variable mass using the example of the motion of a rocket. If at the moment t rocket mass T, and her speed v, then after time dt its mass will decrease by dm and become equal T - dm, and the speed will become equal v+dv. Change in the momentum of the system over a period of time dt

Where And - the speed of gas flow relative to the rocket.

If external forces act on the system, then either

Assuming F = 0 and assuming that the speed of the emitted gases relative to the rocket is constant (the rocket moves in a straight line), we obtain , from which

Integration constant value WITH we determine from the initial conditions. If at the initial moment of time the speed of the rocket is zero, and its launch mass , That C= . Hence,

This relationship is called the Tsiolkovsky formula. It shows that: 1) the greater the final mass of the rocket, the greater the launch mass of the rocket should be; 2) the greater the speed of gas outflow, the greater the final mass can be for a given launch mass of the rocket.

11. Dynamics of rotational motion of a rigid body.

The basic Law.

the motion of a rigid body, like the motion of a point, can be complex.

Let the body make some movement relative to the coordinate system 0 x 1 y 1 z 1, which, in turn, moves relative to the fixed axes 0 xyz.Relative the movement of a body is its movement relative to the moving coordinate system 0 x 1 y 1 z 1 . To find out portable The movement of the body at each moment of time should be considered as rigidly attached to the moving frame of reference, and the movement that the body will make with the moving frame of reference relative to the fixed frame will be portable motion. The movement of a body relative to a fixed coordinate system is called absolute.

The main task of the kinematics of complex motion of a rigid body is to establish relationships between the kinematic characteristics of absolute, relative and translational motion. Complex motion of a rigid body can consist of translational and rotational motions or can be obtained by adding translational and rotational motions. In some kinematics problems, a given complex motion of a rigid body is decomposed into components of motion (analysis); in others, it is required to determine a complex movement as a result of the addition of simpler ones (synthesis). Both in the analysis and in the synthesis of movements we are talking about the decomposition and addition of movements considered at a given moment (instantaneous movements).

Addition of translational motions of a rigid body

Let a rigid body simultaneously participate in two instantaneously translational motions, one of which is translational with a speed v 1, the second - portable with speed v 2 (Figure 2.73). Let's select a point M bodies. Let's find the absolute speed of the point M

v a = v r + v e = v 1 + v 2 . (2.113)

Since both the relative and portable motion of a rigid body are instantly translational, the relative, portable and, therefore, according to formula (2.113), the absolute velocities of all points of the body will be equal to each other at each moment of time (equal in magnitude and parallel in direction) , i.e. the absolute motion of a body is also instantly translational.

Obviously, this conclusion is applicable to complex motion of a rigid body, consisting of three or more instantaneous translational movements, then in the general case

So, as a result of adding the instantaneous translational motions of a rigid body, the resulting motion is instantaneously translational.

Comment. Instantaneous translational motion of a rigid body differs from translational motion in that with translational motion at each moment of time the velocities and accelerations of all points of the body are equal, and with instantaneous translational motion at a given moment of time only the velocities of all points of the body are equal.

66, 67 Addition of rotations around parallel axes

Let us consider the case when the relative motion of the body is rotation

with angular velocity around an axis fixed on the crank (Fig. 1a), and portable - by rotating the crank around an axis parallel to , with angular velocity . Then the motion of the body will be plane-parallel with respect to the plane perpendicular to the axes.

Let us assume that the rotations are directed in one direction. Let us depict the cross section of the body with a plane perpendicular to the axes (Fig. 1 b). The traces of the axes in the section will be denoted by the letters and . Then and. In this case, the vectors are parallel to each other, perpendicular and directed in different directions. Then the point is the instantaneous center of velocities, and therefore, the axis parallel to the axes and is the instantaneous axis of rotation. To determine the angular velocity of the absolute rotation of a body around an axis and the position of the axis itself, i.e. points, we will use the property of the instantaneous velocity center

.

Substituting the values ​​and into these equalities, we finally obtain

So, when adding two rotations directed in the same direction around parallel axes, the resulting motion of the body will be instantaneous rotation with absolute speed around the instantaneous axis parallel to the data, the position of which is determined by proportions (2).

Over time, the instantaneous axis of rotation changes its position, describing a cylindrical surface.

Let us now consider the case when the rotations are directed in different directions (Fig. 2).

Let's assume that . Then, reasoning as in the previous case, for the angular velocity of the absolute motion of a body around an axis and the position of the axis itself, we obtain

Thus, when adding two rotations directed in different directions around parallel axes, the resulting motion of the body will be instantaneous rotation with absolute angular velocity around the instantaneous axis, the position of which is determined by proportions (4).

Note that in this case the point divides the distance between the parallel axes externally.

Let's consider a special case when rotations around parallel axes are directed in different directions, but in absolute value (Fig. 3).

Such a set of rotations is called a pair of rotations, and the vectors form a pair of angular velocities. In this case we get and , that is, = . Then the instantaneous center of velocities is at infinity and all points of the body at a given moment of time have the same velocities.

Consequently, the resulting motion of the body will be translational (or instantly translational) motion with a speed numerically equal to and directed perpendicular to the plane passing through the vectors and . Thus, a pair of rotations is equivalent to instantaneous translational motion with a speed equal to the moment of a pair of angular velocities of these rotations.

An example of a pair of angular velocities is the movement of a bicycle pedal relative to the bicycle frame (Fig. 4).

This movement is a combination of portable rotation with the crank around the axis and relative rotation of the pedal with respect to the crank around the axis. During the entire movement, the pedal remains parallel to its original position, i.e. makes forward movement.

Let's look at a few examples.

Example 1. A crank rotates around an axis clockwise with an angular velocity of , and a disk of radius rotates around an axis clockwise with the same angular velocity relative to the crank. Find the magnitude and direction of the absolute velocities of points and (Fig. 5).

Solution. Since the angular velocities of the portable and relative rotations are equal in magnitude and directed in the same direction, the instantaneous center of rotation of the disk lies in the middle between and , i.e. . The magnitude of the absolute angular velocity of rotation of the disk around a point is equal to . From here we find:

, ,

, .

Example 2. The crank rotates around an axis with angular velocity . A radius gear is loosely mounted on the crank pin and meshed with a stationary radius gear. Find the absolute angular velocity of the gear and its angular velocity relative to the crank (Fig. 6).

Solution. Since the gear is engaged with a stationary wheel, the absolute speed of the point of engagement of the gear with this wheel is zero, i.e. the point is the instantaneous center of rotation for the gear. From here or ,

Note that the direction of rotation of the gear coincides with the direction of rotation of the crank.

Then we find the absolute angular velocity of the gear from the equality

SCREW MOTION- motion of a rigid body, consisting of a rectilinear forward movement at a certain speed And rotational movement with a certain angular velocity around the axis aa 1, parallel to the direction of the postulate. speed (Fig. 1). A body performing a stationary V.D., i.e., V.D., with which the direction of the axis aa 1 remains unchanged, called screw; axis aa 1 called screw axis; distance traveled by any point of the body lying on the axis aa 1, during one revolution, called. step h screw, the value is the screw parameter. If the vector is directed in the direction from which the rotation of the body is seen to occur counterclockwise, then with vectors directed in one direction, the screw is called. right, and in different directions - left.

Speed ​​and acceleration of any point M body distant from the axis aa 1 at a distance r, are numerically equal

When the parameter R constant, propeller pitch is also constant. In this case, every point M body not lying on the axis aa 1, describes a helical line, the tangent to the cut at any point forms with the plane yz, perpendicular to the axis aa 1, angle Any complex motion of a rigid body is generally composed of a series of elementary or instantaneous V.D. The axis of the instantaneous V.D. is called. instantaneous screw axis. In contrast to the axis of a stationary vertical motion, the instantaneous helical axis continuously changes its position both in relation to the reference system in which the movement of the body is considered, and in relation to the body itself, thus forming 2 ruled (touching but straight line) ) surfaces, called respectively, fixed and mobile axoids (Fig. 2). Geom. In the general case, a picture of the movement of a body can be obtained by rolling with longitudinal sliding of a movable axoid over a stationary one, in this way carrying out a series of sequences. V. d., from which the movement of the body is composed.