What are the signs that triangles are equal? The first sign of equality of triangles

A geometric figure formed by three segments that connect three points that do not belong to the same straight line.

The sides of the triangle form three angles at the vertices of the triangle. To paraphrase, triangle is a polygon that has three angles .

Practical significance signs of equality of triangles boils down to the following: according to the wording triangles are equal, in the case when it is possible to superimpose them on each other so that they coincide; however, implementing triangle overlap can sometimes be difficult and sometimes impossible.

Tests for the equality of triangles make it possible to replace the overlap of triangles by finding and comparing individual fundamental components (sides and angles) and thus justify the equality of triangles.

3. All three sides:

They also highlight fourth sign, which is not as widely covered in the school mathematics course as the previous three. It is formulated as follows:

If two sides of the first triangle are respectively equal to two sides of the second triangle and the angle opposite the larger of these sides in the first triangle is equal to the angle opposite the corresponding side equal to it in the second triangle, then these triangles are equal.

Signs of equality of triangles

Triangles whose corresponding sides are equal are called congruent.

Theorem (the first sign of equality of triangles).
If two sides and the angle between them of one triangle are respectively equal to two sides and the angle between them of another triangle, then such triangles are congruent.

Theorem (second criterion for the equality of triangles).
If a side and two adjacent angles of one triangle are respectively equal to a side and two adjacent angles of another triangle, then such triangles are congruent.

Theorem (third criterion for the equality of triangles).
If three sides of one triangle are respectively equal to three sides of another triangle, then such triangles are congruent.

Signs of similarity of triangles

Triangles whose angles are equal and whose similar sides are proportional are called similar: , where is the similarity coefficient.

I sign of similarity of triangles. If two angles of one triangle are respectively equal to two angles of another, then these triangles are similar.

II sign of similarity of triangles. If three sides of one triangle are proportional to three sides of another triangle, then the triangles are similar.

III sign of similarity of triangles. If two sides of one triangle are proportional to two sides of another triangle, and the angles between these sides are equal, then the triangles are similar.

1) on two sides and the angle between them

Proof:

Let triangles ABC and A 1 B 1 C 1 have angle A equal to angle A 1, AB equal to A 1 B 1, AC equal to A 1 C 1. Let us prove that the triangles are congruent.

Let's impose triangle ABC (or symmetrical to it) onto triangle A 1 B 1 C 1 so that angle A is aligned with angle A 1 . Since AB=A 1 B 1, and AC=A 1 C 1, then B will coincide with B 1, and C will coincide with C 1. This means that triangle A 1 B 1 C 1 coincides with triangle ABC, and therefore is equal to triangle ABC.

The theorem is proven.

2) along the side and adjacent corners

Proof:

Let ABC and A 1 B 1 C 1 be two triangles in which AB is equal to A 1 B 1, angle A is equal to angle A 1, and angle B is equal to angle B 1. Let's prove that they are equal.

Let's impose triangle ABC (or symmetrical to it) onto triangle A 1 B 1 C 1 so that AB coincides with A 1 B 1. Since ∠BAC =∠B 1 A 1 C 1 and ∠ABC=∠A 1 B 1 C 1, then ray AC will coincide with A 1 C 1, and BC will coincide with B 1 C 1. It follows that vertex C coincides with C 1. This means that triangle A 1 B 1 C 1 coincides with triangle ABC, and therefore is equal to triangle ABC.

The theorem is proven.

3) on three sides

Proof :

Consider triangles ABC and A l B l C 1, in which AB = A 1 B 1, BC = B l C 1 CA = C 1 A 1. Let us prove that ΔАВС =ΔA 1 B 1 C 1.

Let's apply triangle ABC (or symmetrical to it) to the triangle A 1 B 1 C 1 so that vertex A is aligned with vertex A 1, vertex B is aligned with vertex B 1, and vertices C and C 1 are on opposite sides of straight line A 1 B 1. Let's consider 3 cases:

1) Ray C 1 C passes inside the angle A 1 C 1 B 1. Since, according to the conditions of the theorem, the sides AC and A 1 C 1, BC and B 1 C 1 are equal, then the triangles A 1 C 1 C and B 1 C 1 C are isosceles. By the theorem on the property of the angles of an isosceles triangle, ∠1 = ∠2, ∠3 = ∠4, therefore ∠ACB=∠A 1 C 1 B 1 .

2) Ray C 1 C coincides with one of the sides of this angle. A lies on CC 1. AC=A 1 C 1, BC=B 1 C 1, C 1 BC - isosceles, ∠ACB=∠A 1 C 1 B 1.

3) Ray C 1 C passes outside the angle A 1 C 1 B 1. AC=A 1 C 1, BC=B 1 C 1, which means ∠1 = ∠2, ∠1+∠3 = ∠2+∠4, ∠ACB=∠A 1 C 1 B 1.

So, AC=A 1 C 1, BC=B 1 C 1, ∠C=∠C 1. Therefore, triangles ABC and A 1 B 1 C 1 are equal in
the first criterion for the equality of triangles.

The theorem is proven.

2. Dividing a segment into n equal parts.

Draw a ray through A, lay out n equal segments on it. Draw a straight line through B and A n and parallel lines to it through points A 1 - A n -1. Let us mark their points of intersection with AB. We obtain n segments that are equal according to Thales’ theorem.

Thales's theorem. If several equal segments are laid out in succession on one of two lines and parallel lines are drawn through their ends that intersect the second line, then they will cut off equal segments on the second line.

Proof. AB=CD

1. Draw straight lines through points A and C parallel to the other side of the angle. We get two parallelograms AB 2 B 1 A 1 and CD 2 D 1 C 1. According to the property of a parallelogram: AB 2 = A 1 B 1 and CD 2 = C 1 D 1.

2. ΔABB 2 =ΔCDD 2 ABB 2 CDD 2 BAB 2 DCD 2 and are equal based on the second criterion for the equality of triangles:
AB = CD according to the theorem,
as corresponding ones, formed at the intersection of parallel BB 1 and DD 1 straight line BD.

3. Similarly, each of the angles turns out to be equal to the angle with the vertex at the point of intersection of the secants. AB 2 = CD 2 as corresponding elements in congruent triangles.

4. A 1 B 1 = AB 2 = CD 2 = C 1 D 1

Podgorny Maxim

Research paper material can be used for geometry clubs in 7th grade

Download:

Preview:

MBU DO of the city of Rostov-on-Don "Palace of creativity of children and youth"

Don Academy of Sciences for Young Researchers named after. Yu. A. Zhdanova

Mathematics

Topic: “Non-standard theorems on the equality of triangles”

Podgorny Maxim, 7th grade,

MBOU secondary school No. 3,

Supervisor:

Oleynikova Lyudmila Aleksandrovna,

mathematic teacher,

MBOU secondary school No. 3,

Salsk, Rostov region

Rostov-on-Don

2017

Introduction……………………………………………………….………………3

Main part

Signs of equality of triangles…………………………………………… 4

Non-standard signs of equality of triangles………………………….7

Conclusion……………………………………………………………………………… 10

References…………………………………………………………… 11

Application

Introduction.

Relevance:

The triangle is one of the main figures in planimetry. I heard a lot from high school students that when preparing for the Unified State Exam, they often have to prove the equality of triangles. And knowledge of the basic signs turns out to be insufficient. I wanted to know if it was possible to prove the equality of triangles using other parameters. In the geometry textbook, which students of our school study from (authors L.S. Atanasyan, V.F. Butuzov, etc. Geometry 7-9), only 3 signs of equality of triangles are considered. I looked through teaching kits from other authors. But even in them only three well-known theorems are proposed for study.

Hypothesis:

Is it possible to formulate, in addition to the three well-known ones, other criteria for the equality of triangles?

To make sure that the answer to this question concerns not only me, I conducted a sociological survey among students in grades 7-11 (see Appendix 1).

My assumptions were confirmed. Most students know only three signs that triangles are equal.

Thus, the goal of my research was to find new signs of equality of triangles.

Tasks:

ΘStudy the literature on the topic under study.

ΘSpecify the number of signs that triangles are equal.

ΘDemonstrate to your classmates and students of our school the existence of other signs of equality of triangles and the possibility of proving them.

Object of study:

Studying the signs of equality of triangles.

Subject of study. Triangle is one of the main figures in planimetry.

Research method:Theoretical (study, analysis and synthesis), system-search, practical (proof of theorems).

Historical reference

The triangle is one of the central figures of all geometry.

When solving problems, its wide variety of properties are used.

The properties of a triangle are widely used in practice: in architecture; when developing a building drawing, when planning future apartments; in industry, in the design of various parts, in the manufacture of building materials, in the construction of ships and aircraft; in navigation to plot the correct and most accurate route; in astrology and astronomy, the triangle is a very significant figure; Triangles make the structures of high-voltage power lines and railway bridges reliable.

In addition, there are many other areas where various properties of a triangle are used: when starting a game of billiards, you need to arrange the balls in the form of a triangle, for this they use a special device; the placement of pins in the game of Bowling is also in the form of an equilateral triangle; triangles are used to create beautiful parquet floors; device of Pascal's triangle: each number is equal to the sum of the two numbers located above it (circle the three numbers with a triangle). Everything is elementary, but how many miracles are hidden in it! The computer translated Pascal's triangle into the language of color.

The theme of the triangle can be continued indefinitely.

There are so many triangles in the world!

There are also figurative meanings of this figure: for example, the rule of the “golden triangle” is based on the psychology of the buyer - having found the product he needs, the buyer rushes to the checkout. The task of the sellers is to make him stay in the store longer by placing the goods the buyer needs at the vertices of an imaginary triangle, that is, to “anchor” the buyer. The larger the area of the triangle, the more successful the store layout can be called. In a grocery store, these anchor products are gastronomy, dairy products, and bread. The rear end wall of the sales area is the second most important place and it is there that it is most advisable to place anchor products - precisely in order to force the buyer to go through the entire perimeter of the store.

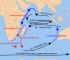
The well-known Bermuda Triangle is an area in the Atlantic Ocean where allegedly mysterious disappearances of ships and aircraft occur. The area is bounded by lines from Florida to Bermuda, on to Puerto Rico and back to Florida through the Bahamas.

Therefore, the study of a triangle and all its properties is a very relevant topic.

The purpose of this work is to talk about the signs of equality of triangles, which is one of their most important properties.

Tests for the equality of triangles are theorems on the basis of which it can be proven that sometriangles are equal.

In geometry, three signs of equality of triangles are used.

This topic has been practically studied, since today there are three criteria for the equality of triangles, which can be proven using the corresponding theorems.

In ancient times, along with astronomy, the science of trigonometry appeared. The word "trigonometry" is derived from the Greek "triangle" and "measure". The literal meaning is “the science of measuring triangles.”

Using stretched ropes 3, 4 and 5 units long, Egyptian priests obtained right angles when building temples, etc.

The art of depicting objects on a plane has attracted human attention since Ancient times; people painted various ornaments, plants, and animals on rocks, walls, vessels and other household items. People sought to ensure that the image correctly reflected the natural shape of the object.

The doctrine of the similarity of figures based on the theory of relationships and proportions was created in Ancient Greece in the 5th-4th centuries BC and still exists and develops today. For example, there are a lot of children's toys similar to items in the adult world, shoes and clothes of the same style are available in different sizes. These examples can be continued further. In the end, all people are similar to each other and, as the Bible states, God created them in his own image and likeness.

Tests for the equality of triangles have long been of great importance in geometry, since the proof of numerous theorems was reduced to proving the equality of certain triangles. The Pythagoreans were already engaged in proving the signs of equality of triangles. According to Proclus, Eudemus of Rhodes attributes to Thales of Miletus a proof of the equality of two triangles having equal sides and two angles adjacent to it (the second sign of the equality of triangles).

Thales used this theorem to determine the distance from the shore to sea ships.It is not known exactly what method Thales used to do this.

Signs of equality of triangles.

Let's start with a definition. Triangles ABC and A1B1C1 are called equal if they can be combined by overlapping.

A triangle consists of six elements: three angles and three sides.

This raises the question: “What is the smallest number of triangle elements needed to take to establish the equality of two triangles?”

We will not be able to establish the equality of two triangles based on one element, because it is unknown: “Will the remaining elements be equal?”

It is also impossible to establish the equality of two triangles using two elements due to the lack of information to establish equality.

It is possible to establish the equality of two triangles using three elements. But this raises the question: “What exactly three elements need to be named to establish the equality of the triangles?”

When studying this issue, I looked through school geometry textbooks of various authors, as well as dictionaries and reference books. In textbooks for the seventh grade, only three criteria for the equality of triangles are proposed for study.

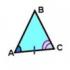
Θ1 Sign : If two sides and the angle between them of one triangle are respectively equal to two sides and the angle between them of another triangle, then such triangles are congruent. Fig.1

Proof. Consider triangles ABC and A 1 B 1 C 1 , (Fig. 1) for which AB = A 1 B 1, AC = A 1 C 1 ∠ A = ∠ A 1 . Let us prove that ΔABC = ΔA 1 B 1 C 1 .

Since ∠A = ∠A 1 , then triangle ABC can be superimposed on triangle A 1 B 1 C 1 so that vertex A coincides with vertex A 1 , and sides AB and AC will overlap rays A, respectively 1 B 1 and A 1 C 1 . Since AB = A 1 B 1, AC = A 1 C 1 , then side AB will align with side A 1 in 1 and side AC is with side A 1 C 1 ; in particular, points B and B will coincide 1, C and C 1 . Therefore, sides BC and B will coincide 1 C 1 . So, triangles ABC and A 1 B 1 C 1 are completely compatible, which means they are equal.

And here’s how the first sign of equality of triangles was used in Ancient Egypt (on two sides and the angle between them), Thales of Miletus is also considered its creator, to measure the height of the pyramid: imagine that we are standing in front of a huge pyramid, how can we measure its height? After all, you can’t attach measuring instruments to it! And here the first sign of equality of triangles comes to the aid of Thales of Miletus: he waited until his shadow exactly coincided with his height, applied the theorem, it turned out that the height of the pyramid is equal to its shadow (Fig. 2).

Rice. 2

Θ2 Sign: If a side and two adjacent angles of one triangle are respectively equal to a side and two adjacent angles of another triangle, then such triangles are congruent.

Proof: If in △ABC and △A 1 B 1 C 1 the following equalities AB=A will take place 1 B 1, ∠BAC=∠B 1 A 1 C 1, ∠АВС= ∠А 1 B 1 C 1 . Let's put triangles A on top of each other 1 B 1 C 1 and ABC so that equal sides AB and A coincide 1 in 1 and the corners that are adjacent to them. As in the previous example already discussed, if necessary, triangle A 1 B 1 C 1 You can “turn it over and put it on the other side.” The triangles will coincide, therefore, they can be considered equal.

Θ3 Sign : If three sides of one triangle are respectively equal to three sides of another triangle, then such triangles are congruent. Proof: Let for △ABC and △A 1 B 1 C 1 equalities A are valid 1 B 1 =AB, B 1 C 1 =BC, C 1 A 1 =SA. Let's move triangle A 1 B 1 C 1 so that side A 1 in 1 coincides with side AB, and vertex B 1 and B, A 1 and A will coincide. Take a circle with center A and radius AC, and a second circle with center B and radius BC. These circles will intersect at two points symmetrical with respect to the segment AB: point C and point C 2 . This means that C1, after moving the triangle A1B1C1, must coincide with either points C or C2. In any case, this will mean the equality △ABC=△A 1 B 1 C 1 , since triangles △ABC=△ABC 2 are equal (after all, these triangles are symmetrical with respect to the segment AB.

This property—the rigidity of a triangle—is widely used in practice. So, in order to secure the pole in a vertical position, a support is placed on it; the same principle is used when installing the bracket.

The property of triangle rigidity is widely used in practice in the construction of iron structures.

From the third criterion for the equality of triangles it follows that a triangle is a rigid figure. Because: we can imagine two slats, the two ends of which are fastened with a nail. This design is not rigid, however, by moving or spreading the free ends of the slats, we can change the angle between them. Now let's take another slats and fasten its ends with the free ends of the first two slats. The resulting structure - a triangle - will already be rigid. It is impossible to move or move apart any two sides, i.e., not a single corner can be changed. Indeed, if this were possible, then we would get a new triangle, not equal to the original one. But this is impossible, since the new triangle must be equal to the original one in the third

In the reference book on elementary mathematics by M. Ya. Vygodsky, I found another sign.

Θ4 Sign: If two sides and the angle opposite the larger of one triangle are respectively equal to two sides and the angle opposite the larger of another triangle, then such triangles are congruent.

I will prove this sign.

Given : ΔABC , ΔA1B1C1 , AB=A1B1,AC=A1C1,∠ B= ∠ B1

Prove: ΔABC=A1B1C1.

Let's arrange the triangles as in Figure 1. Let's connect B and B1, then ΔАВВ1

Isosceles means∠ 1= ∠ 2. ∠ 3= ∠ 4 as remainders of equal angles.

We get ΔВСВ1 - isosceles, hence ВС=В1С1. ΔАВС = ΔА1В1С1 on three sides.

Also in the school course, 4 signs of equality of right triangles are discussed:

Θ1 . If the legs of one right triangle are correspondingly equal to the legs of another, then such triangles are congruent.

Θ2 . If the leg and the adjacent acute angle of one right triangle are respectively equal to the leg and the adjacent acute angle of another, then such triangles are congruent.

Θ3 . If the hypotenuse and acute angle of one right triangle are respectively equal to the hypotenuse and acute angle of another, then such triangles are congruent.

Θ4 . If the hypotenuse and leg of one right triangle are respectively equal to the hypotenuse and leg of another, then such triangles are congruent.

I solved the theoretical basis for the criteria for the equality of triangles, adding other components to the sides and angles used in the classical tests for the equality of triangles: bisector, median and height.

Non-standard criteria for congruence of triangles.

1) On two sides and the height drawn to one of them.

Given: AB=A1B1 , BC=B1C1 , AK=A1K1 ,

Prove: ΔABC= ΔA1B1C1.

Proof: ΔABK=ΔA1B1K1 by hypotenuse and leg, then∠ B= ∠ B1 and get ΔABC= ΔA1B1C1 according to the first sign.

2) On two sides and a median drawn to one of them

Given: AB=A1B1, BC=B1C1, AK=A1K1, AK and A1K1 are medians.

Prove: ΔABC= ΔA1B1C1.

Proof:ΔABK=ΔA1B1K1 on three sides, which means∠ B= ∠ B1 and ΔABC= ΔA1B1C1 according to the first sign.

3) Along two sides and a height drawn from the third corner.

Given: ∠ B= ∠ B1 , ∠ C= ∠ C1 , AK=A1K1 .

Prove: ΔABC= ΔA1B1C1.

Proof: ΔABK=ΔA1B1K1 along the leg and acute angle, which means BK=B1K1,

ΔACK=ΔA1C1K1 by leg and acute angle, which means KC=K1C1, and therefore BC=B1C1, and ΔABC= ΔA1B1C1 by the second sign.

4) Along a side and two heights drawn from the angles adjacent to this side.

Given: AC=A1C1, SM=C1M1, AK=A1K1.

Prove: ΔСC= ΔA1B1C1.

Proof: ΔAMC= ΔA1М1C1 along the leg and hypotenuse, which means∠ A= ∠ A1, and ΔAКC= ΔA1К1C1 along the leg and hypotenuse, which means∠ C= ∠ C1.

So, ΔABC= ΔA1B1C1 according to the second criterion.

5) On two sides and the height drawn to the third side.

Given: AB=A1B1,BC=B1C1,BK=B1K1.

Prove: ΔABC= ΔA1B1C1.

Proof: ΔABK=ΔA1B1K1 on the hypotenuse and leg, which means AK=A1K1,

ΔBКC= ΔB1К1C1 along the leg and hypotenuse, which means KC=K1C1.

So, ΔABC= ΔA1B1C1 on three sides.

6) Along the side, one of the angles adjacent to this side and the bisector from this angle.

Given: AC=A1C1, AK=A1K1,∠ A ∠ A1.

Prove: ΔABC= ΔA1B1C1.

Proof: ΔКАС=ΔК1А1С1 according to the first sign, which means∠ C= ∠ C1,

ΔABC= ΔA1B1C1 according to the second characteristic.

7) By two heights and the angle from which one of the heights is drawn.

Given: SM=S1M1, AK=A1K1, ∠ A ∠ A1.

Prove: ΔABC= ΔA1B1C1.

Proof: ΔAMC= ΔA1М1C1 on the leg and acute angle, ΔКАС=ΔК1А1С1 on the leg and hypotenuse, ΔABC= ΔA1B1C1 on the second sign.

Conclusion.

During the research, I found out that in addition to the three main signs of equality of triangles, it is possible to indicate many others. I formulated and proved the equality of triangles based on the median, altitude, bisector of the triangle in combination with the sides and angles of the triangle, adhering to the presence of three elements. Now I can tell the students of our school that there are other signs that triangles are equal. This will allow school graduates to apply the results of my research in preparation for the Unified State Exam and the Unified State Exam and easily solve geometric problems using these features.

The result of my research: Several criteria for the equality of triangles that are not studied in the school geometry course have been proven.

Bibliography

Vygodsky M.Ya. Handbook of Elementary Mathematics.
Geometry. Grades 7-9: textbook. For general education institutions/L.S.Atanasyan, V.F.Butuzov, S.B. Kadomtsev et al. – 19th ed. – M.: Education, 2009.
Pogorelov A.V. Geometry: Textbook. For 7-9 grades. general education Institutions. – 3rd edition. – M.: Education, 2002.
. Encyclopedia "Avanta" in mathematics, Moscow, 2004.
2. Wikipedia is a free encyclopedia.
3. Glazer G.I. “History of mathematics at school”, Moscow, Prosveshchenie, 1982.
4. Guseva T.M. Signs of similarity of triangles. - Moscow, First of September, supplement “Mathematics”, 1999, No. 28
5. Pogorelov A.V. "Geometry grades 7-9"Moscow, Education, 2003

Annex 1

1. How many signs do you think that triangles are equal?

A) 3 B) more than three C) less than three

2. Would you like to learn new signs for congruence of triangles?

A) yes B) no

Two triangles are said to be congruent if they can be brought together by overlapping. Figure 1 shows equal triangles ABC and A 1 B 1 C 1. Each of these triangles can be superimposed on the other so that they are completely compatible, that is, their vertices and sides match in pairs. It is clear that the angles of these triangles will also match in pairs.

Thus, if two triangles are congruent, then the elements (i.e. sides and angles) of one triangle are respectively equal to the elements of the other triangle. Note that in equal triangles against correspondingly equal sides(i.e., overlapping when superimposed) equal angles lie and back: Equal sides lie opposite respectively equal angles.

So, for example, in equal triangles ABC and A 1 B 1 C 1, shown in Figure 1, opposite equal sides AB and A 1 B 1, respectively, lie equal angles C and C 1. We will denote the equality of triangles ABC and A 1 B 1 C 1 as follows: Δ ABC = Δ A 1 B 1 C 1. It turns out that the equality of two triangles can be established by comparing some of their elements.

Theorem 1. The first sign of equality of triangles. If two sides and the angle between them of one triangle are respectively equal to two sides and the angle between them of another triangle, then such triangles are congruent (Fig. 2).

Proof. Consider triangles ABC and A 1 B 1 C 1, in which AB = A 1 B 1, AC = A 1 C 1 ∠ A = ∠ A 1 (see Fig. 2). Let us prove that Δ ABC = Δ A 1 B 1 C 1 .

Since ∠ A = ∠ A 1, then triangle ABC can be superimposed on triangle A 1 B 1 C 1 so that vertex A is aligned with vertex A 1, and sides AB and AC are respectively superimposed on rays A 1 B 1 and A 1 C 1 . Since AB = A 1 B 1, AC = A 1 C 1, then side AB will align with side A 1 B 1 and side AC will align with side A 1 C 1; in particular, points B and B 1, C and C 1 will coincide. Consequently, sides BC and B 1 C 1 will coincide. So, triangles ABC and A 1 B 1 C 1 are completely compatible, which means they are equal.

Theorem 2 is proved in a similar way using the superposition method.

Theorem 2. The second sign of equality of triangles. If a side and two adjacent angles of one triangle are respectively equal to the side and two adjacent angles of another triangle, then such triangles are congruent (Fig. 34).

Comment. Based on Theorem 2, Theorem 3 is established.

Theorem 3. The sum of any two interior angles of a triangle is less than 180°.

Theorem 4 follows from the last theorem.

Theorem 4. An exterior angle of a triangle is greater than any interior angle not adjacent to it.

Theorem 5. The third sign of equality of triangles. If three sides of one triangle are respectively equal to three sides of another triangle, then such triangles are congruent ().

Example 1. In triangles ABC and DEF (Fig. 4)

∠ A = ∠ E, AB = 20 cm, AC = 18 cm, DE = 18 cm, EF = 20 cm. Compare triangles ABC and DEF. What angle in triangle DEF is equal to angle B?

Solution. These triangles are equal according to the first sign. Angle F of triangle DEF is equal to angle B of triangle ABC, since these angles lie opposite respectively equal sides DE and AC.

Example 2. Segments AB and CD (Fig. 5) intersect at point O, which is the middle of each of them. What is the length of segment BD if segment AC is 6 m?

Solution. Triangles AOC and BOD are equal (according to the first criterion): ∠ AOC = ∠ BOD (vertical), AO = OB, CO = OD (by condition).
From the equality of these triangles it follows that their sides are equal, i.e. AC = BD. But since according to the condition AC = 6 m, then BD = 6 m.