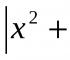Complex derivatives. Logarithmic derivative.
Derivative of the exponential function

We continue to improve our differentiation technique. In this lesson, we will consolidate the material covered, consider more complex derivatives, and also get acquainted with new techniques and tricks for finding the derivative, in particular, with the logarithmic derivative.

Those readers with a low level of training should refer to the article How do I find the derivative? Examples of solutions, which will allow you to raise your skills almost from scratch. Next, you need to carefully study the page Derivative of a complex function, understand and solve everything the examples I gave. This lesson is logically the third in a row, and after mastering it you will confidently differentiate enough complex functions... It is undesirable to adhere to the position “Where else? And that's enough! ", Since all examples and solutions are taken from real control works and are often found in practice.

Let's start with repetition. At the lesson Derivative of a complex function we have looked at a number of examples with detailed comments. In the course of studying differential calculus and other branches of mathematical analysis, you will have to differentiate very often, and it is not always convenient (and not always necessary) to write examples in great detail. Therefore, we will practice verbal finding of derivatives. The most suitable "candidates" for this are derivatives of the simplest of complex functions, for example:

According to the rule of differentiation of a complex function :

When studying other topics of matan in the future, such a detailed record is often not required, it is assumed that the student is able to find similar derivatives on the automatic autopilot. Imagine that at 3 am the phone rang, and a pleasant voice asked: "What is the derivative of the tangent of two Xs?" This should be followed by an almost instant and polite response: .

The first example will immediately target independent decision.

Example 1

Find the following derivatives orally, in one step, for example:. To complete the task, you need to use only table of derivatives of elementary functions(if it is not remembered yet). If you have any difficulties, I recommend rereading the lesson. Derivative of a complex function.

, , ,
, , ,
, , ,

, , ,

, , ,

, , ,

, ,

Answers at the end of the lesson

Complex derivatives

After preliminary artillery preparation, examples with 3-4-5 function attachments will be less scary. Perhaps the following two examples will seem difficult to some, but if you understand them (someone will suffer), then almost everything else in the differential calculus will seem like a child's joke.

Example 2

Find the derivative of a function

As already noted, when finding the derivative of a complex function, first of all, it is necessary right UNDERSTAND the attachments. In cases where there are doubts, I recall a useful technique: we take the experimental value of "X", for example, and try (mentally or on a draft) to substitute this value in the "terrible expression".

1) First, we need to calculate the expression, which means that the amount is the deepest investment.

2) Then you need to calculate the logarithm:

4) Then raise the cosine to a cube:

5) At the fifth step, the difference:

6) Finally, the outermost function is the square root:

Complex function differentiation formula are applied in reverse order, from the outermost function to the innermost. We decide:

It seems without mistakes….

(1) Take the derivative of the square root.

(2) We take the derivative of the difference using the rule

(3) The derivative of the triple is zero. In the second term, we take the derivative of the degree (cube).

(4) Take the derivative of the cosine.

(5) Take the derivative of the logarithm.

(6) Finally, we take the derivative of the deepest nesting.

It may seem too difficult, but this is not the most brutal example. Take, for example, the collection of Kuznetsov and you will appreciate all the charm and simplicity of the analyzed derivative. I noticed that they like to give a similar thing on the exam to check whether the student understands how to find the derivative of a complex function, or does not understand.

The next example is for a do-it-yourself solution.

Example 3

Find the derivative of a function

Hint: First, we apply the linearity rules and the product differentiation rule

Complete solution and answer at the end of the tutorial.

Now is the time to move on to something more compact and cute.
It is not uncommon for an example to give a product of not two, but three functions. How to find the derivative of the product of three factors?

Example 4

Find the derivative of a function

First, let's see if it is possible to turn the product of three functions into the product of two functions? For example, if we had two polynomials in the product, then we could expand the brackets. But in this example, all functions are different: degree, exponent and logarithm.

In such cases, it is necessary consistently apply product differentiation rule twice

The trick is that for "y" we denote the product of two functions:, and for "ve" - ​​the logarithm:. Why can this be done? Is it - this is not a product of two factors and the rule does not work ?! There is nothing complicated:

Now it remains to apply the rule a second time to the parenthesis:

You can still be perverted and put something outside the brackets, but in this case it is better to leave the answer in this form - it will be easier to check.

The considered example can be solved in the second way:

Both solutions are absolutely equivalent.

Example 5

Find the derivative of a function

This is an example for an independent solution, in the sample it is solved in the first way.

Let's look at similar examples with fractions.

Example 6

Find the derivative of a function

Here you can go in several ways:

Or like this:

But the solution will be written more compactly if first of all we use the rule for differentiating the quotient , taking for the entire numerator:

In principle, the example is solved, and if you leave it as it is, it will not be an error. But if you have time, it is always advisable to check on a draft, but is it possible to simplify the answer? Let us bring the expression of the numerator to common denominator and get rid of the three-story fraction:

The disadvantage of additional simplifications is that there is a risk of making a mistake not in finding the derivative, but in banal school transformations. On the other hand, teachers often reject the assignment and ask to "bring to mind" the derivative.

A simpler example for a do-it-yourself solution:

Example 7

Find the derivative of a function

We continue to master the methods of finding the derivative, and now we will consider a typical case when the "terrible" logarithm is proposed for differentiation

Example 8

Find the derivative of a function

Here you can go a long way, using the rule of differentiating a complex function:

But the very first step immediately plunges you into despondency - you have to take an unpleasant derivative from a fractional degree, and then also from a fraction.

therefore before how to take the derivative of the "fancy" logarithm, it is preliminarily simplified using the well-known school properties:

! If you have a practice notebook on hand, copy these formulas right there. If you don't have a notebook, redraw them on a piece of paper, as the rest of the lesson examples will revolve around these formulas.

The solution itself can be styled something like this:

Let's transform the function:

Find the derivative:

Preconfiguration of the function itself has greatly simplified the solution. Thus, when such a logarithm is proposed for differentiation, it is always advisable to "break up" it.

And now a couple of simple examples for an independent solution:

Example 9

Find the derivative of a function

Example 10

Find the derivative of a function

All transformations and answers at the end of the lesson.

Logarithmic derivative

If the derivative of logarithms is such sweet music, then the question arises, is it possible in some cases to organize the logarithm artificially? Can! And even necessary.

Example 11

Find the derivative of a function

We have seen similar examples recently. What to do? You can consistently apply the rule for differentiating the quotient, and then the rule for differentiating the work. The disadvantage of this method is that you get a huge three-story fraction, which you don't want to deal with at all.

But in theory and practice, there is such a wonderful thing as the logarithmic derivative. Logarithms can be organized artificially by "hanging" them on both sides:

Now you need to maximally "destroy" the logarithm of the right side (formulas in front of your eyes?). I will describe this process in great detail:

Actually, we proceed to differentiation.
We enclose both parts under the stroke:

The derivative of the right-hand side is quite simple, I will not comment on it, because if you are reading this text, you should confidently cope with it.

What about the left side?

On the left we have complex function... I foresee the question: "Why, there is also one letter" ygrek "under the logarithm?"

The fact is that this "one letter igrek" - ITSELF IS A FUNCTION(if not very clear, refer to the article Derived from an Implicit Function). Therefore, the logarithm is an external function, and the "game" is an internal function. And we use the rule of differentiating a complex function :

On the left side as if by a wave magic wand we have a derivative. Further, according to the rule of proportion, we throw the "game" from the denominator of the left side to the top of the right side:

And now we recall what kind of “game” -function we discussed in differentiation? We look at the condition:

Final answer:

Example 12

Find the derivative of a function

This is an example for a do-it-yourself solution. A sample of the design of an example of this type at the end of the lesson.

With the help of the logarithmic derivative it was possible to solve any of the examples №№ 4-7, another thing is that the functions there are simpler, and, perhaps, the use of the logarithmic derivative is not very justified.

Derivative of the exponential function

We have not considered this function yet. An exponential function is a function in which and the degree and base depend on "x". Classic example, which will be given to you in any textbook or lecture:

How to find the derivative of an exponential function?

It is necessary to use the technique just considered - the logarithmic derivative. We hang logarithms on both sides:

As a rule, the degree is taken out from under the logarithm on the right side:

As a result, on the right-hand side, we got a product of two functions, which will be differentiated according to the standard formula .

We find the derivative, for this we enclose both parts under the strokes:

Further actions are simple:

Finally:

If any transformation is not entirely clear, please carefully re-read the explanations of Example # 11.

In practical tasks, the exponential function will always be more complicated than the considered lecture example.

Example 13

Find the derivative of a function

We use the logarithmic derivative.

On the right side we have a constant and a product of two factors - "x" and "logarithm of the logarithm of x" (another logarithm is embedded under the logarithm). When differentiating the constant, as we remember, it is better to immediately take out the sign of the derivative so that it does not get in the way under your feet; and of course we apply the familiar rule :

As you can see, the algorithm for applying the logarithmic derivative does not contain any special tricks or tricks, and finding the derivative of the exponential function is usually not associated with "torment".

Calculating the derivative is one of the most important operations in differential calculus. Below is a table of finding derivatives of simple functions. For more complex rules of differentiation, see other lessons:

• Derivative table of exponential and logarithmic functions

Use these formulas as reference values. They will help in solving differential equations and problems. In the picture, in the table of derivatives of simple functions, there is a "cheat sheet" of the main cases of finding a derivative in a form that is understandable for use, along with explanations for each case are given.

Derivatives of simple functions

1. The derivative of a number is zero
s´ = 0
Example:
5´ = 0

Explanation:
The derivative shows the rate at which the value of the function changes when the argument changes. Since the number does not change in any way under any conditions, the rate of its change is always zero.

2. Variable derivative equal to one
x´ = 1

Explanation:
For each increment of the argument (x) by one, the value of the function (the result of calculations) is increased by the same amount. Thus, the rate of change of the value of the function y = x is exactly equal to the rate of change of the value of the argument.

3. The derivative of the variable and the factor is equal to this factor
sx´ = s
Example:
(3x) ´ = 3
(2x) ´ = 2
Explanation:
In this case, each time the argument of the function ( x) its value (y) increases in from time. Thus, the rate of change of the value of the function in relation to the rate of change of the argument is exactly equal to the value from.

Whence it follows that
(cx + b) "= c
that is, the differential linear function y = kx + b is equal to the slope of the straight line (k).

4. Modulus derivative of a variable is equal to the quotient of this variable to its modulus
| x | "= x / | x | provided that x ≠ 0
Explanation:
Since the derivative of the variable (see formula 2) is equal to one, the derivative of the modulus differs only in that the value of the rate of change of the function changes to the opposite when crossing the origin point (try to draw a graph of the function y = | x | and see for yourself. value and returns the expression x / | x |. When x< 0 оно равно (-1), а когда x >0 - one. That is, with negative values ​​of the variable x, with each increase in the change in the argument, the value of the function decreases by exactly the same value, and with positive values, on the contrary, it increases, but by exactly the same value.

5. Derivative of a variable in power is equal to the product of the number of this degree and the variable in the degree reduced by one
(x c) "= cx c-1, provided that x c and cx c-1 are defined and c ≠ 0
Example:
(x 2) "= 2x
(x 3) "= 3x 2
To memorize the formula:
Carry out the power of the variable "down" as a factor, and then decrease the power itself by one. For example, for x 2 - the two was in front of the x, and then the reduced degree (2-1 = 1) just gave us 2x. The same thing happened for x 3 - we "move down" the triple, decrease it by one and instead of a cube we have a square, that is, 3x 2. A bit "unscientific" but very easy to remember.

6.Derivative of a fraction 1 / x
(1 / x) "= - 1 / x 2
Example:
Since a fraction can be thought of as raising to a negative power
(1 / x) "= (x -1)", then you can apply the formula from rule 5 of the table of derivatives
(x -1) "= -1x -2 = - 1 / x 2

7. Derivative of a fraction with variable of arbitrary degree in the denominator
(1 / x c) "= - c / x c + 1
Example:
(1 / x 2) "= - 2 / x 3

8. Derivative of the root(the derivative of the variable under square root)
(√x) "= 1 / (2√x) or 1/2 x -1/2
Example:
(√x) "= (x 1/2)" means you can apply the formula from rule 5
(x 1/2) "= 1/2 x -1/2 = 1 / (2√x)

9. Derivative of a variable under an arbitrary root
(n √x) "= 1 / (n n √x n-1)

Determination of exponential function. Derivation of a formula for calculating its derivative. Examples of calculating the derivatives of exponential functions are discussed in detail.

Exponential function is a function in the form of a power function
y = u v,
where the base u and the exponent v are some functions of the variable x:
u = u (x); v = v (x).
This function is also called exponential or .

Note that the power-law exponential function can be presented in an indicative way:
.
Therefore, it is also called complex exponential function.

Calculation using the logarithmic derivative

Find the derivative of the exponential function
(2) ,
where are the functions of the variable.
To do this, we take the logarithm of equation (2) using the property of the logarithm:
.
We differentiate with respect to the variable x:
(3) .
We apply complex function differentiation rules and works:
;
.

Substitute in (3):
.
From here
.

So, we found the derivative of the exponential function:
(1) .
If exponents are constant, then. Then the derivative is equal to the derivative of a compound power function:
.
If the base degrees are constant, then. Then the derivative is equal to the derivative of a complex exponential function:
.
When and are functions of x, the derivative of the exponential function is equal to the sum of the derivatives of the complex exponential function and the exponential function.

Calculation of the derivative by reduction to a complex exponential function

Now we find the derivative of the exponential function
(2) ,
representing it as a complex exponential function:
(4) .

We differentiate the product:
.
We apply the rule for finding the derivative of a complex function:

.
And we got formula (1) again.

Example 1

Find the derivative of the following function:
.

Decision

Calculated using the logarithmic derivative. Let's take the logarithm of the original function:
(A1.1) .

From the table of derivatives we find:
;
.
By the formula for the derivative of the product, we have:
.
Differentiate (A1.1):
.
Insofar as
,
then
.

Answer

Example 2

Find the derivative of the function
.

Decision

Let's take the logarithm of the original function:
(A2.1) .

Proof and derivation of formulas for the derivative of the exponent (e to the power of x) and the exponential function (a to the power of x). Examples of calculating derivatives of e ^ 2x, e ^ 3x and e ^ nx. Higher order derivative formulas.

The derivative of the exponent is equal to the exponent itself (the derivative of e to the power of x is equal to e to the power of x):
(1) (e x) ′ = e x.

The derivative of an exponential function with a base of degree a is equal to the function itself multiplied by natural logarithm from a:
(2) .

Derivation of the formula for the derivative of the exponent, e to the power of x

An exponent is an exponential function in which the base of the power is equal to the number e, which is the following limit:
.
Here it can be either a natural or a real number. Next, we derive formula (1) for the derivative of the exponential.

Derivation of the derivative exponent formula

Consider the exponent, e to the x power:
y = e x.
This function is defined for everyone. Let us find its derivative with respect to the variable x. By definition, the derivative is the following limit:
(3) .

We transform this expression to reduce it to the well-known mathematical properties and rules. For this we need the following facts:
BUT) Exponent property:
(4) ;
B) Logarithm property:
(5) ;
IN) Continuity of the logarithm and the property of limits for a continuous function:
(6) .
Here is some function that has a limit and this limit is positive.
D) The meaning of the second remarkable limit:
(7) .

We apply these facts to our limit (3). We use property (4):
;
.

Let's make a substitution. Then; ...
Due to the continuity of the exponent,
.
Therefore, for,. As a result, we get:
.

Let's make a substitution. Then. When,. And we have:
.

Let's apply the property of the logarithm (5):
... Then
.

Let us apply property (6). Since there is a positive limit and the logarithm is continuous, then:
.
Here we also used the second remarkable limit (7). Then
.

Thus, we have obtained formula (1) for the derivative of the exponent.

Derivation of the formula for the derivative of the exponential function

Now we derive formula (2) for the derivative of the exponential function with a base of degree a. We believe that and. Then the exponential function
(8)
Defined for everyone.

Let us transform formula (8). To do this, we will use exponential properties and the logarithm.
;
.
So, we have transformed the formula (8) to the following form:
.

Higher-order derivatives of e to the power of x

Now we will find derivatives of higher orders. Let's look at the exponent first:
(14) .
(1) .

We see that the derivative of function (14) is equal to function (14) itself. Differentiating (1), we obtain derivatives of the second and third order:
;
.

Hence, it can be seen that the derivative of the nth order is also equal to the original function:
.

Higher-order derivatives of the exponential function

Now consider an exponential function with a radix of degree a:
.
We found its first-order derivative:
(15) .

Differentiating (15), we obtain derivatives of the second and third order:
;
.

We see that each differentiation leads to the multiplication of the original function by. Therefore, the nth order derivative has the following form:
.

With this video, I begin a long series of tutorials on derivatives. This tutorial is divided into several parts.

First of all, I will tell you what derivatives are in general and how to count them, but not in a sophisticated academic language, but as I understand it myself and how I explain it to my students. Second, we will consider the simplest rule for solving problems in which we will look for derivatives of a sum, derivatives of a difference, and derivatives of a power function.

We will look at more complex combined examples, from which you, in particular, will learn that similar problems containing roots and even fractions can be solved using the formula for the derivative of a power function. In addition, of course, there will be many tasks and examples of solutions of very different levels of complexity.

Actually, initially I was going to record a short 5-minute video, but you can see for yourself what came of it. So enough of the lyrics - let's get down to business.

What is a derivative?

So let's start from afar. Many years ago, when the trees were greener and life was more fun, mathematicians thought about this: consider a simple function given by our graph, let's call it $ y = f \ left (x \ right) $. Of course, the graph does not exist on its own, so you need to draw the $ x $ axes, as well as the $ y $ axis. Now let's choose any point on this graph, absolutely any. The abscissa will be called $ ((x) _ (1)) $, the ordinate, as you might guess, will be $ f \ left (((x) _ (1)) \ right) $.

Consider one more point on the same graph. It doesn't matter which one, the main thing is that it differs from the original one. It, again, has an abscissa, let's call it $ ((x) _ (2)) $, and also an ordinate - $ f \ left (((x) _ (2)) \ right) $.

So, we got two points: they have different abscissas and, therefore, different meanings functions, although the latter is optional. But what is really important is what we know from the planimetry course: through two points you can draw a straight line and, moreover, only one. So let’s conduct it.

And now let's draw a straight line through the very first of them, parallel to the abscissa axis. We get right triangle... Let's call it $ ABC $, right angle $ C $. This triangle has one very interesting property: the fact is that the angle $ \ alpha $ is, in fact, equal to the angle at which the line $ AB $ intersects with the continuation of the abscissa axis. Judge for yourself:

1. line $ AC $ is parallel to the $ Ox $ axis by construction,
2. line $ AB $ meets $ AC $ under $ \ alpha $,
3. therefore, $ AB $ intersects $ Ox $ under the same $ \ alpha $.

What can we say about $ \ text () \! \! \ Alpha \! \! \ Text () $? Nothing concrete, except that in triangle $ ABC $ the ratio of leg $ BC $ to leg $ AC $ is equal to the tangent of this very angle. So we write:

Of course, $ AC $ is easily considered in this case:

Likewise, $ BC $:

In other words, we can write the following:

\ [\ operatorname (tg) \ text () \! \! \ alpha \! \! \ text () = \ frac (f \ left (((x) _ (2)) \ right) -f \ left ( ((x) _ (1)) \ right)) (((x) _ (2)) - ((x) _ (1))) \]

Now that we've figured it all out, let's go back to our graph and look at the new $ B $ point. Erase the old values ​​and take and take $ B $ somewhere closer to $ ((x) _ (1)) $. Let us again denote its abscissa by $ ((x) _ (2)) $, and its ordinate by $ f \ left (((x) _ (2)) \ right) $.

Consider again our little triangle $ ABC $ and $ \ text () \! \! \ Alpha \! \! \ Text () $ inside it. It is quite obvious that this will be a completely different angle, the tangent will also be different because the lengths of the segments $ AC $ and $ BC $ have changed significantly, and the formula for the tangent of the angle has not changed at all - this is still the relationship between the change in the function and the change in the argument ...

Finally, we continue to move $ B $ closer and closer to the original point of $ A $, as a result, the triangle will decrease even more, and the line containing the segment $ AB $ will look more and more like a tangent to the graph of the function.

As a result, if you continue to approach the points, that is, reduce the distance to zero, then the straight line $ AB $ will indeed turn into a tangent to the graph at this point, and $ \ text () \! \! \ Alpha \! \ ! \ text () $ will transform from a regular triangle element to the angle between the tangent to the graph and the positive direction of the $ Ox $ axis.

And here we smoothly pass to the definition of $ f $, namely, the derivative of the function at the point $ ((x) _ (1)) $ is called the tangent of the angle $ \ alpha $ between the tangent to the graph at the point $ ((x) _ ( 1)) $ and the positive direction of the $ Ox $ axis:

\ [(f) "\ left (((x) _ (1)) \ right) = \ operatorname (tg) \ text () \! \! \ alpha \! \! \ text () \]

Returning to our chart, it should be noted that you can select any point on the chart as $ ((x) _ (1)) $. For example, we could just as well have removed a stroke at the point shown in the figure.

The angle between the tangent and the positive direction of the axis is called $ \ beta $. Accordingly, $ f $ in $ ((x) _ (2)) $ will be equal to the tangent of this angle $ \ beta $.

\ [(f) "\ left (((x) _ (2)) \ right) = tg \ text () \! \! \ beta \! \! \ text () \]

Each point of the graph will have its own tangent line, and, therefore, its own value of the function. In each of these cases, in addition to the point at which we are looking for the derivative of the difference or the sum, or the derivative of the power function, it is necessary to take another point located at some distance from it, and then direct this point to the initial one and, of course, find out how in the process such a movement will change the tangent of the inclination angle.

Derivative of a power function

Unfortunately, this definition does not suit us at all. All these formulas, pictures, angles do not give us the slightest idea of ​​how to calculate the real derivative in real problems. Therefore, let's digress a little from the formal definition and consider more effective formulas and techniques with which you can already solve real problems.

Let's start with the simplest constructions, namely, functions of the form $ y = ((x) ^ (n)) $, i.e. power functions. In this case, we can write the following: $ (y) "= n \ cdot ((x) ^ (n-1)) $. In other words, the degree that was in the exponent is shown in the multiplier in front, and the exponent itself is reduced by unit. For example:

\ [\ begin (align) & y = ((x) ^ (2)) \\ & (y) "= 2 \ cdot ((x) ^ (2-1)) = 2x \\\ end (align) \]

Here's another option:

\ [\ begin (align) & y = ((x) ^ (1)) \\ & (y) "= ((\ left (x \ right)) ^ (\ prime)) = 1 \ cdot ((x ) ^ (0)) = 1 \ cdot 1 = 1 \\ & ((\ left (x \ right)) ^ (\ prime)) = 1 \\\ end (align) \]

Using these simple rules, let's try to remove the stroke of the following examples:

So we get:

\ [((\ left (((x) ^ (6)) \ right)) ^ (\ prime)) = 6 \ cdot ((x) ^ (5)) = 6 ((x) ^ (5)) \]

Now let's solve the second expression:

\ [\ begin (align) & f \ left (x \ right) = ((x) ^ (100)) \\ & ((\ left (((x) ^ (100)) \ right)) ^ (\ prime)) = 100 \ cdot ((x) ^ (99)) = 100 ((x) ^ (99)) \\\ end (align) \]

Of course, they were very simple tasks... but real tasks more complex and they are not limited to just the powers of the function.

So, rule number 1 - if the function is presented in the form of the other two, then the derivative of this sum is equal to the sum of the derivatives:

\ [((\ left (f + g \ right)) ^ (\ prime)) = (f) "+ (g)" \]

Similarly, the derivative of the difference of two functions is equal to the difference of the derivatives:

\ [((\ left (f-g \ right)) ^ (\ prime)) = (f) "- (g)" \]

\ [((\ left (((x) ^ (2)) + x \ right)) ^ (\ prime)) = ((\ left (((x) ^ (2)) \ right)) ^ (\ prime)) + ((\ left (x \ right)) ^ (\ prime)) = 2x + 1 \]

In addition, there is one more important rule: if in front of some $ f $ there is a constant $ c $, by which this function is multiplied, then $ f $ of this whole construction is considered as follows:

\ [((\ left (c \ cdot f \ right)) ^ (\ prime)) = c \ cdot (f) "\]

\ [((\ left (3 ((x) ^ (3)) \ right)) ^ (\ prime)) = 3 ((\ left (((x) ^ (3)) \ right)) ^ (\ prime)) = 3 \ cdot 3 ((x) ^ (2)) = 9 ((x) ^ (2)) \]

Finally, one more very important rule: problems often have a separate term that does not contain $ x $ at all. For example, we can observe this in our expressions today. The derivative of a constant, that is, a number that does not depend in any way on $ x $, is always zero, and it does not matter at all what the constant $ c $ is:

\ [((\ left (c \ right)) ^ (\ prime)) = 0 \]

Solution example:

\ [((\ left (1001 \ right)) ^ (\ prime)) = ((\ left (\ frac (1) (1000) \ right)) ^ (\ prime)) = 0 \]

Once again the key points:

1. The derivative of the sum of two functions is always equal to the sum of the derivatives: $ ((\ left (f + g \ right)) ^ (\ prime)) = (f) "+ (g)" $;
2. For similar reasons, the derivative of the difference of two functions is equal to the difference of two derivatives: $ ((\ left (f-g \ right)) ^ (\ prime)) = (f) "- (g)" $;
3. If the function has a constant factor, then this constant can be moved outside the derivative sign: $ ((\ left (c \ cdot f \ right)) ^ (\ prime)) = c \ cdot (f) "$;
4. If the whole function is a constant, then its derivative is always zero: $ ((\ left (c \ right)) ^ (\ prime)) = 0 $.

Let's see how it all works with real-world examples. So:

We write down:

\ [\ begin (align) & ((\ left (((x) ^ (5)) - 3 ((x) ^ (2)) + 7 \ right)) ^ (\ prime)) = ((\ left (((x) ^ (5)) \ right)) ^ (\ prime)) - ((\ left (3 ((x) ^ (2)) \ right)) ^ (\ prime)) + (7) "= \\ & = 5 ((x) ^ (4)) - 3 ((\ left (((x) ^ (2)) \ right)) ^ (\ prime)) + 0 = 5 ((x) ^ (4)) - 6x \\\ end (align) \]

In this example, we see both the derivative of the sum and the derivative of the difference. Total, the derivative is $ 5 ((x) ^ (4)) - 6x $.

Moving on to the second function:

We write down the solution:

\ [\ begin (align) & ((\ left (3 ((x) ^ (2)) - 2x + 2 \ right)) ^ (\ prime)) = ((\ left (3 ((x) ^ ( 2)) \ right)) ^ (\ prime)) - ((\ left (2x \ right)) ^ (\ prime)) + (2) "= \\ & = 3 ((\ left (((x) ^ (2)) \ right)) ^ (\ prime)) - 2 (x) "+ 0 = 3 \ cdot 2x-2 \ cdot 1 = 6x-2 \\\ end (align) \]

So we found the answer.

Let's move on to the third function - it is already more serious:

\ [\ begin (align) & ((\ left (2 ((x) ^ (3)) - 3 ((x) ^ (2)) + \ frac (1) (2) x-5 \ right)) ^ (\ prime)) = ((\ left (2 ((x) ^ (3)) \ right)) ^ (\ prime)) - ((\ left (3 ((x) ^ (2)) \ right )) ^ (\ prime)) + ((\ left (\ frac (1) (2) x \ right)) ^ (\ prime)) - (5) "= \\ & = 2 ((\ left (( (x) ^ (3)) \ right)) ^ (\ prime)) - 3 ((\ left (((x) ^ (2)) \ right)) ^ (\ prime)) + \ frac (1) (2) \ cdot (x) "= 2 \ cdot 3 ((x) ^ (2)) - 3 \ cdot 2x + \ frac (1) (2) \ cdot 1 = 6 ((x) ^ (2)) -6x + \ frac (1) (2) \\\ end (align) \]

We found the answer.

Moving on to the last expression - the most complex and longest one:

So, we consider:

\ [\ begin (align) & ((\ left (6 ((x) ^ (7)) - 14 ((x) ^ (3)) + 4x + 5 \ right)) ^ (\ prime)) = ( (\ left (6 ((x) ^ (7)) \ right)) ^ (\ prime)) - ((\ left (14 ((x) ^ (3)) \ right)) ^ (\ prime)) + ((\ left (4x \ right)) ^ (\ prime)) + (5) "= \\ & = 6 \ cdot 7 \ cdot ((x) ^ (6)) - 14 \ cdot 3 ((x ) ^ (2)) + 4 \ cdot 1 + 0 = 42 ((x) ^ (6)) - 42 ((x) ^ (2)) + 4 \\\ end (align) \]

But the solution does not end there, because we are asked not just to remove the stroke, but to calculate its value at a specific point, so we substitute −1 instead of $ x $ in the expression:

\ [(y) "\ left (-1 \ right) = 42 \ cdot 1-42 \ cdot 1 + 4 = 4 \]

Go ahead and move on to even more complex and interesting examples. The fact is that the formula for solving the power derivative $ ((\ left (((x) ^ (n)) \ right)) ^ (\ prime)) = n \ cdot ((x) ^ (n-1)) $ has an even wider range of applications than is commonly believed. With its help, you can solve examples with fractions, roots, etc. This is what we are going to do now.

To begin with, let's write down the formula once again that will help us find the derivative of the power function:

Now attention: so far we have only considered $ n $ integers, however, we do not interfere with considering fractions and even negative numbers. For example, we can write the following:

\ [\ begin (align) & \ sqrt (x) = ((x) ^ (\ frac (1) (2))) \\ & ((\ left (\ sqrt (x) \ right)) ^ (\ prime)) = ((\ left (((x) ^ (\ frac (1) (2))) \ right)) ^ (\ prime)) = \ frac (1) (2) \ cdot ((x) ^ (- \ frac (1) (2))) = \ frac (1) (2) \ cdot \ frac (1) (\ sqrt (x)) = \ frac (1) (2 \ sqrt (x)) \\\ end (align) \]

Nothing complicated, so let's see how this formula will help us in solving more complex problems. So an example:

We write down the solution:

\ [\ begin (align) & \ left (\ sqrt (x) + \ sqrt (x) + \ sqrt (x) \ right) = ((\ left (\ sqrt (x) \ right)) ^ (\ prime )) + ((\ left (\ sqrt (x) \ right)) ^ (\ prime)) + ((\ left (\ sqrt (x) \ right)) ^ (\ prime)) \\ & ((\ left (\ sqrt (x) \ right)) ^ (\ prime)) = \ frac (1) (2 \ sqrt (x)) \\ & ((\ left (\ sqrt (x) \ right)) ^ ( \ prime)) = ((\ left (((x) ^ (\ frac (1) (3))) \ right)) ^ (\ prime)) = \ frac (1) (3) \ cdot ((x ) ^ (- \ frac (2) (3))) = \ frac (1) (3) \ cdot \ frac (1) (\ sqrt (((x) ^ (2)))) \\ & (( \ left (\ sqrt (x) \ right)) ^ (\ prime)) = ((\ left (((x) ^ (\ frac (1) (4))) \ right)) ^ (\ prime)) = \ frac (1) (4) ((x) ^ (- \ frac (3) (4))) = \ frac (1) (4) \ cdot \ frac (1) (\ sqrt (((x) ^ (3)))) \\\ end (align) \]

Go back to our example and write:

\ [(y) "= \ frac (1) (2 \ sqrt (x)) + \ frac (1) (3 \ sqrt (((x) ^ (2)))) + \ frac (1) (4 \ sqrt (((x) ^ (3)))) \]

Here's a tough decision.

Let's move on to the second example - there are only two terms, but each of them contains both a classical degree and roots.

Now we will learn how to find the derivative of a power function, which, in addition, contains a root:

\ [\ begin (align) & ((\ left (((x) ^ (3)) \ sqrt (((x) ^ (2))) + ((x) ^ (7)) \ sqrt (x) \ right)) ^ (\ prime)) = ((\ left (((x) ^ (3)) \ cdot \ sqrt (((x) ^ (2))) \ right)) ^ (\ prime)) = ((\ left (((x) ^ (3)) \ cdot ((x) ^ (\ frac (2) (3))) \ right)) ^ (\ prime)) = \\ & = (( \ left (((x) ^ (3+ \ frac (2) (3))) \ right)) ^ (\ prime)) = ((\ left (((x) ^ (\ frac (11) (3 ))) \ right)) ^ (\ prime)) = \ frac (11) (3) \ cdot ((x) ^ (\ frac (8) (3))) = \ frac (11) (3) \ cdot ((x) ^ (2 \ frac (2) (3))) = \ frac (11) (3) \ cdot ((x) ^ (2)) \ cdot \ sqrt (((x) ^ (2 ))) \\ & ((\ left (((x) ^ (7)) \ cdot \ sqrt (x) \ right)) ^ (\ prime)) = ((\ left (((x) ^ (7 )) \ cdot ((x) ^ (\ frac (1) (3))) \ right)) ^ (\ prime)) = ((\ left (((x) ^ (7 \ frac (1) (3 ))) \ right)) ^ (\ prime)) = 7 \ frac (1) (3) \ cdot ((x) ^ (6 \ frac (1) (3))) = \ frac (22) (3 ) \ cdot ((x) ^ (6)) \ cdot \ sqrt (x) \\\ end (align) \]

Both terms have been calculated, it remains to write down the final answer:

\ [(y) "= \ frac (11) (3) \ cdot ((x) ^ (2)) \ cdot \ sqrt (((x) ^ (2))) + \ frac (22) (3) \ cdot ((x) ^ (6)) \ cdot \ sqrt (x) \]

We found the answer.

Derivative of a fraction in terms of a power function

But even on this, the possibilities of the formula for solving the derivative of a power function do not end there. The fact is that with its help you can count not only examples with roots, but also with fractions. This is just that rare opportunity that greatly simplifies the solution of such examples, but at the same time it is often ignored not only by students, but also by teachers.

So, now we will try to combine two formulas at once. On the one hand, the classical derivative of the power function

\ [((\ left (((x) ^ (n)) \ right)) ^ (\ prime)) = n \ cdot ((x) ^ (n-1)) \]

On the other hand, we know that an expression of the form $ \ frac (1) (((x) ^ (n))) $ can be represented as $ ((x) ^ (- n)) $. Hence,

\ [\ left (\ frac (1) (((x) ^ (n))) \ right) "= ((\ left (((x) ^ (- n)) \ right)) ^ (\ prime) ) = - n \ cdot ((x) ^ (- n-1)) = - \ frac (n) (((x) ^ (n + 1))) \]

\ [((\ left (\ frac (1) (x) \ right)) ^ (\ prime)) = \ left (((x) ^ (- 1)) \ right) = - 1 \ cdot ((x ) ^ (- 2)) = - \ frac (1) (((x) ^ (2))) \]

Thus, derivatives of simple fractions, where the numerator is a constant, and the denominator is the degree, are also calculated using the classical formula. Let's see how this works in practice.

So the first function:

\ [((\ left (\ frac (1) (((x) ^ (2))) \ right)) ^ (\ prime)) = ((\ left (((x) ^ (- 2)) \ right)) ^ (\ prime)) = - 2 \ cdot ((x) ^ (- 3)) = - \ frac (2) (((x) ^ (3))) \]

The first example is solved, let's move on to the second:

\ [\ begin (align) & ((\ left (\ frac (7) (4 ((x) ^ (4))) - \ frac (2) (3 ((x) ^ (3))) + \ frac (5) (2) ((x) ^ (2)) + 2 ((x) ^ (3)) - 3 ((x) ^ (4)) \ right)) ^ (\ prime)) = \ \ & = ((\ left (\ frac (7) (4 ((x) ^ (4))) \ right)) ^ (\ prime)) - ((\ left (\ frac (2) (3 (( x) ^ (3))) \ right)) ^ (\ prime)) + ((\ left (2 ((x) ^ (3)) \ right)) ^ (\ prime)) - ((\ left ( 3 ((x) ^ (4)) \ right)) ^ (\ prime)) \\ & ((\ left (\ frac (7) (4 ((x) ^ (4))) \ right)) ^ (\ prime)) = \ frac (7) (4) ((\ left (\ frac (1) (((x) ^ (4))) \ right)) ^ (\ prime)) = \ frac (7 ) (4) \ cdot ((\ left (((x) ^ (- 4)) \ right)) ^ (\ prime)) = \ frac (7) (4) \ cdot \ left (-4 \ right) \ cdot ((x) ^ (- 5)) = \ frac (-7) (((x) ^ (5))) \\ & ((\ left (\ frac (2) (3 ((x) ^ (3))) \ right)) ^ (\ prime)) = \ frac (2) (3) \ cdot ((\ left (\ frac (1) (((x) ^ (3))) \ right) ) ^ (\ prime)) = \ frac (2) (3) \ cdot ((\ left (((x) ^ (- 3)) \ right)) ^ (\ prime)) = \ frac (2) ( 3) \ cdot \ left (-3 \ right) \ cdot ((x) ^ (- 4)) = \ frac (-2) (((x) ^ (4))) \\ & ((\ left ( \ frac (5) (2) ((x) ^ (2)) \ right)) ^ (\ prime)) = \ frac (5) (2) \ cdot 2x = 5x \\ & ((\ left (2 ((x) ^ (3)) \ right)) ^ (\ prime)) = 2 \ cdot 3 ((x) ^ (2)) = 6 ((x) ^ (2)) \\ & ((\ left (3 ((x) ^ (4)) \ right)) ^ (\ prime)) = 3 \ cdot 4 ((x) ^ (3)) = 12 ((x) ^ (3)) \\\ end (align) \] ...

Now we collect all these terms into a single formula:

\ [(y) "= - \ frac (7) (((x) ^ (5))) + \ frac (2) (((x) ^ (4))) + 5x + 6 ((x) ^ (2)) - 12 ((x) ^ (3)) \]

We got an answer.

However, before moving on, I would like to draw your attention to the form of writing the original expressions themselves: in the first expression we wrote $ f \ left (x \ right) = ... $, in the second: $ y = ... $ Many students are lost when they see different forms of recording. What is the difference between $ f \ left (x \ right) $ and $ y $? In fact, nothing. They are just different entries with the same meaning. Just when we say $ f \ left (x \ right) $, then it comes, first of all, about a function, and when it comes to $ y $, then most often the graph of a function is meant. Otherwise, it is one and the same, that is, the derivative in both cases is considered the same.

Complex problems with derivatives

In conclusion, I would like to consider a couple of complex combined tasks in which everything that we have considered today is used at once. Roots, fractions, and sums await us in them. However, these examples will be difficult only within the framework of today's video tutorial, because the truly complex functions of derivatives will be waiting for you ahead.

So, the final part of today's video tutorial, consisting of two combined tasks. Let's start with the first one:

\ [\ begin (align) & ((\ left (((x) ^ (3)) - \ frac (1) (((x) ^ (3))) + \ sqrt (x) \ right)) ^ (\ prime)) = ((\ left (((x) ^ (3)) \ right)) ^ (\ prime)) - ((\ left (\ frac (1) (((x) ^ (3) )) \ right)) ^ (\ prime)) + \ left (\ sqrt (x) \ right) \\ & ((\ left (((x) ^ (3)) \ right)) ^ (\ prime) ) = 3 ((x) ^ (2)) \\ & ((\ left (\ frac (1) (((x) ^ (3))) \ right)) ^ (\ prime)) = ((\ left (((x) ^ (- 3)) \ right)) ^ (\ prime)) = - 3 \ cdot ((x) ^ (- 4)) = - \ frac (3) (((x) ^ (4))) \\ & ((\ left (\ sqrt (x) \ right)) ^ (\ prime)) = ((\ left (((x) ^ (\ frac (1) (3))) \ right)) ^ (\ prime)) = \ frac (1) (3) \ cdot \ frac (1) (((x) ^ (\ frac (2) (3)))) = \ frac (1) (3 \ sqrt (((x) ^ (2)))) \\\ end (align) \]

The derivative of the function is:

\ [(y) "= 3 ((x) ^ (2)) - \ frac (3) (((x) ^ (4))) + \ frac (1) (3 \ sqrt (((x) ^ (2)))) \]

The first example is solved. Let's consider the second task:

In the second example, we proceed in the same way:

\ [((\ left (- \ frac (2) (((x) ^ (4))) + \ sqrt (x) + \ frac (4) (x \ sqrt (((x) ^ (3)) )) \ right)) ^ (\ prime)) = ((\ left (- \ frac (2) (((x) ^ (4))) \ right)) ^ (\ prime)) + ((\ left (\ sqrt (x) \ right)) ^ (\ prime)) + ((\ left (\ frac (4) (x \ cdot \ sqrt (((x) ^ (3)))) \ right)) ^ (\ prime)) \]

Let's count each term separately:

\ [\ begin (align) & ((\ left (- \ frac (2) (((x) ^ (4))) \ right)) ^ (\ prime)) = - 2 \ cdot ((\ left ( ((x) ^ (- 4)) \ right)) ^ (\ prime)) = - 2 \ cdot \ left (-4 \ right) \ cdot ((x) ^ (- 5)) = \ frac (8 ) (((x) ^ (5))) \\ & ((\ left (\ sqrt (x) \ right)) ^ (\ prime)) = ((\ left (((x) ^ (\ frac ( 1) (4))) \ right)) ^ (\ prime)) = \ frac (1) (4) \ cdot ((x) ^ (- \ frac (3) (4))) = \ frac (1 ) (4 \ cdot ((x) ^ (\ frac (3) (4)))) = \ frac (1) (4 \ sqrt (((x) ^ (3)))) \\ & ((\ left (\ frac (4) (x \ cdot \ sqrt (((x) ^ (3)))) \ right)) ^ (\ prime)) = ((\ left (\ frac (4) (x \ cdot ((x) ^ (\ frac (3) (4)))) \ right)) ^ (\ prime)) = ((\ left (\ frac (4) (((x) ^ (1 \ frac (3 ) (4)))) \ right)) ^ (\ prime)) = 4 \ cdot ((\ left (((x) ^ (- 1 \ frac (3) (4))) \ right)) ^ ( \ prime)) = \\ & = 4 \ cdot \ left (-1 \ frac (3) (4) \ right) \ cdot ((x) ^ (- 2 \ frac (3) (4))) = 4 \ cdot \ left (- \ frac (7) (4) \ right) \ cdot \ frac (1) (((x) ^ (2 \ frac (3) (4)))) = \ frac (-7) (((x) ^ (2)) \ cdot ((x) ^ (\ frac (3) (4)))) = - \ frac (7) (((x) ^ (2)) \ cdot \ sqrt (((x) ^ (3)))) \\\ end (align) \]

All terms have been calculated. Now we return to the original formula and add all three terms together. We get that the final answer will be like this:

\ [(y) "= \ frac (8) (((x) ^ (5))) + \ frac (1) (4 \ sqrt (((x) ^ (3)))) - \ frac (7 ) (((x) ^ (2)) \ cdot \ sqrt (((x) ^ (3)))) \]

And that is all. This was our first lesson. In the next lessons, we'll look at more complex constructs, as well as find out why derivatives are needed at all.