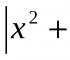وزن یک موقعیت در سیستم اعداد چقدر است. سیستم اعداد چیست؟ چه تعداد سیستم توسط متخصصان برای برقراری ارتباط با رایانه استفاده می شود

آشنایی با لیف

لیستیک مخترع دستگاهی برای انتقال اعداد اختراع کرد. دستگاه وی پیام ها را به صورت زنجیره ای از سیگنال های کوتاه و بلند منتقل می کرد. در یادداشت های خود ، لیستیک یک سیگنال کوتاه با شماره "0" و یک سیگنال بلند با شماره "1" تعیین کرد. هنگام انتقال اعداد ، از کد زیر برای هر رقم استفاده کرد:

شماره 12 ، متشکل از شماره های 1 و 2 ، Leaflet برای انتقال به شرح زیر نوشت:

دستگاه این پیام را در زنجیره ای از این نوع سیگنال ها منتقل می کند: سه کوتاه ، یکی بلند ، دو کوتاه ، یکی بلند و دیگری کوتاه.

شماره 77 طبق سیستم لیستیک به صورت زیر کدگذاری شده است:

کدگذاری اطلاعات

رمزگذاری ترجمه اطلاعات به شکلی است که برای انتقال یا ذخیره سازی مناسب است.

به عنوان مثال ، متن ها با استفاده از حروف و علائم نگارشی رمزگذاری می شوند. علاوه بر این ، یک رکورد مشابه را می توان به روش های مختلف رمزگذاری کرد: به روسی ، به انگلیسی ، به چینی ...

اعداد با استفاده از اعداد رمزگذاری می شوند. به اعدادی که عادت کرده ایم اعداد عربی گفته می شود. بعضی اوقات از اعداد رومی استفاده می شود. در این حالت ، روش رمزگذاری اطلاعات تغییر می کند. به عنوان مثال ، 12 و XII روش های مختلف نوشتن یک عدد است.

موسیقی را می توان با استفاده از نویسه های خاص - نت ها رمزگذاری کرد. علائم راهنمایی جاده با استفاده از پیکتوگرام پیام های رمزگذاری شده ای برای رانندگان و عابران پیاده است.

محصولات موجود در فروشگاه با بارکدی مشخص شده اند که حاوی اطلاعاتی در مورد محصول و سازنده آن است.

بارکد دنباله ای از نوارهای سیاه و سفید است که اطلاعات را به شکلی رمزگذاری می کند که توسط دستگاه های فنی به راحتی قابل خواندن است. علاوه بر این ، یک کد به شکل یک سری اعداد را می توان در زیر بارکد قرار داد.

اطلاعات همیشه به صورت رمز ذخیره و انتقال می یابند. بدون داشتن شرکت مخابراتی ، نمی توانید فقط اطلاعات را ذخیره کنید. به همین ترتیب ، ذخیره و انتقال فقط اطلاعات غیرممکن است: آنها همیشه شکلی دارند ، یعنی رمزگذاری می شوند.

رمزگذاری دودویی

کدگذاری دودویی رمزگذاری اطلاعات با استفاده از صفر و یک است. ثابت شده است که این روش ارائه اطلاعات برای فناوری های رایانه ای بسیار مناسب است.

نکته این است که کامپیوترها بر روی عناصری ساخته شده اند که می توانند در دو حالت ممکن باشند. یک حالت از این دست با عدد 0 و دیگری با شماره 1 تعیین می شود.

یک نمونه از دستگاه های باینری یک لامپ معمولی است. می تواند در یکی از دو حالت باشد: روشن (حالت 1) یا خاموش (حالت 0).

می توانید حافظه الکتریکی را روی لامپ ها بسازید و در آن ذخیره کنید ، به عنوان مثال اعداد را با استفاده از کد باینری Leaf.

برای ذخیره هر رقم اعشاری چهار لامپ مورد نیاز است. به این ترتیب می توانید عدد 6 را به خاطر بسپارید:

کلیدها را در موقعیت دلخواه تنظیم کنید - و بیایید برویم چای بخوریم! اگر برق خاموش نباشد ، اطلاعات صرفه جویی می شود.

لامپ ها ، البته ، برای تولید رایانه مناسب نیستند: آنها بزرگ هستند ، سریع می سوزند ، گران هستند (به هر حال ، میلیون ها عدد از آنها وجود دارد) و محیط را بسیار گرم می کنند.

در رایانه های مدرن ، از دستگاه الکترونیکی ، ترانزیستور ، به عنوان عنصر حافظه استفاده می شود.

ترانزیستور می تواند جریان را از خود عبور دهد (حالت 1) یا نه (حالت 0).

زمانی بود که هر ترانزیستور به طور جداگانه تولید می شد و از نظر اندازه قابل توجه بود.

اکنون ترانزیستورها ، مانند سایر عناصر الکترونیکی ، به روشی مشابه چاپ عکس ساخته می شوند. یکی میکرو مداربه اندازه ناخن ، می توان چندین میلیون ترانزیستور را "حک کرد".

کدی که لیستیک برای رمزگذاری پیام ها استفاده کرده است ، در واقع برای کار با اعداد در رایانه استفاده می شود.

با کدگذاری باینری ، شما مجبور نیستید به طور کلی به این جدول نگاه کنید ، اما قانون ساده ترجمه کد باینری به رقم اعشاری را بخاطر بسپارید.

یکی از کد در وهله اول سمت راست عدد را می دهد
lo 1 ، در دوم - 2 ، در سوم - 4 ، در چهارم - 8. برای به دست آوردن رقم اعشار ، اعداد اضافه می شوند. به عنوان مثال ، کد "0101" به رقم 5 (مجموع اعداد 4 و 1) ترجمه شده است.

همین قانون را می توان برای رمزگشایی نیز استفاده کرد. به عنوان مثال ، رقم 6 به عنوان مجموع اعداد 4 و 2 نوشته شده است ، به این معنی که کد آن "0110" خواهد بود.

لوحی با اعدادی که در سیستم اعداد نوشته شده است و در بابل باستان استفاده شده است. حدود سال 1700 قبل از میلاد رمزگشایی در سال 1945.

سیستم های عددی

کد برگ و کدگذاری اعداد

درس قبلی نحوه نوشتن اعداد را با استفاده از صفر و یک به شما نشان داد. جزوه کدگذاری می شود هر رقمشماره چهار دودوییعلائم

بنابراین ، شماره 102 توسط کد Leaf با استفاده از 12 کاراکتر باینری نوشته می شود:

جزوه کدگذاری می شود بصورت جداگانههر کدام از 10 رقم و از 4 رقم باینری برای این کار استفاده می کند. اما چهار کاراکتر باینری می توانند نه 10 ، بلکه 16 مقدار را رمزگذاری کنند:

به نظر می رسد که 6 کد Leaf (که بیش از نیمی از 10 کد است) هدر می رود!

آیا می توان از نظر اقتصادی کدگذاری بیشتری انجام داد؟

اگر رمزگذاری کنید می توانید نه اعداد(که تعداد آنها جمع می شود) ، و بلافاصله شماره! بنابراین ، شماره 102 ، با این روش رمزگذاری ، نه در دوازده ، بلکه فقط در هفت رقم باینری قابل نوشتن است (ما 5 رقم ذخیره می کنیم):

این برنامه نویسی در این آموزش قرار خواهد گرفت. اما بیایید به ترتیب شروع کنیم.

سیستم اعداد اعشاری

همانطور که می دانید ، اعداد از اعداد ساخته می شوند و فقط ده عدد وجود دارد ، در اینجا آنها وجود دارد:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

چگونه می توان اعداد بزرگ را فقط با ده رقم نوشت؟ اکنون این مورد را خواهیم دید ، اما ابتدا تعریف را بخاطر بسپارید:

به روش نوشتن اعداد گفته می شود سیستم شماره.

کلمه علمی حساب مرده، مطابق با کلمه "محاسبه" در حال حاضر به معنی "یک روش نوشتن اعداد" است. اما به نظر ریاضیدانان این عبارت رسیده است نشانه گذاریبهتر به نظر می رسد مهم نیست ، ما به این اصطلاح دو کلمه تسلط خواهیم یافت! حالا بیایید با آن کنار بیاییم سیستم شماره، که آنها به آن عادت کرده اند.

به عدد 253 نگاه کنید. در این ورودی ، اولین رقم در سمت راست (نامیده می شود) کمترین رقم قابل توجه) به معنای "سه یک" ، پنج به معنای "پنج ده" و دو ( بالاترین رقم) - "دویست".

به نظر می رسد: 253 = 2 · 100 + 5 · 10 + 3 · 1.

ما داریم صحبت می کنیم: "دویست و پنجاه و سه"... این به معنای عددی است که با اضافه کردن:

دویست (2 100 = دویست),

پنج ده (5 10 = پنجاه) و

سه واحد (3 1 = سه).

می بینیم که مقدار رقم در ضبط عدد بستگی دارد موقعیت هاکه رقم در آن قرار دارد. موقعیت های رقمی متفاوت نامیده می شوند تخلیهشماره.

کمترین رقم معنی دار واحدها:

رقم دوم از سمت راست به معنای ده ها است:

رقم سوم از سمت راست به معنای صدها است:

می بینیم که سهم رقم از تعداد به راست به چپ افزایش می یابد.

سیستم های اعدادی که سهم یک رقم در یک عدد به آنها بستگی دارد موقعیت هاشماره های ورودی فراخوانی می شوند سیستم های اعداد موقعیتی.

همانطور که دیدیم سیستم اعدادی که برای ما آشنا است ، موقعیتی است. توجه داشته باشید که در مبناقرار است عدد 10 باشد - تعداد ارقام استفاده شده.

کوچکترین رقم تعداد واحدهای تعداد را نشان می دهد ، دوم از سمت راست - تعداد ده ها (1 · 10). سوم صدها (10 10) ، چهارم هزاران (10 100) و غیره را نشان می دهد.

ما به عنوان واحد حساب می کنیم ، واحد به ده می رسد (ده واحد با یک ده جایگزین می شود) ، ده ها - به صدها (ده ده با صد جایگزین می شود) و غیره.

عدد 10 اساس سیستم اعداد معمول است ، بنابراین نامیده می شود سیستم اعشاری، یا توسط سیستم اعداد مبنا 10.

دوباره به نحوه ترجمه 2789 به یک عدد نگاه کنید.

عدد با جمع شدن بدست می آید سپرده هااعداد موجود در آن:

سهم هر رقم با ضرب آن رقم در یک ضرب وابسته به موقعیت مرتبط با ریشه سیستم بدست می آید.

ضرایب موقعیت با توجه به قانون زیر محاسبه می شوند:

1. ضرب موقعیت اول (راست) است 1 .

2. ضرب هر موقعیت بعدی با ضرب پایه سیستم (عدد) بدست می آید 10 ) توسط یک عامل از موقعیت قبلی.

ضرب موقعیت فراخوانی خواهد شد وزن موقعیت ها، یا وزنه های موقعیتی.

تعداد برابر است با مجموع سپرده ها. سهم برابر است با حاصلضرب شکل و وزن موقعیتی. وزن موقعیت اول 1 ، دومی 10 ، سوم 100 و غیره است. یعنی وزن هر موقعیت (به استثنای حالت اول) از وزن موقعیت قبلی با ضرب در پایه سیستم بدست می آید. وزن موقعیت اول برابر با یک است.

این چگونگی این است: آنها چند برابر شدند ، اضافه شدند و شک نکردند! به نظر می رسد که ما اعداد را در داخل می نویسیم علامت گذاری موقعیت ده پایه! چرا پایه سیستم ما برابر با 10 است؟ خوب ، این قابل درک است: بعد از همه ، ما 10 انگشت داریم ، شمارش با ترتیب خم شدن راحت است.

همانطور که قبلاً می دانید ، برای یک کامپیوتر سیستم باینری بیشتر آشنا است پایه موضعی دو.

سیستم شماره دودویی

فقط دو رقم در سیستم باینری وجود دارد:

اگر در سیستم اعشاری وزن موقعیت با ضرب در ده بدست می آید ، سپس در سیستم باینری - با ضرب در دو:

به نظر می رسد: 1011 2 = 1 2 · 4 + 0· 2 · 2 1+ 2 · 1 1+ 1 .

در سیستم باینری ، آنها به عنوان یک در نظر گرفته می شوند ، یک جمع می شود به دو (دو نفر با یک جایگزین می شوند) ، دو نفر به چهار (دو نفر با یک چهار جایگزین می شوند) و غیره

هنگامی که لازم است مشخص شود که در کدام سیستم یک عدد نوشته شده است ، پایه سیستم از زیر به آن نسبت داده می شود:

1011 2 - شماره در سیستم باینری نوشته شده است.

تبدیل آن به سیستم اعشاری دشوار نیست ، فقط باید عملیات ضرب و جمع را انجام دهید:

1011 2 = 1 2 · 4 + 0· 2 · 2 1+ 2 · 1 1+ 1 =

1 8 + 0 4 + 1 2 + 1 1 = 11 10.

تبدیل باینری به اعشاری

در سیستم باینری ، سهم یک در وهله اول از سمت راست عدد 1 است ، در دوم - 2 ، در سوم - 4 ، در چهارم - 8 ، و غیره. سهم صفر البته بدون در نظر گرفتن موقعیت آنها برابر با صفر است.

ما قانون زیر را دریافت می کنیم:

برای تبدیل از باینری به اعشاری ، باید وزن موقعیت آن را بالای هر رقم دودویی بنویسید و اعداد نوشته شده در بالای اعداد را اضافه کنید.

10111 2 = 16 + 4 + 2 + 1 = 23 10 .

مثال دیگر ، شماره 100110:

100110 2 = 32 + 4 + 2 = 38 10 .

تبدیل دهدهی به باینری

برای تبدیل از اعشاری به باینری ، از طرح قبلی با وزن موقعیت استفاده خواهیم کرد:

فرض کنید شما باید عدد 26 را به سیستم باینری ترجمه کنید ما با توجه به طرح ابتدای عدد باینری (شاخص ترین رقم) را انتخاب می کنیم. 32 بسیار است ، بنابراین ما با 16 شروع می کنیم:

بخشی از شماره اصلی ، یعنی 16 ، کدگذاری شده است ، کدگذاری 26 - 16 = 10 باقی مانده است. 8 را بگیرید (بزرگترین وزن موقعیتی ممکن):

برای کدگذاری 10 - 8 = 2 باقی مانده است. چهار بسیار است. ما در موقعیت 0 می نویسیم و 2 می گیریم:

ما کل شماره را رمزگذاری کرده ایم ، به این معنی که آخرین رقم باید صفر باشد:

به نظر می رسد: 26 10 = 11010 2.

قانون تبدیل از اعشاری به باینری را می توان به صورت زیر تنظیم کرد.

برای درک بهتر این الگوریتم ، روی نیمکت تستر کار کنید. روی دکمه کلیک کنید تنظیم مجدد، یک شماره بگیرید سپس دکمه را فشار دهید شروع کنید: خواهید دید که تستر چگونه گام به گام الگوریتم تبدیل باینری را انجام می دهد.

لطفا توجه داشته باشید: در رکورد الگوریتم ، موردی که اجرا می شود برجسته شده است. بعد ازفشار دادن دکمه شروع کنید... به عنوان مثال ، اگر مورد برجسته شده باشد "تکرار کنید تا عدد به صفر تبدیل شود"، سپس پس از کلیک بر روی شروع کنیدتست کننده عدد فعلی را برای صفر برابر بودن بررسی می کند و در مورد ادامه تکرار تصمیم می گیرد.

(کار با تستر را در صفحه برنامه الکترونیکی انجام دهید.)

سیستم های موقعیتی با پایه های دیگر

واسیا سیستم اعشاری را دوست دارد ، رایانه او باینری است و ریاضیدانان کنجکاو عاشق سیستم های مختلف اعداد موضعی هستند ، زیرا شما می توانید هر عددی را پایه قرار دهید ، نه فقط 2 یا 10.

بیایید یک سیستم اعداد سه گانه را به عنوان مثال در نظر بگیریم.

سیستم اعداد سه گانه

همانطور که حدس می زنید ، سیستم اعداد سه گانه از سه عدد استفاده می کند:

در سیستم سه تایی ، آنها به عنوان یک واحد در نظر گرفته می شوند ، یک به سه اضافه می شود (سه واحد با یک سه جایگزین می شود) ، سه - به نه (سه سه با یک نه جایگزین می شود) و غیره.

جالب اینجاست که در سال 1958 ، تحت رهبری N.P. Brusentsov ، کامپیوتر Setun در دانشگاه دولتی مسکو ایجاد شد و با اعداد نه در باینری بلکه در سیستم اعداد سه گانه کار می کرد! اولین نمونه اولیه "Setun" در عکس نشان داده شده است:

تبدیل از سه تایی به اعشاری

اجازه دهید در نمودار سهم موضعی ارقام در سیستم اعداد سه گانه نشان دهیم:

برای تبدیل به سیستم اعشاری ، اعداد ضرب شده بر وزن موقعیت آنها را اضافه کنید (البته موقعیت های با صفر رقم قابل حذف است):

10212 3 = 1 81 + 2 9 1+ 3 + 2 1 = 104 10 .

در سیستم باینری ، ما ضرب را از دست می دهیم (ضرب در 1 فایده ای ندارد). در سیستم سه تایی یک عدد 2 وجود دارد ، بنابراین شما باید وزنه های موقعیتی مربوطه را دو برابر کنید.

تبدیل ده تا سه

اجازه دهید عدد 196 به سیستم سه تایی ترجمه شود. ما طبق شماره ابتدای شماره سه را انتخاب می کنیم. 243 زیاد است ، بنابراین ما با 81 و عدد 2 (2 81) شروع می کنیم< 196):

بخشی از شماره اصلی ، یعنی 162 = 2 · 81 رمزگذاری شده است ، کدگذاری 196 - 162 = 34 باقی مانده است. 27 را بگیرید و عدد 1 (شماره 2 54 را می دهد ، که خیلی زیاد است):

کدگذاری 34 - 1 · 27 = 7 باقی مانده است. موقعیت با وزن 9 خیلی زیاد می دهد ، 0 را در آن بنویسید و با وزن 3 و شماره 2 موقعیت را بدست آورید:

کدگذاری 7 - 2 · 3 = 1 باقی مانده است. این دقیقاً مقدار رقم کم اهمیت است:

به نظر می رسد: 196 10 = 21021 3.

سیستم های موقعیتی: قوانین اساسی

بیایید قوانین کلی ساخت اعداد را در سیستم های اعداد موقعیتی تدوین کنیم.

شماره به صورت اعداد نوشته شده است ، به عنوان مثال:

برای تعیین مقدار یک عدد ، باید اعداد را در وزن موقعیت های آنها ضرب کنید و نتایج را اضافه کنید.

موقعیت ها از راست به چپ شماره گذاری می شوند. وزن موقعیت اول 1 است.

وزن هر موقعیت بعدی با ضرب در پایه سیستم از وزن موقعیت قبلی بدست می آید.

به نظر می رسد که وزن موقعیت دوم همیشه برابر با پایه سیستم است.

پایه سیستم تعداد ارقامی را که در سیستم داده شده استفاده می شود نشان می دهد. بنابراین ، در یک سیستم پایه 10 ، ده رقم وجود دارد ، در یک سیستم پایه 5 ، پنج رقم.

بیایید به یک مثال نگاه کنیم. اگر ورودی

به معنای یک عدد در سیستم پایه 5 است ، پس آن برابر است با

3242 5 = 3 125 + 2 25 + 4 5 + 2 1 = 447 10 .

همان ورودی در سیستم پایه 6 به معنای عدد است

3242 6 = 3 216 + 2 36 + 4 6 + 2 1 = 746 10 .

سیستم های عددی غیر موضعی

سیستم های اعداد موضعی بلافاصله ظاهر نشدند ، افراد بدوی تعداد برخی از اشیا را برابر با تعداد دیگر تعیین کردند (آنها را سنگریزه ، چوب ، استخوان می دانستند)

روش های راحت تر شمردن نیز مورد استفاده قرار گرفت: بریدگی های چوب ، خط تیره بر روی سنگ ، گره های روی طناب.

بعضی اوقات افراد مدرن نیز از چنین سیستم اعدادی استفاده می کنند ، به عنوان مثال ، تعداد روزهایی را که از ناخن ها گذشته اند ، ذکر می کنند.

این یک نمونه است سیستم شماره واحد غیر موقعیتی: برای شمارش استفاده می شود تنهاتعداد (سنگ ، چوب ، استخوان ، داش ، گره ...) ، و سهم این رقم به مکان (موقعیت) آن بستگی ندارد ، همیشه برابر با یک واحد است.

واضح است که استفاده از سیستم های تعداد موقعیت بسیار راحت تر است.

اقدامات روی اعداد

اقدامات مربوط به اعداد در سیستم موقعیتی با هر پایه به همان روشی که در سیستم اعشاری انجام می شود انجام می شود: آنها بر اساس جداول جمع و ضرب رقم سیستم های عددی مربوطه هستند.

عجیب خواهد بود اگر در سیستم های مختلف مجبور شوید به روش های مختلف جمع ، تفریق ، ضرب و تقسیم کنید! در واقع ، در همه سیستم های اعدادی ، اعداد به همان صورت ساخته می شوند ، به این معنی که اعمال روی آنها باید به همان روش انجام شود.

بیایید به چند نمونه نگاه کنیم.

اضافه کردن

5 + 7 = 12. در کمترین بیت 2 را می نویسیم و یکی را به بیت بعدی اضافه می کنیم.

بیایید یک جدول جمع هشت ضلعی بسازیم:

طبق جدول جمع 5 + 7 = 14 8. ما 4 را با حداقل رقم قابل توجه می نویسیم ، و یک را به رقم بعدی اضافه می کنیم.

منها کردن

ما در مقام دوم 1 را اشغال می کنیم و 7 را از عدد 15 کم می کنیم. به همین ترتیب در سیستم اکتال:

ما در رقم دوم 1 را اشغال می کنیم و 7 را از عدد 15 8 کم می کنیم. با توجه به جدول جمع در خط 7 ، شماره 15 را پیدا می کنیم. تعداد ستون مربوطه نتیجه اختلاف را می دهد - عدد 6.

این احتمالاً برای استفاده عنکبوت ها مناسب است
سیستم اکتال شماره!

ضرب

2 7 = 14. ما 4 را می نویسیم ، و 1 به "ذهن" می رود (به دسته بعدی اضافه می شود). 4 · 7 = 28. ما 9 (8 به علاوه 1 از "ذهن") را می نویسیم و 2 را به گروه بعدی منتقل می کنیم.

بیایید یک جدول ضرب هشت ضلعی بسازیم:

2 7 = 16 8. ما 6 را می نویسیم ، و 1 به "ذهن" می رود (به دسته بعدی اضافه می شود). 4 7 = 34 8. ما 5 (4 به علاوه 1 از "ذهن") می نویسیم و 3 را به رقم بعدی منتقل می کنیم.

لشکر

3 5< 17 < 4·5, поэтому первая цифра результата - 3. Из 17 вычитаем 5·3 = 15. К разности 2 приписываем цифру 5, получается 25. 25 = 5 ·5. Из 25 вычитаем 25=5·5, получается 0 - деление закончено.

در جدول ضرب در خط 5 عدد مناسب 17 8 = 5 3 را پیدا می کنیم:

این به این معنی است که رقم اول نتیجه 3 است. از 17 8 17 8 = 5 · 3 را کم می کنیم. به اختلاف 0 آخرین رقم 5 را اختصاص می دهیم. 5 = 5 · 1. 5 را از 5 کم کنید ، معلوم می شود 0 - تقسیم تمام شده است.

پرسش و پاسخ

1. به اصطلاح "سیستم اعداد" تعریفی بدهید.

2. به اصطلاح "سیستم اعداد موقعیتی" تعریفی بدهید.

3- اصول ساخت اعداد را در علامت اعشاری با استفاده از مثال عدد 548 توضیح دهید.

4- وزن یک موقعیت چیست؟ الگوریتم پیدا کردن وزن یک موقعیت را به ما بگویید. وزن موقعیت سوم از سمت راست در علامت اعشاری عدد چقدر است؟ و باینری؟ و در سه تایی؟

5. منظور از ترشح چیست؟ عدد 5 در عدد اعشاری 1532 کدام مکان است؟

6. سهم اعداد را چه می نامند؟ سهم تعداد 7 به 1745 10 چقدر است؟ و سهم عدد 4 به عدد 1432 5؟

7. به اصطلاح "پایه سیستم اعداد موضعی" تعریفی ارائه دهید. ارتباط پایه یک سیستم با تعداد ارقام موجود در این سیستم چگونه است؟ چند رقم در سیستم اعداد 5 گانه وجود دارد؟ و در هگزادسیمال؟ سیستم پایه 25 چطور؟

8- کمترین رقم قابل توجه در ثبت اعداد کجاست؟ و بزرگترین؟

9. الگوریتم تبدیل یک عدد باینری به سیستم اعداد اعشاری را به ما بگویید و این الگوریتم را برای شماره 101101 2 انجام دهید.

10. به الگوریتم تبدیل عدد اعشاری به سیستم اعداد باینری بگویید و این الگوریتم را برای شماره 50 10 انجام دهید.

11. چگونه می توان یک عدد را از هر سیستم اعداد موضعی به سیستم اعشاری تبدیل کرد؟ توضیحات بر اساس مثال سیستمی با پایه 4 است.

Hometasks

گزینه 1. بدون کامپیوتر ، "روی کاغذ" انجام می شود

1. پیچهای زبان را بخوانید ، اعداد باینری را با اعشار جایگزین کنید:

خوب غذا بخور
100001 2 پای با پای ،
بله ، همه با پنیر پنیر.

101000 2 موش وجود داشت ،
حمل شده 101000 2 grosz ،
موش های 10 2 کوچکتر هستند
آنها هر کدام 10 گروس داشتند.

2. معماهای باینری را حل کنید:

3. محاسبات را انجام دهید و پاسخ را با علامت اعشاری بنویسید:

1) 100 2 5 8 =

2) 100 3 + 100 5 =

3) 10 9 10 100 - 10 900 =

4) 33 4 + 44 5 =

5) 15 6 + 51 8 =

4- اعداد داده شده را به سیستم های اعدادی نشان داده شده ترجمه کنید:

گزینه 2. اجرا در رایانه

1. برای حل مسئله زیر عبارت حسابی را بنویسید و پاسخ را محاسبه کنید:

مالوینای باهوش ما
از بوراتینو مراقبت می کند
و من آن را برای او خریداری کردم
آنچه او بیش از همه به آن نیاز دارد:
10 2 جلد ، 11 2 حاکم
و برای 111 برچسب 2 روبل.
روی جلدها - Barmaley ،
قیمت هر یک 101 2 روبل است.
روی حاکمانی که من خریدم
101010 2 روبل کافی بود.
هزینه خریدها چقدر بود؟
در هنگام بازتاب - نیم دقیقه.

2. سعی کنید از برنامه استاندارد ماشین حساب برای تبدیل اعداد از یک شعر به علامت گذاری اعشاری معمول استفاده کنید ( چشم انداز- مهندسی، صندوقچه- نمایش دودویی یک عدد ، دسامبر- نمایش اعشاری عدد). از ماشین حساب برای نوشتن الگوریتم های تبدیل اعداد از دودویی به اعشاری و بالعکس ، از اعشاری به باینری استفاده کنید.

گزینه 3. برای کنجکاوها

1. ثابت کنید که نوشتن 10 در هر سیستم اعداد موضعی به معنای عددی برابر با پایه این سیستم است.

2. پایه سیستم اعداد موقعیتی را تعیین کنید ببرای هر برابری:

1) 10 ب = 50 10 ;

2) 11 ب = 6 10 ;

3) 100 ب = 64 10 ;

4) 101 ب = 26 10 ;

5) 50 ب = 30 10 ;

6) 99 ب = 909 10 ;

7) 21 ب = 15 6 ;

8) 10 2 ب = 100 ب ;

9) 12 2 ب = 22 ب ;

10) 14 ب· ب = 104 ب .

p ALIGN = "JUSTIFY"> 3. سیستم اعداد هگزادسیمال از 16 رقم استفاده می کند. ده رقم اول با ارقام سیستم اعشاری مطابقت دارد و آخرین آنها با حروف الفبای لاتین مشخص می شوند:

0 ، 1 ، 2 ، 3 ، 4 ، 5 ، 6 ، 7 ، 8 ، 9 ، A ، B ، C ، D ، E ، F

	مقدار

بیایید به عنوان مثال ، شماره A8 16 را به سیستم اعشاری ترجمه کنیم:

A8 16 = 10 16 8+ 1 = 168 10 .

در هر کار مقدار عدد را پیدا کنید ایکس:

1) 25 16 = ایکس 10 ; 4) 170 10 = ایکس 16 ;

2) AB 16 = ایکس 10 ; 5) 2569 10 = ایکس 16 ;

3) FD 16 = ایکس 10 ; 6) 80 32 = ایکس 16 .

4- کارهای زیر را انجام دهید.

1) اگر مشخص شود که وزن موقعیت دوم 7 است ، موقعیت موقعیت سوم را پیدا کنید. شماره گذاری موقعیت ها از راست به چپ.

2) سیستم اعداد از 5 رقم استفاده می کند. وزن موقعیت چهارم را از سمت راست در علامت گذاری عدد پیدا کنید.

3) عدد به صورت دو واحد نوشته می شود: 11- در کدام سیستم اعداد نوشته می شود اگر به دهده برابر 21 باشد؟

4) در یک سیستم اعداد خاص ، عدد 100 به نظر می رسد. اگر در سیستم اعشاری عدد 2500 باشد ، این سیستم اعداد از چند رقم استفاده می کند؟

5) دو عدد به صورت 100 نوشته می شوند ، اما در سیستم هایی با شعاع متفاوت. شناخته شده است که پایه سیستم اول دو برابر پایه دوم است. کدام عدد بیشتر است و چند بار؟

6) پایه سیستم را پیدا کنید ، اگر مشخص باشد که عدد 101 ، نوشته شده در این سیستم ، به معنای عدد اعشاری 37 است.

7) در کدام سیستم اعداد ، برای دو برابر کردن یک عدد ، باید صفر را در سمت راست ورودی آن اضافه کنید؟

8) ضرب در 10 در سیستم اعشاری به معنای افزودن صفر به سمت راست عدد است. قانون ضرب را بر 10 فرموله کنید بدر یک سیستم با پایه ب.

5- الگوریتمی برای تبدیل عددی از سیستم اعشاری به سه گانه فرموله کنید.

6. جداول جمع و ضرب را برای سیستم اعداد چهار برابر بسازید. با استفاده از این جداول ، اقدامات زیر را روی اعداد یک ستون انجام دهید (در حالی که در سیستم اعداد رباعی باقی مانده است):

1. الف) 1021 4 + 333 4 ؛

ب) 3333 4 + 3210 4 ؛

2. الف) 321 4 - 123 4 ؛

ب) 1000 4 - 323 4 ؛

3. الف) 13 4 · 12 4؛

ب) 302 4 23 4 ؛

4. الف) 1123 4:13 4 ؛

ب) 112003 4: 101 4.

7. برای سیستم اعداد باینری جداول جمع و ضرب بسازید. با استفاده از این جداول ، مراحل زیر را روی اعداد موجود در یک ستون (باقیمانده در سیستم اعداد باینری) انجام دهید:

1. الف) 1001 2 + 1010 2 ؛

ب) 10111 2 + 1110 2 ؛

2. الف) 1110 2 - 101 2؛

ب) 10000 2 - 111 2 ؛

3. الف) 101 2 · 11 2؛

ب) 1110 2 · 101 2؛

4. الف) 1000 110 2: 101 2؛

ب) 100000100 2: 1101 2.

کارگاه

در صفحات برنامه الکترونیکی ، با مجری Encoder کار کنید.

تمرینات شامل گروههای زیر از وظایف است:

اعشاری

1. از دودویی تا اعشاری

2. از سه تایی تا اعشاری

3. از پنج تا اعشاری

4. از هگزادسیمال به اعشاری

از دهدهی

1. اعشاری به باینری

2. از اعشاری تا سه تایی

3. از اعشاری تا پنج

4. اعشاری تا هگزادسیمال

اعتبار کلاس 1

2. 1101 2 = ? 10

3. 11101 2 = ? 10

اعتبار کلاس 2

10. 1001 2 = ? 16

مطالب معلم

سیستم های اعداد موقعیتی

در سیستم اعداد موقعیتی ، یک عدد به صورت زنجیره ای از کاراکترهای خاص نوشته می شود:

a n a n - 1 ... آ 2 آ 1 (1)

نمادها a مننامیده می شوند ارقام... آنها مقادیر قابل شمارش ترتیبی را نشان می دهند ، از صفر شروع می شوند و تا مقدار یک عدد کمتر. سنامیده می شود مبناسیستم شماره یعنی اگر س- پایه ، مقادیر ارقام در فاصله قرار می گیرند (از جمله مرزها).

موقعیت رقم در ثبت عدد (1) نامیده می شود موقعیت، یا تخلیه.

توجه 1. در این صفحات ، اصطلاح "موقعیت" ترجیح داده می شود. اولاً ، کلمه "موقعیت" با مفهوم "سیستم تعداد موقعیت" مطابقت دارد ، و ثانیا ، اصطلاح "وزن موقعیت" یا "وزن موقعیت" بهتر از "وزن بیت" یا "وزن بیت" بهتر ، واضح و ساده به نظر می رسد . با این حال ، معلم می تواند و باید هر از گاهی به دانش آموزان یادآوری کند که "موقعیت" و "رتبه" اصطلاحات معادل هستند.

نكته 2. تعريف سيستم اعداد موضعي ارائه شده در متون براي دانشجو كاملاً دقيق نيست. وابستگی سهم شکل فقط به موقعیت کافی نیست. به عنوان مثال ، در سیستم اعداد رومی ، سهم رقم نیز به موقعیت بستگی دارد (اعداد IV و VI متفاوت است) ، اما این سیستم موقعیتی نیست. یک تعریف دقیق را می توان کل قوانین ساخت یک عدد در نظر گرفت که در این زمینه برای یک معلم آورده شده است (یعنی همراه با واقعیت وابستگی موقعیتی ، تعریف شامل: محدود بودن مجموعه ارقام و قانون برای پیدا کردن یک عدد با ضبط آن).

موقعیت ها از راست به چپ شماره گذاری می شوند. به شماره در موقعیت اول فراخوانی می شود جوان تررقم یک عدد ، در آخرین - ارشد.

هر موقعیت با یک عدد همراه است ، که ما آن را وزن آن می نامیم ( موقعیت وزنی).

وزن موقعیت با توجه به قانون بازگشتی زیر تعیین می شود:

1. وزن کمترین موقعیت 1 است.

2. وزن هر موقعیت بعدی با ضرب در پایه سیستم از وزن موقعیت قبلی بدست می آید.

بگذار س- پایه سیستم اعداد. سپس قانون محاسبه وزن موقعیتی من منبه طور خلاصه تر می تواند به عنوان یک فرمول تکراری نوشته شود:

1. w 1 = 1.

2. من من = من من-یکی · س(برای همه من > 1).

در سیستم اعداد موقعیتی ، رکورد

a n a n - 1 ... آ 2 آ 1 (1)

به معنی عدد است N، برابر با مجموع محصولات رقم با توجه به وزن موقعیتی آنها:

N = a n· w n + a n-یکی · w n–1 + ... + آ 2 w 2 + آیکی · w 1 . (2)

حاصلضرب یک رقم بر اساس وزن موقعیت آن (یعنی a من· من من) فراخوانی خواهد شد سهم موقعیتی اعداد.

فرمول (2) مبنایی برای قوانین ترجمه اعداد از یک سیستم به سیستم دیگر است که در متن برای دانش آموز پیشنهاد شده است.

در سیستم اعشاری ، اعداد با استفاده از ده حرف عربی نوشته می شوند: 0 ، 1 ، 2 ، 3 ، 4 ، 5 ، 6 ، 7 ، 8 ، 9.
وزنهای موقعیتی این سیستم عبارتند از: ... ، 1000 ، 100 ، 10 ، 1.

4627 10 = 4 1000 + 6 100 + 2 10 + 7 1.

در سیستم باینری ، اعداد با استفاده از دو حرف عربی نوشته می شوند: 0 و 1. وزنهای موقعیتی این سیستم: ... ، 256 ، 128 ، 64 ، 32 ، 16 ، 8 ، 4 ، 2 ، 1.

به عنوان مثال ، ورودی 10101 مانند این "رمزگشایی" شده است:

10101 2 = 1 16 + 0 8 + 1 4 + 0 2 + 1 1.

توجه داشته باشید که قانون بازگشتی برای محاسبه وزن به این معنی است من من = q من–1 و بنابراین ، علامت گذاری (2) معادل علامت گذاری سنتی در قالب یک چند جمله ای قدرت است:

N = a n· q n–1 + a n-یکی · q n–2 + ... + آ 2 س + آ 1 . (3)

بگذارید این را با استقرا ثابت کنیم. پایه القاییدر من= 1 مستقیماً بررسی می شود: w 1 = س 0 = 1.

فرضیه استقرا:: بگذارید این جمله برای برخی درست باشد n:

w n = q n–1 .

بگذارید ثابت کنیم که برای آن نیز معتبر خواهد بود n + 1.
یعنی ما اعتبار برابری را ثابت خواهیم کرد:

w n + 1 = q n.

در واقع، w n+1 = w n· س(با توجه به تعریف بازگشتی از وزن موقعیت) ، و w n = q n–1 با فرضیه استقرایی. به نظر می رسد:

w n + 1 = w n· س = q n-یکی · س = q n.

بگذارید ثابت کنیم که هر عددی در شکل (1) (قضیه 1) به روشی منحصر به فرد قابل نمایش است (قضیه 2).

قضیه 1 (وجود). هر عددی متربرای هر کس می تواند در فرم (1) نشان داده شود س > 1.

شواهد و مدارک. بگذارید با استقرا آن را ثابت کنیم. برای متر = 0
و متر= 1 ساخت نمایش مورد نیاز آسان است - اینها به ترتیب 0 و 1 هستند (برای هر کدام) س> 1) بگذارید بگوییم ما موفق به نشان دادن عدد شدیم متربه شکل (1). سپس یک نمایندگی برای پیدا می کنیم متر+ 1. برای انجام این کار ، تبدیل مبلغ کافی است

a n q n–1 + a n-یکی · q n–2 + ... + آ 2 س + آ 1 + 1 برای تشکیل (1).

اگر یک آ 1 < (س-1) ، سپس با جایگزینی رقم نمایش دلخواه بدست می آید آ 1 در آ " 1 = آ 1 + 1.

اگر یک آ 1 = (س–1) ، انتقال واحد را به موقعیت بعدی می رسانیم:

a n q n F - 1 + a n-یکی · q n–2 + ... + (آ 2 + 1) س + 0.

بعد ، ما به روشی مشابه استدلال می کنیم. اگر یک آ 2 < (س-1) ، سپس با جایگزینی رقم نمایش دلخواه بدست می آید آ 2 در آ " 2 = آ 2 + 1. اگر آ 2 = (س–1) ، پس آ 2 با صفر جایگزین می شود و یکی به موقعیت بعدی منتقل می شود.

یا روی بعضی من < nما ساخت را به پایان می رسانیم ، یا رکورد 1000 ... 0 - یک و nصفر به سمت راست اثبات کامل است.

قبل از قضیه 2 ، لمی را اثبات می کنیم.

لما سهم هر رقم غیر صفر در رکورد (1) از مجموع سهم ارقام واقع در سمت راست آن بیشتر است.

a n a n - 1 ... آ 2 آ 1 . (1)

شواهد و مدارک. بگذارید این را برای هر کس ثابت کنیم n > 1:

a n q n–1 > a n-یکی · q n–2 + ... + آ 2 س+ آ 1 .

شماره a مندر فاصله قرار بگیرید ، به این معنی که اثبات نابرابری برای کوچکترین رقم غیر صفر در سمت چپ و حداکثر رقم در سمت راست کافی است:

q n - 1> ( س-یک) · q n–2 + ... + (س-یک) · س + (س–1).

در سمت راست ، فاکتور را خارج می کنیم ( س–1) در خارج از براکت:

(س-یک) · q n–2 + ... + (س-یک) · س + (س–1) =

= (س-یک) · ( q n–2 + ... + س + 1).

ما با استفاده از فرمول معروف مجموع پیشرفت هندسی را در آخرین براکت محاسبه می کنیم:

(س-یک) · ( q n–2 + ... + س + 1) =

= (س-یک) · ( q n–1 –1)/(س–1) = q n–1 – 1.

ما یک نابرابری آشکار به دست می آوریم که لمی را ثابت می کند:

q n - 1> q n–1 – 1.

قضیه 2 (منحصر به فرد). عدد موجود در فرم (1) تنها به روش نشان داده می شود.

شواهد و مدارک. از لما نتیجه می گیرد که اعداد با تعداد مختلف رقم در علامت گذاری خود (صفرهای غیر قابل توجه در سمت چپ محاسبه نمی شوند) نمی توانند برابر باشند: یک عدد با تعداد زیادی رقم همیشه بیشتر است. از این رو ، فقط لازم است که ثابت شود اگر a مننا برابر ب منبرای همه مناز 1 تا nسپس ثبت می کند

a n a n - 1 ... آ 2 آ 1 (4)

b n b n - 1 ... ب 2 ب 1 (5)

نمی تواند به همان تعداد باشد.

بیایید سوابق (4) و (5) را از چپ به راست در جستجوی ارقام ناسازگار بررسی کنیم. بگذارید باشد a kو ب کرهایش کن a k – ب ک = د.

در ک-مین مکان در رکورد ، تفاوت در وجود دارد د· q k-یک این اختلاف باید با کمک موقعیت های واقع در سمت راست جبران شود. اما این غیرممکن است ، زیرا طبق نظر لما ، مجموع کمک های موقعیت های واقع در سمت راست همیشه کمتر از کمک موقعیت فعلی است. قضیه اثبات شده است.

تبدیل به اعشاری

برای ترجمه اعداد از سیستم radix سدر سیستم اعشاری ، می توانید از فرمول (2) استفاده کنید ، ضرب و جمع را در آن انجام دهید.

N = a n· w n + a n-یکی · w n–1 + ... + آ 2 w 2 + آیکی · w 1 (2)

هنگام ترجمه از یک سیستم باینری ، فقط جمع درگیر می شود (زیرا نمی توانید در 1 ضرب کنید). بنابراین ، ما قانون ترجمه را در اتاق خواندن به دست می آوریم:

بنابراین ، به عنوان مثال ، برای شماره 10111 دریافت می کنیم:

10111 2 = 16 + 4 + 2 + 1 = 23 10

قانون کلی انتقال از سسیستم اری به اعشاری مانند این است:

برای انتقال از سسیستم اصلی به صورت اعشاری ، باید وزن موقعیت آن را بالای هر رقم یادداشت کنید و مجموع محصولات رقم را با توجه به وزن موقعیتی آنها پیدا کنید (یعنی مجموع مشارکتهای موقعیتی را پیدا کنید).

بنابراین ، به عنوان مثال ، برای شماره 10212 3 بدست می آوریم:

ما اعداد ضرب شده بر وزن موقعیت آنها را اضافه می کنیم (البته موقعیت هایی با رقم صفر قابل حذف است):

10212 3 = 1 81 + 2 9 1+ 3 + 2 1 = 104 10 .

ترجمه به س- شخصی

برای تبدیل اعداد از اعشاری به رادیکس سما به فرمول (2) ادامه خواهیم داد:

N = a n· w n + a n-یکی · w n–1 + ... + آ 2 w 2 + آیکی · w 1 . (2)

الگوریتم ترجمه.

I. تکرار کنید تا شماره به صفر تبدیل شود:

1. موقعیت اول را در سمت چپ پیدا کنید ، وزن آن بیشتر از تعداد فعلی نیست. حداکثر رقم ممکن را در موقعیت بنویسید ، به طوری که سهم موقعیتی آن (حاصلضرب رقم بر اساس وزن) از عدد فعلی بیشتر نشود.

2. تعداد فعلی را با مشارکت موقعیت ساخته شده کاهش دهید.

دوم صفرها را در موقعیت هایی که توسط ارقام ساخته شده اشغال نشده اند بنویسید.

در هر موقعیت ، حداکثر رقم ممکن گرفته می شود ، زیرا ، با توجه به لما ، سهم این رقم را نمی توان با ارقام واقع در سمت راست جبران کرد. الگوریتم به دلیل وجود اثبات شده (قضیه 1) و منحصر به فرد بودن (قضیه 2) نمایش عددی در فرم (1) کار خواهد کرد.

برای یک سیستم باینری ، ما یک نوع الگوریتم ارائه شده در این ماده برای دانش آموز می گیریم.

برای تبدیل به باینری ، باید الگویی با وزن ارقام باینری بسازید:

تعداد مطابق الگوریتم زیر ترجمه شده است:

I. تکرار کنید تا شماره به صفر تبدیل شود:

1. 1 را در اولین موقعیت در سمت چپ بنویسید ، که وزن آن بیشتر از عدد فعلی نیست.

2. تعداد فعلی را با توجه به وزن واحد ساخته شده کاهش دهید.

دوم صفرها را در موقعیت هایی که توسط آنها اشغال نشده است بنویسید.

در عمل ، این روش ترجمه با یافتن پس مانده ها بسیار ساده تر و سریعتر از الگوریتم سنتی است.

هنگام تبدیل از یک سیستم اعشاری به یک سیستم سه تایی ، باید هم وزن های موقعیتی و هم دو برابر آنها را در نظر گرفت. برای ترجمه سریع ، می توانید جدولی بسازید که خطوط آن با موقعیت اعداد ، ستون ها - با اعداد و سلول ها - با مشارکت تعداد با تعداد مطابقت دارد ، بسته به موقعیت آن در رکورد تعداد:


729
243
موقعیت 81
موقعیت 27
موقعیت 9
موقعیت 3
موقعیت 1

بیایید بگوییم سهم شماره 2 در موقعیت 243 عدد 486 و در موقعیت 9 عدد 18 است.

برای ترجمه به یک سیستم سه تایی ، باید جدول را خط به خط جستجو کنید تا بیشترین تعداد را که از مقدار فعلی بیشتر نیست جستجو کنید.

به عنوان مثال ، بیایید شماره 183 را به سیستم سه تایی تبدیل کنیم. یک مقدار مناسب در ردیف سوم و ستون اول قرار دارد:


729
243
موقعیت 81
موقعیت 27
موقعیت 9
موقعیت 3
موقعیت 1

از این رو ، شماره سه گانه با رقم 2 شروع می شود:

183 10 = 202?? 3

برای عدد 21-18 = 3 یک معنی دقیق در جدول وجود دارد ، ترجمه به پایان رسیده است:

183 10 = 20210 3 .

برای سیستم های دارای پایه بزرگ ، جداول مربوطه البته حجیم ترند. به عنوان مثال آخر ، بیایید جدولی برای تبدیل به سیستم اعداد هگزادسیمال ایجاد کنیم:

اجازه دهید عدد 4255 به سیستم هگزادسیمال تبدیل شود. ما به دنبال اولین شماره در جدول هستیم (از چپ به راست ، ردیف به ردیف ، از بالا شروع می شود) ، که معلوم است بیش از عدد اصلی 4255 نیست:

اولین رقم 1 را در موقعیت 4096 بدست می آوریم:

برای کدگذاری 4255 - 4096 = 159 باقی مانده است.

از خط 256 عبور کنید (رقم مربوط به آن 0 خواهد بود) و در خط 16 مقدار مناسب 144 را پیدا می کنیم:

اعداد را در موقعیت های 256 و 16 بدست می آوریم:

برای کدگذاری 159 - 144 = 15 باقی مانده است. روشن است که این مقدار کمترین رقم قابل توجه است:

به نظر می رسد: 4255 10 = 109F 16.

اقدامات روی اعداد

این بخش در مطالب برای دانش آموز به صورت شماتیک ، برای اهداف اطلاعاتی ارائه شده است.

یک درس جداگانه ، بزرگ و بسیار جالب می تواند به این موضوع اختصاص یابد ، اما در حال حاضر مطالب زیادی وجود دارد - درک بی اندازه بودن کار دشواری است!

در یک نسخه مقدماتی ساده ، نشان داده شده است که اعمال روی اعداد در هر سیستم عددی به همان روشی است که در سیستم اعشاری انجام می شود. اگر غیر از این باشد عجیب است ، زیرا اعداد در همه سیستم های موقعیتی طبق همان قوانین ساخته می شوند ، به این معنی که اعمال روی آنها باید به همان روش انجام شود.

این بخش با انجام تکالیف درسی برای گزینه 3 پشتیبانی می شود. این تمرینات را می توان به عنوان تکالیف جداگانه به دانش آموزان کنجکاو توصیه کرد.

فصل 4. مبانی حسابی رایانه ها

4.1 سیستم اعداد چیست؟

سیستم های اعداد موضعی و غیر موضعی وجود دارد.

در سیستم های عددی غیر موضعیوزن یک رقم (یعنی سهمی که در مقدار عدد دارد) به موقعیت او بستگی ندارددر علامت گذاری شماره. بنابراین ، در سیستم اعداد رومی ، در عدد XXXII (سی و دو) ، وزن شکل X در هر موقعیت فقط ده است.

در سیستم های اعداد موقعیتیوزن هر رقم بسته به موقعیت آن (موقعیت) در توالی ارقام نشان دهنده تعداد تغییر می کند. به عنوان مثال ، در عدد 757.7 ، هفت اول به معنای 7 صد ، دوم - 7 واحد و سوم - 7 دهم یک است.

همان علامت گذاری همان عدد 757.7 به معنای بیان مختصر است

700 + 50 + 7 + 0,7 = 7 . 10 2 + 5 . 10 1 + 7 . 10 0 + 7 . 10 -1 = 757,7.

هر سیستم اعداد موضعی با آن مشخص می شود مبنا

هر عدد طبیعی را می توان به عنوان پایه سیستم در نظر گرفت - دو ، سه ، چهار و غیره. از این رو ، تعداد بیشماری سیستم موقعیت یابی امکان پذیر است: باینری ، سه تایی ، کواترنری و ... نوشتن اعداد در هر یک از سیستم های radix سبه معنی بیان مختصر است

آ n-1 س n-1 + a n-2 س n-2 + ... + a 1 س 1 + a 0 س 0 + a -1 س -1 + ... + a -م س -م ,

جایی که آ من - اعداد عددی ؛ n و متر - به ترتیب تعداد ارقام صحیح و کسری.
مثلا:

4.2 چگونه عدد صحیح در سیستم های اعداد موقعیتی تولید می شود؟

در هر سیستم اعداد ، اعداد با توجه به معنی آنها ترتیب داده می شوند: 1 بزرگتر از 0 ، 2 بزرگتر از 1 و غیره

پیشبرد عدد 1 به معنای جایگزینی آن با 2 ، پیشبرد عدد 2 به معنای جایگزینی آن با 3 و غیره است. ارتقاit رقم بالا(به عنوان مثال ، اعداد 9 در اعشاری) به معنی جایگزینی آن با 0 است... در یک سیستم باینری که فقط از دو رقم 0 و 1 استفاده می کند ، پیشرفت 0 به معنای جایگزینی آن با 1 و پیشرفت 1 به معنای جایگزینی آن با 0 است.

عدد صحیح در هر سیستم عددی با استفاده از تولید می شود قوانین حساب [44 ]:

با استفاده از این قانون ، بیایید ده عدد اول را بنویسیم

در باینری: 0 ، 1 ، 10 ، 11 ، 100 ، 101 ، 110 ، 111 ، 1000 ، 1001 ؛

در سیستم سه تایی: 0 ، 1 ، 2 ، 10 ، 11 ، 12 ، 20 ، 21 ، 22 ، 100 ؛

در سیستم پنج برابر: 0 ، 1 ، 2 ، 3 ، 4 ، 10 ، 11 ، 12 ، 13 ، 14 ؛

در هشت درجه: 0 ، 1 ، 2 ، 3 ، 4 ، 5 ، 6 ، 7 ، 10 ، 11.

4.3 متخصصان از چه سیستم شماره ای برای برقراری ارتباط با رایانه استفاده می کنند؟

علاوه بر اعشاری ، سیستم هایی با پایه که قدرت صحیح 2 دارند به طور گسترده ای استفاده می شوند ، یعنی:

دودویی(اعداد 0 ، 1 استفاده می شود) ؛

هشت ضلعی(اعداد 0 ، 1 ، ... ، 7 استفاده می شود) ؛

هگزادسیمال(برای اولین عدد صحیح از صفر تا نه ، از ارقام 0 ، 1 ، ... ، 9 استفاده می شود و برای عددهای صحیح بعدی ، از ده تا پانزده ، از شخصیت های A ، B ، C ، D ، E ، F استفاده می شود) به عنوان رقم)

یادآوری ورودی در این سیستم های عددی برای دو ده اول عدد صحیح مفید است:

از همه سیستم های عددی به خصوص سادهو بنابراین جالب برای پیاده سازی فنی در سیستم تعداد دودویی رایانه ها.

4.4 چرا مردم از اعشاری و کامپیوترها از باینری استفاده می کنند؟

مردم سیستم اعشاری را ترجیح می دهند ، احتمالاً به این دلیل که از زمان های بسیار قدیم با انگشتان خود می شمردند و مردم ده انگشت بر روی دست و پا دارند. همیشه و نه در همه جا مردم از سیستم اعداد اعشاری استفاده می کنند. به عنوان مثال در چین مدت ها از سیستم اعداد پنج برابر استفاده می شد.

و رایانه ها از یک سیستم باینری استفاده می کنند زیرا دارای مزایای زیادی نسبت به سایر سیستم ها است:

برای اجرای آن ، شما نیاز دارید دستگاه های فنی با دو حالت ثابت(یک جریان وجود دارد - هیچ جریانی ، مغناطیسی نشده - مغناطیسی نشده است ، و غیره) ، و نه ، به عنوان مثال ، با ده ، مانند اعشاری ؛

ارائه اطلاعات فقط با استفاده از دو حالت بطرزی قابل اعتمادو ضد پارازیت;

احتمالاً برنامه دستگاه جبر بولیبرای انجام تحولات منطقی اطلاعات ؛

حساب دودویی بسیار ساده تر از اعشاری است.

عیب سیستم باینری است افزایش سریع تعداد ارقامبرای نوشتن اعداد لازم است.

4.5 چرا رایانه ها از سیستم اعداد هشت و هگزادسیمال نیز استفاده می کنند؟

یک سیستم باینری ، مناسب برای رایانه ها ، به دلیل دست و پا گیر بودن و ضبط غیرمعمول برای انسان ناخوشایند است.

تبدیل اعداد از اعشاری به باینری و بالعکس توسط دستگاه انجام می شود. با این حال ، برای استفاده حرفه ای از رایانه ، باید یاد بگیرید که کلمه ماشین را بفهمید. برای این منظور ، سیستمهای هشت و هگزادسیمال ایجاد شده است.

اعداد در این سیستم ها تقریباً به راحتی اعداد اعشاری خوانده می شوند ، به ترتیب به سه (هشت عددی) و چهار (هگزادسیمال) برابر رقم کمتر از سیستم باینری نیاز دارند (به هر حال ، اعداد 8 و 16 به ترتیب سوم هستند و قدرت های چهارم شماره 2) ...

مثلا:

مثلا،

4.6 چگونه یک عدد صحیح را از سیستم اعشاری به سیستم عددی موضعی دیگری تبدیل کنیم؟

مثال:بیایید عدد 75 را از سیستم اعشاری به باینری ، هشت و هگزادسیمال تبدیل کنیم:

پاسخ: 75 10 = 1 001 011 2 = 113 8 = 4B 16.

4.7 چگونه عدد اعشاری صحیح را به هر سیستم اعداد موضعی دیگری ترجمه کنیم؟

برای ترجمه صحیح عدد اعشاریF به رادیکسس لازمF ضربدرس ، در همان سیستم اعشاری نوشته شده است ، سپس قسمت کسری محصول حاصل را در ضرب می کنیمq ، و به همین ترتیب ، تا زمانی که قسمت کسری محصول بعدی برابر با صفر شود ، یا دقت مورد نیاز عدد حاصل نشود F که درس سیستم جفت شده نمایش بخش کسری یک عددF در سیستم شماره جدید ، دنباله ای از قسمتهای کامل آثار دریافت شده وجود دارد که به ترتیب دریافت آنها نوشته شده و توسط یک نفر به تصویر کشیده شده است س -یک عدد. در صورت دقت مورد نیاز در تبدیل عددF استک رقم اعشار ، پس حداکثر خطای مطلق برابر است باس - (k + 1) / 2.

مثال.بیایید عدد 0.36 را از سیستم اعشاری به باینری ، هشت و هگزادسیمال تبدیل کنیم:

4.8 چگونه می توان یک عدد را از سیستم باینری (هشت ، هگزادسیمال) به اعشاری تبدیل کرد؟

تبدیل یک عدد به سیستم اعشاریایکس ثبت شده درس سیستم اعداد دومی (س = 2 ، 8 یا 16) در فرمایکس س = (الف n آ n-1 ... آ 0 ، آ -1 آ -2 ... آ -م ) س به محاسبه مقدار چند جمله ای کاهش می یابد

ایکس 10 = الف n س n + a n-1 س n-1 + ... + a 0 س 0 + a -1 س -1 + a -2 س -2 + ... + a -م س -م

با استفاده از حساب اعشاری.

مثال ها:

4.9 جدول خلاصه ترجمه اعداد صحیح از یک سیستم عددی به سیستم دیگر

فقط سیستم های اعدادی را که در رایانه استفاده می شوند - اعشار ، دودویی ، هشت و هگزادسیمال در نظر بگیرید. برای مشخص بودن ، ما یک عدد اعشاری دلخواه ، به عنوان مثال 46 ، می گیریم و برای آن همه ترجمه های متوالی ممکن را از یک سیستم عددی به سیستم دیگر انجام می دهیم. ترتیب ترجمه ها مطابق با شکل تعیین می شود:

این شکل از قراردادهای زیر استفاده می کند:

مبنای سیستم های عددی به صورت دایره ای نوشته شده است.

فلش ها جهت ترجمه را نشان می دهند.

عدد کنار پیکان به معنی شماره سریال مثال مربوطه در جدول خلاصه 4.1 است.

به عنوان مثال: به معنی ترجمه از باینری به هگزادسیمال است که دنباله شماره 6 آن در جدول است.

جدول محوری ترجمه های عدد صحیحدوبخشها- نظریه آمار ... آمار ، انفورماتیکبه عنوان رشته ... KR (الکترونیکی نسخهنسخه ها) ".... EP اقتصاد خرد اقتصاد: کتاب درسی. کمک هزینه... - م.: Delo ، 2000. ... مجله. اینترنت- وب سایت های Rosstat ...

& quot ؛ شکل گیری پایگاه داده های باز منابع اطلاعاتی & quot؛

گزارش

نسخه های مرجع کتابشناسی فواید. بخش 1. انتشارات مرجع ... رویه های سازش. اینترنت-نسخهمجله دسترسی به ... URSS / اینترنت-نمره تشکیل شده استازدوبخشها: ... متخصصان دفتر انفورماتیکو ارتباطات از راه دور ...

نشانه گذاریروشی است برای نوشتن یک عدد با استفاده از مجموعه مشخصی از کاراکترهای خاص (اعداد).

نشانه گذاری:

نمایش مجموعه ای از اعداد (عدد صحیح و / یا واقعی) را نشان می دهد.

به هر شماره یک نمایش منحصر به فرد می دهد (یا حداقل یک نمایش استاندارد).

ساختار جبری و حسابی یک عدد را نمایش می دهد.

نوشتن یک عدد در سیستم اعداد خاص نامیده می شود کد شماره.

یک موقعیت جداگانه در نمایش یک عدد نامیده می شود تخلیه، به این معنی که شماره موقعیت است شماره رتبه.

به تعداد بیت های یک عدد گفته می شود لقمهو با طول آن مطابقت دارد.

سیستم های اعداد به تقسیم می شوند موضعیو غیر موضعیسیستم های تعداد موقعیت تقسیم می شوند

در همگنو مختلط.

سیستم اعداد هشت ضلعی ، سیستم اعداد هگزادسیمال و سایر سیستم های اعدادی.

ترجمه سیستم های عددی.اعداد را می توان از یک سیستم اعداد به سیستم دیگر ترجمه کرد.

جدول مطابقت اعداد در سیستم های مختلف اعداد.

سیستم اعداد موضعی و غیر موضعی وجود دارد.

در سیستم های اعداد موقعیتیوزن هر رقم بسته به موقعیت آن (موقعیت) در توالی ارقام نشان دهنده تعداد تغییر می کند. به عنوان مثال ، در عدد 757.7 ، هفت اول به معنای 7صد ، دوم - 7 واحد و سوم - 7 دهم یک است.