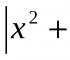چگونه می توان a1 را در فرمول پیشرفت حساب پیدا کرد. ماتریس معکوس

بنابراین ، خدمات برای حل آنلاین ماتریس:

سرویس کار با ماتریس به شما امکان می دهد تبدیل ماتریس ابتدایی را انجام دهید.
اگر وظیفه دارید تحول پیچیده تری انجام دهید ، از این سرویس باید به عنوان سازنده استفاده کنید.

مثال... ماتریس های داده شده آو ب، نیاز به پیدا کردن ج = آ -1 * ب + ب T ،

ابتدا باید پیدا کنید ماتریس معکوسA1 = آ-1 ، با استفاده از سرویس برای پیدا کردن ماتریس معکوس ؛
علاوه بر این ، پس از پیدا کردن ماتریس A1انجام دهید ضرب ماتریسA2 = A1 * ببا استفاده از سرویس ضرب ماتریس.
بیایید اجرا کنیم جابجایی ماتریسA3 = ب T (سرویس پیدا کردن ماتریس جابجا شده) ؛
و آخرین مورد - جمع ماتریس ها را پیدا کنید با = A2 + A3(سرویس محاسبه مجموع ماتریس ها) - و ما با دقیق ترین راه حل پاسخی دریافت می کنیم!

محصول ماتریس ها

این یک سرویس آنلاین در است دو مرحله:

ماتریس عامل اول را معرفی کنید آ
ماتریس عامل دوم یا بردار ستون را معرفی کنید ب

ضرب ماتریس-بردار

با استفاده از سرویس می توان ضرب ماتریس بردار را پیدا کرد ضرب ماتریس
(عامل اول ماتریس داده شده خواهد بود ، عامل دوم ستونی متشکل از عناصر بردار داده شده خواهد بود)

این یک سرویس آنلاین در است دو مرحله:

وارد ماتریس شوید آ، برای آن شما باید ماتریس معکوس را پیدا کنید
برای یافتن ماتریس معکوس با یک راه حل دقیق پاسخ دهید

تعیین کننده ماتریس

این یک سرویس آنلاین در است یک قدم:

وارد ماتریس شوید آ، برای آن شما باید تعیین کننده ماتریس را پیدا کنید

انتقال ماتریس

در اینجا می توانید الگوریتم جابجایی ماتریس را ردیابی کنید و یاد بگیرید چگونه خودتان چنین مشکلاتی را حل کنید.
این یک سرویس آنلاین در است یک قدم:

وارد ماتریس شوید آجابجا شدن

رتبه ماتریس

این یک سرویس آنلاین در است یک قدم:

وارد ماتریس شوید آ، برای آن شما باید رتبه را پیدا کنید

مقادیر ویژه ماتریس و بردارهای ویژه ماتریس

این یک سرویس آنلاین در است یک قدم:

وارد ماتریس شوید آ، برای آن شما باید بردارهای ویژه و مقادیر ویژه (مقادیر ویژه) را پیدا کنید

نمایش ماتریس

این یک سرویس آنلاین در است دو مرحله:

وارد ماتریس شوید آ، که شما آن را به قدرت می رسانید
یک عدد صحیح وارد کنید س- درجه

اگر شرط $ A ^ (- 1) \ cdot A = A \ cdot A ^ (- 1) = E $ راضی باشد ، ماتریس $ A ^ (- 1) $ را با توجه به ماتریس مربع $ A معکوس می نامیم ، جایی که $ E $ ماتریس هویت است ، ترتیب آن برابر با ترتیب ماتریس $ A $ است.

ماتریس غیر انحطاطی - ماتریسی که تعیین کننده آن برابر با صفر نیست. بر این اساس ، یک ماتریس منحط یکی با تعیین کننده صفر است.

ماتریس معکوس $ A ^ (- 1) $ وجود دارد در صورتی که ماتریس $ A $ جدید نیست. اگر ماتریس معکوس $ A ^ (- 1) $ وجود داشته باشد ، بی نظیر است.

روش های مختلفی برای پیدا کردن عکس یک ماتریس وجود دارد ، و ما دو مورد را بررسی خواهیم کرد. در این صفحه روش ماتریس الحاقی بحث می شود که در اکثر دروس ریاضیات بالاتر استاندارد تلقی می شود. روش دوم برای یافتن ماتریس معکوس (روش تحولات اولیه) ، که شامل استفاده از روش گاوس یا روش گاوس- جوردن است ، در قسمت دوم بحث شده است.

روش ماتریس الحاقی (الحاقی)

اجازه دهید ماتریس $ A_ (n \ times n) $ داده شود. برای یافتن عکس ماتریس $ A ^ (- 1) $ ، سه مرحله لازم است:

تعیین کننده ماتریس $ A $ و مطمئن شوید که $ \ Delta A \ neq 0 $ ، یعنی. که ماتریس A غیر منحط است.
مکمل های جبری $ A_ (ij) $ از هر عنصر ماتریس $ A $ را بسازید و ماتریس $ A_ (n \ times n) ^ (*) = \ چپ (A_ (ij) \ سمت راست) $ را از مکمل های جبری پیدا کرد.
ماتریس معکوس را با در نظر گرفتن فرمول $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $ بنویسید.

ماتریس $ (A ^ (*)) ^ T $ اغلب به عنوان متصل (متقابل ، مجاور) به ماتریس $ A $ گفته می شود.

اگر راه حل به صورت دستی انجام شود ، روش اول فقط برای ماتریس هایی با ترتیب نسبتاً کوچک مناسب است: دوم () ، سوم () ، چهارم (). از روشهای دیگر برای یافتن عکس یک ماتریس مرتبه بالاتر استفاده می شود. به عنوان مثال ، روش گاوس ، که در قسمت دوم مورد بحث قرار گرفته است.

مثال شماره 1

معکوس $ A = \ left (\ start (array) (cccc) 5 & -4 & 1 & 0 \\ 12 & -11 & 4 & 0 \\ -5 و 58 & 4 & 0 \\ 3 & - 1 & -9 و 0 \ end (آرایه) \ راست) $.

از آنجا که تمام عناصر ستون چهارم برابر با صفر هستند ، بنابراین $ \ Delta A = 0 $ (یعنی ماتریس $ A $ تحلیل رفته است). از آنجا که $ \ Delta A = 0 $ ، ماتریس معکوس با ماتریس $ A $ وجود ندارد.

پاسخ: ماتریس $ A ^ (- 1) $ وجود ندارد.

مثال شماره 2

معکوس ماتریس $ A = \ left (\ start (آرایه) (cc) -5 و 7 \\ 9 & 8 \ end (آرایه) \ right) $ پیدا کنید. بررسی.

ما از روش ماتریس الحاقی استفاده می کنیم. ابتدا ، تعیین کننده ماتریس داده شده $ A $ پیدا می کنیم:

$ $ \ دلتا A = \ چپ | \ start (آرایه) (cc) -5 و 7 \\ 9 & 8 \ end (آرایه) \ right | = -5 \ cdot 8-7 \ cdot 9 = -103. $ $

از آنجا که $ \ Delta A \ neq 0 $ ، پس ماتریس معکوس وجود دارد ، بنابراین ما راه حل را ادامه می دهیم. یافتن مکمل های جبری

\ start (تراز شده) & A_ (11) = (- 1) ^ 2 \ cdot 8 = 8؛ \؛ A_ (12) = (- 1) ^ 3 \ cdot 9 = -9؛ \\ & A_ (21) = (- 1) ^ 3 \ cdot 7 = -7؛ \؛ A_ (22) = (- 1) ^ 4 \ cdot (-5) = - 5. \\ \ پایان (تراز شده)

ما یک ماتریس از مکمل های جبری می سازیم: $ A ^ (*) = \ left (\ start (array) (cc) 8 & -9 \\ -7 & -5 \ end (array) \ right) $.

ماتریس حاصل را جابجا کنید: $ (A ^ (*)) ^ T = \ left (\ start (array) (cc) 8 & -7 \\ -9 & -5 \ end (array) \ right) $ (نتیجه ماتریس اغلب به ماتریس الحاقی یا الحاقی ماتریس $ A $ گفته می شود). با استفاده از فرمول $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $ ، ما باید:

$ $ A ^ (- 1) = \ frac (1) (- 103) \ cdot \ سمت چپ (\ start (آرایه) (cc) 8 & -7 \\ -9 & -5 \ end (آرایه) \ right) = \ چپ (\ شروع (آرایه) (cc) -8/103 و 7/103 \\ 9/103 و 5/103 \ پایان (آرایه) \ راست) $ $

بنابراین معکوس پیدا می شود: $ A ^ (- 1) = \ left (\ start (array) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $ برای بررسی حقیقت نتیجه ، کافی است که حقیقت یکی از برابری ها را بررسی کنید: $ A ^ (- 1) \ cdot A = E $ یا $ A \ cdot A ^ (- 1) = E $. اجازه دهید برابری $ A ^ (- 1) \ cdot A = E $ را بررسی کنیم. برای اینکه کمتر با کسر کار کنیم ، ماتریس $ A ^ (- 1) $ را به شکل $ \ left جایگزین نخواهیم کرد (\ start (آرایه) (cc) -8/103 و 7/103 \\ 9/103 & 5/103 \ end (آرایه) \ سمت راست) $ ، و به عنوان $ - \ frac (1) (103) \ cdot \ left (\ start (آرایه) (cc) 8 & -7 \\ -9 & -5 \ end (آرایه) \ سمت راست) $:

$ $ A ^ (- 1) \ cdot (A) = - \ frac (1) (103) \ cdot \ سمت چپ (\ start (آرایه) (cc) 8 & -7 \\ -9 & -5 \ پایان ( آرایه) \ راست) \ cdot \ چپ (\ شروع (آرایه) (سی سی) -5 و 7 \\ 9 و 8 \ پایان (آرایه) \ راست) = - \ frac (1) (103) \ cdot \ چپ ( \ start (آرایه) (cc) -103 و 0 \\ 0 & -103 \ end (آرایه) \ راست) = \ چپ (\ start (آرایه) (cc) 1 & 0 \\ 0 & 1 \ end (آرایه ) \ راست) = E $ $

پاسخ: $ A ^ (- 1) = \ چپ (\ شروع (آرایه) (cc) -8/103 و 7/103 \\ 9/103 و 5/103 \ پایان (آرایه) \ سمت راست) $.

مثال شماره 3

معکوس ماتریس $ A = \ left (\ start (array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (array) \ right) $ پیدا کنید. بررسی.

بیایید با محاسبه مقدار ماتریس $ A $ شروع کنیم. بنابراین ، تعیین کننده ماتریس $ A $ به شرح زیر است:

$ $ \ دلتا A = \ چپ | \ start (آرایه) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (آرایه) \ سمت راست | = 18-36 + 56-12 = 26. $ $

از آنجا که $ \ Delta A \ neq 0 $ ، پس ماتریس معکوس وجود دارد ، بنابراین ما راه حل را ادامه می دهیم. مکمل های جبری هر یک از عناصر ماتریس داده شده را پیدا می کنیم:

$$ \ start (تراز شده) & A_ (11) = (- 1) ^ (2) \ cdot \ left | \ start (آرایه) (cc) 9 & 4 \\ 3 & 2 \ end (آرایه) \ right | = 6 ؛ \؛ A_ (12) = (- 1) ^ (3) \ cdot \ left | \ start (آرایه) (cc) -4 & 4 \\ 0 & 2 \ end (آرایه) \ right | = 8؛ \؛ A_ (13) = (- 1) ^ (4) \ cdot \ left | \ start (array) (cc) -4 & 9 \\ 0 & 3 \ end (array) \ right | = -12؛ \\ & A_ (21) = (- 1) ^ (3) \ cdot \ سمت چپ | \ start (آرایه) (cc) 7 و 3 \\ 3 & 2 \ end (آرایه) \ right | = -5؛ \؛ A_ (22) = (- 1) ^ (4) \ cdot \ left | \ start (آرایه) (cc) 1 & 3 \\ 0 & 2 \ end (آرایه) \ right | = 2؛ \؛ A_ (23) = (- 1) ^ (5) \ cdot \ left | \ start (آرایه) (cc) 1 & 7 \\ 0 & 3 \ end (آرایه) \ right | = -3؛ \\ & A_ (31) = (- 1) ^ (4) \ cdot \ سمت چپ | \ start (آرایه) (cc) 7 & 3 \\ 9 & 4 \ end (آرایه) \ right | = 1؛ \؛ A_ (32) = (- 1) ^ (5) \ cdot \ left | \ start (array) (cc) 1 & 3 \\ -4 & 4 \ end (array) \ right | = -16؛ \؛ A_ (33) = (- 1) ^ (6) \ cdot \ سمت چپ | \ start (آرایه) (cc) 1 & 7 \\ -4 & 9 \ end (آرایه) \ right | = 37. \ پایان (تراز شده) $ $

ما یک ماتریس از مکمل های جبری می سازیم و آن را جابجا می کنیم:

$$ A ^ * = \ چپ (\ شروع (آرایه) (ccc) 6 و 8 و -12 \\ -5 و 2 و -3 \\ 1 & -16 و 37 \ end (آرایه) \ سمت راست)؛ \؛ (A ^ *) ^ T = \ چپ (\ شروع (آرایه) (ccc) 6 & -5 و 1 \\ 8 & 2 & -16 \\ -12 & -3 و 37 \ end (آرایه) \ سمت راست) ... $ $

با استفاده از فرمول $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $ ، به دست می آوریم:

$ $ A ^ (- 1) = \ frac (1) (26) \ cdot \ سمت چپ (\ start (آرایه) (ccc) 6 & -5 و 1 \\ 8 & 2 & -16 \\ -12 & - 3 و 37 \ پایان (آرایه) \ راست) = \ چپ (\ شروع (آرایه) (ccc) 3/13 و -5/26 و 1/26 \\ 4/13 و 1/13 و -8/13 \ \ -6/13 و -3/26 و 37/26 \ پایان (آرایه) \ راست) $ $

بنابراین $ A ^ (- 1) = \ چپ (\ شروع (آرایه) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 / 13 & -3/26 و 37/26 \ end (آرایه) \ سمت راست) $. برای بررسی حقیقت نتیجه کافی است که حقیقت یکی از برابری ها را بررسی کنید: $ A ^ (- 1) \ cdot A = E $ یا $ A \ cdot A ^ (- 1) = E $. بگذارید برابری $ A \ cdot A ^ (- 1) = E $ را بررسی کنیم. برای اینکه کمتر با کسر کار کنیم ، ماتریس $ A ^ (- 1) $ را به شکل $ \ left جایگزین نخواهیم کرد (\ start (آرایه) (ccc) 3/13 & -5/26 & 1/26 \ \ 4/13 و 1/13 و -8/13 \\ -6/13 و -3/26 و 37/26 \ end (آرایه) \ سمت راست) $ و به عنوان $ \ frac (1) (26) \ cdot \ left (\ start (آرایه) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ end (آرایه) \ right) $:

$ $ A \ cdot (A ^ (- 1)) = \ left (\ start (array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (array) \ راست) \ cdot \ frac (1) (26) \ cdot \ چپ (\ start (آرایه) (ccc) 6 & -5 و 1 \\ 8 & 2 & -16 \\ -12 & -3 و 37 \ پایان (آرایه) \ راست) = \ frac (1) (26) \ cdot \ چپ (\ شروع (آرایه) (ccc) 26 و 0 و 0 \\ 0 & 26 و 0 \\ 0 & 0 & 26 \ پایان (آرایه) \ راست) = \ چپ (\ شروع (آرایه) (ccc) 1 و 0 و 0 \\ 0 & 1 و 0 \\ 0 & 0 & 1 \ پایان (آرایه) \ راست) = E $ $

بررسی موفقیت آمیز بود ، معکوس $ A ^ (- 1) $ به درستی پیدا شد.

پاسخ: $ A ^ (- 1) = \ چپ (\ شروع (آرایه) (ccc) 3/13 & -5/26 و 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 / 13 & -3/26 و 37/26 \ end (آرایه) \ سمت راست) $.

مثال شماره 4

معکوس $ A = \ چپ (\ شروع (آرایه) (cccc) 6 و -5 و 8 و 4 \\ 9 و 7 و 5 و 2 \\ 7 و 5 و 3 و 7 \\ -4 و 8 را پیدا کنید & -8 و -3 \ end (آرایه) \ سمت راست) $.

برای یک ماتریس مرتبه چهارم ، یافتن ماتریس معکوس با استفاده از مکمل های جبری تا حدودی دشوار است. با این حال ، نمونه هایی از این دست در مقاله های آزمایشی یافت می شود.

برای پیدا کردن عکس یک ماتریس ، ابتدا باید تعیین کننده ماتریس $ A را محاسبه کنید. بهترین روش برای انجام این کار در این شرایط ، گسترش تعیین کننده به ردیف (ستون) است. ما هر ردیف یا ستونی را انتخاب می کنیم و مکمل های جبری هر یک از عناصر ردیف یا ستون انتخاب شده را پیدا می کنیم.

به عنوان مثال ، برای خط اول:

$$ A_ (11) = \ چپ | \ start (آرایه) (ccc) 7 & 5 & 2 \\ 5 & 3 & 7 \\ 8 & -8 & -3 \ end (آرایه) \ سمت راست | = 556؛ \؛ A_ (12) = - \ چپ | \ شروع (آرایه) (ccc) 9 و 5 و 2 \\ 7 و 3 و 7 \\ -4 و -8 و -3 \ پایان (آرایه) \ راست | = -300 ؛ $ $ $ $ A_ (13) = \ چپ | \ شروع (آرایه) (ccc) 9 و 7 و 2 \\ 7 و 5 و 7 \\ -4 و 8 و -3 \ پایان (آرایه) \ راست | = -536؛ \؛ A_ (14) = - \ چپ | \ شروع (آرایه) (ccc) 9 و 7 و 5 \\ 7 و 5 و 3 \\ -4 و 8 & -8 \ پایان (آرایه) \ راست | = -112. $ $

تعیین کننده ماتریس $ A $ با فرمول زیر محاسبه می شود:

$ $ \ دلتا (A) = a_ (11) \ cdot A_ (11) + a_ (12) \ cdot A_ (12) + a_ (13) \ cdot A_ (13) + a_ (14) \ cdot A_ (14 ) = 6 \ cdot 556 + (- 5) \ cdot (-300) +8 \ cdot (-536) +4 \ cdot (-112) = 100. $ $

$ $ \ start (تراز شده) & A_ (21) = - 77؛ \؛ A_ (22) = 50؛ \؛ A_ (23) = 87؛ \؛ A_ (24) = 4؛ \\ & A_ (31) = -93؛ \؛ A_ (32) = 50؛ \؛ A_ (33) = 83؛ \؛ A_ (34) = 36؛ \\ & A_ (41) = 473؛ \؛ A_ (42) = - 250 ؛ \؛ A_ (43) = - 463؛ \؛ A_ (44) = - 96. \ پایان (تراز شده) $ $

ماتریس مکمل جبری: $ A ^ * = \ left (\ start (array) (cccc) 556 & -300 & -536 & -112 \\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36 \\ 473 & -250 & -463 & -96 \ end (آرایه) \ سمت راست) $.

ماتریس پیوسته: $ (A ^ *) ^ T = \ left (\ start (array) (cccc) 556 & -77 & -93 & 473 \\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 و -463 \\ -112 و 4 و 36 و -96 \ پایان (آرایه) \ سمت راست) $.

ماتریس معکوس:

$ $ A ^ (- 1) = \ frac (1) (100) \ cdot \ left (\ start (array) (cccc) 556 & -77 & -93 & 473 \\ -300 & 50 & 50 & -250 \\ -536 و 87 و 83 و -463 \\ -112 و 4 و 36 و -96 \ پایان (آرایه) \ راست) = \ چپ (\ شروع (آرایه) (cccc) 139/25 و -77/100 & -93/100 و 473/100 \\ -3 و 1/2 و 1/2 و -5/2 \\ -134/25 و 87/100 و 83/100 و -463/100 \\ -28 / 25 و 1/25 و 9/25 و -24/25 \ پایان (آرایه) \ راست) $ $

در صورت تمایل ، بررسی می تواند به همان روشی که در نمونه های قبلی انجام شده است ، انجام شود.

پاسخ: $ A ^ (- 1) = \ left (\ start (آرایه) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 و 87/100 و 83/100 و -463/100 \\ -28/25 و 1/25 و 9/25 و -24/25 \ پایان (آرایه) \ سمت راست) $

در قسمت دوم ، روش دیگری برای یافتن ماتریس معکوس در نظر گرفته خواهد شد که شامل استفاده از تحولات روش گاوس یا روش گاوس- جوردن است.

برای حل سیستم معادلات خطی (3) با توجه به x 1ما از روش Gauss استفاده خواهیم کرد.

سیستم های باقیمانده معادلات خطی (2) به روشی مشابه حل می شوند.

سرانجام گروهی از بردارهای ستون x 1 ، x 2 ، ... ، x nمعکوس را تشکیل می دهد A -1.

توجه داشته باشید که پس از پیدا کردن ماتریس های جایگشت P 1 ، P 2 ، ... ، P n-1و ماتریس های محرومیت M 1 ، M 2 ، ... ، M n-1(به روش حذف گاوسی صفحه مراجعه کنید) و ساخت یک ماتریس

M = M n-1 P n-1 ... M 2 P 2 M 1 P 1 ،

سیستم (2) را می توان به فرم تبدیل کرد

حداکثر 1 = من 1 ،
MAx 2 = من 2 ،
......
MAX n = Me n

از اینجا هستند x 1 ، x 2 ، ... ، x n، با دو طرف راست متفاوت من 1 ، من 2 ، ... ، Me n.

هنگام محاسبه ماتریس معکوس ، راحت تر است که ماتریس هویت را در سمت راست ماتریس اصلی اضافه کنید و روش گاوسی را در جهت جلو و عقب اعمال کنید.

بیایید به یک مثال نگاه کنیم.

نمونه ای از محاسبه ماتریس معکوس

اجازه دهید ماتریس معکوس پیدا شود A -1برای یک ماتریس معین آ:

بیایید ماتریس هویت را در سمت راست بنویسیم:

ما عنصر محوری "4" را انتخاب می کنیم (از آنجا که بزرگترین مقدار مطلق است) و خطوط اول و سوم را مرتب می کنیم:

استثنا column گاوسی را برای ستون اول اعمال کنید:

ردیف های دوم و سوم را عوض کنید و برای ستون دوم محرومیت گاوسی را اعمال کنید.

روش های پیدا کردن ماتریس معکوس. یک ماتریس مربع در نظر بگیرید

ما Δ = det A را نشان می دهیم.

ماتریس مربع A نامیده می شود غیر منحط ،یا غیر مفرداگر تعیین کننده آن غیر صفر باشد ، و انحطاطیا خاص، اگرΔ = 0.

یک ماتریس مربع B برای یک ماتریس مربع A با همان ترتیب وجود دارد اگر محصول آنها A B = B A = E باشد ، جایی که E ماتریس هویت همان نظم ماتریس های A و B است.

قضیه . برای اینکه ماتریس A دارای یک ماتریس معکوس باشد ، لازم و کافی است که تعیین کننده آن غیر صفر باشد.

ماتریس معکوس ماتریس A ، با A نشان داده می شود- 1 ، به طوری که B = A - 1 و با فرمول محاسبه می شود

, (1)

که در آن А i j مکمل های جبری عناصر a i j ماتریس A است.

محاسبه A-1 طبق فرمول (1) برای ماتریس های مرتبه بالا بسیار کارساز است ، بنابراین در عمل یافتن A-1 با استفاده از روش تحولات اولیه (EP) راحت است. هر ماتریس غیر منفرد A را می توان با استفاده از EP تنها در ستون ها (یا فقط ردیف ها) به ماتریس هویت E تقلیل داد. اگر EP های کامل روی ماتریس A به همان ترتیب برای ماتریس هویت E اعمال شوند ، نتیجه یک ماتریس معکوس انجام EP بر روی ماتریس های A و E به طور همزمان ، نوشتن هر دو ماتریس در کنار هم از طریق یک خط راحت است. مجدداً توجه داشته باشید که هنگام یافتن فرم متعارف ماتریس به منظور یافتن ، می توانید از تغییر شکل سطرها و ستون ها استفاده کنید. در صورت نیاز به یافتن معکوس یک ماتریس ، فقط ردیف ها یا فقط ستون ها باید در فرآیند تبدیل استفاده شوند.

مثال 1... برای ماتریس پیدا کردن A -1.

راه حل.ابتدا تعیین کننده ماتریس A را پیدا می کنیم
بنابراین ، ماتریس معکوس وجود دارد و ما می توانیم آن را با فرمول پیدا کنیم: ، جایی که A i j (i ، j = 1،2،3) مکمل های جبری عناصر a i j ماتریس اصلی هستند.

جایی که .

مثال 2... با استفاده از روش تحولات ابتدایی ، A-1 را برای ماتریس پیدا کنید: A =.

راه حل.ما به ماتریس اصلی در سمت راست ماتریس هویت با همان ترتیب اختصاص می دهیم: ... با کمک تحولات ستون ابتدایی ، "نیمه" سمت چپ را به واحد می رسانیم ، همزمان دقیقاً همان تحولات را روی ماتریس سمت راست انجام می دهیم.
برای این کار ، بیایید ستون های اول و دوم را عوض کنیم: ~ ... ستون اول را به ستون سوم اضافه کنید و ستون اول را در -2 ضرب کنید: ... از ستون اول ، دوم را دو برابر می کنیم و از سوم - دوم ضرب در 6 ؛ ... بیایید ستون سوم را به ستون اول و دوم اضافه کنیم: ... بیایید ستون آخر را در 1 ضرب کنیم: ... ماتریس مربع به دست آمده در سمت راست میله عمودی معکوس ماتریس داده شده A است. بنابراین ،
.

هنگام مطالعه جبر در یک مدرسه آموزش عمومی (کلاس 9) ، یکی از مباحث مهم مطالعه توالی های عددی است که شامل پیشرفت ها - هندسی و حساب است. در این مقاله ، پیشرفت حساب و مثالها را با راه حل در نظر خواهیم گرفت.

پیشرفت حسابی چیست؟

برای درک این موضوع ، لازم است تعریفی از پیشرفت در نظر گرفته شده و همچنین فرمولهای اساسی ارائه شود که بیشتر در حل مشکلات استفاده خواهد شد.

پیشرفت حسابی یا جبری مجموعه ای از اعداد منطقی مرتب است که هر اصطلاح با مقداری ثابت با اصطلاح قبلی متفاوت است. این مقدار تفاوت نامیده می شود. یعنی ، با دانستن هر عضو از مجموعه اعداد مرتب شده و تفاوت ، می توانید کل پیشرفت حساب را بازیابی کنید.

بیایید مثالی بزنیم. دنباله اعداد زیر یک پیشرفت حسابی خواهد بود: 4 ، 8 ، 12 ، 16 ، ... ، زیرا تفاوت در این مورد 4 است (8 - 4 = 12 - 8 = 16 - 12). اما مجموعه اعداد 3 ، 5 ، 8 ، 12 ، 17 دیگر نمی تواند به نوع پیشرفت در نظر گرفته شود ، زیرا تفاوت برای آن یک مقدار ثابت نیست (5 - 3 ≠ 8 - 5 ≠ 12 - 8 ≠ 17 - 12)

فرمول های مهم

حال اجازه دهید فرمول های اساسی مورد نیاز برای حل مشکلات را با استفاده از یک پیشرفت حساب ارائه دهیم. بگذارید با n n ترمینه دنباله را نشان دهیم ، جایی که n یک عدد صحیح است. تفاوت را با حرف لاتین d نشان می دهند. سپس عبارات زیر معتبر هستند:

برای تعیین مقدار ترم n ، فرمول مناسب است: a n = (n-1) * d + a 1.
برای تعیین مجموع n اصطلاحات اول: S n = (a n + a 1) * n / 2.

برای درک هر یک از نمونه های پیشرفت حساب با یک راه حل در درجه 9 ، کافی است این دو فرمول را بخاطر بسپارید ، زیرا هر نوع مشکلی از نوع مورد استفاده بر اساس استفاده از آنها است. همچنین باید به یاد داشته باشید که تفاوت پیشرفت با فرمول تعیین می شود: d = a n - a n-1.

مثال شماره 1: یافتن عضو ناشناخته

بیایید یک مثال ساده از پیشرفت حساب و فرمولهایی ارائه دهیم که باید برای حل آنها استفاده شود.

بگذارید توالی 10 ، 8 ، 6 ، 4 ، ... داده شود ، یافتن پنج اصطلاح در آن ضروری است.

قبلاً از بیان مسئله مشخص شده است که 4 اصطلاح اول شناخته شده است. پنجم را می توان به دو روش تعریف کرد:

ابتدا تفاوت را محاسبه می کنیم. ما داریم: d = 8 - 10 = -2. به همین ترتیب ، می توان هر دو عضوی دیگر را که کنار یکدیگر ایستاده اند ، گرفت. به عنوان مثال ، d = 4 - 6 = -2. از آنجا که مشخص شده است d = a n - a n-1 ، پس d = a 5 - a 4 ، از این رو به دست می آوریم: a 5 = a 4 + d. مقادیر شناخته شده را جایگزین کنید: a 5 = 4 + (-2) = 2.
روش دوم نیز نیاز به دانستن تفاوت پیشرفت در نظر گرفته شده دارد ، بنابراین ابتدا باید آن را همانطور که در بالا نشان داده شده تعیین کنید (-2 = d). با دانستن اینکه ترم اول a 1 = 10 ، از فرمول n تعداد دنباله استفاده می کنیم. ما داریم: a n = (n - 1) * d + a 1 = (n - 1) * (-2) + 10 = 12 - 2 * n. n = 5 را با آخرین عبارت جایگزین می کنیم: a 5 = 12-2 * 5 = 2.

همانطور که می بینید ، هر دو روش حل به یک نتیجه منجر شدند. توجه داشته باشید که در این مثال ، اختلاف d پیشرفت منفی است. چنین توالی هایی در حال کاهش نامیده می شوند ، زیرا هر ترم بعدی کمتر از اصطلاح قبلی است.

مثال شماره 2: تفاوت پیشرفت

حالا بیایید کار را کمی پیچیده کنیم ، بیایید مثالی بزنیم که چگونه

مشخص شده است که در بعضی ترم های 1 برابر 6 و ترم 7 برابر 18 است. لازم است تفاوت را پیدا کنیم و این توالی را به ترم 7 بازگردانیم.

بیایید از فرمول برای تعیین اصطلاح ناشناخته استفاده کنیم: a n = (n - 1) * d + a 1. ما داده های شناخته شده از شرط را جایگزین می کنیم ، یعنی اعداد a 1 و 7 ، ما داریم: 18 = 6 + 6 * d. از این عبارت می توانید تفاوت را به راحتی محاسبه کنید: d = (18 - 6) / 6 = 2. بنابراین ، ما به قسمت اول مسئله پاسخ داده ایم.

برای بازگرداندن یک دنباله تا 7 اصطلاح ، باید از تعریف پیشرفت جبری استفاده کنید ، یعنی a 2 = a 1 + d ، 3 = a 2 + d و غیره. در نتیجه ، کل دنباله را بازیابی می کنیم: a 1 = 6 ، a 2 = 6 + 2 = 8 ، a 3 = 8 + 2 = 10 ، a 4 = 10 + 2 = 12 ، 5 = 12 + 2 = 14 ، 6 = 14 + 2 = 16 ، 7 = 18.

مثال شماره 3: پیشرفت

بگذارید وضعیت مشکل را بیش از پیش پیچیده کنیم. اکنون لازم است به این سوال پاسخ دهیم که چگونه می توان پیشرفت حساب را پیدا کرد. می توانید مثال زیر را بیاورید: برای مثال دو عدد - 4 و 5. لازم است یک پیشرفت جبری ایجاد کنید تا سه اصطلاح دیگر بین اینها جا بیفتد.

قبل از شروع به حل این مشکل ، لازم است درک کنیم که اعداد داده شده در پیشرفت آینده چه جایگاهی را اشغال می کنند. از آنجا که سه اصطلاح دیگر بین آنها وجود خواهد داشت ، پس 1 = -4 و 5 = 5. پس از ایجاد این مشکل ، به مسئله ای می پردازیم که مشابه مورد قبلی است. مجدداً ، برای دوره نهم ، از فرمول استفاده می کنیم ، بدست می آوریم: a 5 = a 1 + 4 * d. از کجا: d = (a 5 - a 1) / 4 = (5 - (-4)) / 4 = 2.25. در اینجا مقدار عددی صحیح از تفاوت را دریافت نکردیم ، اما یک عدد منطقی است ، بنابراین فرمول های پیشرفت جبری ثابت هستند.

اکنون تفاوت پیدا شده را به 1 اضافه کرده و اعضای گمشده پیشرفت را بازیابی کنید. ما بدست می آوریم: a 1 = - 4 ، a 2 = - 4 + 2.25 = - 1.75 ، 3 = -1.75 + 2.25 = 0.5 ، 4 = 0.5 + 2.25 = 2.75 ، 5 = 2.75 + 2.25 = 5 ، که همزمان است با شرایط مشکل

مثال شماره 4: اولین دوره پیشرفت

بیایید به مثال هایی از پیشرفت حساب با یک راه حل ادامه دهیم. در تمام مشکلات قبلی ، اولین شماره از پیشرفت جبری شناخته شده بود. حال مسئله ای از نوع دیگر را در نظر بگیرید: بگذارید دو عدد داده شود ، جایی که 15 = 50 و 43 = 37 باشد. لازم است عددی را پیدا کنید که این توالی از آن آغاز می شود.

فرمول های استفاده شده تاکنون دانش 1 و d را فرض می کنند. در بیانیه مسئله چیزی درباره این اعداد مشخص نیست. با این وجود ، ما عباراتی را برای هر عضوی که اطلاعاتی در مورد آنها وجود دارد ، می نویسیم: a 15 = a 1 + 14 * d و 43 = a 1 + 42 * d. دو معادله دریافت کرد که در آن 2 مقدار ناشناخته (a 1 و d). این بدان معناست که مسئله به حل یک سیستم معادلات خطی کاهش می یابد.

ساده ترین راه حل این سیستم بیان 1 در هر معادله و سپس مقایسه عبارات بدست آمده است. معادله اول: a 1 = a 15 - 14 * d = 50 - 14 * d؛ معادله دوم: a 1 = a 43 - 42 * d = 37 - 42 * d. با برابر کردن این عبارات ، به دست می آوریم: 50 - 14 * d = 37 - 42 * d ، از آنجا اختلاف d = (37 - 50) / (42 - 14) = - 0.464 (فقط 3 رقم اعشار داده می شود).

با دانستن d ، می توانید از هر دو عبارت بالا برای 1 استفاده کنید. به عنوان مثال ، اولین مورد: a 1 = 50 - 14 * d = 50 - 14 * (- 0.464) = 56.496.

اگر در نتیجه تردید دارید ، می توانید آن را بررسی کنید ، برای مثال ، 43 مدت پیشرفت را تعیین کنید ، که در شرایط مشخص شده است. ما بدست می آوریم: a 43 = a 1 + 42 * d = 56.496 + 42 * (- 0.464) = 37.008. یک خطای کوچک به دلیل این واقعیت است که از محاسبات استفاده شده از دور هزارم استفاده شده است.

مثال شماره 5: مقدار

حال بیایید به چند مثال با راه حل برای جمع پیشرفت محاسبات نگاه کنیم.

اجازه دهید یک پیشرفت عددی از شکل زیر ارائه شود: 1 ، 2 ، 3 ، 4 ، ... ،. جمع این 100 عدد را چگونه محاسبه می کنید؟

با تشکر از پیشرفت فناوری رایانه ، حل این مشکل امکان پذیر است ، یعنی می توان تمام اعداد را به صورت متوالی جمع کرد ، این کار به محض فشار دادن کلید ورود به سیستم ، توسط رایانه انجام می شود. اگر توجه کنیم که مجموعه اعداد ارائه شده یک پیشرفت جبری است و تفاوت آن در 1 است ، می توان مشکل را در ذهن حل کرد. با استفاده از فرمول جمع ، به دست می آوریم: S n = n * (a 1 + an) / 2 = 100 * (1 + 100) / 2 = 5050.

جالب است بدانید که این مشکل "Gaussian" نامیده می شود ، زیرا در آغاز قرن هجدهم آلمانی معروف ، در حالی که هنوز تنها 10 سال سن نداشت ، توانست در عرض چند ثانیه آن را در سر خود حل کند. پسر فرمول جمع یک پیشرفت جبری را نمی دانست ، اما متوجه شد که اگر اعداد حاشیه دنباله را به صورت جفت جمع کنید ، همیشه یک نتیجه می گیرید ، یعنی 1 + 100 = 2 + 99 = 3 + 98 = ... ، و از آنجایی که این مقادیر دقیقاً 50 خواهد بود (100/2) ، بنابراین برای دریافت پاسخ صحیح ، کافی است 50 را در 101 ضرب کنید.

مثال شماره 6: مجموع اعضا از n تا m

مثال معمول دیگری از جمع پیشرفت حساب به شرح زیر است: با توجه به یک سری اعداد: 3 ، 7 ، 11 ، 15 ، ... ، باید پیدا کنید که مجموع اعضای آن از 8 تا 14 برابر باشد.

مشکل از دو طریق حل می شود. اولین آنها شامل پیدا کردن اصطلاحات ناشناخته از 8 تا 14 و سپس جمع بندی متوالی آنها است. از آنجا که اصطلاحات کمی وجود دارد ، این روش به اندازه کافی پر زحمت نیست. با این وجود پیشنهاد می شود این مشکل با روش دوم که جهانی تر است حل شود.

ایده این است که فرمولی برای مجموع پیشرفت جبری بین اصطلاحات m و n بدست آورید ، جایی که n> m عدد صحیح است. بیایید برای هر دو مورد دو عبارت برای مجموع بنویسیم:

S m = m * (a m + a 1) / 2.
S n = n * (a n + a 1) / 2.

از آنجا که n> m ، بدیهی است که 2 جمع شامل اولین است. نتیجه گیری آخر به این معنی است که اگر اختلاف بین این مبالغ را بگیریم ، و اصطلاح a m را به آن اضافه کنیم (در صورت گرفتن اختلاف از مجموع S n کم می شود) ، در این صورت پاسخ لازم را برای مسئله می گیریم. ما داریم: S mn = S n - S m + am = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am = a 1 * (n - m) / 2 + an * n / 2 + am * (1- m / 2). در این عبارت لازم است فرمولها را جایگزین n و m کنید. سپس بدست می آوریم: S mn = a 1 * (n - m) / 2 + n * (a 1 + (n - 1) * d) / 2 + (a 1 + (m - 1) * d) * (1 - m / 2) = 1 * (n - m + 1) + d * n * (n - 1) / 2 + d * (3 * m - m 2 - 2) / 2.

فرمول حاصل تا حدی دست و پا گیر است ؛ با این وجود ، مجموع S mn فقط به n ، m ، a 1 و d بستگی دارد. در حالت ما ، a 1 = 3، d = 4، n = 14، m = 8. با جایگزینی این اعداد ، بدست می آوریم: S mn = 301.

همانطور که از راه حلهای ارائه شده مشاهده می شود ، همه مشکلات مبتنی بر دانش بیان برای ترم نهم و فرمول مجموع of مجموعه اصطلاحات اول است. قبل از شروع به حل هر یک از این مشکلات ، توصیه می شود شرایط را به دقت بخوانید ، آنچه را که لازم است به وضوح درک کنید و فقط پس از آن به راه حل بروید.

نکته دیگر تلاش برای سادگی است ، یعنی اگر می توانید بدون استفاده از محاسبات پیچیده ریاضی به س questionالی پاسخ دهید ، پس باید این کار را بکنید ، زیرا در این حالت احتمال خطا کمتر است. به عنوان مثال ، در یک مثال از پیشرفت حساب با راه حل شماره 6 ، می توان در فرمول S mn = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am متوقف شد ، و شکست مسئله کلی را به کارهای فرعی جداگانه (در این مورد ، ابتدا اعضای an و am را پیدا کنید).

اگر در نتیجه به دست آمده تردید دارید ، توصیه می شود آن را بررسی کنید ، همانطور که در برخی از مثال های ذکر شده انجام شد. ما فهمیدیم که چگونه می توان پیشرفت حسابی را پیدا کرد. اگر آن را بفهمید ، چندان دشوار نیست.