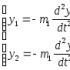ارتعاشات آزاد سیستم های با دو درجه آزادی. نوسانات آزاد کوچک یک سیستم با دو درجه آزادی فرکانس بحرانی نیروی مزاحم

نوسانات با چندین درجه آزادی.

اطلاعات مختصری از نظریه

سیستم هایی با n قدرتآزادیدر دینامیک مرسوم است که چنین سیستم هایی را صدا می زنند تا به طور کامل حالت هندسی آنها را در هر لحظه از زمان تنظیم کنید. پپارامترها، به عنوان مثال موقعیت (انحرافات) پنکته ها. موقعیت سایر نقاط با تکنیک های استاتیکی معمولی تعیین می شود.

نمونه ای از سیستم با پدرجات آزادی می تواند یک پرتو یا یک قاب صاف باشد اگر توده های تک تک اجزا یا عناصر آن به طور مشروط (برای تسهیل محاسبات دینامیکی) متمرکز در نظر گرفته شوند. پنقاط، یا اگر حامل n جرم بزرگ (موتورها، موتورها) باشد، در مقایسه با آنها می توان وزن خود عناصر را نادیده گرفت. اگر جرمهای متمرکز ("نقطه") منفرد بتوانند هنگام نوسان در دو جهت حرکت کنند، تعداد درجات آزادی سیستم برابر با تعداد اتصالاتی خواهد بود که باید به سیستم تحمیل شود تا جابجایی ها حذف شود. از همه توده ها

اگر سیستمی با n درجه آزادی از حالت تعادل خارج شود، متعهد می شود ارتعاشات رایگان، و هر "نقطه" (جرم) نوسانات پیچیده چند هارمونیک از نوع زیر را انجام می دهد:

ثابت A منو ب منبه شرایط اولیه حرکت (انحراف جرم ها از سطح ایستا و سرعت در لحظه زمان) بستگی دارد. تی=0). فقط در برخی موارد خاص از تحریک نوسانات می تواند حرکت چند هارمونیک برای توده های منفرد به هارمونیک تبدیل شود، یعنی. مانند یک سیستم با یک درجه آزادی:

تعداد فرکانس های طبیعی یک سیستم برابر است با تعداد درجات آزادی آن.

برای محاسبه فرکانس های طبیعی، لازم است که به اصطلاح تعیین کننده فرکانس را حل کنیم که به این شکل نوشته شده است:

این شرط به صورت بسط یافته معادله را نشان می دهد پدرجه هفتم برای تعیین پمقادیر ω 2 که معادله فرکانس نامیده می شود.

از طریق δ 11، δ 12، δ 22 و غیره. حرکات احتمالی نشان داده شده است. بنابراین، δ12 جابجایی در جهت اول از نقطه محل جرم اول از یک واحد نیروی اعمال شده در جهت دوم به نقطه محل جرم دوم و غیره است.

با دو درجه آزادی، معادله فرکانس به شکل زیر است:

جایی که برای دو فرکانس داریم:

در موردی که توده های منفرد M منهمچنین می تواند حرکات چرخشی یا فقط چرخشی را در ترکیب با حرکات خطی انجام دهد، سپس من-که مختصات زاویه چرخش و در فرکانس تعیین کننده جرم خواهد بود

م منباید با ممان اینرسی جرم J جایگزین شود من; بر این اساس، حرکات ممکن در جهت من-ام مختصات ( δ من 2 , δ من 2 و غیره) حرکات زاویه ای خواهد بود.

اگر جرمی در چند جهت نوسان کند - من-مو و ک-th (مثلاً عمودی و افقی)، سپس چنین جرمی چندین بار تحت اعداد M در تعیین کننده شرکت می کند. منآنها کو با چندین حرکت ممکن مطابقت دارد ( δ ii, δ kk, δ ik، و غیره.).

توجه داشته باشید که هر فرکانس طبیعی شکل خاص خود را از نوسان دارد (ماهیت یک محور منحنی، خط انحراف، جابجایی، و غیره)، که در موارد خاص ممکن است یک شکل معتبر از نوسان باشد، اگر فقط آزاد باشد. نوسانات به درستی برانگیخته می شوند (تکانه های انتخاب مناسب، نقاط کاربرد آنها و غیره). در این صورت سیستم طبق قوانین حرکتی سیستم با یک درجه آزادی نوسان خواهد کرد.

در حالت کلی، همانطور که از عبارت (9.1) به دست می آید، سیستم نوسانات چند هارمونیک را انجام می دهد، اما بدیهی است که هر خط الاستیک پیچیده ای که تأثیر همه فرکانس های طبیعی را منعکس می کند، می تواند به اجزای منفرد فرم، هر یک از آنها، تجزیه شود. که با فرکانس خودش مطابقت دارد فرآیند چنین تجزیه حالت واقعی ارتعاش به اجزاء (که هنگام حل مسائل پیچیده دینامیک سازه ضروری است) تجزیه به حالت های ارتعاشات طبیعی نامیده می شود.

اگر در هر جرم، به طور دقیق تر - در جهت هر درجه آزادی، یک نیروی مزاحم اعمال شود که بر اساس قانون هارمونیک در زمان تغییر می کند.

یا که برای اهداف بعدی بی تفاوت است و دامنه نیروها برای هر جرم متفاوت است و فرکانس و فازها یکسان است، در این صورت با اثر طولانی چنین نیروهای مزاحم، سیستم نوسانات اجباری حالت پایدار را با فرکانس انجام خواهد داد. از نیروی محرکه دامنه حرکات در هر جهت من-این مدرک در این مورد خواهد بود:

که در آن تعیین کننده D مطابق (9.2) نوشته می شود و ω با θ جایگزین می شود و بنابراین، D≠0. D منبا عبارت مشخص می شود:

آن ها منستون دهم تعیین کننده D با ستونی متشکل از عبارت های شکل جایگزین می شود: برای حالت دو درجه آزادی: (9.6)

و به همین ترتیب

هنگام محاسبه ارتعاشات اجباری تیرهایی با سطح مقطع ثابت حامل جرمهای متمرکز (شکل 9.1).

با این حال، استفاده از فرمول های زیر برای دامنه انحراف، زاویه چرخش، لنگر خمشی و نیروی برشی در هر مقطعی از تیر آسان تر است:

(9.7)

جایی که y 0 , φ 0 , م 0 , س 0 - دامنه انحراف، چرخش، گشتاور و نیروی برشی مقطع اولیه (پارامترهای اولیه). M iو جی آی- جرم و گشتاور اینرسی آن (جرم های متمرکز)؛ علامت ∑ برای تمام نیروها و جرم های متمرکز واقع از مقطع اولیه تا سوژه اعمال می شود.

فرمول های نشان داده شده (9.7) را می توان در هنگام محاسبه فرکانس های طبیعی نیز استفاده کرد که برای آنها لازم است نیروهای مزاحم در نظر گرفته شوند. آرمنو لحظات ∑ ممنبرابر صفر، فرکانس نوسانات اجباری θ را با فرکانس نوسانات طبیعی ω جایگزین کنید و با فرض وجود نوسانات (نوسانات آزاد)، عبارات (9.7) را در رابطه با مقاطعی بنویسید که توده های متمرکز در آن قرار دارند و دامنه ها از قبل مشخص شده است. بخش های مرجع، محور تقارن و غیره). ما یک سیستم معادلات خطی همگن به دست می آوریم. با معادل سازی دترمینان این سیستم با صفر، قادر به محاسبه فرکانس های طبیعی خواهیم بود.

استفاده از عبارات (9.4) و (9.5) برای تعیین دامنه توصیه می شود. y 0 , φ 0 , و غیره) در ایکس= 0، و سپس با استفاده از (9.7) تمام عناصر انحراف دیگر را محاسبه کنید.

پیچیده تر، مشکل محاسبه حرکات یک سیستم با چندین درجه آزادی تحت عمل یک بار دلخواه است که در طول زمان تغییر می کند و به توده های مختلف اعمال می شود.

هنگام حل چنین مشکلی باید به صورت زیر عمل کنید:

الف) فرکانس های طبیعی و حالت های ارتعاشات طبیعی را تعیین کنید.

ب) بار داده شده را بین توده ها مجدداً جمع کنید یا به قول آنها آن را مطابق با حالت های ارتعاشات طبیعی تجزیه کنید. تعداد گروه های بار برابر با تعداد فرکانس های طبیعی سیستم است.

ج) پس از انجام دو عمل کمکی فوق، برای هر گروه از بارها با استفاده از فرمول های شناخته شده از تئوری نوسانات یک سیستم با یک درجه آزادی، یک محاسبه انجام دهید و بسامد نوسانات طبیعی در این فرمول ها یک در نظر گرفته شود. که این گروه بار مربوط به آن است.

د) راه حل های جزئی از هر دسته از بارها خلاصه می شود که راه حل نهایی مسئله را تعیین می کند.

تعیین فرکانس های طبیعی مطابق (9.2) انجام می شود. در مورد شناسایی اشکال ارتعاشات طبیعی، در اینجا لازم است که توسط ویژگی اصلی هر شکلی از ارتعاشات طبیعی هدایت شود، که نشان دهنده خط نفوذ انحراف از نیروها است (تعداد آنها برابر است با تعداد درجات آزادی) متناسب با حاصلضرب توده ها و مختصات انحرافات نقاط اتصال توده ها. برای جرم‌های مساوی، شکل ارتعاشات طبیعی نشان‌دهنده خط انحراف از نیروهای متناسب با مختصات انحراف است. نمودار بار مشابه نمودار انحراف است.

کمترین فرکانس مربوط به ساده ترین شکل ارتعاش است. برای تیرها، اغلب این شکل با محور منحنی سیستم تحت تأثیر وزن خود مطابقت دارد. اگر این ساختار در هر جهتی، به عنوان مثال در افقی، کمتر صلب باشد، برای شناسایی ماهیت محور منحنی مورد نظر، باید به طور مشروط وزن خود را در این جهت اعمال کرد.

سیستم‌های با دو درجه آزادی، حالت خاصی از سیستم‌های دارای چند درجه آزادی هستند. اما این سیستم‌ها ساده‌ترین سیستم‌ها هستند و به فرد اجازه می‌دهند تا فرمول‌های محاسباتی نهایی را برای تعیین فرکانس‌های ارتعاش، دامنه‌ها و انحرافات دینامیکی به دست آورند.

انحراف پرتو y در اثر نیروهای اینرسی:

P 2 = 1 (1)

علائم (-) در عبارات (1) به این دلیل است که نیروها و واحدهای اینرسی. حرکات در جهت مخالف هستند.

ما معتقدیم که ارتعاشات جرمی طبق قانون هارمونیک رخ می دهد:

(2)

بیایید شتاب حرکت جرم را پیدا کنیم:

(3)

با جایگزینی عبارات (2) و (3) به معادله (1) به دست می آوریم:

(5)

دامنه نوسانات A 1 و A 2 را مجهول در نظر می گیریم و معادلات را تبدیل می کنیم:

(6)

جواب سیستم معادلات همگن A 1 = A 2 = 0 برای ما مناسب نیست؛ برای به دست آوردن جواب غیر صفر، عوامل تعیین کننده سیستم (6) را با صفر برابر می کنیم:

(7)

اجازه دهید معادله (8) را با در نظر گرفتن فرکانس دایره ای نوسانات طبیعی  ناشناخته تبدیل کنیم:

معادله (9) معادله بی هارمونیک نوسانات آزاد سیستم های با دو درجه آزادی نامیده می شود.

با جایگزینی متغیر  2 =Z به دست می آوریم

از اینجا Z 1 و Z 2 را تعیین می کنیم.

در نتیجه می توان نتایج زیر را به دست آورد:

1. ارتعاشات آزاد سیستم های با دو درجه آزادی با دو فرکانس  1 و  2 رخ می دهد. فرکانس پایین‌تر 1 را تون بنیادی یا بنیادی می‌گویند و فرکانس بالاتر 2 را فرکانس دوم یا اوورتون می‌گویند.

ارتعاشات آزاد سیستم های با n درجه آزادی، n-ton هستند که از n-ارتعاشات آزاد تشکیل شده اند.

2. حرکات جرم های m 1 و m 2 با فرمول های زیر بیان می شود:

به عنوان مثال، اگر نوسانات با فرکانس  1 رخ دهد، در هر لحظه از زمان حرکات جرم دارای علائم مشابه هستند.

اگر نوسانات فقط با فرکانس  2 رخ دهند، در این صورت حرکت جرم در هر زمان دارای علائم مخالف است.

با نوسانات همزمان جرم ها با فرکانس های  1 و  2، سیستم عمدتاً در فرکانس  1 نوسان می کند و یک نور با فرکانس  2 در این نوسانات قرار می گیرد.

اگر سیستمی با دو درجه آزادی تحت نیروی محرکه با فرکانس  باشد، لازم است که:

  0.7  1.

سخنرانی 9

نوسانات سیستم هایی با تعداد بی نهایت درجه آزادی.

تئوری ارتعاشات مکانیکی کاربردهای متعدد و بسیار متنوعی تقریباً در تمامی زمینه های فناوری دارد. صرف نظر از هدف و راه حل طراحی انواع سیستم های مکانیکی، ارتعاشات آنها تابع قوانین فیزیکی یکسانی است که بررسی آنها موضوع تئوری ارتعاشات سیستم های الاستیک است. نظریه خطی نوسانات به طور کامل توسعه یافته است. تئوری نوسانات سیستم‌هایی با درجات آزادی در قرن 18 توسط لاگرانژ در اثر کلاسیک خود "مکانیک تحلیلی" ارائه شد.

جوزف لوئیس لاگرانژ (1736 - 1813) - استاد ریاضیات در تورین از سن 19 سالگی. از سال 1759 - عضو، و از سال 1766 - رئیس آکادمی علوم برلین. از سال 1787 در پاریس زندگی می کرد. در سال 1776 او به عنوان عضو افتخاری خارجی آکادمی علوم سن پترزبورگ انتخاب شد.

در پایان قرن نوزدهم، ریلی پایه‌های تئوری خطی نوسانات سیستم‌ها را با درجه آزادی بی‌نهایت (یعنی با توزیع پیوسته جرم در کل حجم سیستم تغییر شکل‌پذیر) پایه‌گذاری کرد. در قرن بیستم، می توان گفت که نظریه خطی تکمیل شده است (روش Bubnov-Galerkin، که همچنین تعیین فرکانس های نوسان بالاتر را با استفاده از تقریب های متوالی ممکن می سازد).

جان ویلیام استرت (لرد ریلی) (1842 - 1919) - فیزیکدان انگلیسی، نویسنده تعدادی از آثار در نظریه نوسانات.

ایوان گریگوریویچ بوبنوف (1872 - 1919) - یکی از بنیانگذاران مکانیک سازه کشتی. استاد مؤسسه پلی تکنیک سنت پترزبورگ، از سال 1910 - در آکادمی دریایی.

بوریس گریگوریویچ گالرکین (1871-1945) - استاد موسسه پلی تکنیک لنینگراد.

فرمول ریلی در تئوری ارتعاشات و پایداری سیستم های الاستیک محبوبیت بیشتری دارد. ایده زیربنای اشتقاق فرمول رایلی به موارد زیر می رسد. با نوسانات آزاد تک هارمونیک (یک تن) یک سیستم الاستیک با فرکانس ، حرکات نقاط آن در زمان بر اساس قانون هارمونیک اتفاق می افتد:

که در آن  1 (x,y,z)،  2 (x,y,z)،  3 (x,y,z) توابعی از مختصات فضایی نقطه ای هستند که شکل نوسان مورد نظر (دامنه) را تعیین می کنند.

اگر این توابع شناخته شده باشند، فرکانس  ارتعاشات آزاد را می توان از شرط ثابت بودن مجموع انرژی جنبشی و پتانسیل بدن پیدا کرد. این شرط منجر به معادله ای می شود که فقط یک کمیت مجهول دارد.

با این حال، این توابع از قبل شناخته شده نیستند. ایده راهنمای روش ریلی این است که این توابع را مشخص کند و انتخاب آنها را با شرایط مرزی و شکل مورد انتظار ارتعاشات مطابقت دهد.

اجازه دهید اجرای این ایده را برای ارتعاشات خمشی صفحه یک میله با جزئیات بیشتری در نظر بگیریم؛ شکل ارتعاشات با تابع =(x) توصیف می شود. نوسانات آزاد با وابستگی توصیف می شوند

انرژی پتانسیل یک میله خم شده

(2)

انرژی جنبشی

(3)

جایی که ل- طول میله، m=m(x) شدت جرم توزیع شده میله؛

انحنای محور منحنی میله؛ - سرعت ارتعاشات عرضی.

داده شده (1)

.

(4)

(5)

با گذشت زمان، هر یک از این کمیت ها به طور مداوم تغییر می کنند، اما، طبق قانون بقای انرژی، مجموع آنها ثابت می ماند، یعنی.

یا با جایگزین کردن عبارات (4)، (5) در اینجا

(7)

این منجر به فرمول ریلی می شود:

(8)

اگر بارهای متمرکز با جرم M i با میله ای با جرم توزیع شده m همراه باشد، فرمول ریلی به شکل زیر در می آید:

(9)

کل سیر اشتقاق نشان می دهد که در چارچوب مفروضات پذیرفته شده (اعتبار نظریه فنی خمش میله ها، عدم وجود مقاومت غیر کشسان)، این فرمول در صورتی دقیق است که (x) شکل واقعی ارتعاشات باشد. . با این حال، تابع(x) از قبل ناشناخته است. اهمیت عملی فرمول ریلی این است که می توان از آن برای یافتن فرکانس طبیعی با توجه به شکل ارتعاش(x) استفاده کرد. در عین حال، یک عنصر کم و بیش جدی از نزدیکی به تصمیم وارد می شود. به همین دلیل، فرمول رایلی را گاهی فرمول تقریبی می نامند.

m=cosnt اجازه دهید تابع :(x)=ax 2 را به عنوان شکل ارتعاش در نظر بگیریم که شرایط مرزی سینماتیکی مسئله را برآورده می کند.

تعریف می کنیم:

طبق فرمول (8)

این نتیجه به طور قابل توجهی با نتیجه دقیق متفاوت است

فرمول گرامل دقیق تر است، که هنوز به اندازه فرمول ریلی محبوب نشده است (شاید به دلیل "جوانی" نسبی آن - در سال 1939 پیشنهاد شد).

اجازه دهید دوباره به همان مشکل ارتعاشات خمشی آزاد یک میله بپردازیم.

فرض کنید (x) شکل مشخص شده نوسانات آزاد میله باشد. سپس شدت حداکثر نیروهای اینرسی با عبارت m 2  تعیین می شود، که در آن، مانند قبل، m=m(x) شدت جرم توزیع شده میله است؛  2 مجذور فرکانس طبیعی است. این نیروها در لحظه ای که انحرافات حداکثر هستند، به مقدار مشخص شده می رسند، یعنی. توسط تابع(x) تعیین می شوند.

اجازه دهید عبارت بالاترین انرژی خمشی پتانسیل را بر حسب ممان خمشی ناشی از حداکثر نیروهای اینرسی بنویسیم:

. (10)

اینجا - گشتاورهای خمشی ناشی از بار m 2 . اجازه دهید ممان خمشی ناشی از بار مشروط m را نشان دهیم، یعنی.  2 برابر کمتر از نیروی اینرسی.

, (11)

و عبارت (10) را می توان به صورت زیر نوشت:

. (12)

بالاترین انرژی جنبشی، مانند بالا

. (13)

با معادل سازی عبارات (12) و (13) به فرمول گرامل می رسیم:

(14)

برای محاسبه با استفاده از این فرمول، ابتدا باید یک تابع مناسب (x) را مشخص کنید. پس از این، بار شرطی m=m(x)(x) تعیین می شود و عبارات خمش ناشی از بار شرطی m نوشته می شود. با استفاده از فرمول (14) فرکانس نوسان طبیعی سیستم تعیین می شود.

مثال: (قبلی را در نظر بگیرید)

y

m(x)·(x)=max 2

با توجه به (3.7)، سیستم معادلات برای II = 2دارای فرم:

از آنجایی که ما در مورد نوسانات آزاد صحبت می کنیم، سمت راست سیستم (3.7) برابر با صفر در نظر گرفته می شود.

ما به دنبال راه حل در فرم هستیم

پس از جایگزینی (4.23) به (4.22) دریافت می کنیم:

این سیستم معادلات برای یک دلخواه معتبر است تی،بنابراین، عبارات محصور در پرانتز برابر با صفر است. بنابراین ما یک سیستم خطی از معادلات جبری برای A و به دست می آوریم که در.

یک راه حل بی اهمیت آشکار برای این سیستم L= اوه، B = O مطابق (4.23) مربوط به عدم وجود نوسان است. با این حال، در کنار این راه حل، یک راه حل غیر ضروری L * O نیز وجود دارد، V F 0 به شرطی که تعیین کننده سیستم A ( به 2) برابر با صفر:

این تعیین کننده نامیده می شود فرکانس، و معادله نسبی است k - معادله فرکانس.عملکرد گسترش یافته A(k 2) می تواند به صورت نمایش داده شود

برنج. 4.5

برای YatsYad - ^2 > ® و با n ^-4>0 نمودار A (k 2)شکل سهمی دارد که محور آبسیسا را ​​قطع می کند (شکل 4.5).

اجازه دهید نشان دهیم که برای نوسانات حول یک موقعیت تعادلی پایدار، نابرابری های بالا برآورده می شوند. اجازه دهید بیان انرژی جنبشی را به صورت زیر تبدیل کنیم:

در q, = 0 داریم T = 0، 5 الف.

در مرحله بعد، ثابت می کنیم که ریشه های معادله فرکانس (4.25) دو مقدار مثبت هستند به 2 و به 2(در تئوری نوسانات، شاخص کمتر مربوط به فرکانس کمتر است، به عنوان مثال. k ( برای این منظور ابتدا مفهوم فرکانس جزئی را معرفی می کنیم. این اصطلاح به عنوان فرکانس طبیعی یک سیستم با یک درجه آزادی درک می شود که از سیستم اصلی با ثابت کردن همه مختصات تعمیم یافته به جز یک به دست می آید. به عنوان مثال، اگر در اولین معادلات سیستم باشد ما (4.22) قبول می کنیم q 2 = 0، سپس فرکانس جزئی خواهد بود p ( =yjc u /a n. به طور مشابه، ثابت کردن p 2 ~^c n /a 21.

برای اینکه معادله فرکانس (4.25) دو ریشه واقعی داشته باشد k xو ک 2، لازم و کافی است که اولاً نمودار تابع A (تا 2)در k = 0 دارای یک ارتین مثبت است و دوم اینکه محور x را قطع می کند. مورد فرکانس های متعدد k (= k. ) و همچنین تبدیل کمترین فرکانس به صفر در اینجا در نظر گرفته نشده است. اولین مورد از این شرایط برآورده می شود، زیرا d (0) = c„c 22 - با و> 0 تأیید صحت شرط دوم با جایگزین کردن (4.25) آسان است. k = k = p 2 ; در این مورد، اطلاعات A(p, 2) از این نوع در محاسبات مهندسی، پیش بینی ها و برآوردها را تسهیل می کند.

دو مقدار فرکانس حاصل به، و به 2مربوط به راه حل های خاص شکل (4.23) است، بنابراین راه حل کلی به شکل زیر است:

بنابراین، هر یک از مختصات تعمیم یافته در یک فرآیند نوسانی پیچیده شرکت می کند، که اضافه کردن حرکات هارمونیک با فرکانس ها، دامنه ها و فازهای مختلف است (شکل 4.6). فرکانس ها k tو به 2بنابراین در حالت کلی غیرقابل قیاس هستند q v cتوابع تناوبی نیستند

برنج. 4.6

نسبت دامنه ارتعاشات آزاد در یک فرکانس ثابت طبیعی را ضریب شکل می گویند. برای سیستمی با دو درجه آزادی، ضرایب شکل (3.= BJA."مستقیماً از معادلات (4.24) تعیین می شوند:

بنابراین، ضرایب شکل p، = V 1 /A [و r.,= V., / A.,فقط به پارامترهای سیستم بستگی دارد و به شرایط اولیه بستگی ندارد. ضرایب شکل برای فرکانس طبیعی در نظر گرفته شده است به.توزیع دامنه ها در طول مدار نوسانی ترکیب این دامنه ها به اصطلاح را تشکیل می دهد فرم ارتعاش

مقدار فاکتور شکل منفی به این معنی است که نوسانات خارج از فاز هستند.

هنگام استفاده از برنامه های کامپیوتری استاندارد، آنها گاهی اوقات استفاده می کنند ضرایب شکل نرمال شدهاین اصطلاح به معنی

در شاخص ضریب p'g منمربوط به عدد مختصات و شاخص است G-شماره فرکانس بدیهی است که یا به راحتی می توان متوجه شد که p*

در سیستم معادلات (4.28)، چهار مجهول باقی مانده A g A 2، oc، cx 2 با استفاده از شرایط اولیه تعیین می شوند:

وجود یک نیروی مقاومت خطی، درست مانند سیستم با یک درجه آزادی، منجر به میرایی نوسانات آزاد می شود.

برنج. 4.7

مثال. اجازه دهید فرکانس های طبیعی، فرکانس های جزئی و فاکتورهای شکل را برای سیستم نوسانی نشان داده شده در شکل مشخص کنیم. 4.7، آ.در نظر گرفتن جابجایی های مطلق جرم.g به عنوان مختصات تعمیم یافته، = q v x 2 = q. rاجازه دهید عبارات انرژی جنبشی و بالقوه را بنویسیم:

بدین ترتیب،

پس از جایگزینی در معادلات فرکانس (4.25) به دست می آوریم

علاوه بر این، طبق (4.29)

در شکل 4.7، بحالت های ارتعاش داده شده است. در شکل اول نوسان، جرم ها به طور همزمان در یک جهت و در جهت دوم در جهت مخالف حرکت می کنند. علاوه بر این، در مورد دوم یک مقطع ظاهر شد N،با فرکانس خاص خود در فرآیند نوسانی شرکت نمی کند k rاین به اصطلاح است واحد ارتعاش

همانطور که می دانید جسمی که به هیچ وجه در حرکاتش محدودیت نداشته باشد، آزاد نامیده می شود، زیرا می تواند در هر جهتی حرکت کند. از این رو، هر جسم صلب آزاد دارای شش درجه آزادی حرکت است. توانایی ایجاد حرکات زیر را دارد: سه حرکت انتقالی مربوط به سه سیستم مختصات اصلی و سه حرکت چرخشی حول این سه محور مختصات.

تحمیل اتصالات (تثبیت) تعداد درجات آزادی را کاهش می دهد. بنابراین، اگر جسمی در یک نقطه ثابت باشد، نمی تواند در امتداد محورهای مختصات حرکت کند، حرکات آن فقط به چرخش حول این محورها محدود می شود، یعنی. بدن سه درجه آزادی دارد. در حالتی که دو نقطه ثابت هستند، جسم فقط یک درجه آزادی دارد، فقط می تواند حول یک خط (محوری) که از هر دو نقطه عبور می کند بچرخد. و در نهایت، با سه نقطه ثابت که روی یک خط قرار نمی گیرند، تعداد درجات آزادی صفر است و هیچ حرکت بدنی نمی تواند رخ دهد. در انسان، دستگاه غیرفعال حرکت از قسمت هایی از بدن او به نام پیوند تشکیل شده است. همه آنها به یکدیگر متصل هستند، بنابراین توانایی انجام سه نوع حرکت در امتداد محورهای مختصات را از دست می دهند. آنها فقط توانایی چرخش حول این محورها را دارند. بنابراین، حداکثر درجه آزادی که یک پیوند بدنه می تواند در رابطه با پیوند دیگر مجاور آن داشته باشد، سه درجه است.

این به متحرک ترین مفاصل بدن انسان اشاره دارد که شکل کروی دارند.

اتصالات متوالی یا منشعب اعضای بدن (پیوندها) زنجیره های سینماتیکی را تشکیل می دهند.

در انسان وجود دارد:

• - زنجیره های سینماتیک بازداشتن یک انتهای متحرک آزاد، ثابت فقط در یک انتها (به عنوان مثال، یک بازو در رابطه با بدن).
• - زنجیره های سینماتیک بسته، در دو انتها ثابت شده است (مثلاً مهره - دنده - جناغ - دنده - مهره).

لازم به ذکر است که این به دامنه بالقوه حرکات در مفاصل مربوط می شود. در واقعیت، در یک فرد زنده، این شاخص ها همیشه کمتر است، که توسط کارهای متعدد محققان داخلی - P. F. Lesgaft، M. F. Ivanitsky، M. G. Prives، N. G. Ozolin و غیره در مورد میزان تحرک مفاصل استخوان در یک زندگی ثابت شده است. فرد تحت تأثیر تعدادی از عوامل مرتبط با سن، جنسیت، ویژگی های فردی، وضعیت عملکردی سیستم عصبی، میزان کشش عضلات، دمای محیط، زمان روز و در نهایت آنچه برای ورزشکاران مهم است، درجه آموزش بنابراین، در تمام اتصالات استخوانی (ناپیوسته و پیوسته)، میزان تحرک در افراد جوان بیشتر از افراد مسن است. به طور متوسط ​​زنان بیشتر از مردان هستند. میزان تحرک تحت تأثیر میزان کشش عضلاتی است که در سمت مخالف حرکت قرار دارند و همچنین قدرت عضلات تولید کننده این حرکت. هرچه عضلات اولی الاستیک‌تر و دومی قوی‌تر باشند، دامنه حرکات در یک اتصال استخوانی بیشتر است و بالعکس. مشخص است که حرکات در اتاق سرد نسبت به اتاق گرم دامنه کمتری دارد و در صبح کمتر از عصر است. استفاده از تمرینات مختلف اثرات متفاوتی بر تحرک مفاصل دارد. بنابراین، تمرین سیستماتیک با تمرینات "انعطاف پذیری" دامنه حرکت را در مفاصل افزایش می دهد، در حالی که تمرینات "قدرت"، برعکس، آن را کاهش می دهد و منجر به "سفتی" مفاصل می شود. با این حال، کاهش دامنه حرکتی مفاصل هنگام استفاده از تمرینات قدرتی مطلقاً اجتناب ناپذیر نیست. می توان با ترکیب مناسب تمرینات قدرتی و تمرینات کششی برای همان گروه های عضلانی از آن جلوگیری کرد.

در زنجیره های سینماتیک باز بدن انسان، تحرک در ده ها درجه آزادی محاسبه می شود. به عنوان مثال، تحرک مچ نسبت به کتف و تحرک تارس نسبت به لگن دارای هفت درجه آزادی و نوک انگشتان دست نسبت به سینه دارای 16 درجه آزادی است. اگر تمام درجات آزادی اندام و سر را نسبت به بدن جمع کنیم، آنگاه با عدد 105 که از موقعیت های زیر تشکیل شده است بیان می شود:

• - سر - 3 درجه آزادی؛
• - بازوها - 14 درجه آزادی؛
• - پاها - 12 درجه آزادی؛
• - دست و پا - 76 درجه آزادی.

برای مقایسه، اشاره می کنیم که اکثریت قریب به اتفاق ماشین ها تنها یک درجه آزادی حرکت دارند.

در اتصالات توپی و سوکتی، چرخش حول سه محور متقابل عمود بر هم امکان پذیر است. تعداد کل محورهایی که چرخش حول آنها در این اتصالات امکان پذیر است بی نهایت زیاد است. در نتیجه در مورد اتصالات کروی می توان گفت که پیوندهای مفصل بندی شده در آنها، از شش درجه آزادی حرکت ممکن، دارای سه درجه آزادی و سه درجه جفت هستند.

مفاصل با دو درجه آزادی حرکت و چهار درجه کوپلینگ تحرک کمتری دارند. اینها شامل مفاصل بیضی یا بیضی شکل و زین هستند، یعنی. دو محوری آنها اجازه حرکت در اطراف این دو محور را می دهند.

پیوندهای بدن در آن مفاصلی که یک محور چرخش دارند، یعنی یک درجه آزادی تحرک و در عین حال پنج درجه اتصال دارند. دارای دو نقطه ثابت

اکثر مفاصل بدن انسان دارای دو یا سه درجه آزادی هستند. با چندین درجه آزادی حرکت (دو یا بیشتر)، تعداد بی نهایت مسیر ممکن است. اتصالات استخوان های جمجمه شش درجه اتصال دارند و بی حرکت هستند. اتصال استخوان ها با کمک غضروف ها و رباط ها (سینکوندروز و سیندسموز) در برخی موارد می تواند تحرک قابل توجهی داشته باشد که بستگی به خاصیت ارتجاعی و اندازه تشکیلات غضروفی یا بافت همبند بین این استخوان ها دارد.

اجازه دهید یک سیستم با دو درجه آزادی داده شود و مختصات تعمیم یافته باشد. انرژی جنبشی و پتانسیل سیستم با فرمول (10.2) به دست می آید:

توابع T و P قطعا مثبت هستند و بنابراین:

با جایگزینی (10.2) به (10.12)، معادلات دیفرانسیل را برای نوسانات کوچک یک سیستم با دو درجه آزادی بدست می آوریم:

این سیستم دارای یک راه حل صفر A=B=0 است که مربوط به یک موقعیت تعادلی پایدار است. برای جواب های غیر صفر، از (10.15) رابطه را می سازیم:

به دلیل نابرابری های پایداری، معادله درجه دوم (با توجه به ) (10.18) دارای دو ریشه واقعی مثبت است. بیایید آنها را به ترتیب صعودی مرتب کنیم:

برای ارتعاش اصلی دوم:

(10.21)

ارتعاشات اصلی ارتعاشات هارمونیک هستند.

با جایگزینی و به نوبه خود در (10.16)، اتصالات بین دامنه های A و B را در ارتعاشات اصلی پیدا می کنیم: . فاکتورها را ضرایب شکل ویژه (ضرایب توزیع دامنه) می نامند. آنها می توانند هم مثبت و هم منفی باشند. هنگامی که هر دو مختصات در نوسان اصلی در یک فاز باشند. در - در آنتی فاز.

حرکت حاصل در امتداد هر مختصات مجموع دو نوسان اصلی خواهد بود:

(10.22)

که در آن - به شرایط اولیه بستگی دارد، - به شرایط اولیه بستگی ندارد و توسط پارامترهای خود سیستم نوسانی تعیین می شود. در حالت کلی، فرکانس ها و غیرقابل قیاس هستند و بنابراین حرکت حاصل دوره ای نخواهد بود.

1. فرکانس های طبیعی و حالت های طبیعی ارتعاش (کوچک) یک آونگ ریاضی دوتایی که توسط دو نقطه مادی با جرم مساوی m و دو میله به طول هر کدام تشکیل شده است را تعیین کنید.

یک سیستم مشابه در شکل کلی در مثال 2 (§34) در نظر گرفته شد. اجازه دهید از فرمول های (2) و (3) به دست آمده در آنجا استفاده کنیم.

وقتی، دریافت می کنیم:

از آنجایی که نوسانات کوچک هستند، بنابراین، تا نوسانات کوچک مرتبه دوم شامل:

(3)

با در نظر گرفتن (3) از (1)، توجه می کنیم:

(4)

با مقایسه (4) و (2) متوجه می شویم:

با بسط معادله (7.52) فرکانس ها، به دست می آوریم:

از (9.50) ضرایب توزیع را پیدا می کنیم: .

اولین نوسان عمده:

حرکت در فاز - در هر لحظه میله ها در یک جهت می چرخند.

تردید اصلی دوم:

حرکت در آنتی فاز - در هر لحظه میله ها دقیقاً در جهت مخالف می چرخند.

حالت های ارتعاش در شکل نشان داده شده است. 50. در ارتعاش اصلی دوم یک نقطه خاص F وجود دارد که بی حرکت می ماند. به چنین نقاطی گره می گویند. نقطه پایانی O یک گره نیست.

2. دو جسم صلب با جرم و و دو فنر با سفتی و ترکیب شده و در سیستمی که در یک صفحه افقی صاف قرار دارد و می تواند نوسانات خطی کوچک انجام دهد.

اولین نوسان عمده:

اجسام به صورت فازی به سمت راست یا چپ حرکت می کنند. دامنه نوسان جسم دوم 1.62 برابر بیشتر است.

تردید اصلی دوم:

اجسام در پادفاز حرکت می کنند: یا به سمت یکدیگر، به سمت گره، یا از گره منحرف می شوند. دامنه نوسانات جسم دوم 0.62 از دامنه بدن اول است.