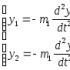Drgania swobodne układów o dwóch stopniach swobody. Małe swobodne oscylacje układu o dwóch stopniach swobody Częstotliwości krytyczne siły zakłócającej

Oscylacje o kilku stopniach swobody.

Krótka informacja z teorii.

Układy o n potęgachwolność w dynamice zwyczajowo nazywa się takie układy, aby całkowicie ustalić stan geometryczny, którego w dowolnym momencie należy ustawić P parametry, np. położenie (ugięcia) P zwrotnica. Położenie pozostałych punktów określa się konwencjonalnymi technikami statycznymi.

Przykład systemu z P stopniami swobody może być belka lub płaska rama, jeżeli masy poszczególnych jej części lub elementów warunkowo (w celu ułatwienia obliczeń dynamicznych) rozważy się skupione w P punktów, lub jeśli przenosi n dużych mas (silniki, silniki), w porównaniu z którymi można pominąć ciężar własny elementów. Jeżeli poszczególne masy skupione („punktowe”) mogą podczas oscylacji poruszać się w dwóch kierunkach, to liczba stopni swobody układu będzie równa liczbie połączeń, jakie należy nałożyć na układ, aby wyeliminować przemieszczenia wszystkich mas.

Jeśli układ z n stopniami swobody zostanie wytrącony z równowagi, popełni błąd darmowe wibracje, a każdy „punkt” (masa) będzie wykonywał złożone oscylacje poliharmoniczne typu:

Stałe A I oraz b I zależą od początkowych warunków ruchu (odchylenia mas od poziomu statycznego i prędkości w chwili T=0). Tylko w niektórych szczególnych przypadkach wzbudzenia oscylacji ruch poliharmoniczny dla poszczególnych mas może zamienić się w harmoniczny, tj. jak w układzie o jednym stopniu swobody:

Liczba częstotliwości własnych układu jest równa liczbie jego stopni swobody.

Aby obliczyć częstotliwości własne, należy rozwiązać tzw. wyznacznik częstotliwości, zapisany w postaci:

Warunek ten w postaci rozszerzonej daje równanie P stopień do ustalenia P wartości ω 2, co nazywa się równaniem częstotliwości.

Przez δ 11, δ 12, δ 22 itd. wskazane są możliwe ruchy. Zatem δ 12 jest przemieszczeniem w pierwszym kierunku punktu położenia pierwszej masy od siły jednostkowej przyłożonej w drugim kierunku do punktu położenia drugiej masy itd.

Przy dwóch stopniach swobody równanie częstotliwości przyjmuje postać:

Gdzie dla dwóch częstotliwości mamy:

W przypadku gdy poszczególne masy M I może wówczas wykonywać także ruchy obrotowe lub tylko obrotowe w połączeniu z ruchami liniowymi I- tą współrzędną będzie kąt obrotu, a w wyznaczniku częstotliwości masa

M I należy zastąpić momentem bezwładności masy J I; odpowiednio możliwe ruchy w kierunku I-te współrzędne ( δ I 2 , δ I 2 itp.) będą ruchy kątowe.

Jeśli jakakolwiek masa oscyluje w kilku kierunkach - I-mu i k-th (na przykład pionowa i pozioma), wówczas taka masa uczestniczy w wyznaczniku kilka razy pod liczbami M I ich k i odpowiada kilku możliwym ruchom ( δ II, δ kk, δ ja itp.).

Należy zauważyć, że każda częstotliwość drgań własnych ma swoją własną, specjalną formę oscylacji (charakter zakrzywionej osi, linia odchylenia, przemieszczenie itp.), która w indywidualnych, szczególnych przypadkach może okazać się ważną formą oscylacji, jeśli tylko jest swobodna drgania są odpowiednio wzbudzone (odpowiedni wybór impulsów, punkty ich przyłożenia itp.). W takim przypadku układ będzie oscylował zgodnie z prawami ruchu układu z jednym stopniem swobody.

W ogólnym przypadku, jak wynika z wyrażenia (9.1), układ wykonuje drgania poliharmoniczne, ale jest oczywiste, że dowolną złożoną linię sprężystą, która odzwierciedla wpływ wszystkich częstotliwości własnych, można rozłożyć na poszczególne składowe postaci, z których każda co odpowiada jego własnej częstotliwości Proces takiego rozkładu prawdziwego trybu drgań na składowe (co jest konieczne przy rozwiązywaniu złożonych problemów dynamiki konstrukcji) nazywany jest rozkładem na postacie drgań własnych.

Jeżeli w każdej masie, a dokładniej - w kierunku każdego stopnia swobody, przyłożona zostanie siła zakłócająca, zmienna w czasie zgodnie z prawem harmonicznym

lub, co jest obojętne dla dalszych celów, a amplitudy sił dla każdej masy są różne, a częstotliwość i fazy są takie same, to przy długotrwałym działaniu takich sił zakłócających układ będzie wykonywał wymuszone oscylacje w stanie ustalonym z częstotliwością siły napędowej. Amplitudy ruchów w dowolnym kierunku I-stopień ten w tym przypadku będzie wynosił:

gdzie wyznacznik D zapisuje się zgodnie z (9.2) zastępując ω przez θ, a zatem D≠0; D I określa się za pomocą wyrażenia:

te. I Kolumnę wyznacznika D zastępuje się kolumną złożoną z wyrazów postaci: Dla przypadku dwóch stopni swobody: (9.6)

I odpowiednio

Przy obliczaniu drgań wymuszonych belek o stałym przekroju poprzecznym przenoszących masy skupione (rys. 9.1).

Łatwiej jest jednak skorzystać z następujących wzorów na amplitudy ugięcia, kąt obrotu, moment zginający i siłę ścinającą w dowolnym przekroju belki:

(9.7)

Gdzie y 0 , φ 0 , M 0 , Q 0 – amplitudy ugięcia, obrotu, momentu i siły ścinającej przekroju początkowego (parametry początkowe); M ja I J- masa i jej moment bezwładności (masy skupione); znak ∑ dotyczy wszystkich sił i skupionych mas znajdujących się od odcinka początkowego do obiektu.

Wskazane wzory (9.7) można wykorzystać także przy obliczaniu częstotliwości drgań własnych, dla których konieczne jest uwzględnienie sił zakłócających ∑ RI i momenty ∑ MI równą zeru, zastąp częstotliwość drgań wymuszonych θ częstotliwością drgań własnych ω i zakładając istnienie oscylacji (oscylacji swobodnych) zapisz wyrażenia (9.7) w odniesieniu do odcinków, w których znajdują się skupione masy i znane są już amplitudy ( przekroje referencyjne, oś symetrii itp.). Otrzymujemy układ jednorodnych równań liniowych. Przyrównując wyznacznik tego układu do zera, będziemy mogli obliczyć częstotliwości własne.

Okazuje się, że wskazane jest użycie wyrażeń (9.4) i (9.5) do określenia amplitud ( y 0 , φ 0 , itp.) o godz X=0, a następnie korzystając z (9.7) obliczyć wszystkie pozostałe elementy uginające.

Bardziej złożony jest problem obliczania ruchów układu o kilku stopniach swobody pod działaniem dowolnego, zmieniającego się w czasie obciążenia, przyłożonego do różnych mas.

Rozwiązując taki problem, należy postępować w następujący sposób:

a) wyznaczać częstotliwości własne i postacie drgań własnych;

b) przegrupować dany ładunek pomiędzy masy lub, jak to się mówi, rozłożyć go zgodnie z modami drgań własnych. Liczba grup obciążeń jest równa liczbie częstotliwości własnych systemu;

c) po wykonaniu powyższych dwóch operacji pomocniczych należy dla każdej grupy obciążeń dokonać obliczeń korzystając ze znanych wzorów z teorii drgań układu o jednym stopniu swobody i przyjąć, że częstotliwość drgań własnych w tych wzorach jest częstotliwością któremu odpowiada ta grupa obciążeń;

d) rozwiązania cząstkowe z każdej kategorii obciążeń sumuje się, co wyznacza ostateczne rozwiązanie problemu.

Wyznaczanie częstotliwości własnych przeprowadza się zgodnie z (9.2). Jeśli chodzi o identyfikację postaci drgań własnych, to tutaj należy kierować się podstawową właściwością każdej formy drgań własnych, że reprezentuje ona linię wpływu ugięcia od sił (których liczba jest równa liczbie stopnie swobody) proporcjonalne do iloczynu mas i rzędnych ugięcia punktów mocowania mas. Dla równych mas postać drgań własnych przedstawia linię odchylenia od sił proporcjonalnych do rzędnych ugięcia; wykres obciążenia jest podobny do wykresu ugięcia.

Najniższa częstotliwość odpowiada najprostszej formie wibracji. W przypadku belek kształt ten najczęściej odpowiada zakrzywionej osi układu pod wpływem własnego ciężaru. Jeśli konstrukcja ta okaże się mniej sztywna w jakimkolwiek kierunku, na przykład w poziomie, to aby określić charakter pożądanej zakrzywionej osi, należy warunkowo przyłożyć swój własny ciężar w tym kierunku.

Układy o dwóch stopniach swobody są szczególnym przypadkiem układów o kilku stopniach swobody. Układy te są jednak najprostsze i pozwalają w ostatecznej formie otrzymać wzory obliczeniowe służące do wyznaczania częstotliwości, amplitud i ugięć dynamicznych drgań.

yUgięcia belek pod wpływem sił bezwładności:

P2 =1 (1)

Znaki (-) w wyrażeniach (1) wynikają z istnienia sił i jednostek bezwładności. ruchy są w przeciwnym kierunku.

Uważamy, że drgania mas zachodzą zgodnie z prawem harmonicznym:

(2)

Znajdźmy przyspieszenie ruchu masowego:

(3)

Podstawiając wyrażenia (2) i (3) do równania (1) otrzymujemy:

(5)

Rozważamy nieznane amplitudy oscylacji A 1 i A 2 i przekształcamy równania:

(6)

Rozwiązanie układu równań jednorodnych A 1 = A 2 =0 nam nie odpowiada, aby otrzymać rozwiązanie niezerowe, przyrównujemy wyznaczniki układu (6) do zera:

(7)

Przekształćmy równanie (8), biorąc pod uwagę częstotliwość kołową drgań własnych  nieznaną:

Równanie (9) nazywane jest równaniem biharmonicznym drgań swobodnych układów o dwóch stopniach swobody.

Zastępując zmienną  2 =Z, otrzymujemy

stąd określamy Z 1 i Z 2.

W rezultacie można wyciągnąć następujące wnioski:

1. Drgania swobodne układów o dwóch stopniach swobody występują z dwiema częstotliwościami  1 i  2. Niższa częstotliwość 1 nazywana jest tonem podstawowym lub podstawowym, wyższa częstotliwość 2 nazywana jest drugą częstotliwością lub alikwotem.

Drgania swobodne układów o n-stopniach swobody są n-tonowe i składają się z n-drgań swobodnych.

2. Ruchy mas m 1 i m 2 wyrażają następujące wzory:

tj. jeśli oscylacje występują z częstotliwością  1, to w dowolnym momencie ruchy mas mają te same znaki.

Jeśli oscylacje występują tylko z częstotliwością  2, wówczas ruchy mas w dowolnym momencie mają przeciwne znaki.

Przy równoczesnych oscylacjach mas o częstotliwościach  1 i  2, układ oscyluje głównie z częstotliwością  1, a alikwot o częstotliwości  2 wpisuje się w te oscylacje.

Jeżeli na układ o dwóch stopniach swobody działa siła napędowa o częstotliwości , to konieczne jest, aby:

  0,7  1 .

Wykład 9

Drgania układów o nieskończonej liczbie stopni swobody.

Teoria drgań mechanicznych ma liczne i bardzo różnorodne zastosowania w niemal wszystkich obszarach techniki. Niezależnie od przeznaczenia i rozwiązania konstrukcyjnego różnych układów mechanicznych, ich drgania podlegają tym samym prawom fizycznym, których badanie jest przedmiotem teorii drgań układów sprężystych. Najpełniej rozwinięta została liniowa teoria oscylacji. Teorię oscylacji układów o kilku stopniach swobody przedstawił już w XVIII wieku Lagrange w swoim klasycznym dziele „Mechanika analityczna”.

Joseph Louis Lagrange (1736 - 1813) - od 19 roku życia profesor matematyki w Turynie. Od 1759 r. członek, a od 1766 r. prezes Berlińskiej Akademii Nauk; od 1787 mieszkał w Paryżu. W 1776 roku został wybrany honorowym członkiem zagranicznym Akademii Nauk w Petersburgu.

Pod koniec XIX wieku Rayleigh położył podwaliny pod liniową teorię drgań układów o nieskończonym stopniu swobody (tj. o ciągłym rozkładzie masy w całej objętości odkształcalnego układu). W XX wieku można powiedzieć, że teoria liniowa została zakończona (metoda Bubnova-Galerkina, która umożliwia także wyznaczanie wyższych częstotliwości drgań za pomocą kolejnych przybliżeń).

John William Strett (Lord Rayleigh) (1842 - 1919) - fizyk angielski, autor szeregu prac z zakresu teorii oscylacji.

Iwan Grigoriewicz Bubnow (1872 - 1919) - jeden z twórców mechaniki konstrukcji okrętowych. Profesor Instytutu Politechnicznego w Petersburgu, od 1910 r. – Akademii Morskiej.

Borys Grigoriewicz Galerkin (1871-1945) - profesor Instytutu Politechnicznego w Leningradzie.

Wzór Rayleigha jest najbardziej popularny w teorii drgań i stabilności układów sprężystych. Idea leżąca u podstaw wyprowadzenia wzoru Rayleigha sprowadza się do następujących kwestii. Przy monoharmonicznych (jednotonowych) swobodnych oscylacjach układu sprężystego o częstotliwości  ruchy jego punktów zachodzą w czasie zgodnie z prawem harmonicznym:

gdzie  1 (x,y,z),  2 (x,y,z),  3 (x,y,z) są funkcjami współrzędnych przestrzennych punktu, które określają kształt drgań (amplitudę).

Jeżeli znane są te funkcje, to częstotliwość drgań swobodnych  można wyznaczyć z warunku, że suma energii kinetycznej i potencjalnej ciała jest stała. Warunek ten prowadzi do równania zawierającego tylko jedną nieznaną wielkość.

Funkcje te nie są jednak znane z góry. Ideą przewodnią metody Rayleigha jest określenie tych funkcji, dopasowanie ich wyboru do warunków brzegowych i oczekiwanego kształtu drgań.

Rozważmy bardziej szczegółowo realizację tego pomysłu dla drgań zginających pręta w płaszczyźnie, kształt drgań opisuje funkcja =(x). Swobodne oscylacje opisuje zależność

energia potencjalna zgiętego pręta

(2)

energia kinetyczna

(3)

Gdzie l- długość pręta, m=m(x) intensywność rozłożonej masy pręta;

Krzywizna osi zakrzywionej pręta, - prędkość drgań poprzecznych.

Biorąc pod uwagę (1)

.

(4)

(5)

Z biegiem czasu każda z tych wielkości zmienia się w sposób ciągły, ale zgodnie z prawem zachowania energii ich suma pozostaje stała, tj.

lub zastępując tutaj wyrażenia (4), (5).

(7)

Prowadzi to do wzoru Rayleigha:

(8)

Jeżeli obciążenia skupione o masach M i powiążemy z prętem o rozłożonej masie m, to wzór Rayleigha przyjmuje postać:

(9)

Z całego przebiegu wyprowadzenia wynika, że ​​w ramach przyjętych założeń (ważność technicznej teorii zginania prętów, brak oporów niesprężystych) wzór ten jest trafny, jeśli (x) jest prawdziwą postacią drgań . Jednak funkcja (x) jest z góry nieznana. Praktyczne znaczenie wzoru Rayleigha polega na tym, że można go zastosować do obliczenia częstotliwości drgań własnych , znając kształt drgań (x). Jednocześnie do decyzji wprowadzany jest mniej lub bardziej poważny element bliskości. Z tego powodu wzór Rayleigha nazywany jest czasem wzorem przybliżonym.

m=koszt Przyjmijmy za drgania funkcję:(x)=ax 2, która spełnia kinematyczne warunki brzegowe problemu.

Definiujemy:

Według wzoru (8)

Wynik ten znacznie różni się od dokładnego

Dokładniejsza jest formuła Grammela, która nie stała się jeszcze tak popularna jak formuła Rayleigha (być może ze względu na jej względną „młodość” - zaproponowano ją w 1939 r.).

Zastanówmy się jeszcze nad tym samym problemem swobodnych drgań zginających pręta.

Niech (x) będzie określoną formą drgań swobodnych pręta. Następnie intensywność maksymalnych sił bezwładności określa się za pomocą wyrażenia m 2 , gdzie jak poprzednio m=m(x) jest natężeniem rozłożonej masy pręta,  2 jest kwadratem częstotliwości drgań własnych. Siły te osiągają określoną wartość w momencie, gdy ugięcia są maksymalne, tj. są określone przez funkcję (x).

Zapiszmy wyrażenie na największą potencjalną energię zginania w postaci momentów zginających wywołanych maksymalnymi siłami bezwładności:

. (10)

Tutaj - momenty zginające wywołane obciążeniem m 2 . Oznaczmy moment zginający wywołany obciążeniem warunkowym m, tj.  2 razy mniejsza niż siła bezwładności.

, (11)

a wyrażenie (10) można zapisać jako:

. (12)

Najwyższa energia kinetyczna, taka sama jak powyżej

. (13)

Porównując wyrażenia (12) i (13) dochodzimy do wzoru Grammela:

(14)

Aby obliczyć za pomocą tego wzoru, należy najpierw określić odpowiednią funkcję (x). Następnie wyznaczane jest obciążenie warunkowe m=m(x)(x) i zapisywane są wyrażenia na zginanie spowodowane obciążeniem warunkowym m. Korzystając ze wzoru (14) wyznacza się częstotliwość drgań własnych układu.

Przykład: (rozważ poprzedni)

y

m(x)·(x)=max 2

Zgodnie z (3.7) układ równań dla II =2 ma postać:

Ponieważ mówimy o oscylacjach swobodnych, przyjmuje się, że prawa strona układu (3.7) jest równa zeru.

Szukamy rozwiązania w formie

Po podstawieniu (4.23) do (4.22) otrzymujemy:

Ten układ równań obowiązuje dla dowolnego T, dlatego wyrażenia ujęte w nawiasy kwadratowe są równe zero. W ten sposób otrzymujemy liniowy układ równań algebraicznych dla A i W.

Oczywiste trywialne rozwiązanie tego układu L= Och, B = O zgodnie z (4.23) odpowiada brakowi oscylacji. Jednak wraz z tym rozwiązaniem istnieje również rozwiązanie nietrywialne L*O, V F 0 pod warunkiem, że wyznacznik układu A ( Do 2) równe zeru:

Ten wyznacznik nazywa się częstotliwość, a równanie jest względne k - równanie częstotliwości. Rozbudowana funkcja A (ok 2) można przedstawić jako

Ryż. 4,5

Dla YatsYad - ^2 > ® i przy n ^-4>0 wykres A (k 2) ma postać paraboli przecinającej oś odciętych (ryc. 4.5).

Pokażmy, że dla oscylacji wokół stabilnego położenia równowagi spełnione są powyższe nierówności. Przekształćmy wyrażenie na energię kinetyczną w następujący sposób:

Na Q, = 0 mamy T = 0,5a.

Następnie udowadniamy, że pierwiastkami równania częstotliwości (4.25) są dwie wartości dodatnie Do 2 i do 2(w teorii oscylacji niższy wskaźnik odpowiada niższej częstotliwości, tj. k ( W tym celu najpierw wprowadzamy pojęcie częstotliwości cząstkowej. Pod tym pojęciem rozumie się częstotliwość drgań własnych układu o jednym stopniu swobody, uzyskaną z układu pierwotnego poprzez ustalenie wszystkich współrzędnych uogólnionych z wyjątkiem jednego. A więc np. jeśli w pierwszym z równań układu my (4.22) akceptujemy q 2 = 0, wówczas częstotliwość częściowa będzie wynosić p ( =yjc u /a n. Podobnie ustalenie p 2 ~^c n /a 21.

Aby równanie częstotliwości (4.25) miało dwa pierwiastki rzeczywiste k x I k 2, konieczne i wystarczające jest, aby w pierwszej kolejności narysować wykres funkcji A (do 2) Na k = 0 miałby dodatnią rzędną, a po drugie, przecinałby oś x. Przypadek wielu częstotliwości k ( = k. ), jak również zwrócenie najniższej częstotliwości do zera, nie są tutaj brane pod uwagę. Pierwszy z tych warunków jest spełniony, gdyż d (0) = c„c 22 - z I> 0 Ważność drugiego warunku łatwo sprawdzić podstawiając (4.25) k = k = p 2; w tym przypadku A(p, 2) Informacje tego typu w obliczeniach inżynierskich ułatwiają prognozowanie i szacunki.

Wynikowe dwie wartości częstotliwości Do, I do 2 odpowiadają poszczególnym rozwiązaniom postaci (4.23), zatem rozwiązanie ogólne ma postać:

Zatem każda z uogólnionych współrzędnych uczestniczy w złożonym procesie oscylacyjnym, polegającym na dodawaniu ruchów harmonicznych o różnych częstotliwościach, amplitudach i fazach (ryc. 4.6). Częstotliwości k t I do 2 w ogólnym przypadku są więc niewspółmierne qvc, nie są funkcjami okresowymi.

Ryż. 4.6

Stosunek amplitud drgań swobodnych przy ustalonej częstotliwości drgań własnych nazywany jest współczynnikiem kształtu. W przypadku układu o dwóch stopniach swobody współczynniki kształtu (3.= BJA.” wyznacza się bezpośrednio z równań (4.24):

Zatem współczynniki postaci p, = V1/A [ i r.,= V.,/A., zależą wyłącznie od parametrów systemu i nie zależą od warunków początkowych. Dla rozpatrywanej częstotliwości drgań własnych scharakteryzowano współczynniki kształtu Do. rozkład amplitud wzdłuż obwodu oscylacyjnego. Połączenie tych amplitud tworzy tzw forma wibracji.

Ujemna wartość współczynnika kształtu oznacza, że ​​oscylacje są przesunięte w fazie.

Podczas korzystania ze standardowych programów komputerowych czasami używają znormalizowane współczynniki kształtu. Termin ten oznacza

We współczynniku p'g indeks I odpowiada numerowi współrzędnej i indeksowi G- numer częstotliwości. To oczywiste lub Łatwo zauważyć, że p*

W układzie równań (4.28) pozostałe cztery niewiadome AG A 2, oc, cx 2 wyznacza się korzystając z warunków początkowych:

Występowanie liniowej siły oporu, podobnie jak w układzie o jednym stopniu swobody, prowadzi do tłumienia drgań swobodnych.

Ryż. 4.7

Przykład. Wyznaczmy częstotliwości własne, częstotliwości cząstkowe i współczynniki kształtu układu oscylacyjnego pokazanego na ryc. 4,7, A. Przyjmując bezwzględne przemieszczenia masy.g jako uogólnione współrzędne, = q v x 2 = q. R Zapiszmy wyrażenia na energię kinetyczną i potencjalną:

Zatem,

Po podstawieniu do równań częstotliwościowych (4.25) otrzymujemy

Co więcej, zgodnie z (4.29)

Na ryc. 4,7, B podane są tryby wibracji. W pierwszej formie drgań masy poruszają się synchronicznie w jednym kierunku, a w drugiej w przeciwnym. Dodatkowo w tym drugim przypadku pojawił się przekrój N, nie uczestniczy w procesie oscylacyjnym z własną częstotliwością k r Jest to tzw jednostka wibracyjna.

Jak wiadomo, ciało, które nie jest w żaden sposób ograniczone w swoich ruchach, nazywa się wolnym, ponieważ może poruszać się w dowolnym kierunku. Zatem każde swobodne ciało sztywne ma sześć stopni swobody ruchu. Posiada zdolność do wykonywania następujących ruchów: trzech ruchów translacyjnych, odpowiadających trzem głównym układom współrzędnych oraz trzech ruchów obrotowych wokół tych trzech osi współrzędnych.

Nałożenie połączeń (mocowanie) zmniejsza liczbę stopni swobody. Zatem jeśli ciało jest nieruchome w jednym punkcie, nie może poruszać się po osiach współrzędnych, jego ruchy ograniczają się jedynie do obrotu wokół tych osi, tj. ciało ma trzy stopnie swobody. W przypadku, gdy dwa punkty są ustalone, ciało ma tylko jeden stopień swobody, może obracać się jedynie wokół prostej (osi) przechodzącej przez oba te punkty. I wreszcie, w przypadku trzech stałych punktów, które nie leżą na tej samej linii, liczba stopni swobody wynosi zero i nie mogą wystąpić żadne ruchy ciała. U człowieka bierny aparat ruchu składa się z części ciała zwanych ogniwami. Wszystkie są ze sobą połączone, przez co tracą możliwość wykonywania trzech rodzajów ruchów wzdłuż osi współrzędnych. Mają jedynie możliwość obracania się wokół tych osi. Zatem maksymalna liczba stopni swobody, jaką może mieć jedno ogniwo ciała w stosunku do innego ogniwa sąsiadującego z nim, wynosi trzy.

Dotyczy to najbardziej ruchomych stawów ludzkiego ciała, które mają kulisty kształt.

Sekwencyjne lub rozgałęzione połączenia części ciała (ogniwa) tworzą łańcuchy kinematyczne.

U ludzi występują:

• - otwarte łańcuchy kinematyczne posiadający swobodnie ruchomy koniec, zamocowany tylko na jednym końcu (na przykład ramię w stosunku do ciała);
• - zamknięte łańcuchy kinematyczne, zamocowane na obu końcach (na przykład kręg - żebro - mostek - żebro - kręg).

Należy zaznaczyć, że dotyczy to potencjalnego zakresu ruchów w stawach. W rzeczywistości u żywej osoby wskaźniki te są zawsze niższe, co potwierdzają liczne prace krajowych badaczy - P. F. Lesgafta, M. F. Ivanitsky'ego, M. G. Privesa, N. G. Ozolina itp. O wielkości ruchomości w stawach kostnych w życiu człowieka, ma na niego wpływ szereg czynników związanych z wiekiem, płcią, cechami indywidualnymi, stanem funkcjonalnym układu nerwowego, stopniem rozciągnięcia mięśni, temperaturą otoczenia, porą dnia i wreszcie, co dla sportowców ważne, stopień wyszkolenia. Zatem we wszystkich połączeniach kostnych (nieciągłych i ciągłych) stopień ruchomości u osób młodych jest większy niż u osób starszych; Kobiety mają średnio więcej niż mężczyźni. Na wielkość ruchomości wpływa stopień rozciągnięcia mięśni znajdujących się po stronie przeciwnej do ruchu, a także siła mięśni wykonujących ten ruch. Im bardziej elastyczny jest pierwszy z tych mięśni i silniejszy drugi, tym większy jest zakres ruchów w danym połączeniu kostnym i odwrotnie. Wiadomo, że w chłodni ruchy mają mniejszy zasięg niż w ciepłym, rano są mniejsze niż wieczorem. Stosowanie różnych ćwiczeń ma różny wpływ na mobilność stawów. Tym samym systematyczny trening z ćwiczeniami „uelastyczniającymi” zwiększa zakres ruchu w stawach, natomiast ćwiczenia „siłowe” wręcz przeciwnie, zmniejszają go, prowadząc do „usztywnienia” stawów. Jednak zmniejszenie zakresu ruchu w stawach podczas stosowania ćwiczeń siłowych nie jest absolutnie nieuniknione. Można temu zapobiec poprzez odpowiednie połączenie treningu siłowego i ćwiczeń rozciągających dla tych samych grup mięśni.

W otwartych łańcuchach kinematycznych ciała ludzkiego mobilność oblicza się w dziesiątkach stopni swobody. Na przykład ruchomość nadgarstka względem łopatki i ruchomość stępu względem miednicy mają siedem stopni swobody, a czubków palców ręki względem klatki piersiowej mają 16 stopni swobody. Jeśli zsumujemy wszystkie stopnie swobody kończyn i głowy w stosunku do ciała, wówczas zostanie to wyrażone liczbą 105, złożoną z następujących pozycji:

• - głowa - 3 stopnie swobody;
• - ramiona - 14 stopni swobody;
• - nogi - 12 stopni swobody;
• - dłonie i stopy - 76 stopni swobody.

Dla porównania zwracamy uwagę, że zdecydowana większość maszyn ma tylko jeden stopień swobody ruchu.

W przegubach kulowych możliwe są obroty wokół trzech wzajemnie prostopadłych osi. Całkowita liczba osi, wokół których możliwe są obroty w tych przegubach, jest nieskończenie duża. W związku z tym w odniesieniu do przegubów kulistych można powiedzieć, że przegubowe w nich ogniwa, spośród możliwych sześciu stopni swobody ruchu, posiadają trzy stopnie swobody i trzy stopnie sprzężenia.

Stawy o dwóch stopniach swobody ruchu i czterech stopniach sprzężenia mają mniejszą ruchliwość. Należą do nich stawy o kształcie jajowatym lub eliptycznym oraz siodłowe, tj. dwuosiowy. Umożliwiają ruch wokół tych dwóch osi.

Ciało łączy się w tych stawach, które mają jedną oś obrotu, czyli mają jeden stopień swobody ruchu i jednocześnie pięć stopni łączności. mają dwa punkty stałe.

Większość stawów w ludzkim ciele ma dwa lub trzy stopnie swobody. Przy kilku stopniach swobody ruchu (dwa lub więcej) możliwa jest nieskończona liczba trajektorii. Połączenia kości czaszki mają sześć stopni połączenia i są nieruchome. Połączenie kości za pomocą chrząstki i więzadeł (synchondroza i syndesmoza) może w niektórych przypadkach wykazywać znaczną ruchliwość, która zależy od elastyczności i wielkości formacji chrzęstnych lub tkanki łącznej znajdujących się pomiędzy tymi kościami.

Niech będzie dany układ o dwóch stopniach swobody i są to współrzędne uogólnione. Energię kinetyczną i potencjalną układu wyrażają wzory (10.2):

Funkcje T i P są zdecydowanie dodatnie, a zatem:

Podstawiając (10.2) do (10.12) otrzymujemy równania różniczkowe dla małych drgań układu o dwóch stopniach swobody:

Układ ma rozwiązanie zerowe A=B=0, odpowiadające stabilnemu położeniu równowagi. Dla rozwiązań niezerowych tworzymy z (10.15) relację:

Ze względu na nierówności stabilności równanie kwadratowe (ze względu na ) (10.18) ma dwa rzeczywiste pierwiastki dodatnie. Uporządkujmy je rosnąco:

Dla drugiej wibracji głównej:

(10.21)

Główne wibracje to drgania harmoniczne.

Podstawiając i z kolei w (10.16) znajdujemy powiązania pomiędzy amplitudami A i B w drganiach głównych: . Czynniki te nazywane są współczynnikami postaci własnej (współczynnikami rozkładu amplitudy). Mogą być zarówno pozytywne, jak i negatywne. Gdy obie współrzędne w oscylacji głównej są w tej samej fazie; w - w przeciwfazie.

Wynikowy ruch wzdłuż każdej współrzędnej będzie sumą dwóch głównych oscylacji:

(10.22)

gdzie - zależą od warunków początkowych, - nie zależą od warunków początkowych i są określone przez parametry samego układu oscylacyjnego. W ogólnym przypadku częstotliwości i są niewspółmierne i dlatego powstały ruch nie będzie okresowy.

1. Wyznacz częstotliwości własne i drgania własne (małe) podwójnego wahadła matematycznego utworzonego przez dwa punkty materialne o jednakowych masach m i dwa pręty o długości każdy.

Podobny system w ogólnej formie rozważano w przykładzie 2 (§34). Skorzystajmy z uzyskanych tam wzorów (2) i (3).

Kiedy dostaniemy:

Ponieważ oscylacje są małe, to aż do małych oscylacji drugiego rzędu włącznie:

(3)

Biorąc pod uwagę (3) z (1), zauważamy:

(4)

Porównując (4) i (2) zauważamy:

Rozwijając równanie (7.52) częstotliwości, otrzymujemy:

Z (9.50) znajdujemy współczynniki rozkładu: .

Pierwsza duża oscylacja:

Ruch w fazie - w każdym momencie pręty obracają się w jednym kierunku.

Drugie główne wahanie:

Ruch w przeciwfazie - w każdej chwili pręty obracają się w dokładnie przeciwnych kierunkach.

Tryby wibracji pokazano na rys. 50. W drugiej wibracji głównej znajduje się specjalny punkt F, który pozostaje nieruchomy. Takie punkty nazywane są węzłami. Punkt końcowy O nie jest węzłem.

2. Dwa sztywne ciała z masami i dwie sprężyny o sztywności połączone są w układ umieszczony na gładkiej płaszczyźnie poziomej i mogący wykonywać niewielkie oscylacje liniowe.

Pierwsza duża oscylacja:

Ciała poruszają się w fazie, albo w prawo, albo w lewo. Amplituda drgań drugiego ciała jest 1,62 razy większa.

Drugie główne wahanie:

Ciała poruszają się w przeciwfazie: albo ku sobie, w kierunku węzła, albo odbiegają od węzła. Amplituda drgań drugiego ciała wynosi 0,62 amplitudy pierwszego.