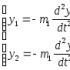Вільні коливання систем із двома ступенями свободи. Малі вільні коливання системи з двома ступенями свободи Критичні частоти сили, що обурює
Коливання з кількома ступенями свободи.
Короткі відомості із теорії.
Системами з п ступенямисвободиприйнято в динаміці називати такі системи, для повної фіксації геометричного стану яких у будь-який момент часу потрібно задати ппараметрів, наприклад положення (прогини) пточок. Положення інших точок визначається звичайними статичними прийомами.
Прикладом системи з пступенями свободи може служити балка або плоска рама, якщо маси її окремих частин або елементів умовно (для полегшення динамічного розрахунку) вважаються зосередженими в пточках, або якщо вона несе п великих мас (двигуни, мотори), в порівнянні з якими можна знехтувати власною вагою елементів. Якщо окремі зосереджені («точкові») маси можуть при коливаннях здійснювати переміщення за двома напрямами, то число ступенів свободи системи дорівнюватиме кількості зв'язків, які слід накласти на систему, щоб ліквідувати зміщення всіх мас.
Якщо вивести з рівноваги систему з ступенями свободи, то вона буде здійснювати вільні коливання, причому кожна «точка» (маса) здійснюватиме складні полігармонічні коливання типу:
Постійні А iі В iзалежать від початкових умов руху (відхилень мас від статичного рівня та швидкостей у момент часу t=0). Лише деяких, особливих, випадках порушення коливань полігармонійний рух окремих мас може перейти в гармонійне, тобто. як у системі з одним ступенем свободи:
Число власних частот системи дорівнює числу її ступенів свободи.
Для обчислення власних частот необхідно вирішити так званий визначник частот, що записується у такому вигляді:
Ця умова у розгорнутому вигляді дає рівняння п-ого ступеня для визначення пзначень 2, яке називається рівнянням частот.
Через δ 11 , δ 12 , δ 22 і т.д. позначені можливі переміщення. Так, 12 є переміщення по першому напрямку точки розташування першої маси від одиничної сили, прикладеної по другому напрямку до точки розташування другої маси і т.д.
При двох ступенях свободи рівняння частот набуває вигляду:
Звідки для двох частот маємо:
У тому випадку, коли окремі маси М iможуть здійснювати разом із лінійними переміщеннями також обертальні чи лише обертальні руху, то i-тою координатою буде кут обертання, і в визначнику частот масу
М iслід замінити моментом інерції маси J i; відповідно можливі переміщення за напрямом iтієї координати ( δ i 2 , δ i 2 і т.д.) будуть кутовими переміщеннями.
Якщо будь-яка маса буде робити коливання за кількома напрямками - i-му і k-му (наприклад, по вертикальному та горизонтальному), то така маса бере участь у визначнику кілька разів під номерами М iта М kі їй відповідає кілька можливих переміщень ( δ ii, δ kk, δ ik, і т.д.).
Зауважимо, що кожній власній частоті властива своя особлива форма коливань (характер вигнутої осі, лінії прогинів, переміщень тощо), яка в окремих, особливих випадках може виявитися дійсною формою коливань, якщо тільки належним чином або збуджені вільні коливання (належний підбір імпульсів, точок їх застосування і т.п.). В цьому випадку коливання системи відбуватимуться за законами руху системи з одним ступенем свободи.
У загальному випадку, як це випливає з виразу (9.1), система здійснює полігармонічні коливання, але, очевидно, що будь-яка складна пружна лінія, в якій відображається вплив усіх власних частот, може бути розкладена на окремі складові форми, кожна з яких відповідає своїй власній частоті. Процес такого розкладання справжньої форми коливань на складові (що необхідно при вирішенні складних завдань будівельної динамі) зветься розкладання за формами власних коливань.
Якщо в кожній масі, точніше – за кожним ступенем свободи, докласти обурливу силу, що змінюється за часом за гармонічним законом
або , що для подальшого байдуже, причому амплітуди сил при кожній мас різні, а частота і фаз однакові, то при тривалій дії таких збурювальних сил система буде здійснювати вимушені коливання з частотою змушує сили. Амплітуди переміщень за напрямком будь-який i-Такої міри в цьому випадку буде:де визначник D записується по (9.2) із заміною ω на θ і, отже, D≠0; D iвизначається виразом:
тобто. i-й стовпець визначника D замінюється стовпцем, складеним із членом виду: Для випадку двох ступенів свободи: (9.6)І відповідно
Розраховуючи на вимушені коливання балок постійного перерізу, що несуть зосереджені маси (рис.9.1).
Простіше, однак, користуватися нижченаведеними формулами для амплітуд прогину, кута повороту, згинального моменту та поперечної сили в будь-якому перерізі балки:
(9.7)де y 0 , φ 0 , M 0 , Q 0 – амплітуди прогину, повороту, моменту та поперечної сили початкового перерізу (початкові параметри); M iі J i- маса та її момент інерції (зосереджені маси); знак ∑ поширюється на всі сили та зосереджені маси, розташовані від початкового перерізу до обстежуваного.
Зазначеними формулами (9.7) можна користуватися і при обчисленні власних частот, для чого необхідно вважати сили, що обурюють ∑ Рiта моменти ∑ Мiрівними нулю, замінити частоту вимушених коливань θ частотою власних коливань ω і, припускаючи існування коливань (вільних коливань), написати вирази (9.7) стосовно перерізів, де розташовані зосереджені маси і вже відомі амплітуди (опорні перерізи, ось. ). Отримаємо систему однорідних лінійних рівнянь. Прирівнюючи до нуля визначник цієї системи, матимемо можливість обчислити власні частоти.
Доцільним, виявляється використовувати вирази (9.4) та (9.5) для визначення амплітуд ( y 0 , φ 0 , і т.п.) при х=0, а потім за допомогою (9.7) обчислити всі інші елементи прогину.
Більш складною є завдання розрахунку рухів системи з декількома ступенями свободи на дію довільного навантаження, що змінюється в часі та додається до різних мас.
При розв'язанні такого завдання слід чинити так:
а) визначити власні частоти та форми власних коливань;
б) задане навантаження перегрупувати між масами або, як кажуть, розкласти за формами власних коливань. Число груп навантажень дорівнює числу власних частот системи;
в) після виконання зазначених вище двох допоміжних операцій зробити розрахунок для кожної групи навантажень за відомими формулами з теорії коливань системи з одним ступенем свободи, причому частота власних коливань у цих формулах приймається та, якій відповідає дана група навантаження;
г) приватні рішення від кожної категорії навантажень підсумовують, чим визначається остаточне рішення задачі.
Визначення власних частот виконується згідно (9.2). Що стосується виявлення форм власних коливань, то тут необхідно керуватися тим основним властивістю будь-якої форми власних коливань, що вона є лінією впливу прогину від сил (число яких дорівнює числу ступенів свободи), пропорційних добутку мас на ординати прогинів точок прикріплення мас. За рівних мас форма власних коливань представляє лінію прогину від сил, пропорційних ординатам прогину; епюра навантаження подібна до епюрі прогину.
Нижчій частоті відповідає найпростіша форма коливань. Для балок найчастіше ця форма близько відповідає вигнутій осі системи під впливом власної ваги. Якщо дана конструкція виявляється менш жорсткою в якомусь напрямку, наприклад, у горизонтальному, то для виявлення характеру шуканої вигнутої осі слід умовно власну вагу докласти в цьому напрямку.
Системи з двома ступенями свободи є окремим випадком систем з кількома ступенями свободи. Але ці системи є найпростішими, що дозволяють отримати в кінцевому вигляді розрахункові формули для визначення частот коливань, амплітуд і динамічних прогинів.
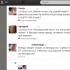
yПрогини балки від дії інерційних сил:
P 2 = 1  (1)
(1)
Знаки (-) у виразах (1) викликані тим, що інерційні сили та од. переміщення мають протилежний напрямок.
Вважаємо, що коливання мас відбуваються за гармонійним законом:
 (2)
(2)
Знайдемо прискорення руху мас:
 (3)
(3)
Підставляючи вираз (2) та (3) в рівняння (1) отримаємо:
 (5)
(5)
Невідомими вважаємо амплітуди коливань А1 і А2, перетворюємо рівняння:
 (6)
(6)
Розв'язання системи однорідних рівнянь А 1 = А 2 =0 нас не влаштовує, щоб отримає не нульове рішення, прирівняємо нулю детермінант системи (6):
 (7)
(7)
перетворимо рівняння (8), вважаючи невідомою кругову частоту власних коливань :
Рівняння (9) називається бігармонічним рівнянням вільних коливань систем із двома ступенями свободи.
Замінюючи змінну 2 =Z, отримаємо
звідси визначаємо Z1 і Z2.
![]()
У результаті можна зробити такі висновки:
1. Вільні коливання систем із двома ступенями свободи відбуваються із двома частотами 1 та 2 . Нижча частота 1 називається основний або основним тоном, більш висока частота 2 - називається другою частотою або обертоном.
Вільні коливання систем з n-ступенями свободи є n-тонними, що складаються з вільних коливань.
2. Переміщення мас m 1 іm 2 виражаються такими формулами:

тобто, якщо коливання відбуваються з частотою 1 , то в будь-який момент часу переміщення мас мають однакові знаки.
Якщо коливання відбуваються лише з частотою 2 , то переміщення мас у будь-який момент часу мають протилежні знаки.
При одночасному коливанні мас з частотами 1 і 2 система в основному коливається по частоті 1 і в ці коливання вписується обертон з частотою 2 .
Якщо на систему з двома ступенями свободи діють сила з частотою , то необхідно щоб:
0,7 1 .
Лекція 9
Коливання систем із нескінченним числом ступенів свободи.
Теорія механічних коливань має багаточисельні та дуже різноманітні додатки чи не у всіх галузях техніки. Незалежно від призначення та конструктивного рішення різних механічних систем їх коливання підпорядковуються одним і тим же фізичним закономірностям, вивчення яких і є предметом теорії коливань пружних систем. Найбільш повно розроблено лінійну теорію коливань. Теорія коливань систем з кількома ступенями свободи була дана ще у XVIII столітті Лагранжем у його класичній праці "Аналітична механіка".
Жозеф Луї Лагранж (1736 – 1813) – з 19-річного віку професор математики в Турині. З 1759 - член, а з 1766 - президент Берлінської Академії наук; з 1787 жив у Парижі. У 1776 був обраний почесним іноземним членом Петербурзької Академії наук.
Наприкінці ХІХ століття Релеєм було закладено основи лінійної теорії коливань систем із нескінченним ступенем ступенів свободи (тобто з безперервним розподілом маси з усього обсягу деформируемой системи). У XX столітті лінійну теорію, можна сказати, було завершено (метод Бубнова-Галеркіна, який дозволяє за допомогою послідовних наближень визначати також вищі частоти коливань).
Джон Вільям Стретт (лорд Релей) (1842 – 1919) – англійський фізик, автор низки робіт з теорії коливань.
Іван Григорович Бубнов (1872 – 1919) – один із основоположників будівельної механіки корабля. Професор Петербурзького політехнічного інституту, з 1910 року – Морської академії.
Борис Григорович Галеркін (1871-1945) – професор Ленінградського політехнічного інституту.
Формула Релея найбільш популярна в теорії коливань та стійкості пружних систем. Ідея, що лежить в основі виведення формули Релея, зводиться до наступного. При моногармонійних (однотонних) вільних коливаннях пружної системи з частотою , переміщення її точок відбуваються в часі за гармонічним законом:

де 1 (x, y, z), 2 (x, y, z), 3 (x, y, z) - функції просторових координат точки, що визначають розглянуту форму коливань (амплітудну).
Якщо ці функції відомі, то частоту вільних коливань можна знайти з умови сталості суми кінетичної та потенційної енергії тіла. Ця умова призводить до рівняння, що містить лише одну невідому величину.
Однак ці функції заздалегідь невідомі. Керівна ідея методу Релея полягає в тому, щоб задаватися цими функціями, узгоджуючи їх вибір із граничними умовами та очікуваною формою коливань.
Докладніше розглянемо реалізацію цієї ідеї для плоских згинальних коливань стрижня, форма коливань описується функцією =(x). Вільні коливання описуються залежністю
потенційна енергія вигнутого стрижня
 (2)
(2)
кінетична енергія
 (3)
(3)
де l- Довжина стрижня, m=m(x) інтенсивність розподіленої маси стрижня;
Кривизна вигнутої осі стрижня; - Швидкість поперечних коливань.
Враховуючи (1)
![]() .
.
 (4)
(4)
![]() (5)
(5)
З часом кожна з цих величин безперервно змінюється, але, відповідно до закону збереження енергії, їх сума залишається постійною, тобто.
або підставляючи сюди вирази (4), (5)
 (7)
(7)
Звідси випливає формула Релея:
 (8)
(8)
Якщо зі стрижнем з розподіленою масою m, пов'язані зосереджені вантажі з масами M i , то формула Релея набуває вигляду:
 (9)
(9)
Весь хід висновку показує, що в рамках прийнятих припущень (справедливість технічної теорії згинання стрижнів, відсутності непружних опорів) ця формула точна, якщо (x) – справжня форма коливань. Однак функція (x) заздалегідь невідома. Практичне значення формули Релея у тому, що з її допомогою можна знайти власну частоту, задаючись формою коливань(x). При цьому рішення вноситься більш-менш серйозний елемент наближеності. Тому формулу Релея іноді називають наближеною.
 m=cosntПриймемо як форму коливань функцію:(x)=ax 2 , яка задовольняє кінематичним граничним умовам завдання.
m=cosntПриймемо як форму коливань функцію:(x)=ax 2 , яка задовольняє кінематичним граничним умовам завдання.
Визначаємо:

За формулою (8)
Цей результат значно відрізняється від точного
Точнішою є формула Граммеля, яка досі ще не стала такою популярною, як формула Релея (можливо, внаслідок своєї відносної "молодості" - вона запропонована у 1939 році).
Знову зупинимося на тій самій задачі про вільні згинальні коливання стрижня.
Нехай (x) - задається форма вільних коливань стрижня. Тоді інтенсивність максимальних сил інерції визначається виразом m 2 , де як і раніше m=m(x) - інтенсивність розподіленої маси стрижня; 2 - квадрат власної частоти. Ці сили досягають зазначеного значення на той час, коли прогини максимальні, тобто. визначаються функцією (x).
Запишемо вираз найбільшої потенційної енергії вигину через згинальні моменти, що викликаються максимальними силами інерції:
 . (10)
. (10)
Тут ![]() - згинальні моменти, що викликаються навантаженням m 2 . Позначимо изг - згинальний момент, викликаний умовним навантаженням m, тобто. в 2 разів менший, ніж сили інерції.
- згинальні моменти, що викликаються навантаженням m 2 . Позначимо изг - згинальний момент, викликаний умовним навантаженням m, тобто. в 2 разів менший, ніж сили інерції.
![]() ,
(11)
,
(11)
і вираз (10) можна записати у вигляді:
 . (12)
. (12)
Найбільша кінетична енергія, як і вище
![]() . (13)
. (13)
Прирівнюючи вирази (12) та (13) приходимо до формули Граммеля:
 (14)
(14)
Для обчислень за цією формулою необхідно насамперед поставити відповідну функцію (x). Після цього визначається умовне навантаження m=m(x)(x) і записуються вирази ізг викликані умовним навантаженням m. За формулою (14) визначають частоту своїх коливань системи.
Приклад: (Розглядаємо попередній)
y 
m(x)·(x)=max 2


Згідно (3.7), система рівнянь при II = 2має вигляд:
Оскільки йдеться про вільні коливання, права частина системи (3.7) прийнята рівною нулю.
Рішення шукаємо у вигляді
Після підстановки (4.23) (4.22) отримаємо:
Ця система рівнянь справедлива при довільному t,тому вирази, укладені у квадратні дужки, дорівнюють нулю. Тим самим отримуємо лінійну систему рівнянь алгебри щодо Л і Ст.
Очевидне тривіальне вирішення цієї системи Л= О, В =Про відповідно (4.23) відповідає відсутності коливань. Однак поряд із цим рішенням існує і нетривіальне рішення Л*О, У Ф 0 за умови, що визначник системи А ( до 2) дорівнює нулю:

Цей визначник називають частотним, а рівняння щодо k – частотним рівнянням.У розкритому вигляді функція A(k 2) може бути представлена як


Мал. 4.5
При ЯцЯд - ^2 > ® і з п ^-4>0 графік A (k 2)має вигляд параболи, що перетинає вісь абсцис (рис. 4.5).
Покажемо, що з коливань біля стійкого становища рівноваги наведені вище нерівності дотримуються. Перетворення вираз для кінетичної енергії наступним чином:

При q, = 0 маємо Т = 0,5a.
Далі доведемо, що корінням частотного рівняння (4.25) є два позитивні значення до 2 та до 2(Теорією коливань меншому індексу відповідає менша частота, тобто. k ( З цією метою введемо спочатку поняття парціальної частоти. Під цим терміном розуміють власну частоту системи з одним ступенем свободи, отриманої з вихідної системи закріпленням всіх узагальнених координат, крім однієї. Так, наприклад, якщо в першому з рівнянь системи ми (4.22) прийняти q 2 = 0, то парціальною частотою буде p (= yjc u /a n. Аналогічно, закріплюючи р 2 ~^с п /а 21 .
Щоб частотне рівняння (4.25) мало два дійсні корені до хі k 2 необхідно і достатньо, щоб, по-перше, графік функції А (До 2)при до = 0 мав би позитивну ординату, а по-друге, щоб він перетинав вісь абсцис. Випадок кратних частот до ( = до. ) , і навіть звернення нижчої частоти на нуль, тут розглядається. Перше з цих умов дотримується, оскільки д (0) = с„з 22 - з і> 0 У справедливості другої умови легко переконатися, підставивши залежність (4.25) до = до = р 2; при цьому А(р, 2) Інформація такого роду при інженерному розрахунку полегшує прогнози та оцінки.
Отриманим двом значенням частот до, і до 2відповідають приватні рішення виду (4.23), тому загальне рішення має таку форму:
Таким чином, кожна з узагальнених координат бере участь у складному коливальному процесі, що є додаванням гармонійних рухів з різними частотами, амплітудами і фазами (рис. 4.6). Частоти k tі до 2у загальному випадку непорівнянні, тому q v ц,є періодичними функціями.

Мал. 4.6
Відношення амплітуд вільних коливань при фіксованій частоті називають коефіцієнтом форми. Для системи з двома ступенями свободи коефіцієнти форми (3.= BJA."визначаються безпосередньо з рівнянь (4.24):
Таким чином, коефіцієнти форми р = У 1/А [та р.,= Ст,/А.,залежать лише від параметрів системи та не залежать від початкових умов. Коефіцієнти форми характеризують для власної частоти, що розглядається. до.розподіл амплітуд за коливальним ланцюгом. Сукупність цих амплітуд утворює так звану форму коливань.
Негативне значення коефіцієнта форми означає, що коливання перебувають у протифазах.
При використанні стандартних програм на ЕОМ іноді використовують нормовані коефіцієнти форми.Під цим терміном розуміють

У коефіцієнті р′г індекс iвідповідає номеру координати, а індекс г-номер частоти. Очевидно, що ![]() або Легко помітити, що р *
або Легко помітити, що р *
У системі рівнянь (4.28) чотири невідомі залишилися А г А 2 , ос, сх 2 визначаються за допомогою початкових умов:
Наявність лінійної сили опору так само, як і в системі з одним ступенем свободи, призводить до загасання вільних коливань.

Мал. 4.7
приклад. Визначимо власні частоти, парціальні частоти та коефіцієнти форми для коливальної системи, показаної на рис. 4.7, а.Приймаючи як узагальнені координати абсолютні переміщення мас.г, = q v x 2 = q. rзапишемо вирази для кінетичної та потенційної енергій:

Таким чином,
Після підстановки частотні рівняння (4.25) отримуємо
![]()
При цьому Згідно (4.29)
На рис. 4.7, бнаведено форми коливань. При першій формі коливань маси переміщуються синхронно в одному напрямку, а при другій – зустрічно. Крім того, в останньому випадку з'явився перетин N,що не бере участі в коливальному процесі з власною частотою k rЦе так званий вузол коливань.
Як відомо, тіло, нічим не обмежене в рухах, називається вільним, оскільки може рухатися у будь-якому напрямку. Звідси кожне вільне тверде тіло має шість ступенів свободи руху. Воно має можливість проводити такі переміщення: три переміщення поступального характеру, відповідно трьом основним системам координат, і три обертальних руху навколо цих трьох координатних осей.
Накладення зв'язків (закріплення) зменшує кількість ступенів свободи. Так, якщо тіло в одній своїй точці закріплено, воно не може переміщатися вздовж координатних осей, його рухи обмежуються лише обертанням навколо цих осей, тобто. тіло має три ступені свободи. У тому випадку, коли закріпленими є дві точки, тіло має лише один ступінь свободи, воно може лише обертатися навколо лінії (осі), що проходить через обидві ці точки. І нарешті, при трьох закріплених точках, що не лежать на одній лінії, кількість ступенів свободи дорівнює нулю, і ніяких рухів тіла не може бути. Людина пасивний апарат руху становлять частини його тіла, звані ланками. Всі вони з'єднані між собою, тому втрачають можливість до трьох видів рухів уздовж координатних осей. Вони залишаються лише можливості обертання навколо цих осей. Таким чином, максимальна кількість ступенів свободи, якою може мати одну ланку тіла по відношенню до іншої ланки, суміжної з нею, дорівнює трьом.
Це відноситься до найбільш рухливих суглобів людського тіла, що мають кулясту форму.
Послідовно або розгалужені сполуки частин тіла (ланок) утворюють кінематичні ланцюги.
У людини розрізняють:
- - відкриті кінематичні ланцюги, що мають вільний рухомий кінець, закріплений лише на одному своєму кінці (наприклад, рука по відношенню до тулуба);
- - замкнені кінематичні ланцюги, закріплені на обох кінцях (наприклад, хребець – ребро – грудина – ребро – хребець).
Слід зазначити, що це потенційно можливих розмахів рухів у суглобах. Насправді ж у живої людини ці показники завжди менші, що доведено численними роботами вітчизняних дослідників - П. Ф. Лесгафтом, М. Ф. Іваницьким, М. Г. Привагою, Н. Г. Озоліним та ін. На величину рухливості у з'єднаннях кісток у живої людини впливає ряд факторів, пов'язаних із віком, статтю, індивідуальними особливостями, функціональним станом нервової системи, ступенем розтягування м'язів, температурою навколишнього середовища, часом дня і, нарешті, що важливо для спортсменів, ступенем тренованості. Так, у всіх сполуках кісток (перервних та безперервних) ступінь рухливості в осіб молодого віку більший, ніж у старшого віку; у жінок у середньому більше, ніж у чоловіків. На величину рухливості впливає ступінь розтягування м'язів, що знаходяться на стороні, протилежній руху, а також сила м'язів, що виробляють цей рух. Чим еластичніші перші з названих м'язів і сильніші за другі, тим розмах рухів у даному з'єднанні кісток більше, і навпаки. Відомо, що у холодному приміщенні руху мають менший розмах, ніж у теплому, вранці вони менші, ніж увечері. Застосування різних вправ по-різному впливає рухливість сполук. Так, систематичні тренування вправами «на гнучкість» збільшують амплітуду рухів у з'єднаннях, тоді як «силові» вправи, навпаки, зменшують її, призводячи до «закріпачення» суглобів. Однак зменшення амплітуди рухів у суглобах при застосуванні силових вправ не є абсолютно неминучим. Його можна запобігти правильним поєднанням силових вправ з вправами на розтягнення тих самих м'язових груп.
У відкритих кінематичних ланцюгах людського тіла рухливість обчислюється десятками ступенів волі. Наприклад, рухливість зап'ястя щодо лопатки та рухливість передплюсни щодо тазу налічує по сім ступенів свободи, а кінчики пальців кисті щодо грудної клітки – 16 ступенів свободи. Якщо підсумовувати всі ступені свободи кінцівок і голови щодо тулуба, то це виразиться числом 105, що складається з наступних позицій:
- - голова – 3 ступеня свободи;
- - руки – 14 ступенів свободи;
- - ноги – 12 ступенів свободи;
- - кисті та стопи - 76 ступенів свободи.
Для порівняння вкажемо, що переважна більшість машин має лише один ступінь свободи рухів.
У кулястих суглобах можливі обертання близько трьох взаємно перпендикулярних осей. Загальна кількість осей, біля яких можливі в цих суглобах обертання, до нескінченності велика. Отже, щодо кулястих суглобів можна сказати, що ланки, що зчленовуються в них, з можливих шести ступенів свободи рухів мають три ступені свободи і три ступені пов'язаності.
Меншу рухливість мають суглоби з двома ступенями свободи рухів і чотирма ступенями зв'язаності. До них відносяться суглоби яйцеподібної або еліпсоподібної та сідловиної форм, тобто. двовісні. Вони можливі рухи навколо цих двох осей.
Один ступінь свободи рухливості разом із цим п'ять ступенів пов'язаності мають ланки тіла у тих суглобах, які мають однієї віссю обертання, тобто. мають дві закріплені точки.
У переважній частині суглобів тіла людини два або три ступені свободи. При кількох ступенях свободи рухів (двох або більше) можливе безліч траєкторій. З'єднання кісток черепа мають шість ступенів зв'язаності та є нерухомими. З'єднання кісток за допомогою хрящів і зв'язок (синхондрози та синдесмози) можуть мати в деяких випадках значну рухливість, яка залежить від еластичності та від розмірів хрящових або сполучнотканинних утворень, що знаходяться між даними кістками.
Нехай дана система з двома ступенями свободи та - узагальнені координати. Кінетична та потенційна енергія системи дається формулами (10.2):
Функції Т і П виразно позитивні, а тому:
Підставивши (10.2) (10.12), отримаємо диференціальні рівняння малих коливань системи з двома ступенями свободи:
Система має нульове рішення A=B=0, що відповідає стійкому положенню рівноваги. Для ненульових рішень складемо з (10.15) відношення:
Квадратне (щодо ) рівняння (10.18) з нерівностей стійкості має два речовинних позитивних кореня. Розташуємо їх у порядку зростання:
Для другого головного вагання:
| (10.21) |
Головні коливання є коливаннями гармонійними.
Підставивши послідовно й у (10.16), знайдемо зв'язок між амплітудами A і B у головних коливаннях: . Множники називають коефіцієнтами власних форм (коефіцієнтами розподілу амплітуд). Вони можуть бути як позитивними, і негативними. Обидві координати в головному коливанні знаходяться в одній фазі; при – у протифазі.
Результуючий рух за кожною координатою буде сумою двох головних коливань:
| (10.22) |
де - Залежать від початкових умов, - від початкових умов не залежать і визначаються параметрами самої коливальної системи. У загальному випадку частоти і непорівнянні, а тому результуючий рух не буде періодичним.
1. Визначити власні частоти та власні форми коливань (малих) подвійного математичного маятника, утвореного двома матеріальними точками рівної маси m та двома стрижнями завдовжки кожен.
Подібна система у загальному вигляді була розглянута у прикладі 2 (§34). Скористаємося отриманими там формулами (2) та (3).
При , отримаємо:
Так як коливання малі, то з точністю до малих другого порядку включно:
| (3) |
З урахуванням (3) із (1), помічаємо:
| (4) |
Порівнюючи (4) і (2), помічаємо:
Розкриваючи рівняння (7.52) частот, отримаємо:
З (9.50) знаходимо коефіцієнти розподілу: .
Перше головне коливання:
Рух у фазі - кожну мить стрижні обертаються в одному напрямку.
Друге головне коливання:
Рух у протифазі – кожної миті стрижні обертаються у прямо протилежних напрямках.
Форми коливань показано на рис. 50. У другому головному коливанні є особлива точка F, яка залишається нерухомою. Такі точки називають вузлами. Кінцева точка O до вузлів не належить.
2. Два тверді тіла з масами і дві пружини, жорсткістю і , об'єднані в систему, яка розташовується на гладкій горизонтальній площині і може здійснювати малі прямолінійні коливання.
Перше головне коливання:
Тіла рухаються у фазі, або праворуч або ліворуч. Амплітуда коливань другого тіла у 1,62 рази більша.
Друге головне коливання:
Тіла рухаються у протифазі: або назустріч один одному, до вузла, або розходяться від вузла. Амплітуда коливань другого тіла становить 0,62 амплітуди першого.