Аксіома перша спосіб встановлення площини в просторі. Способи завдання площини на кресленні

Положення площини в просторі може бути визначено на кресленні одним із таких способів:

1. Трьома точками, що не лежать на одній прямій ( мал. 35).

2. Прямий і точкою, що не лежить на цій прямій ( мал. 36).

3. Двома пересічними прямими ( мал. 37).

4. Двома паралельними прямими (рис. 38 ).

5. Плоскою фігурою ( мал. 39).

6. Слідами ( мал. 40, 41).

7. Параметрами площині.

сліди площини

слідом площині називається лінія перетину площини з площиною проекцій . Слід площині позначається тією ж буквою, що і площину з підрядковим знаком, відповідним імені площині проекцій, з якої перетинається дана. Якщо площину (назвемо її P ) Не паралельна, будь-якої площини проекцій, то вона перетинає всі три площини проекцій і, отже, має три сліду - горизонтальний P H , фронтальний P V і профільний P W (мал. 40, 41). Як і будь-яка пряма, будь-який слід площині має три проекції, але, для полегшення читання епюра, прийнято позначати тільки ту проекцію сліду, яка не збігається з віссю проекцій. Положення будь-якого сліду площини, як і будь-якої прямої, визначається положенням двох її точок. Для слідів площини такими точками можуть бути точки, звані точками сходу слідів, Тобто точки, в яких площина перетинає осі координат - P x , P y , P z . Чисельні значення координат x , y , і z точок сходу слідів називаються параметрами площині.

Положення площини в просторі визначається:

• трьома крапками, що не лежать на одній прямій;
• прямий і точкою, взятої поза прямою;
• двома пересічними прямими;
• двома паралельними прямими;
• плоскою фігурою.

Відповідно до цього на епюрі площина може бути задана:

• проекціями трьох точок, які не лежать на одній прямій (Малюнок 3.1, а);
• проекціями точки і прямої (Малюнок 3.1, б);
• проекціями двох пересічних прямих (Малюнок 3.1, в);
• проекціями двох паралельних прямих (Малюнок 3.1, г);
• плоскою фігурою (Малюнок 3.1, д);
• слідами площини;
• лінією найбільшого скату площини.

Малюнок 3.1 - Способи завдання площин

Площина загального положення - це площина, яка не паралельна і не перпендикулярна ні однієї з площин проекцій.

слідом площині називається пряма, отримана в результаті перетину заданої площини з однією з площин проекцій.

Площина загального положення може мати три сліди: горизонтальний – απ 1, фронтальний – απ 2 і профільний – απ 3, які вона утворює при перетині з відомими площинами проекцій: горизонтальної π 1, фронтальної π 2 і профільної π 3 (Малюнок 3.2).

Малюнок 3.2 - Сліди площини загального положення

3.2. Площині приватного положення

Площина приватного положення - площина, перпендикулярна або паралельна площині проекцій.

Площина, перпендикулярна площині проекцій, називається проецирующей і на цю площину проекцій вона буде проектуватися у вигляді прямої лінії.

Властивість проецирующей площині: Все точки, лінії, плоскі фігури, що належать проецирующей площині, мають проекції на похилому сліді площини (Малюнок 3.3).

Малюнок 3.3 - Фронтально-проектує площину, якій належать: точки А, В, З; лінії АС, АВ, ВС; площину трикутника АВС

Фронтально-проектує площину – площину, перпендикулярна фронтальної площини проекцій (Малюнок 3.4, а).

Горизонтально-проектує площину – площину, перпендикулярна горизонтальної площини проекцій (Малюнок 3.4, б).

Профільно-проектує площину – площину, перпендикулярна профільної площини проекцій.

Площині, паралельні площинам проекцій, називаються площинами рівня або двічі проектується площинами.

Фронтальна площина рівня – площину, паралельна фронтальній площині проекцій(Малюнок 3.4, в).

Горизонтальна площина рівня – площину, паралельна горизонтальній площині проекцій (Малюнок 3.4, г).

Профільна площину рівня – площину, паралельна профільної площини проекцій (Малюнок 3.4, д).

Малюнок 3.4 - Епюри площин приватного положення

3.3. Точка і пряма в площині. Належність точки і прямої площині

Точка належить площині, якщо вона належить будь-якої прямої, що лежить у цій площині (Малюнок 3.5).

Пряма належить площині, якщо вона має з площиною хоча б дві загальні точки (Малюнок 3.6).

Малюнок 3.5 - Належність точки площині

α = m // n

D∈ n⇒ D∈ α

Малюнок 3.6 - Належність прямої площині

Вправа

Дана площину, задана чотирикутником (Малюнок 3.7, а). Необхідно добудувати горизонтальну проекцію вершини З.

а	б

Малюнок 3.7 - Рішення задачі

Рішення :

1. ABCD - плоский чотирикутник, що задає площину.
2. Проведемо в ньому діагоналі AC і BD (Малюнок 3.7, б), які є пересічними прямими, також задають ту ж площину.
3. Згідно ознакою пересічних прямих, побудуємо горизонтальну проекцію точки перетину цих прямих - K по її відомою фронтальної проекції: A 2 C 2 ∩ B 2 D 2 \u003d K 2 .
4. Відновимо лінію проекційної зв'язку до перетину з горизонтальною проекцією прямої BD: На проекції діагоналі B 1 D 1 будуємо До 1 .
5. через А 1 До 1 проводимо проекцію діагоналі А 1 З 1 .
6. крапку З 1 отримуємо, за допомогою лінії проекційної зв'язку до перетину її з горизонтальною проекцією продовженої діагоналі А 1 До 1 .

3.4. Головні лінії площини

У площині можна побудувати безліч прямих, але є особливі прямі, що лежать в площині, звані головними лініями площині (Малюнок 3.8 - 3.11).

Прямий рівня або паралеллю площині називається пряма, що лежить у цій площині і паралельна одній з площин проекцій.

горизонталь або горизонтальна пряма рівня h(Перша паралель) - це пряма, що лежить у цій площині і паралельна горизонтальній площині проекцій (π 1) (Малюнок 3.8, а; 3.9).

фронталь або фронтальна пряма рівня f (Друга паралель) - це пряма лежить у цій площині і паралельна фронтальній площині проекцій (π 2) (Малюнок 3.8, б; 3.10).

Профільна пряма рівня p (Третя паралель) - це пряма лежить у цій площині і паралельна профільної площини проекцій (π 3) (Малюнок 3.8, в; 3.11).

Малюнок 3.8 а - Горизонтальна пряма рівня в площині, заданої трикутником

Малюнок 3.8 б - Фронтальна пряма рівня в площині, заданої трикутником

Малюнок 3.8 в - Профільна пряма рівня в площині, заданої трикутником

Малюнок 3.9 - Горизонтальна пряма рівня в площині, заданої слідами

Малюнок 3.10 - Фронтальна пряма рівня в площині, заданої слідами

Малюнок 3.11 - Профільна пряма рівня в площині, заданої слідами

3.5. Взаємне розміщення прямої і площини

Пряма по відношенню до заданої площині може бути паралельною і може з нею мати спільну точку, тобто перетинатися.

3.5.1. Паралельність прямої площині

Ознака паралельності прямої площини: Пряма паралельна площині, якщо вона паралельна будь-якої прямої, що належить цій площині (Малюнок 3.12).

Малюнок 3.12 - Паралельність прямої площині

3.5.2. Перетин прямої з площиною

Для побудови точки перетину прямої з площиною загального положення (Малюнок 3.13), необхідно:

1. укласти пряму аудопоміжну площину β (в якості допоміжної площини слід вибирати площині приватного положення);
2. Знайти лінію перетину допоміжної площини β із заданою площиною α;
3. Знайти точку перетину заданої прямої а з лінією перетину площин MN.

Малюнок 3.13 - Побудова точки зустрічі прямої з площиною

Вправа

Задані: пряма АВ загального положення, площину σ⊥π 1. (Малюнок 3.14). Побудувати точку перетину прямої АВ з площиною σ.

Рішення :

1. Площина σ - горизонтально-проектує, отже, горизонтальною проекцією площини σ є пряма σ 1 (горизонтальний слід площини);
2. Крапка До повинна належати прямій АВ ⇒ До 1 ∈А 1 В 1 і заданої площині σ ⇒ До 1 ∈σ 1, отже, До 1 знаходиться в точці перетину проекцій А 1 В 1 і σ 1;
3. Фронтальну проекцію точки До знаходимо за допомогою лінії проекційної зв'язку: До 2 ∈А 2 В 2 .

Малюнок 3.14 - Перетин прямої загального положення з площиною приватного положення

Вправа

Задані: площину σ \u003d Δ АВС - загального положення, пряма EF (Малюнок 3.15).

Потрібно побудувати точку перетину прямої EF з площиною σ.

а	б

Малюнок 3.15 - Перетин прямої з площиною

1. укладемо пряму EFудопоміжну площину, в якості якої скористаємося горизонтально-проецирующей площиною α (Малюнок 3.15, а);
2. Якщо α⊥π 1, то на площину проекцій π 1 площину α проектується в пряму (горизонтальний слід площини απ 1 або α 1), збігається з E 1 F 1 ;
3. Знайдемо пряму перетину (1-2) проецирующей площині α з площиною σ (рішення такого завдання буде розглянуто);
4. Пряма (1-2) і задана пряма EF лежать в одній площині α і перетинаються в точці K.

Алгоритм рішення задачі (Малюнок 3.15, б):

через EF проведемо допоміжну площину α:

3.6. Визначення видимості методом конкуруючих точок

При оцінці стану даної прямий, необхідно визначити - точка якої ділянки прямої розташована ближче (далі) до нас, як до спостерігачів, при погляді на площину проекцій π 1 або π 2.

Точки, які належать різним об'єктам, а на одній з площин проекцій їх проекції збігаються (тобто, дві точки проектуються в одну), називаються конкуруючими на цій площині проекцій.

Необхідно окремо визначити видимість на кожній площині проекцій.

Видимість на π 2 (рис. 3.15)

Виберемо точки, конкуруючі на π 2 - точки 3 і 4. Нехай точка 3∈ ВС∈σ, Точка 4∈ EF.

Щоб визначити видимість точок на площині проекцій π 2 треба визначити розташування цих точок на горизонтальній площині проекцій при погляді на π 2.

Напрямок погляду на π 2 показано стрілкою.

За горизонтальним проекція точок 3 і 4, при погляді на π 2, видно, що точка 4 1 розташовується ближче до спостерігача, ніж 3 Розділ 1.

4 1 ∈E 1 F 1 ⇒ 4∈EF ⇒ на π 2 буде видима точка 4, що лежить на прямій EF, Отже, пряма EF на ділянці розглянутих конкуруючих точок розташована перед площиною σ і буде видима до точки K

Видимість на π 1

Для визначення видимості виберемо точки, конкуруючі на π 1 - точки 2 і 5.

Щоб визначити видимість точок на площині проекцій π 1 треба визначити розташування цих точок на фронтальній площині проекцій при погляді на π 1.

Напрямок погляду на π 1 показано стрілкою.

За фронтальним проекція точок 2 і 5, при погляді на π 1, видно, що точка 2 2 розташовується ближче до спостерігача, ніж 5 2.

2 1 ∈А 2 В 2 ⇒ 2∈АВ ⇒ на π 1 буде видима точка 2, що лежить на прямій АВ, Отже, пряма EF на ділянці розглянутих конкуруючих точок розташована під площиною σ і буде невидима до точки K - точки перетину прямої з площиною σ.

Видимої з двох конкуруючих точок буде та, у якої координата «Z» або (і) «Y» більше.

3.7. Перпендикулярність прямої площині

Ознака перпендикулярності прямої площині: Пряма перпендикулярна площині, якщо вона перпендикулярна двом пересічним прямим, лежачим в даній площині.

а	б

Малюнок 3.16 - Завдання прямий, перпендикулярної площині

Теорема. Якщо пряма перпендикулярна площині, то на епюрі: горизонтальна проекції прямої перпендикулярна горизонтальної проекції горизонталі площини, а фронтальна проекція прямої перпендикулярна фронтальної проекції фронталі (Малюнок 3.16, б)

Теорема доводиться через теорему про проектуванні прямого кута в окремому випадку.

Якщо площину задана слідами, то проекції прямої перпендикулярної площині перпендикулярні відповідним слідах площині (Малюнок 3.16, а).

нехай пряма p перпендикулярна площині σ \u003d Δ АВС і проходить через точку K.

1. Побудуємо горизонталь і фронталь в площині σ \u003d Δ АВС : A-1∈σ; A-1// π 1; З-2∈σ; З-2// π 2.
2. Відновимо з точки K перпендикуляр до заданої площині: p 1⊥h 1 і p 2⊥f 2, або p 1⊥απ 1 і p 2⊥απ 2

3.8. Взаємне положення двох площин

3.8.1. паралельність площин

Дві площини можуть бути паралельними і пересічними між собою.

Ознака паралельності двох площин: Дві площини взаємно паралельні, якщо дві пересічні прямі площині відповідно рівнобіжні двом пересічним прямим іншій площині.

Вправа

Задана площина загального положення α \u003d Δ АВС і крапка F∉α (Малюнок 3.17).

через точку F провести площину β, паралельну площині α.

Малюнок 3.17 - Побудова площині, паралельної заданої

Рішення :

Як пересічних прямих площині α візьмемо, наприклад, сторони трикутника АВ і ВС.

1. через точку F проводимо пряму m, Паралельну, наприклад, АВ.
2. через точку F, Або ж через будь-яку точку, що належить m, Проводимо пряму n, Паралельну, наприклад, ВС, причому m∩n \u003d F.
3. β = m∩n і β // α за визначенням.

3.8.2. перетин площин

Результатом перетину 2-х площин є пряма. Будь-яка пряма на площині або в просторі може бути однозначно задана двома точками. Тому для того, щоб побудувати лінію перетину двох площин, слід знайти дві точки, загальні для обох площин, після чого з'єднати їх.

Розглянемо приклади перетину двох площин при різних способах їх завдання: слідами; трьома крапками, що не лежать на одній прямій; паралельними прямими; пересічними прямими і ін.

Вправа

Дві площини α і β задані слідами (Малюнок 3.18). Побудувати лінію перетину площин.

Малюнок 3.18 - Перетин площин загального положення, заданих слідами

Порядок побудови лінії перетину площин:

1. Знайти точку перетину горизонтальних слідів - це точка М(Її проекції М 1 і М 2, при цьому М 1 \u003d М, Тому що М -точка приватного положення, що належить площині π 1).
2. Знайти точку перетину фронтальних слідів - це точка N (Її проекції N 1 і N 2, при цьому N 2 = N, Тому що N - точка приватного положення, що належить площині π 2).
3. Побудувати лінію перетину площин, з'єднавши однойменні проекції отриманих точок: М 1 N 1 і М 2 N 2 .

МN - лінія перетину площин.

Вправа

Задана площина σ \u003d Δ АВС, Площина α - горизонтально проектує (α⊥π 1) ⇒α 1 - горизонтальний слід площини (Малюнок 3.19).

Побудувати лінію перетину цих площин.

Рішення :

Так як площину α перетинає сторони АВ і АС трикутника АВС, То точки перетину K і L цих сторін з площиною α є загальними для обох заданих площин, що дозволить, з'єднавши їх, знайти шукану лінію перетину.

Точки можуть бути знайдені як точки перетину прямих з проецирующей площиною: знаходимо горизонтальні проекції точок K і L, тобто K 1 і L 1, на перетині горизонтального сліду (α 1) заданої площині α з горизонтальними проекціями сторін Δ АВС: А 1 В 1 і A 1 C 1. Після чого за допомогою ліній проекційної зв'язку знаходимо фронтальні проекції цих точок K 2і L 2 на фронтальних проекціях прямих АВ і АС. З'єднаємо однойменні проекції: K 1 і L 1 ; K 2і L 2. Лінія перетину заданих площин побудована.

Алгоритм рішення задачі:

KL - лінія перетину Δ АВС і σ (α∩σ \u003d KL).

Малюнок 3.19 - Перетин площин загального і приватного положення

Вправа

Задані площини α \u003d m // n і площину β \u003d Δ АВС (Малюнок 3.20).

Побудувати лінію перетину заданих площин.

Рішення :

1. Щоб знайти точки, загальні для обох заданих площин і задають лінію перетину площин α і β, необхідно скористатися допоміжними площинами приватного положення.
2. В якості таких площин виберемо дві допоміжні площині приватного положення, наприклад: σ // τ; σ⊥π 2; τ⊥π 2.
3. Знову введені площині перетинаються з кожної з заданих площин α і β за прямими, паралельним один одному, так як σ // τ:

- результатом перетину площин α, σ і τ є прямі (4-5) і (6-7);

- результатом перетину площин β, σ і τ є прямі (3-2) і (1-8).

1. Прямі (4-5) і (3-2) лежать в площині σ; точка їх перетину М одночасно лежить в площинах α і β, тобто на прямий перетину цих площин;
2. Аналогічно знаходимо точку N, Загальну для площин α і β.
3. Поєднавши точки M і N, Побудуємо пряму перетину площин α і β.

Малюнок 3.20 - Перетин двох площин загального положення (загальний випадок)

Алгоритм рішення задачі:

Вправа

Задані площини α \u003d Δ АВС і β \u003d a//b. Побудувати лінію перетину заданих площин (Малюнок 3.21).

Малюнок 3.21 Рішення завдання на перетин площин

Рішення :

Скористаємося допоміжними січними площинами приватного положення. Введемо їх так, щоб скоротити кількість побудов. Наприклад, введемо площину σ⊥π 2, уклавши пряму a удопоміжну площину σ (σ∈ a). Площина σ перетинає площину α по прямій (1-2), а σ∩β \u003d а. Отже (1-2) ∩ а=K.

Крапка До належить обом площинам α та β.

Отже, точка K, Є однією з шуканих точок, через які проходить пряма перетину заданих площин α і β.

Для знаходження другої точки, що належить прямій перетину α і β, укладемо пряму b удопоміжну площину τ⊥π 2 (τ∈ b).

Поєднавши точки K і L, Отримаємо пряму перетину площин α і β.

3.8.3. Взаємно перпендикулярні площини

Площині взаємно перпендикулярні, якщо одна з них проходить через перпендикуляр до іншої.

Вправа

Задана площина σ⊥π 2 і пряма загального положення - DE (Малюнок 3.22)

Потрібно побудувати через DE площину τ⊥σ.

Рішення .

проведемо перпендикуляр CD до площини σ - C 2 D 2 ⊥σ 2 (на підставі).

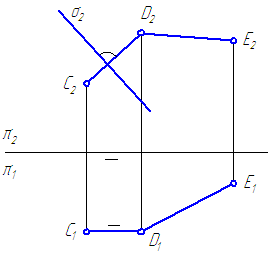
Малюнок 3.22 - Побудова площині, перпендикулярній до заданої площини

По теоремі про проектуванні прямого кута C 1 D 1 повинна бути паралельна осі проекцій. пересічні прямі CD∩DE задають площину τ. Отже, τ⊥σ.

Аналогічні міркування, в разі площині загального положення.

Вправа

Задана площина α \u003d Δ АВС і крапка K поза площиною α.

Потрібно побудувати площину β⊥α, що проходить через точку K.

алгоритм рішення (Малюнок 3.23):

1. побудуємо горизонталь h і фронталь f в заданій площині α = Δ АВС;
2. через точку Kпроведемо перпендикуляр b до площини α (по теоремі про перпендикуляр до площини: Якщо пряма перпендикулярна площині, то її проекції перпендикулярні до похилих проекцій горизонталі і фронталі, що лежать в площині:b 2⊥f 2; b 1⊥h 1;
3. Задаємо площину β будь-яким способом, наприклад, β \u003d a∩b, Таким чином, площина, перпендикулярна до заданої, побудована: α⊥β.

Малюнок 3.23 - Побудова площині, перпендикулярній до заданої Δ АВС

3.9. Завдання для самостійного рішення

1. Задана площина α \u003d m//n(Малюнок 3.24). Відомо що K∈α.

Побудуйте фронтальну проекцію точки До.

малюнок 3.24

2. Побудуйте сліди прямої, заданої відрізком CB, І визначте квадранти, через які вона проходить (Малюнок 3.25).

малюнок 3.25

3. Побудуйте проекції квадрата, що належить площині α⊥π 2, якщо його діагональ MN// π 2 (Малюнок 3.26).

малюнок 3.26

4. Побудувати прямокутник ABCD з більшою стороною ВС на прямий m, Виходячи з умови, що відношення його сторін дорівнює 2 (Малюнок 3.27).

малюнок 3.27

5. Задана площина α \u003d a//b (Малюнок 3.28). Побудувати площину β паралельну площині α і віддалену від неї на відстані 20 мм.

малюнок 3.28

6. Задана площина α \u003d Δ АВС і крапка D D площину β⊥α і β⊥π 1.

7. Задана площина α \u003d Δ АВС і крапка D поза площиною. Побудувати через точку D пряму DE// α і DE// π 1.

Будь-яка геометрична фігура, занурена в простір, складається з певної кількості точок простору. Площина як одна з геометричних фігур, являє собою сукупність безлічі точок. З цього визначення площини можна встановити способи завдання її положення в просторі. Для цього достатньо згадати аксіому поєднання - через три точки, що не лежать на одній прямій, можна провести площину і до того ж тільки одну.

На рис. 21 представлені способи завдання положення площини в просторі:

а - трьома крапками, що не лежать на одній прямій;

б - прямий і точкою, взятої поза прямою;

в - двома пересічними прямими;

г - двома паралельними прямими.

На комплексному кресленні (рис. 22) площину може бути задана:

а - проекціями трьох точок, які не лежать на одній прямій;

б - проекціями прямої і точки, взятої поза прямою;

в - проекціями двох пересічних прямих;

г - проекціями двох паралельних прямих.

Кожен з представлених на рис. 22 способів встановлення площини на кресленні може бути перетворений з одного в інший. Так, наприклад, провівши через точки А і В (рис. 22, а) пряму, отримують завдання площині, представлене на рис. 22, б. Від нього можна перейти до способу, представленого на рис. 22, г, якщо через точку С провести пряму, паралельну прямій АВ. Якщо точки А, В і С з'єднати попарно прямими, то отримують трикутник АВС - плоску фігуру (рис. 23), проекціями якої може бути задана площина на кресленні.

При цьому завжди слід пам'ятати про те, що площина, як геометрична фігура, безмежна і тому не можна обмежуватися побудовами тільки в межах площі цього трикутника, так як в загальному випадку проекції площини займають всю кожну з площин проекцій: горизонтальну П I, фронтальну П 2 і профільну П 3.

Більш наочно площину може бути задана за допомогою прямих, за якими вона перетинає площині проекцій (рис. 24, а).

Ці прямі називаються слідами площини. У загальному випадку обидва сліду повинні перетинатися між собою в точці на осі проекцій, яку називають «точкою сходу слідів».

З усього різноманіття положень площині щодо заданої системи площин проекцій зазвичай виділяють такі, коли.

5.1 Завдання площині

Площина задається трьома довільними точками, що не належать одній прямій. Площина в просторі можна задати:

· Трьома крапками, що не лежать на одній прямій (рисунок 5.1, а);

· Прямий і не належить їй точкою (рисунок 5.1, б);

· Двома пересічними прямими (рисунок 5.1, в);

· Двома паралельними прямими (рисунок 5.1, г);

· Будь-якій плоскій фігурою (рисунок 5.1, д).

малюнок 5.1

Кожен з перерахованих способів встановлення площини допускає перехід до будь-якого іншого, тому що розміщення прямої в площині визначається двома її точками або однією точкою і напрямом цієї прямої.

Часто застосовується спосіб встановлення площини за допомогою прямих ліній (взаємно перетинаються або паралельні), за якими дана площину перетинається з площинами проекцій П 1 П 2, П 3. Крім цього - це завдання площині слідами, при цьому зберігається наочність зображення (малюнок 5.2).

малюнок 5.2

5.2 Сліди площини.

Лінія перетину даної площини з площиною проекцій (П 1 , П 2, П 3 ) називається слідом площини. Іншими словами, слід площині - це пряма, що лежить в площині проекцій. Сліду присвоюється найменування тій площині проекцій, якій він належить. Наприклад, горизонтальний слід отриманий при перетині заданої площині з площиною П 1 і позначається, фронтальний - з площиною П 2 (), профільний - з площиною П 3 (). Два сліду однієї і тієї ж площині перетинаються на осі проекції в точці, яка називається точкою сходу слідів. Кожен з слідів площини збігається зі своєю однойменної проекцією, інші проекції виявляються лежать на осях. Наприклад, горизонтальний слід площини Σ (рисунок 5.2) збігається зі своєю горизонтальною проекцією, фронтальна його проекція знаходиться на осі х, А профільна на осі у.По розташуванню слідів площини можна судити про становище даної площини в просторі щодо площин проекцій П 1, П 2, П 3.

5.3 Положення площині щодо площин проекцій

Будь-яка, довільно взята в просторі площину, може займати загальне або приватна положення. Площиною загального положення називається площина, яка перпендикулярна до жодної з площин проекцій (див. Рисунок 5.2). Всі інші площини (крім площин проекцій) відносяться до площин приватного положення і підрозділяються на проектують площині і площині рівня. | Проектується називається площина, перпендикулярна до однієї
з площин проекцій. Наприклад, горизонтально-проектує плоскостьперпендікулярна до горизонтальної площини проекції П 1 (рисунок 5.3).

малюнок 5.3

Горизонтальні проекції всіх геометричних образів (точок, прямих, фігур), що лежать в цій площині, збігаються з горизонтальним слідом 1. Кут, який утворюється між площинами і П 2, проектується на П1 без спотворення. Фронтальний слід 2 перпендикулярний до осі x.

Фронтально-проектує площину () перпендикулярна до фронтальної площини П 2 показана на малюнку 5.4. Фронтальні проекції всіх геометричних образів (точок, прямих, фігур), що лежать в цій площині, збігаються з фронтальним слідом площини 2. Кут, який утворюється між заданою площиною і П 1, проектується на П 2 без спотворення. Горизонтальний слід площини 1 перпендикулярний до осі x.

малюнок 5.4

Профільно-проектує площину Т (T 1, T 2) перпендикулярна до профільної площини проекції П 3 (рисунок 5.5).

малюнок 5.5

Профільні проекції всіх геометричних образів (точок, прямих, фігур), що лежать в цій площині, збігаються з профільним слідом площині Т 3 . Кути і, які утворюються між заданою площиною і площинами проекцій П 1 і П 2 (\u003d T ^ П 1 ; = Т ^ П 2 ), проектуються на площину П 3 без спотворень. Горизонтальний і фронтальний сліди площини паралельні осі х.

Профільно-проектує площину може проходити через вісь x: (рисунок 5.6).

малюнок 5.6

Сліди цієї площини 1 \u003d 2 збігаються один з одним і з віссю x, тому не визначають положення площини. Необхідно крім слідів задати в площині точку (рисунок 5.6). В окремому випадку ця площину може бути биссекторной площиною. Кут ° \u003d °, а точка А рівновіддалена від площин проекцій П 1 і П 2 . Площиною рівня називається площина, перпендикулярна одночасно до двох площинах проекцій і паралельна третій. Таких площин три різновиди (рисунок 5.7):

· Горизонтальна площина рівня перпендикулярна до П2, П3 і паралельна П 1 (Рисунок 5.7, а);

· Фронтальна площину рівня перпендикулярна до П1, П 3 і паралельна П 2 (рисунок 5.7, б);

· Профільна площина рівня перпендикулярна до П1, П2 і паралельна П 3 (рисунок 5.7 в).

малюнок 5.7

З визначення площин рівня слід, що одна з проекцій точки, лінії, фігури, які належать цим площинах, буде збігатися з однойменною слідом площини рівня, а інша проекція буде натуральною величиною цих геометричних образів.

5.4 Ознаки приналежності точки і прямої площині

Для визначення приналежності точки і прямої площині, розташованої в просторі, слід керуватися наступними положеннями:

· Точка належить площині, якщо через неї можна провести лінію, що лежить в площині;

· Пряма належить площині, якщо вона має з площиною хоча б дві загальні точки;

· Пряма належить площині, якщо вона проходить через точку даної площині паралельно прямий, що належить цій площині.

Через одну точку на площині можна провести безліч ліній. Це можуть бути довільні лінії і лінії, що займають особливе становище стосовно площин проекцій П 1 П 2, П 3 . Пряма, що належить даної площини, проведена паралельно горизонтальній площині проекцій, називається г орізонталью площині.

Пряма, що належить даної площини, проведена паралельно фронтальній площині проекцій, називається фронтале площині.

Горизонталь і фронталь є лініями рівня.

Горизонталь площини слід починати будувати з фронтальної проекції, тому що вона паралельна осі x, Горизонтальна проекція горизонталі паралельна горизонтальному сліду площині.

А так як всі горизонталі площини паралельні між собою, можна вважати горизонтальний слід площини нульовий горизонталлю (рисунок 5.8).

Фронталь площини слід починати будувати з горизонтальної проекції, тому що вона паралельна осі x, фронтальна проекція фронталі паралельна фронтальному сліду. Фронтальний слід площини - нульова фронталь. Все фронталі площині паралельні між собою (малюнок 5.9).

малюнок 5.8

малюнок 5.9

До лінії рівня відноситься і профільна пряма, що лежить в заданій площині і паралельна П 3 .

До головних лініях особливого становища в площині, крім лінії рівня, відносяться лінії найбільшого нахилу площини до площини проекцій.

5.5 Визначення кута нахилу площини до площин проекцій

Площина загального положення, розташована в просторі довільно, нахилена до площин проекцій. Для визначення величини двухгранний кута нахилу заданої площині до будь-якої площини проекції використовуються лінії найбільшого нахилу площини до площини проекцій: до П 1 - лінія ската, до П 2 - лінія найбільшого нахилу площини до площини П 2.

Лінії найбільшого нахилу площини - це прямі, що утворюють з площиною проекцій найбільший кут, проводяться в площині перпендикулярно до відповідної лінії рівня. Лінії найбільшого нахилу і її відповідна проекція утворюють лінійний кут, яким вимірюється величина двухгранний кута, складеного даної площиною і площиною проекцій (рисунок 5.10).

Положення площини в просторі визначається трьома її точками, що не лежать на одній прямій. Тому щоб поставити на епюрі площина, досить задати три її точки (рис. 206). Площина можна задати точкою і прямою (рис. 207, а), двома паралельними прямими (рис. 207, б), двома пересічними прямими (рис. 207, в), трикутником (рис. 207, г).

Можна задати площину слідами. Слідом площині називають пряму, по якій дана площину перетинає площину проекцій. На рис. 208 Pv - фронтальний слід площини Р, Р н - горизонтальний слід площини Р, Pw - профільний слід площини Р.

Різні випадки розташування площин щодо площин проекцій

Площина загального положення - площина, розташована похило до всіх площинах проекцій (рис. 208). Така площину перетинається з трьома площинами проекцій за прямими, які є слідами цієї площини. Кожна пара слідів сходиться в точці, яка називається точкою сходу слідів площини і розташовується на осі проекцій. Площина загального положення має три точки сходу, які позначаються Рх, Ру, Рz. У цих точках площину перетинає осі координат. Плоскі фігури, що лежать в площині загального положення, проектуються проекцій з спотворенням.

проектує площину - площина, перпендикулярна будь-якої площини проекцій.

Горизонтально - проектує площину - площина, перпендикулярна горизонтальної площини проекцій Н (рис. 209).

Фронтально - проектує площину - площина, перпендикулярна фронтальної площини проекції (рис. 210).

Профільно-проектує площину - площина, перпендикулярна профільної площини проекцій (рис. 211).

Проектує площину проектується на площину проекцій, до якої вона перпендикулярна, в пряму. Па рис. 209 площину Р горизонтально-проектує, ΔАВС, що лежить в площині Р, проектується у відрізок прямої лінії, який збігається зі слідом площини Рн. На рис. 210 ΔDEF, що належить фронтально-проектує площині R, проектується у відрізок, що співпадає зі слідом площини Rv. На рис. 211 ΔKMN, що лежить в профільно-проецирующей площині Q, проектується на площину W в відрізок, що співпадає зі слідом площини Qw. Тому проектують площині часто використовуються в якості допоміжних при різних побудовах. Наприклад, щоб через пряму AB провести горизонтально-проецирующую площину (рис. 212), досить через горизонтальну проекцію прямої ab провести горизонтальний слід цій площині, так як все, що в цій площині лежить, в тому числі і пряма AB, проектується на її горизонтальний слід. Фронтальний слід фронтально-проектує площині збігається з фронтальною проекцією прямої a "b" (рис. 213). Сліди проектують площин на інших площинах проекцій перпендикулярні відповідним осях проекцій (див. Рис. 209, 210, 211).

Мал. 212 Рис. 213

Площині, перпендикулярні двох площинах проекцій, паралельні третій площині проекцій . Геометричні фігури, що лежать в цих площинах, проектуються без спотворення на ту площину проекцій, якій паралельна дана площину (рис. 214, 215; 216). Називаються такі площини так само, як і площину проекцій, паралельно якій вони розташовані: горизонтальна площина (рис. 214), фронтальна площину (рис. 215), профільна площина (рис. 216).