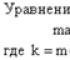Практична робота №2

"Диференціал функції"

Мета заняття: Навчитися вирішувати приклади та завдання з даної теми

Питання теорії (початковий рівень):

1. Застосування похідних на дослідження функцій на екстремум.

2. Диференціал функції, його геометричний та фізичний зміст.

3. Повний диференціал функції багатьох змінних.

4. Стан організму як багато змінних.

5. Наближені обчислення.

6. Знаходження приватних похідних та повного диференціалу.

7. Приклади використання зазначених понять у фармакокінетиці, мікробіології та ін.

(Самостійна підготовка)

1. відповісти на запитання на тему заняття;

2. розв'язати приклади.

Приклади

Знайти диференціали наступних функцій:

1)	2)	3)
4)	5)	6)
7)	8)	9)
10)	11)	12)
13)	14)	15)
16)	17)	18)
19)	20)

Застосування похідних на дослідження функцій

Умова зростання функції y = f(x) на відрізку [а, b]

Умова зменшення функції y=f(x)на відрізку [а, b]

Умова максимуму функції y=f(x)при x= а

f"(a)=0 та f"" (a)<0

Якщо при х=а похідні f"(а) = 0 і f"(а) = 0, то необхідно дослідити f"(x)в околицях точки x = а. Функція у=f(х)при х=а має максимум , якщо при переході через точку х= а похідна f"(x) змінює знак з "+" на "-", у разі мінімуму - з "-" на "+" Якщо f"(x) не змінює знака при переході через точку х = а, то в цій точці функції екстремуму немає

Диференціал функції.

Диференціал незалежної змінної дорівнює її прирощенню:

Диференціал функції y=f(x)

Диференціал суми (різниці) двох функцій y=u±v

Диференціал добутку двох функцій у=uv

Диференціал частки двох функцій y=u/v

dy=(vdu-udv)/v 2

Збільшення функції

Δy = f(x + Δx) - f(x) ≈ dy ≈ f"(x) Δx

де Δx: - Збільшення аргументу.

Наближене обчислення значення функції:

f(x + Δx) ≈ f(x) + f"(x) Δx

Застосування диференціала у наближених обчисленнях

Диференціал застосовується для обчислення абсолютної та відносної похибок при непрямих вимірах u = f(x, y, z). Абсолютна похибка результату виміру

du≈Δu≈|du/dx|Δx+|du/dy|Δy+|du/dz|Δz+…

Відносна похибка результату виміру

du/u≈Δu/u≈(|du/dx|Δx+|du/dy|Δy+|du/dz|Δz+…)/u

ДИФЕРЕНЦІАЛ ФУНКЦІЇ.

Диференціал функції як головна частина збільшення функції в.З поняттям похідної тісно пов'язане поняття диференціалу функції. Нехай функція f(x)безперервна при даних значеннях хі має похідну

D f/Dx = f¢(x) + a(Dx), звідки збільшення функції Df = f(x)Dx + a(Dx)Dx,де a(Dх) ® 0при Dх ® 0. Визначимо порядок нескінченно малої f¢(x)Dx Dх.:

Отже, нескінченно малі f¢(x)Dxі Dxмають однаковий порядок малості, тобто f¢(x)Dx = O.

Визначимо порядок нескінченно малої a(Dх)Dхпо відношенню до нескінченно малої Dх:

Отже, нескінченно мала a(Dх)Dхмає більш високий порядок дещиці порівняно з нескінченно малою Dх, тобто a(Dх)Dх = о.

Таким чином, нескінченно мале прирощення Dfдиференційованої функції може бути представлено у вигляді двох доданків: нескінченно малої f¢(x)Dxоднакового порядку малості з Dхі нескінченно малою a(Dх)Dхвищого порядку малості порівняно з нескінченно малою Dх.Це означає, що у рівності Df=f¢(x)Dx + a(Dx)Dxпри Dх® 0другий доданок прагне нуля «швидше», ніж перше, тобто a(Dх)Dх = о.

Перший доданок f¢(x)Dx,лінійне відносно Dх, називають диференціалом функції f(x) у точці хі позначають dyабо df(читається "де ігрек" або "де еф"). Отже,

dy = df = f (x) Dx.

Аналітичний зміст диференціалуполягає в тому, що диференціал функції є головною частиною збільшення функції Df, лінійна щодо збільшення аргументу Dx. Диференціал функції відрізняється від збільшення функції на нескінченно малу вищого порядку малості, ніж Dx. Справді, Df=f¢(x)Dx + a(Dx)Dxабо Df = df + a(Dx)Dx . Диференціал аргументу dxдорівнює його прирощенню Dx: dx = Dx.

приклад.Обчислити значення диференціалу функції f(x) = x 3 + 2x,коли хзмінюється від 1 до 1,1.

Рішення.Знайдемо загальний вираз для диференціалу цієї функції:

Підставляючи значення dx = Dx = 1,1-1 = 0,1і x = 1в останню формулу, отримаємо потрібне значення диференціала: df½ x=1; = 0,5.

ПРИВАТНІ ВИРОБНИЧІ ТА ДИФЕРЕНЦІАЛИ.

Приватні похідні першого порядку. Приватної похідної першого порядку функції z = f (x, y ) за аргументом ху точці, що розглядається (х; у)називається межа

якщо вона існує.

Приватна похідна функції z = f(x, y)за аргументом хпозначається одним із наступних символів:

Аналогічно приватна похідна по упозначається та визначається формулою:

Оскільки приватна похідна – це похідна функції одного аргументу, її неважко обчислити. Для цього потрібно користуватися всіма розглянутими досі правилами диференціювання, враховуючи в кожному випадку, який із аргументів приймається за «постійне число», а який є «змінною диференціювання».

Зауваження.Для знаходження приватної похідної, наприклад, за аргументом х – df/dx, Досить визначити звичайну похідну функції f(x, y),вважаючи останню функцією одного аргументу х, а у- Постійною; для знаходження df/dy- Навпаки.

приклад.Знайти значення окремих похідних від функції f(x,y) = 2x 2 + y 2у точці Р(1; 2).

Рішення.Вважаючи f(x, y)функцією одного аргументу хта користуючись правилами диференціювання, знаходимо

У точці Р(1; 2)значення похідної

Вважаючи f(x;y) функцією одного аргументу у, знаходимо

У точці Р(1; 2)значення похідної

ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ СТУДЕНТА:

Знайдіть диференціали наступних функцій:

Розв'язати такі завдання:

1. На скільки зменшиться площа квадрата зі стороною х=10см, якщо сторону зменшити на 0,01 см?

2. Дано рівняння руху тіла: y=t 3 /2+2t 2 , де s – виражено у метрах, t-у секундах. Знайти шлях s, пройдений тілом за t=1,92 з початку руху.

ЛІТЕРАТУРА

1. Лобоцька Н.Л. Основи вищої математики – М.: «Вища школа», 1978. C198-226.

2. Бейлі Н. Математика в біології та медицині. Пров. з англ. М.: "Світ", 1970.

3. Ремізов А.М., Ісакова Н.Х., Максіна Л.Г. Збірник завдань з медичної та біологічної фізики - М.: «Вища школа», 1987. С16-20.

Приватні похідні функції двох змінних.
Поняття та приклади рішень

На цьому уроці ми продовжимо знайомство з функцією двох змінних і розглянемо, мабуть, найпоширеніше тематичне завдання – знаходження приватних похідних першого та другого порядку, а також повного диференціалу функції. Студенти-заочники, як правило, стикаються з приватними похідними на 1 курсі у 2 семестрі. Причому, за моїми спостереженнями, завдання перебування приватних похідних практично завжди зустрічається на іспиті.

Для ефективного вивчення нижченаведеного матеріалу вам необхідновміти більш менш впевнено знаходити «звичайні» похідні функції однієї змінної. Навчитися правильно поводитися з похідними можна під час уроків Як знайти похідну?і Похідна складної функції. Також нам знадобиться таблиця похідних елементарних функцій та правил диференціювання, найзручніше, якщо вона буде під рукою в роздрукованому вигляді. Здобути довідковий матеріал можна на сторінці Математичні формули та таблиці.

Швиденько повторимо поняття функції двох змінних, я постараюся обмежитися найменшим. Функція двох змінних зазвичай записується як , у своїй змінні , називаються незалежними зміннимиабо аргументами.

Приклад: - Функція двох змінних.

Іноді використовують запис. Також зустрічаються завдання, де замість букви використовується буква .

З геометричної точки зору функція двох змінних найчастіше є поверхнею тривимірного простору (площина, циліндр, куля, параболоїд, гіперболоїд і т. д.). Але, власне, це вже більше аналітична геометрія, а у нас на порядку денному математичний аналіз, який ніколи не давав списувати мій викладач вузу є моїм «ковзаном».

Переходимо до питання перебування приватних похідних першого та другого порядків. Повинен повідомити хорошу новину для тих, хто випив кілька чашок кави і налаштувався на неймовірно важкий матеріал: приватні похідні – це майже те саме, що й «звичайні» похідні функції однієї змінної.

Для приватних похідних справедливі всі правила диференціювання та таблиця похідних елементарних функцій. Є тільки кілька невеликих відмінностей, з якими ми познайомимося прямо зараз:

…так, до речі, для цієї теми я таки створив маленьку pdf-книжку, яка дозволить "набити руку" буквально за пару годин. Але, користуючись сайтом, ви, безумовно, теж отримаєте результат - тільки може трохи повільніше:

Приклад 1

Знайти приватні похідні першого та другого порядку функції

Спочатку знайдемо приватні похідні першого порядку. Їх дві.

Позначення:
або - приватна похідна по "ікс"
або – приватна похідна за «ігроком»

Почнемо з . Коли ми знаходимо приватну похідну по «ікс», то змінна вважається константою (постійним числом).

Коментарі до виконаних дій:

(1) Перше, що ми робимо під час перебування приватної похідної – укладаємо всюфункцію в дужки під штрих з підрядковим індексом.

Увага, важливо!Підрядкові індекси НЕ ВТРАЮЄМО по ходу рішення. В даному випадку, якщо ви десь намалюєте «штрих» без , то викладач, як мінімум, може поставити поруч із завданням (відразу відкусити частину бала за неуважність).

(2) Використовуємо правила диференціювання , . Для простого прикладу, як цей, обидва правила можна застосувати на одному кроці. Зверніть увагу на перший доданок: оскільки вважається константою, а будь-яку константу можна винести за знак похідної, то ми виносимо за дужки. Тобто в цій ситуації нічим не краще за звичайне число. Тепер подивимося на третій доданок: тут, навпаки, нічого не виносити. Оскільки константа, то – теж константа, і в цьому сенсі вона нічим не краща за останній доданок – «сімки».

(3) Використовуємо табличні похідні та .

(4) Спрощуємо, або, як я люблю говорити, «зачісуємо» відповідь.

Тепер. Коли ми знаходимо приватну похідну за «ігроком», то зміннавважається константою (постійним числом).

(1) Використовуємо самі правила диференціювання , . У першому доданку виносимо константу за знак похідної, у другому доданку нічого винести не можна оскільки – вже константа.

(2) Використовуємо таблицю похідних функцій. Уявно поміняємо в таблиці всі «ікси» на «ігреки». Тобто дана таблиця рівно справедлива і для (та й взагалі майже для будь-якої літери). Зокрема, формули, які ми використовуємо, виглядають так: і .

У чому сенс приватних похідних?

По суті приватні похідні 1-го порядку нагадують «звичайну» похідну:

– це функції, які характеризують швидкість змінифункції у напрямку осей та відповідно. Так, наприклад, функція характеризує крутість «підйомів» та «схилів» поверхніу напрямку осі абсцис, а функція повідомляє нам про «рельєф» цієї ж поверхні у напрямку осі ординат.

! Примітка : тут маються на увазі напрямки, які паралельнікоординатним осям.

З метою кращого розуміння розглянемо конкретну точку площини та обчислимо в ній значення функції (висоту):
– а тепер уявіть, що ви тут знаходитесь (НА САМІЙ поверхні).

Обчислимо приватну похідну по «ікс» у цій точці:

Негативний знак «іксової» похідної повідомляє про спаданняфункції в точці за напрямом осі абсцис. Іншими словами, якщо ми зробимо маленький-маленький (Безмежно малий)крок у бік вістря осі (паралельно даної осі), то спустимося вниз схилом поверхні.

Тепер дізнаємося характер «місцевості» у напрямку осі ординат:

Похідна за «ігроком» позитивна, отже, в точці за напрямком осі функція зростає. Якщо дуже просто, то тут нас чекає підйом у гору.

Крім того, приватна похідна в точці характеризує швидкість змінифункції за відповідним напрямом. Чим набуте значення більше за модулем– тим поверхня крутіша, і навпаки, чим вона ближче до нуля – тим поверхня більш полога. Так, у нашому прикладі «схил» у напрямку осі абсцис крутіший, ніж «гора» у напрямку осі ординат.

Але то були два приватні шляхи. Цілком зрозуміло, що з точки, в якій ми знаходимося, (і взагалі з будь-якої точки даної поверхні)ми можемо зрушити і в якомусь іншому напрямку. Таким чином, виникає інтерес скласти загальну «навігаційну карту», ​​яка повідомляла б нам про «ландшафт» поверхні по можливостіу кожній точці області визначення цієї функціїпо всіх доступних шляхах. Про це та інші цікаві речі я розповім на одному з наступних уроків, а поки що повернемося до технічного боку питання.

Систематизуємо елементарні прикладні правила:

1) Коли ми диференціюємо по , то змінна вважається константою.

2) Коли ж диференціювання здійснюється зато константою вважається.

3) Правила та таблиця похідних елементарних функцій справедливі і застосовні для будь-якої змінної (або будь-якої іншої), за якою ведеться диференціювання.

Крок другий. Знаходимо приватні похідні другого порядку. Їх чотири.

Позначення:
або – друга похідна з «ікс»
або – друга похідна за «ігроком»
або – змішанапохідна «ікс із ігрок»
або – змішанапохідна «ігрок з ікс»

З другої похідної немає жодних проблем. Говорячи простою мовою, друга похідна – це похідна від першої похідної.

Для зручності я перепишу вже знайдені приватні похідні першого порядку:

Спочатку знайдемо змішані похідні:

Як бачите, все просто: беремо приватну похідну та диференціюємо її ще раз, але в даному випадку – вже за «ігроком».

Аналогічно:

У практичних прикладах можна орієнтуватися на таку рівність:

Таким чином, через змішані похідні другого порядку дуже зручно перевірити, чи правильно ми знайшли приватні похідні першого порядку.

Знаходимо другу похідну по «ікс».
Жодних винаходів, беремо і диференціюємо її по «ікс» ще раз:

Аналогічно:

Слід зазначити, що при знаходженні потрібно проявити підвищена увага, оскільки жодних чудових рівностей для їхньої перевірки не існує.

Другі похідні також знаходять широке практичне застосування, зокрема вони використовуються в задачі відшукання екстремумів функції двох змінних. Але всьому свій час:

Приклад 2

Обчислити приватні похідні першого порядку функції у точці. Знайти похідні другого порядку.

Це приклад самостійного рішення (відповіді наприкінці уроку). Якщо виникли труднощі з диференціюванням коріння, поверніться до уроку Як знайти похідну?А взагалі, незабаром ви навчитеся знаходити подібні похідні «з льоту».

Набиваємо руку на складніших прикладах:

Приклад 3

Перевірити, що . Записати повний диференціал першого порядку.

Рішення: Знаходимо приватні похідні першого порядку:

Зверніть увагу на підрядковий індекс: , поряд з «іксом» можна в дужках записувати, що - константа. Ця позначка може бути дуже корисною для початківців, щоб легше було орієнтуватися у вирішенні.

Подальші коментарі:

(1) Виносимо всі константи за знак похідної. У разі і , отже, та його твір вважається постійним числом.

(2) Не забуваємо, як правильно диференціювати коріння.

(1) Виносимо всі константи за знак похідної, у разі константою є .

(2) Під штрихом у нас залишився добуток двох функцій, отже, потрібно використовувати правило диференціювання твору .

(3) Не забуваємо, що це складна функція (хоча і найпростіша зі складних). Використовуємо відповідне правило: .

Тепер знаходимо змішані похідні другого порядку:

Отже, всі обчислення виконані правильно.

Запишемо повний диференціал. У контексті завдання не має сенсу розповідати, що таке повний диференціал функції двох змінних. Важливо, що цей диференціал дуже часто потрібно записати в практичних завданнях.

Повний диференціал першого порядкуфункції двох змінних має вигляд:

В даному випадку:

Тобто, у формулу треба тупо просто підставити вже знайдені похідні приватні першого порядку. Значки диференціалів і в цій та схожих ситуаціях по можливості краще записувати в чисельниках:

І на неодноразові прохання читачів, повний диференціал другого порядку.

Він виглядає так:

УВАЖНО знайдемо «однолітерні» похідні 2-го порядку:

і запишемо «монстра», акуратно «прикріпивши» квадрати, твір і не забувши подвоїти змішану похідну:

Нічого страшного, якщо щось здалося важким, до похідних завжди можна повернутися пізніше, після того, як підніміть техніку диференціювання:

Приклад 4

Знайти приватні похідні першого порядку функції . Перевірити, що . Записати повний диференціал першого порядку.

Розглянемо серію прикладів зі складними функціями:

Приклад 5

Знайти приватні похідні першого порядку функції.

Рішення:

Приклад 6

Знайти приватні похідні першого порядку функції .
Записати повний диференціал.

Це приклад самостійного рішення (відповідь наприкінці уроку). Повне рішення не наводжу, оскільки воно досить просте

Досить часто всі вищерозглянуті правила застосовують у комбінації.

Приклад 7

Знайти приватні похідні першого порядку функції .

(1) Використовуємо правило диференціювання суми

(2) Перше доданок у разі вважається константою, оскільки у виразі немає нічого, залежить від «ікс» – лише «ігреки». Знаєте, завжди приємно, коли дріб вдається перетворити на нуль). Для другого доданку застосовуємо правило диференціювання твору. До речі, у цьому сенсі нічого б не змінилося, якби натомість була дана функція – важливо, що тут добуток двох функцій, КОЖНА з яких залежить від «ікс», А тому потрібно використовувати правило диференціювання твору. Для третього доданку застосовуємо правило диференціювання складної функції.

(1) У першому доданку і в чисельнику і в знаменнику міститься «гравець», отже потрібно використовувати правило диференціювання приватного: . Другий доданок залежить ТІЛЬКИ від «ікс», значить, вважається константою і перетворюється на нуль. Для третього доданку використовуємо правило диференціювання складної функції.

Для тих читачів, які мужньо дісталися майже кінця уроку, розповім старий мехматовский анекдот для разрядки:

Одного разу в просторі функцій з'явилася зла похідна і як пішла всіх диференціювати. Усі функції розбігаються хто куди, нікому не хочеться перетворюватися! І лише одна функція нікуди не тікає. Підходить до неї похідна і запитує:

– А чому це ти від мене нікуди не тікаєш?

– Ха. А мені все одно, адже я «е в ступені ікс», і ти зі мною нічого не вдієш!

На що зла похідна з підступною посмішкою відповідає:

- Ось тут ти помиляєшся, я тебе продиференціюю по "ігрок", так що тобі бути нулем.

Хто зрозумів анекдот, той освоїв похідні щонайменше на «трійку»).

Приклад 8

Знайти приватні похідні першого порядку функції .

Це приклад самостійного рішення. Повне рішення та зразок оформлення завдання – наприкінці уроку.

Ну ось майже все. Насамкінець не можу не порадувати любителів математики ще одним прикладом. Справа навіть не в любителях, у всіх різний рівень математичної підготовки - зустрічаються люди (і не так вже й рідко), які люблять потягатися із завданнями складніше. Хоча, останній цьому уроці приклад не так складний, скільки громіздкий з погляду обчислень.

Для спрощення запису та викладення матеріалу обмежимося випадком функцій двох змінних. Все подальше справедливо також для функцій будь-якої кількості змінних.

Визначення. Приватна похіднафункції z = f(х, у) по незалежній змінній хназивається похідна

обчислена при постійному у.

Аналогічно визначається приватна похідна за змінною у.

Для окремих похідних справедливі звичайні правила і формули диференціювання.

Визначення.Добуток приватної похідної на збільшення аргументу х(y) називається приватним диференціаломпо змінній х(у) функції двох змінних z = f(x, y) (Позначення: ):

Якщо під диференціалом незалежної змінної dx(dy) розуміти збільшення х(у), то

Для функції z = f(x, y) з'ясуємо геометричний зміст її частотних похідних та .

Розглянемо точку, точку P 0 (х 0 ,y 0 , z 0) на поверхні z = f(x,у) та криву Lяка вийде при перерізі поверхні площиною у = у 0 . Цю криву можна розглядати як графік функції однієї змінної z = f(x, y) у площині у = у 0 . Якщо провести у точці Р 0 (х 0 , у 0 , z 0) дотичну до кривої L, то, згідно з геометричним змістом похідної функції однієї змінної , де a – кут, утворений дотичною з позитивним напрямком осі Ох.

Або: аналогічно зафіксуємо іншу змінну, тобто. проведемо переріз поверхні z = f(x, y) площиною х = х 0 . Тоді функцію

z = f(x 0 , y) можна розглянути як функцію однієї змінної у:

де b- Кут, утворений дотичної в точці М 0 (х 0 , у 0) з позитивним напрямом осі Ой(Рис. 1.2).

Мал. 1.2. Ілюстрація геометричного значення приватних похідних.

приклад 1.6.Дана функція z = х 2 – 3ху - 4у 2 - х + 2у + 1. Знайти та .

Рішення.Розглядаючи уяк постійну величину, отримаємо

Вважаючи хпостійною, знаходимо

Лекція 3 ФНП, приватні похідні, диференціал

Що головне ми дізналися на минулій лекції

Ми дізналися, що таке функція кількох змінних з аргументом з евклідового простору. Вивчили, що таке межа та безперервність для такої функції

Що ми дізнаємось на цій лекції

Продовжуючи вивчення ФНП, ми вивчимо приватні похідні та диференціали для цих функцій. Дізнаємося, як написати рівняння дотичної площини та нормалі до поверхні.

Приватна похідна повний диференціал ФНП. Зв'язок диференційованості функції із існуванням приватних похідних

Для функції однієї речової змінної після вивчення тем «Межі» та «Безперервність» (Вступ до математичного аналізу) вивчалися похідні та диференціали функції. Перейдемо до розгляду аналогічних питань функції декількох змінних. Зауважимо, що якщо у ФНП зафіксувати всі аргументи, крім одного, то ФНП породжує функцію одного аргументу, для якої можна розглядати збільшення, диференціал та похідну. Їх ми називатимемо відповідно приватним збільшенням, приватним диференціалом та приватною похідною. Перейдемо до точним визначенням.

Визначення 10. Нехай задана функція змінних де - Елемент евклідова простору і відповідні збільшення аргументів , , ..., . При величині називаються приватними прирощеннями функція. Повне збільшення функції - це величина.

Наприклад, для функції двох змінних , де - точка на площині і , відповідні збільшення аргументів, приватними будуть збільшення , . При цьому величина є повним збільшенням функції двох змінних.

Визначення 11. Приватної похідної функції змінних за змінною називається межа відношення приватного збільшення функції за цією змінною до збільшення відповідного аргументу , коли прагне до 0.

Запишемо визначення 11 у вигляді формули або у розгорнутому вигляді. (2) Для функції двох змінних визначення 11 запишеться у вигляді формул , . З практичної точки зору це визначення означає, що при обчисленні приватної похідної по одній змінній решта всіх змінних фіксуються і ми розглядаємо цю функцію як функцію однієї обраної змінної. За цією змінною і береться звичайна похідна.

Приклад 4. Для функції , де знайдіть приватні похідні та точку, де обидві приватні похідні дорівнюють 0.

Рішення . Обчислимо приватні похідні, і систему запишемо у вигляді Рішенням цієї системи є дві точки і .

Розглянемо тепер, як поняття диференціала узагальнюється ФНП. Згадаймо, що функція однієї змінної називається диференційованою, якщо її збільшення представляється у вигляді при цьому величина є головною частиною збільшення функції і називається її диференціалом. Величина є функцією від , має ту властивість, що , тобто є функцією, нескінченно малою в порівнянні з . Функція однієї змінної диференційована в точці і тоді, коли має похідну в цій точці. У цьому константа і дорівнює цієї похідної, т. е. для диференціала справедлива формула .

Якщо розглядається приватне збільшення ФНП, то змінюється лише один з аргументів, і це приватне збільшення можна розглядати як збільшення функції однієї змінної, тобто працює та ж теорія. Отже, умова диференційності виконано тоді і лише тоді, коли існує приватна похідна , і в цьому випадку приватний диференціал визначається формулою .

А що таке повний диференціал функції кількох змінних?

Визначення 12. Функція змінних називається диференційованою в точці , якщо її збільшення представляється як . У цьому головна частина збільшення називається диференціалом ФНП.

Отже, диференціалом ФНП є величина . Уточнимо, що ми розуміємо під величиною , яку ми називатимемо нескінченно малою в порівнянні з приростами аргументів . Це функція, яка має ту властивість, що якщо всі прирощення, крім одного , дорівнюють 0, то справедлива рівність . По суті це означає, що = = + +…+ .

А як пов'язані між собою умова диференційності ФНП та умови існування приватних похідних цієї функції?

Теорема 1. Якщо функція змінних диференційована у точці , то в неї існують приватні похідні за всіма змінними в цій точці і при цьому .

Доведення. Рівність запишемо при та у вигляді та розділи обидві частини отриманої рівності на . В отриманій рівності перейдемо до межі при . У результаті ми й отримаємо необхідну рівність. Теорему доведено.

Слідство. Диференціал функції змінних обчислюється за формулою . (3)

У прикладі 4 диференціал функції дорівнював. Зауважимо, що цей же диференціал у точці дорівнює . А от якщо ми його обчислимо в точці з приростами, то диференціал дорівнюватиме. Зауважимо, що точне значення заданої функції в точці одно , а це ж значення, приблизно обчислене з допомогою 1-го диференціала, одно . Ми бачимо, що, замінюючи збільшення функції її диференціалом, ми можемо приблизно обчислювати значення функції.

А чи буде функція кількох змінних диференційована у точці, якщо вона має приватні похідні у цій точці. На відміну від функції однієї змінної у відповідь це питання негативний. Точне формулювання взаємозв'язку дає така теорема.

Теорема 2. Якщо у функції змінних у точці існують безперервні похідні приватні по всіх змінних, то функція диференційована в цій точці.

у вигляді . У кожній дужці змінюється лише одна змінна, тому ми можемо і там і там застосувати формулу кінцевих приростів Лагранжа. Суть цієї формули в тому, що для безперервно диференційованої функції однієї змінної різниця значень функції у двох точках дорівнює значенню похідної в деякій проміжній точці, помноженому на відстань між точками. Застосовуючи цю формулу кожної з дужок, отримаємо . Через безперервність приватних похідних похідна в точці і похідна в точці відрізняються від похідних і в точці на величини і , що прагнуть 0 при , що прагнуть 0. Але тоді і, очевидно, . Теорему доведено. , А координата. Перевірте, чи ця точка належить поверхні. Напишіть рівняння дотичної площини та рівняння нормалі до поверхні у зазначеній точці.

Рішення. Справді, . Ми вже обчислювали у минулій лекції диференціал цієї функції у довільній точці, у заданій точці він дорівнює . Отже, рівняння дотичної площини запишеться як або , а рівняння нормалі - як .

Кожна приватна похідна (по xі по y) функції двох змінних є звичайною похідною функції однієї змінної при фіксованому значенні іншої змінної:

(де y= const),

(де x= Const).

Тому приватні похідні обчислюють за формулам та правилам обчислення похідних функцій однієї змінної, Вважаючи при цьому іншу змінну постійною (константою).

Якщо Вам не потрібен розбір прикладів та необхідного для цього мінімуму теорії, а потрібне лише вирішення Вашого завдання, то переходьте до калькулятор приватних похідних онлайн .

Якщо важко зосередитися, щоб відстежувати, де у функції константа, то можна в чорновому рішенні прикладу замість змінної з фіксованим значенням підставити будь-яке число - тоді можна буде швидше обчислити приватну похідну як похідну звичайну функції однієї змінної. Треба тільки не забути при чистовому оформленні повернути місце константу (змінну з фіксованим значенням).

Описана вище властивість приватних похідних випливає з визначення приватної похідної, яка може потрапити в екзаменаційні питання. Тож ознайомлення з визначенням нижче можна відкрити теоретичну довідку.

Поняття безперервності функції z= f(x, y) у точці визначається аналогічно до цього поняття для функції однієї змінної.

Функція z = f(x, y) називається безперервною в точці якщо

Різниця (2) називається повним збільшенням функції z(Воно виходить в результаті прирощень обох аргументів).

Нехай задані функції z= f(x, y) і крапка

Якщо зміна функції zвідбувається при зміні лише одного з аргументів, наприклад, x, при фіксованому значенні іншого аргументу y, то функція отримає збільшення

зване приватним збільшенням функції f(x, y) за x.

Розглядаючи зміну функції zЗалежно від зміни лише одного з аргументів, ми фактично переходимо до функції однієї змінної.

Якщо існує кінцева межа

то він називається приватною похідною функції f(x, y) за аргументом xі позначається одним із символів

(4)

Аналогічно визначаються приватне збільшення zпо y:

та приватна похідна f(x, y) за y:

(6)

приклад 1.

Рішення. Знаходимо приватну похідну за змінною "ікс":

(yфіксовано);

Знаходимо приватну похідну за змінною "гравець":

(xфіксовано).

Як видно, не має значення, якою мірою змінна, яка фіксована: в даному випадку це просто деяке число, що є множником (як у випадку звичайної похідної) при змінній, за якою знаходимо приватну похідну. Якщо ж фіксована змінна не помножена на змінну, за якою знаходимо приватну похідну, то ця самотня константа, байдуже, якою мірою, як і у випадку звичайної похідної, звертається в нуль.

приклад 2.Дана функція

Знайти приватні похідні

(за іксом) та (за гріком) і обчислити їх значення в точці А (1; 2).

Рішення. При фіксованому yпохідна першого доданка знаходиться як похідна статечної функції ( таблиця похідних функцій однієї змінної):

.

При фіксованому xпохідна першого доданка знаходиться як похідна показової функції, а другого – як похідна постійної:

Тепер обчислимо значення цих приватних похідних у точці А (1; 2):

Перевірити розв'язання задач з приватними похідними можна на калькулятор приватних похідних онлайн .

приклад 3.Знайти приватні похідні функції

Рішення. За один крок знаходимо

(y xніби аргументом синуса було 5 x: так само 5 виявляється перед знаком функції);

(xфіксовано і є в даному випадку множником при y).

Перевірити розв'язання задач з приватними похідними можна на калькулятор приватних похідних онлайн .

Аналогічно визначаються приватні похідні функції трьох і більше змінних.

Якщо кожному набору значень ( x; y; ...; t) незалежних змінних з множини Dвідповідає одне певне значення uз множини E, то uназивають функцією змінних x, y, ..., tі позначають u= f(x, y, ..., t).

Для функцій трьох і більше змінних геометричної інтерпретації немає.

Приватні похідні функції кількох змінних визначаються і обчислюються також у припущенні, що змінюється лише одне із незалежних змінних, інші при цьому фіксовані.

приклад 4.Знайти приватні похідні функції

.

Рішення. yі zфіксовані:

xі zфіксовані:

xі yфіксовані:

Знайти приватні похідні самостійно, а потім переглянути рішення

Приклад 5.

Приклад 6.Знайти приватні похідні функції.

Приватна похідна функції кількох змінних має той самий механічний зміст, як і похідна функції однієї змінної, - це швидкість зміни функції щодо зміни одного із аргументів.

Приклад 8.Кількісна величина потоку Ппасажирів залізниць може бути виражена функцією

де П- кількість пасажирів, N– кількість жителів кореспондуючих пунктів, R- Відстань між пунктами.

Приватна похідна функції Ппо R, рівна

показує, що зменшення потоку пасажирів обернено пропорційно квадрату відстані між кореспондуючими пунктами за однієї і тієї ж чисельності жителів у пунктах.

Приватна похідна Ппо N, рівна

показує, що збільшення потоку пасажирів пропорційно подвоєному числу жителів населених пунктів при тому самому відстані між пунктами.

Перевірити розв'язання задач з приватними похідними можна на калькулятор приватних похідних онлайн .

Повний диференціал

Твір приватної похідної на збільшення відповідної незалежної змінної називається приватним диференціалом. Приватні диференціали позначаються так:

Сума приватних диференціалів за всіма незалежними змінними дає повний диференціал. Для функції двох незалежних змінних повний диференціал виражається рівністю

(7)

Приклад 9.Знайти повний диференціал функції

Рішення. Результат використання формули (7):

Функція, що має повний диференціал у кожній точці певної області, називається диференційованою в цій галузі.

Знайти повний диференціал самостійно, а потім переглянути рішення

Як і у разі функції однієї змінної, з диференційованості функції у певній області випливає її безперервність у цій галузі, але з навпаки.

Сформулюємо без доказів достатню умову диференціювання функції.

Теорема.Якщо функція z= f(x, y) має безперервні приватні похідні

у цій галузі, вона диференційована у цій галузі та її диференціал виражається формулою (7).

Можна показати, що подібно до того, як у випадку функції однієї змінної диференціал функції є головною лінійною частиною прирощення функції , так і у випадку декількох змінних повний диференціал є головною, лінійною щодо прирощень незалежних змінних частиною повного прирощення функції.

Для функції двох змінних повне збільшення функції має вигляд

(8)

де α і β - нескінченно малі при і.

Приватні похідні вищих порядків

Приватні похідні та функції f(x, y) самі є деякими функціями тих самих змінних і, у свою чергу, можуть мати похідні за різними змінними, які називаються приватними похідними вищих порядків.